giaitoan.edu.vn giới thiệu đến quý thầy, cô giáo và các em học sinh đề cương ôn thi cuối học kì 1 môn Toán 6 năm học 2025 – 2026 trường THCS Lê Quang Cường, thành phố Hồ Chí Minh.
CHƯƠNG I: SỐ TỰ NHIÊN.
1. Tập hợp.
– Nhận biết được tập hợp các số tự nhiên.
– Viết được tập hợp số tự nhiên bằng 2 cách: Liệt kê các phần tử của tập hợp; Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
– Nhận biết được phần tử thuộc (không thuộc) một tập.
2. Tập hợp số tự nhiên.
– Thực hiện được các phép tính: cộng, trừ, nhân, chia, nâng lên lũy thừa trong tập hợp số tự nhiên.
– Vận dụng các tính chất của phép cộng và phép nhân số tự nhiên để tính nhanh, tính hợp lý.
5. Lũy thừa.
– Nhân, chia hai lũy thừa cùng cơ số.
– Quy ước.
6. Thứ tự thực hiện các phép tính trong biểu thức.
– Đối với biểu thức không có dấu ngoặc.
– Đối với biểu thức có dấu ngoặc.
7. Tính chất chia hết của một tổng.
8. Các dấu hiệu chia hết cho 2, 3, 5, 9.
9. Ước và bội.
+ Cách tìm ước: Muốn tìm các ước của số tự nhiên a (a /> 1), ta có thể lần lượt chia a cho các số tự nhiên từ 1 đến a, nếu a chia hết cho các số nào thì các số ấy là ước của a.
+ Cách tìm bội: Muốn tìm các bội của số tự nhiên a khác 0, ta có thể nhân a lần lượt với 0; l; 2; ….
10. Số nguyên tố. Hợp số.
– Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
– Hợp số là số tự nhiên lớn hơn 1 có nhiều hơn hai ước.
11. Ước chung, bội chung, ước chung lớn nhất, bội chung nhỏ nhất.
– Tìm ƯCLN bằng cách phân tích các số ra thừa số nguyên tố.
– Tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố.
CHƯƠNG II: SỐ NGUYÊN.
1. Tập hợp các số nguyên được kí hiệu là Z.
2. So sánh hai số nguyên.
+ Số nguyên dương /> 0; Số nguyên âm < 0; Số nguyên âm < Số nguyên dương.
+ Với hai số nguyên âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.
3. Phép cộng hai số nguyên.
– Cộng hai số nguyên dương, ta thực hiện như cộng hai số tự nhiên.
– Cộng hai số nguyên âm, ta cộng hai số đối của chúng rồi thêm dấu trừ đẳng trước kết quả.
– Tổng hai số nguyên đối nhau luôn luôn bằng 0.
– Cộng hai số nguyên trái dấu:
+ Nếu số dương lớn hơn số đối của số âm thì ta lấy số dương trừ đi số đối của số âm.
+ Nếu số dương bé hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ trước kết quả.
4. Tính chất phép cộng của các số nguyên.
a) Giao hoán.
b) Kết hợp.
5. Phép trừ hai số nguyên.
6. Quy tắc bỏ dấu ngoặc.
– Có dấu “+” thì giữ nguyên dấu của các số hạng trong ngoặc.
– Có dấu “−” thì phải đổi dấu tất cả các số hạng trong ngoặc.
7. Phép nhân hai số nguyên.
– Nhân hai số nguyên khác dấu:
+ Tích của hai số nguyên khác dấu luôn luôn là một số nguyên âm.
+ Khi nhân hai số nguyên khác dấu, ta nhân số dương với số đối của số âm rồi thêm dấu trừ (−) trước kết quả nhận được.
– Nhân hai số nguyên cùng dấu:
+ Khi nhân hai số nguyên cùng dương, ta nhân chúng như nhân hai số tự nhiên.
+ Khi nhân hai số nguyên cùng âm, ta nhân hai số đối của chúng.
9. Tính chất của phép nhân các số nguyên.
a) Giao hoán.
b) Kết hợp.
c) Phân phối của phép nhân đối với phép cộng.
10. Quan hệ chia hết và phép chia hết trong tập hợp số nguyên.
CHƯƠNG III: CÁC HÌNH PHẲNG TRONG THỰC TIỄN.
+ Hình chữ nhật.
+ Hình vuông.
+ Hình tam giác.
+ Hình thang.
+ Hình thoi.
+ Hình bình hành.
CHƯƠNG IV: MỘT SỐ YẾU TỐ THỐNG KÊ.
– Thực hiện được việc thu thập, phân loại dữ liệu theo các tiêu chí cho trước từ những nguồn: bảng biểu, kiến thức trong các môn học khác.
– Nhận biết được tính hợp lí của dữ liệu theo các tiêu chí đơn giản.
– Đọc và mô tả thành thạo các dữ liệu ở dạng: bảng thống kê; biểu đồ tranh.
– Lựa chọn và biểu diễn được dữ liệu vào bảng, biểu đồ thích hợp ở dạng: bảng thống kê; biểu đồ tranh.
– Giải quyết được những vấn đề đơn giản liên quan đến các số liệu thu được ở dạng: bảng thống kê; biểu đồ tranh.





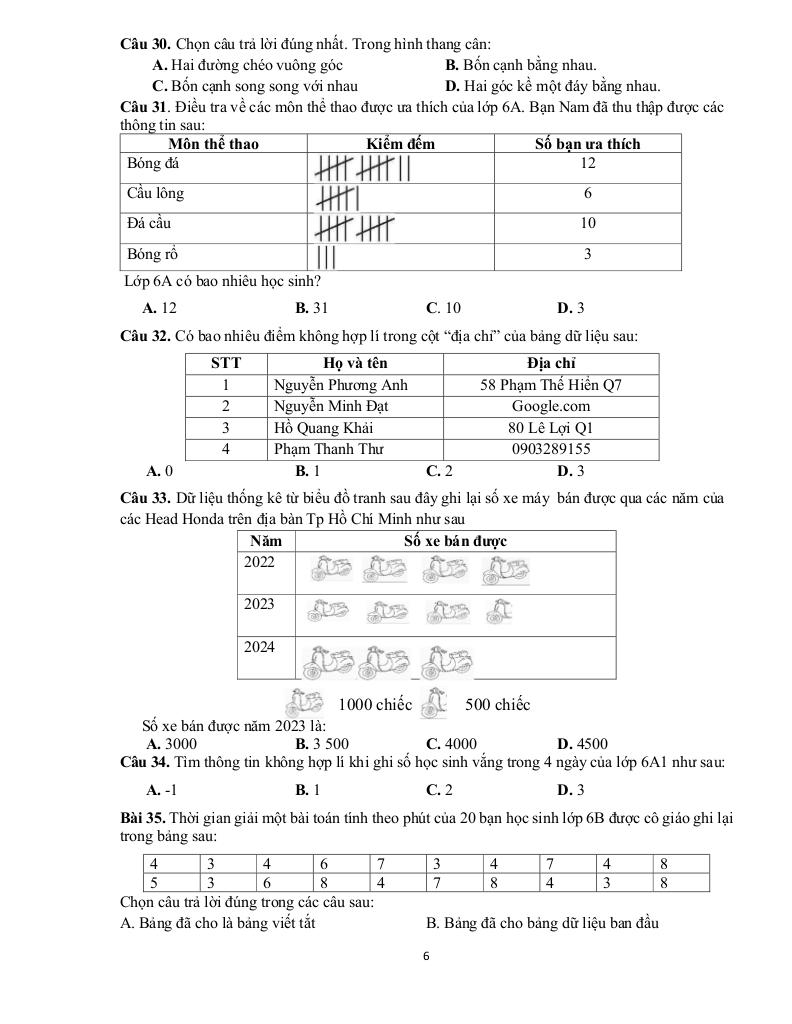




Giải Toán đề cương học kì 1 toán 6 năm 2025 – 2026 trường thcs lê quang cường – tp hcm với Đáp Án Mới Nhất
Toán học luôn là một môn học quan trọng, giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề. Để hỗ trợ các bạn học sinh và giáo viên trong việc học tập và giảng dạy, bài viết này sẽ cung cấp lời giải chi tiết và đáp án chính xác cho chủ đề đề cương học kì 1 toán 6 năm 2025 – 2026 trường thcs lê quang cường – tp hcm, giúp bạn hiểu sâu và tự tin hơn khi làm bài tập.
đề cương học kì 1 toán 6 năm 2025 – 2026 trường thcs lê quang cường – tp hcm là một trong những phần kiến thức quan trọng trong chương trình toán học, thường xuất hiện trong các bài kiểm tra và kỳ thi lớn. Việc nắm vững phần này không chỉ giúp bạn đạt điểm cao mà còn tạo nền tảng vững chắc để học các nội dung nâng cao hơn.
Chúng tôi cung cấp hướng dẫn từng bước giải bài tập, bao gồm:
Mỗi bài giải đều kèm theo lời giải thích chi tiết, giúp bạn hiểu không chỉ cách làm mà còn cả lý do tại sao nên áp dụng phương pháp đó.
Tất cả các bài tập đều đi kèm đáp án mới nhất, được kiểm tra kỹ lưỡng để đảm bảo độ chính xác cao. Điều này giúp bạn tự kiểm tra kết quả và khắc phục lỗi sai một cách nhanh chóng.
Ngoài ra, bài viết còn cung cấp các tài liệu bổ trợ như:
Chủ đề đề cương học kì 1 toán 6 năm 2025 – 2026 trường thcs lê quang cường – tp hcm là một phần kiến thức thú vị và hữu ích trong toán học. Hãy sử dụng bài viết này như một công cụ hỗ trợ để bạn chinh phục mọi thử thách trong môn Toán. Đừng quên ôn tập thường xuyên và luyện tập nhiều dạng bài tập khác nhau để thành thạo hơn!
Chúc các bạn học tốt và đạt kết quả cao! 😊
>> Xem thêm đáp án chi tiết về: đề cương học kì 1 toán 6 năm 2025 – 2026 trường thcs lê quang cường – tp hcm.