Tài liệu gồm 31 trang, được sưu tầm và biên soạn bởi thầy giáo Huỳnh Văn Ánh, tuyển tập một số bài tập toán thực tế giới hạn, hàm số liên tục môn Toán 11, có đáp án và lời giải chi tiết.
Trích dẫn Toán thực tế giới hạn, hàm số liên tục Toán 11:
+ Cho đường tròn (C) tâm O, bán kính r = 20cm. Vẽ đường tròn (C1) đi qua tâm O và tiếp xúc với (C), vẽ đường tròn (C2) đi qua tâm của (C1) và tiếp xúc với (C1). Tiếp tục quá trình này đến vô hạn. Ta tô màu phần ngoài của hình tròn mới theo quy luật như hình vẽ dưới đây. Tính diện tích toàn bộ phần tô màu.
+ Một bệnh nhân hàng ngày phải uống một viên thuốc 150mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
+ Người ta làm lỗ thông gió của một ngôi nhà bằng cách ghép một dãy hình tròn có cùng bán kính là 3cm, theo các bước như Hình 2. Kí hiệu un (đơn vị diện tích) là diện tích hình tròn ghép được ở bước thứ n. a) Với n như thế nào thì un vượt quá 90000π; 9000000π? b) Với n như thế nào thì un vượt quá 45m2?









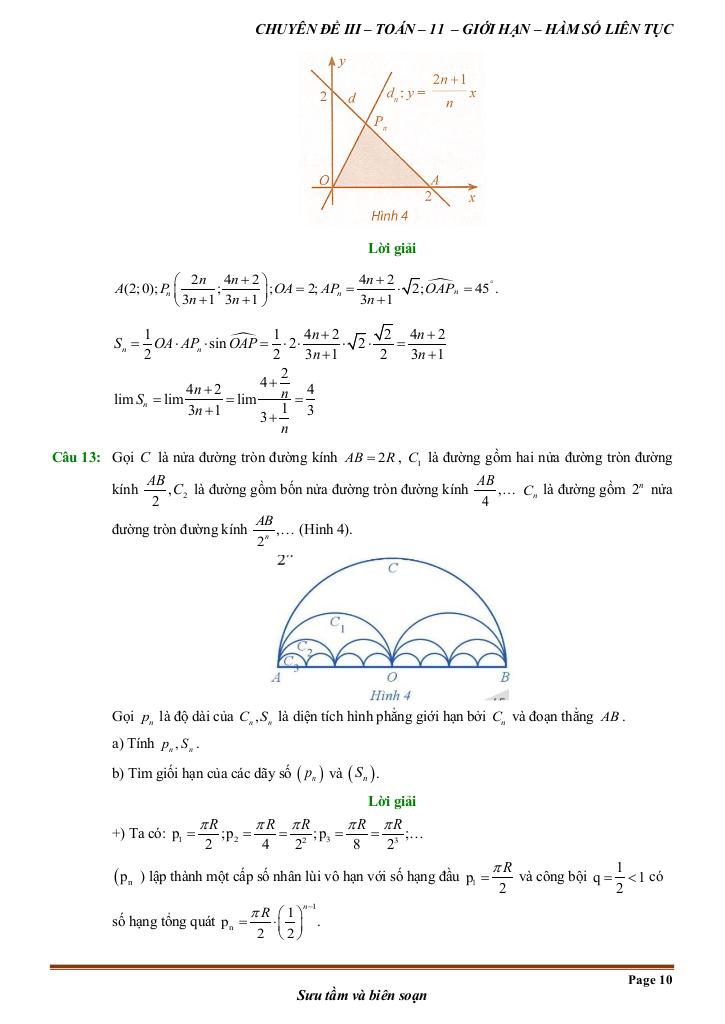
Giải Toán toán thực tế giới hạn, hàm số liên tục toán 11 với Đáp Án Mới Nhất
Toán học luôn là một môn học quan trọng, giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề. Để hỗ trợ các bạn học sinh và giáo viên trong việc học tập và giảng dạy, bài viết này sẽ cung cấp lời giải chi tiết và đáp án chính xác cho chủ đề toán thực tế giới hạn, hàm số liên tục toán 11, giúp bạn hiểu sâu và tự tin hơn khi làm bài tập.
toán thực tế giới hạn, hàm số liên tục toán 11 là một trong những phần kiến thức quan trọng trong chương trình toán học, thường xuất hiện trong các bài kiểm tra và kỳ thi lớn. Việc nắm vững phần này không chỉ giúp bạn đạt điểm cao mà còn tạo nền tảng vững chắc để học các nội dung nâng cao hơn.
Chúng tôi cung cấp hướng dẫn từng bước giải bài tập, bao gồm:
Mỗi bài giải đều kèm theo lời giải thích chi tiết, giúp bạn hiểu không chỉ cách làm mà còn cả lý do tại sao nên áp dụng phương pháp đó.
Tất cả các bài tập đều đi kèm đáp án mới nhất, được kiểm tra kỹ lưỡng để đảm bảo độ chính xác cao. Điều này giúp bạn tự kiểm tra kết quả và khắc phục lỗi sai một cách nhanh chóng.
Ngoài ra, bài viết còn cung cấp các tài liệu bổ trợ như:
Chủ đề toán thực tế giới hạn, hàm số liên tục toán 11 là một phần kiến thức thú vị và hữu ích trong toán học. Hãy sử dụng bài viết này như một công cụ hỗ trợ để bạn chinh phục mọi thử thách trong môn Toán. Đừng quên ôn tập thường xuyên và luyện tập nhiều dạng bài tập khác nhau để thành thạo hơn!
Chúc các bạn học tốt và đạt kết quả cao! 😊
>> Xem thêm đáp án chi tiết về: toán thực tế giới hạn, hàm số liên tục toán 11.