Tài liệu gồm 174 trang tuyển tập các bài toán ứng dụng thực tiễn chọn lọc trong các đề thi thử THPT Quốc gia năm 2017, có lời giải chi tiết. Các bài toán được phân dạng thành các chủ đề:
+ Chủ đề 1. Liên quan di chuyển – quãng đường đi
+ Chủ đề 2. Liên quan cắt – ghép các khối hình
+ Chủ đề 3. Lãi suất ngân hàng – trả góp
+ Chủ đề 4. Bài toán tăng trưởng
+ Chủ đề 5. Bài toán tối ưu chi phí sản xuất
+ Chủ đề 6. Bài toán thực tế min – max
[ads]
Trích dẫn tài liệu:
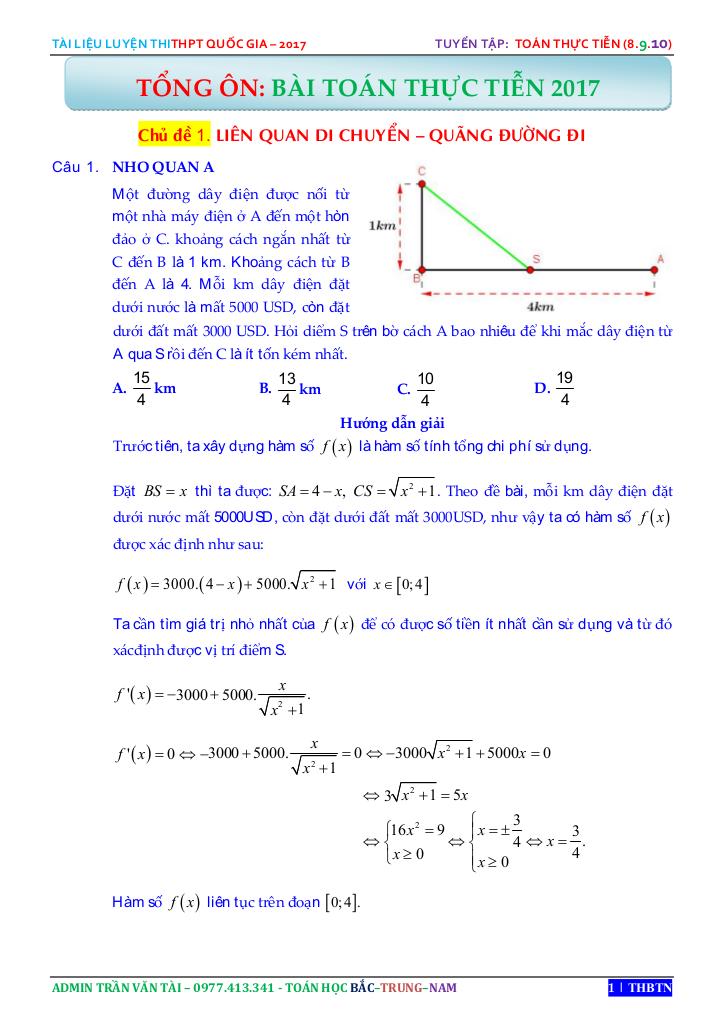
+ Một kho hàng được đặt tại ví trí A trên bến cảng cần được chuyển tới kho C trên một đảo, biết rằng khoảng cách ngắn nhất từ kho C đến bờ biển AB bằng độ dài CB = 60 km và khoảng cách giữa 2 điểm A, B là AB = 130km. Chi phí để vận chuyển toàn bộ kho hàng bằng đường bộ là 300.000 đồng/km, trong khi đó chi phí vận chuyển hàng bằng đường thủy là 500.000 đồng/km. Hỏi phải chọn điểm trung chuyển hàng D (giữa đường bộ và đường thủy) cách kho A một khoảng bằng bao nhiêu thì tổng chi phí vận chuyển hàng từ kho A đến kho C là ít nhất?
+ Một vùng đất hình chữ nhật ABCD có AB = 25km, BC = 20 km và M, N lần lượt là trung điểm của AD, BC. Một người cưỡi ngựa xuất phát từ A đi đến C bằng cách đi thẳng từ A đến một điểm X thuộc đoạn MN rồi lại đi thẳng từ X đến C. Vận tốc của ngựa khi đi trên phần ABNM là 15km/h, vận tốc của ngựa khi đi trên phần MNCD là 30km/h. Thời gian ít nhất để ngựa di chuyển từ A đến C là mấy giờ?
+ Trong Công viên Toán học có những mảnh đất mang hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán học. Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemmiscate có phương trình trong hệ tọa độ Oxy là 16y^2 = x^2.(25 – x^2) như hình vẽ bên. Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ tọa độ Oxy tương ứng với chiều dài 1 mét.
Xem thêm đáp án: tuyển tập và giải chi tiết các bài toán thực tiễn trong đề thi thử – trần văn tài








Giải Toán tuyển tập và giải chi tiết các bài toán thực tiễn trong đề thi thử – trần văn tài với Đáp Án Mới Nhất
Toán học luôn là một môn học quan trọng, giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề. Để hỗ trợ các bạn học sinh và giáo viên trong việc học tập và giảng dạy, bài viết này sẽ cung cấp lời giải chi tiết và đáp án chính xác cho chủ đề tuyển tập và giải chi tiết các bài toán thực tiễn trong đề thi thử – trần văn tài, giúp bạn hiểu sâu và tự tin hơn khi làm bài tập.
tuyển tập và giải chi tiết các bài toán thực tiễn trong đề thi thử – trần văn tài là một trong những phần kiến thức quan trọng trong chương trình toán học, thường xuất hiện trong các bài kiểm tra và kỳ thi lớn. Việc nắm vững phần này không chỉ giúp bạn đạt điểm cao mà còn tạo nền tảng vững chắc để học các nội dung nâng cao hơn.
Chúng tôi cung cấp hướng dẫn từng bước giải bài tập, bao gồm:
Mỗi bài giải đều kèm theo lời giải thích chi tiết, giúp bạn hiểu không chỉ cách làm mà còn cả lý do tại sao nên áp dụng phương pháp đó.
Tất cả các bài tập đều đi kèm đáp án mới nhất, được kiểm tra kỹ lưỡng để đảm bảo độ chính xác cao. Điều này giúp bạn tự kiểm tra kết quả và khắc phục lỗi sai một cách nhanh chóng.
Ngoài ra, bài viết còn cung cấp các tài liệu bổ trợ như:
Chủ đề tuyển tập và giải chi tiết các bài toán thực tiễn trong đề thi thử – trần văn tài là một phần kiến thức thú vị và hữu ích trong toán học. Hãy sử dụng bài viết này như một công cụ hỗ trợ để bạn chinh phục mọi thử thách trong môn Toán. Đừng quên ôn tập thường xuyên và luyện tập nhiều dạng bài tập khác nhau để thành thạo hơn!
Chúc các bạn học tốt và đạt kết quả cao! 😊
>> Xem thêm đáp án chi tiết về: tuyển tập và giải chi tiết các bài toán thực tiễn trong đề thi thử – trần văn tài.