Bài viết trình bày lý thuyết và một số bài tập điển hình có lời giải chi tiết chủ đề vectơ trong không gian – đây là nội dung thuộc chương trình Hình học 11 chương 3.
Kiến thức cần nắm vững:
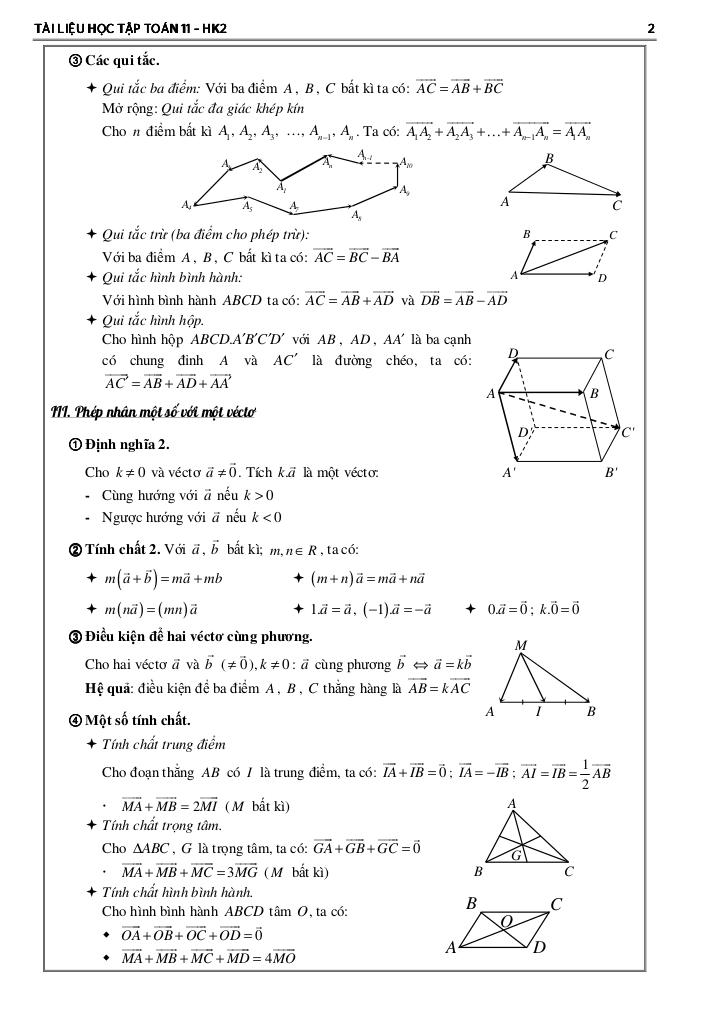
Cho các vectơ \(\vec a\), \(\vec b\), \(\vec c\) trong không gian và \(l,k \in R.\)
1. Phép cộng vectơ:
Lấy \(O\) tùy ý trong không gian.
Vẽ \(\overrightarrow {OA} = \vec a\), \(\overrightarrow {AB} = \vec b\) thì \(\overrightarrow {OB} = \vec a + \vec b.\)
Quy tắc ba điểm: Cho ba điểm bất kì \(M\), \(N\), \(K\) thì \(\overrightarrow {MN} = \overrightarrow {MK} + \overrightarrow {KN} .\)
2. Phép trừ vectơ:
\(\vec a – \vec b = \vec a + ( – \overrightarrow b ).\)
Quy tắc ba điểm: \(\overrightarrow {MN} = \overrightarrow {KN} – \overrightarrow {KM} .\)
3. Tích của một vectơ với một số:
Tích vectơ \(\vec a\) với số thực \(k\) là một vectơ kí hiệu \(k\vec a\):
+ Cùng hướng \(\vec a\) nếu \(k /> 0.\)
+ Ngược hướng \(\vec a\) nếu \(k < 0.\)
+ \(\left| {k\overrightarrow a } \right| = \left| k \right|\left| {\overrightarrow a } \right|.\)
Tính chất:
\(k(\vec a + \vec b) = k\vec a + k\vec b.\)
\((l + k)\vec a = l\overrightarrow a + k\vec a.\)
Hệ quả: Nếu \(I\) là trung điểm của \(AB\), \(O\) tùy ý thì \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OI} .\)
4. Tích vô hướng của hai vectơ:
Định nghĩa: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \widehat {\left( {\overrightarrow a ,\overrightarrow b } \right)}.\)
Hệ quả:
\(\vec a \bot \vec b \Leftrightarrow \vec a.\vec b = 0.\)
\({\vec a^2} = \vec a.\vec a = {\left| {\vec a} \right|^2}.\)
Tính chất:
\(\vec a(\vec b + \vec c) = \overrightarrow a \overrightarrow b + \overrightarrow a \overrightarrow c .\)
\(\vec a(k\vec b) = (k\vec a)\vec b = k(\vec a.\vec b).\)
\({(\vec a + \vec b)^2} = {\left| {\vec a} \right|^2} + 2\vec a.\vec b + {\left| {\vec b} \right|^2}.\)
5. Sự đồng phẳng của các vectơ:
Ba vectơ \(\vec a\), \(\vec b\), \(\vec c\) gọi là đồng phẳng nếu giá của chúng cùng song song hoặc nằm trên một mặt phẳng.
Cho \(\vec a\), \(\vec b\) không cùng phương: \(\vec a\), \(\vec b\), \(\vec c\) đồng phẳng \( \Leftrightarrow \exists !m,n \in R:\vec c = m\vec a + n\vec b.\)
Nếu ba vectơ \(\vec a\), \(\vec b\), \(\vec c\) không đồng phẳng thì mọi vectơ đều được biểu diễn dưới dạng \(\vec d = m\vec a + n\vec b + k\vec c\) với \(m\), \(n\), \(k\) xác định duy nhất.
Ví dụ minh họa:
Ví dụ 1: Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm các cạnh \(BC\), \(CA\), \(AB\) của \(ΔABC\) và \(O\) là điểm bất kì trong không gian. Chứng minh: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} .\)
Do \(M\) là trung điểm \(BC\), ta có: \(\overrightarrow {OB} + \overrightarrow {OC} \) \( = (\overrightarrow {OM} + \overrightarrow {MB} ) + (\overrightarrow {OM} + \overrightarrow {MC} )\) \( = 2\overrightarrow {OM} + (\overrightarrow {MB} + \overrightarrow {MC} ) = 2\overrightarrow {OM} \) \((1).\)
Tương tự:
\(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OP} \) \((2).\)
\(\overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow {ON} \) \((3).\)
Lấy \((1) + (2) + (3)\) ta được: \(2(\overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {OC} )\) \( = 2(\overrightarrow {OM} + \overrightarrow {OP} + 2\overrightarrow {ON} )\) \( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \) \( = \overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {ON} .\)
Ví dụ 2: Cho tứ diện \(ABCD\) và mặt phẳng \((P).\) Gọi \(E\), \(F\) lần lượt là trung điểm \(AB\) và \(CD.\) Gọi \(I\) là trung điểm \(EF.\)
a) Chứng minh: \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \vec 0.\)
b) Trên mặt phẳng \((P)\) tìm điểm \(M\) sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right|\) đạt giá trị nhỏ nhất.
a)
Do \(E\) là trung điểm \(AB\) nên \(\overrightarrow {IA} + \overrightarrow {IB} = 2\overrightarrow {IE} .\)
Do \(F\) là trung điểm \(CD\) nên \(\overrightarrow {IC} + \overrightarrow {ID} = 2\overrightarrow {IF} .\)
Vậy \((\overrightarrow {IA} + \overrightarrow {IB} ) + (\overrightarrow {IC} + \overrightarrow {ID} )\) \( = 2\overrightarrow {IE} + 2\overrightarrow {IF} \) \( = 2(\overrightarrow {IE} + \overrightarrow {IF} )\) \( = \vec 0\) (do \(I\) là trung điểm \(EF\)).
b)
Ta có: \((\overrightarrow {MA} + \overrightarrow {MB} ) + (\overrightarrow {MC} + \overrightarrow {MD} )\) \( = 2\overrightarrow {ME} + 2\overrightarrow {MF} \) \( = 2(\overrightarrow {ME} + \overrightarrow {MF} ) = 4\overrightarrow {MI} .\)
Do đó: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right|\) \( = \left| {4\overrightarrow {MI} } \right| = 4MI.\)
Gọi \(H\) là hình chiếu vuông góc của \(I\) lên mặt phẳng \((P)\) ta có \(IM ≥ IH.\)
Vậy MÁ + MB + MG + MD] ngắn nhất \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right|\) ngắn nhất \( \Leftrightarrow MI\) ngắn nhất \( \Leftrightarrow M \equiv H.\)
Ví dụ 3: Cho ba điểm \(A\), \(B\), \(C\) cố định trên mặt phẳng \((α)\) và \(M\) di động trong không gian.
a) Xác định điểm \(I\) sao cho \(3\overrightarrow {IA} – 2\overrightarrow {IB} + \overrightarrow {IC} = \vec 0.\)
b) Cho điểm \(N\) sao cho \(\overrightarrow {MN} = 3\overrightarrow {MA} – 2\overrightarrow {MB} + \overrightarrow {MC} .\) Chứng minh đường thẳng \(MN\) luôn qua một điểm cố định.
a) Ta có: \(3\overrightarrow {IA} – 2\overrightarrow {IB} + \overrightarrow {IC} = \vec 0\) \( \Leftrightarrow 3\overrightarrow {IA} – 2(\overrightarrow {IA} + \overrightarrow {AB} ) + (\overrightarrow {IA} + \overrightarrow {AC} ) = \vec 0\) \( \Leftrightarrow 2\overrightarrow {IA} = \overrightarrow {AB} + \overrightarrow {AB} – \overrightarrow {AC} \) \( \Leftrightarrow 2\overrightarrow {IA} = \overrightarrow {AB} + \overrightarrow {CB} \) \( \Leftrightarrow 2\overrightarrow {AI} = \overrightarrow {BA} + \overrightarrow {BC} = 2\overrightarrow {BE} \) (với \(E\) là trung điểm \(AC\)).
Vậy \(I\) là điểm cố định sao cho \(\overrightarrow {AI} = \overrightarrow {BE} .\)
b) Ta có: \(\overrightarrow {MN} = 3\overrightarrow {MA} – 2\overrightarrow {MB} + \overrightarrow {MC} \) \( \Leftrightarrow \overrightarrow {MN} = 3(\overrightarrow {MI} + \overrightarrow {IA} )\) \( – 2(\overrightarrow {MI} + \overrightarrow {IB} ) + (\overrightarrow {MI} + \overrightarrow {IC} )\) \( \Leftrightarrow \overrightarrow {MN} = 2\overrightarrow {MI} + (3\overrightarrow {IA} – 2\overrightarrow {IB} + \overrightarrow {IC} )\) \( \Leftrightarrow \overrightarrow {MN} = 2\overrightarrow {MI} .\)
Do đó ba điểm \(M\), \(N\), \(I\) thẳng hàng nên đường thẳng \(MN\) luôn qua điểm \(I\) cố định.
Ví dụ 4: Cho tứ diện \(ABCD\) có \(I\) và \(J\) là trung điểm \(AB\) và \(CD.\) Gọi \(M\) và \(N\) là hai điểm chia đoạn \(BC\) và \(AD\) theo tỉ số \(k.\) Chứng minh \(I\), \(J\), \(M\) và \(N\) cùng nằm trên mặt phẳng.
Ta có: \(M\) chia đoạn \(BC\) theo tỉ số \(k\) \( \Leftrightarrow \overrightarrow {MB} = k\overrightarrow {MC} .\)
\(N\) chia đoạn \(AD\) theo tỉ số \(k\) \( \Leftrightarrow \overrightarrow {NA} = k\overrightarrow {ND} .\)
Ta có: \(\overrightarrow {JI} = \frac{1}{2}(\overrightarrow {JA} + \overrightarrow {JB} )\) \( = \frac{1}{2}(\overrightarrow {JD} + \overrightarrow {DA} + \overrightarrow {JC} + \overrightarrow {CB} )\) \( = \frac{1}{2}(\overrightarrow {DA} + \overrightarrow {CB} )\) \( = \frac{1}{2}(\overrightarrow {NA} – \overrightarrow {ND} + \overrightarrow {MB} – \overrightarrow {MC} )\) \( = \frac{1}{2}(k\overrightarrow {ND} – \overrightarrow {ND} + k\overrightarrow {MC} – \overrightarrow {MC} )\) \( = \frac{{k – 1}}{2}(\overrightarrow {NJ} + \overrightarrow {JD} + \overrightarrow {MJ} + \overrightarrow {JC} )\) \( = \frac{{k – 1}}{2}(\overrightarrow {NJ} + \overrightarrow {MJ} ).\)
Do đó \(\overrightarrow {JI} \), \(\overrightarrow {JN} \), \(\overrightarrow {JM} \) đồng phẳng.
Suy ra \(J\), \(I\), \(M\), \(N\) cùng thuộc một mặt phẳng.
Ví dụ 5: Cho hình hộp \(ABCD.A’B’C’D’.\) Gọi \(M\) và \(N\) lần lượt là trung điểm \(CD\) và \(DD’.\) Gọi \(G\) và \(G’\) lần lượt là trọng tâm tứ diện \(A’D’MN\) và \(BCC’D’.\) Chứng minh \(GG’\) song song mặt phẳng \((ABB’A’).\)
Đặt \(\overrightarrow {AB} = \vec a\), \(\overrightarrow {AD} = \vec b\), \(\overrightarrow {AA’} = \vec c.\)
Ta có: \(G\) trọng tâm tứ diện \(A’D’MN\) \( \Leftrightarrow \overrightarrow {GA’} + \overrightarrow {GD’} + \overrightarrow {GM} + \overrightarrow {GN} = \vec 0.\)
Do đó: \(4\overrightarrow {AG} = \overrightarrow {AG} + \overrightarrow {AG} + \overrightarrow {AG} + \overrightarrow {AG} \) \( \Leftrightarrow 4\overrightarrow {AG} = \left( {\overrightarrow {AA’} + \overrightarrow {A’G} } \right)\) \( + \left( {\overrightarrow {AD’} + \overrightarrow {D’G} } \right)\) \( + (\overrightarrow {AM} + \overrightarrow {MG} )\) \( + (\overrightarrow {AN} + \overrightarrow {NG} )\) \( \Leftrightarrow 4\overrightarrow {AG} = \overrightarrow {AA’} + \overrightarrow {AD’} + \overrightarrow {AM} + \overrightarrow {AN} \) \( \Leftrightarrow 4\overrightarrow {AG} = \vec c + (\vec b + \vec c) + \left( {\vec b + \frac{{\vec a}}{2}} \right) + \left( {\vec b + \frac{{\vec c}}{2}} \right)\) \( \Leftrightarrow 4\overrightarrow {AG} = 3\vec b + \frac{5}{2}\vec c + \frac{{\vec a}}{2}.\)
Tương tự: \(4\overrightarrow {AG’} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AC’} + \overrightarrow {AD’} \) \( \Leftrightarrow 4\overrightarrow {AG’} = \vec a + (\vec a + \vec b)\) \( + (\vec a + \vec b + \vec c) + (\vec b + \vec c)\) \( \Leftrightarrow 4\overrightarrow {AG’} = 3(\overrightarrow a + \overrightarrow b + \overrightarrow c ).\)
Do đó: \(4\left( {\overrightarrow {AG} – \overrightarrow {AG’} } \right) = – \frac{5}{2}\vec a – \frac{1}{2}\vec c\) \( \Leftrightarrow 4\overrightarrow {G’G} = \frac{5}{2}\overrightarrow {AB} – \frac{1}{2}\overrightarrow {A{A^\prime }} .\)
Vậy ba vectơ \(\overrightarrow {G’G} \), \(\overrightarrow {AB} \), \(\overrightarrow {AA’} \) đồng phẳng.
Mặt khác \(G \notin mp\left( {ABB’A’} \right).\)
Do đó \(GG’//mp\left( {ABB’A’} \right).\)
Ví dụ 6: Cho hình lập phương \(ABCD.A’B’C’D’.\) Lấy hai điểm \(M\) và \(N\) lần lượt trên hai cạnh \(B’C’\) và \(CD\) sao cho \(B’M = CN.\) Chứng minh \(AM\) vuông góc \(BN.\)
Gọi \(a\) là cạnh hình lập phương.
Gọi \(\vec u = \overrightarrow {AB} \), \(\vec v = \overrightarrow {AD} \), \(\vec w = \overrightarrow {AA’} \) thì \(|\vec u| = |\vec v| = |\vec w| = a.\)
Đặt \(x = B’M = CN\) \((0 \le x \le a).\)
Ta có: \(B’M = \frac{x}{a} \cdot B’C’\) và \(M\) nằm giữa hai điểm \(B’\) và \(C’\) nên \(\overrightarrow {B’M} = \frac{x}{a}\overrightarrow {B’C’} = \frac{x}{a}.\overrightarrow v .\)
Tương tự: \(\overrightarrow {CN} = \frac{x}{a} \cdot \overrightarrow {CD} = – \frac{x}{a} \cdot \vec u.\)
Vậy \(\overrightarrow {AM} = \overrightarrow {AA’} + \overrightarrow {A’B’} + \overrightarrow {B’M} \) \( = \vec w + \vec u + \frac{x}{a}\vec v\) và \(\overrightarrow {BN} = \overrightarrow {BC} + \overrightarrow {CN} = \vec v – \frac{x}{a} \cdot \vec u.\)
Do đó: \(\overrightarrow {AM} .\overrightarrow {BN} = \left( {\vec w + \vec u + \frac{x}{a}\vec v} \right).\left( {\vec v – \frac{x}{a}\vec u} \right)\) \( = \overrightarrow w .\overrightarrow v – \frac{x}{a}\overrightarrow w .\overrightarrow u + \overrightarrow u .\overrightarrow v \) \(- \frac{x}{a}.{\overrightarrow u ^2} + \frac{x}{a}.{\overrightarrow v ^2} – \frac{{{x^2}}}{{{a^2}}}\overrightarrow v .\overrightarrow u .\)
Mà \(\vec u \bot \vec v\), \(\vec u \bot \overrightarrow w \) và \(\vec w \bot \vec v\) nên \(\overrightarrow {AM} .\overrightarrow {BN} = – \frac{x}{a}|\vec u{|^2} + \frac{x}{a}|\vec v{|^2}\) \( = – xa + xa = 0.\)
Do đó: \(AM \bot BN.\)
Ví dụ 7: Cho bốn điểm \(A\), \(B\), \(C\), \(D\) tùy ý trong không gian. Chứng minh:
a) \(AB ⊥ CD\) khi và chỉ khi \(A{C^2} + B{D^2} = A{D^2} + B{C^2}.\)
b) Nếu \(AB ⊥ CD\) và \(AD ⊥ BC\) thì \(AC ⊥ BD.\)
a) Ta có: \(A{C^2} + B{D^2} = {\overrightarrow {AC} ^2} + {\overrightarrow {BD} ^2}\) \( = {(\overrightarrow {AD} + \overrightarrow {DC} )^2} + {(\overrightarrow {BC} + \overrightarrow {CD} )^2}\) \( = {\overrightarrow {AD} ^2} + {\overrightarrow {DC} ^2} + 2\overrightarrow {AD} .\overrightarrow {DC} \) \( + {\overrightarrow {BC} ^2} + {\overrightarrow {CD} ^2} + 2\overrightarrow {BC} .\overrightarrow {CD} \) \( = A{D^2} + B{C^2} + 2{\overrightarrow {DC} ^2}\) \( + 2\overrightarrow {AD} .\overrightarrow {DC} – 2\overrightarrow {BC} .\overrightarrow {DC} \) \( = A{D^2} + B{C^2} + 2\overrightarrow {DC} (\overrightarrow {DC} + \overrightarrow {AD} – \overrightarrow {BC} )\) \( = A{D^2} + B{C^2} + 2\overrightarrow {DC} (\overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {CB} )\) \( = A{D^2} + B{C^2} + 2\overrightarrow {DC} .\overrightarrow {AB} .\)
Do \(AB \bot CD \Leftrightarrow \overrightarrow {DC} .\overrightarrow {AB} = 0\) nên \(AB \bot CD\) \( \Leftrightarrow A{C^2} + B{D^2} = A{D^2} + B{C^2}.\)
b) Ta có: \(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AD} .\overrightarrow {BC} + \overrightarrow {AC} .\overrightarrow {DB} \) \( = \overrightarrow {AB} (\overrightarrow {AD} – \overrightarrow {AC} )\) \( + \overrightarrow {AD} (\overrightarrow {AC} – \overrightarrow {AB} )\) \( + \overrightarrow {AC} (\overrightarrow {AB} – \overrightarrow {AD} )\) \( = \overrightarrow {AB} .\overrightarrow {AD} – \overrightarrow {AB} .\overrightarrow {AC} \) \( + \overrightarrow {AD} .\overrightarrow {AC} – \overrightarrow {AD} .\overrightarrow {AB} \) \( + \overrightarrow {AC} .\overrightarrow {AB} – \overrightarrow {AC} .\overrightarrow {AD} \) \(=0\) (đây là hệ thức Euler) \((*).\)
Do đó \(AB \bot CD\) và \(AD \bot BC\) thì \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AD} .\overrightarrow {BC} = 0.\)
Từ \((*)\) suy ra \(\overrightarrow {AC} .\overrightarrow {DB} = 0\) \( \Rightarrow AC \bot DB.\)
Ví dụ 8: Cho \(ABCD.A’B’C’D’\) là hình lập phương cạnh có độ dài \(1.\) Trên \(BB’\), \(CD\), \(A’D’\) lấy \(M\), \(N\), \(P\) sao cho \(B’M = CN = D’P = a\) \((0 < a < 1).\) Chứng minh:
a) \(\overrightarrow {MN} = – a\overrightarrow {AB} + \overrightarrow {AD} + (a – 1)\overrightarrow {AA} .\)
b) \(AC’\) vuông góc với \(MN\) và \(NP.\)
Đặt \(\overrightarrow {AB} = \vec u\), \(\overrightarrow {AD} = \vec v\), \(\overrightarrow {AA’} = \vec w.\)
a) Ta có: \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} .\)
Ta có: \(\frac{{MB}}{{BB’}} = \frac{{1 – a}}{1}\) \( \Rightarrow \overrightarrow {MB} = (1 – a)\overrightarrow {B’B} = (a – 1)\overrightarrow {AA’} \) và \(\overrightarrow {BC} = \overrightarrow {AD} .\)
Ta có: \(\frac{{CN}}{{CD}} = \frac{a}{1}\) \( \Rightarrow \overrightarrow {CN} = a\overrightarrow {CD} = – a\overrightarrow {AB} .\)
Do đó: \(\overrightarrow {MN} = (a – 1)\overrightarrow {AA’} + \overrightarrow {AD} – a\overrightarrow {AB} .\)
b) Ta có: \(\overrightarrow {AC’} = \overrightarrow {AB} + \overrightarrow {AD’} \) \( = \overrightarrow {AB} + \left( {\overrightarrow {AD} + \overrightarrow {AA’} } \right)\) \( = \vec u + \vec v + \vec w.\)
Mà \(\overrightarrow {MN} = (a – 1)\vec w + \vec v – a\vec u.\)
Do đó: \(\overrightarrow {AC’} .\overrightarrow {MN} \) \( = (\vec u + \vec v + \vec w).[(a – 1)\vec w + \vec v – a\vec u]\) \( = – a + 1 + (a – 1) = 0\) \((1)\) (do \(\vec u.\vec w = 0\), \(\vec u.\vec v = 0\), \(\vec w.\vec v = 0\), \(|\vec u| = |\vec v| = |\vec w| = 1.\))
Tương tự: \(\overrightarrow {NP} = \overrightarrow {ND} + \overrightarrow {DD’} + \overrightarrow {D’P} \) \( = (a – 1)\vec v + \vec w – a\vec u\) nên \(\overrightarrow {AC’} .\overrightarrow {NP} \) \( = (\vec u + \vec v + \vec w)[(a – 1)\vec v + \vec w – a\vec u]\) \( = – a + (a – 1) + 1 = 0.\)
Từ \((1)\) và \((2)\) suy ra \(AC’ \bot MN\) và \(AC’ \bot NP.\)
Ví dụ 9: Cho tam giác \(ABC\) trong không gian.
a) Cho điểm \(M\) thỏa: \(\overrightarrow {AB} .\overrightarrow {CM} = \overrightarrow {CB} .\overrightarrow {AM} \). Chứng minh \(BM\) vuông góc \(AC.\)
b) Gọi \(AD\) là đường phân giác trong của \(\widehat {BAC}\). Hãy biểu diễn \(\overrightarrow {AD} \) theo \(\overrightarrow {AB} \), \(\overrightarrow {AC} .\)
a) Ta có: \(\overrightarrow {AB} .\overrightarrow {CM} = \overrightarrow {CB} .\overrightarrow {AM} \) \( \Leftrightarrow \overrightarrow {AB} .(\overrightarrow {AM} – \overrightarrow {AC} ) = \overrightarrow {CB} .\overrightarrow {AM} \) \( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AM} – \overrightarrow {AB} .\overrightarrow {AC} – \overrightarrow {AM} .\overrightarrow {CB} = \vec 0\) \( \Leftrightarrow \overrightarrow {AM} (\overrightarrow {AB} + \overrightarrow {BC} ) – \overrightarrow {AB} .\overrightarrow {AC} = 0\) \( \Leftrightarrow \overrightarrow {AM} .\overrightarrow {AC} – \overrightarrow {AB} .\overrightarrow {AC} = 0\) \( \Leftrightarrow \overrightarrow {AC} (\overrightarrow {AM} – \overrightarrow {AB} ) = 0\) \( \Leftrightarrow \overrightarrow {AC} .\overrightarrow {BM} = 0\) \( \Leftrightarrow AC \bot BM.\)
b) Gọi \(AB = c\), \(AC = b\), \(BC = a.\)
Do tính chất chân đường phân giác trong nên: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow DB = \frac{c}{b}DC.\)
Mà \(D\) nằm giữa \(B\) và \(C\) nên \(\overrightarrow {DB} = – \frac{c}{b}\overrightarrow {DC} \) \( \Leftrightarrow \overrightarrow {AB} – \overrightarrow {AD} = – \frac{c}{b}(\overrightarrow {AC} – \overrightarrow {AD} )\) \( \Leftrightarrow \overrightarrow {AB} + \frac{c}{b}\overrightarrow {AC} \) \( = \left( {1 + \frac{c}{b}} \right)\overrightarrow {AD} \) \( = \frac{{b + c}}{b}\overrightarrow {AD} \) \( \Leftrightarrow \overrightarrow {AD} = \frac{b}{{b + c}}\overrightarrow {AB} + \frac{c}{{b + c}}\overrightarrow {AC} .\)



















Giải Toán vectơ trong không gian với Đáp Án Mới Nhất
Toán học luôn là một môn học quan trọng, giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề. Để hỗ trợ các bạn học sinh và giáo viên trong việc học tập và giảng dạy, bài viết này sẽ cung cấp lời giải chi tiết và đáp án chính xác cho chủ đề vectơ trong không gian, giúp bạn hiểu sâu và tự tin hơn khi làm bài tập.
vectơ trong không gian là một trong những phần kiến thức quan trọng trong chương trình toán học, thường xuất hiện trong các bài kiểm tra và kỳ thi lớn. Việc nắm vững phần này không chỉ giúp bạn đạt điểm cao mà còn tạo nền tảng vững chắc để học các nội dung nâng cao hơn.
Chúng tôi cung cấp hướng dẫn từng bước giải bài tập, bao gồm:
Mỗi bài giải đều kèm theo lời giải thích chi tiết, giúp bạn hiểu không chỉ cách làm mà còn cả lý do tại sao nên áp dụng phương pháp đó.
Tất cả các bài tập đều đi kèm đáp án mới nhất, được kiểm tra kỹ lưỡng để đảm bảo độ chính xác cao. Điều này giúp bạn tự kiểm tra kết quả và khắc phục lỗi sai một cách nhanh chóng.
Ngoài ra, bài viết còn cung cấp các tài liệu bổ trợ như:
Chủ đề vectơ trong không gian là một phần kiến thức thú vị và hữu ích trong toán học. Hãy sử dụng bài viết này như một công cụ hỗ trợ để bạn chinh phục mọi thử thách trong môn Toán. Đừng quên ôn tập thường xuyên và luyện tập nhiều dạng bài tập khác nhau để thành thạo hơn!
Chúc các bạn học tốt và đạt kết quả cao! 😊
>> Xem thêm đáp án chi tiết về: vectơ trong không gian.