Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 12 Cánh diều - Đề số 2, được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, tập trung vào các chủ đề quan trọng như tích phân, số phức, và hình học không gian. Học sinh có thể sử dụng đề thi này để tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Nguyên hàm của hàm số f(x) = \({e^x}\) là
\(\frac{{{e^{x + 1}}}}{{x + 1}} + C\)
\(\frac{{{{(e + 1)}^x}}}{{e + 1}} + C\)
\( - {e^{ - x}} + C\)
\({e^x} + C\)
Hàm số F(x) = cos3x là một nguyên hàm của hàm số nào dưới đây?
\(f(x) = 3\sin 3x\)
\(f(x) = \sin {x^2}\)
\(f(x) = - 3\sin 3x\)
\(f(x) = - \frac{1}{3}\sin 3x\)
Cho hai hàm số f(x) và g(x) liên tục trên \(\mathbb{R}\). Khẳng định nào dưới đây đúng?
\(\int\limits_a^b {\left[ {f(x) + g(x)} \right]dx} = \int\limits_a^b {f(x)dx} + \int\limits_a^b {g(x)dx} \)
\(\int\limits_a^b {\left[ {f(x) - g(x)} \right]dx} = \int\limits_a^b {f(x)dx} + \int\limits_a^b {g(x)dx} \)
\(\int\limits_a^b {f(x).g(x)dx} = \int\limits_a^b {f(x)dx} .\int\limits_a^b {g(x)dx} \)
\(\int\limits_a^b {\left[ {f(x) - g(x)} \right]dx} = \int\limits_a^b {g(x)dx} - \int\limits_a^b {f(x)dx} \)
Cho hàm số \(f(x) = 3 + \frac{1}{x}\). Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của f(x) trên \((0; + \infty )\)?
\(F(x) = 3x - \frac{1}{{{x^2}}}\)
\(F(x) = 3x + \ln x\)
\(F(x) = 3x + \frac{1}{{{x^2}}}\)
\(F(x) = 3x - \ln x\)
Cho hàm số \(\frac{{2{x^2}}}{3}\). Kết quả của \(\int\limits_0^3 {\frac{{f(x)}}{2}dx} \) là
9
3
27
\(\frac{1}{3}\)
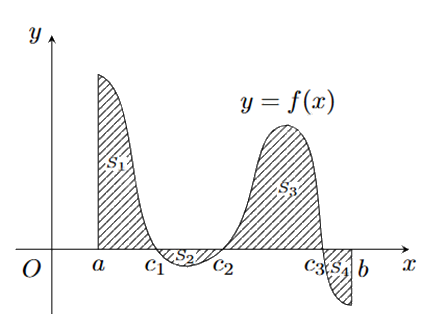
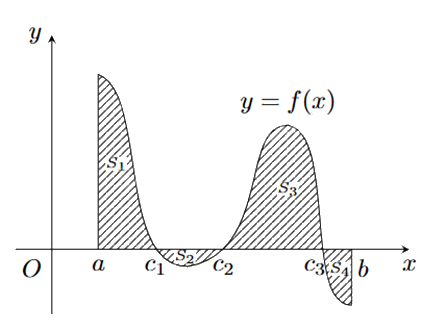
Cho hàm số y = f(x) có đồ thị như hình bên. \({S_1}\), \({S_2}\), \({S_3}\), \({S_4}\) lần lượt là phần diện tích tương ứng của đồ thị hàm số với trục hoành. Tích phân \(\int\limits_a^b {f(x)dx} \) có kết quả là
\({S_1} + {S_2} + {S_3} + {S_4}\)
\( - {S_1} + {S_2} - {S_3} + {S_4}\)
\({S_1} - {S_2} + {S_3} - {S_4}\)
\( - {S_1} - {S_2} - {S_3} - {S_4}\)
Trong không gian Oxyz , mặt phẳng \((\alpha )\): x + 2y + 3z – 12 = 0 cắt trục tung tại điểm có tung độ bằng
2
6
3
1
Trong không gian Oxyz, khoảng cách từ điểm M(-2;1;2) đến mặt phẳng \((\alpha )\): x – 5y + 2z – 7 = 0 là
\(\frac{{\sqrt {10} }}{3}\)
\(\frac{{\sqrt {10} }}{{\sqrt 3 }}\)
\(\frac{{\sqrt 3 }}{{\sqrt {10} }}\)
\(\frac{{\sqrt 3 }}{{10}}\)
Trong không gian Oxyz, một vecto chỉ phương của mặt phẳng \((\beta )\): 2x + 3y – z + 5 = 0 là
\(\overrightarrow u = ( - 2; - 3;1)\)
\(\overrightarrow u = (0;2;6)\)
\(\overrightarrow u = (2;2;2)\)
\(\overrightarrow u = ( - 1;3;2)\)
Góc giữa hai mặt phẳng (P): x + 2y + z – 1 = 0 và (Q): -x + y + 2z + 2 = 0 bằng
\({30^o}\)
\({45^o}\)
\({60^o}\)
\({90^o}\)
Trong không gian Oxyz, cho mặt phẳng (P): x – 2y + z – 1 = 0. Điểm nào sau đây không thuộc mặt phẳng (P)?
E(0;0;1)
F(3;1;0)
M(2;-1;3)
N(3;2;2)
Trong không gian Oxyz, phương trình nào sau đây là phương trình tổng quát của một mặt phẳng?
\({x^2} + 2{y^2} - 3{z^2} + 1 = 0\)
\(\frac{1}{x} + \frac{2}{y} + \frac{3}{z} + 2 = 0\)
\(x - y + 1 = 0\)
\(xy + 5 = 0\)
Cho khối tròn xoay như hình bên.
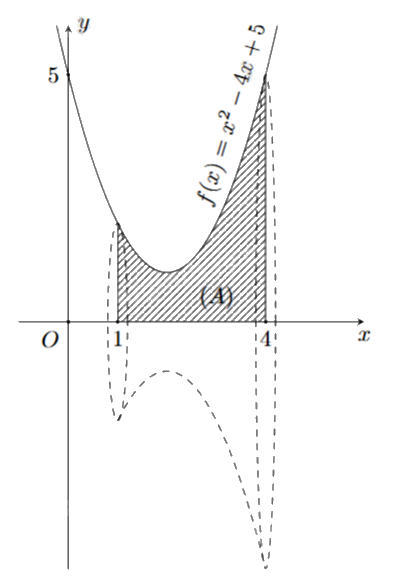
a) Hình phẳng (A) được giới hạn các đường \(y = f(x) = {x^2} - 4x + 5\), y = 0, x = 0, x = 4.
b) Diện tích hình phẳng (A) được giới hạn là 6.
c) Tổng diện tích đáy trên và đáy dưới của khối tròn xoay là \(17\pi \).
d) Thể tích khối tròn xoay này khi quay hình phẳng (A) quanh trục Ox là \(\frac{{78}}{5}\pi \).
Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí A(4;0;0). Vùng phủ sóng của thiết bị có bán kính bằng 4.
a) Điểm M(4;2;2) thuộc vùng phủ sóng.
b) Tập hợp tất cả các điểm thuộc vùng phủ sóng của thiết bị được giới hạn bởi mặt cầu có phương trình \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4\).
c) Một bức tường được xây gần đó có phương trình (P): x + y – z = 6 sẽ chắn sóng của thiết bị.
d) Vùng nhận được tín hiệu trên mặt phẳng (P) là hình tròn có bán kính bằng 4.
Tại một nhà máy sản xuất phân bón, gọi P(x) là lợi nhuận (tính theo triệu đồng) thu được từ việc bán x tấn sản phẩm trong một tuần. Khi đó, đạo hàm P’(x), gọi là là lợi nhuận cận biên, cho biết tốc độ tăng lợi nhuận theo lượng sản phẩm bán được. Giả sử lợi nhuận cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức P’(x) = 16 – 0,02x với \(0 \le x \le 100\). Tính lợi nhuận chênh lệch có được khi nhà máy bán 90 tấn sản phẩm trong tuần so với bán 20 tấn sản phẩm trong tuần (tính theo triệu đồng).
Đáp án:
Một xe ô tô chuyển động với vận tốc tại giây thứ t là \(v(t) = 4{t^3} + 2t + 3\) (m/s). Hỏi xe đã đi được quãng đường là bao nhiêu (đơn vị: mét) kể từ lúc bắt đầu (t = 0) cho đến lúc t = 5 (s)?
Đáp án:
Một sinh viên thiết kế đồ họa 3D của một cánh đồng điện mặt trời trong không gian Oxyz, một tấm pin nằm trên mặt phẳng (P): x + 2y + 3z + 2 = 0; một tấm pin khác nằm trên mặt phẳng (Q) đi qua điểm M(1;2;3) và song song với mặt phẳng (P). Biết rằng phương trình mặt phẳng (Q) có dạng ax + 2y + bz + c = 0. Khi đó giá trị a + b + c bằng bao nhiêu?
Đáp án:
Trong không gian Oxyz, cho điểm M (1;2;3). Mặt phẳng (P): ax + by + cz − 14 = 0 đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Tính giá trị biểu thức S = 2a + 3b − 4c.
Đáp án:
Cho \(f(x) = \left\{ \begin{array}{l}1\\2x - 1\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ge 1\\x < 1\end{array}\). Tính \(J = \int\limits_{ - 1}^2 {f(x)dx} \).
Trong chương trình nông thôn mới, tại một xã Y có xây một đoạn đường hầm bằng bê tông như hình vẽ. Tính thể tích \(({m^3})\) khối bê tông để đổ đủ đoạn đường hầm, biết đường cong trong hình vẽ là các đường parabol.
Trong không gian Oxyz, cho ba điểm A(1;1;1), B(−1;2;0), C(3;−1;2) và M là điểm thuộc mặt phẳng \((\alpha )\): 2x − y + 2z + 7 = 0. Tính giá trị nhỏ nhất của \(P = \left| {3\overrightarrow {MA} + 5\overrightarrow {MB} - 7\overrightarrow {MC} } \right|\).
Nguyên hàm của hàm số f(x) = \({e^x}\) là
\(\frac{{{e^{x + 1}}}}{{x + 1}} + C\)
\(\frac{{{{(e + 1)}^x}}}{{e + 1}} + C\)
\( - {e^{ - x}} + C\)
\({e^x} + C\)
Đáp án : D
Áp dụng công thức nguyên hàm của hàm số mũ: \(\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\).
\(\int {{e^x}dx} = \frac{{{e^x}}}{{\ln e}} + C = {e^x} + C\).
Hàm số F(x) = cos3x là một nguyên hàm của hàm số nào dưới đây?
\(f(x) = 3\sin 3x\)
\(f(x) = \sin {x^2}\)
\(f(x) = - 3\sin 3x\)
\(f(x) = - \frac{1}{3}\sin 3x\)
Đáp án : C
F(x) là nguyên hàm của f(x) nếu F’(x) = f(x).
Vì \(F'(x) = (\cos 3x)' = - 3\sin 3x\) nên F(x) là một nguyên hàm của hàm số \(f(x) = - 3\sin 3x\).
Cho hai hàm số f(x) và g(x) liên tục trên \(\mathbb{R}\). Khẳng định nào dưới đây đúng?
\(\int\limits_a^b {\left[ {f(x) + g(x)} \right]dx} = \int\limits_a^b {f(x)dx} + \int\limits_a^b {g(x)dx} \)
\(\int\limits_a^b {\left[ {f(x) - g(x)} \right]dx} = \int\limits_a^b {f(x)dx} + \int\limits_a^b {g(x)dx} \)
\(\int\limits_a^b {f(x).g(x)dx} = \int\limits_a^b {f(x)dx} .\int\limits_a^b {g(x)dx} \)
\(\int\limits_a^b {\left[ {f(x) - g(x)} \right]dx} = \int\limits_a^b {g(x)dx} - \int\limits_a^b {f(x)dx} \)
Đáp án : A
Áp dụng tính chất của tích phân \(\int\limits_a^b {\left[ {f(x) \pm g(x)} \right]dx} = \int\limits_a^b {f(x)dx} \pm \int\limits_a^b {g(x)dx} \).
\(\int\limits_a^b {f(x) + g(x)dx} = \int\limits_a^b {f(x)dx} + \int\limits_a^b {g(x)dx} \) là khẳng định đúng.
Cho hàm số \(f(x) = 3 + \frac{1}{x}\). Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của f(x) trên \((0; + \infty )\)?
\(F(x) = 3x - \frac{1}{{{x^2}}}\)
\(F(x) = 3x + \ln x\)
\(F(x) = 3x + \frac{1}{{{x^2}}}\)
\(F(x) = 3x - \ln x\)
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lũy thừa: \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
Áp dụng công thức nguyên hàm của hàm số \(y = \frac{1}{x}\): \(\int {\frac{1}{x}dx} = \ln \left| x \right| + C\).
\(\int {f(x)dx} = \int {\left( {3 + \frac{1}{x}} \right)dx} = 3x + \ln \left| x \right| + C\).
Cho hàm số \(\frac{{2{x^2}}}{3}\). Kết quả của \(\int\limits_0^3 {\frac{{f(x)}}{2}dx} \) là
9
3
27
\(\frac{1}{3}\)
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
Áp dụng tính chất của tích phân \(\int\limits_a^b {kf(x)dx} = k\int\limits_a^b {f(x)dx} \).
\(\int\limits_0^3 {\frac{{f(x)}}{2}dx} = \frac{1}{2}\int\limits_0^3 {f(x)dx} = \frac{1}{2}\int\limits_0^3 {\frac{{2{x^2}}}{3}dx} = \frac{1}{3}\int\limits_0^3 {{x^2}dx} = \frac{1}{3}.\frac{{{x^3}}}{3}\left| {\begin{array}{*{20}{c}}{^3}\\{_0}\end{array}} \right. = \frac{1}{3}.\frac{{{3^3}}}{3} = 3\).
Cho hàm số y = f(x) có đồ thị như hình bên. \({S_1}\), \({S_2}\), \({S_3}\), \({S_4}\) lần lượt là phần diện tích tương ứng của đồ thị hàm số với trục hoành. Tích phân \(\int\limits_a^b {f(x)dx} \) có kết quả là
\({S_1} + {S_2} + {S_3} + {S_4}\)
\( - {S_1} + {S_2} - {S_3} + {S_4}\)
\({S_1} - {S_2} + {S_3} - {S_4}\)
\( - {S_1} - {S_2} - {S_3} - {S_4}\)
Đáp án : C
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f(x), y = g(x) liên tục trên [a;b] và hai đường thẳng x = a, x = b được tính bằng công thức \(S\int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \).
\({S_1} = \int\limits_a^{{c_1}} {\left| {f(x)} \right|dx} \Rightarrow {S_1} = \int\limits_a^{{c_1}} {f(x)dx} \);
\({S_2} = \int\limits_{{c_1}}^{{c_2}} {\left| {f(x)} \right|dx} \Rightarrow {S_2} = - \int\limits_{{c_1}}^{{c_2}} {f(x)dx} \Rightarrow - {S_2} = \int\limits_{{c_1}}^{{c_2}} {f(x)dx} \);
\({S_3} = \int\limits_{{c_3}}^{{c_3}} {\left| {f(x)} \right|dx} \Rightarrow {S_3} = \int\limits_{{c_3}}^{{c_3}} {f(x)dx} \);
\({S_4} = \int\limits_{{c_3}}^b {\left| {f(x)} \right|dx} \Rightarrow {S_4} = - \int\limits_{{c_3}}^b {f(x)dx} \Rightarrow - {S_4} = \int\limits_{{c_3}}^b {f(x)dx} \).
Ta có: \(\int\limits_a^b {f(x)dx} = \int\limits_a^{{c_1}} {f(x)dx} + \int\limits_{{c_1}}^{{c_2}} {f(x)dx} + \int\limits_{{c_2}}^{{c_3}} {f(x)dx} + \int\limits_{{c_3}}^b {f(x)dx} = {S_1} - {S_2} + {S_3} - {S_4}\).
Trong không gian Oxyz , mặt phẳng \((\alpha )\): x + 2y + 3z – 12 = 0 cắt trục tung tại điểm có tung độ bằng
2
6
3
1
Đáp án : B
Lập phương trình tham số của trục tung. Thay tọa độ x, y, z theo t của phương trình vừa lập vào phương trình mặt phẳng để tìm t. Từ đó kết luận tung độ giao điểm.
Trục tung có phương trình tham số là \(\left\{ \begin{array}{l}x = 0\\y = t\\z = 0\end{array} \right.\) \((t \in \mathbb{R})\).
Xét phương trình \(0 + 2t + 3.0 - 12 = 0 \Leftrightarrow 2t - 12 = 0 \Leftrightarrow t = 6\).
Vậy tung độ giao điểm của trục tung và mặt phẳng \((\alpha )\) là y = 6.
Trong không gian Oxyz, khoảng cách từ điểm M(-2;1;2) đến mặt phẳng \((\alpha )\): x – 5y + 2z – 7 = 0 là
\(\frac{{\sqrt {10} }}{3}\)
\(\frac{{\sqrt {10} }}{{\sqrt 3 }}\)
\(\frac{{\sqrt 3 }}{{\sqrt {10} }}\)
\(\frac{{\sqrt 3 }}{{10}}\)
Đáp án : B
Áp dụng công thức tính khoảng cách từ một điểm tới một đường thẳng.
\(d\left( {M,(\alpha )} \right) = \frac{{\left| {1.( - 2) - 5.1 + 2.2 - 7} \right|}}{{\sqrt {{1^2} + {{( - 5)}^2} + {2^2}} }} = \frac{{10}}{{\sqrt {30} }} = \frac{{\sqrt {10} }}{{\sqrt 3 }}\).
Trong không gian Oxyz, một vecto chỉ phương của mặt phẳng \((\beta )\): 2x + 3y – z + 5 = 0 là
\(\overrightarrow u = ( - 2; - 3;1)\)
\(\overrightarrow u = (0;2;6)\)
\(\overrightarrow u = (2;2;2)\)
\(\overrightarrow u = ( - 1;3;2)\)
Đáp án : B
Từ phương trình tổng quát, xác định vecto pháp tuyến của mặt phẳng, từ đó tìm vecto có giá vuông góc với vecto pháp tuyến vừa tìm.
Vecto pháp tuyến của \((\beta )\) là \(\overrightarrow n = (2;3; - 1)\).
Xét các phương án, thấy chỉ có 0.2 + 2.3 + 6.(-1) = 0, tức \(\overrightarrow u = (0;2;6)\) có giá vuông góc với \(\overrightarrow n = (2;3; - 1)\).
Vậy \(\overrightarrow u = (0;2;6)\) là một vecto chỉ phương của \((\beta )\).
Góc giữa hai mặt phẳng (P): x + 2y + z – 1 = 0 và (Q): -x + y + 2z + 2 = 0 bằng
\({30^o}\)
\({45^o}\)
\({60^o}\)
\({90^o}\)
Đáp án : C
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\vec n{\rm{\;}} = \left( {A;B;C} \right),\vec n'{\rm{\;}} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {(P),(Q)} \right) = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\).
\(\cos \left( {(P),(Q)} \right) = \frac{{\left| {1.( - 1) + 2.1 + 1.2} \right|}}{{\sqrt {{1^2} + {2^2} + {1^2}} .\sqrt {{{( - 1)}^2} + {1^2} + {2^2}} }} = \frac{1}{2} \Rightarrow \left( {(P),(Q)} \right) = {60^o}\).
Trong không gian Oxyz, cho mặt phẳng (P): x – 2y + z – 1 = 0. Điểm nào sau đây không thuộc mặt phẳng (P)?
E(0;0;1)
F(3;1;0)
M(2;-1;3)
N(3;2;2)
Đáp án : C
Thay tọa độ các điểm vào phương trình, nếu thỏa mãn thì điểm đó thuộc mặt phẳng
Thay tọa độ các điểm vào phương trình mặt phẳng, thấy chỉ có tọa độ điểm M(2;-1;3) không thỏa mãn phương trình mặt phẳng, do: 1.2 – 2.(-1) + 1.3 – 1 \( \ne \) 0.
Trong không gian Oxyz, phương trình nào sau đây là phương trình tổng quát của một mặt phẳng?
\({x^2} + 2{y^2} - 3{z^2} + 1 = 0\)
\(\frac{1}{x} + \frac{2}{y} + \frac{3}{z} + 2 = 0\)
\(x - y + 1 = 0\)
\(xy + 5 = 0\)
Đáp án : C
Phương trình tổng quát của mặt phẳng có dạng Ax + By + Cz + D = 0, với A, B, C không đồng thời bằng 0.
Chỉ có phương trình \(x - y + 1 = 0\) ở đáp án C có dạng phương trình tổng quát của mặt phẳng.
Cho khối tròn xoay như hình bên.
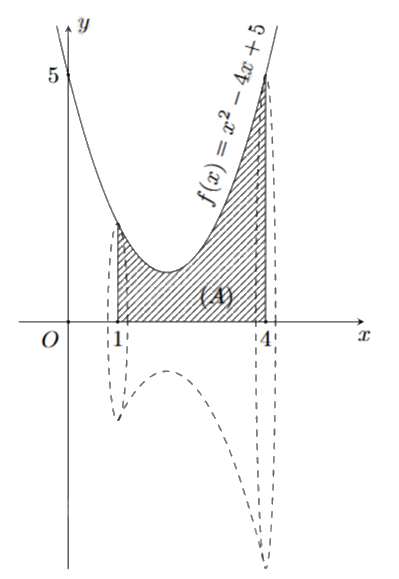
a) Hình phẳng (A) được giới hạn các đường \(y = f(x) = {x^2} - 4x + 5\), y = 0, x = 0, x = 4.
b) Diện tích hình phẳng (A) được giới hạn là 6.
c) Tổng diện tích đáy trên và đáy dưới của khối tròn xoay là \(17\pi \).
d) Thể tích khối tròn xoay này khi quay hình phẳng (A) quanh trục Ox là \(\frac{{78}}{5}\pi \).
a) Hình phẳng (A) được giới hạn các đường \(y = f(x) = {x^2} - 4x + 5\), y = 0, x = 0, x = 4.
b) Diện tích hình phẳng (A) được giới hạn là 6.
c) Tổng diện tích đáy trên và đáy dưới của khối tròn xoay là \(17\pi \).
d) Thể tích khối tròn xoay này khi quay hình phẳng (A) quanh trục Ox là \(\frac{{78}}{5}\pi \).
Cho hình phẳng được giới hạn bởi các đồ thị hàm số liên tục trên [a;b] y = f(x), y = 0, đường thẳng x = a, x = b.
a) Quan sát đồ thị và nhận xét.
b) Áp dụng công thức tính diện tích của hình phẳng \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
c) Bán kính hai đáy lần lượt là f(1) và f(4).
d) Áp dụng công thức tính thể tích vật thể quay quanh trục Ox \(V = \pi \int\limits_a^b {{f^2}(x)dx} \).
a)Sai. Hình phẳng (A) được giới hạn các đường \(y = f(x) = {x^2} - 4x + 5\), y = 0, x = 1, x = 4.
b) Đúng. Quan sát đoạn [1;4], thấy đồ thị y = f(x) nằm phía trên trục hoành.
Do đó, trên đoạn [1;4] ta có f(x) > 0, suy ra |f(x)| = f(x).
Diện tích hình phẳng (A) là:
\(S = \int\limits_1^4 {\left| {{x^2} - 4x + 5} \right|dx} = \int\limits_1^4 {\left( {{x^2} - 4x + 5} \right)dx} = \left( {\frac{{{x^3}}}{3} - 2{x^2} + 5x} \right)\left| {\begin{array}{*{20}{c}}{^4}\\{_1}\end{array}} \right.\)
\( = \left( {\frac{{{4^3}}}{3} - {{2.4}^2} + 5.4} \right) - \left( {\frac{{{1^3}}}{3} - {{2.1}^2} + 5.1} \right) = 6\).
c) Sai. Bán kính đáy nhỏ của khối tròn xoay là \(f(1) = {1^2} - 4.1 + 5 = 2\), bán kính đáy lớn là \(f(4) = {4^2} - 4.4 + 5 = 5\).
Tổng diện tích hai đáy là \(S = \pi {.2^2} + \pi {.5^2} = 41\pi \).
d) Đúng. Thể tích khối tròn xoay khi quay hình phẳng (A) quanh trục Ox là:
\(V = \pi \int\limits_1^4 {{{\left( {{x^2} - 4x + 5} \right)}^2}dx} = \frac{{78\pi }}{5}\).
Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí A(4;0;0). Vùng phủ sóng của thiết bị có bán kính bằng 4.
a) Điểm M(4;2;2) thuộc vùng phủ sóng.
b) Tập hợp tất cả các điểm thuộc vùng phủ sóng của thiết bị được giới hạn bởi mặt cầu có phương trình \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4\).
c) Một bức tường được xây gần đó có phương trình (P): x + y – z = 6 sẽ chắn sóng của thiết bị.
d) Vùng nhận được tín hiệu trên mặt phẳng (P) là hình tròn có bán kính bằng 4.
a) Điểm M(4;2;2) thuộc vùng phủ sóng.
b) Tập hợp tất cả các điểm thuộc vùng phủ sóng của thiết bị được giới hạn bởi mặt cầu có phương trình \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4\).
c) Một bức tường được xây gần đó có phương trình (P): x + y – z = 6 sẽ chắn sóng của thiết bị.
d) Vùng nhận được tín hiệu trên mặt phẳng (P) là hình tròn có bán kính bằng 4.
a) Áp dụng biểu thức tính khoảng cách giữa hai điểm. Nếu khoảng cách đó nhỏ hơn bán kính phủ sóng thì điểm M thuộc vùng phủ sóng.
b) Áp dụng quy tắc lập phương trình mặt cầu biết tâm và bán kính.
c) Tính khoảng cách từ điểm A tới mặt phẳng (P). Nếu khoảng cách đỏ nhỏ nhỏ hơn bán kính phủ sóng thì bức tường chắn được sóng của thiết bị.
d) Áp dụng định lí Pythagore.
a)Đúng. \(AM = \sqrt {{{(4 - 4)}^2} + {{(2 - 0)}^2} + {{(2 - 0)}^2}} = 2\sqrt 2 < 4\).
Khoảng cách từ M đến A nhỏ hơn bán kính phủ sóng nên M thuộc vùng phủ sóng.
b) Sai. Vùng phủ sóng là mặt cầu tâm A(4;0;0), bán kính R = 4 nên có phương trình:
\({\left( {x - 4} \right)^2} + {y^2} + {z^2} = 16\).
c) Đúng. \(d\left( {A,(P)} \right) = \frac{{\left| {1.4 + 1.0 - 1.0 - 6} \right|}}{{\sqrt {{1^2} + {1^2} + {{( - 1)}^2}} }} = \frac{{2\sqrt 3 }}{3} < 4\).
Vì khoảng cách từ bức tường tới thiết bị phát sóng nhỏ hơn bán kính phủ sóng nên bức tường đó chắn được sóng của thiết bị.
d) Sai. Bán kính vùng nhận được tín hiệu trên mặt phẳng (P) là \(\sqrt {{4^2} - {{\left( {\frac{{2\sqrt 3 }}{3}} \right)}^2}} = \frac{{2\sqrt {33} }}{3}\).
Tại một nhà máy sản xuất phân bón, gọi P(x) là lợi nhuận (tính theo triệu đồng) thu được từ việc bán x tấn sản phẩm trong một tuần. Khi đó, đạo hàm P’(x), gọi là là lợi nhuận cận biên, cho biết tốc độ tăng lợi nhuận theo lượng sản phẩm bán được. Giả sử lợi nhuận cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức P’(x) = 16 – 0,02x với \(0 \le x \le 100\). Tính lợi nhuận chênh lệch có được khi nhà máy bán 90 tấn sản phẩm trong tuần so với bán 20 tấn sản phẩm trong tuần (tính theo triệu đồng).
Đáp án:
Đáp án:
Tính \(\int\limits_{20}^{90} {P'(x)dx} \).
\(P(x) = \int\limits_{20}^{90} {P'(x)dx} = \int\limits_{20}^{90} {\left( {16 - 0,02x} \right)dx} = \left( {16x - \frac{{{x^2}}}{{100}}} \right)\left| {\begin{array}{*{20}{c}}{^{90}}\\{_{20}}\end{array} = 1043} \right.\).
Một xe ô tô chuyển động với vận tốc tại giây thứ t là \(v(t) = 4{t^3} + 2t + 3\) (m/s). Hỏi xe đã đi được quãng đường là bao nhiêu (đơn vị: mét) kể từ lúc bắt đầu (t = 0) cho đến lúc t = 5 (s)?
Đáp án:
Đáp án:
Tính \(\int\limits_0^5 {v(t)dt} \).
\(s(5) = \int\limits_0^5 {v(t)dt} = \int\limits_0^5 {\left( {4{t^3} + 2t + 3} \right)dt} = 665\) (m).
Một sinh viên thiết kế đồ họa 3D của một cánh đồng điện mặt trời trong không gian Oxyz, một tấm pin nằm trên mặt phẳng (P): x + 2y + 3z + 2 = 0; một tấm pin khác nằm trên mặt phẳng (Q) đi qua điểm M(1;2;3) và song song với mặt phẳng (P). Biết rằng phương trình mặt phẳng (Q) có dạng ax + 2y + bz + c = 0. Khi đó giá trị a + b + c bằng bao nhiêu?
Đáp án:
Đáp án:
Mặt phẳng (Q) có cùng vecto pháp tuyến với mặt phẳng (Q) do hai mặt phẳng song song với nhau.
(Q) // (P) và M(1;2;3) thuộc (Q) nên phương trình mặt phẳng (Q) là:
\(1(x - 1) + 2(y - 2) + 3(z - 3) = 0 \Leftrightarrow x + 2y + 3z - 14 = 0\).
Vậy a + b + c = 1 + 3 + (-14) = -10.
Trong không gian Oxyz, cho điểm M (1;2;3). Mặt phẳng (P): ax + by + cz − 14 = 0 đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Tính giá trị biểu thức S = 2a + 3b − 4c.
Đáp án:
Đáp án:
Chứng minh \(OM \bot (P)\) và \(\overrightarrow {OM} \) là một vecto pháp tuyến của (P). Từ đó viết phương trình tổng quát của (P).
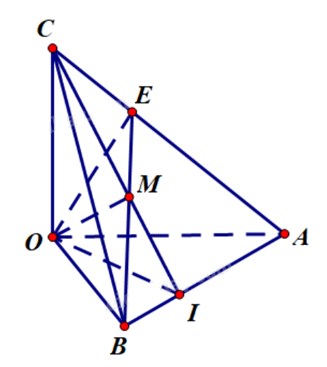
Lấy \(I \in AB\) sao cho \(CI \bot AB\). Khi đó, CI là đường cao của tam giác ABC và trực tâm M thuộc CI.
Ta có \(\left\{ \begin{array}{l}OC \bot (OAB) \Rightarrow OC \bot AB\\CI \bot AB\end{array} \right. \Rightarrow AB \bot (OCI) \Rightarrow AB \bot OM\) (vì OM thuộc (OCI)) (1)
Gọi E là giao điểm của BM và AC. Khi đó \(BE \bot AC\) vì M là trực tâm tam giác ABC.
Ta có \(\left\{ \begin{array}{l}BE \bot AC\\OB \bot (OAC) \Rightarrow OB \bot AC\end{array} \right. \Rightarrow AC \bot (OBE) \Rightarrow AC \bot OM\) (vì OM thuộc (OBE)) (2)
Từ (1) và (2) suy ra \(OM \bot (ABC)\) hay \(OM \bot (P)\).
Do đó, \(\overrightarrow {OM} = (1;2;3)\) là một vecto pháp tuyến của (P).
Mặt phẳng (P) đi qua M(1;2;3) và nhận \(\overrightarrow {OM} = (1;2;3)\) làm vecto pháp tuyến có phương trình:
\(1(x - 1) + 2(y - 2) + 3(z - 3) = 0 \Leftrightarrow x + 2y + 3z - 14 = 0\).
Vậy S = 2a + 3b – 4c = 2.1 + 3.2 – 4.3 = -4.
Cho \(f(x) = \left\{ \begin{array}{l}1\\2x - 1\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ge 1\\x < 1\end{array}\). Tính \(J = \int\limits_{ - 1}^2 {f(x)dx} \).
Áp dụng tính chất của tích phân: \(\int\limits_a^b {f(x)dx} = \int\limits_a^c {f(x)dx} + \int\limits_c^b {f(x)dx} \).
Áp dụng công thức nguyên hàm của hàm số lũy thừa: \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int\limits_{ - 1}^2 {f(x)dx} = \int\limits_{ - 1}^1 {f(x)dx} + \int\limits_1^2 {f(x)dx} = \int\limits_{ - 1}^1 {(2x - 1)dx} + \int\limits_1^2 {1dx} \)
\(\left( {{x^2} - x} \right)\left| {\begin{array}{*{20}{c}}{^1}\\{_{ - 1}}\end{array}} \right. + x\left| {\begin{array}{*{20}{c}}{^2}\\{_1}\end{array}} \right. = \left( {{1^2} - 1} \right) - \left( {{{( - 1)}^2} - ( - 1)} \right) + 2 - 1 = 0 - 2 + 2 - 1 = - 1\).
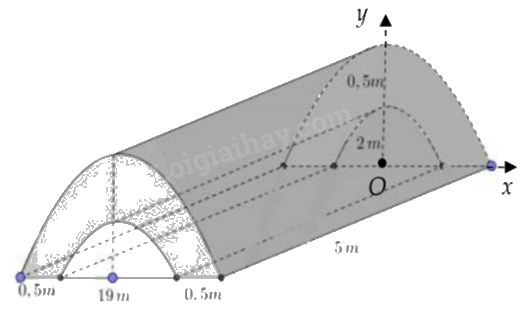
Trong chương trình nông thôn mới, tại một xã Y có xây một đoạn đường hầm bằng bê tông như hình vẽ. Tính thể tích \(({m^3})\) khối bê tông để đổ đủ đoạn đường hầm, biết đường cong trong hình vẽ là các đường parabol.
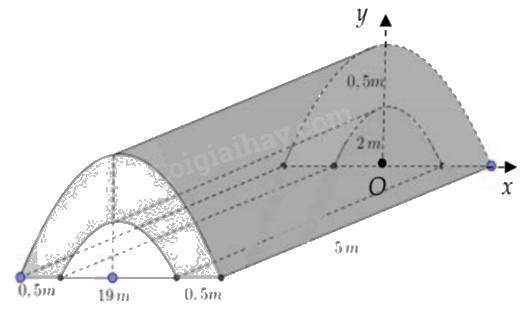
Ứng dụng tích phân, tính diện tích mặt cắt khối bê tông.
Áp dụng công thức tính thể tích: V = Sh.
Gọi parabol giới hạn mặt cắt của khối bê tông lần lượt là (P) và (Q). Giả sử (P) là parabol nằm phía trên.
(P) đi qua điểm có tọa độ (10;0) và tọa độ đỉnh là (0;2,5) nên ta có hệ:
\(\left\{ \begin{array}{l}0 = a{.10^2} + b.10 + c\\\frac{5}{2} = a{.0^2} + b.0 + c\\ - \frac{b}{{2a}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = \frac{5}{2}\\b = 0\\100a + 10b = - 2,5\end{array} \right. \Rightarrow (P):y = - \frac{1}{{40}}{x^2} + \frac{5}{2} = 0\).
(Q) đi qua điểm có tọa độ (9,5;0) và tọa độ đỉnh là (0;2) nên ta có hệ:
\(\left\{ \begin{array}{l}0 = a.{\left( {\frac{{19}}{2}} \right)^2} + b.\frac{{19}}{2} + c\\2 = a{.0^2} + b.0 + c\\ - \frac{b}{{2a}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 2\\b = 0\\\frac{{361}}{4}a + \frac{{19}}{2}b = - 2\end{array} \right. \Rightarrow (Q):y = - \frac{8}{{361}}{x^2} + 2 = 0\).
Diện tích hình phẳng giới hạn bởi (P) và trục hoành là:
\({S_P} = \int\limits_{ - 10}^{10} {\left( { - \frac{1}{{40}}{x^2} + \frac{5}{2}} \right)dx} = \frac{{100}}{3}\).
Diện tích hình phẳng giới hạn bởi (Q) và trục hoành là:
\({S_Q} = \int\limits_{ - 9,5}^{9,5} {\left( { - \frac{8}{{361}}{x^2} + 2} \right)dx} = \frac{{76}}{3}\).
Diện tích mặt cắt khối bê tông là:
\(S = {S_P} - {S_Q} = \frac{{100}}{3} - \frac{{76}}{3} = 8\) \(({m^2})\).
Thể tích khối bê tông là:
\(V = Sh = 8.5 = 40\) \(({m^3})\).
Trong không gian Oxyz, cho ba điểm A(1;1;1), B(−1;2;0), C(3;−1;2) và M là điểm thuộc mặt phẳng \((\alpha )\): 2x − y + 2z + 7 = 0. Tính giá trị nhỏ nhất của \(P = \left| {3\overrightarrow {MA} + 5\overrightarrow {MB} - 7\overrightarrow {MC} } \right|\).
Gọi I(a;b;c) là điểm thỏa mãn \(3\overrightarrow {IA} + 5\overrightarrow {IB} - 7\overrightarrow {IC} = \overrightarrow 0 \).
Biến đổi biểu thức P theo điểm I.
Gọi điểm I(a;b;c) là điểm thỏa mãn \(3\overrightarrow {IA} + 5\overrightarrow {IB} - 7\overrightarrow {IC} = \overrightarrow 0 \).
Khi đó \(\left\{ \begin{array}{l}3(1 - a) + 5( - 1 - a) - 7(3 - a) = 0\\3(1 - b) + 5(2 - b) - 7( - 1 - b) = 0\\3(1 - c) + 5(0 - c) - 7(2 - c) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 23\\b = 20\\c = - 11\end{array} \right. \Rightarrow I( - 23;20; - 11)\).
Ta có \(P = \left| {3\overrightarrow {MA} + 5\overrightarrow {MB} - 7\overrightarrow {MC} } \right|\)
\( = \left| {3\overrightarrow {MI} + \overrightarrow {3IA} + 5\overrightarrow {MI} + 5\overrightarrow {BI} - 7\overrightarrow {MI} - 7\overrightarrow {IC} } \right|\)
\( = \left| {\overrightarrow {MI} + 3\overrightarrow {IA} + 5\overrightarrow {IB} - 7\overrightarrow {IC} } \right| = \left| {\overrightarrow {MI} } \right| = MI\).
P đạt giá trị nhỏ nhất khi MI nhỏ nhất. Mà M thuộc mặt phẳng \((\alpha )\) nên MI nhỏ nhất khi và chỉ khi M là hình chiếu vuông góc của I lên mặt phẳng \((\alpha )\), hay MI là khoảng cách từ I đến mặt phẳng \((\alpha )\).
Ta có \(d\left( {I;(\alpha )} \right) = \frac{{\left| {2.( - 23) - 1.20 + 2.( - 11) + 7} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = 27\).
Vậy giá trị nhỏ nhất của P là 27.
Đề thi giữa kì 2 Toán 12 Cánh diều - Đề số 2 đóng vai trò quan trọng trong việc đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kỳ. Đề thi này không chỉ kiểm tra khả năng tính toán mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế.
Đề thi thường bao gồm hai phần chính: trắc nghiệm và tự luận. Phần trắc nghiệm thường chiếm khoảng 40-50% tổng số điểm, tập trung vào các kiến thức cơ bản và các công thức quan trọng. Phần tự luận chiếm khoảng 50-60% tổng số điểm, yêu cầu học sinh trình bày chi tiết các bước giải và giải thích rõ ràng lý do tại sao lại chọn phương pháp giải đó.
Nội dung đề thi giữa kì 2 Toán 12 Cánh diều - Đề số 2 thường bao gồm các chủ đề sau:
Để đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 12 Cánh diều - Đề số 2, học sinh cần:
Câu 1: (Trắc nghiệm) Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm của hàm số tại x = 1.
A. 0
B. -1
C. 1
D. 2
Giải: y' = 3x2 - 6x. Thay x = 1 vào, ta được y'(1) = 3(1)2 - 6(1) = -3. Vậy đáp án là B.
Để chuẩn bị tốt nhất cho kỳ thi giữa kì 2 Toán 12 Cánh diều - Đề số 2, học sinh có thể tham khảo các tài liệu sau:
Hãy dành thời gian ôn tập kiến thức một cách kỹ lưỡng và luyện tập giải nhiều bài tập khác nhau. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 12 Cánh diều - Đề số 2!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Tích phân | Cao |
| Số phức | Trung bình |
| Hình học không gian | Cao |
| Tổng kết | Cần nắm vững kiến thức và luyện tập thường xuyên |