Chào mừng các em học sinh lớp 9 đến với đề thi giữa kì 2 môn Toán chương trình Cánh diều - Đề số 3.
Đề thi này được thiết kế bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho bảng thống kê sản lượng muối (đơn vị: tấn) của một xã của tỉnh Nam Định 3 tháng đầu năm 2020 và 2021.

Tính tỉ số phần trăm sản lượng muối tháng 2 năm 2020 với cùng kì năm 2021 (làm tròn đến hàng phần mười).
142,7%
54,3%.
76,9%.
130,1%.
Các số liệu thống kê kích thước (đơn vị: cm) của 24 con mực được nuôi cấy thử nghiệm của trung tâm A được ghi lại như sau:
12, 11, 11, 12, 8, 11, 12, 7, 7, 10, 11, 12, 9, 12, 5, 9, 9, 12, 8, 9, 7, 10, 12, 10.
Trong 24 số liệu trên có bao nhiêu giá trị khác nhau?
Có 5 giá trị khác nhau.
Có 6 giá trị khác nhau.
Có 7 giá trị khác nhau.
Có 8 giá trị khác nhau.
Một doanh nghiệp sản xuất xe ô tô khảo sát lượng xăng tiêu thụ trên 100 km của một số loại xe ô tô trên thị trường. Kết quả khảo sát 100 chiếc xe được biểu diễn trong hình dưới đây:
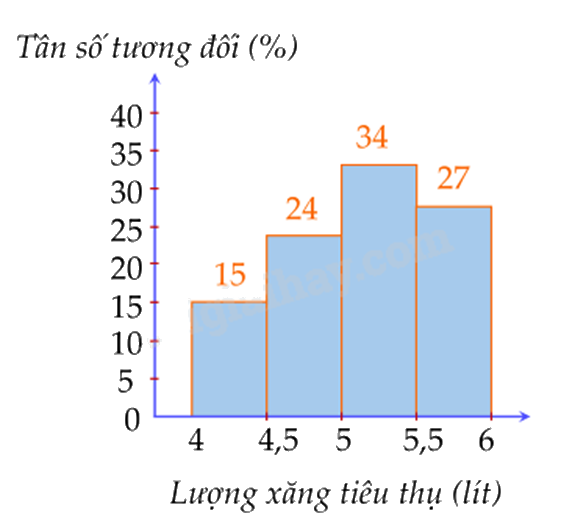
Tần số tương đối của số lượng xe ô tô tiêu thụ dưới 5 lít xăng cho 100km là:
76%.
39%.
61%.
24%.
Cho tập hợp A là tập các số tự nhiên có hai chữ số khác nhau được lập ra từ các chữ số 0; 5; 7. Chọn ngẫu nhiên một phần tử của tập hợp A. Số phần tử của không gian mẫu là:
1.
2.
4.
8.
Cho tứ giác \(BEGH\) nội tiếp đường tròn tâm \((I)\), biết \(\widehat B = 116^\circ \), \(\widehat E = 92^\circ \), tính số đo \(\widehat G\).
\(\widehat G = 78^\circ \).
\(\widehat G = 64^\circ \).
\(\widehat G = 88^\circ \).
\(\widehat G = 84^\circ \).
Cho tam giác ABC nội tiếp đường tròn (O). Biết \(\widehat {BOC} = 120^\circ \) và \(\widehat {OCA} = 40^\circ \). Tính số đo góc BAO.
\(40^\circ \).
\(60^\circ \).
\(20^\circ \).
\(80^\circ \).
Lớp 9A định tổ chức một trò chơi dân gian khi đi dã ngoại. Lớp trưởng đã yêu cầu mỗi bạn đề xuất một trò chơi bằng cách ghi vào phiếu. Sau khi thu phiếu và tổng hợp kết quả, lớp trưởng thu được biểu đồ cột như sau:
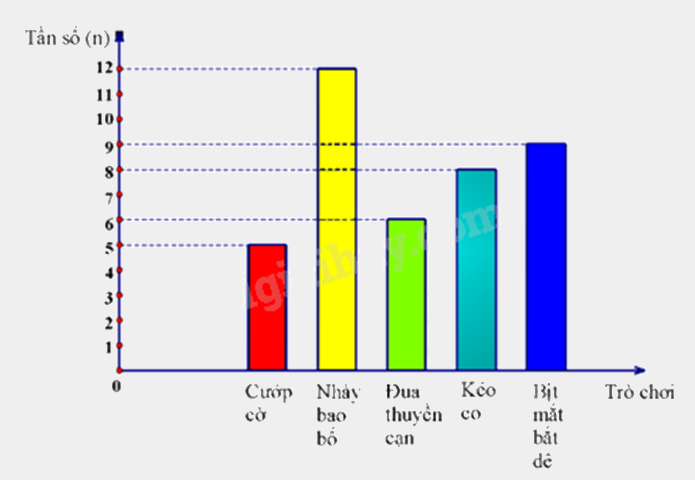
a) Số học sinh lớp 9A là 40 học sinh.
b) Bảng tần số của biểu đồ tần số trên là:

c) Tần số tương đối của trò Nhảy bao bố là 15%.
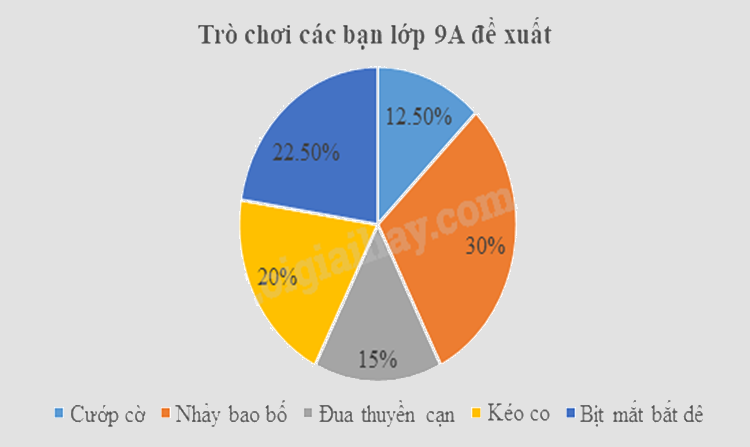
d) Biểu đồ hình quạt biểu diễn tần số tương đối của trò chơi các bạn lớp 9A đề xuất là:
Cho tứ giác ABCD có \(\widehat A = \widehat C = 90^\circ \) nội tiếp đường tròn tâm O.
a) \(\widehat {ABD} = \widehat {ACD}\).
b) Đường tròn \(\left( O \right)\) là đường tròn nội tiếp tam giác ABC.
c) Nếu \(\widehat {ABC} = 80^\circ \) thì \(\widehat {ADC} = 100^\circ \).
d) Bán kính đường tròn ngoại tiếp tam giác ACD bằng \(\frac{{BD}}{2}\).
Hà có 4 hộp kẹo dẻo với 4 vị khác nhau là: vị dâu, vị cam, vị nho, vị việt quất. Hà lấy ngẫu nhiên một hộp kẹo trong 4 hộp kẹo này cho em trai. Em trai Hà ghi lại vị của hộp kẹo nhận được rồi lại trả hộp kẹo lại cho chị và bảo chi lại lấy ngẫu nhiên một hộp kẹo trong 4 hộp kẹo đó đưa cho mình và ghi lại vị của hộp kẹo nhận được trong lần thứ hai. Quan sát vị của hộp kẹo qua hai lần lấy. Không gian mẫu của phép thử này có số phần tử là…
Đáp án:
Biểu đồ tranh thể hiện số ti vi (TV) bán được qua các năm của 1 siêu thị điện máy như sau:

Tần số tương đối của số ti vi bán được trong năm 2022 là: …. (không điền dấu %)
Đáp án:
Cho biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng về chiều cao của học sinh nữ lớp 9C.
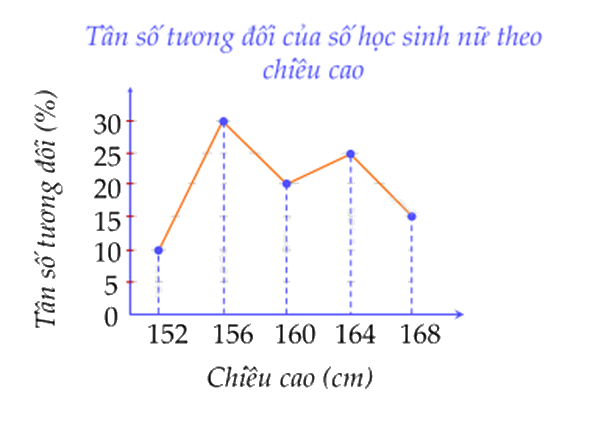
Lớp 9C cần chọn ra những bạn nữ cao từ 160cm trở lên để tham gia đội tuyển thi đấu bóng chuyền. Nếu lớp 9C có 20 bạn nữ thì số bạn được tham gia đội tuyển bằng bao nhiêu.
Đáp án:
Cho tứ giác ABCD nội tiếp đường tròn (O;R) có AB = BC = R. Số đo \(\widehat {ABC}\) bằng bao nhiêu độ? (không cần ghi độ)
Đáp án:
Khối lượng (đơn vị: gam) của 30 củ khoai tây thu hoạch được ở gia đình bác Ngọc là:

Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm theo năm nhóm sau:
\(\left[ {70;80} \right),\,\left[ {80;90} \right),\,\left[ {90;100} \right),\,\left[ {100;110} \right),\,\left[ {110;120} \right).\)
Một bó hoa gồm \(3\) bông hoa màu đỏ và \(1\) bông hoa màu vàng. Bạn Trúc Linh chọn ngẫu nhiên \(2\) bông hoa từ bó hoa đó.
a) Liệt kê các cách chọn mà bạn Trúc Linh thực hiện.
b) Tính xác suất của mỗi biến cố sau:
\(R\): “Trong \(2\) bông hoa được chọn, có đúng \(1\) bông hoa màu đỏ”;
\(T\): “Trong \(2\) bông hoa được chọn, có ít nhất \(1\) bông hoa màu đỏ”.
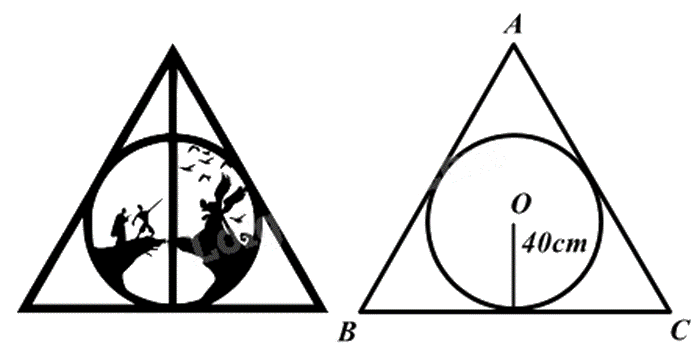
Một bức ảnh hình tròn có bán kính 40 cm, người ta làm một khung gỗ hình tam giác đều bao bên ngoài bức ảnh sao cho bức ảnh hình tròn tiếp xúc với các cạnh của khung gỗ. Tính độ dài cạnh khung gỗ (làm tròn đến số thập phân thứ nhất).
Cho bảng thống kê sản lượng muối (đơn vị: tấn) của một xã của tỉnh Nam Định 3 tháng đầu năm 2020 và 2021.

Tính tỉ số phần trăm sản lượng muối tháng 2 năm 2020 với cùng kì năm 2021 (làm tròn đến hàng phần mười).
142,7%
54,3%.
76,9%.
130,1%.
Đáp án : D
Để tính tỉ số phần trăm sản lượng muối tháng 2 năm 2020 với cùng kì năm 2021, ta lấy (sản lượng muối tháng 2 năm 2020 . 100) : sản lượng muối tháng 2 năm 2021 (%).
Tỉ số phần trăm sản lượng muối tháng 2 năm 2020 với cùng kì năm 2021 là:
\(\frac{{588.100}}{{452}}\% \approx 130,1\% \).
Đáp án D
Các số liệu thống kê kích thước (đơn vị: cm) của 24 con mực được nuôi cấy thử nghiệm của trung tâm A được ghi lại như sau:
12, 11, 11, 12, 8, 11, 12, 7, 7, 10, 11, 12, 9, 12, 5, 9, 9, 12, 8, 9, 7, 10, 12, 10.
Trong 24 số liệu trên có bao nhiêu giá trị khác nhau?
Có 5 giá trị khác nhau.
Có 6 giá trị khác nhau.
Có 7 giá trị khác nhau.
Có 8 giá trị khác nhau.
Đáp án : C
Lập bảng tần số, xác định các giá trị khác nhau và tần số xuất hiện của các giá trị.
Ta có bảng tần số:

Có 7 giá trị khác nhau.
Đáp án C
Một doanh nghiệp sản xuất xe ô tô khảo sát lượng xăng tiêu thụ trên 100 km của một số loại xe ô tô trên thị trường. Kết quả khảo sát 100 chiếc xe được biểu diễn trong hình dưới đây:
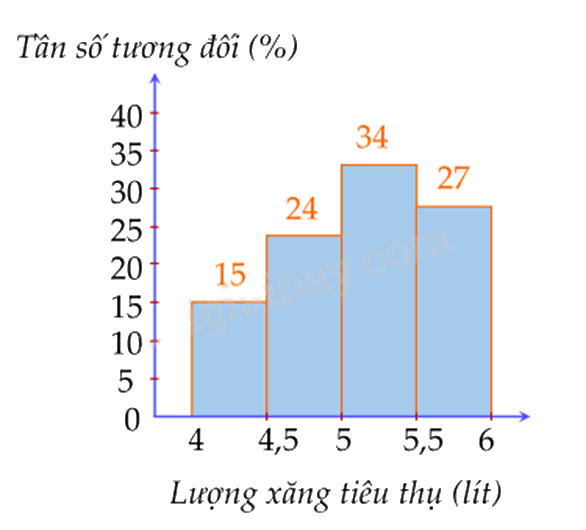
Tần số tương đối của số lượng xe ô tô tiêu thụ dưới 5 lít xăng cho 100km là:
76%.
39%.
61%.
24%.
Đáp án : B
Tính tổng tần số tương đối của lượng xe ô tô tiêu thụ dưới 5 lít xăng cho 100km.
Tần số tương đối của số lượng xe ô tô tiêu thụ dưới 5 lít xăng cho 100km là:
15% + 24% = 39%.
Đáp án B
Cho tập hợp A là tập các số tự nhiên có hai chữ số khác nhau được lập ra từ các chữ số 0; 5; 7. Chọn ngẫu nhiên một phần tử của tập hợp A. Số phần tử của không gian mẫu là:
1.
2.
4.
8.
Đáp án : C
Liệt kế các số có thể tạo thành.
Không gian mẫu của phép thử là:
\(\Omega = \left\{ {50;57;70;75} \right\}\)
Vậy không gian mẫu có \(4\) phần tử.
Đáp án C
Cho tứ giác \(BEGH\) nội tiếp đường tròn tâm \((I)\), biết \(\widehat B = 116^\circ \), \(\widehat E = 92^\circ \), tính số đo \(\widehat G\).
\(\widehat G = 78^\circ \).
\(\widehat G = 64^\circ \).
\(\widehat G = 88^\circ \).
\(\widehat G = 84^\circ \).
Đáp án : B
Sử dụng tổng hai góc đối của tứ giác nội tiếp bằng \(180^\circ \).
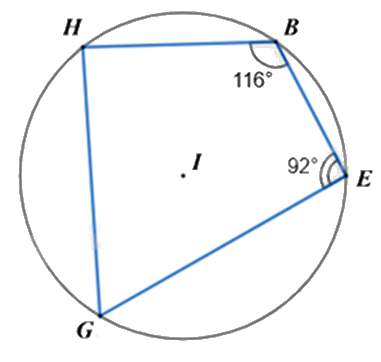
Tứ giác BEGH nội tiếp đường tròn (I) nên ta có:
\(\widehat G + \widehat B = 180^\circ \)
Suy ra \(\widehat G = 180^\circ - \widehat B = 180^\circ - 116^\circ = 64^\circ \)
Đáp án B
Cho tam giác ABC nội tiếp đường tròn (O). Biết \(\widehat {BOC} = 120^\circ \) và \(\widehat {OCA} = 40^\circ \). Tính số đo góc BAO.
\(40^\circ \).
\(60^\circ \).
\(20^\circ \).
\(80^\circ \).
Đáp án : C
Từ tam giác cân OAC, tính góc OAC.
Tính góc nội tiếp BAC = \(\frac{1}{2}\) góc ở tâm chắn cung đó.
Ta tính được số đo góc BAO.

Vì tam giác AOC cân nên \(\widehat {OAC} = \widehat {OCA} = 40^\circ \)
Vì tam giác ABC nội tiếp đường tròn (O) nên \(\widehat {BAC}\) là góc nội tiếp chắn cung BC. Mà \(\widehat {BOC}\) là góc ở tâm chắn cung BC nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}.120^\circ = 60^\circ \).
Mà \(\widehat {BAO} + \widehat {OAC} = \widehat {BAC}\) nên ta có:
\(\widehat {BAO} = \widehat {BAC} - \widehat {OAC} = 60^\circ - 40^\circ = 20^\circ \).
Đáp án C
Lớp 9A định tổ chức một trò chơi dân gian khi đi dã ngoại. Lớp trưởng đã yêu cầu mỗi bạn đề xuất một trò chơi bằng cách ghi vào phiếu. Sau khi thu phiếu và tổng hợp kết quả, lớp trưởng thu được biểu đồ cột như sau:
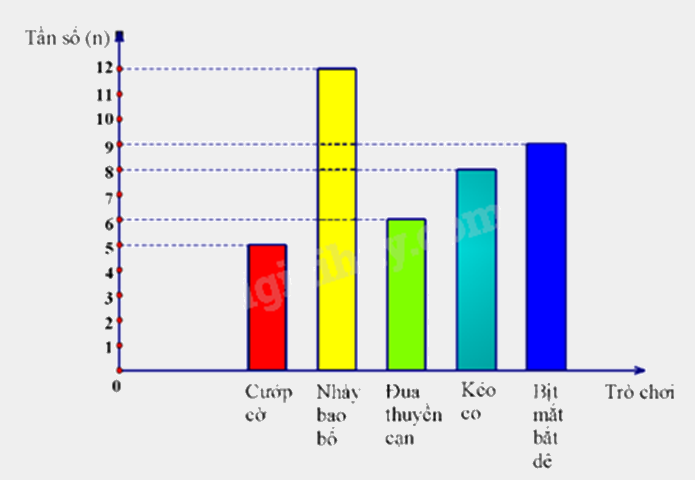
a) Số học sinh lớp 9A là 40 học sinh.
b) Bảng tần số của biểu đồ tần số trên là:

c) Tần số tương đối của trò Nhảy bao bố là 15%.
d) Biểu đồ hình quạt biểu diễn tần số tương đối của trò chơi các bạn lớp 9A đề xuất là:
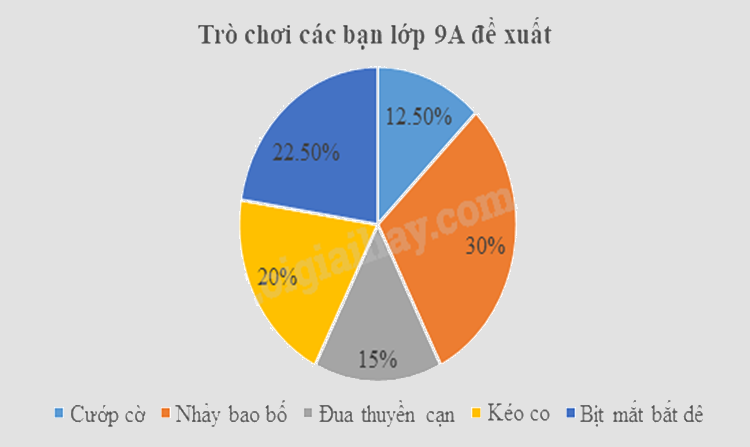
a) Số học sinh lớp 9A là 40 học sinh.
b) Bảng tần số của biểu đồ tần số trên là:

c) Tần số tương đối của trò Nhảy bao bố là 15%.
d) Biểu đồ hình quạt biểu diễn tần số tương đối của trò chơi các bạn lớp 9A đề xuất là:
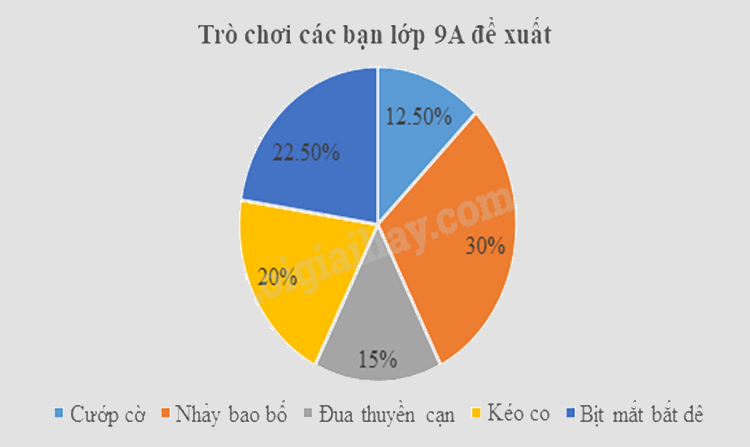
a) Tính tổng số học sinh cả lớp dựa vào tần số các giá trị.
b) Quan sát biểu đồ tần số để xác định tần số của các giá trị và lập bảng tần số.
c) Tần số tương đối của giá trị bằng tần số của giá trị với tổng tần số.
d) Tính tần số tương đối của các giá trị để vẽ biểu đồ tần số tương đối.
a) Đúng
Lớp 9A có số học sinh là:
5 + 12 + 6 + 8 + 9 = 40 (học sinh)
Vậy a) đúng.
b) Sai
Quan sát biểu đồ, ta lập được bảng tần số:

Vậy b) sai.
c) Sai
Tần số tương đối của trò Nhảy bao bố là: \(\frac{{12}}{{40}}.100\% = 30\% \).
Vậy c) sai.
d) Đúng
Tần số tương đối của trò chơi Cướp cờ; Nhảy bao bố; Đua thuyền cạn; Kéo co; Bịt mắt bắt dê lần lượt là:
\({f_1} = \frac{{5.100}}{{40}}\% = 12,5\% \); \({f_2} = \frac{{12.100}}{{40}} = 30\% \); \({f_3} = \frac{{6.100}}{{40}}\% = 15\% \); \({f_4} = \frac{{8.100}}{{40}}\% = 20\% \); \({f_5} = \frac{{9.100}}{{40}}\% = 22,5\% \).
Ta có bảng tần số tương đối là:

Vậy biểu đồ hình quạt tròn biểu diễn tần số tương đối của trò chơi các bạn lớp 9A đề xuất là:
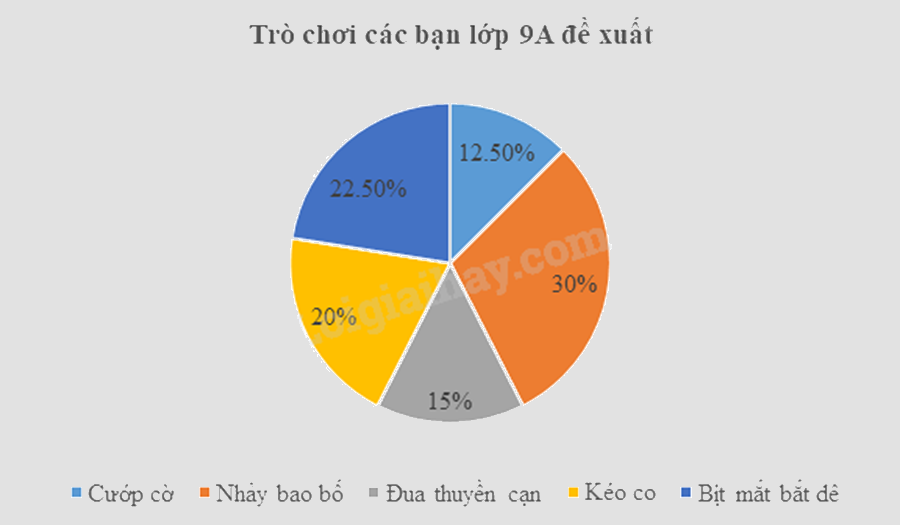
Đáp án: ĐSSĐ
Cho tứ giác ABCD có \(\widehat A = \widehat C = 90^\circ \) nội tiếp đường tròn tâm O.
a) \(\widehat {ABD} = \widehat {ACD}\).
b) Đường tròn \(\left( O \right)\) là đường tròn nội tiếp tam giác ABC.
c) Nếu \(\widehat {ABC} = 80^\circ \) thì \(\widehat {ADC} = 100^\circ \).
d) Bán kính đường tròn ngoại tiếp tam giác ACD bằng \(\frac{{BD}}{2}\).
a) \(\widehat {ABD} = \widehat {ACD}\).
b) Đường tròn \(\left( O \right)\) là đường tròn nội tiếp tam giác ABC.
c) Nếu \(\widehat {ABC} = 80^\circ \) thì \(\widehat {ADC} = 100^\circ \).
d) Bán kính đường tròn ngoại tiếp tam giác ACD bằng \(\frac{{BD}}{2}\).
a) Sử dụng hai góc nội tiếp chắn cùng một cung thì bằng nhau.
b) Đường tròn đi qua ba đỉnh của một tam giác là đường tròn ngoại tiếp tam giác đó.
c) Dựa vào tổng hai góc đối của tứ giác nội tiếp bằng \(180^\circ \).
d) Bán kính đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền.
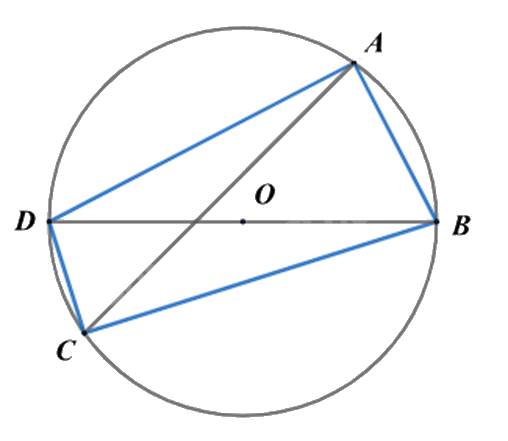
a) Đúng
Vì \(\widehat {ABD}\) và \(\widehat {ACD}\) là hai góc nội tiếp cùng chắn cung AD nên \(\widehat {ABD} = \widehat {ACD}\).
b) Sai
Đường tròn \(\left( O \right)\) đi qua ba đỉnh của tam giác ABC nên là đường tròn ngoại tiếp tam giác ABC.
c) Đúng
Vì tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat {ABC} + \widehat {ADC} = 180^\circ \).
Suy ra \(\widehat {ADC} = 180^\circ - \widehat {ABC} = 180^\circ - 80^\circ = 100^\circ \).
d) Đúng
Xét tam giác ABD nội tiếp đường tròn (O) (vì ABCD là tứ giác nội tiếp) có \(\widehat A = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên tam giác ABD vuông tại A.
Do đó bán kính đường tròn ngoại tiếp tam giác ABD bằng \(\frac{{BD}}{2}\), hay bán kính đường tròn (O) bằng \(\frac{{BD}}{2}\).
Đường tròn \(\left( O \right)\) đi qua ba đỉnh của tam giác ACD nên là đường tròn ngoại tiếp tam giác ACD.
Vậy bán kính đường tròn ngoại tiếp tam giác ACD bằng \(\frac{{BD}}{2}\).
Đáp án: ĐSĐĐ
Hà có 4 hộp kẹo dẻo với 4 vị khác nhau là: vị dâu, vị cam, vị nho, vị việt quất. Hà lấy ngẫu nhiên một hộp kẹo trong 4 hộp kẹo này cho em trai. Em trai Hà ghi lại vị của hộp kẹo nhận được rồi lại trả hộp kẹo lại cho chị và bảo chi lại lấy ngẫu nhiên một hộp kẹo trong 4 hộp kẹo đó đưa cho mình và ghi lại vị của hộp kẹo nhận được trong lần thứ hai. Quan sát vị của hộp kẹo qua hai lần lấy. Không gian mẫu của phép thử này có số phần tử là…
Đáp án:
Đáp án:
Liệt kê các kết quả có thể của phép thử.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng:
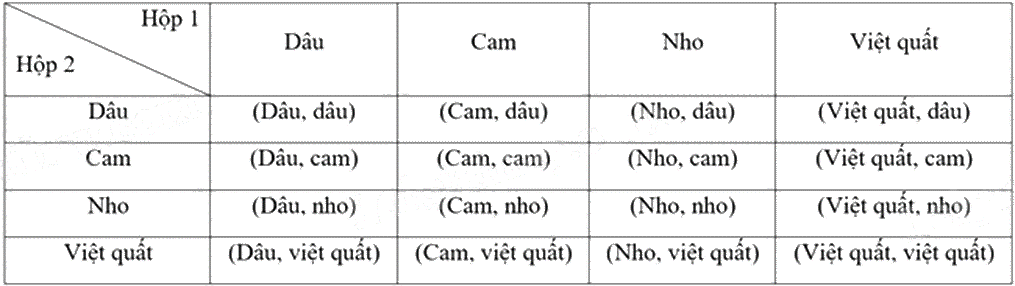
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp gồm 4.4 16 = (phần tử)
Đáp án: 16
Biểu đồ tranh thể hiện số ti vi (TV) bán được qua các năm của 1 siêu thị điện máy như sau:

Tần số tương đối của số ti vi bán được trong năm 2022 là: …. (không điền dấu %)
Đáp án:
Đáp án:
Từ biểu đồ tranh, tính tổng số ti vi bán được từ năm 2018 đến năm 2022 và số ti vi bán được trong năm 2022.
Tần số tương đối của số ti vi bán được trong năm 2022 bằng tỉ số phần trăm giữa số ti vi bán được năm 2022 với tổng số ti vi bán được.
Từ biểu đồ tranh, ta thấy số ti vi bán được của các năm 2018; 2019; 2020; 2021; 2022 lần lượt là: 500; 600; 250; 300; 350.
Tổng số ti vi bán được từ năm 2018 đến 2022 là: 500 + 600 + 250 + 300 + 350 = 2000 (chiếc)
Tần số tương đối của số ti vi bán được trong năm 2022 là: \(\frac{{350}}{{2000}}.100\% = 17,5\% \)
Đáp án: 17,5
Cho biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng về chiều cao của học sinh nữ lớp 9C.
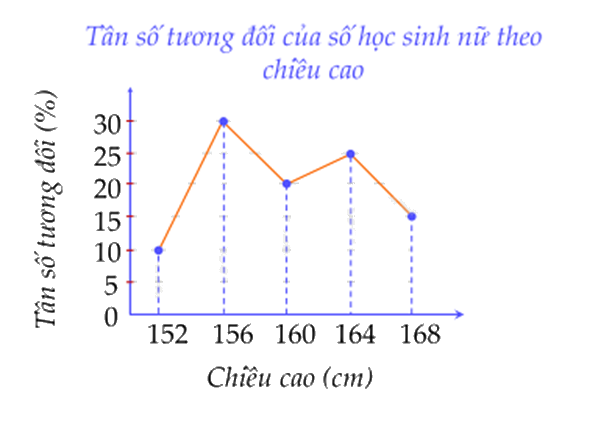
Lớp 9C cần chọn ra những bạn nữ cao từ 160cm trở lên để tham gia đội tuyển thi đấu bóng chuyền. Nếu lớp 9C có 20 bạn nữ thì số bạn được tham gia đội tuyển bằng bao nhiêu.
Đáp án:
Đáp án:
Xác định tần số tương đối của các bạn nữ cao từ 160cm trở lên.
Tính số bạn nữ được tham gia bằng tổng số bạn nữ nhân với tần số tương đối các bạn nữ cao từ 160cm trở lên.
Tần số tương đối của số bạn nữ có chiều cao từ 160cm là:
25 + 15 = 40(%)
Số bạn được tham gia đội tuyển là:
20.40% = 8 (bạn).
Vậy có 8 bạn được tham gia đội tuyển.
Đáp án: 8
Cho tứ giác ABCD nội tiếp đường tròn (O;R) có AB = BC = R. Số đo \(\widehat {ABC}\) bằng bao nhiêu độ? (không cần ghi độ)
Đáp án:
Đáp án:
Chứng minh tam giác BCO, BAO đều nên tính được số đo góc BOC, BOA.
Ta tính được số đo góc AOC, từ đó suy ra số đo góc ADC (liên hệ giữa góc ở tâm và góc nội tiếp cùng một cung).
Kết hợp với tính chất hai góc đối của tứ giác nội tiếp, ta có số đo góc ABC.
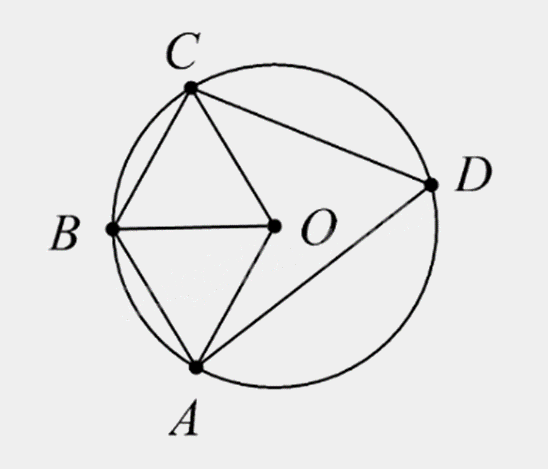
Xét tam giác BCO có: BC = CO = BO = R nên tam giác BCO đều, do đó \(\widehat {BOC} = 60^\circ \).
Xét tam giác BAO có: BA = AO = BO = R nên tam giác BAO đều, do đó \(\widehat {BAC} = 60^\circ \).
\(\widehat {AOC} = \widehat {AOB} + \widehat {BOC} = 60^\circ + 60^\circ = 120^\circ \)
Mà \(\widehat {AOC}\) là góc ở tâm chắn cung AC, \(\widehat {ADC}\) là góc nội tiếp chắn cung AC nên \(\widehat {ADC} = \frac{1}{2}\widehat {AOC} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì tứ giác ABCD nội tiếp đường tròn nên \(\widehat {ABC} + \widehat {ADC} = 180^\circ \)
Suy ra \(\widehat {ABC} = 180^\circ - \widehat {ADC} = 180^\circ - 60^\circ = 120^\circ \)
Đáp án: 120
Khối lượng (đơn vị: gam) của 30 củ khoai tây thu hoạch được ở gia đình bác Ngọc là:

Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm theo năm nhóm sau:
\(\left[ {70;80} \right),\,\left[ {80;90} \right),\,\left[ {90;100} \right),\,\left[ {100;110} \right),\,\left[ {110;120} \right).\)
Xác định các tần số của mỗi nhóm để lập bảng.
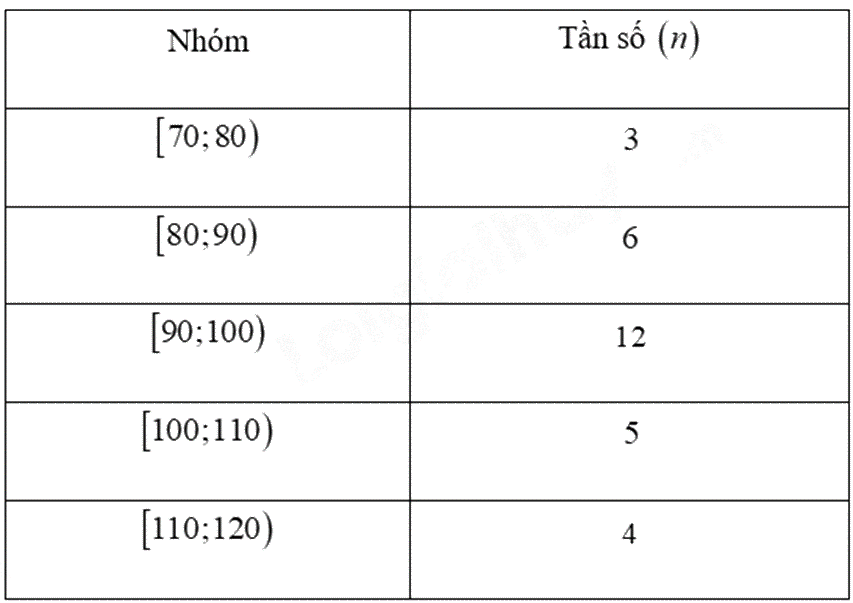
Các nhóm \(\left[ {70;80} \right),\,\,\left[ {80;90} \right),\,\,\left[ {90;100} \right),\,\,\left[ {100;110} \right),\,\,\left[ {110;120} \right)\) có tần số lần lượt là: \(n{}_1\, = \,3\) , \(n{}_2\, = \,6\), \({n_3}\, = \,12\), \({n_4}\, = \,5\), \(n{}_5\, = \,4\).
Ta được bảng tần số ghép nhóm của mẫu số liệu ghép nhóm sau:
Một bó hoa gồm \(3\) bông hoa màu đỏ và \(1\) bông hoa màu vàng. Bạn Trúc Linh chọn ngẫu nhiên \(2\) bông hoa từ bó hoa đó.
a) Liệt kê các cách chọn mà bạn Trúc Linh thực hiện.
b) Tính xác suất của mỗi biến cố sau:
\(R\): “Trong \(2\) bông hoa được chọn, có đúng \(1\) bông hoa màu đỏ”;
\(T\): “Trong \(2\) bông hoa được chọn, có ít nhất \(1\) bông hoa màu đỏ”.
a) Xác định các kết quả có thể.
b) Xác định các kết quả thuận lợi cho biến cố.
Tính xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
a) Các cách chọn có thể có là: đỏ \(1\) và vàng, đỏ \(2\) và vàng, đỏ \(3\) và vàng, đỏ \(1\) và đỏ \(2\), đỏ \(2\) và đỏ \(3\), đỏ \(1\) và đỏ \(3\).
b) Có \(3\) kết quả thuận lợi cho biến cố R là: đỏ \(1\) và vàng, đỏ \(2\) và vàng, đỏ \(3\) và vàng.
Vậy \(P\left( R \right) = \frac{3}{6} = \frac{1}{2}\).
Có tất cả \(4\) kết quả thuận lợi cho biến cố \(T\).
Vậy \(P\left( T \right) = \frac{4}{6} = \frac{2}{3}\) .
Một bức ảnh hình tròn có bán kính 40 cm, người ta làm một khung gỗ hình tam giác đều bao bên ngoài bức ảnh sao cho bức ảnh hình tròn tiếp xúc với các cạnh của khung gỗ. Tính độ dài cạnh khung gỗ (làm tròn đến số thập phân thứ nhất).
Tính độ dài cạnh khung gỗ chính là tính cạnh của tam giác đều ngoại tiếp đường tròn.
Từ công thức tính bán kính đường tròn nội tiếp tam giác đều cạnh a bằng \(\frac{{\sqrt 3 }}{3}a\), ta tính cạnh a theo bán kính đường tròn nội tiếp.
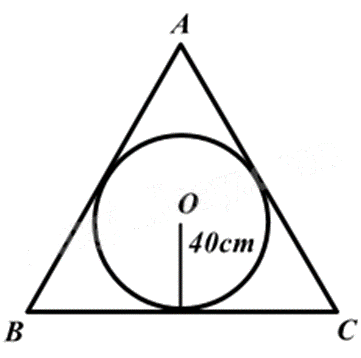
Vì khung ảnh hình tròn tiếp xúc với các cạnh của tam giác đều nên ta có đường tròn nội tiếp tam giác đều.
Vì bán kính đường tròn nội tiếp tam giác đều là \(R = \frac{{a\sqrt 3 }}{6}\) với a là độ dài cạnh tam giác đều nên ta có:
\(\begin{array}{l}40 = \frac{{a\sqrt 3 }}{6}\\a\sqrt 3 = 240\\a = \frac{{240}}{{\sqrt 3 }} \approx 138,6\left( {cm} \right)\end{array}\)
Vậy độ dài cạnh khung gỗ khoảng 138,6cm.
Đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 3 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau nửa học kỳ. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, phương trình bậc hai một ẩn, và các ứng dụng thực tế của đại số.
Thông thường, đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 3 có cấu trúc gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 3:
Ví dụ 1: Giải phương trình bậc hai 2x2 - 5x + 2 = 0
Giải:
Phương trình có dạng ax2 + bx + c = 0 với a = 2, b = -5, c = 2.
Tính delta: Δ = b2 - 4ac = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + 3) / (2 * 2) = 2
x2 = (-b - √Δ) / 2a = (5 - 3) / (2 * 2) = 0.5
Vậy phương trình có hai nghiệm là x1 = 2 và x2 = 0.5
Để chuẩn bị tốt nhất cho đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 3, học sinh nên:
Đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 3 là một cơ hội để học sinh đánh giá năng lực và kiến thức của mình. Việc ôn tập kỹ lưỡng và làm bài thi một cách cẩn thận sẽ giúp các em đạt được kết quả tốt nhất. Chúc các em thành công!