Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 5, một công cụ ôn luyện tuyệt vời dành cho học sinh lớp 9. Đề thi được biên soạn theo chương trình Cánh diều, bám sát kiến thức trọng tâm và cấu trúc đề thi chính thức.
Với đề thi này, các em học sinh có thể tự đánh giá năng lực, rèn luyện kỹ năng giải đề và làm quen với áp lực phòng thi. Đồng thời, đáp án chi tiết đi kèm sẽ giúp các em hiểu rõ phương pháp giải và khắc phục những sai lầm.
Cho bảng thống kê chiều cao của học sinh lớp 6A:

Lớp 6A có bao nhiêu bạn có chiều cao trên 1m50?
23 bạn.
13 bạn.
22 bạn.
9 bạn.
Thống kê số lần truy cập Internet của 30 người trong một tuần là:

Có bao nhiêu người có số lần truy cập thuộc nhóm [30; 40)?
8.
6.
5.
10.
Gieo một con xúc xắc cân đối và đồng chất 2 lần. Tính xác suất để tổng số chấm trong hai lần gieo nhỏ hơn 6.
\(\frac{2}{9}\).
\(\frac{{11}}{{36}}\).
\(\frac{1}{6}\).
\(\frac{5}{{18}}\).
Một cửa hàng đồ chơi trong tháng qua bán được 60 hộp lego thuộc nhiều thương hiệu đồ chơi khác nhau. Dưới đây là bảng thống kê của đại lí:

Lego và Hot Wheel.
Lego và Sembo Block.
Hot Wheel và Moyu Block.
Lego và Moyu Block.
Trong các đường tròn dưới đây, đường tròn nào là đường tròn ngoại tiếp tam giác ABC.
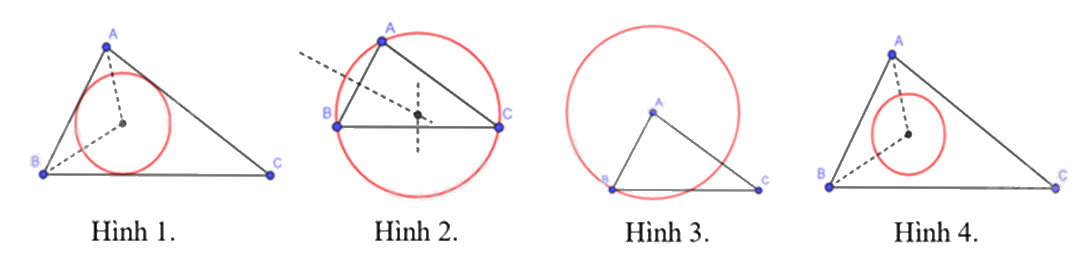
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho đường tròn \(\left( O \right)\). Biết \(MA;MB\) là các tiếp tuyến của \(\left( O \right)\) cắt nhau tại \(M\) và \(\widehat {AMB} = 58^\circ \) Khi đó số đo \(\widehat {ABO}\) bằng:
\(24^\circ \).
\(29^\circ \).
\(30^\circ \).
\(31^\circ \).
Điều tra về chiều cao của các bạn học sinh nam khối 9 của một trường trong hai năm 2023 và 2024 được kết quả minh họa bằng hai biểu đồ cột sau đây cho biết
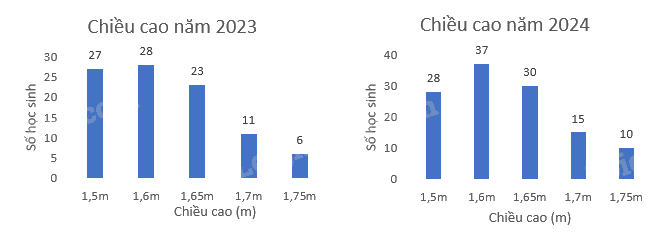
Lựa chọn đúng, sai
a) Tần số tương đối của 1,5m năm 2024 là 23,3%.
b) Tỉ lệ chiều cao 1,5m năm 2024 cao hơn năm 2023.
c) Tỉ lệ chiều cao 1,65m năm 2024 và năm 2023 bằng nhau.
d) Tỉ lệ chiều cao từ 1,65m trở lên năm 2024 cao hơn năm 2023 là 3,7%.
Cho \(\Delta ABC\) đều có cạnh \(4\,cm\) ngoại tiếp \(\left( {O;r} \right)\) và nội tiếp \(\left( {O;R} \right)\) khi đó:
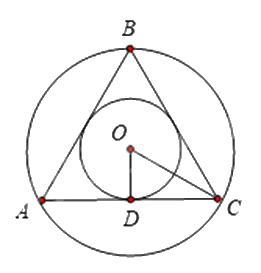
a) Khoảng cách từ tâm \(O\) đến \(AB\) bằng \(\sqrt 3 \).
b) Chu vi đường tròn nội tiếp \(\Delta ABC\) bằng \(\frac{{4\sqrt 3 }}{3}\pi \).
c) \(OA + OB + OC - OD = 10\sqrt 3 \).
d) Gọi \(x, y, z\) lần lượt là khoảng cách từ điểm \(O\) tới \(AB, BC, CA.\) Giá trị của biểu thức \(xy + \sqrt 3 z\) là \(\frac{{10}}{3}\).
Thống kê về phần trăm khối lượng các loại hoa quả bán được trong 1 tháng của một cửa hàng được ghi lại như sau: 25% khối lượng bán được là Cam; 32% khối lượng bán được là Xoài; 10% là Thanh long; còn lại là Ổi. Biết tổng khối lượng hoa quả bán được trong tháng đó là 200kg. Khi đó khối lượng Ổi đã bán là … kg.
Đáp án:
Thời gian đi từ nhà tới trường (đơn vị: phút) của các bạn học sinh lớp 9C được biểu diễn bởi biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng như sau:
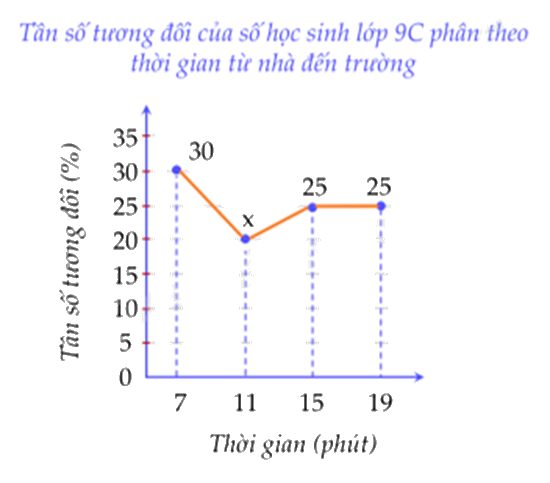
Biết lớp 9C có 40 học sinh. Số học sinh tương ứng với tần số tương đối x là:
Đáp án:
Có hai túi \(I\) và \(II\). Túi \(I\) chứa bốn tấm thẻ , đánh số \(1;2;3;4\). Túi \(II\)chứa năm tấm thẻ ghi số \(1;2;3;4;5\). Rút ngẫu nhiên một tấm thẻ từ mỗi túi \(I\) và \(II\). Xác suất để cả hai tấm thẻ rút ra đều ghi số chẵn là bao nhiêu? (viết dưới dạng số thập phân)
Đáp án:
Cho tam giác ABC nội tiếp nửa đường tròn (O;R). Biết \(\widehat {AOC} = 116^\circ \). Độ dài cạnh AC là \(2R.\sin ...^\circ \). Số còn thiếu là:
Đáp án:
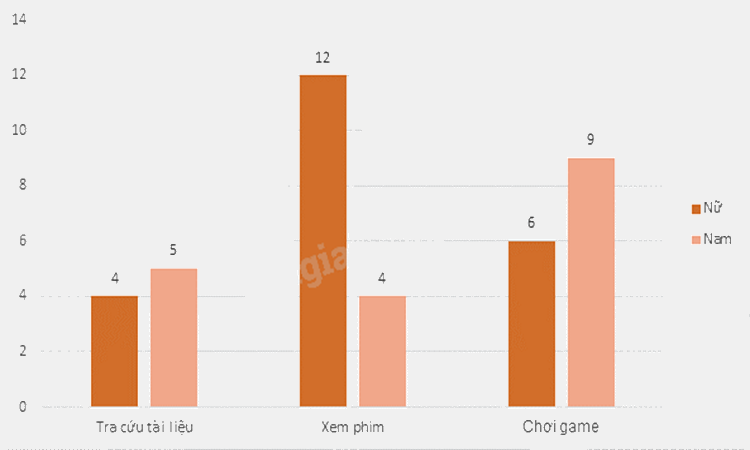
Khảo sát mục đích sử dụng Internet của học sinh lớp 9C (mỗi học sinh chỉ nêu một mục đích hay sử dụng nhất). Biểu đồ cột kép dưới đây biểu diễn số học sinh nam và số học sinh nữ của lớp 9C với 3 mục đích chính: tra cứu tài liệu, xem phim, chơi game.
a) Tính xác suất của biến cố A: “Học sinh được chọn là nam”.
b) Tính xác suất của biến cố B: “Học sinh được chọn là nữ và có mục đích là xem phim”.
c) Tính xác suất của biến cố C: “Học sinh được chọn là nam và có mục đích là chơi game hoặc tra cứu tài liệu”.
Cho đường tròn \(\left( {O;R} \right)\) đường kính\(AB\), gọi \(I\) là trung điểm của \(OA\), dây \(CD\) vuông góc với \(AB\) tại I. Lấy \(K\) tùy ý trên cung \(BC\) nhỏ, \(AK\) cắt \(CD\) tại \(H\).
a) Chứng minh tứ giác \(BIHK\) là tứ giác nội tiếp.
b) Chứng minh \(AH.AK\) có giá trị không phụ thuộc vị trí điểm \(K\).
Cho bảng thống kê chiều cao của học sinh lớp 6A:

Lớp 6A có bao nhiêu bạn có chiều cao trên 1m50?
23 bạn.
13 bạn.
22 bạn.
9 bạn.
Đáp án : C
Quan sát bảng thống kê, xác định số bạn có chiều cao trên 1m50.
Lớp 6A có số bạn có chiều cao trên 1m50 là:
13 + 8 + 1 = 22 (bạn)
Đáp án C
Thống kê số lần truy cập Internet của 30 người trong một tuần là:

Có bao nhiêu người có số lần truy cập thuộc nhóm [30; 40)?
8.
6.
5.
10.
Đáp án : C
Từ dãy số liệu xác định số người thuộc nhóm [30; 40).
Có 5 người thuộc nhóm [30; 40).
Đáp án C
Gieo một con xúc xắc cân đối và đồng chất 2 lần. Tính xác suất để tổng số chấm trong hai lần gieo nhỏ hơn 6.
\(\frac{2}{9}\).
\(\frac{{11}}{{36}}\).
\(\frac{1}{6}\).
\(\frac{5}{{18}}\).
Đáp án : D
Tính số phần tử của không gian mẫu.
Tính số phần tử của biến cố “Tổng số chấm trong hai lần gieo nhỏ hơn 6”.
Xác suất của biến cố A bằng tỉ số giữa số phần tử của biến cố A với số phần tử của không gian mẫu.
Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = {6^2} = 36\).
Gọi A là biến cố “Tổng số chấm trong hai lần gieo nhỏ hơn 6”.
Tập hợp các quả của biến cố A là:
\(A = \left\{ {\left( {1;1} \right);\left( {1;2} \right);\left( {1;3} \right);\left( {1;4} \right);\left( {2;1} \right);\left( {2;2} \right);\left( {2;3} \right);\left( {3;1} \right);\left( {3;2} \right);\left( {4;1} \right)} \right\}\).
Số phần tử của biến cố A là: \(n\left( A \right) = 10\).
Xác suất của biến cố A là: \(P\left( A \right) = \frac{{10}}{{36}} = \frac{5}{{18}}\).
Đáp án D
Một cửa hàng đồ chơi trong tháng qua bán được 60 hộp lego thuộc nhiều thương hiệu đồ chơi khác nhau. Dưới đây là bảng thống kê của đại lí:

Lego và Hot Wheel.
Lego và Sembo Block.
Hot Wheel và Moyu Block.
Lego và Moyu Block.
Đáp án : D
Quan sát bảng tần số để xác định hai thương hiệu nào có tần số lớn nhất.
Theo bảng tần số, tần số của Lego, Hot Wheel, Cada, Moyu Block, Wange, Sembo Block lần lượt là 18; 9; 5; 18; 3; 7.
Mà 18 > 9 > 7 > 5 > 3 nên tần số của Lego và Moyu Block là lớn nhất.
Vậy cửa hàng nên nhập lego của các hãng Lego và Moyu Block.
Đáp án D
Trong các đường tròn dưới đây, đường tròn nào là đường tròn ngoại tiếp tam giác ABC.
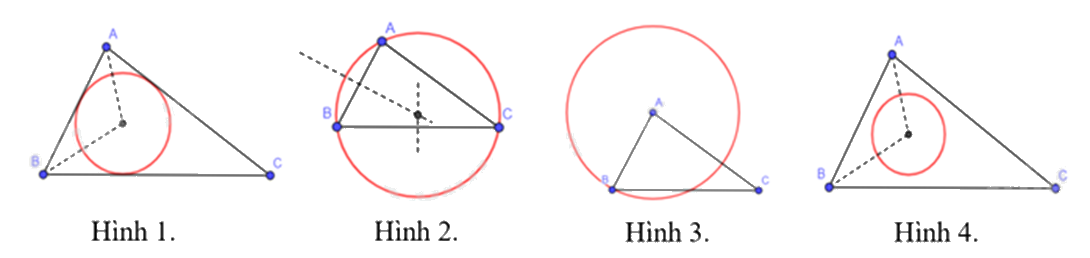
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đáp án : B
Đường tròn ngoại tiếp tam giác đi qua tất cả các đỉnh của tam giác đó.
Đường tròn ở hình 2 là đường tròn ngoại tiếp tam giác ABC.
Đáp án B
Cho đường tròn \(\left( O \right)\). Biết \(MA;MB\) là các tiếp tuyến của \(\left( O \right)\) cắt nhau tại \(M\) và \(\widehat {AMB} = 58^\circ \) Khi đó số đo \(\widehat {ABO}\) bằng:
\(24^\circ \).
\(29^\circ \).
\(30^\circ \).
\(31^\circ \).
Đáp án : B
Chứng minh tam giác AMO, BMO nội tiếp đường tròn nên tứ giác AMBO nội tiếp đường tròn.
Sử dụng định lí tổng hai góc đối của tứ giác nội tiếp để tính góc AOB.
Sử dụng định lí tổng ba góc của tam giác bằng \(180^\circ \) và tính chất tam giác cân để tính \(\widehat {ABO}\).
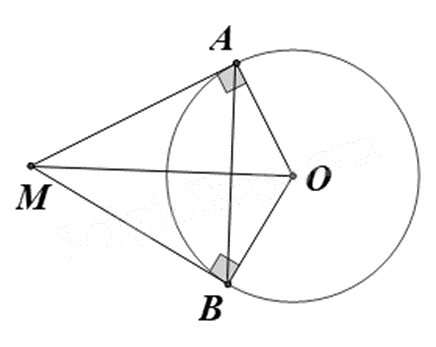
Vì MA; MB là các tiếp tuyến của (O) nên \(MA \bot OA,MB \bot OB\).
Do đó \(\Delta AMO;\Delta BMO\) lần lượt vuông tại A và B, do đó \(\Delta AMO;\Delta BMO\) ngoại tiếp đường tròn đường kính OM hay 4 điểm A, M, B, O thuộc cùng một đường tròn.
Do đó AMBO là tứ giác nội tiếp.
Áp dụng định lí tổng hai góc đối của tứ giác nội tiếp, ta có: \(\widehat {AMB} + \widehat {AOB} = 180^\circ \).
Suy ra \(\widehat {AOB} = 180^\circ - \widehat {AMB} = 180^\circ - 58^\circ = 122^\circ \)
Tam giác AOB cân tại O (do OA = OB) nên \(\widehat {ABO} = \frac{{180^\circ - \widehat {AOB}}}{2} = \frac{{180^\circ - 122^\circ }}{2} = 29^\circ \).
Đáp án B
Điều tra về chiều cao của các bạn học sinh nam khối 9 của một trường trong hai năm 2023 và 2024 được kết quả minh họa bằng hai biểu đồ cột sau đây cho biết
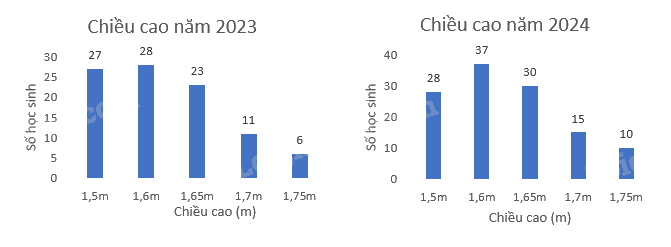
Lựa chọn đúng, sai
a) Tần số tương đối của 1,5m năm 2024 là 23,3%.
b) Tỉ lệ chiều cao 1,5m năm 2024 cao hơn năm 2023.
c) Tỉ lệ chiều cao 1,65m năm 2024 và năm 2023 bằng nhau.
d) Tỉ lệ chiều cao từ 1,65m trở lên năm 2024 cao hơn năm 2023 là 3,7%.
a) Tần số tương đối của 1,5m năm 2024 là 23,3%.
b) Tỉ lệ chiều cao 1,5m năm 2024 cao hơn năm 2023.
c) Tỉ lệ chiều cao 1,65m năm 2024 và năm 2023 bằng nhau.
d) Tỉ lệ chiều cao từ 1,65m trở lên năm 2024 cao hơn năm 2023 là 3,7%.
Lập bảng tần số tương đối năm 2023 và 2024.
Quan sát bảng trên để xác định tính đúng sai của các khẳng định.
Lập bảng tần số tương đối năm 2023:
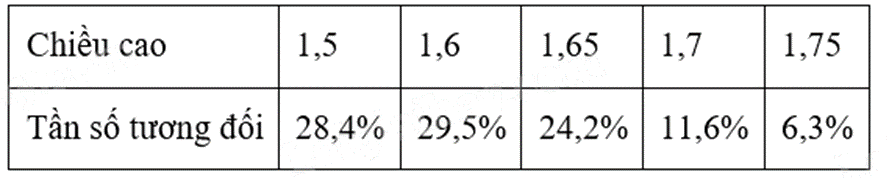
Lập được bảng tần số tương đối năm 2024:
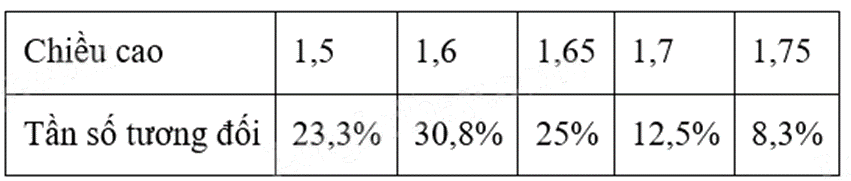
Quan sát bảng trên:
- Tần số tương đối của 1,5m năm 2024 là 23,3%. a) đúng
- Tỉ lệ chiều cao 1,5m năm 2024 cao hơn năm 2023. b) sai
- Tỉ lệ chiều cao 1,65m năm 2024 và năm 2023 bằng nhau. c) sai
- Tỉ lệ chiều cao từ 1,65m trở lên năm 2024 cao hơn năm 2023 là 3,7%. d) đúng
Đáp án ĐSSĐ
Cho \(\Delta ABC\) đều có cạnh \(4\,cm\) ngoại tiếp \(\left( {O;r} \right)\) và nội tiếp \(\left( {O;R} \right)\) khi đó:
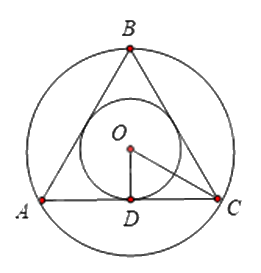
a) Khoảng cách từ tâm \(O\) đến \(AB\) bằng \(\sqrt 3 \).
b) Chu vi đường tròn nội tiếp \(\Delta ABC\) bằng \(\frac{{4\sqrt 3 }}{3}\pi \).
c) \(OA + OB + OC - OD = 10\sqrt 3 \).
d) Gọi \(x, y, z\) lần lượt là khoảng cách từ điểm \(O\) tới \(AB, BC, CA.\) Giá trị của biểu thức \(xy + \sqrt 3 z\) là \(\frac{{10}}{3}\).
a) Khoảng cách từ tâm \(O\) đến \(AB\) bằng \(\sqrt 3 \).
b) Chu vi đường tròn nội tiếp \(\Delta ABC\) bằng \(\frac{{4\sqrt 3 }}{3}\pi \).
c) \(OA + OB + OC - OD = 10\sqrt 3 \).
d) Gọi \(x, y, z\) lần lượt là khoảng cách từ điểm \(O\) tới \(AB, BC, CA.\) Giá trị của biểu thức \(xy + \sqrt 3 z\) là \(\frac{{10}}{3}\).
a) Khoảng cách từ tâm O đến AB chính là tâm đường tròn nội tiếp tam giác đều ABC. \(r = \frac{{\sqrt 3 }}{6}\). độ dài cạnh tam giác.
b) Từ bán kính đường tròn nội tiếp, tính chu vi đường tròn: \(C = 2\pi r\).
c) Từ độ dài các đoạn thẳng để tính giá trị biểu thức.
d) Tính bán kính đường tròn nội tiếp, đường tròn ngoại tiếp tam giác ABC để xác định khoảng cách từ điểm \(O\) tới \(AB, BC, CA.\)
Tính giá trị biểu thức.
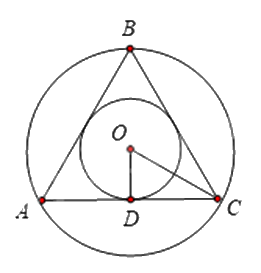
a) Sai
Khoảng cách từ tâm \(O\) đến \(AB\) bằng khoảng cách từ tâm \(O\) đến \(AC\) và bằng \(OD\)
Mà \(OD = r = \frac{{\sqrt 3 }}{6}.4 = \frac{{2\sqrt 3 }}{3}\) nên khoảng cách từ tâm \(O\) đến \(AB\) bằng \(\frac{{2\sqrt 3 }}{3}\).
b) Đúng
Chu vi đường tròn nội tiếp \(\Delta ABC\) là: \(C = 2\pi r = 2\pi .\frac{{2\sqrt 3 }}{3} = \frac{{4\sqrt 3 }}{3}\pi \).
c) Sai
Ta có: OA = OB = OC = R nên OC = \(OC = R = \frac{{\sqrt 3 }}{3}.4 = \frac{{4\sqrt 3 }}{3}\).
Do đó: \(OA + OB + OC - OD = 3.\frac{{4\sqrt 3 }}{3} - \frac{{2\sqrt 3 }}{3} = \frac{{10\sqrt 3 }}{3}\).
d) Đúng
Gọi \(x, y, z\) lần lượt là khoảng cách từ điểm \(O\) tới \(AB, BC, CA\) và bằng \(OD\) (bán kính đường tròn nội tiếp tam giác ABC.
Mà \(OD = \frac{{2\sqrt 3 }}{3}\).
Do đó \(xy + \sqrt 3 z = \frac{{2\sqrt 3 }}{3}.\frac{{2\sqrt 3 }}{3} + \sqrt 3 .\frac{{2\sqrt 3 }}{3} = \frac{4}{3} + 2 = \frac{{10}}{3}\).
Đáp án SĐSĐ
Thống kê về phần trăm khối lượng các loại hoa quả bán được trong 1 tháng của một cửa hàng được ghi lại như sau: 25% khối lượng bán được là Cam; 32% khối lượng bán được là Xoài; 10% là Thanh long; còn lại là Ổi. Biết tổng khối lượng hoa quả bán được trong tháng đó là 200kg. Khi đó khối lượng Ổi đã bán là … kg.
Đáp án:
Đáp án:
Xác định tần số tương đối của khối lượng Ổi đã bán.
Tính khối lượng Ổi đã bán.
Tần số tương đối của khối lượng Ổi là: \(100\% - 25\% - 32\% - 10\% = 33\% \).
Khối lượng Ổi đã bán là: \(200.33\% = 66\left( {kg} \right)\)
Đáp án: 66
Thời gian đi từ nhà tới trường (đơn vị: phút) của các bạn học sinh lớp 9C được biểu diễn bởi biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng như sau:
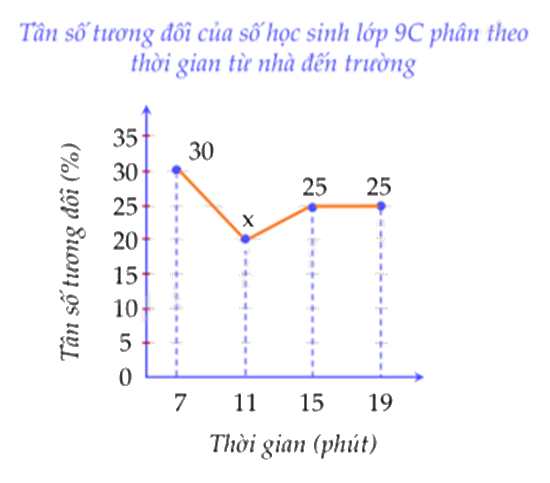
Biết lớp 9C có 40 học sinh. Số học sinh tương ứng với tần số tương đối x là:
Đáp án:
Đáp án:
Xác định giá trị của x.
Tính số học sinh đi đến trường tương ứng với tần số tương đối x = 40.x%
Giá trị của x là: 100 - 30 - 25 - 25 = 20.
Số học sinh tương ứng với tần số tương đối 20% là: \(40.20\% = 8\) (học sinh)
Đáp án: 8
Có hai túi \(I\) và \(II\). Túi \(I\) chứa bốn tấm thẻ , đánh số \(1;2;3;4\). Túi \(II\)chứa năm tấm thẻ ghi số \(1;2;3;4;5\). Rút ngẫu nhiên một tấm thẻ từ mỗi túi \(I\) và \(II\). Xác suất để cả hai tấm thẻ rút ra đều ghi số chẵn là bao nhiêu? (viết dưới dạng số thập phân)
Đáp án:
Đáp án:
Xác định không gian mẫu. Xác định các kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi và các phần tử của không gian mẫu.
Kết quả phép thử được viết dưới dạng \(\left( {a,b} \right)\) trong đó \(a,b\)lần lượt là các số trên các thẻ ở hai túi \(I\) và \(II\).
Bảng mô tả không gian mẫu
Số phần tử của không gian mẫu là \(20\).
Vì rút ngẫu nhiên một tấm thẻ từ mỗi túi \(I\) và \(II\)nên các kết quả có thể xảy ra ở trên đồng khả năng.
Có 4 kết quả thuận lợi cho biến cố “hai tấm thẻ rút ra đều ghi số chẵn” là \(\left( {2;2} \right)\);\(\left( {2;4} \right)\);\(\left( {4;2} \right)\);\(\left( {4;4} \right)\).
Do đó \(P = \frac{4}{{20}} = \frac{1}{5} = 0,2\).
Đáp án: 0,2
Cho tam giác ABC nội tiếp nửa đường tròn (O;R). Biết \(\widehat {AOC} = 116^\circ \). Độ dài cạnh AC là \(2R.\sin ...^\circ \). Số còn thiếu là:
Đáp án:
Đáp án:
Tính góc nội tiếp ABC theo góc ở tâm AOC.
Chứng minh tam giác ABC vuông tại C. Sử dụng hệ thức lượng để tính AC theo R.
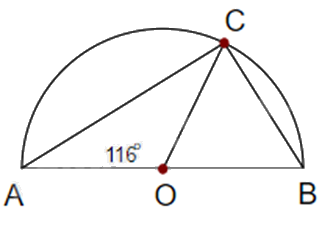
Vì \(\widehat {AOC}\) là góc ở tâm chắn cung AC, \(\widehat {ABC}\) là góc nội tiếp chắn cung AC nên \(\widehat {ABC} = \frac{1}{2}\widehat {AOC} = \frac{1}{2}.116^\circ = 58^\circ \).
Ta có: \(\widehat {ACB}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACB} = 90^\circ \).
Do đó tam giác ABC vuông tại C.
Áp dụng hệ thức lượng vào tam giác vuông ABC, ta được: \(AC = AB.\sin B = 2R.\sin 58^\circ \).
Đáp án: 58
Khảo sát mục đích sử dụng Internet của học sinh lớp 9C (mỗi học sinh chỉ nêu một mục đích hay sử dụng nhất). Biểu đồ cột kép dưới đây biểu diễn số học sinh nam và số học sinh nữ của lớp 9C với 3 mục đích chính: tra cứu tài liệu, xem phim, chơi game.
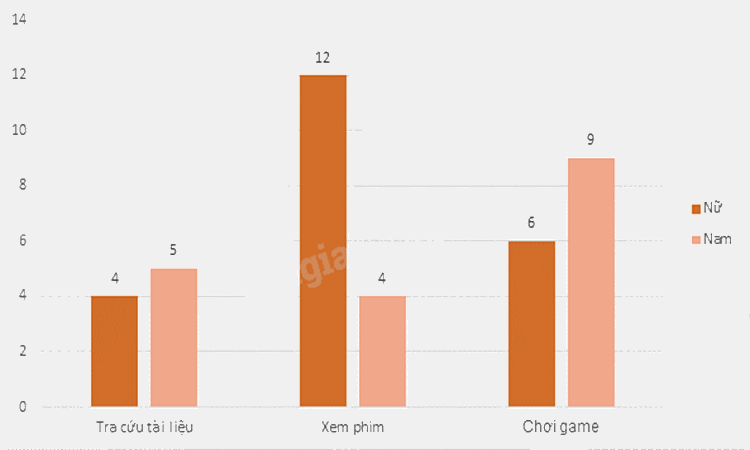
a) Tính xác suất của biến cố A: “Học sinh được chọn là nam”.
b) Tính xác suất của biến cố B: “Học sinh được chọn là nữ và có mục đích là xem phim”.
c) Tính xác suất của biến cố C: “Học sinh được chọn là nam và có mục đích là chơi game hoặc tra cứu tài liệu”.
Xác định số kết quả thuận lợi cho biến cố.
Xác định số phần tử của không gian mẫu.
Xác suất của biến cố bằng tỉ lệ giữa số kết quả thuận lợi cho biến cố với số phần tử của không gian mẫu.
Tổng số học sinh lớp 9C là: 4 + 5 + 12 + 4 + 6 + 9 = 40 (học sinh)
a) Số kết quả thuận lợi cho biến cố A: “Học sinh được chọn là nam” là:
5 + 4 + 9 = 18
Xác suất của biến cố A: “Học sinh được chọn là nam” là: \(\frac{{18}}{{40}} = \frac{9}{{20}}\).
b) Số kết quả thuận lợi cho biến cố B: “Học sinh được chọn là nữ và có mục đích là xem phim” là: 12
Xác suất của biến cố B: “Học sinh được chọn là nữ và có mục đích là xem phim” là: \(\frac{{12}}{{40}} = \frac{3}{{10}}\).
c) Số kết quả thuận lợi cho biến cố C: “Học sinh được chọn là nam và có mục đích là chơi game hoặc tra cứu tài liệu” là: 9 + 5 = 14
Xác suất của biến cố C: “Học sinh được chọn là nam và có mục đích là chơi game hoặc tra cứu tài liệu” là: \(\frac{{14}}{{40}} = \frac{7}{{20}}\).
Cho đường tròn \(\left( {O;R} \right)\) đường kính\(AB\), gọi \(I\) là trung điểm của \(OA\), dây \(CD\) vuông góc với \(AB\) tại I. Lấy \(K\) tùy ý trên cung \(BC\) nhỏ, \(AK\) cắt \(CD\) tại \(H\).
a) Chứng minh tứ giác \(BIHK\) là tứ giác nội tiếp.
b) Chứng minh \(AH.AK\) có giá trị không phụ thuộc vị trí điểm \(K\).
a) Chứng minh tứ giác nội tiếp thông qua hai tam giác vuông nội tiếp cùng một đường tròn.
b) Chứng minh $\Delta AHI\backsim \Delta ABK\left( g.g \right)$ suy ra tỉ số liên quan đến \(AH,AK\).
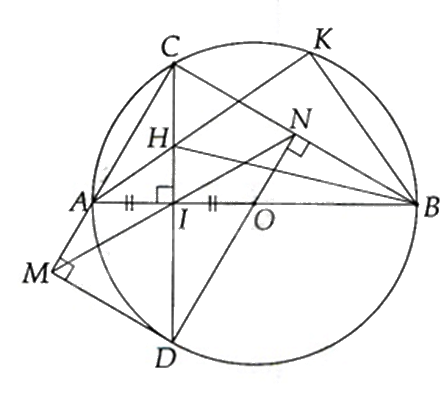
a) Ta có: \(\widehat {HKB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta HKB\) vuông tại K.
\(\widehat {HIB} = 90^\circ \) (dây CD vuông góc với AB tại I) nên \(\Delta HIB\) vuông tại I.
Do đó \(\Delta HKB,\Delta HIB\) cùng nội tiếp đường tròn đường kính HB, suy ra H, I, B, K thuộc một đường tròn hay tứ giác \(BIHK\) là tứ giác nội tiếp.
b) Xét tam giác AHI và tam giác ABK có:
\(\widehat {HIB} = \widehat {HKB} = 90^\circ \)
\(\widehat A\) chung
nên $\Delta AHI\backsim \Delta ABK$ (g.g)
Suy ra \(\frac{{AH}}{{AI}} = \frac{{AB}}{{AK}}\). Do đó \(AH.AK = AI.AB\).
Mà I là trung điểm của AO nên \(AI = \frac{{AO}}{2} = \frac{R}{2}\).
Suy ra \(AH.AK = AI.AB = \frac{R}{2}.2R = {R^2}\) (không đổi).
Vậy \(AH.AK\) có giá trị không phụ thuộc vị trí điểm \(K\).
Đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 5 là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau nửa học kỳ 2. Đề thi thường bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, phương trình bậc hai một ẩn, và các ứng dụng thực tế của đại số.
Đề thi thường được chia thành các phần sau:
Để đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 9 Cánh diều - Đề số 5, học sinh cần:
Việc ôn tập kỹ lưỡng trước kỳ thi là rất quan trọng. Học sinh nên dành thời gian để xem lại các bài giảng, làm lại các bài tập đã học, và giải các đề thi thử. Điều này sẽ giúp các em tự tin hơn và đạt kết quả tốt hơn trong kỳ thi.
Giaitoan.edu.vn cung cấp đầy đủ tài liệu ôn tập, đề thi thử, và đáp án chi tiết cho kỳ thi giữa kì 2 Toán 9 Cánh diều - Đề số 5. Chúng tôi cam kết mang đến cho học sinh một môi trường học tập hiệu quả và chất lượng.
Bài toán: Giải hệ phương trình sau:
| x | y |
|---|---|
| 2x + y = 5 | |
| x - y = 1 |
Lời giải:
Cộng hai phương trình, ta được: 3x = 6 => x = 2
Thay x = 2 vào phương trình x - y = 1, ta được: 2 - y = 1 => y = 1
Vậy nghiệm của hệ phương trình là (x; y) = (2; 1)
Hãy luôn giữ tinh thần thoải mái và tự tin khi làm bài thi. Chúc các em học sinh đạt kết quả tốt nhất!