Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 2, một công cụ ôn luyện tuyệt vời dành cho học sinh lớp 9. Đề thi được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi này bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, giúp học sinh đánh giá được kiến thức đã học và xác định những phần cần củng cố thêm. Đáp án chi tiết đi kèm sẽ giúp các em tự kiểm tra và rút kinh nghiệm sau khi làm bài.
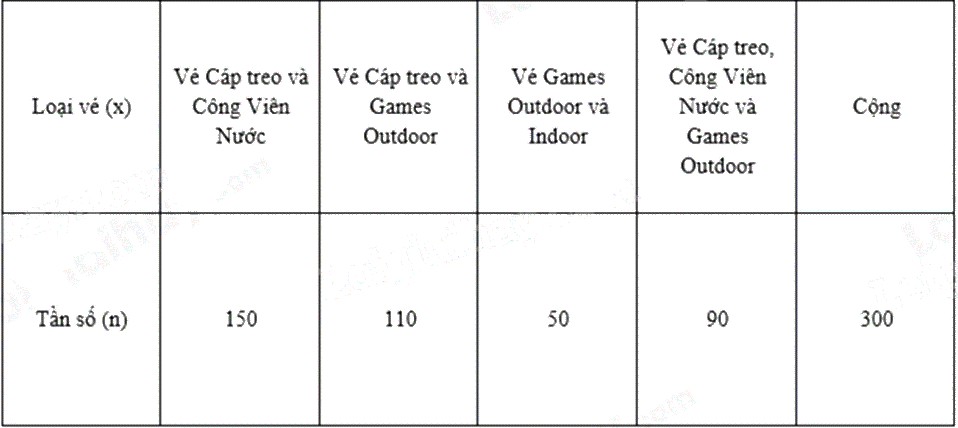
Bảng dưới đây thể hiện vé xuất ra trong 1 ngày của VinWonders Cửa Hội tại Cửa Lò. Bảng thống kê này được gọi là loại bảng thống kê nào?
Bảng tần số.
Bảng tần số tương đối.
Bảng thống kê.
Bảng tần suất.
Nguyên tắc chuyển đổi số liệu của mỗi đối tượng thống kê (tính theo tỉ số phần trăm) về số đo cung tương ứng với đối tượng thống kê đó (tính theo độ) là:
\(x\% \) tương ứng với \(x\% .90^\circ \).
\(x\% \) tương ứng với \(\frac{{360^\circ }}{{x\% }}\).
\(x\% \) tương ứng với \(x\% .180^\circ \).
\(x\% \) tương ứng với \(x\% .360^\circ \).
Cho biểu đồ tần số tương đối dạng cột về chiều cao của 40 cây keo mới trồng trong một khu công nghiệp:
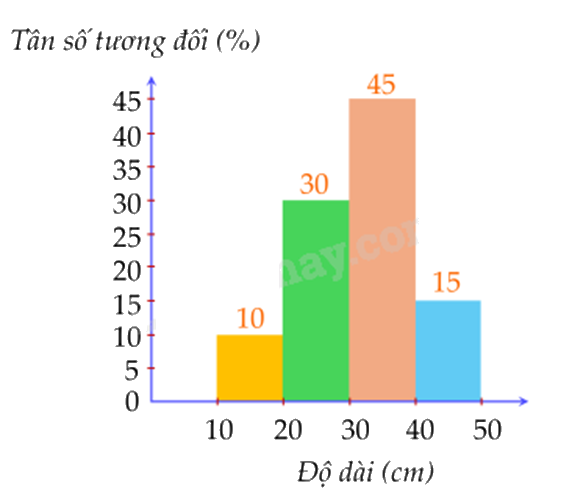
Số cây có chiều cao từ 30 cm trở lên bằng bao nhiêu?
10 cây.
20 cây.
24 cây.
12 cây.
Kích thước không gian mẫu của phép thử “Bạn An liệt kê các số chính phương có hai chữ số” là:
100.
10.
12.
6.
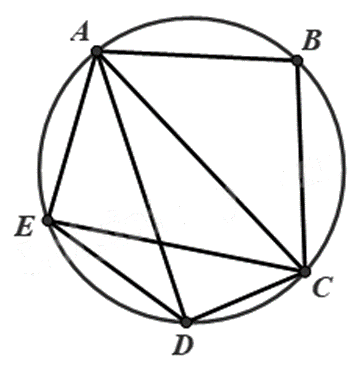
Có bao nhiêu tứ giác nội tiếp trong hình sau:
1.
2.
3.
4.
Cho tam giác ABC, gọi G là giao điểm ba đường phân giác của tam giác đó. Từ G kẻ GH, GI, GK lần lượt vuông góc với AB, AC, BC (\(H \in AB,I \in AC,K \in BC\)). So sánh độ dài GH, GI, GK.
GH < GI < GK.
GH = GI = GK.
GH > GI > GK.
GH = GI > GK.
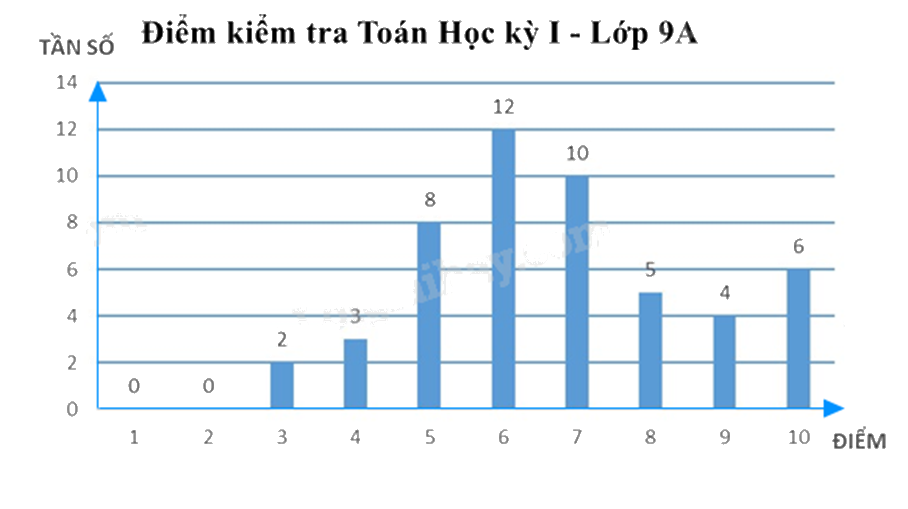
Kết quả điểm kiểm tra môn Toán cuối học kì 1 của học sinh lớp 9A được biểu diễn bằng biểu đồ cột dưới đây.
a) Bảng tần số biểu thị mẫu dữ liệu trong biểu đồ cột là:

b) Tổng số học sinh lớp 9A tham gia làm bài kiểm tra môn toán là 48.
c) Tần số tương đối của số học sinh đạt 8 điểm là 10%.
d) Số học sinh đạt điểm giỏi (điểm 8; 9; 10) bằng 50% số học sinh đạt điểm trung bình và khá (điểm 5; 6; 7).
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O), đường cao BD của tam giác cắt (O) tại điểm thứ hai là \(E\) (\(E\) khác \(B\)), vẽ EF vuông góc với BC (\(F\) thuộc BC).
a) DFCE là tứ giác nội tiếp.
b) Số đo của \(\widehat {ABD} = \widehat {ECF}\).
c) Gọi I là trung điểm của EC thì EC vuông góc OI.
d) \(BD.BE = BF.BC\).
Một cửa hàng khảo sát mức độ hài lòng của khách hàng thông qua việc khách hàng đánh giá từ ★ đến ★★★★★. Kết quả được thống kê bởi bảng số liệu sau:

Tần số tương đối của mức độ ★★★★★ là …
(không điền dấu %)
Đáp án:
Sau khi thống kê số lượt truy cập Internet của 30 người trong một tuần, người ta thu được bảng tần số ghép nhóm như sau:

Tần số tương đối của nhóm [30;40) (làm tròn đến hàng đơn vị) là …%.
Đáp án:
Bạn Hà Gieo hai con xúc xắc 6 mặt cân đối và đồng chất. Xác suất để tích số chấm trên mặt xuất hiện của hai con xúc xắc là một số chia hết cho 6 là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai).
Đáp án:
Cho tam giác ABC vuông tại A có AB = 5cm, AC = 7cm. Tính bán kính đường tròn đi qua 3 điểm A, B, C (làm tròn đơn vị đến hàng phần mười của cm).
Đáp án:
Một siêu thị thống kê hóa đơn mua hàng (đơn vị: nghìn đồng) của \(150\) khách hàng đầu tiên trong ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm sau:
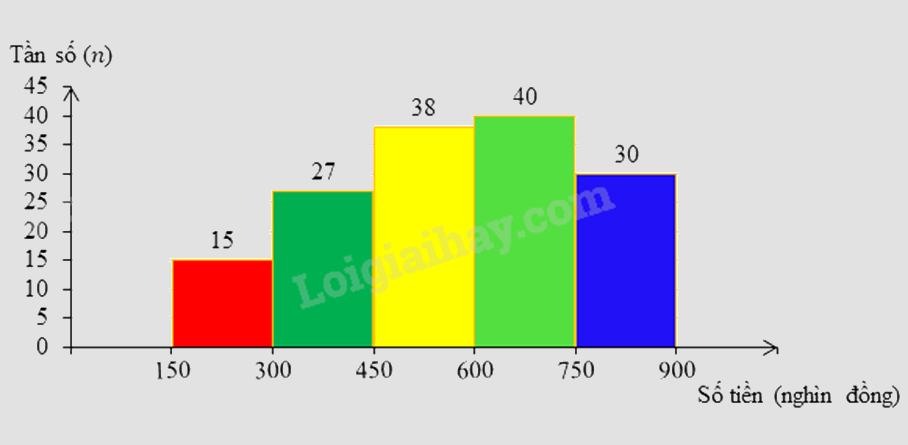
Tính tần số tương đối của nhóm có tần số lớn nhất (làm tròn đến số thập phân thứ nhất).
Cho tập hợp \(A = \left\{ {4;5;6} \right\}\). Từ các chữ số của tập hợp \(A\) viết ngẫu nhiên một số tự nhiên có \(2\) chữ số. Tính xác suất để số được viết có hai chữ số khác nhau.
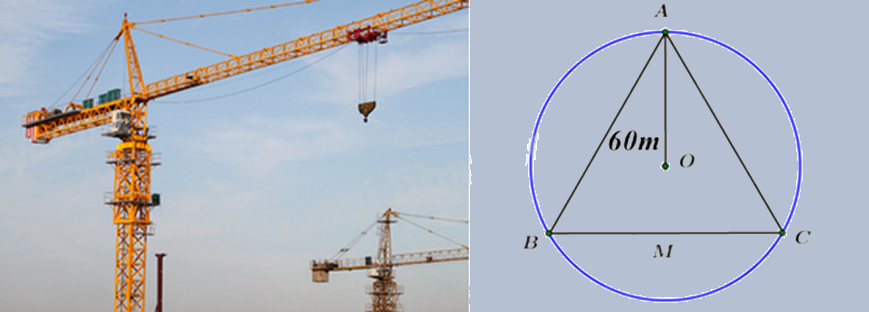
Cẩu tháp là một loại thiết bị nâng hạ được thiết kế để nâng, hạ và di chuyền vật liệu xây dựng tại các công trường, đặc biệt là trong xây dựng các công trình cao tầng. Có khả năng hoạt động ở độ cao lớn và với tải trọng nặng, cẩu tháp được lắp đặt cố định hoặc có thể di chuyển trên ray tại công trường, giúp tăng hiệu quả công việc và đảm bảo an toàn lao động. Ba vị trí A, B, C của một công trình là ba đỉnh của một tam giác đều. Trên công trình, người ta muốn đặt cẩu tháp tại điểm O sao cho bán kính quay của cẩu tháp đến các vị trí điểm A, B, C bằng nhau và bằng 60 m (hình bên). Tính khoảng cách từ A đến B (làm tròn đến số hàng đơn vị).
Bảng dưới đây thể hiện vé xuất ra trong 1 ngày của VinWonders Cửa Hội tại Cửa Lò. Bảng thống kê này được gọi là loại bảng thống kê nào?
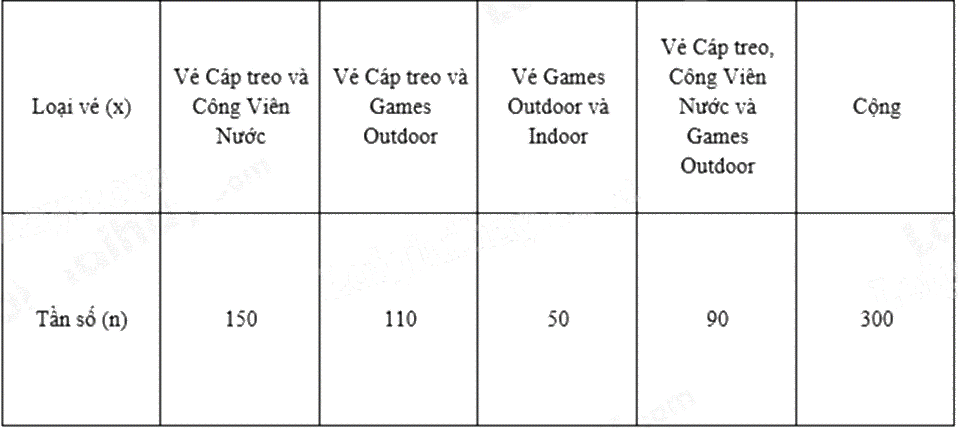
Bảng tần số.
Bảng tần số tương đối.
Bảng thống kê.
Bảng tần suất.
Đáp án : A
Dựa vào khái niệm các loại bảng đã học.
Bảng trên là bảng tần số.
Đáp án A
Nguyên tắc chuyển đổi số liệu của mỗi đối tượng thống kê (tính theo tỉ số phần trăm) về số đo cung tương ứng với đối tượng thống kê đó (tính theo độ) là:
\(x\% \) tương ứng với \(x\% .90^\circ \).
\(x\% \) tương ứng với \(\frac{{360^\circ }}{{x\% }}\).
\(x\% \) tương ứng với \(x\% .180^\circ \).
\(x\% \) tương ứng với \(x\% .360^\circ \).
Đáp án : D
Dựa vào quy tắc đổi % sang độ.
Chuyển đổi số liệu của mỗi đối tượng thống kê (tính theo tỉ số phần trăm) về số đo cung tương ứng với đối tượng thống kê đó (tính theo độ) dựa theo nguyên tắc sau: \(x\% \) tương ứng với \(x\% .360^\circ \).
Đáp án D
Cho biểu đồ tần số tương đối dạng cột về chiều cao của 40 cây keo mới trồng trong một khu công nghiệp:
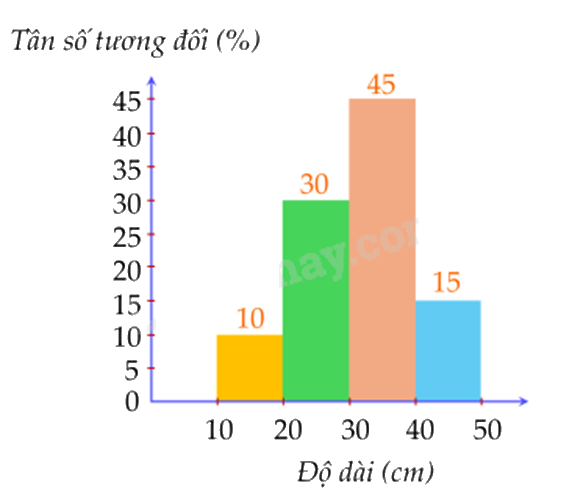
Số cây có chiều cao từ 30 cm trở lên bằng bao nhiêu?
10 cây.
20 cây.
24 cây.
12 cây.
Đáp án : C
Tính tần số tương đối của số cây có chiều cao từ 30 cm trở lên.
Tính số cây dựa vào công thức tính tỉ số phần trăm a% của một số m bằng a%.m.
Tần số tương đối của số cây cao từ 30cm trở lên bằng: \(45\% + 15\% = 60\% \)
Số cây có chiều cao từ 30 cm trở lên là: 60%.40 = 24.
Đáp án C
Kích thước không gian mẫu của phép thử “Bạn An liệt kê các số chính phương có hai chữ số” là:
100.
10.
12.
6.
Đáp án : D
Số chính phương là số bình phương của một số nguyên.
Xác định các số chính phương có 2 chữ số.
Có 6 số chính phương có hai chữ số, đó là: 16; 25; 36; 49; 64; 81.
Vậy kích thước không gian mẫu là 6.
Đáp án D
Có bao nhiêu tứ giác nội tiếp trong hình sau:
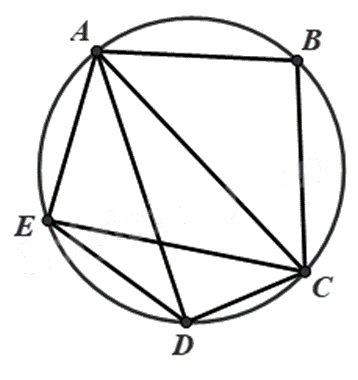
1.
2.
3.
4.
Đáp án : C
Quan sát hình vẽ để xác định các tứ giác nội tiếp.
Hình trên có 3 tứ giác nội tiếp, đó là: ABCD, ABCE, ACDE.
Đáp án C
Cho tam giác ABC, gọi G là giao điểm ba đường phân giác của tam giác đó. Từ G kẻ GH, GI, GK lần lượt vuông góc với AB, AC, BC (\(H \in AB,I \in AC,K \in BC\)). So sánh độ dài GH, GI, GK.
GH < GI < GK.
GH = GI = GK.
GH > GI > GK.
GH = GI > GK.
Đáp án : B
Giao điểm của ba đường phân giác của tam giác chính là tâm đường tròn nội tiếp tam giác và GH, GI, GK chính là giao của đường tròn với ba cạnh của tam giác.
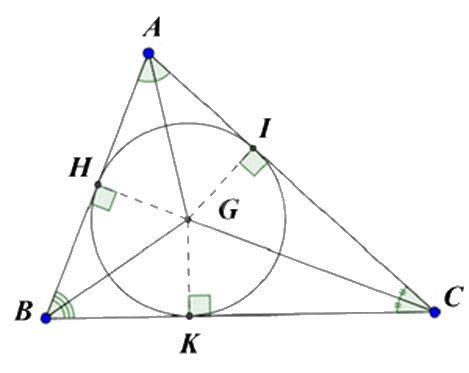
Vì G là giao điểm ba đường phân giác của tam giác nên G là tâm đường tròn nội tiếp tam giác.
GH, GI, GK lần lượt vuông góc với AB, AC, BC tại H, I, K nên GH = GI = GK = bán kính đường tròn nội tiếp tam giác ABC.
Đáp án B
Kết quả điểm kiểm tra môn Toán cuối học kì 1 của học sinh lớp 9A được biểu diễn bằng biểu đồ cột dưới đây.
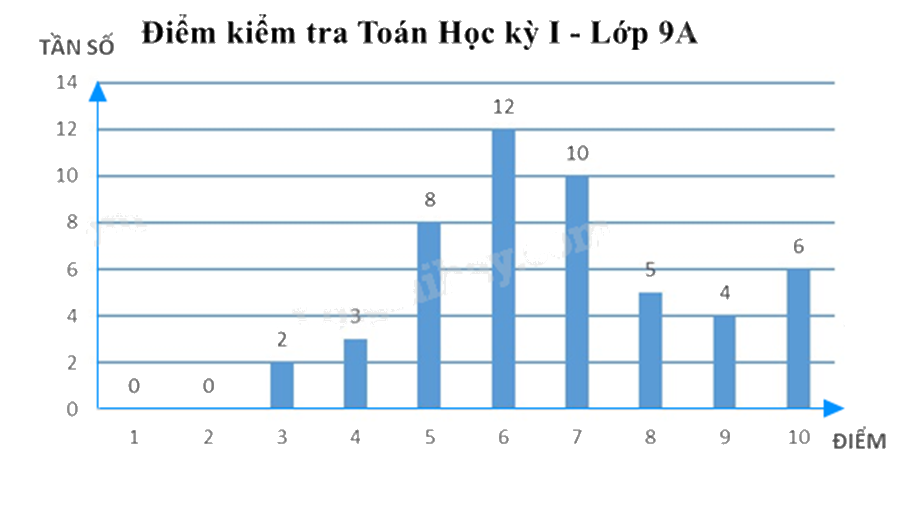
a) Bảng tần số biểu thị mẫu dữ liệu trong biểu đồ cột là:

b) Tổng số học sinh lớp 9A tham gia làm bài kiểm tra môn toán là 48.
c) Tần số tương đối của số học sinh đạt 8 điểm là 10%.
d) Số học sinh đạt điểm giỏi (điểm 8; 9; 10) bằng 50% số học sinh đạt điểm trung bình và khá (điểm 5; 6; 7).
a) Bảng tần số biểu thị mẫu dữ liệu trong biểu đồ cột là:

b) Tổng số học sinh lớp 9A tham gia làm bài kiểm tra môn toán là 48.
c) Tần số tương đối của số học sinh đạt 8 điểm là 10%.
d) Số học sinh đạt điểm giỏi (điểm 8; 9; 10) bằng 50% số học sinh đạt điểm trung bình và khá (điểm 5; 6; 7).
a) Quan sát biểu đồ tần số để xác định tần số của các giá trị và lập bảng tần số.
b) Tổng số học sinh tham gia làm bài kiểm tra bằng tổng tần số của các điểm.
c) Tần số tương đối của giá trị bằng tần số của giá trị với tổng tần số.
d) Xác định số học sinh đạt điểm giỏi, điểm trung bình và khá.
Tính tỉ số phần trăm giữa số học sinh đạt điểm giỏi với số học sinh đạt điểm trung bình và khá.
a) Đúng
Bảng tần số biểu thị mẫu dữ liệu trong biểu đồ cột là:
Vậy a) đúng.
b) Sai
Tổng số các tần số trong bảng là:
\(2 + 3 + 8 + 12 + 10 + 5 + 4 + 6 = 50\) (học sinh)
Vậy b) sai.
c) Đúng
Tần số tương đối của số học sinh đạt điểm 8 là: \(\frac{5}{{50}}.100\% = 10\% \).
Vậy c) đúng.
d) Đúng
Tổng số học sinh đạt điểm giỏi (điểm 8; 9; 10) là: \(5 + 4 + 6 = 15\) (học sinh)
Tổng số HS đạt điểm trung bình và khá (điểm 5; 6; 7) là: \(8 + 12 + 10 = 30\) (học sinh)
Vậy số học sinh đạt điểm giỏi (điểm 8; 9; 10) bằng:
\(\frac{{15}}{{30}} = 50\% \) số học sinh đạt điểm trung bình và khá (điểm 5; 6; 7).
Vậy d) đúng.
Đáp án ĐSĐĐ
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O), đường cao BD của tam giác cắt (O) tại điểm thứ hai là \(E\) (\(E\) khác \(B\)), vẽ EF vuông góc với BC (\(F\) thuộc BC).
a) DFCE là tứ giác nội tiếp.
b) Số đo của \(\widehat {ABD} = \widehat {ECF}\).
c) Gọi I là trung điểm của EC thì EC vuông góc OI.
d) \(BD.BE = BF.BC\).
a) DFCE là tứ giác nội tiếp.
b) Số đo của \(\widehat {ABD} = \widehat {ECF}\).
c) Gọi I là trung điểm của EC thì EC vuông góc OI.
d) \(BD.BE = BF.BC\).
a) Chứng minh tam giác DEC và tam giác EFC cùng nội tiếp một đường tròn nên DFCE là tứ giác nội tiếp.
b) Xác định cung chắn hai góc trên để kiểm tra.
c) Dựa vào tính chất đường trung trực của đoạn thẳng để kiểm tra.
d) Dựa vào 2 tam giác đồng dạng tam giác \(BDC\) và tam giác \(BFE\) suy tỉ số và dựa tính chất tỉ lệ thức.
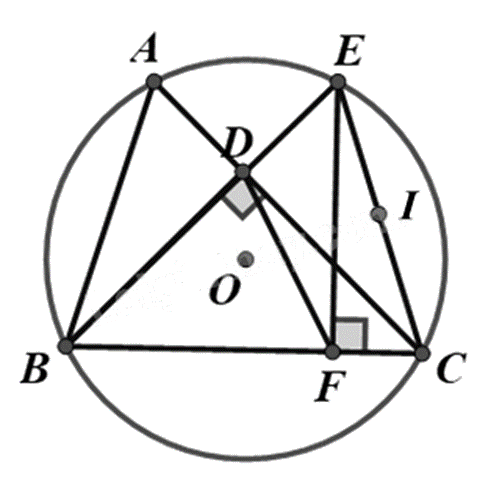
a) Đúng
Xét tam giác DEC có \(\widehat {CDE} = 90^\circ \) nên nội tiếp đường tròn đường kính EC.
Xét tam giác EFC có \(\widehat {EFC} = 90^\circ \) nên nội tiếp đường tròn đường kính EC.
Do đó 4 điểm D, F, C, E cùng thuộc đường tròn đường kính EC hay DFCE là tứ giác nội tiếp.
b) Sai
Ta có: \(\widehat {ABD}\) hay \(\widehat {ABE}\) chắn cung AE, \(\widehat {ECF}\) hay \(\widehat {ECB}\) chắn cung BE.
Mà cung BE và cung AE không bằng nhau nên \(\widehat {ABD} \ne \widehat {ECF}\).
c) Đúng
Vì E, C thuộc đường tròn (O) nên OE = OC hay O cách đều hai điểm E, C.
Vì I là trung điểm của EC nên IE = IC hay I cách đều hai điểm E, C.
Suy ra OI là đường trung trực của EC nên \(EC \bot OI\).
d) Đúng
Xét tam giác BDC và tam giác BFE có:
\(\widehat {BDC} = \widehat {BFE}\left( { = 90^\circ } \right)\)
\(\widehat B\) chung
Suy ra $\Delta BDC\backsim \Delta BFE\left( g.g \right)$
Do đó \(\frac{{BD}}{{BC}} = \frac{{BF}}{{BE}}\) nên \(BD.BE = BF.BC\).
Đáp án: ĐSĐĐ
Một cửa hàng khảo sát mức độ hài lòng của khách hàng thông qua việc khách hàng đánh giá từ ★ đến ★★★★★. Kết quả được thống kê bởi bảng số liệu sau:

Tần số tương đối của mức độ ★★★★★ là …
(không điền dấu %)
Đáp án:
Đáp án:
Tần số tương đối của một giá trị bằng tỉ số phần trăm giữa tần số của giá trị đó với tổng tần số.
Tần số tương đối của mức độ ★★★★★ là: \(\frac{{312}}{{500}}.100\% = 62,4\% \).
Đáp án: 62,4
Sau khi thống kê số lượt truy cập Internet của 30 người trong một tuần, người ta thu được bảng tần số ghép nhóm như sau:

Tần số tương đối của nhóm [30;40) (làm tròn đến hàng đơn vị) là …%.
Đáp án:
Đáp án:
Tính tổng các tần số, xác định tần số của nhóm [30;40).
Xác định tần số tương đối bằng tỉ số phần trăm của tần số nhóm với tổng các tần số.
Cộng các tần số ghép nhóm ta được tổng tần số là: \(N = 5 + 6 + 6 + 4 + 3 + 6 = 30\).
Quan sát bảng trên ta thấy nhóm [30;40) có tần số là 5, tổng tần số là 30.
Vì vậy tần số tương đối của nhóm này là: \(\frac{{5.100}}{{30}}\% \approx 17\% \)
Đáp án: 17
Bạn Hà Gieo hai con xúc xắc 6 mặt cân đối và đồng chất. Xác suất để tích số chấm trên mặt xuất hiện của hai con xúc xắc là một số chia hết cho 6 là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai).
Đáp án:
Đáp án:
Xác định số phần tử của không gian mẫu của phép thử, số kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số phần tử của không gian mẫu.
Không gian mẫu của phép thử là:
\(\begin{array}{l}\Omega = \{ (1;1),(1;2),(1;3),(1;4),(1;5),(1;6),\\(2;1),(2;2),(2;3),(2;4),(2;5),(2;6),\\(3;1),(3;2),(3;3),(3;4),(3;5),(3;6),\\(4;1),(4;2),(4;3),(4;4),(4;5),(4;6),\\(5;1),(5;2),(5;3),(5;4),(5;5),(5;6),\\(6;1),(6;2),(6;3),(6;4),(6;5),(6;6)\} \end{array}\)
Số phần tử không gian mẫu \(n(\Omega ) = 36\).
Có 15 kết quả thuận lợi cho biến cố trên là:
\(\begin{array}{l}A = {\rm{\{ }}\left( {1;6} \right),\left( {6;1} \right),\left( {6;2} \right),\left( {2;6} \right),\left( {6;3} \right),\left( {3;6} \right),\left( {6;4} \right),\left( {4;6} \right),\\\left( {6;5} \right),\left( {5;6} \right),\left( {6;6} \right),\left( {2;3} \right),\left( {3;2} \right),\left( {3;4} \right),\left( {4;3} \right){\rm{\} }}\end{array}\)
Vậy xác suất của biến cố trên là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{15}}{{36}} \approx 0.42\).
Đáp án: 0,42
Cho tam giác ABC vuông tại A có AB = 5cm, AC = 7cm. Tính bán kính đường tròn đi qua 3 điểm A, B, C (làm tròn đơn vị đến hàng phần mười của cm).
Đáp án:
Đáp án:
Áp dụng định lí Pythagore vào tam giác vuông để tính BC.
Đường tròn ngoại tiếp tam giác vuông có bán kính bằng một nửa cạnh huyền của tam giác vuông.
Áp dụng định lí Pythagore vào tam giác ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {7^2} = 74\)
Suy ra \(BC = \sqrt {74} \) (cm).
Đường tròn đi qua 3 điểm A, B, C là đường tròn ngoại tiếp tam giác ABC.
Vì tam giác ABC vuông tại A nên đường tròn ngoại tiếp tam giác ABC có đường kính là cạnh huyền BC.
Bán kính đường tròn ngoại tiếp tam giác ABC là: \(\frac{{\sqrt {74} }}{2} \approx 4,3\) (cm).
Đáp án: 4,3
Một siêu thị thống kê hóa đơn mua hàng (đơn vị: nghìn đồng) của \(150\) khách hàng đầu tiên trong ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm sau:
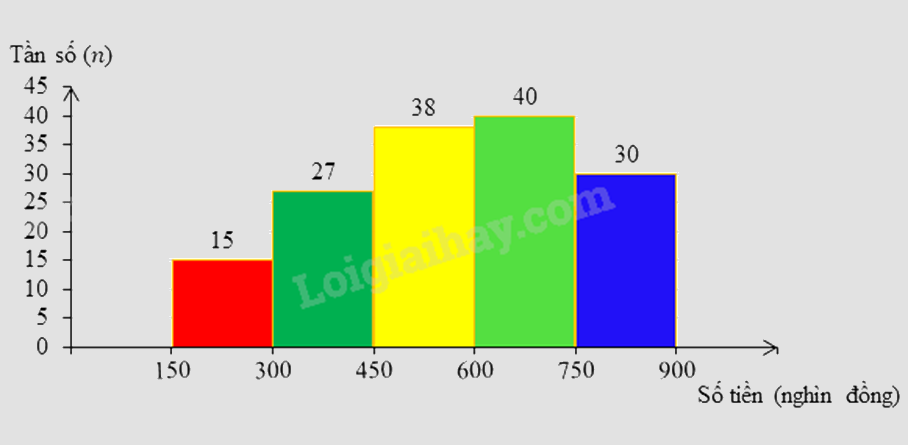
Tính tần số tương đối của nhóm có tần số lớn nhất (làm tròn đến số thập phân thứ nhất).
Xác định nhóm có tần số lớn nhất và tính tần số tương đối của nhóm đó.
Nhóm có tần số lớn nhất là nhóm \(\left[ {600\,;\,750} \right)\) với tần số \(40\).
Tần số tương đối của nhóm có tần số lớn nhất là \(\frac{{40.100}}{{150}}\% \approx 26,7\% \).
Cho tập hợp \(A = \left\{ {4;5;6} \right\}\). Từ các chữ số của tập hợp \(A\) viết ngẫu nhiên một số tự nhiên có \(2\) chữ số. Tính xác suất để số được viết có hai chữ số khác nhau.
Xác định không gian mẫu, các kết quả thuận lợi cho biến cố.
Tính xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố và số phần tử của không gian mẫu.
Không gian mẫu là \(\Omega = \left\{ {44;45;46;54;55;56;64;65;66} \right\}\), suy ra \(n\left( \Omega \right) = 9\)
Có \(6\) kết quả thuận lợi của biến cố “Số được viết có hai chữ số khác nhau” là\(\left\{ {45;46;54;56;64;65} \right\}.\) Vậy \(P = \frac{6}{9} = \frac{2}{3}\).
Cẩu tháp là một loại thiết bị nâng hạ được thiết kế để nâng, hạ và di chuyền vật liệu xây dựng tại các công trường, đặc biệt là trong xây dựng các công trình cao tầng. Có khả năng hoạt động ở độ cao lớn và với tải trọng nặng, cẩu tháp được lắp đặt cố định hoặc có thể di chuyển trên ray tại công trường, giúp tăng hiệu quả công việc và đảm bảo an toàn lao động. Ba vị trí A, B, C của một công trình là ba đỉnh của một tam giác đều. Trên công trình, người ta muốn đặt cẩu tháp tại điểm O sao cho bán kính quay của cẩu tháp đến các vị trí điểm A, B, C bằng nhau và bằng 60 m (hình bên). Tính khoảng cách từ A đến B (làm tròn đến số hàng đơn vị).
Tính khoảng cách giữa hai vị trí A và B chính là tìm cạnh của tam giác đều ABC khi biết bán kính đường tròn ngoại tiếp tam giác.
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).
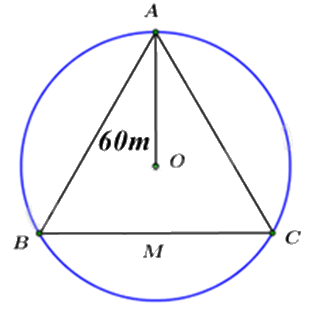
Vì O cách đều 3 đỉnh của tam giác ABC nên O là tâm đường tròn ngoại tiếp tam giác đều ABC.
Gọi a (m) là độ dài cạnh của tam giác đều ABC (a > 0)
Ta có bán kính đường tròn ngoại tiếp tam giác đều là 60m nên \(R = \frac{{a\sqrt 3 }}{3}\), suy ra \(60 = \frac{{a\sqrt 3 }}{3}\)
Do đó\(\begin{array}{l}a\sqrt 3 = 60.3 = 180\\a = 180:\sqrt 3 \approx 104\left( {TM} \right)\end{array}\)
Vậy khoảng cách từ A đến B khoảng 104 m.
Đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 2 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau nửa học kỳ. Đề thi này thường bao gồm các chủ đề chính như hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, phương trình bậc hai một ẩn, và các ứng dụng thực tế của đại số.
Cấu trúc đề thi thường được chia thành hai phần chính: phần trắc nghiệm và phần tự luận. Phần trắc nghiệm thường chiếm khoảng 30-40% tổng số điểm, tập trung vào việc kiểm tra khả năng hiểu và vận dụng các khái niệm cơ bản. Phần tự luận chiếm khoảng 60-70% tổng số điểm, yêu cầu học sinh trình bày chi tiết các bước giải và giải thích rõ ràng lý do tại sao lại chọn phương pháp giải đó.
Để giải phương trình bậc hai ax2 + bx + c = 0, ta sử dụng công thức nghiệm:
x = (-b ± √(b2 - 4ac)) / 2a
Trong đó, Δ = b2 - 4ac là biệt thức của phương trình. Nếu Δ > 0, phương trình có hai nghiệm phân biệt. Nếu Δ = 0, phương trình có nghiệm kép. Nếu Δ < 0, phương trình vô nghiệm.
Có hai phương pháp phổ biến để giải hệ phương trình bậc nhất hai ẩn:
Để đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 9 Cánh diều, học sinh cần:
Làm đề thi thử là một bước quan trọng trong quá trình ôn thi. Nó giúp học sinh:
Giaitoan.edu.vn cung cấp một kho đề thi giữa kì 2 Toán 9 Cánh diều - Đề số 2 và nhiều đề thi khác với đáp án chi tiết, giúp học sinh ôn luyện và chuẩn bị tốt nhất cho kỳ thi. Chúng tôi cam kết mang đến cho học sinh những tài liệu học tập chất lượng và hiệu quả nhất.
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số bậc nhất | Cao |
| Hệ phương trình bậc nhất hai ẩn | Cao |
| Phương trình bậc hai một ẩn | Trung bình |
| Ứng dụng thực tế | Trung bình |
| Nguồn: Giaitoan.edu.vn | |