Giaitoan.edu.vn xin giới thiệu bộ đề khảo sát chất lượng Toán 11 năm học 2024 - 2025 do sở Giáo dục và Đào tạo Hà Nội ban hành. Đây là tài liệu vô cùng quan trọng giúp học sinh lớp 11 rèn luyện kỹ năng, làm quen với cấu trúc đề thi và đánh giá năng lực bản thân.
Bộ đề này bao gồm các đề thi thử với độ khó và cấu trúc tương tự như đề thi chính thức, giúp học sinh chuẩn bị tốt nhất cho các kỳ thi sắp tới.
Với a là số thực dương tùy ý, \({\log _3}\frac{a}{3}\) bằng
\(1 - {\log _3}a\)
\(1 + {\log _3}a\)
\(\frac{{{{\log }_2}a}}{3}\)
\({\log _3}a - 1\)
Cho tứ diện ABCD. Gọi M là trung điểm của đoạn thẳng BC. Giao tuyến của hai mặt phẳng (AMD) và (BCD) là đường thẳng nào dưới đây?
CD
BC
MA
MD
Cho hàm số y = cos 2x có đồ thị như hình vẽ:
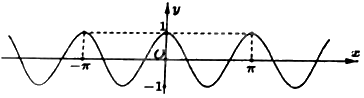
Số nghiệm của phương trình \(\cos 2x = \frac{1}{3}\) trên đoạn \([ - \pi ;\pi ]\) là
6
2
4
Vô số
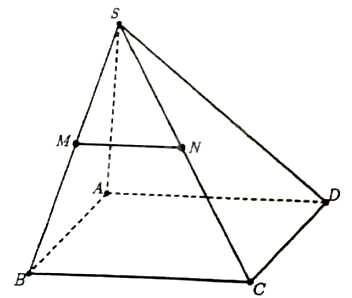
Cho hình chóp S.ABCD có đáy là hình bình hành. Hai điểm M, N lần lượt là trung điểm của SB và SC. Đường thẳng MN song song với mặt phẳng nào sau đây?
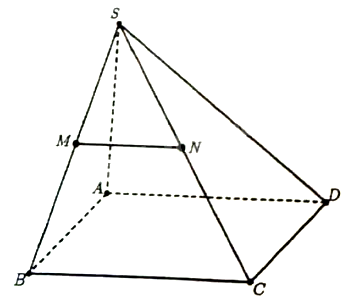
(SAB)
(SCD)
(SAD)
(SBD)
Điểm thi môn Toán trong Kỳ thi Tốt nghiệp trung học phổ thông của 690 học sinh trường THPT X được thống kê bởi bảng số liệu như sau:

Điểm trung bình môn Toán của mẫu số liệu trên xấp xỉ bằng
5,4
6,4
7,4
7,0
Giá trị của \(\mathop {\lim }\limits_{x \to {\rm{ \;}} + \infty } \frac{{{2^n} + 1}}{{{3^n}}}\) bằng
2
1
-1
0
Từ thành phố A đến thành phố B có 4 con đường đi, từ thành phố B đến thành phố C có 3 con đường đi. Số cách đi từ thành phố A đến thành phố C mà phải đi qua thành phố B là
12
1
42
7
Tập xác định của hàm số \(y = \frac{4}{{\sin x}}\) là
\(D = R\backslash \left\{ {k\pi ,k \in Z} \right\}\)
\(D = \mathbb{R}\)
\(D = R\backslash \left\{ {k2\pi ,k \in Z} \right\}\)
\(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}\)
Cho dãy số \(({u_n})\) với \({u_n} = 3n + 1,\forall n \in {N^*}\). Giá trị của \({u_3}\) bằng
7
28
10
12
Thống kê thời gian hoàn thành một đề thi online của 25 học sinh, ta được bảng sau:

Mốt của mẫu số liệu ghép nhóm trên thuộc nhóm nào dưới đây?
[25; 30)
[15; 20)
[5; 10)
[10; 15)
Cho cấp số nhân \(({u_n})\) với \({u_2} = 3\) và \({u_3} = 6\). Công bội của cấp số nhân đã cho là
\(\frac{1}{2}\)
2
-2
\( - \frac{1}{2}\)
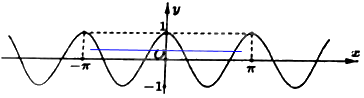
Hàm số nào dưới đây có đồ thị là đường cong như hình vẽ?
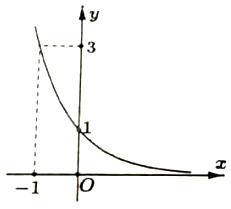
\(y = {\left( {\frac{1}{3}} \right)^x}\)
\(y = {\log _3}x\)
\(y = {\log _{\frac{1}{3}}}x\)
\(y = {3^x}\)
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{{x^2} - 3x + 2}}{{x - 2}}}\\1\end{array}} \right.\) \(\begin{array}{*{20}{l}}{khi}\\{khi}\end{array}\) \(\begin{array}{*{20}{l}}{x \ne 2}\\{x = 2}\end{array}\).
a) Giá trị của \(f(2)\) bằng 1.
b) Giá trị của \(\mathop {\lim }\limits_{x \to 2} f(x)\) bằng -1.
c) Hàm số đã cho liên tục trên \(\mathbb{R}\).
d) Giá trị của \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {xf(x) + 1} }}{{x + 1}}\) bằng 1.
Cho hình H là một tam giác đều cạnha) Người ta lần lượt thực hiện các bước như sau:
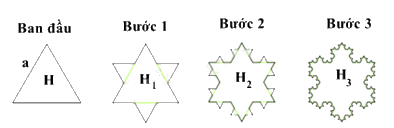
Bước 1: Chia mỗi cạnh của hình H thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài hình H, sau đó xóa bỏ đoạn ở giữa, ta được hình \({H_1}\) (tham khảo hình vẽ).
Bước 2: Tiếp tục lặp lại quá trình trên với mỗi cạnh của hình \({H_1}\) ta được hình \({H_2}\).
Sau nhiều bước thực hiện như trên, ta được một hình giống như bông tuyết, gọi là bông tuyết Von Koch.
a) Độ dài mỗi cạnh của hình \({H_1}\) là \(\frac{a}{3}\).
b) Với mọi số tự nhiên\(\;n \ge 2\) thì độ dài mỗi cạnh của hình \({H_{n - 1}}\) gấp 3 lần độ dài mỗi cạnh của hình \({H_n}\).
c) Gọi \({u_1},{u_2},.....,{u_n},....\) lần lượt là số cạnh của các hình \({H_1},{H_2},....{H_n},...\). Khi đó, dãy số \({u_1},{u_2},{u_3},{u_4},....\) theo thứ tự lập thành một cấp số nhân có công bội \(q = 4\).
d) Chu vi của hình bông tuyết Von Koch \({H_{16}}\) lớn hơn 100 lần chu vi của hìnhH.
Giả sử số lượng của một quần thể vi sinh vật tại môi trường nuôi cấy trong phòng thí nghiệm (phụ thuộc vào thời gian nuôi cấy) được mô hình hóa bằng hàm số \(P(t) = \frac{{25}}{{a + {e^{ - 0.8t}}}}\;\) trong đó thời gian t được tính bằng giờ, a là hệ số điều chỉnh mật độ vi sinh vật ban đầu. Biết rằng, tại thời điểm ban đầu \(t = 0\) quần thể có 20 vi sinh vật.
a) Giá trị của \(a\) bằng 0,25.
b) Sau 2 giờ, quần thể có nhiều hơn 60 vi sinh vật.
c) Với quy trình nuôi cấy theo mô hình trên thì số lượng vi khuẩn trong quần thể không lớn hơn 100.
d) Để số lượng vi sinh vật trong quần thể lớn hơn 90 thì cần nuôi cấy ít nhất 6 giờ.
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD // BC, AD = 2BC. Gọi O là giao điểm của hai đường chéo AC và BD, điểm M là trung điểm của đoạn thẳng SC.
a) Đường thẳng AM nằm trong mặt phẳng (SAC).
b) Giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng SO.
c) Giao điểm của đường thẳng AM và mặt phẳng (SBD) là giao điểm của AM và SO.
d) Gọi \(\left( {\alpha {\rm{\;}}} \right)\) là mặt phẳng chứa đường thẳng AM và song song với đường thẳng BD. Mặt phẳng \(\left( {\alpha {\rm{\;}}} \right)\) cắt SB tại P. Khi đó \(\frac{{SP}}{{SB}} = \frac{2}{3}\).
Cho cấp số cộng (\({u_n}\)) có \({u_3} = 9\) và \({u_7} = 17\). Tổng của 20 số hạng đầu tiên của cấp số cộng đã cho bằng bao nhiêu?
Đáp án:
Anh An gửi 100 triệu vào ngân hàng với kì hạn 1 năm và hưởng lãi suất 5,4%/năm theo thể thức lãi kép. Sau khi gửi được tròn 9 tháng, anh cần dùng đến 100 triệu trên để sửa nhà. Nhân viên ngân hàng đã đưa ra cho anh hai phương án như sau:
*Phương án 1: Anh rút hết tiền trước kì hạn. Khi đó toàn bộ số tiền anh gửi sẽ được tính lãi với lãi suất không kì hạn là \(0,2\% \)/năm (tính theo thể thức lãi kép với kì hạn 1 tháng).
*Phương án 2: Anh thế chấp sổ tiết kiệm đó để vay ngân hàng 100 triệu. Khi đó, toàn bộ số tiền vay sẽ phải chịu lãi suất \(8\% \)/năm (tính theo thể thức lãi kép với kì hạn 1 tháng). Đủ kì hạn 1 năm của khoản tiền gửi, anh sẽ rút hết tiền và trả hết nợ cho ngân hàng.
Nếu làm theo phương án 2 thì anh được lợi bao nhiêu triệu đồng so với phương án 1 (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
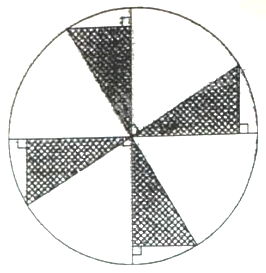
Một khu phố có kế hoạch tu sửa một sân chơi hình tròn, bán kính 10m. Theo bản thiết kế dự kiến thì công (như hình vẽ), người ta lát gạch trang trí ở phần kẻ sọc (với \({0^\circ } < \alpha {\rm{ \;}} < {45^\circ }\)) và phần còn lại đổ xi măng. Chi phí lát gạch là 1 triệu đồng/\(1{m^2}\) và chi phí đổ xi măng là 300 nghìn đồng/\(1{m^2}\) (giả sử phần chi phí khác không đáng kể). Hỏi góc \(\alpha \) lớn nhất là bao nhiêu độ để chi phí tu sửa không lớn hơn 150 triệu đồng (làm tròn kết quả đến hàng đơn vị).
Đáp án:
Trong kỳ thi vấn đáp, bạn Bình phải bốc thăm ngẫu nhiên và trả lời 3 chủ đề trong số 10 chủ đề đã được chuẩn bị trước. Bạn Bình chỉ chuẩn bị được 7 trong 10 chủ đề trên. Xác suất để Bình bốc được ít nhất hai chủ đề trong những chủ đề đã chuẩn bị bằng bao nhiêu (làm tròn đến hàng phần trăm)?
Đáp án:
Bất phương trình \({\log _2}(2x - 1) < {\log _2}(14 - x)\) có bao nhiêu nghiệm nguyên?
Đáp án:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 6. Gọi M là trung điểm của đoạn thẳng SB và điểm N thuộc đoạn thẳng SC sao cho NS = 2NC. Phép chiếu song song lên mặt phẳng (SCD) theo phương chiếu BD biến điểm M thành điểm P. Phép chiếu song song lên mặt phẳng (ABCD) theo phương chiếu SA biến tam giác MNP thành hình T. Khi đó diện tích hình T bằng bao nhiêu?
Đáp án:
Với a là số thực dương tùy ý, \({\log _3}\frac{a}{3}\) bằng
\(1 - {\log _3}a\)
\(1 + {\log _3}a\)
\(\frac{{{{\log }_2}a}}{3}\)
\({\log _3}a - 1\)
Đáp án : D
Tính chất của logarit.
\({\log _3}\frac{a}{3} = {\log _3}a - {\log _3}3 = {\log _3}a - 1\).
Cho tứ diện ABCD. Gọi M là trung điểm của đoạn thẳng BC. Giao tuyến của hai mặt phẳng (AMD) và (BCD) là đường thẳng nào dưới đây?
CD
BC
MA
MD
Đáp án : D
Tìm 2 điểm chung của 2 mặt phẳng.
Ta có (AMD) và (BCD) có điểm chung là M, D nên giao tuyến là MD.
Cho hàm số y = cos 2x có đồ thị như hình vẽ:
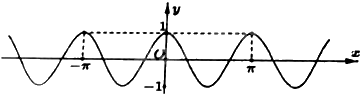
Số nghiệm của phương trình \(\cos 2x = \frac{1}{3}\) trên đoạn \([ - \pi ;\pi ]\) là
6
2
4
Vô số
Đáp án : C
Sử dung tương giao đồ thị hàm số.
Ta thấy đồ thị hàm số cắt \(y = \frac{1}{3}\) tại 4 điểm trong \([ - \pi ;\pi ]\) nên có tất cả 4 nghiệm.
Cho hình chóp S.ABCD có đáy là hình bình hành. Hai điểm M, N lần lượt là trung điểm của SB và SC. Đường thẳng MN song song với mặt phẳng nào sau đây?
(SAB)
(SCD)
(SAD)
(SBD)
Đáp án : C
Tính chất đường trung bình.
Ta thấy MN là đường trung bình của \(\Delta SBC \Rightarrow\) MN // BC // AD, suy ra MN // (SAD).
Điểm thi môn Toán trong Kỳ thi Tốt nghiệp trung học phổ thông của 690 học sinh trường THPT X được thống kê bởi bảng số liệu như sau:

Điểm trung bình môn Toán của mẫu số liệu trên xấp xỉ bằng
5,4
6,4
7,4
7,0
Đáp án : B
Công thức tìm giá trị trung bình.
Ta có \(\bar x = \frac{{15.1 + 55.3 + 190.5 + 290.7 + 140.9}}{{15 + 55 + 190 + 290 + 140}} = 6,4\).
Giá trị của \(\mathop {\lim }\limits_{x \to {\rm{ \;}} + \infty } \frac{{{2^n} + 1}}{{{3^n}}}\) bằng
2
1
-1
0
Đáp án : D
Chia cả tử và mẫu cho \({3^n}\).
\(\mathop {\lim }\limits_{x \to {\rm{ \;}} + \infty } \frac{{{2^n} + 1}}{{{3^n}}} = \mathop {\lim }\limits_{x \to {\rm{ \;}} + \infty } \frac{{{{\left( {\frac{2}{3}} \right)}^n} + {{\left( {\frac{1}{3}} \right)}^n}}}{1} = 0\).
Từ thành phố A đến thành phố B có 4 con đường đi, từ thành phố B đến thành phố C có 3 con đường đi. Số cách đi từ thành phố A đến thành phố C mà phải đi qua thành phố B là
12
1
42
7
Đáp án : D
Quy tắc cộng xác suất.
Theo quy tắc cộng có tất cả 4 + 3 = 7 cách.
Tập xác định của hàm số \(y = \frac{4}{{\sin x}}\) là
\(D = R\backslash \left\{ {k\pi ,k \in Z} \right\}\)
\(D = \mathbb{R}\)
\(D = R\backslash \left\{ {k2\pi ,k \in Z} \right\}\)
\(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}\)
Đáp án : A
Giải phương trình \(\sin x \ne 0\).
Ta có \(\sin x \ne 0 \Leftrightarrow x \ne k\pi {\rm{ \;}} \Rightarrow D = \mathbb{R}\backslash \left\{ {k\pi ,k \in Z} \right\}\).
Cho dãy số \(({u_n})\) với \({u_n} = 3n + 1,\forall n \in {N^*}\). Giá trị của \({u_3}\) bằng
7
28
10
12
Đáp án : C
Thay \(n = 3\) vào \({u_n} = 3n + 1,\forall n \in {N^*}\).
Thay \(n = 3\) vào \({u_n} = 3n + 1,\forall n \in {N^*}\) ta được \({u_4} = 3.3 + 1 = 10\).
Thống kê thời gian hoàn thành một đề thi online của 25 học sinh, ta được bảng sau:

Mốt của mẫu số liệu ghép nhóm trên thuộc nhóm nào dưới đây?
[25; 30)
[15; 20)
[5; 10)
[10; 15)
Đáp án : B
Tìm nhóm có tần số lớn nhất.
Nhóm [15;20] có 10 học sinh nhiều nhất nên là nhóm chứa mốt.
Cho cấp số nhân \(({u_n})\) với \({u_2} = 3\) và \({u_3} = 6\). Công bội của cấp số nhân đã cho là
\(\frac{1}{2}\)
2
-2
\( - \frac{1}{2}\)
Đáp án : B
Công bội \(q = \frac{{{u_{n + 1}}}}{{{u_n}}}\).
Công bội \(q = \frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{6}{3} = 2\).
Hàm số nào dưới đây có đồ thị là đường cong như hình vẽ?
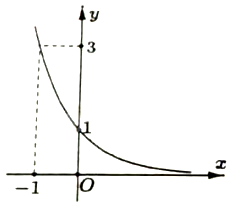
\(y = {\left( {\frac{1}{3}} \right)^x}\)
\(y = {\log _3}x\)
\(y = {\log _{\frac{1}{3}}}x\)
\(y = {3^x}\)
Đáp án : A
Dựa vào tập xác định và các điểm mà đồ thị đi qua.
Từ đồ thị ta thấy hàm số xác định trên \(\mathbb{R}\), nghịch biến và đi qua \(\left( { - 1,3} \right)\) nên \(y = {\left( {\frac{1}{3}} \right)^x}\).
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{{x^2} - 3x + 2}}{{x - 2}}}\\1\end{array}} \right.\) \(\begin{array}{*{20}{l}}{khi}\\{khi}\end{array}\) \(\begin{array}{*{20}{l}}{x \ne 2}\\{x = 2}\end{array}\).
a) Giá trị của \(f(2)\) bằng 1.
b) Giá trị của \(\mathop {\lim }\limits_{x \to 2} f(x)\) bằng -1.
c) Hàm số đã cho liên tục trên \(\mathbb{R}\).
d) Giá trị của \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {xf(x) + 1} }}{{x + 1}}\) bằng 1.
a) Giá trị của \(f(2)\) bằng 1.
b) Giá trị của \(\mathop {\lim }\limits_{x \to 2} f(x)\) bằng -1.
c) Hàm số đã cho liên tục trên \(\mathbb{R}\).
d) Giá trị của \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {xf(x) + 1} }}{{x + 1}}\) bằng 1.
Tính biểu thức \(f(x)\) tại \(x = 2\).
Tính \(\mathop {\lim }\limits_{x \to 2} f(x)\), xét tính liên tục của hàm số.
a) Đúng. Khi \(x = 2\) thì \(f(x) = 1\). Do đó \(f(2) = 1\).
b) Sai. Có \(\mathop {\lim }\limits_{x \to 2} f(x) = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 3x + 2}}{{x - 2}}\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2)(x - 1)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} (x - 1) = 2 - 1 = 1\).
c) Đúng. Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to 2} f(x) = 1}\\{f(2) = 1}\end{array}} \right.\) suy ra \(\mathop {\lim }\limits_{x \to 2} f(x) = f(2) = 1\).
Vậy hàm số liên tục trên \(\mathbb{R}\).
d) Sai. Khi \(x \ne 2\) thì \(f(x) = \frac{{{x^2} - 3x + 2}}{{x - 2}} = x - 1\) nên ta có:
\(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {xf(x) + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {x(x - 1) + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {{x^2} - x + 1} }}{{x + 1}}\)
\( = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\sqrt {{x^2}\left( {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} \right)} }}{{x + 1}} = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{\left| x \right|\sqrt {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} }}{{x + 1}} = \mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \frac{{ - x\sqrt {1 - \frac{1}{x} + \frac{1}{{{x^2}}}} }}{{x + 1}} = {\rm{\;}} - 1\).
Cho hình H là một tam giác đều cạnha) Người ta lần lượt thực hiện các bước như sau:
Bước 1: Chia mỗi cạnh của hình H thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài hình H, sau đó xóa bỏ đoạn ở giữa, ta được hình \({H_1}\) (tham khảo hình vẽ).
Bước 2: Tiếp tục lặp lại quá trình trên với mỗi cạnh của hình \({H_1}\) ta được hình \({H_2}\).
Sau nhiều bước thực hiện như trên, ta được một hình giống như bông tuyết, gọi là bông tuyết Von Koch.
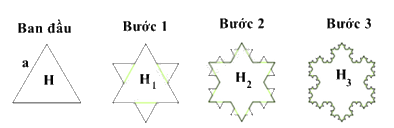
a) Độ dài mỗi cạnh của hình \({H_1}\) là \(\frac{a}{3}\).
b) Với mọi số tự nhiên\(\;n \ge 2\) thì độ dài mỗi cạnh của hình \({H_{n - 1}}\) gấp 3 lần độ dài mỗi cạnh của hình \({H_n}\).
c) Gọi \({u_1},{u_2},.....,{u_n},....\) lần lượt là số cạnh của các hình \({H_1},{H_2},....{H_n},...\). Khi đó, dãy số \({u_1},{u_2},{u_3},{u_4},....\) theo thứ tự lập thành một cấp số nhân có công bội \(q = 4\).
d) Chu vi của hình bông tuyết Von Koch \({H_{16}}\) lớn hơn 100 lần chu vi của hìnhH.
a) Độ dài mỗi cạnh của hình \({H_1}\) là \(\frac{a}{3}\).
b) Với mọi số tự nhiên\(\;n \ge 2\) thì độ dài mỗi cạnh của hình \({H_{n - 1}}\) gấp 3 lần độ dài mỗi cạnh của hình \({H_n}\).
c) Gọi \({u_1},{u_2},.....,{u_n},....\) lần lượt là số cạnh của các hình \({H_1},{H_2},....{H_n},...\). Khi đó, dãy số \({u_1},{u_2},{u_3},{u_4},....\) theo thứ tự lập thành một cấp số nhân có công bội \(q = 4\).
d) Chu vi của hình bông tuyết Von Koch \({H_{16}}\) lớn hơn 100 lần chu vi của hìnhH.
Phân tích đề bài, suy ra độ dài cạnh và số cạnh của các hình \({H_n}\).
a) Đúng. Chia mỗi cạnh của hình H thành ba đoạn thẳng bằng nhau nên mỗi đoạn là có độ dài \(\frac{a}{3}\) và trên mỗi đoạn thẳng đó, dựng một tam giác đều nằm ngoài hình H, ta được hình \({H_1}\) nên độ dài mỗi cạnh của hình \({H_1}\) là \(\frac{a}{3}\).
b) Đúng. Độ dài mỗi cạnh của hình \({H_{n - 1}}\) là \(\frac{a}{{{3^{n - 1}}}}\).
Độ dài mỗi cạnh của hình \({H_n}\) là \(\frac{a}{{{3^n}}}\).
Suy ra độ dài hình \({H_{n - 1}}\) gấp 3 lần độ dài mỗi cạnh của hình \({H_n}\).
c) Đúng. \({u_1},{u_2},.....,{u_n},....\) lần lượt là số cạnh của các hình \({H_1},{H_2},....{H_n},...\)
Có \(u = 3;{u_1} = 12 = 3.4;{u_2} = 48 = {3.4^2},...,{u_n} = {3.4^n}\).
Vậy dãy số \({u_1},{u_2},{u_3},{u_4},....\) theo thứ tự lập thành một cấp số nhân có công bội q = 4.
d) Sai. Hình \(H\) có chu vi là 3a.
Hình \({H_{16}}\) có số cạnh là \({3.4^{16}}\) cạnh và độ dài mỗi cạnh là \(\frac{a}{{{3^{16}}}}\).
Chu vi hình \({H_{16}}\) là \({3.4^{16}}.\frac{a}{{{3^{16}}}} \approx 299a\).
Vậy hình \({H_{16}}\) có chu vi gấp 99,67 lần chu vi hình H.
Giả sử số lượng của một quần thể vi sinh vật tại môi trường nuôi cấy trong phòng thí nghiệm (phụ thuộc vào thời gian nuôi cấy) được mô hình hóa bằng hàm số \(P(t) = \frac{{25}}{{a + {e^{ - 0.8t}}}}\;\) trong đó thời gian t được tính bằng giờ, a là hệ số điều chỉnh mật độ vi sinh vật ban đầu. Biết rằng, tại thời điểm ban đầu \(t = 0\) quần thể có 20 vi sinh vật.
a) Giá trị của \(a\) bằng 0,25.
b) Sau 2 giờ, quần thể có nhiều hơn 60 vi sinh vật.
c) Với quy trình nuôi cấy theo mô hình trên thì số lượng vi khuẩn trong quần thể không lớn hơn 100.
d) Để số lượng vi sinh vật trong quần thể lớn hơn 90 thì cần nuôi cấy ít nhất 6 giờ.
a) Giá trị của \(a\) bằng 0,25.
b) Sau 2 giờ, quần thể có nhiều hơn 60 vi sinh vật.
c) Với quy trình nuôi cấy theo mô hình trên thì số lượng vi khuẩn trong quần thể không lớn hơn 100.
d) Để số lượng vi sinh vật trong quần thể lớn hơn 90 thì cần nuôi cấy ít nhất 6 giờ.
Có P(0) = 20, tính \(a\). Thay giá trị \(t\) để tính \(P(t).\)
Tính giới hạn tại vô cùng của hàm \(P(t).\)
Giải bất phương trình \(P(t) > 90.\)
a) Đúng. Ta có \(P(t) = \frac{{25}}{{a + {e^{ - 0.8t}}}}\), và \(P(0) = 20\) nên \(\frac{{25}}{{a + {e^{ - 0,8.0}}}} = 20 \Leftrightarrow a = \frac{{25}}{{20}} - 1 = 0,25\)
b) Sai. Sau 2 giờ, số vi sinh vật là \(P(2) = \frac{{25}}{{0,25 + {e^{ - 0,8.2}}}} \approx 55,3\)
c) Đúng. Ta cần tính \(\mathop {\lim }\limits_{t \to {\rm{\;}} + \infty } P(t) = \mathop {\lim }\limits_{t \to {\rm{\;}} + \infty } \frac{{25}}{{0,25 + {e^{ - 0,8.t}}}}\).
Khi \(t \to {\rm{\;}} + \infty \) thì \({e^{ - 0,8t}} \to 0\), nên \(\mathop {\lim }\limits_{t \to {\rm{\;}} + \infty } P(t) = \mathop {\lim }\limits_{t \to {\rm{\;}} + \infty } \frac{{25}}{{0,25 + {e^{ - 0,8.t}}}} = \frac{{25}}{{0,25}} = 100\)
Vậy số lượng vi khuẩn trong quần thể không lớn hơn 100.
d) Sai. Ta có:
\(\begin{array}{*{20}{l}}{P(t) = \frac{{25}}{{0,25 + {e^{ - 0.8t}}}} > 90 \Leftrightarrow {e^{ - 0,8.t}} < \frac{{25}}{{90}} - 0,25}\\{ \Leftrightarrow {e^{ - 0,8.t}} < \frac{1}{{36}} \Leftrightarrow t > 4,48}\end{array}\)
Để số lượng vi sinh vật trong quần thể lớn hơn 90 thì cần nuôi cấy ít nhất 4,48 giờ.
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD // BC, AD = 2BC. Gọi O là giao điểm của hai đường chéo AC và BD, điểm M là trung điểm của đoạn thẳng SC.
a) Đường thẳng AM nằm trong mặt phẳng (SAC).
b) Giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng SO.
c) Giao điểm của đường thẳng AM và mặt phẳng (SBD) là giao điểm của AM và SO.
d) Gọi \(\left( {\alpha {\rm{\;}}} \right)\) là mặt phẳng chứa đường thẳng AM và song song với đường thẳng BD. Mặt phẳng \(\left( {\alpha {\rm{\;}}} \right)\) cắt SB tại P. Khi đó \(\frac{{SP}}{{SB}} = \frac{2}{3}\).
a) Đường thẳng AM nằm trong mặt phẳng (SAC).
b) Giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng SO.
c) Giao điểm của đường thẳng AM và mặt phẳng (SBD) là giao điểm của AM và SO.
d) Gọi \(\left( {\alpha {\rm{\;}}} \right)\) là mặt phẳng chứa đường thẳng AM và song song với đường thẳng BD. Mặt phẳng \(\left( {\alpha {\rm{\;}}} \right)\) cắt SB tại P. Khi đó \(\frac{{SP}}{{SB}} = \frac{2}{3}\).
Vẽ hình.
Xét điểm A, M có thuộc mặt phẳng (SAC) không.
Xét hai điểm S, O cùng thuộc mặt phẳng (SAC) và mặt phẳng (SBD) không
Gọi giao điểm của AM và SO là I, chứng minh \(I \in (SBD)\).
Sử dụng phương pháp phản chứng: Giả sử \(\frac{{SP}}{{SB}} = \frac{2}{3}\) rồi chứng minh điều đó vô lí.
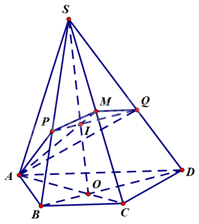
a) Đúng. Vì \(M \in SC\) nên \(M \in (SAC)\), lại có \(A \in (SAC)\) nên AM nằm trong mặt phẳng (SAC).
b) Đúng. Ta có \(O \in AC\) nên \(O \in (SAC)\); \(O \in BD\) nên \(O \in (SBD)\). Do đó O thuộc cả hai mặt phẳng (SAC) và (SBD).
Mà S cũng thuộc cả hai mặt phẳng (SAC) và (SBD).
Vậy SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
c) Đúng. Theo chứng minh ở các phần trên, SO và MA cùng thuộc mặt phẳng (SAC), hai đường thẳng đó không song song với nhau nên gọi giao điểm của chúng là I.
Khi đó, \(I \in AM\) (1).
Vì \(I \in SO\), mà \(SO \subset (SBD)\) nên \(I \in (SBD)\) (2).
Từ (1) và (2) suy ra I là giao điểm của AM và mặt phẳng (SBD), đồng thời là giao điểm của SO và MA.
d) Sai. Vì AD // BC nên theo hệ quả của định lý Thales, ta có:
\(\frac{{CO}}{{OA}} = \frac{{BC}}{{AD}} = \frac{1}{2}\) (vì AD = 2BC theo giả thiết).
Suy ra \(\frac{{CO}}{{CA}} = \frac{1}{3}\), tức O không phải trung điểm của AC.
Gọi giao điểm của \(\left( {\alpha {\rm{\;}}} \right)\) và SD là Q. Khi đó, PQ là giao tuyến của \(\left( {\alpha {\rm{\;}}} \right)\) và (SBD).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{(\alpha )//BD}\\\begin{array}{l}BD \subset (SBD)\\(SBD) \cap (\alpha ) = PQ\end{array}\end{array}} \right.\) suy ra BD // PQ (3).
Vì \(I \in AM\) và \(AM \subset \left( {\alpha {\rm{\;}}} \right)\) nên \(I \in \left( {\alpha {\rm{\;}}} \right)\), mà \(I \in (SBD)\) nên I thuộc giao tuyến của \(\left( {\alpha {\rm{\;}}} \right)\) và (SBD), hay \(I \in PQ\) (4).
Từ (3) và (4) suy ra PI // BO.
Giả sử \(\frac{{SP}}{{SB}} = \frac{2}{3}\).
Vì PI // BO nên theo định lí Thales ta có: \(\frac{{SI}}{{SO}} = \frac{{SP}}{{SB}} = \frac{2}{3}\).
Vì M là trung điểm của SC suy ra AM là đường trung tuyến của \(\Delta SAC\).
Mặt khác, \(I \in AM\) và \(\frac{{SI}}{{SO}} = \frac{2}{3}\) nên I là trọng tâm \(\Delta SAC\).
Do đó, SO là đường trung tuyến của \(\Delta SAC\), hay O là trung điểm của AC (vô lí).
Vậy \(\frac{{SP}}{{SB}} \ne \frac{2}{3}\).
Cho cấp số cộng (\({u_n}\)) có \({u_3} = 9\) và \({u_7} = 17\). Tổng của 20 số hạng đầu tiên của cấp số cộng đã cho bằng bao nhiêu?
Đáp án:
Đáp án:
Áp dụng công thức số hạng tổng quát \({u_n} = {u_1} + (n - 1)d\) để tìm \({u_1}\) và \(d\).
Áp dụng công thức tính tổng của n số hạng đầu của cấp số cộng.
Có \({u_3} = 9\) và \({u_7} = 17\) nên \(\left\{ {\begin{array}{*{20}{l}}{{u_1} + 2d = 9}\\{{u_1} + 6d = 17}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{u_1} = 5}\\{d = 2}\end{array}} \right.\).
Áp dụng công thức tính tổng, có \({S_{20}} = \frac{{20}}{2}(2.5 + 19.2) = 480\).
Anh An gửi 100 triệu vào ngân hàng với kì hạn 1 năm và hưởng lãi suất 5,4%/năm theo thể thức lãi kép. Sau khi gửi được tròn 9 tháng, anh cần dùng đến 100 triệu trên để sửa nhà. Nhân viên ngân hàng đã đưa ra cho anh hai phương án như sau:
*Phương án 1: Anh rút hết tiền trước kì hạn. Khi đó toàn bộ số tiền anh gửi sẽ được tính lãi với lãi suất không kì hạn là \(0,2\% \)/năm (tính theo thể thức lãi kép với kì hạn 1 tháng).
*Phương án 2: Anh thế chấp sổ tiết kiệm đó để vay ngân hàng 100 triệu. Khi đó, toàn bộ số tiền vay sẽ phải chịu lãi suất \(8\% \)/năm (tính theo thể thức lãi kép với kì hạn 1 tháng). Đủ kì hạn 1 năm của khoản tiền gửi, anh sẽ rút hết tiền và trả hết nợ cho ngân hàng.
Nếu làm theo phương án 2 thì anh được lợi bao nhiêu triệu đồng so với phương án 1 (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Đáp án:
Áp dụng công thức lãi kép \(T = A{\left( {1 + r} \right)^n}\).
Xét phương án 1: Với số tiền gửi là 100 triệu, lãi suất theo tháng là \(\frac{{5,4}}{{12}} = \frac{1}{{60}}\% \), gửi trong 6 tháng thì toàn bộ số tiền anh An nhận được sau 9 tháng là:
\(T = A{\left( {1 + r} \right)^n} = 100{\left( {1 + \frac{1}{{60}}\% } \right)^9} = 100,1501\) triệu tức là lợi được 0,1501 triệu.
Xét phương án 2: Số tiền anh An nhận được khi gửi với lãi suất 5,4% trong 1 năm là
\(T = 100.5,4\% {\rm{ \;}} = 105,4\) triệu.
Anh An cần vay ngân hàng trong 3 tháng với lãi suất 8%/năm tức là \(\frac{8}{{12}}\% \)/tháng.
\( \Rightarrow T = 100{\left( {1 + \frac{8}{{12}}\% } \right)^3}\).
Vậy số tiền anh An dư sau khi trả ngân hàng là \(105,4 - 100{\left( {1 + \frac{8}{{12}}\% } \right)^3} = 3,386\) triệu.
Khi đó so với phương án 1 thì anh An lợi được \(3,386 - 0,1501 \approx 3,24\) triệu.
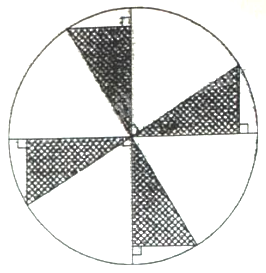
Một khu phố có kế hoạch tu sửa một sân chơi hình tròn, bán kính 10m. Theo bản thiết kế dự kiến thì công (như hình vẽ), người ta lát gạch trang trí ở phần kẻ sọc (với \({0^\circ } < \alpha {\rm{ \;}} < {45^\circ }\)) và phần còn lại đổ xi măng. Chi phí lát gạch là 1 triệu đồng/\(1{m^2}\) và chi phí đổ xi măng là 300 nghìn đồng/\(1{m^2}\) (giả sử phần chi phí khác không đáng kể). Hỏi góc \(\alpha \) lớn nhất là bao nhiêu độ để chi phí tu sửa không lớn hơn 150 triệu đồng (làm tròn kết quả đến hàng đơn vị).
Đáp án:
Đáp án:
Tính diện tích của phần làm gạch và phần còn lại theo \(\alpha \). Từ đó lập hàm chi phí và tìm GTNN.
Xét 1 phần gạch hình tam giác là \(\Delta OAB\) vuông tại A, có \(OB = 10,\angle AOB = \alpha \).
\(\begin{array}{*{20}{l}}{ \Rightarrow OA = 10.\sin \alpha ;AB = 10.\cos \alpha }\\{ \Rightarrow {S_{\Delta OAB}} = \frac{1}{2}.10.\sin \alpha .10.\cos \alpha {\rm{ \;}} = 25\sin 2\alpha }\end{array}\)
Khi đó diện tích phần gạch lát là \(S = 4.25\sin 2\alpha {\rm{ \;}} = 100\sin 2\alpha \).
Diện tích của cả hình tròn là \(S = \pi {.10^2} = 100\pi \).
Diện tích phần lát xi măng là \(S = 100\pi {\rm{ \;}} - 100.\sin 2\alpha \).
Vậy chi phí cần bỏ ra là \(T = 100.\sin 2\alpha .1 + \left( {100 - 100\sin 2\alpha } \right).0,3 = 70\sin 2\alpha {\rm{ \;}} + 30\pi \).
Do chi phí nhỏ hơn 150 triệu nên ta có
\(\begin{array}{*{20}{l}}{70\sin 2\alpha {\rm{ \;}} + 30\pi {\rm{ \;}} < 150}\\{ \Leftrightarrow \sin 2\alpha {\rm{ \;}} < 0,79}\\{ \Leftrightarrow 2\alpha {\rm{ \;}} < 52,{{79}^o}}\\{ \Leftrightarrow \alpha {\rm{ \;}} < 26,{{39}^o}}\end{array}\)
Vậy góc \(\alpha \) nhỏ nhất bằng \({26^o}\).
Trong kỳ thi vấn đáp, bạn Bình phải bốc thăm ngẫu nhiên và trả lời 3 chủ đề trong số 10 chủ đề đã được chuẩn bị trước. Bạn Bình chỉ chuẩn bị được 7 trong 10 chủ đề trên. Xác suất để Bình bốc được ít nhất hai chủ đề trong những chủ đề đã chuẩn bị bằng bao nhiêu (làm tròn đến hàng phần trăm)?
Đáp án:
Đáp án:
Ta chia thành 2 trường hợp:
TH1: Bình bốc trúng hai chủ đề trong 7 chủ đề đã chuẩn bị và 1 chủ đề trong 3 chủ đề không chuẩn bị.
TH2: Bình bốc trúng ba chủ đề trong 7 chủ đề đã chuẩn bị.
Không gian mẫu là \(C_{10}^3\).
Để Bình bốc được ít nhất hai chủ đề trong những chủ đề đã chuẩn bị thì có 2 TH
TH1: Bình bốc trúng hai chủ đề trong 7 chủ đề đã chuẩn bị và 1 chủ đề trong 3 chủ đề không chuẩn bị. Khi đó có \(C_7^2.C_3^1\) cách.
TH2: Bình bốc trúng ba chủ đề trong 7 chủ đề đã chuẩn bị \( \Rightarrow \) Có \(C_7^3\) cách.
Vậy xác suất cần tính là \(P = \frac{{C_7^2.C_3^1 + C_7^3}}{{C_{10}^3}} = 0,8166 \approx 0,82\).
Bất phương trình \({\log _2}(2x - 1) < {\log _2}(14 - x)\) có bao nhiêu nghiệm nguyên?
Đáp án:
Đáp án:
Tìm ĐKXĐ và giải bất phương trình cơ bản.
ĐKXĐ: \(\frac{1}{2} < x < 14\).
\(\begin{array}{*{20}{l}}{{{\log }_2}(2x - 1) < {{\log }_2}(14 - x)}\\{ \Leftrightarrow 2x - 1 < 14 - x}\\{ \Leftrightarrow 3x < 15}\\{ \Leftrightarrow x < 5}\end{array}\)
\( \Rightarrow \frac{1}{2} < x < 5\).
Do \(x \in \mathbb{Z} \Rightarrow x \in \left\{ {1,2,3,4} \right\}\).
Vậy có tất cả 4 nghiệm nguyên.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 6. Gọi M là trung điểm của đoạn thẳng SB và điểm N thuộc đoạn thẳng SC sao cho NS = 2NC. Phép chiếu song song lên mặt phẳng (SCD) theo phương chiếu BD biến điểm M thành điểm P. Phép chiếu song song lên mặt phẳng (ABCD) theo phương chiếu SA biến tam giác MNP thành hình T. Khi đó diện tích hình T bằng bao nhiêu?
Đáp án:
Đáp án:
Sử dụng tính chất đường trung bình kẻ các đường thẳng song song tìm M, N, P. Từ đó tính diện tích tam giác.
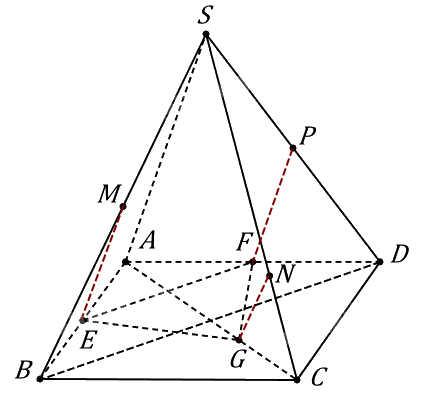
Xét trong (SBD) kẻ \(MP\parallel BD\) với \(P \in SD\).
Khi đó P là hình chiếu của M xuống (SBD) với phương chiếu BD.
Do M là trung điểm của SB nên MP là đường trung bình của \(\Delta SBD\).
Suy ra P là trung điểm của SD.
Tương tự xét trong (SAB) kẻ \(ME\parallel SA \Rightarrow E\) là trung điểm AB.
Trong (SAD) kẻ \(PF\parallel SA \Rightarrow F\) là trung điểm AD.
Trong \(\left( {SAC} \right)\) kẻ \(NG\parallel SA \Rightarrow \frac{{GC}}{{GA}} = \frac{{NC}}{{SC}} = \frac{1}{3}\) (Thales).
Khi đó hình chiếu của M, N, P xuống (ABCD) theo phương chiếu SA lần lượt là E, G, F.
Ta sẽ tính diện tích \(\Delta GEF\).
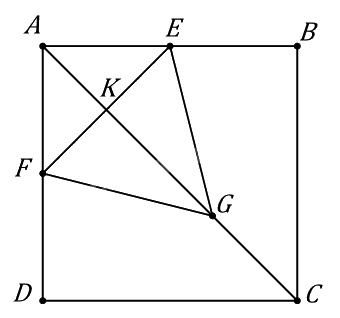
Ta có \(\Delta GEF\) cân tại G nên \({S_{\Delta GEF}} = \frac{1}{2}GK.EF\).
\(AF = AE = \frac{1}{2}AB = 3 \Rightarrow EF = 3\sqrt 2 ;AK = \frac{1}{2}EF = \frac{3}{2}\sqrt 2 \).
\(AC = 6\sqrt 2 ;AG = \frac{2}{3}.6\sqrt 2 {\rm{ \;}} = 4\sqrt 2 {\rm{ \;}} \Rightarrow GK = 4\sqrt 2 {\rm{ \;}} - \frac{3}{2}\sqrt 2 {\rm{ \;}} = \frac{5}{2}\sqrt 2 \).
\( \Rightarrow {S_{\Delta GEF}} = \frac{1}{2}GK.EF = \frac{1}{2}.\frac{5}{2}\sqrt 2 .3\sqrt 2 {\rm{ \;}} = \frac{{15}}{2} = 7,5\).
Đề khảo sát chất lượng Toán 11 năm 2024 - 2025 do sở GD&ĐT Hà Nội tổ chức đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh, đồng thời giúp giáo viên có cái nhìn tổng quan về chất lượng giảng dạy. Bài viết này sẽ phân tích chi tiết cấu trúc đề thi, các dạng bài tập thường gặp và cung cấp hướng dẫn giải chi tiết để học sinh có thể tự tin đối phó với kỳ thi.
Thông thường, đề khảo sát chất lượng Toán 11 của sở GD&ĐT Hà Nội bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề khảo sát bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong đề khảo sát chất lượng Toán 11:
Để giải quyết các bài tập trong đề khảo sát chất lượng Toán 11, học sinh cần nắm vững các kiến thức cơ bản, rèn luyện kỹ năng giải toán và áp dụng các phương pháp giải toán phù hợp. Dưới đây là một số hướng dẫn giải chi tiết cho một số dạng bài tập thường gặp:
Phương trình bậc hai có dạng ax2 + bx + c = 0. Để giải phương trình này, ta có thể sử dụng công thức nghiệm:
x = (-b ± √(b2 - 4ac)) / 2a
Nếu b2 - 4ac > 0, phương trình có hai nghiệm phân biệt.
Nếu b2 - 4ac = 0, phương trình có nghiệm kép.
Nếu b2 - 4ac < 0, phương trình vô nghiệm.
Để chứng minh đẳng thức lượng giác, ta có thể sử dụng các công thức lượng giác cơ bản và các phép biến đổi đại số. Ví dụ, ta có thể sử dụng công thức sin2x + cos2x = 1 để biến đổi vế trái của đẳng thức về vế phải hoặc ngược lại.
Tập xác định của hàm số là tập hợp tất cả các giá trị của x sao cho hàm số có nghĩa. Để tìm tập xác định của hàm số, ta cần xác định các điều kiện để hàm số có nghĩa, ví dụ như mẫu số khác 0, căn thức không âm, logarit có cơ số lớn hơn 0 và khác 1.
Hy vọng với những phân tích và hướng dẫn trên, học sinh có thể tự tin hơn khi làm bài thi khảo sát chất lượng Toán 11 năm 2024 - 2025 của sở GD&ĐT Hà Nội. Chúc các em học tập tốt và đạt kết quả cao!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số bậc hai | Cao |
| Phương trình và bất phương trình | Cao |
| Vectơ | Trung bình |
| Hàm số lượng giác | Trung bình |
| Nguồn: Giaitoan.edu.vn | |