Giaitoan.edu.vn xin giới thiệu đến quý thầy cô và các em học sinh đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 của trường THPT Triệu Sơn 4, Thanh Hóa. Đây là một đề thi quan trọng giúp các em đánh giá năng lực hiện tại và làm quen với cấu trúc đề thi THPT Quốc gia.
Đề thi được biên soạn bám sát chương trình học, có độ khó phù hợp, giúp các em rèn luyện kỹ năng giải đề và tự tin hơn trong kỳ thi sắp tới.
Với a là số thực dương tuỳ ý, \(\sqrt {{a^3}} \) bằng
\({a^{\frac{3}{2}}}\)
\({a^{\frac{2}{3}}}\)
\({a^6}\)
\({a^{\frac{1}{6}}}\)
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\(\left( {0; + \infty } \right)\)
\(\left( { - 3;0} \right)\)
\(\left( {0;2} \right)\)
\(\left( { - \infty ; - 3} \right)\)
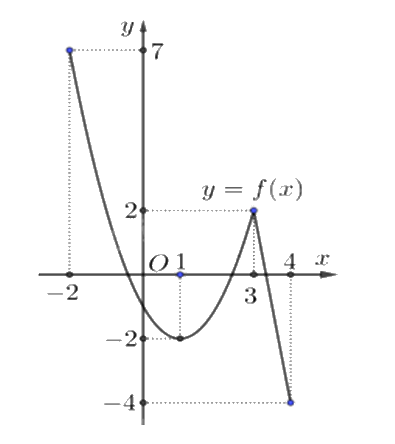
Cho hàm số y = f(x) liên tục và có đồ thị trên đoạn [-2;4] như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên đoạn [-2;4] bằng
-2
5
3
0
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA = SC, SB = SD. Trong các khẳng định sau khẳng định nào đúng?
\(SC \bot \left( {ABCD} \right)\)
\(SA \bot \left( {ABCD} \right)\)
\(SB \bot \left( {ABCD} \right)\)
\(SO \bot \left( {ABCD} \right)\)
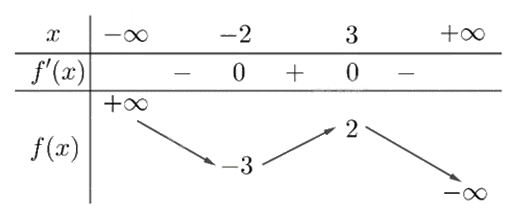
Cho hàm số y = f(x) có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
-2
-3
3
2
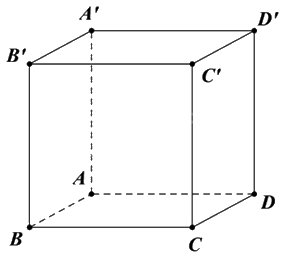
Cho hình lập phương ABCD.A’B’C’D’ (minh họa như hình bên). Mệnh đề nào sau đây sai?
\(\overrightarrow {AB} = \overrightarrow {CD} \)
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
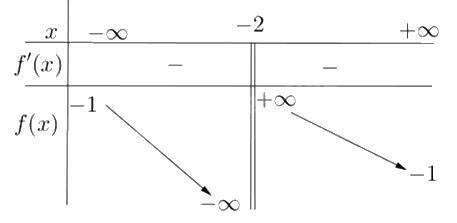
Cho hàm số y = f(x) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình
x = -1
x = -2
y = -1
y = -2
Một nhóm học sinh gồm 20 học sinh nam và 10 học sinh nữ. Có bao nhiêu cách chọn một học sinh nam trong nhóm đó tham gia đội thanh niên tình nguyện của trường?
30
10
20
200
Cho hàm số \(f(x) = {e^x} + 2\). Khẳng định nào dưới đây là đúng?
\(\int f (x)dx = {e^x} + C\)
\(\int f (x)dx = {e^x} + 2x + C\)
\(\int f (x)dx = {e^{x - 2}} + C\)
\(\int f (x)dx = {e^x} - 2x + C\)
Cho cấp số nhân $\left( {{u}_{n}} \right)$ với \({u_1} = 2\) và công bội \(q = 3\). Tìm số hạng thứ \(4\) của cấp số nhân?
54
48
24
162
Cho hàm số $y=\frac{ax+b}{cx+d}$ $(c\ne 0,ad-bc\ne 0)$ có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị hàm số là
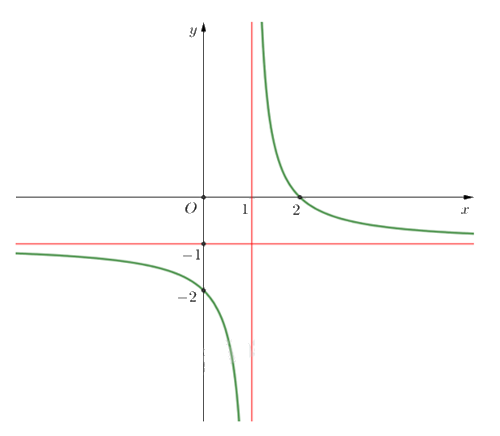
x = -1
y = -1
x = 1
y = 1
Tập nghiệm của bất phương trình \({\log _5}\left( {2x - 1} \right) < {\log _5}\left( {x + 2} \right)\) là
\(S=\left( 3;+\infty \right)\)
\(S = \left( { - 2;3} \right)\)
\(S=\left( \frac{1}{2};3 \right)\)
\(S = \left( { - \infty ;3} \right)\)
Cho hàm số có đạo hàm ${f}'\left( x \right)={{\left( x-1 \right)}^{2}}\left( {{x}^{2}}-3x+2 \right)$ với mọi \(x \in \mathbb{R}\).
a) Hàm số đồng biến trên khoảng \(( - \infty ;2)\).
b) Hàm số \(y = f\left( {{x^2} - 4x + 1} \right)\) có ba điểm cực tiểu.
c) Hàm số f(x) có hai điểm cực trị.
d) Điểm cực đại của đồ thị hàm số là x = 1.
Thầy giáo thống kê lại điểm trung bình cuối năm của các học sinh lớp 11A và 11B ở bảng sau:

a) So sánh theo độ lệch chuẩn thì các học sinh lớp 11A học đồng đều hơn lớp 11B.
b) Điểm trung bình của lớp 11A nhỏ hơn lớp 11B.
c) Phương sai của mẫu số liệu lớp 11B là 1,05 (làm tròn đến hàng phần trăm).
d) Điểm trung bình của lớp 11A là 8,3 (làm tròn đến hàng phần chục).
Cho phương trình lượng giác \(\cos 2x = - \frac{1}{2}\) (*).
a) Phương trình (*) tương đương với phương trình: \(\cos 2x = \cos \left( { - \frac{\pi }{3}} \right)\).
b) Nghiệm dương nhỏ nhất của phương trình (*) bằng \(\frac{\pi }{3}\).
c) Tổng các nghiệm của phương trình (*) trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{3\pi }}{2}\).
d) Trong khoảng \(\left( {0;\pi } \right)\) phương trình (*) có 3 nghiệm.
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 1, có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho $MO=\frac{1}{2}MI$. Gắn hệ trục A’xyz như hình vẽ.
a) Tọa độ điểm $M\left( \frac{1}{2};\frac{1}{2};\frac{1}{4} \right).$
b) Tọa độ các điểm A’(0;0;0), B’(1;0;0), D’(0;1;0) và A(0;0;1).
c) Trong không gian giả sử điểm P, Q sao cho \(\overrightarrow {A'P} = \overrightarrow {A'B'} + 2\overrightarrow {A'D'} - 2\overrightarrow {A'A} \); \(\overrightarrow {A'Q} = \frac{8}{3}\overrightarrow {A'B'} + \frac{4}{3}\overrightarrow {A'D'} + \frac{8}{3}\overrightarrow {A'A} \) và J(a;b;c) là tâm đường tròn nội tiếp tam giác A’PQ, khi đó a – b + c = 0.
d) Trong không gian có đúng 2 điểm N sao cho N không trùng với các điểm A, B’, D’ và \(\widehat {ANB'} = \widehat {B'ND'} = \widehat {D'NA} = 90^\circ \).
Cho hàm số y = f(x) có đạo hàm liên tục trên $\mathbb{R}$ và có bảng biến thiên của đạo hàm như hình vẽ.
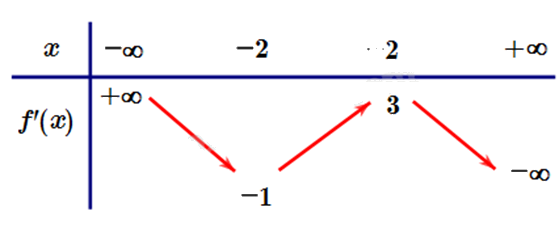
Đặt \(g\left( x \right)=f\left( \frac{{{x}^{2}}+1}{x} \right)\). Tìm số điểm cực trị của hàm số \(y=g\left( x \right).\)
Đáp án:
Độ dốc của mái nhà (mặt sân, con đường thẳng…) là tan của góc tạo bởi mái nhà (mặt sân, con đường thẳng…) đó với mặt phẳng nằm ngang. Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều, biết rằng diện tích để lát tất cả các mặt của kim tự tháp bằng 80300 ${{m}^{2}}$ và độ dốc của mặt bên kim tự tháp bằng \(\frac{{49}}{{45}}\). Tính chiều cao (đơn vị m) của kim tự tháp (làm tròn đến hàng đơn vị).

Đáp án:
Một đoàn tàu gồm 3 toa đỗ ở sân ga. Có 5 hành khách bước lên tàu, mỗi hành khách độc lập với nhau chọn ngẫu nhiên 1 toa. Tính xác suất để mỗi toa có ít nhất 1 hành khách bước lên tàu (kết quả làm tròn đến hàng phần trăm).
Đáp án:
Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100 m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Biết dòng sông là thẳng, mục tiêu cách chiến sỹ 1 km theo đường chim bay và chiến sỹ cách bờ bên kia 100 m. Hãy cho biết chiến sỹ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất (làm tròn kết quả đến hàng đơn vị).
Đáp án:
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(3;1;0), B(3;6;6), C(4;6;2), D(6;2;14) và điểm M(a;b;c) thỏa mãn MA = 3, MB = 6, MC = 5, MD = 13. Khoảng cách từ điểm M đến điểm O bằng bao nhiêu (làm tròn đến hàng phàn trăm)?
Đáp án:
Một xe ô tô chở khách du lịch có sức chứa tối đa là 16 hành khách. Trong một khu du lịch, một đoàn khách gồm 24 người đang đi bộ và muốn thuê xe về khách sạn. Lái xe đưa ra thỏa thuận với đoàn khách du lịch như sau: Nếu một chuyến xe chở x (người) thì giá tiền cho mỗi người là \(\frac{{{(40-x)}^{2}}}{2}\)(nghìn đồng). Với thỏa thuận như trên thì lái xe có thể thu được nhiều nhất bao nhiêu triệu đồng từ một chuyến chở khách (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Với a là số thực dương tuỳ ý, \(\sqrt {{a^3}} \) bằng
\({a^{\frac{3}{2}}}\)
\({a^{\frac{2}{3}}}\)
\({a^6}\)
\({a^{\frac{1}{6}}}\)
Đáp án : A
Áp dụng công thức \(\sqrt[n]{{{a^m}}} = {a^{\frac{m}{n}}}\).
\(\sqrt {{a^3}} = {a^{\frac{3}{2}}}\).
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\(\left( {0; + \infty } \right)\)
\(\left( { - 3;0} \right)\)
\(\left( {0;2} \right)\)
\(\left( { - \infty ; - 3} \right)\)
Đáp án : B
Hàm số y = f(x) nghịch biến trên khoảng f’(x) < 0.
Hàm số nghịch biến trên khoảng (-3;0) vì f’(x) < 0 trên (-3;0).
Cho hàm số y = f(x) liên tục và có đồ thị trên đoạn [-2;4] như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên đoạn [-2;4] bằng
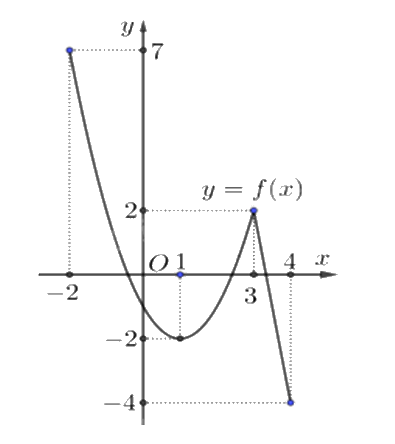
-2
5
3
0
Đáp án : C
Quan sát đồ thị và nhận xét.
Trên [-2;4], giá trị lớn nhất của hàm số là 7, giá trị nhỏ nhất của hàm số là -4, tổng là 7 + (-4) = 3.
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA = SC, SB = SD. Trong các khẳng định sau khẳng định nào đúng?
\(SC \bot \left( {ABCD} \right)\)
\(SA \bot \left( {ABCD} \right)\)
\(SB \bot \left( {ABCD} \right)\)
\(SO \bot \left( {ABCD} \right)\)
Đáp án : D
Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng đó.
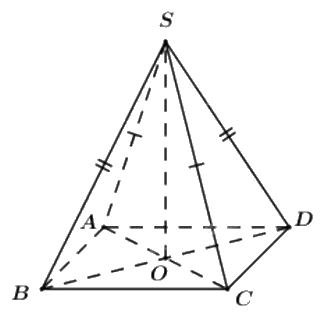
Vì ABCD là hình bình hành nên O là trung điểm của AC và BD.
Khi đó, SO vừa là trung tuyến, vừa là đường cao của tam giác SAC và SBD.
Suy ra \(\left\{ \begin{array}{l}SO \bot AC\\SO \bot BD\end{array} \right. \Rightarrow SO \bot (ABCD)\).
Cho hàm số y = f(x) có bảng biến thiên như sau:
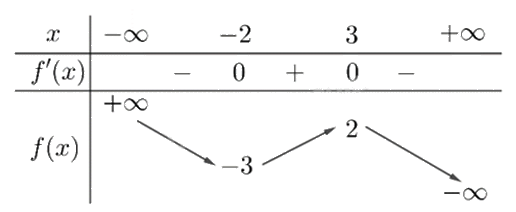
Giá trị cực đại của hàm số đã cho bằng
-2
-3
3
2
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Giá trị cực đại của hàm số đã cho bằng 2.
Cho hình lập phương ABCD.A’B’C’D’ (minh họa như hình bên). Mệnh đề nào sau đây sai?
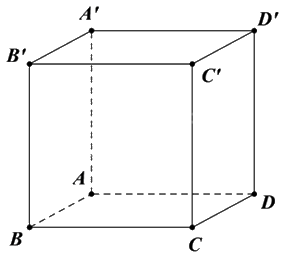
\(\overrightarrow {AB} = \overrightarrow {CD} \)
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
Đáp án : A
Áp dụng định nghĩa hai vecto bằng nhau, quy tắc ba điểm, quy tắc hình hộp và độ dài vecto.
Vì \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng nên \(\overrightarrow {AB} \ne \overrightarrow {CD} \).
Cho hàm số y = f(x) có bảng biến thiên như sau:
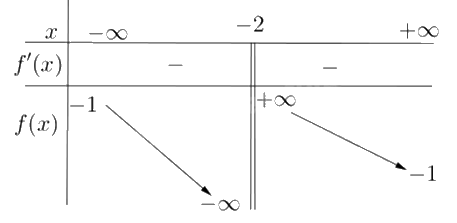
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình
x = -1
x = -2
y = -1
y = -2
Đáp án : B
\(x={{x}_{0}}\) là tiệm cận đứng của đồ thị hàm số y = f(x) nếu thỏa mãn một trong các điều kiện: \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \).
Quan sát bảng biến thiên, thấy \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = + \infty \) nên x = -2 là tiệm cận đứng của đồ thị hàm số.
Một nhóm học sinh gồm 20 học sinh nam và 10 học sinh nữ. Có bao nhiêu cách chọn một học sinh nam trong nhóm đó tham gia đội thanh niên tình nguyện của trường?
30
10
20
200
Đáp án : C
Áp dụng quy tắc cộng.
Có 20 cách chọn một học sinh nam tham gia đội thanh niên tình nguyện của trường.
Cho hàm số \(f(x) = {e^x} + 2\). Khẳng định nào dưới đây là đúng?
\(\int f (x)dx = {e^x} + C\)
\(\int f (x)dx = {e^x} + 2x + C\)
\(\int f (x)dx = {e^{x - 2}} + C\)
\(\int f (x)dx = {e^x} - 2x + C\)
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lũy thừa $\int{{{x}^{\alpha }}dx}=\frac{{{x}^{\alpha +1}}}{\alpha +1}+C$, hàm số mũ \(\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\).
\(\int f (x)dx = \int {\left( {{e^x} + 2} \right)dx} = {e^x} + 2x + C\).
Cho cấp số nhân $\left( {{u}_{n}} \right)$ với \({u_1} = 2\) và công bội \(q = 3\). Tìm số hạng thứ \(4\) của cấp số nhân?
54
48
24
162
Đáp án : A
Áp dụng công thức số hạng tổng quát của cấp số nhân ${{u}_{n}}={{u}_{1}}{{q}^{n-1}}$.
${{u}_{4}}={{u}_{1}}{{q}^{3}}={{2.3}^{3}}=54$.
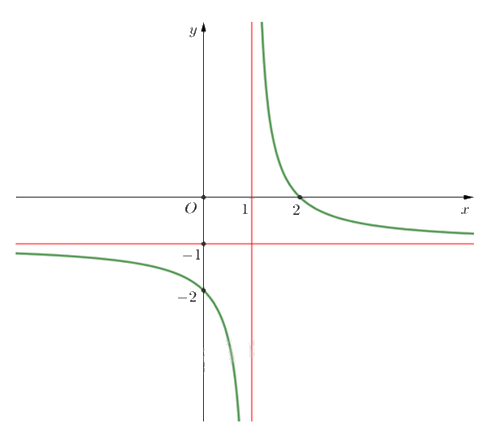
Cho hàm số $y=\frac{ax+b}{cx+d}$ $(c\ne 0,ad-bc\ne 0)$ có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị hàm số là
x = -1
y = -1
x = 1
y = 1
Đáp án : C
Quan sát đồ thị rồi nhận xét.
Tiệm cận đứng của đồ thị hàm số là x = 1.
Tập nghiệm của bất phương trình \({\log _5}\left( {2x - 1} \right) < {\log _5}\left( {x + 2} \right)\) là
\(S=\left( 3;+\infty \right)\)
\(S = \left( { - 2;3} \right)\)
\(S=\left( \frac{1}{2};3 \right)\)
\(S = \left( { - \infty ;3} \right)\)
Đáp án : C
Tìm tập xác định.
Với a > 1, ta có \({{\log }_{a}}x<{{\log }_{a}}y\Leftrightarrow x<y\).
ĐKXĐ: \(\left\{ \begin{array}{l}2x - 1 > 0\\x + 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > \frac{1}{2}\\x > - 2\end{array} \right. \Leftrightarrow x > \frac{1}{2}\).
\({\log _5}\left( {2x - 1} \right) < {\log _5}\left( {x + 2} \right) \Leftrightarrow 2x - 1 < x + 2 \Leftrightarrow x < 3\).
Kết hợp ĐKXĐ ta được tập nghiệm \(S=\left( \frac{1}{2};3 \right)\).
Cho hàm số có đạo hàm ${f}'\left( x \right)={{\left( x-1 \right)}^{2}}\left( {{x}^{2}}-3x+2 \right)$ với mọi \(x \in \mathbb{R}\).
a) Hàm số đồng biến trên khoảng \(( - \infty ;2)\).
b) Hàm số \(y = f\left( {{x^2} - 4x + 1} \right)\) có ba điểm cực tiểu.
c) Hàm số f(x) có hai điểm cực trị.
d) Điểm cực đại của đồ thị hàm số là x = 1.
a) Hàm số đồng biến trên khoảng \(( - \infty ;2)\).
b) Hàm số \(y = f\left( {{x^2} - 4x + 1} \right)\) có ba điểm cực tiểu.
c) Hàm số f(x) có hai điểm cực trị.
d) Điểm cực đại của đồ thị hàm số là x = 1.
Tính đạo hàm, lập bảng biến thiên của hàm số rồi kết luận.
a) Sai. Ta có \({f}'\left( x \right)={{\left( x-1 \right)}^{2}}\left( {{x}^{2}}-3x+2 \right)={{\left( x-1 \right)}^{3}}\left( x-2 \right)\).
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\).
Bảng biến thiên :
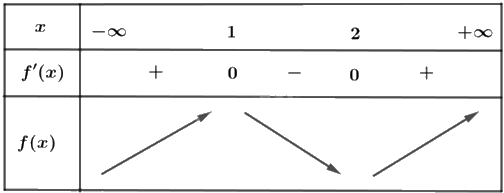
Dựa vào bảng biến thiên của hàm số $y=f\left( x \right)$ ta thấy hàm số đồng biến trên các khoảng $\left( -\infty ;1 \right),\left( 2;+\infty \right)$.
b) Đúng. Ta có \(y = f\left( {{x^2} - 6x + 1} \right) \Rightarrow y' = {\left( {{x^2} - 4x + 1} \right)^\prime }f'\left( {{x^2} - 4x + 1} \right) = \left( {2x - 4} \right)f'\left( {{x^2} - 4x + 1} \right)\).
\(y' = 0 \Leftrightarrow \left( {2x - 4} \right)f'\left( {{x^2} - 4x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2x - 4 = 0\\{x^2} - 4x + 1 = 1\\{x^2} - 4x + 1 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 0\\x = 4\\x = 2 + \sqrt 5 \\x = 2 - \sqrt 5 \end{array} \right.\).
Bảng biến thiên $y=f\left( {{x}^{2}}-4x+1 \right)$:
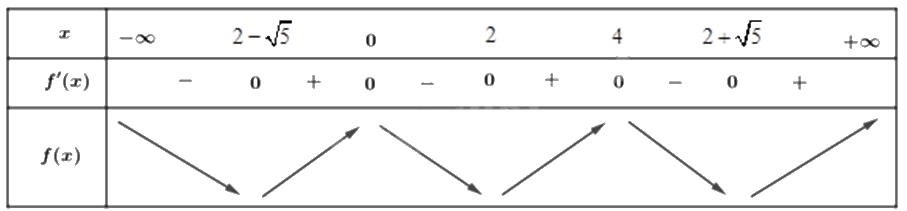
Dựa vào bảng biến thiên của hàm số $y=f\left( {{x}^{2}}-4x+1 \right)$ ta thấy hàm số có ba điểm cực tiểu.
c) Đúng. Theo bảng biến thiên ở câu a), hàm số f(x) có hai điểm cực trị là x = 1 và x = 2.
d) Sai. Điểm cực đại của đồ thị hàm số là \(\left( {1;f(1)} \right)\).
Thầy giáo thống kê lại điểm trung bình cuối năm của các học sinh lớp 11A và 11B ở bảng sau:

a) So sánh theo độ lệch chuẩn thì các học sinh lớp 11A học đồng đều hơn lớp 11B.
b) Điểm trung bình của lớp 11A nhỏ hơn lớp 11B.
c) Phương sai của mẫu số liệu lớp 11B là 1,05 (làm tròn đến hàng phần trăm).
d) Điểm trung bình của lớp 11A là 8,3 (làm tròn đến hàng phần chục).
a) So sánh theo độ lệch chuẩn thì các học sinh lớp 11A học đồng đều hơn lớp 11B.
b) Điểm trung bình của lớp 11A nhỏ hơn lớp 11B.
c) Phương sai của mẫu số liệu lớp 11B là 1,05 (làm tròn đến hàng phần trăm).
d) Điểm trung bình của lớp 11A là 8,3 (làm tròn đến hàng phần chục).
Áp dụng công thức tính số trung bình, phương sai, độ lệch chuẩn của từng mẫu số liệu rồi so sánh.
Ta có bảng thống kê điểm trung bình theo giá trị đại diện:

Điểm trung bình của lớp 11A là \({\bar x_1} = \frac{{1 \cdot 5,5 + 11 \cdot 7,5 + 22 \cdot 8,5 + 6 \cdot 9,5}}{{40}} = 8,3.\)
Điểm trung bình của lớp 11B là \({\bar x_2} = \frac{{6 \cdot 6,5 + 8 \cdot 7,5 + 14 \cdot 8,5 + 12 \cdot 9,5}}{{40}} = 8,3.\)
Phương sai của mẫu số liệu lớp 11A là \(s_1^2 = \frac{1}{{40}}\left( {1 \cdot 5,{5^2} + 11 \cdot 7,{5^2} + 22 \cdot 8,{5^2} + 6 \cdot 9,{5^2}} \right) - 8,{3^2} = 0,61.\)
Phương sai của mẫu số liệu lớp 11B là \(s_2^2 = \frac{1}{{40}}\left( {6 \cdot 6,{5^2} + 8 \cdot 7,{5^2} + 14 \cdot 8,{5^2} + 12 \cdot 9,{5^2}} \right) - 8,{3^2} = 1,06.\)
Độ lệch chuẩn của mẫu số liệu lớp 11A là \({s_1} = \sqrt {0,61} \).
Độ lệch chuẩn của mẫu số liệu lớp 11B là \({s_2} = \sqrt {1,06} \).
a) Đúng. Do \({s_1} < {s_2}\) nên nếu so sánh theo độ lệch chuẩn thì học sinh lớp 11A có điểm trung bình ít phân tán hơn học sinh lớp 11B, nghĩa là lớp 11A học đồng đều hơn lớp 11B.
b) Sai. Hai lớp 11A và 11B có điểm trung bình bằng nhau.
c) Sai. Phương sai của mẫu số liệu lớp 11B là 1,06 (làm tròn đến hàng phần trăm).
d) Đúng. Điểm trung bình của lớp 11A là 8,3 (làm tròn đến hàng phần chục).
Cho phương trình lượng giác \(\cos 2x = - \frac{1}{2}\) (*).
a) Phương trình (*) tương đương với phương trình: \(\cos 2x = \cos \left( { - \frac{\pi }{3}} \right)\).
b) Nghiệm dương nhỏ nhất của phương trình (*) bằng \(\frac{\pi }{3}\).
c) Tổng các nghiệm của phương trình (*) trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{3\pi }}{2}\).
d) Trong khoảng \(\left( {0;\pi } \right)\) phương trình (*) có 3 nghiệm.
a) Phương trình (*) tương đương với phương trình: \(\cos 2x = \cos \left( { - \frac{\pi }{3}} \right)\).
b) Nghiệm dương nhỏ nhất của phương trình (*) bằng \(\frac{\pi }{3}\).
c) Tổng các nghiệm của phương trình (*) trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{3\pi }}{2}\).
d) Trong khoảng \(\left( {0;\pi } \right)\) phương trình (*) có 3 nghiệm.
Áp dụng công thức nghiệm của phương trình lượng giác cơ bản: \(\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + k2\pi \), \(k \in \mathbb{Z}\).
a) Sai. \(\cos 2x=-\frac{1}{2}\Leftrightarrow \cos 2x=\cos \left( \frac{2\pi }{3} \right)\).
b) Đúng. \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x = \frac{{2\pi }}{3} + k2\pi }\\{2x = - \frac{{2\pi }}{3} + k2\pi }\end{array}(k \in \mathbb{Z}) \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{3} + k\pi }\\{x = - \frac{\pi }{3} + k\pi }\end{array}(k \in \mathbb{Z})} \right.} \right.\).
\(0 < x < \pi \Rightarrow \left[ {\begin{array}{*{20}{l}}{0 < \frac{\pi }{3} + k\pi < \pi }\\{0 < - \frac{\pi }{3} + k\pi < \pi }\end{array}(k \in \mathbb{Z}) \Rightarrow \left[ {\begin{array}{*{20}{l}}{k = 0}\\{k = 1}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{3}}\\{x = \frac{{2\pi }}{3}}\end{array}} \right.} \right.\).
Do \(\frac{{2\pi }}{3} > \frac{\pi }{3}\) nên phương trình có nghiệm dương nhỏ nhất trong khoảng là .
c)Sai. Tổng các nghiệm của phương trình trong khoảng \(\left( {0;\pi } \right)\) là: $S=\frac{\pi }{3}+\frac{2\pi }{3}=\pi $.
d) Sai. Trong khoảng \(\left( {0;\pi } \right)\) phương trình (*) có 2 nghiệm là \(x = \frac{\pi }{3}\) và \(x = \frac{{2\pi }}{3}\).
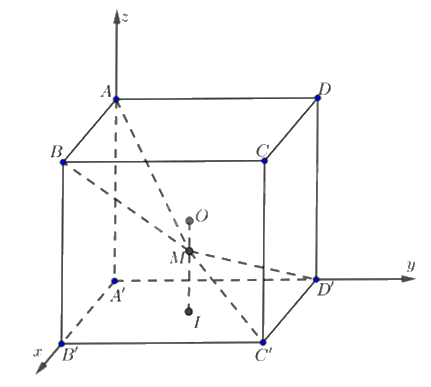
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 1, có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho $MO=\frac{1}{2}MI$. Gắn hệ trục A’xyz như hình vẽ.
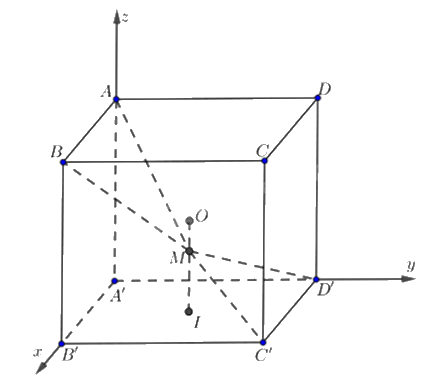
a) Tọa độ điểm $M\left( \frac{1}{2};\frac{1}{2};\frac{1}{4} \right).$
b) Tọa độ các điểm A’(0;0;0), B’(1;0;0), D’(0;1;0) và A(0;0;1).
c) Trong không gian giả sử điểm P, Q sao cho \(\overrightarrow {A'P} = \overrightarrow {A'B'} + 2\overrightarrow {A'D'} - 2\overrightarrow {A'A} \); \(\overrightarrow {A'Q} = \frac{8}{3}\overrightarrow {A'B'} + \frac{4}{3}\overrightarrow {A'D'} + \frac{8}{3}\overrightarrow {A'A} \) và J(a;b;c) là tâm đường tròn nội tiếp tam giác A’PQ, khi đó a – b + c = 0.
d) Trong không gian có đúng 2 điểm N sao cho N không trùng với các điểm A, B’, D’ và \(\widehat {ANB'} = \widehat {B'ND'} = \widehat {D'NA} = 90^\circ \).
a) Tọa độ điểm $M\left( \frac{1}{2};\frac{1}{2};\frac{1}{4} \right).$
b) Tọa độ các điểm A’(0;0;0), B’(1;0;0), D’(0;1;0) và A(0;0;1).
c) Trong không gian giả sử điểm P, Q sao cho \(\overrightarrow {A'P} = \overrightarrow {A'B'} + 2\overrightarrow {A'D'} - 2\overrightarrow {A'A} \); \(\overrightarrow {A'Q} = \frac{8}{3}\overrightarrow {A'B'} + \frac{4}{3}\overrightarrow {A'D'} + \frac{8}{3}\overrightarrow {A'A} \) và J(a;b;c) là tâm đường tròn nội tiếp tam giác A’PQ, khi đó a – b + c = 0.
d) Trong không gian có đúng 2 điểm N sao cho N không trùng với các điểm A, B’, D’ và \(\widehat {ANB'} = \widehat {B'ND'} = \widehat {D'NA} = 90^\circ \).
Áp dụng biểu thức tọa độ tổng, hiệu, tích của vecto; đẳng thức vecto liên quan đến tâm đường tròn nội tiếp tam giác.
a) Sai. $O\left( \frac{1}{2};\frac{1}{2};\frac{1}{2} \right)$, \(I\left( {\frac{1}{2};\frac{1}{2};0} \right)\).
\(\overrightarrow {MO} = \left( {\frac{1}{2} - {x_M};\frac{1}{2} - {y_M};\frac{1}{2} - {z_M}} \right)\), \(\overrightarrow {MI} = \left( {\frac{1}{2} - {x_M};\frac{1}{2} - {y_M}; - {z_M}} \right) \Rightarrow - \frac{1}{2}\overrightarrow {MI} = \left( { - \frac{1}{4} + \frac{1}{2}{x_M}; - \frac{1}{4} + \frac{1}{2}{y_M};\frac{1}{2}{z_M}} \right)\).
\(\overrightarrow {MO} = 2\overrightarrow {MI} \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{2} - {x_M} = - \frac{1}{4} + \frac{1}{2}{x_M}\\\frac{1}{2} - {y_M} = - \frac{1}{4} + \frac{1}{2}{y_M}\\\frac{1}{2} - {z_M} = \frac{1}{2}{z_M}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = \frac{1}{2}\\{y_M} = \frac{1}{2}\\{x_M} = \frac{1}{3}\end{array} \right. \Rightarrow M\left( {\frac{1}{2};\frac{1}{2};\frac{1}{3}} \right)\).
b) Đúng. Tọa độ các điểm A’(0;0;0), B’(1;0;0), D’(0;1;0) và A(0;0;1).
c) Đúng. Ta có \(\overrightarrow {A'P} = \left( {1;\,\,2;\,\, - 2} \right)\), \(\overrightarrow {A'Q} = \left( {\frac{8}{3};\,\frac{4}{3};\,\,\frac{8}{3}} \right)\), do đó $A'P=3,\,\,A'Q=4,\,\,PQ=5$. Với\(J(a;b;c)\) là tâm đường tròn nội tiếp tam giác A’PQ ta lại có
\(PQ.\overrightarrow {JA'} + A'P.\overrightarrow {JQ} + A'Q.\overrightarrow {JP} = \overrightarrow 0 \) ta giải tìm được tọa độ \(J(1;1;0)\).
Vậy \(a - b + c = 0\).
d) Đúng. Gọi \(N({x_0};{y_0};{z_0})\).
\(\overrightarrow {AN} = ({x_0};{y_0};{z_0} - 1)\); \(\overrightarrow {B'N} = ({x_0} - 1;{y_0};{z_0})\); \(\overrightarrow {D'N} = ({x_0};{y_0} - 1;{z_0})\).
Do\(\widehat {ANB'} = \widehat {B'ND'} = \widehat {D'NA} = 90^\circ \) nên \(\left\{ \begin{array}{l}\overrightarrow {AN} .\overrightarrow {B'N} = 0\\\overrightarrow {AN} .\overrightarrow {D'N} = 0\\\overrightarrow {D'N} .\overrightarrow {B'N} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0}({x_0} - 1) + y_0^2 + ({z_0} - 1){z_0} = 0\\x_0^2 + {y_0}({y_0} - 1) + ({z_0} - 1){z_0} = 0\\{x_0}({x_0} - 1) + ({y_0} - 1){y_0} + z_0^2 = 0\end{array} \right.\).
Giải hệ ta được \({x_0} = {y_0} = {z_0} = 0\); \({x_0} = {y_0} = {z_0} = \frac{2}{3}\).
Khi đó có hai điểm \(N\) thỏa mãn điều kiện trên.
Cho hàm số y = f(x) có đạo hàm liên tục trên $\mathbb{R}$ và có bảng biến thiên của đạo hàm như hình vẽ.
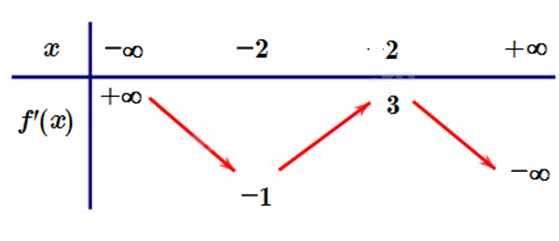
Đặt \(g\left( x \right)=f\left( \frac{{{x}^{2}}+1}{x} \right)\). Tìm số điểm cực trị của hàm số \(y=g\left( x \right).\)
Đáp án:
Đáp án:
Tính đạo hàm g’(x) và lập bảng biến thiên.
Đặt \(g'\left( x \right) = \left( {\frac{{{x^2} - 1}}{{{x^2}}}} \right)f'\left( {\frac{{{x^2} + 1}}{x}} \right)\).
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\left( {\frac{{{x^2} - 1}}{{{x^2}}}} \right) = 0\\f'\left( {\frac{{{x^2} + 1}}{x}} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm 1\\\frac{{{x^2} + 1}}{x} = a\,\,\left( {a < - 2} \right)\\\frac{{{x^2} + 1}}{x} = b\,\,\left( { - 2 < b < 2} \right)\\\frac{{{x^2} + 1}}{x} = c\,\,\left( {c > 2} \right)\end{array} \right.\).
Xét hàm số \(h\left( x \right) = \frac{{{x^2} + 1}}{x}\): \(h'\left( x \right) = \frac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow x = \pm 1\).
Bảng biến thiên của hàm số \(h\left( x \right) = \frac{{{x^2} + 1}}{x}\):
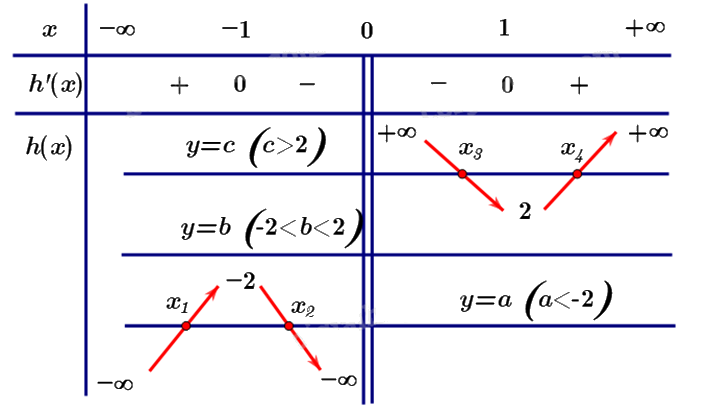
Dựa vào bảng biến thiến trên ta thấy phương trình $h\left( x \right)=a,h\left( x \right)=c$, mỗi phương trình có hai nghiệm phân biệt khác \( \pm 1\), mà \(a \ne c\) \( \Rightarrow f'\left( {\frac{{{x^2} + 1}}{x}} \right) = 0\) có 4 nghiệm đơn phân biệt \({x_1},{x_2},{x_3},{x_4}\) khác \( \pm 1\) và phương trình \(h\left( x \right) = b\) vô nghiệm.
Do đó phương trình $g'\left( x \right)=0$ có 6 nghiệm đơn phân biệt lần lượt theo thứ tự từ nhỏ đến lớn là \({x_1}, - 1,{x_2},{x_3},1,{x_4}\).
Vậy hàm số \(g\left( x \right) = f\left( {\frac{{{x^2} + 1}}{x}} \right)\) có 6 cực trị.
Độ dốc của mái nhà (mặt sân, con đường thẳng…) là tan của góc tạo bởi mái nhà (mặt sân, con đường thẳng…) đó với mặt phẳng nằm ngang. Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều, biết rằng diện tích để lát tất cả các mặt của kim tự tháp bằng 80300 ${{m}^{2}}$ và độ dốc của mặt bên kim tự tháp bằng \(\frac{{49}}{{45}}\). Tính chiều cao (đơn vị m) của kim tự tháp (làm tròn đến hàng đơn vị).

Đáp án:
Đáp án:
Mô hình hóa mái nhà dưới dạng hình chóp tứ giác đều. Áp dụng hệ thức lượng trong tam giác vuông, định lí Pythagore, công thức tính diện tích tam giác.
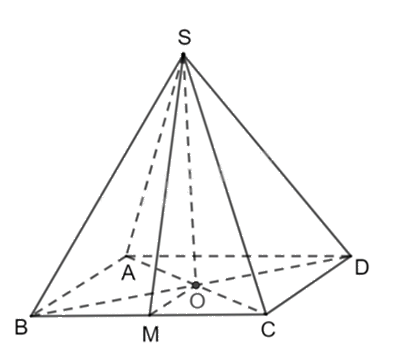
Mô hình hoá kim tự tháp bằng chóp tứ giác đều S.ABCD với O là tâm của đáy.
Kẻ \(OM \bot BC\).
Ta có góc tạo bởi mặt bên và mặt đáy của kim tự tháp là góc \(\widehat {SMO} \Rightarrow \tan \widehat {SMO} = \frac{{49}}{{45}} = \frac{{SO}}{{OM}}\).
Đặt \(\left\{ \begin{array}{l}SO = 49x\\OM = 45x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}SM = \sqrt {S{O^2} + O{M^2}} = \sqrt {4426} x\\AB = 2OM = 90x\end{array} \right.\)
Diện tích tất cả các mặt của kim tự tháp là:
\(S = 4{S_{\Delta SBC}} + {S_{ABCD}} \Leftrightarrow 4.\frac{1}{2}SM.BC + A{B^2} = 80300\)
\( \Leftrightarrow 2x\sqrt {4426} .90x + {\left( {90x} \right)^2} = 80300\)
\( \Rightarrow x \approx 2 \Rightarrow SO = 49x \approx 98\) (m).
Một đoàn tàu gồm 3 toa đỗ ở sân ga. Có 5 hành khách bước lên tàu, mỗi hành khách độc lập với nhau chọn ngẫu nhiên 1 toa. Tính xác suất để mỗi toa có ít nhất 1 hành khách bước lên tàu (kết quả làm tròn đến hàng phần trăm).
Đáp án:
Đáp án:
Áp dụng phương pháp tổ hợp và tính xác suất bằng biến cố đối.
Mỗi hành khách có 3 cách chọn toa tàu nên 5 hành khách có tất cả $n\left( \Omega \right)={{3}^{5}}=243$ cách chọn.
A: “Mỗi toa có ít nhất 1 hành khách”.
\(\overline A \): “Có toa không có hành khách nào bước lên”. Ta có:
TH1: Có 2 toa không có hành khách bước lên.
- Chọn 2 trong 3 toa để không có khách bước lên, có \(C_3^2\) cách.
- Sau đó cả 5 hành khách lên toa còn lại, có 1 cách.
Do đó trường hợp này có \(C_3^2.1 = 3\) cách.
TH2: Có 1 toa không có hành khách bước lên:
- Chọn 1 trong 3 toa để không có khách bước lên, có \(C_3^1\) cách.
- 2 toa còn lại ta cần xếp 5 hành khách lên và mỗi toa có ít nhất 1 hành khách, có \({2^5} - C_2^1.1 = 30\) cách.
Do đó trường hợp này có \(C_3^1.30 = 90\) cách.
Vậy \(n\left( {\overline A } \right) = 3 + 90 = 93\), suy ra \(n\left( A \right) = n\left( \Omega \right) - n\left( {\overline A } \right) = 243 - 93 = 150\).
Xác suất cần tính là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{150}}{{243}} = \frac{{50}}{{81}} \approx 0,62\).
Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100 m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Biết dòng sông là thẳng, mục tiêu cách chiến sỹ 1 km theo đường chim bay và chiến sỹ cách bờ bên kia 100 m. Hãy cho biết chiến sỹ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất (làm tròn kết quả đến hàng đơn vị).
Đáp án:
Đáp án:
Lập hàm số tính thời gian di chuyển theo x và tìm x để hàm số đạt giá trị nhỏ nhất.
Gọi A là mục tiêu; B là vị trí chiến sỹ và BD là đường bơi của chiến sỹ.Chọn một đơn vị độ dài là 100m, suy ra BC = 1; AB = 10; \(AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {{{10}^2} - {1^2}} = 3\sqrt {11} \).
Gọi vận tốc bơi của chiến sỹ là 1 đơn vị vận tốc thì vận tốc chạy của chiến sỹ là 3 đơn vị vận tốc. Gọi x là quãng đường chiến sỹ bơi, hay BD = x (1 < x < 10).
\(CD = \sqrt {{x^2} - 1} \); \(AD = AC - CD = 3\sqrt {11} - \sqrt {{x^2} - 1} \).
Thời gian chiến sỹ đến được mục tiêu là: \(t = \frac{{3\sqrt {11} - \sqrt {{x^2} - 1} }}{3} + \frac{x}{1} = \sqrt {11} - \frac{1}{3}\sqrt {{x^2} - 1} + x\).
Xét hàm \(f(x) = \sqrt {11} - \frac{1}{3}\sqrt {{x^2} - 1} + x\) có \(f'(x) = 1 - \frac{x}{{3\sqrt {{x^2} - 1} }} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3\sqrt 2 }}{4}\\x = - \frac{{3\sqrt 2 }}{4}\end{array} \right.\).
Bảng biến thiên:
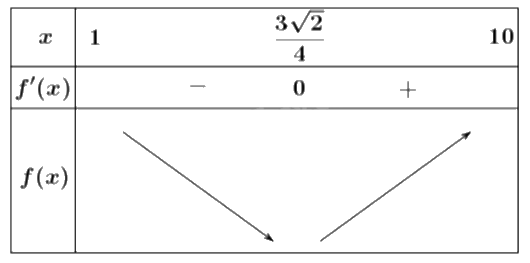
Thời gian chiến sỹ đến mục tiêu ngắn nhất khi f(x) đạt giá trị nhỏ nhất, hay \(x = \frac{{3\sqrt 2 }}{4}\).
Vậy chiến sĩ phải bơi \(\frac{{3\sqrt 2 }}{4}.100 = 75\sqrt 2 \approx 106\) (m).
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(3;1;0), B(3;6;6), C(4;6;2), D(6;2;14) và điểm M(a;b;c) thỏa mãn MA = 3, MB = 6, MC = 5, MD = 13. Khoảng cách từ điểm M đến điểm O bằng bao nhiêu (làm tròn đến hàng phàn trăm)?
Đáp án:
Đáp án:
Áp dụng công thức tính khoảng cách giữa hai điểm trong không gian: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).
Ta có \(\left\{ {\begin{array}{*{20}{c}}{MA = 3}\\{MB = 6}\\{MC = 5}\\{MD = 13}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\left( {a - 3} \right)}^2} + {{\left( {b - 1} \right)}^2} + {c^2} = 9}\\{{{\left( {a - 3} \right)}^2} + {{\left( {b - 6} \right)}^2} + {{\left( {c - 6} \right)}^2} = 36}\\{{{\left( {a - 4} \right)}^2} + {{\left( {b - 6} \right)}^2} + {{\left( {c - 2} \right)}^2} = 25}\\{{{\left( {a - 6} \right)}^2} + {{\left( {b - 2} \right)}^2} + {{\left( {c - 14} \right)}^2} = 169}\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{a^2} + {b^2} + {c^2} - 6a - 2b = - 1}\\{{a^2} + {b^2} + {c^2} - 6a - 12b - 12c = - 45}\\{{a^2} + {b^2} + {c^2} - 8a - 12b - 4c = - 31}\\{{a^2} + {b^2} + {c^2} - 12a - 4b - 28c = - 67}\end{array}} \right.\).
Đặt \(d = {a^2} + {b^2} + {c^2}\) ta được \(\left\{ {\begin{array}{*{20}{c}}{d - 6a - 2b = - 1}\\{d - 6a - 12b - 12c = - 45}\\{d - 8a - 12b - 4c = - 31}\\{d - 12a - 4b - 28c = - 67}\end{array}} \right.\).
Giải hệ, tìm được a = 1; b = 2; c = 2; d = 9 suy ra M(1;2;2).
Vậy \(OM = \sqrt {{a^2} + {b^2} + {c^2}} = \sqrt d = 3\).
Một xe ô tô chở khách du lịch có sức chứa tối đa là 16 hành khách. Trong một khu du lịch, một đoàn khách gồm 24 người đang đi bộ và muốn thuê xe về khách sạn. Lái xe đưa ra thỏa thuận với đoàn khách du lịch như sau: Nếu một chuyến xe chở x (người) thì giá tiền cho mỗi người là \(\frac{{{(40-x)}^{2}}}{2}\)(nghìn đồng). Với thỏa thuận như trên thì lái xe có thể thu được nhiều nhất bao nhiêu triệu đồng từ một chuyến chở khách (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Đáp án:
Lập hàm tính lợi nhuận của lái xe khi chở x khách. Tìm giá trị lớn nhất của hàm số đó.
Gọi f(x) là lợi nhuận mà lái xe có thể thu về khi chở x (người) \(\left( {x \in {\mathbb{N}^*}} \right)\) trong chuyến xe đó. Khi đó:
\(f\left( x \right) = \frac{1}{2}x{\left( {40 - x} \right)^2}\), với \(0 < x \le 16\).
Ta có:
\(f'\left( x \right) = \left[ {\frac{1}{2}x{{\left( {40 - x} \right)}^2}} \right]' = \frac{1}{2}\left[ {x{{\left( {40 - x} \right)}^2}} \right]'\)
\( = \frac{1}{2}\left\{ {\left( x \right)'{{\left( {40 - x} \right)}^2} + x\left[ {{{\left( {40 - x} \right)}^2}} \right]'} \right\}\)
\( = \frac{1}{2}\left[ {{{\left( {40 - x} \right)}^2} - 2x\left( {40 - x} \right)} \right] = \frac{1}{2}\left( {40 - x} \right)\left( {40 - 3x} \right)\).
Với thì \(f'\left( x \right) = 0 \Leftrightarrow x = \frac{{40}}{3}\). Mà \(13 < \frac{{40}}{3} < 14\) nên ta có bảng biến thiên như sau:
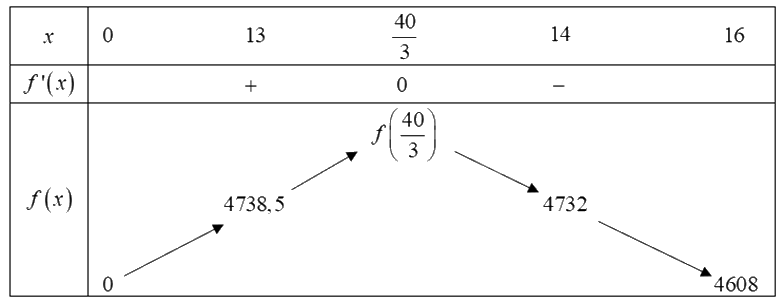
Với f(13) = 4738,5, f(4) = 4732. Căn cứ vào bảng biến thiên ta có \(\mathop {max}\limits_{\left( {0;16} \right]} f\left( x \right) = 4738,5\) (nghìn đồng). Vậy người lái xe đó có thể thu được nhiều nhất khoảng 4,74 triệu đồng từ một chuyến xe chở 13 khách.
Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 4 - Thanh Hóa là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau một thời gian học tập. Đề thi này không chỉ giúp học sinh tự đánh giá năng lực mà còn là cơ sở để giáo viên điều chỉnh phương pháp giảng dạy, đảm bảo học sinh được trang bị đầy đủ kiến thức và kỹ năng cần thiết cho kỳ thi THPT Quốc gia sắp tới.
Đề thi thường bao gồm các dạng câu hỏi trắc nghiệm và tự luận, tập trung vào các chủ đề chính của chương trình Toán 12 như:
Tỷ lệ câu hỏi trắc nghiệm và tự luận có thể thay đổi tùy theo từng trường, nhưng nhìn chung, đề thi thường có sự cân bằng giữa các dạng câu hỏi để đánh giá toàn diện năng lực của học sinh.
Để giúp học sinh hiểu rõ hơn về cấu trúc và nội dung đề thi, chúng ta sẽ phân tích một số câu hỏi điển hình từ đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 4 - Thanh Hóa.
Cho hàm số y = f(x) có đạo hàm f'(x) = x(x - 1)(x + 2). Hàm số f(x) đạt cực đại tại điểm nào?
A. x = -2
B. x = 0
C. x = 1
D. x = 2
Hướng dẫn giải: Để tìm điểm cực đại của hàm số, ta cần tìm các điểm mà đạo hàm đổi dấu từ dương sang âm. Dựa vào bảng xét dấu của f'(x), ta thấy f'(x) đổi dấu từ dương sang âm tại x = -2. Vậy hàm số f(x) đạt cực đại tại x = -2.
Giải phương trình: log2(x + 1) + log2(x - 1) = 3
Hướng dẫn giải: Sử dụng tính chất logab + logac = loga(bc), ta có:
log2[(x + 1)(x - 1)] = 3
log2(x2 - 1) = 3
x2 - 1 = 23
x2 - 1 = 8
x2 = 9
x = ±3
Tuy nhiên, điều kiện xác định của log2(x + 1) và log2(x - 1) là x > 1. Vậy nghiệm duy nhất của phương trình là x = 3.
Để đạt kết quả tốt nhất trong kỳ thi THPT Quốc gia, học sinh cần:
Ngoài đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 4 - Thanh Hóa, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng, với những phân tích và hướng dẫn trên, học sinh sẽ có thêm kiến thức và kỹ năng để tự tin chinh phục kỳ thi THPT Quốc gia sắp tới. Chúc các em thành công!