Chào mừng các em học sinh đến với đề tham khảo thi THPT môn Toán - Đề số 7 tại giaitoan.edu.vn. Đề thi này được biên soạn theo cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo, giúp các em làm quen với dạng đề và rèn luyện kỹ năng giải quyết các bài toán khó.
Đề thi số 7 tập trung vào các chủ đề quan trọng như Đại số, Hình học, Giải tích, và các bài toán thực tế. Bài giải chi tiết đi kèm sẽ giúp các em hiểu rõ phương pháp giải và tránh những sai lầm thường gặp.
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa đường thẳng CD’ và mặt phẳng (ABCD) bằng?
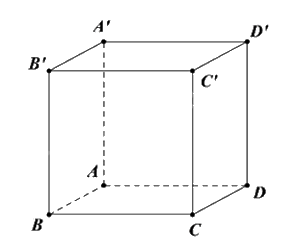
\({60^o}\)
\({90^o}\)
\({30^o}\)
\({45^o}\)
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3a. Tính thể tích khối chóp S.ABCD.
\(\frac{{\sqrt 2 {a^3}}}{6}\)
\(3{a^3}\)
\({a^3}\)
\(\frac{{\sqrt 2 {a^3}}}{3}\)
Nguyên hàm của hàm số \(f\left( x \right) = {x^3} - x\) là
\(\frac{1}{4}{x^4} - \frac{1}{2}{x^2} + C\)
\(3{x^2} - 1 + C\)
\(\frac{{{x^4}}}{4} + C\)
\({x^4} + {x^2} + C\)
Bảng sau thống kê cân nặng của 50 quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
40
540
200
450
Không gian với trục hệ tọa độ \(Oxyz\), cho \(\overrightarrow a = 2\overrightarrow j - \overrightarrow i + 3\overrightarrow k .\) Tọa độ của vectơ \(\overrightarrow a \) là
\(\overrightarrow a \left( { - 1;2; - 3} \right)\)
\(\overrightarrow a \left( {2; - 1;3} \right)\)
\(\overrightarrow a \left( { - 1;2;3} \right)\)
\(\overrightarrow a \left( {2; - 1; - 3} \right)\)
Tập nghiệm của bất phương trình \({\left( {\frac{1}{3}} \right)^x} > 9\) là
\(\left( {2;\, + \infty } \right)\)
\(\left( { - \infty ;\, - 2} \right)\)
\(\left( { - 2;\, + \infty } \right)\)
\(\left( { - 2;\,0} \right)\)
Cho hàm số \(f\left( x \right) = {e^x}\). Tính f’(2).
\(f'\left( 2 \right) = 2e\)
\(f'\left( 2 \right) = - {e^2}\)
\(f'\left( 2 \right) = e\)
\(f'\left( 2 \right) = {e^2}\)
Phương trình \(\sin x = - \frac{1}{2}\) có tập nghiệm là
\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ;\frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)s
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ;\frac{{7\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
\(S = \left\{ {\frac{1}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
Trong không gian, với mọi vecto \(\overrightarrow a ,\,\overrightarrow b \) ta có
\(\overrightarrow a .\vec b = \left| {\overrightarrow a } \right|.\left| {\vec b} \right|\)
\(\overrightarrow a .\vec b = \left| {\overrightarrow a } \right|.\left| {\vec b} \right|.\sin (\overrightarrow a .\overrightarrow b )\)
\(\overrightarrow a .\vec b = \left| {\overrightarrow a } \right|.\left| {\vec b} \right|.\cos (\overrightarrow a .\overrightarrow b )\)
\(\overrightarrow a .\vec b = - \left| {\overrightarrow a } \right|.\left| {\vec b} \right|\)
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
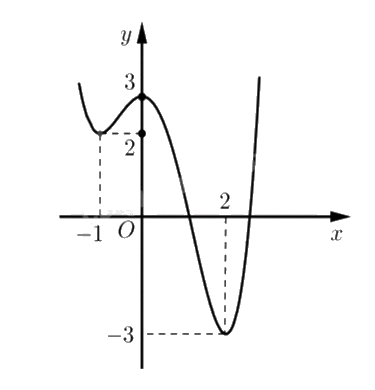
Hàm số y = f(x) nghịch biến trên khoảng nào sau đây?
\(\left( {2; + \infty } \right)\)
\(\left( {0;2} \right)\)
\(\left( { - \infty ;2} \right)\)
\(\left( {2;3} \right)\)
Trong không gian với hệ tọa độ Oxyz, cho hai vecto \(\overrightarrow u = \left( {2;0; - 3} \right)\) và \(\overrightarrow v = \left( {0;2; - 1} \right)\). Tìm tọa độ của vecto \(\overrightarrow a = \overrightarrow u + 2\overrightarrow v \).
\(\overrightarrow a = \left( {2;4; - 1} \right)\)
\(\overrightarrow a = \left( {2;2; - 4} \right)\)
\(\overrightarrow a = \left( {0;1; - 1} \right)\)
\(\overrightarrow a = \left( {2;4; - 5} \right)\)
Trong không gian Oxy, cho điểm M(1;0;2) và mặt phẳng (P): 2x – y + 3z + 5 = 0. Mặt phẳng đi qua M và song song với (P) có phương trình là
\(2x - y + 3z + 8 = 0\)
\(2x + y + 3z - 3 = 0\)
\(2x + y + 3z + 5 = 0\)
\(2x - y + 3z - 8 = 0\)
Giá của một chiếc máy photocopy lúc mới mua là 50 triệu đồng. Biết rằng giá trị của nó sau mỗi năm sử dụng chỉ còn 75% giá trị trong năm liền trước đó.
a) Giá trị của máy photocopy sau 1 năm sử dụng là: \({T_1} = 37,5\) triệu đồng.
b) Giá trị của máy photocopy sau 2 năm sử dụng lớn hơn 30 triệu đồng.
c) Giá trị tiêu hao của chiếc máy photocopy đó sau khoảng thời gian 5 năm kể từ khi mua là \(11,8652\) triệu đồng.
d) Sau 7 năm thì giá trị của máy photocopy con 10% có với giá trị ban đầu.
Cho hình lăng trụ ABCD.A’B’C’D’ có đáy là hình thoi cạnh 3a, \(\widehat {ABC} = {60^o}\), AA’ = 2a. Đỉnh A’ cách đều ba đỉnh A, B, C. Gọi G là trọng tâm của tam giác ABC.
a) A’G là đường cao của hình lăng trụ ABCD.A’B’C’D’.
b) Độ dài đường cao của hình lăng trụ ABCD.A’B’C’D’ bằng \(a\sqrt 3 \).
c) Diện tích hình thoi ABCD bằng \(\frac{{9{a^2}\sqrt 3 }}{2}\).
d) Thể tích của khối chóp B’BCD bằng \(\frac{{3{a^3}\sqrt 3 }}{2}\).
Trưởng Câu lạc bộ Thể thao đã tiến hành điều tra tuổi thọ (đơn vị: năm) của máy chạy bộ do hai hãng X, Y sản xuất và thu được hai mẫu số liệu sau đây:

a) Tuổi thọ của máy chạy bộ do hãng Y có độ phân tán lớn hơn tuổi thọ của máy chạy bộ do hãng X sản xuất.
b) Tuổi thọ trung bình của máy chạy bộ do hãng Y sản xuất lớn hơn tuổi thọ trung bình của máy chạy bộ do hãng X sản xuất.
c) Khoảng tứ phân vị của mẫu số liệu về tuổi thọ của máy chạy bộ do hãng X sản xuất là 2,5.
d) Tuổi thọ máy chạy bộ do hãng X sản xuất đồng đều hơn tuổi thọ máy chạy bộ do hãng Y sản xuất.
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC. Biết \(MN = \frac{{a\sqrt 6 }}{2}\).
a) Gọi I hình chiếu của M lên (ABCD) nên \(CI = \frac{2}{3}AC\).
b) \(SO = \frac{{a\sqrt {14} }}{2}\).
c) Khoảng cách giữa IN và SC bằng \(\frac{{\sqrt {14} }}{4}\).
d) Giá trị sin của góc giữa đường thẳng \(MN\) và mặt phẳng \((SBD)\) là \(\frac{{\sqrt 6 }}{3}\).
Khối rubik như hình vẽ có độ dài cạnh bằng 2. Khi gắn rubik vào hệ trục tọa độ trong không gian Oxyz, cho hình lập phương ABCD.A’B’C’D’ có A(0;0;0), B(2;0;0), D(0;2;0), A’(0;0;2). Gọi M, N lần lượt là trung điểm của CD, AA’ (xem hình vẽ bên dưới). Biết rằng cos[B,MN,D’] = m, tính giá trị 14m.

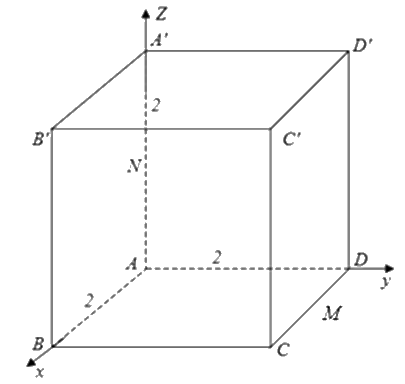
Đáp án:
Phương trình \(\cos \left( {2x + \frac{\pi }{3}} \right) = -2\sin \left( {x + \frac{\pi }{6}} \right) + 1\) có bao nhiêu nghiệm trên đoạn [0;2024]?
Đáp án:
Một hình tam giác đều màu trắng có cạnh 2 đơn vị dài được chia thành bốn hình tam giác nhỏ hơn bằng nhau và hình tam giác ở chính giữa được tô màu đỏ (như hình vẽ).
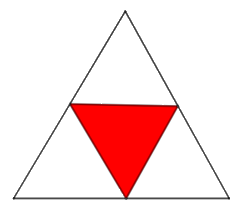
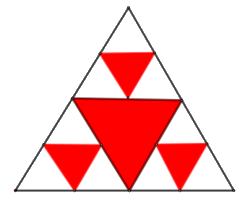
Mỗi hình tam giác màu trắng nhỏ hơn lại được chia thành bốn hình tam giác con bằng nhau, và mỗi hình tam giác con ở chính giữa lại được tô màu đỏ. Nếu quá trình này được tiếp tục lặp lại sáu lần, thì tổng diện tích các hình tam giác không được tô màu đỏ là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
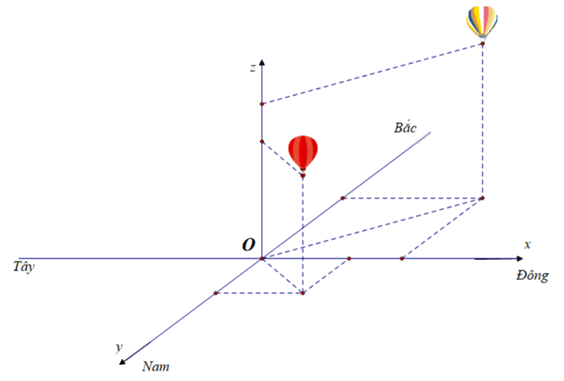
Cho hệ trục tọa độ Oxyz mặt phẳng Oxy trùng với mặt đất với trục Ox hướng về phía Đông, trục Oy hướng về phía Nam và trục Oz hướng thẳng đứng lên trời (như hình minh họa bên dưới), đơn vị đo lấy theo kilomet. Hai khinh khí cầu bay lên cùng thời điểm chiếc thứ nhất xuất phát tại điểm O, chiếc thứ hai xuất phát từ điểm I(1;0;0). Sau 20 phút chiếc thứ nhất cách điểm xuất phát 1 km về phía Nam và 1 km về phía Đông, đồng thời cách mặt đất 0,5 km. Chiếc thứ hai cách điểm xuất phát 2 km về phía Bắc và 2 km về phía Đông, đồng thời cách mặt đất 0,8 km. Hỏi nếu giữ nguyên vận tốc và hướng bay thì sau 10 phút nữa 2 khinh khí cầu cách nhau bao km (kết quả làm tròn đến chữ số thập phân thứ nhất)?
Đáp án:
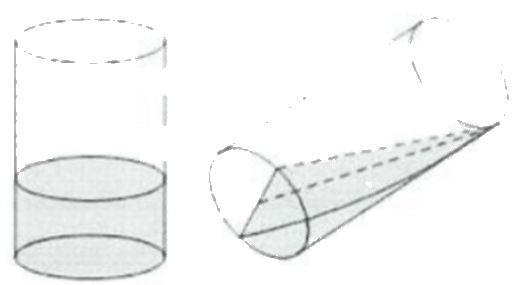
Bạn Nam có một ống thủy tinh hình trụ, đường kính trong lòng đáy cốc là 10 cm, chiều cao cốc là 15 cm đang đựng nước. Khi bạn Nam nghiêng cốc nước thì thấy mặt nước đi qua đường kính đáy và chạm miệng cốc. Thể tích lượng nước trong cốc là bao nhiêu \(c{m^3}\)?
Đáp án:
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,4 và khả năng thắng thầu của dự án 2 là 0,5. Khả năng thắng thầu cả 2 dự án là 0,3. Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là a. Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là b. Khi đó biểu thức P = 4a + 3b là bao nhiêu?
Đáp án:
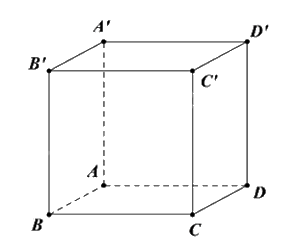
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa đường thẳng CD’ và mặt phẳng (ABCD) bằng?
\({60^o}\)
\({90^o}\)
\({30^o}\)
\({45^o}\)
Đáp án : D
Xác định hình chiếu vuông góc của CD’ lên mặt phẳng (ABCD).
CD là hình chiếu vuông góc của CD’ lên (ABCD) nên góc giữa đường thẳng \(CD'\) và mặt phẳng \(\left( {ABCD} \right)\) bằng: \((CD',(ABCD)) = (CD',CD) = \widehat {D'CD} = {45^o}\)\((CD',CD) = \widehat {D'CD} = {45^o}\).
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3a. Tính thể tích khối chóp S.ABCD.
\(\frac{{\sqrt 2 {a^3}}}{6}\)
\(3{a^3}\)
\({a^3}\)
\(\frac{{\sqrt 2 {a^3}}}{3}\)
Đáp án : C
Áp dụng công thức tính thể tích khối chóp \(V = \frac{1}{3}Bh\).
\(V = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}3a.{a^2} = {a^3}\).
Nguyên hàm của hàm số \(f\left( x \right) = {x^3} - x\) là
\(\frac{1}{4}{x^4} - \frac{1}{2}{x^2} + C\)
\(3{x^2} - 1 + C\)
\(\frac{{{x^4}}}{4} + C\)
\({x^4} + {x^2} + C\)
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int {({x^3} - x)dx = \frac{{{x^4}}}{4}} - \frac{{{x^2}}}{2} + C\).
Bảng sau thống kê cân nặng của 50 quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
40
540
200
450
Đáp án : C
Để tính khoảng biến thiên của mẫu số liệu ghép nhóm, ta lấy đầu mút phải của nhóm cuối cùng trừ đi đầu mút trái của nhóm đầu tiên.
R = 450 – 250 = 200.
Không gian với trục hệ tọa độ \(Oxyz\), cho \(\overrightarrow a = 2\overrightarrow j - \overrightarrow i + 3\overrightarrow k .\) Tọa độ của vectơ \(\overrightarrow a \) là
\(\overrightarrow a \left( { - 1;2; - 3} \right)\)
\(\overrightarrow a \left( {2; - 1;3} \right)\)
\(\overrightarrow a \left( { - 1;2;3} \right)\)
\(\overrightarrow a \left( {2; - 1; - 3} \right)\)
Đáp án : C
\(\overrightarrow a = m\overrightarrow i + n\overrightarrow j + p\overrightarrow k = \left( {m;n;p} \right)\).
\(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j + 3\overrightarrow k = \left( { - 1;2;3} \right)\).
Tập nghiệm của bất phương trình \({\left( {\frac{1}{3}} \right)^x} > 9\) là
\(\left( {2;\, + \infty } \right)\)
\(\left( { - \infty ;\, - 2} \right)\)
\(\left( { - 2;\, + \infty } \right)\)
\(\left( { - 2;\,0} \right)\)
Đáp án : B
Với 0 < a < 1 thì \({a^x} > b \Leftrightarrow x < {\log _a}b\).
\({\left( {\frac{1}{3}} \right)^x} > 9 \Leftrightarrow x < {\log _{\frac{1}{3}}}9 \Leftrightarrow x < - 2\). Vậy tập nghiệm \(S = \left( { - \infty ;\, - 2} \right)\).
Cho hàm số \(f\left( x \right) = {e^x}\). Tính f’(2).
\(f'\left( 2 \right) = 2e\)
\(f'\left( 2 \right) = - {e^2}\)
\(f'\left( 2 \right) = e\)
\(f'\left( 2 \right) = {e^2}\)
Đáp án : D
Áp dụng công thức tính đạo hàm của hàm số mũ \(\left( {{a^x}} \right)' = {a^x}\ln a\).
\(f'\left( x \right) = \left( {{e^x}} \right)' = {e^x} \Rightarrow f'\left( 2 \right) = {e^2}\).
Phương trình \(\sin x = - \frac{1}{2}\) có tập nghiệm là
\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ;\frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)s
\(S = \left\{ { - \frac{\pi }{6} + k2\pi ;\frac{{7\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
\(S = \left\{ {\frac{1}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)
Đáp án : A
Áp dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\).
\(\sin x = - \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{6} + k2\pi \\x = \pi - \left( { - \frac{\pi }{6}} \right) + k2\pi = \frac{{7\pi }}{6} + k2\pi \end{array} \right.\) \(\left( {k \in \mathbb{Z}} \right)\).
Trong không gian, với mọi vecto \(\overrightarrow a ,\,\overrightarrow b \) ta có
\(\overrightarrow a .\vec b = \left| {\overrightarrow a } \right|.\left| {\vec b} \right|\)
\(\overrightarrow a .\vec b = \left| {\overrightarrow a } \right|.\left| {\vec b} \right|.\sin (\overrightarrow a .\overrightarrow b )\)
\(\overrightarrow a .\vec b = \left| {\overrightarrow a } \right|.\left| {\vec b} \right|.\cos (\overrightarrow a .\overrightarrow b )\)
\(\overrightarrow a .\vec b = - \left| {\overrightarrow a } \right|.\left| {\vec b} \right|\)
Đáp án : C
Áp dụng công thức tích vô hướng của hai vecto.
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
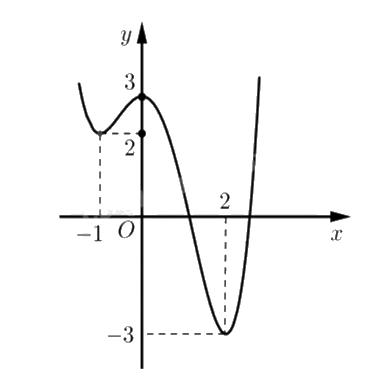
Hàm số y = f(x) nghịch biến trên khoảng nào sau đây?
\(\left( {2; + \infty } \right)\)
\(\left( {0;2} \right)\)
\(\left( { - \infty ;2} \right)\)
\(\left( {2;3} \right)\)
Đáp án : B
Hàm số nghịch biến trên khoảng đồ thị đi xuống từ trái sang phải.
Quan sát thấy đồ thị đi xuống trên khoảng (0;2) nên hàm số nghịch biến trên khoảng (0;2).
Trong không gian với hệ tọa độ Oxyz, cho hai vecto \(\overrightarrow u = \left( {2;0; - 3} \right)\) và \(\overrightarrow v = \left( {0;2; - 1} \right)\). Tìm tọa độ của vecto \(\overrightarrow a = \overrightarrow u + 2\overrightarrow v \).
\(\overrightarrow a = \left( {2;4; - 1} \right)\)
\(\overrightarrow a = \left( {2;2; - 4} \right)\)
\(\overrightarrow a = \left( {0;1; - 1} \right)\)
\(\overrightarrow a = \left( {2;4; - 5} \right)\)
Đáp án : D
Áp dụng biểu thức tọa độ các phép cộng, trừ, tích của vecto với một số.
\(\overrightarrow a = \overrightarrow u + 2\overrightarrow v = \left( {2;0; - 3} \right) + 2.\left( {0;2; - 1} \right) = (2 + 0;0 + 2.2; - 3 + 2.( - 1)) = (2;4; - 5)\).
Trong không gian Oxy, cho điểm M(1;0;2) và mặt phẳng (P): 2x – y + 3z + 5 = 0. Mặt phẳng đi qua M và song song với (P) có phương trình là
\(2x - y + 3z + 8 = 0\)
\(2x + y + 3z - 3 = 0\)
\(2x + y + 3z + 5 = 0\)
\(2x - y + 3z - 8 = 0\)
Đáp án : D
Phương trình mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
Mặt phẳng cần tìm song song với (P) nên nhận \(\overrightarrow n = (2; - 1;3)\) làm vecto pháp tuyến.
Phương trình mặt phẳng đó là \(2\left( {x - 1} \right) - 1\left( {y - 0} \right) + 3\left( {z - 2} \right) = 0 \Leftrightarrow 2x - y + 3z - 8 = 0\).
Giá của một chiếc máy photocopy lúc mới mua là 50 triệu đồng. Biết rằng giá trị của nó sau mỗi năm sử dụng chỉ còn 75% giá trị trong năm liền trước đó.
a) Giá trị của máy photocopy sau 1 năm sử dụng là: \({T_1} = 37,5\) triệu đồng.
b) Giá trị của máy photocopy sau 2 năm sử dụng lớn hơn 30 triệu đồng.
c) Giá trị tiêu hao của chiếc máy photocopy đó sau khoảng thời gian 5 năm kể từ khi mua là \(11,8652\) triệu đồng.
d) Sau 7 năm thì giá trị của máy photocopy con 10% có với giá trị ban đầu.
a) Giá trị của máy photocopy sau 1 năm sử dụng là: \({T_1} = 37,5\) triệu đồng.
b) Giá trị của máy photocopy sau 2 năm sử dụng lớn hơn 30 triệu đồng.
c) Giá trị tiêu hao của chiếc máy photocopy đó sau khoảng thời gian 5 năm kể từ khi mua là \(11,8652\) triệu đồng.
d) Sau 7 năm thì giá trị của máy photocopy con 10% có với giá trị ban đầu.
Áp dụng công thức số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\).
a) Đúng. Giá trị của máy photocopy sau 1 năm sử dụng là \({T_1} = 50.75\% = 37,5\) (triệu đồng).
b) Sai. Giá trị của máy photocopy sau 2 năm sử dụng là \({T_2} = {T_1}.75\% = 28,125\) (triệu đồng).
c) Sai. Giá trị của máy photocopy sau n năm sử dụng lập thành một cấp số nhân với số hạng đầu bằng 50 (triệu đồng), công bội 75%.
Giá trị của máy photocopy sau 5 năm sử dụng là \(50.{\left( {75\% } \right)^5}\) (triệu đồng).
Giá trị tiêu hao là \(50 - 50.{\left( {75\% } \right)^5} \approx 38,1348\) (triệu đồng).
d) Sai. Giá trị của máy photocopy sau 7 năm sử dụng là \(50.{\left( {75\% } \right)^7}\) (triệu đồng).
Giá trị của máy photocopy sau 7 năm so với giá ban đầu là \(\frac{{50.{{\left( {75\% } \right)}^7}}}{{50}} \approx 13,35\% \).
Cho hình lăng trụ ABCD.A’B’C’D’ có đáy là hình thoi cạnh 3a, \(\widehat {ABC} = {60^o}\), AA’ = 2a. Đỉnh A’ cách đều ba đỉnh A, B, C. Gọi G là trọng tâm của tam giác ABC.
a) A’G là đường cao của hình lăng trụ ABCD.A’B’C’D’.
b) Độ dài đường cao của hình lăng trụ ABCD.A’B’C’D’ bằng \(a\sqrt 3 \).
c) Diện tích hình thoi ABCD bằng \(\frac{{9{a^2}\sqrt 3 }}{2}\).
d) Thể tích của khối chóp B’BCD bằng \(\frac{{3{a^3}\sqrt 3 }}{2}\).
a) A’G là đường cao của hình lăng trụ ABCD.A’B’C’D’.
b) Độ dài đường cao của hình lăng trụ ABCD.A’B’C’D’ bằng \(a\sqrt 3 \).
c) Diện tích hình thoi ABCD bằng \(\frac{{9{a^2}\sqrt 3 }}{2}\).
d) Thể tích của khối chóp B’BCD bằng \(\frac{{3{a^3}\sqrt 3 }}{2}\).
Áp dụng định lý Pythagore, các công thức tính diện tích, thể tích.
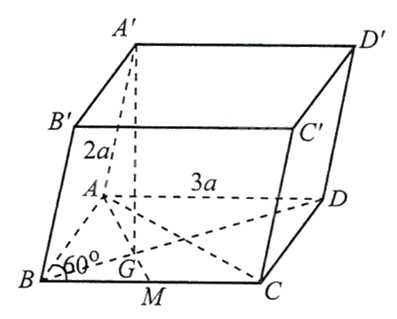
a) Đúng. Ta có G, A’ cùng cách đều ba đỉnh A, B, C nên A’G là trục đường tròn ngoại tiếp tam giác ABC và \(A'G \bot (ABC)\).
b) Sai. Vì AB = BC = 3a và \(\widehat {ABC} = {60^o}\) nên tam giác ABC đều.
Khi đó \(AG = \frac{2}{3}.\frac{{3a\sqrt 3 }}{2} = a\sqrt 3 \).
Xét tam giác AA’G vuông tại G có \({A^\prime }G = \sqrt {A'{A^2} - A{G^2}} = \sqrt {{{(2a)}^2} - {{(a\sqrt 3 )}^2}} = a\).
c) Đúng. Diện tích hình thoi \(ABCD\) bằng \(3a.3a.\sin {60^o} = \frac{{9{a^2}\sqrt 3 }}{2}\).
d) Sai. \({V_{B'.BCD}} = \frac{1}{3}{S_{BCD}}.d\left( {B',(BCD)} \right) = \frac{1}{3}.\frac{1}{2}{S_{ABCD}}.d\left( {A',(BCD)} \right) \)
\(= \frac{1}{6}{S_{ABCD}}.A'G = \frac{1}{6}.\frac{{9{a^2}\sqrt 3 }}{2}.a = \frac{{3{a^3}\sqrt 3 }}{4}\).
Trưởng Câu lạc bộ Thể thao đã tiến hành điều tra tuổi thọ (đơn vị: năm) của máy chạy bộ do hai hãng X, Y sản xuất và thu được hai mẫu số liệu sau đây:

a) Tuổi thọ của máy chạy bộ do hãng Y có độ phân tán lớn hơn tuổi thọ của máy chạy bộ do hãng X sản xuất.
b) Tuổi thọ trung bình của máy chạy bộ do hãng Y sản xuất lớn hơn tuổi thọ trung bình của máy chạy bộ do hãng X sản xuất.
c) Khoảng tứ phân vị của mẫu số liệu về tuổi thọ của máy chạy bộ do hãng X sản xuất là 2,5.
d) Tuổi thọ máy chạy bộ do hãng X sản xuất đồng đều hơn tuổi thọ máy chạy bộ do hãng Y sản xuất.
a) Tuổi thọ của máy chạy bộ do hãng Y có độ phân tán lớn hơn tuổi thọ của máy chạy bộ do hãng X sản xuất.
b) Tuổi thọ trung bình của máy chạy bộ do hãng Y sản xuất lớn hơn tuổi thọ trung bình của máy chạy bộ do hãng X sản xuất.
c) Khoảng tứ phân vị của mẫu số liệu về tuổi thọ của máy chạy bộ do hãng X sản xuất là 2,5.
d) Tuổi thọ máy chạy bộ do hãng X sản xuất đồng đều hơn tuổi thọ máy chạy bộ do hãng Y sản xuất.
a) So sánh khoảng biến thiên của hai mẫu số liệu.
b) Tính số trung bình của hai mẫu số liệu rồi so sánh.
c) Tính khoảng tứ phân vị của mẫu số liệu hãng X.
d) Tính độ lệch chuẩn của hai mẫu số liệu rồi so sánh.
a) Sai. Khoảng biến thiên của tuổi thọ máy chạy bộ do hãng \(X\) sản xuất là \({R_X} = 12 - 2 = 10\).
Khoảng biến thiên của tuổi thọ máy chạy bộ do hãng \(Y\) sản xuất là \({R_Y} = 12 - 4 = 8\).
Vì \({R_X} > {R_Y}\) nên tuổi thọ của máy chạy bộ do hãng \(X\) có độ phân tán lớn hơn tuổi thọ của máy chạy bộ do hãng \(Y\) sản xuất.
b) Đúng. Chọn giá trị đại diện cho các nhóm số liệu, ta có bảng thống kê sau:
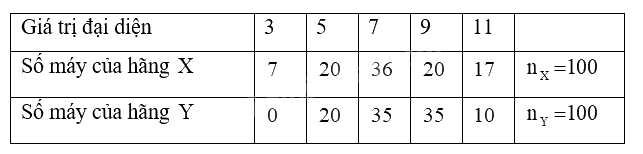
Tuổi thọ trung bình của máy chạy bộ do hãng \(X\) sản xuất là
\(\overline {{x_X}} = \frac{{3.7 + 5.20 + 7.36 + 9.20 + 11.17}}{{100}} = 7,4\).
Tuổi thọ trung bình của máy chạy bộ do hãng \(Y\) sản xuất là
\(\overline {{x_Y}} = \frac{{3.0 + 5.20 + 7.35 + 9.35 + 11.10}}{{100}} = 7,7\).
Như vậy, tuổi thọ trung bình của máy chạy bộ do hãng \(Y\) sản xuất lớn hơn tuổi thọ trung bình của máy chạy bộ do hãng \(X\) sản xuất.
c) Sai. Tính các tần số tích lũy của mẫu số liệu về tuổi thọ của máy chạy bộ do hãng \(X\) sản xuất, ta có bảng thống kê sau:
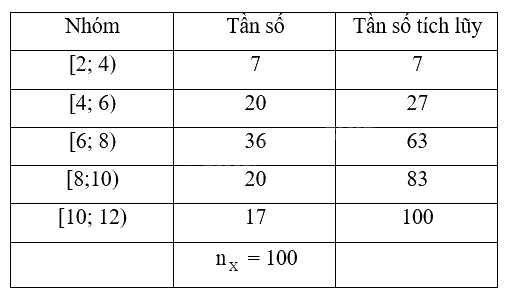
Ta có \(\frac{{{n_X}}}{4} = 25\) mà 7 < 25 < 27 nên nhóm \(2\) là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 25. Xét nhóm \(2\) là nhóm \(\left[ {4;6} \right)\) có \(s = 4;h = 2;{n_2} = 20\) và nhóm \(1\) là nhóm [2;4) có \(c{f_1} = 7.\)
Ta có tứ phân vị thứ nhất là \({Q_1} = 4 + \left( {\frac{{25 - 7}}{{20}}} \right).2 = 5,8\).
Ta có \(\frac{{3{n_X}}}{4} = 75\) mà 63 < 75 , 83 nên nhóm \(4\) là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 75. Xét nhóm 4 là nhóm \(\left[ {8;10} \right)\) có \(s = 8;l = 2;{n_4} = 20\) và nhóm \(3\) là nhóm \(\left[ {6;8} \right)\) có \(c{f_3} = 63.\)
Ta có tứ phân vị thứ ba là \({Q_3} = 8 + \left( {\frac{{75 - 63}}{{20}}} \right).2 = 9,2\).
Vậy khoảng tứ phân vị là \({{\rm{\Delta }}_Q} = {Q_3} - {Q_1} = 3,4\).
d) Sai. chuẩn của tuổi thọ máy chạy bộ do hãng \(X\) sản xuất là
\({s_X} = \sqrt {\frac{{7.{{(3 - 7,4)}^2} + 20.{{(5 - 7,4)}^2} + 36.{{(7 - 7,4)}^2} + 20.{{(9 - 7,4)}^2} + 17{{(11 - 7,4)}^2}}}{{100}}} \approx 2,3\).
Độ lệch chuẩn của tuổi thọ máy chạy bộ do hãng \(Y\) sản xuất là
\({s_Y} = \sqrt {\frac{{20.{{(5 - 7,7)}^2} + 35.{{(7 - 7,7)}^2} + 35{{(9 - 7,7)}^2} + 10{{(11 - 7,7)}^2}}}{{100}}} \approx 1,82\).
Vậy tuổi thọ máy chạy bộ do hãng \(Y\) sản xuất đồng đều hơn tuổi thọ máy chạy bộ do hãng \(X\) sản xuất.
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC. Biết \(MN = \frac{{a\sqrt 6 }}{2}\).
a) Gọi I hình chiếu của M lên (ABCD) nên \(CI = \frac{2}{3}AC\).
b) \(SO = \frac{{a\sqrt {14} }}{2}\).
c) Khoảng cách giữa IN và SC bằng \(\frac{{\sqrt {14} }}{4}\).
d) Giá trị sin của góc giữa đường thẳng \(MN\) và mặt phẳng \((SBD)\) là \(\frac{{\sqrt 6 }}{3}\).
a) Gọi I hình chiếu của M lên (ABCD) nên \(CI = \frac{2}{3}AC\).
b) \(SO = \frac{{a\sqrt {14} }}{2}\).
c) Khoảng cách giữa IN và SC bằng \(\frac{{\sqrt {14} }}{4}\).
d) Giá trị sin của góc giữa đường thẳng \(MN\) và mặt phẳng \((SBD)\) là \(\frac{{\sqrt 6 }}{3}\).
Áp dụng định lý cosin, phương pháp tọa độ hóa.
a) Sai. Gọi I hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.
Khi đó \(CI = \frac{3}{4}AC = \frac{{3a\sqrt 2 }}{4}\).
b) Đúng. Áp dụng định lý cosin ta có:
\(NI = \sqrt {C{N^2} + C{I^2} - 2CN.CI.\cos 45^\circ } = \sqrt {\frac{{{a^2}}}{4} + \frac{{9{a^2}}}{8} - 2 \cdot \frac{a}{2} \cdot \frac{{3a\sqrt 2 }}{4} \cdot \frac{{\sqrt 2 }}{2}} = \frac{{a\sqrt {10} }}{4}\).
Do \(\Delta MIN\) vuông tại I nên \(MI = \sqrt {M{N^2} - N{I^2}} = \sqrt {\frac{{3{a^2}}}{2} - \frac{{5{a^2}}}{8}} = \frac{{a\sqrt {14} }}{4}\).
Mà MI // SO, \(MI = \frac{1}{2}SO \Rightarrow SO = \frac{{a\sqrt {14} }}{2}\).
c) Sai. Chọn hệ trục tọa độ \(Oxyz\) như hình vẽ.
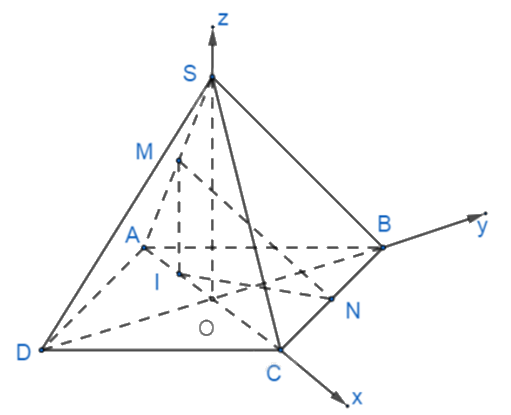
Khi đó ta có tọa độ các điểm: \(O(0;0;0),B\left( {0;\frac{{\sqrt 2 }}{2};0} \right),D\left( {0; - \frac{{\sqrt 2 }}{2};0} \right),C\left( {\frac{{\sqrt 2 }}{2};0;0} \right)\), \(N\left( {\frac{{\sqrt 2 }}{4};\frac{{\sqrt 2 }}{4};0} \right),A\left( { - \frac{{\sqrt 2 }}{2};0;0} \right),S\left( {0;0;\frac{{\sqrt {14} }}{2}} \right),M\left( { - \frac{{\sqrt 2 }}{4};0;\frac{{\sqrt {14} }}{4}} \right)\), \(I\left( { - \frac{{\sqrt 2 }}{4};0;0} \right)\).
Suy ra\({\rm{ }}\left[ {\overrightarrow {IN} ,\overrightarrow {SC} } \right] = \left( {\frac{{\sqrt 7 }}{4}; - \frac{{\sqrt 7 }}{2};\frac{1}{4}} \right);\overrightarrow {IC} = \left( {\frac{{3\sqrt 2 }}{4};0;0} \right)\)
Khoảng cách giữa \(IN\) và \(SC\) bằng \(d = \frac{{\left| {\left[ {\overrightarrow {IN} ,\overrightarrow {SC} } \right].\overrightarrow {IC} } \right|}}{{\left| {\left[ {\overrightarrow {IN} ,\overrightarrow {SC} } \right]} \right|}} = \frac{{\sqrt {14} }}{8}\).
d) Sai. \(\overrightarrow {MN} = \left( {\frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{4}; - \frac{{\sqrt {14} }}{4}} \right),\overrightarrow {SB} = \left( {0;\frac{{\sqrt 2 }}{2}; - \frac{{\sqrt {14} }}{2}} \right),\overrightarrow {SD} = \left( {0; - \frac{{\sqrt 2 }}{2}; - \frac{{\sqrt {14} }}{2}} \right)\).
Vecto pháp tuyến mặt phẳng \(\left( {SBD} \right):\vec n = \left[ {\overrightarrow {SB} ,\overrightarrow {SD} } \right] = \left( { - \sqrt 7 ;0;0} \right)\).
Suy ra \(\sin \left( {MN,\left( {SBD} \right)} \right) = \frac{{|\overrightarrow {MN} .\vec n|}}{{|\overrightarrow {MN} |.|\vec n|}} = \frac{{\left| {\frac{{\sqrt 2 }}{2} \cdot \left( { - \sqrt 7 } \right)} \right|}}{{\frac{{\sqrt 6 }}{2} \cdot \sqrt 7 }} = \frac{{\sqrt 3 }}{3}\).
Khối rubik như hình vẽ có độ dài cạnh bằng 2. Khi gắn rubik vào hệ trục tọa độ trong không gian Oxyz, cho hình lập phương ABCD.A’B’C’D’ có A(0;0;0), B(2;0;0), D(0;2;0), A’(0;0;2). Gọi M, N lần lượt là trung điểm của CD, AA’ (xem hình vẽ bên dưới). Biết rằng cos[B,MN,D’] = m, tính giá trị 14m.

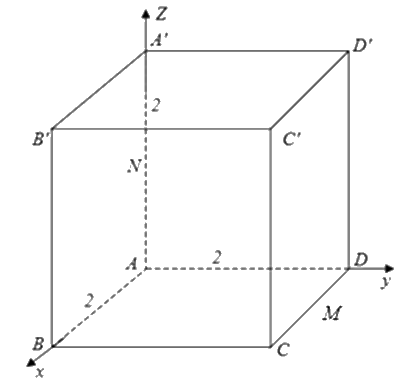
Đáp án:
Đáp án:
Gọi H, H’ lần lượt là hình chiếu của B, D’ trên MN.
Tính \(\cos \left( {\overrightarrow {BH} ,\overrightarrow {D'H'} } \right)\).
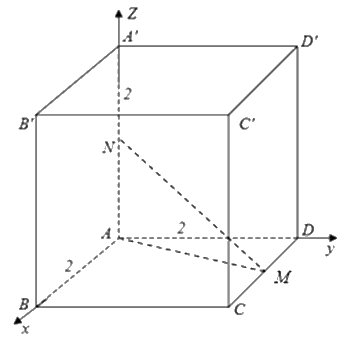
Gọi M, N lần lượt là trung điểm của CD, AA’, suy ra M(1;2;0), N(0;0;1).
\( \Rightarrow \overrightarrow {MN} = \left( { - 1;\, - 2;\,1} \right)\) \( \Rightarrow MN:\left\{ \begin{array}{l}x = t\\y = 2t\\z = 1 - t\end{array} \right.\).
Gọi \(H\left( {t;2t;1 - t} \right)\), \(H'\left( {u;2u;1 - u} \right)\) theo thứ tự là hình chiếu của B, D’ trên MN.
\(\overrightarrow {BH} \left( {t - 2;2t;1 - t} \right);\overrightarrow {D'H'} \left( {u;2u - 2; - 1 - u} \right)\) vuông góc với \(\overrightarrow {MN} = \left( { - 1;\, - 2;\,1} \right)\)
\( \Leftrightarrow \left\{ \begin{array}{l}2 - t - 4t + 1 - t = 0\\ - u - 4u + 4 - 1 - u = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = \frac{1}{2}\\u = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow \overrightarrow {BH} \left( { - \frac{3}{2};1;\frac{1}{2}} \right);\overrightarrow {D'H'} \left( {\frac{1}{2}; - 1; - \frac{3}{2}} \right)\)\( \Rightarrow \cos \left[ {B,MN,D'} \right] = \cos \left( {\overrightarrow {BH} ,\overrightarrow {D'H'} } \right) = \frac{{ - \frac{3}{4} - 1 - \frac{3}{4}}}{{\sqrt {\frac{9}{4} + 1 + \frac{1}{4}} .\sqrt {\frac{9}{4} + 1 + \frac{1}{4}} }} = - \frac{5}{7}\)
\( \Rightarrow \cos \left[ {B,MN,D'} \right] = - \frac{5}{7} = m \Rightarrow 14m = - 10\).
Phương trình \(\cos \left( {2x + \frac{\pi }{3}} \right) = -2\sin \left( {x + \frac{\pi }{6}} \right) + 1\) có bao nhiêu nghiệm trên đoạn [0;2024]?
Đáp án:
Đáp án:
Đưa về phương trình bậc hai đối với một hàm số lượng giác.
\(\cos \left( {2x + \frac{\pi }{3}} \right) =- 2\sin \left( {x + \frac{\pi }{6}} \right) + 1\)
\( \Leftrightarrow 1 - 2{\sin ^2}\left( {x + \frac{\pi }{6}} \right) = -2\sin \left( {x + \frac{\pi }{6}} \right) + 1\)
\( \Leftrightarrow \left[ \begin{array}{l}\sin \left( {x + \frac{\pi }{6}} \right) = 1\\\sin \left( {x + \frac{\pi }{6}} \right) = 0\end{array} \right.\) \( \Leftrightarrow \) \(\left[ \begin{array}{l}x = \frac{\pi }{3}\, + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\\x = - \frac{\pi }{6}\, + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\end{array} \right.\)
Vì \(x \in \left[ {0;2024} \right]\) nên:
+ Với \(x = \frac{\pi }{3}\, + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\):
\(0 \le \frac{\pi }{3}\, + k2\pi \le 2024 \Leftrightarrow - \frac{1}{6} \le k \le \frac{{1012}}{\pi } - \frac{1}{6}\).
Vì \(k \in \mathbb{Z}\) nên có \(322\) nghiệm thỏa mãn.
+ Với \(x = - \frac{\pi }{6}\, + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\):
\(0 \le x = - \frac{\pi }{6}\, + k\pi \,\, \le 2024 \Leftrightarrow \frac{1}{6} \le k \le \frac{{2024}}{\pi } + \frac{1}{6}\).
Vì \(k \in \mathbb{Z}\) nên có \(642\) nghiệm thỏa mãn.
Vậy có \(642 + 322 = 964\) nghiệm thỏa mãn.
Một hình tam giác đều màu trắng có cạnh 2 đơn vị dài được chia thành bốn hình tam giác nhỏ hơn bằng nhau và hình tam giác ở chính giữa được tô màu đỏ (như hình vẽ).
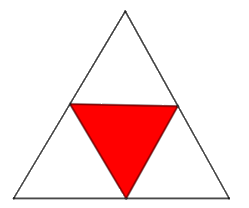
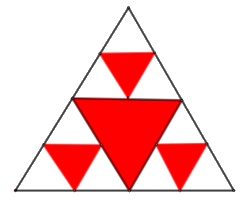
Mỗi hình tam giác màu trắng nhỏ hơn lại được chia thành bốn hình tam giác con bằng nhau, và mỗi hình tam giác con ở chính giữa lại được tô màu đỏ. Nếu quá trình này được tiếp tục lặp lại sáu lần, thì tổng diện tích các hình tam giác không được tô màu đỏ là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Đáp án:
Áp dụng công thức tính tổng n số hạng đầu của cấp số nhân.
Lần phân chia thứ nhất, 1 hình tam giác thành 4 hình tam giác con, diện tích hình tam giác tô màu đỏ là \({u_1} = \frac{1}{4}.\frac{{\sqrt 3 }}{4}{.2^2} = \frac{{\sqrt 3 }}{4}.\)Lần phân chia thứ hai, 3 hình tam giác thành 12 hình tam giác con, diện tích hình tam giác tô màu đỏ tăng thêm là \({u_2} = 3.\frac{1}{4}.\frac{1}{4}.\frac{{\sqrt 3 }}{4}{.2^2} = \frac{{\sqrt 3 }}{4}.\left( {\frac{3}{4}} \right).\)
Lần phân chia thứ ba, 9 hình tam giác thành 36 hình tam giác con, diện tích hình tam giác tô màu đỏ tăng thêm là \({u_3} = 9.\frac{1}{4}.\frac{1}{4}.\frac{1}{4}\frac{{\sqrt 3 }}{4}{.2^2} = \frac{{\sqrt 3 }}{4}.{\left( {\frac{3}{4}} \right)^2}.\)
Lần phân chia thứ tư, 27 hình tam giác thành 108 hình tam giác con, diện tích hình tam giác tô màu đỏ tăng thêm là \({u_4} = 27.\frac{1}{4}\frac{1}{4}\frac{1}{4}.\frac{1}{4}.\frac{{\sqrt 3 }}{4}{.2^2} = \frac{{\sqrt 3 }}{4}.{\left( {\frac{3}{4}} \right)^3}.\)
Tương tự ta thu được diện tích các phần tô màu đỏ theo thứ tự lập thành cấp số nhân có \(\,{u_1} = \frac{{\sqrt 3 }}{4}\), \(q = \frac{3}{4}\).
Do đó, tổng diện tích hình tam giác tô màu đỏ sau 6 lần chia là \({S_6} = {u_1}.\frac{{{q^6} - 1}}{{q - 1}}\).
Diện tích phần không bị tô là \(S\, = \,\frac{1}{2}2.2.{\mathop{\rm Sin}\nolimits} 60^\circ - {S_6}\, \approx 0,31\,\).
Cho hệ trục tọa độ Oxyz mặt phẳng Oxy trùng với mặt đất với trục Ox hướng về phía Đông, trục Oy hướng về phía Nam và trục Oz hướng thẳng đứng lên trời (như hình minh họa bên dưới), đơn vị đo lấy theo kilomet. Hai khinh khí cầu bay lên cùng thời điểm chiếc thứ nhất xuất phát tại điểm O, chiếc thứ hai xuất phát từ điểm I(1;0;0). Sau 20 phút chiếc thứ nhất cách điểm xuất phát 1 km về phía Nam và 1 km về phía Đông, đồng thời cách mặt đất 0,5 km. Chiếc thứ hai cách điểm xuất phát 2 km về phía Bắc và 2 km về phía Đông, đồng thời cách mặt đất 0,8 km. Hỏi nếu giữ nguyên vận tốc và hướng bay thì sau 10 phút nữa 2 khinh khí cầu cách nhau bao km (kết quả làm tròn đến chữ số thập phân thứ nhất)?
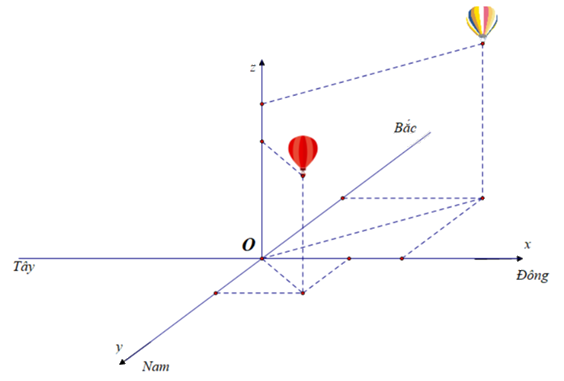
Đáp án:
Đáp án:
Xác định tọa độ hai chiếc khinh khí cầu dựa vào dữ liệu đề bài cho. Áp dụng biểu thức tọa độ các phép toán vecto và công thức tính khoảng cách giữa hai điểm.
Gọi vị trí chiếc khinh khí cầu thứ nhất và thứ hai sau khi bay 20 phút lần lượt là M và N.
Sau 20 phút:
+ Chiếc thứ nhất cách điểm xuất phát 1 km về phía Nam, 1 km về phía Đông, cách mặt đất 0,5 km nên M(1;1;0,5).
+ Chiếc thứ hai cách điểm xuất phát 2 km về phía Bắc, 2 km về phía Đông, cách mặt đất 0,8 km nên N(2;-2;0,8).
Gọi \(A\left( {{x_A};{y_A};{z_A}} \right) \), \(B\left( {{x_B};{y_B};{z_B}} \right)\) lần lượt là vị trí của khinh khí cầu thứ nhất, thứ hai sau khi bay 10 phút tiếp theo. Do đó, thời gian hai chiếc khinh khí cầu bay từ O đến A, B mất 30 phút.
Suy ra \(\overrightarrow {OA} = \frac{3}{2}\overrightarrow {OM} {\rm{\;}} \Rightarrow A\left( {\frac{3}{2};\frac{3}{2};\frac{1}{4}} \right)\); \(\overrightarrow {IB} = \frac{3}{2}\overline {IN} {\rm{\;}} \Rightarrow B\left( {\frac{5}{2}; - 3;1,2} \right)\) .
Ta có \(AB = {\sqrt {{{\left( {\frac{5}{2} - \frac{3}{2}} \right)}^2} + {{\left( { - 3 - \frac{3}{2}} \right)}^2} + {{\left( {1,2 - \frac{1}{4}} \right)}^2}} ^{}} \approx 4,7\).
Bạn Nam có một ống thủy tinh hình trụ, đường kính trong lòng đáy cốc là 10 cm, chiều cao cốc là 15 cm đang đựng nước. Khi bạn Nam nghiêng cốc nước thì thấy mặt nước đi qua đường kính đáy và chạm miệng cốc. Thể tích lượng nước trong cốc là bao nhiêu \(c{m^3}\)?
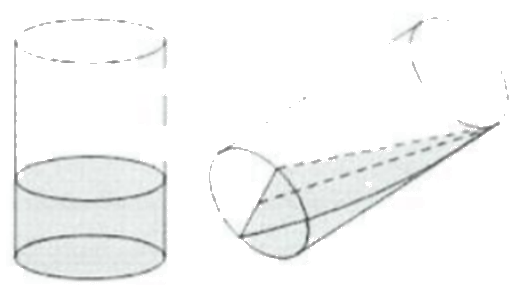
Đáp án:
Đáp án:
Áp dụng công thức tính thể tích vật thể \(V = \int\limits_a^b {S(x)dx} \).
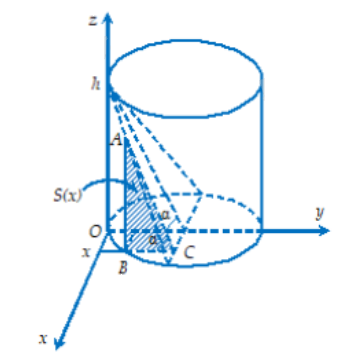
Chọn hệ trục tọa độ như hình vẽ. Ta có: R = 5 cm là bán kính đáy cốc, h = 15 cm là chiều cao của cốc.
Thiết diện của khối nước, cắt bởi mặt phẳng bất kì vuông góc với trục Ox tại điểm có hoành độ \(x\,\,\left( { - 5 \le x \le 5} \right)\) là tam giác ABC vuông tại B, với độ dài cạnh \(BC = \sqrt {{R^2} - {x^2}} = \sqrt {25 - {x^2}} \) và góc \(\alpha = \widehat {BCA} = \arctan \frac{h}{R}\).
Ta có: \(\tan \alpha = \frac{h}{R} = 3\), suy ra \(BA = BC.\tan \alpha = 3\sqrt {25 - {x^2}} \)
Vậy diện tích thiết diện là \(S\left( x \right) = \frac{1}{2}BC\,.\,BA = \frac{3}{2}\left( {25 - {x^2}} \right)\).
Thể tích lượng nước trong cốc là: \(V = \int\limits_{ - 5}^5 {S\left( x \right)dx} = \frac{3}{2}.\int\limits_{ - 5}^5 {\left( {25 - {x^2}} \right)dx} = 250\,\,c{m^3}\).
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,4 và khả năng thắng thầu của dự án 2 là 0,5. Khả năng thắng thầu cả 2 dự án là 0,3. Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là a. Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là b. Khi đó biểu thức P = 4a + 3b là bao nhiêu?
Đáp án:
Đáp án:
Áp dụng công thức tính xác suất có điều kiện \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\).
Gọi \(A\) là biến cố: “Thắng thầu dự án 1”.
Gọi \(B\) là biến cố: “Thắng thầu dự án 2”.
Theo giả thiết suy ra: \(P\left( A \right) = 0,4\); \(P\left( B \right) = 0,5\) và \(P\left( {AB} \right) = 0,3\).
Gọi \(D\) là biến cố: “Thắng thầu dự án 2 biết công ty thắng thầu dự án 1” \( \Rightarrow D = B|A\).
Khi đó: \(P\left( D \right) = P\left( {B|A} \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{{0,3}}{{0,4}} = \frac{3}{4}\).
Gọi \(E\) là biến cố: “Thắng thầu dự án 2 biết công ty không thắng thầu dự án 1” \( \Rightarrow E = B|\overline A \).
Khi đó: \(P\left( E \right) = P\left( {B|\overline A } \right) = \frac{{P\left( {\overline A B} \right)}}{{P\left( {\overline A } \right)}} = \frac{{P\left( B \right) - P\left( {AB} \right)}}{{1 - P\left( A \right)}} = \frac{{0,5 - 0,3}}{{1 - 0,4}} = \frac{{0,2}}{{0,6}} = \frac{1}{3}\).
Vậy \(P = 4.\frac{3}{4} + 3.\frac{1}{3} = 4\).
Đề tham khảo thi THPT môn Toán - Đề số 7 là một công cụ luyện thi vô cùng hữu ích cho các em học sinh đang chuẩn bị cho kỳ thi quan trọng này. Đề thi được xây dựng dựa trên cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp các em làm quen với nhiều loại bài tập và rèn luyện kỹ năng giải quyết vấn đề.
Đề thi số 7 bao gồm các chủ đề chính sau:
Câu hỏi này yêu cầu các em giải phương trình bậc hai. Để giải quyết bài toán này, các em cần nắm vững các công thức nghiệm của phương trình bậc hai và các điều kiện để phương trình có nghiệm. Ngoài ra, các em cũng cần chú ý đến việc kiểm tra lại nghiệm để đảm bảo tính chính xác.
Câu hỏi này liên quan đến đường tròn và các tính chất của đường tròn. Để giải quyết bài toán này, các em cần nắm vững các định nghĩa, định lý và công thức liên quan đến đường tròn, như bán kính, đường kính, dây cung, tiếp tuyến, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung.
Câu hỏi này yêu cầu các em tính đạo hàm của một hàm số. Để giải quyết bài toán này, các em cần nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản, như hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit. Ngoài ra, các em cũng cần chú ý đến việc áp dụng quy tắc chuỗi để tính đạo hàm của các hàm số hợp.
Câu hỏi này yêu cầu các em áp dụng kiến thức toán học để giải quyết một bài toán thực tế. Để giải quyết bài toán này, các em cần phân tích bài toán, xác định các yếu tố toán học liên quan, và xây dựng mô hình toán học phù hợp. Sau đó, các em cần giải mô hình toán học và diễn giải kết quả để trả lời câu hỏi của bài toán.
Sau mỗi câu hỏi, chúng tôi cung cấp bài giải chi tiết và hướng dẫn giải cụ thể. Bài giải này không chỉ cung cấp đáp án đúng mà còn giải thích rõ ràng các bước giải, giúp các em hiểu rõ phương pháp giải và tránh những sai lầm thường gặp. Các em có thể tham khảo bài giải này để tự kiểm tra kiến thức và rèn luyện kỹ năng giải đề.
Đề tham khảo thi THPT môn Toán - Đề số 7 là một tài liệu luyện thi quan trọng và hữu ích cho các em học sinh. Hy vọng rằng, với đề thi này và bài giải chi tiết đi kèm, các em sẽ tự tin hơn khi bước vào kỳ thi THPT sắp tới. Chúc các em thành công!