Giaitoan.edu.vn xin giới thiệu bộ đề thi thử THPT môn Toán năm 2025 do Sở GD Quảng Bình biên soạn. Đây là tài liệu ôn tập vô cùng quan trọng, giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải quyết bài toán và đánh giá năng lực bản thân.
Bộ đề này được thiết kế bám sát chương trình học THPT, bao gồm các dạng bài tập thường gặp trong kỳ thi THPT Quốc gia. Việc luyện tập thường xuyên với các đề thi thử sẽ giúp các em tự tin hơn khi bước vào phòng thi.
Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là:
2,10
4,84
2,09
6,94
Nghiệm của phương trình \({\log _2}x = 3\) là
x = 3
x = 2
x = \({3^2}\)
x = \({2^3}\)
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (1; - 2;1)\) và \(\overrightarrow b = (2; - 4; - 2)\). Khi đó \(\overrightarrow a .\overrightarrow b \) bằng
8
-8
12
-12
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có ba đỉnh A(2;1;-3). B(4;2;1), C(3;0;5). Tọa độ trọng tâm G của tam giác ABC là
G(3;1;-1)
G(3;1;1)
G(1;3;1)
G(-1;3;1)
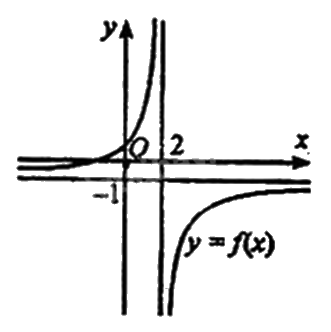
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\), \((c \ne 0,ad - bc \ne 0)\) có đồ thị như hình bên. Tiệm cận đứng của đồ thị hàm số đã cho là
y = -1
y = 2
x = -1
x = 2
Tập nghiệm của bất phương trình \(\log \left( {x - 1} \right) \ge 1\) là
\(\left[ {11; + \infty } \right)\)
\(\left( { - \infty ;11} \right)\)
\(\left( {11; + \infty } \right)\)
\(\left( {1; + \infty } \right)\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M và N theo thứ tự là trung điểm của cạnh SA và SD. Mặt phẳng nào sau đây song song với mặt phẳng (MNO)?
(SCD)
(SBC)
(SAB)
(SAD)
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\). Biết \(\int\limits_5^9 {f(x)dx} = 25\) thì \(\int\limits_9^5 {f(x)dx} \) bằng
9
25
-25
5
Cho cấp số nhân \(\left( {{u_n}} \right)\) biết \({u_2}.{u_6} = 64\). Giá trị của \({u_3}.{u_5}\) bằng
-64
64
-8
8
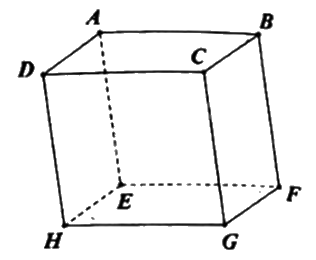
Cho hình hộp ABCD.EFGH (minh họa như hình bên). Vecto nào sau đây bằng vecto \(\overrightarrow {FH} \)?
\(\overrightarrow {BD} \)
\(\overrightarrow {DB} \)
\(\overrightarrow {BA} \)
\(\overrightarrow {AB} \)
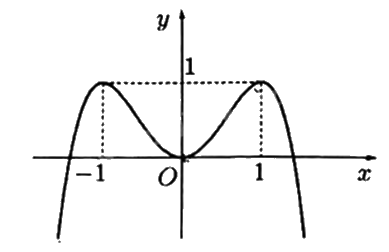
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - 1;1} \right)\)
\(\left( {0;1} \right)\)
\(\left( { - \infty ;1} \right)\)
\(\left( {0; + \infty } \right)\)
Nguyên hàm của hàm số \(f(x) = {x^5}\) là
\(F(x) = \frac{{{x^6}}}{6} + C\)
\(F(x) = 5{x^6} + C\)
\(F(x) = 5{x^4} + C\)
\(F(x) = \frac{{{x^4}}}{4} + C\)
Một sợi dây kim loại dài 6 (cm). Người ta cắt sợi dây thành hai đoạn. Đoạn có độ dài x (cm) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông (0 < x < 6).
a) Bán kính đường tròn là \(r = \frac{x}{\pi }\).
b) Diện tích hình vuông là \({\left( {\frac{{6 - x}}{4}} \right)^2}\).
c) Tổng diện tích hai hình là \(\frac{{(4 + \pi ){x^2} - 12\pi x + 36\pi }}{{16\pi }}\).
d) Khi \(x = \frac{{6\pi }}{{2 + \pi }}\) thì hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
Cho hàm số f(x) = sin2x – x.
a) \(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( {\frac{\pi }{2}} \right) = - \frac{\pi }{2}\).
b) Đạo hàm của hàm số đã cho là f’(x) = cos2x – 1.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{6}\) hoặc \(\frac{\pi }{6}\).
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{2}\).
Cho hàm số \(y = {x^3} - 3{x^2} + 4\).
a) Hàm số y = f(x) nghịch biến trên khoảng (0;2).
b) Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
c) Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số y = f(x). Khi đó độ dài AB bằng \(\sqrt 5 \).
d) Đồ thị hàm số \(y = \frac{{x + 1}}{{f(x)}}\) có đúng hai đường tiệm cận đứng.
Hai bạn Bảo và Nam của lớp 12A cùng tham gia giải bóng bàn đơn nam do nhà trường tổ chức. Hai bạn đó không cùng thuộc một bảng đấu vòng loại và mỗi bảng đấu vòng loại chỉ chọn một người vào vòng chung kết. Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và bạn Nam lần lượt là 0,8 và 0,6.
Gọi A là biến cố “Có ít nhất một bạn lọt vào vòng chung kết".
Gọi B là biến cố “Chỉ có bạn Bảo lọt vào vòng chung kết".
a) Xác suất để bạn Nam không lọt vào vòng chung kết là 0,4.
b) Xác suất để cả hai bạn lọt vào vòng chung kết là 0,8.
c) Xác suất của biến cố A là 0,48.
d) Xác suất của biến cố B là 0,32.
Một máy bay không người lái bay lên tại một điểm. Sau một thời gian bay, máy bay cách điểm xuất phát về phía Bắc 50 (km) và về phía Tây 20 (km), đồng thời cách mặt đất 1 (km). Lúc đó máy bay cách vị trí tại điểm xuất phát của nó là a (km), giá trị của a là bao nhiêu (kết quả làm tròn đến hàng phần mười)?
Đáp án:
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng 2, cạnh bên bằng \(2\sqrt 2 \). Tính khoảng cách giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần mười).
Đáp án:
Cho f(x) là hàm số liên tục trên \(\mathbb{R}\), biết \(f(x) = 16{x^3} - 15{x^2} + 2x\int\limits_1^2 {f(t)dt} - 21\). Giá trị của f(2) bằng bao nhiêu?
Đáp án:
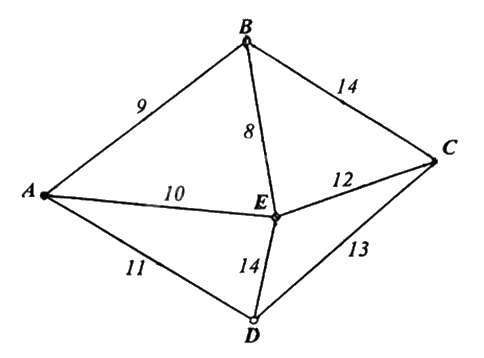
Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hình vẽ bên dưới). Chi phí di chuyển giữa các thành phố được mô tả trên hình. Xe giao hàng của công ty xuất phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố ban đầu. Tìm chi phí thấp nhất của xe giao hàng.
Đáp án:
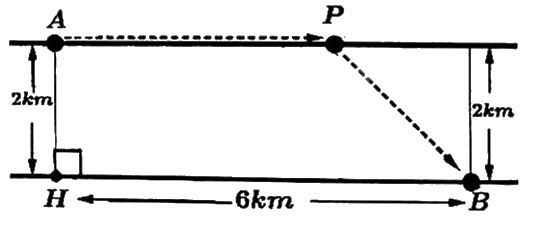
Người ta muốn lắp một ống dẫn dầu từ nhà máy lọc dầu ở vị trí A đến kho chứa dầu đặt ở vị trí B qua một con sông rộng 2 km, dài 6 km. Chi phí lắp đặt đường ống dẫn dầu trên mặt đất để nối từ nhà máy lọc dầu đến trạm trung chuyển tại vị trí P là 4 tỷ VNĐ/km và chi phí lắp đặt ống dẫn dầu dưới dòng sông để nối từ P đến kho chứa dầu tại vị trí B là 8 tỷ VNĐ/km (như hình vẽ dưới). Hỏi để chi phí lắp đặt ít nhất, cần đặt vị trí P cách nhà máy lọc dầu là bao nhiêu kilômét (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Trong đợt ủng hộ sách giáo khoa cho những học sinh bị ảnh hưởng do trận lũ lụt vừa qua, lớp 12A nhận được 20 cuốn gồm 5 cuốn sách Toán học, 7 cuốn sách Vật lí, 8 cuốn sách Hóa học, các sách cùng môn học là giống nhau. Số sách này được chia đều cho 10 học sinh, mỗi học sinh chỉ được nhận đúng 2 cuốn sách khác môn học. Trong số 10 học sinh nhận sách đợt này có bạn Hưng và bạn Thành. Tính xác suất để 2 cuốn sách mà bạn Hưng nhận được giống 2 cuốn sách của bạn Thành (làm tròn kết quả đến hàng phần trăm).
Đáp án:
Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là:
2,10
4,84
2,09
6,94
Đáp án : B
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.({u_{m + 1}} - {u_m})\).
Mẫu số liệu ghép nhóm có cỡ mẫu n = 3 + 8 + 7 + 12 + 7 + 1 + 1 = 39.
Gọi \({x_1},{x_2},...,{x_{39}}\) là điểm của 39 học sinh, giả sử dãy này đã được sắp xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{10}} \in [4;5)\).
Vậy \({Q_1} = 4 + \frac{{\frac{{39}}{4} - 3}}{8}.(5 - 4) = \frac{{155}}{{32}} \approx 4,84\).
Nghiệm của phương trình \({\log _2}x = 3\) là
x = 3
x = 2
x = \({3^2}\)
x = \({2^3}\)
Đáp án : D
ĐKXĐ: x > 0.
\({\log _a}x = b \Leftrightarrow x = {a^b}\).
ĐKXĐ: x > 0.
\({\log _2}x = 3 \Leftrightarrow x = {2^3}\) (thỏa mãn).
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (1; - 2;1)\) và \(\overrightarrow b = (2; - 4; - 2)\). Khi đó \(\overrightarrow a .\overrightarrow b \) bằng
8
-8
12
-12
Đáp án : A
\(\overrightarrow a .\overrightarrow b = {x_a}.{x_b} + {y_a}.{y_b} + {z_a}.{z_b}\).
\(\overrightarrow a .\overrightarrow b = 1.2 - 2.( - 4) + 1.( - 2) = 8\).
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có ba đỉnh A(2;1;-3). B(4;2;1), C(3;0;5). Tọa độ trọng tâm G của tam giác ABC là
G(3;1;-1)
G(3;1;1)
G(1;3;1)
G(-1;3;1)
Đáp án : B
Với G là trọng tâm tam giác ABC, ta có \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3}\end{array} \right.\).
\(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{2 + 4 + 3}}{3} = 3\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{1 + 2 + 0}}{3} = 1\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{ - 3 + 1 + 5}}{3} = 1\end{array} \right. \Rightarrow G(3;1;1)\).
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\), \((c \ne 0,ad - bc \ne 0)\) có đồ thị như hình bên. Tiệm cận đứng của đồ thị hàm số đã cho là
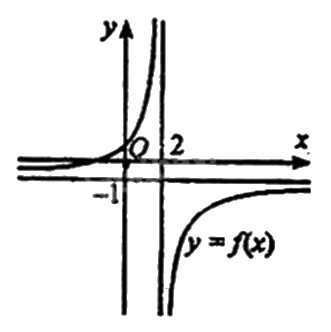
y = -1
y = 2
x = -1
x = 2
Đáp án : D
Quan sát đồ thị và nhận xét.
Tiệm cận đứng của đồ thị hàm số đã cho là x = 2.
Tập nghiệm của bất phương trình \(\log \left( {x - 1} \right) \ge 1\) là
\(\left[ {11; + \infty } \right)\)
\(\left( { - \infty ;11} \right)\)
\(\left( {11; + \infty } \right)\)
\(\left( {1; + \infty } \right)\)
Đáp án : A
Xét phương trình \({\log _a}x \ge b\) (a > 1).
ĐKXĐ: x > 0.
Ta có \({\log _a}x \ge b \Leftrightarrow x \ge {a^b}\).
ĐKXĐ: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\).
\(\log \left( {x - 1} \right) \ge 1 \Leftrightarrow x - 1 \ge {10^1} \Leftrightarrow x \ge 11\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M và N theo thứ tự là trung điểm của cạnh SA và SD. Mặt phẳng nào sau đây song song với mặt phẳng (MNO)?
(SCD)
(SBC)
(SAB)
(SAD)
Đáp án : B
Mặt phẳng (P) song song với mặt phẳng (Q) nếu trong (P) chứa hai đường thẳng cắt nhau cùng song song với (Q).
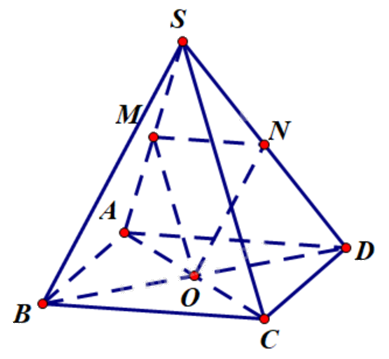
Ta có MN là đường trung bình tam giác SAD nên MN // AD (1).
Mà ABCD là hình bình hành nên AD // BC (2).
Từ (1) và (2) suy ra MN // BC, do đó MN // (SBC) (3).
O là tâm hình bình hành ABCD nên O là trung điểm của AC, suy ra MO là đường trung bình của tam giác SAC. Vì vậy, MO // SC và từ đó ta có MO // (SBC) (4).
Mặt khác, MN cắt MO tại M (5).
Từ (3), (4) và (5) suy ra (MNO) // (SBC).
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\). Biết \(\int\limits_5^9 {f(x)dx} = 25\) thì \(\int\limits_9^5 {f(x)dx} \) bằng
9
25
-25
5
Đáp án : C
Áp dụng tính chất của tích phân \(\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} \).
\(\int\limits_5^9 {f(x)dx} = 25 \Rightarrow \int\limits_9^5 {f(x)dx} = - 25\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) biết \({u_2}.{u_6} = 64\). Giá trị của \({u_3}.{u_5}\) bằng
-64
64
-8
8
Đáp án : B
Áp dụng công thức truy hồi của cấp số nhân \({u_n} = {u_{n - 1}}.q\).
\({u_3}.{u_5} = \left( {{u_2}.q} \right).\left( {\frac{{{u_6}}}{q}} \right) = {u_2}.{u_6} = 64\).
Cho hình hộp ABCD.EFGH (minh họa như hình bên). Vecto nào sau đây bằng vecto \(\overrightarrow {FH} \)?
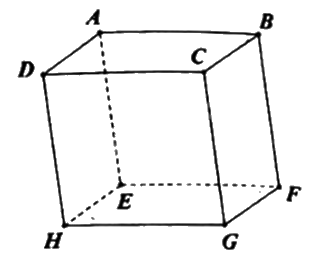
\(\overrightarrow {BD} \)
\(\overrightarrow {DB} \)
\(\overrightarrow {BA} \)
\(\overrightarrow {AB} \)
Đáp án : A
Hai vecto bằng nhau nếu chúng cùng hướng và có độ dài bằng nhau.
\(\overrightarrow {FH} = \overrightarrow {BD} \) vì chúng cùng hướng và FH = BD.
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
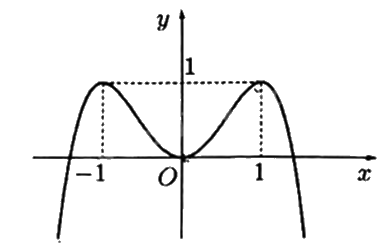
\(\left( { - 1;1} \right)\)
\(\left( {0;1} \right)\)
\(\left( { - \infty ;1} \right)\)
\(\left( {0; + \infty } \right)\)
Đáp án : B
Hàm số đồng biến trên khoảng đồ thị đi lên từ trái sang phải.
Hàm số đã cho đồng biến trên khoảng (0;1) vì đồ thị hàm số đi lên từ trái sang phải.
Nguyên hàm của hàm số \(f(x) = {x^5}\) là
\(F(x) = \frac{{{x^6}}}{6} + C\)
\(F(x) = 5{x^6} + C\)
\(F(x) = 5{x^4} + C\)
\(F(x) = \frac{{{x^4}}}{4} + C\)
Đáp án : A
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int {f(x)dx} = \int {{x^5}dx} = \frac{{{x^{5 + 1}}}}{{5 + 1}} + C = \frac{{{x^6}}}{6} + C\).
Một sợi dây kim loại dài 6 (cm). Người ta cắt sợi dây thành hai đoạn. Đoạn có độ dài x (cm) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông (0 < x < 6).
a) Bán kính đường tròn là \(r = \frac{x}{\pi }\).
b) Diện tích hình vuông là \({\left( {\frac{{6 - x}}{4}} \right)^2}\).
c) Tổng diện tích hai hình là \(\frac{{(4 + \pi ){x^2} - 12\pi x + 36\pi }}{{16\pi }}\).
d) Khi \(x = \frac{{6\pi }}{{2 + \pi }}\) thì hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
a) Bán kính đường tròn là \(r = \frac{x}{\pi }\).
b) Diện tích hình vuông là \({\left( {\frac{{6 - x}}{4}} \right)^2}\).
c) Tổng diện tích hai hình là \(\frac{{(4 + \pi ){x^2} - 12\pi x + 36\pi }}{{16\pi }}\).
d) Khi \(x = \frac{{6\pi }}{{2 + \pi }}\) thì hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
Áp dụng công thức tính chu vi, diện tích của hình tròn và hình vuông. Lập hàm số biểu diễn tổng diện tích hai hình rồi ứng dụng đạo hàm tìm giá trị nhỏ nhất.
a) Sai. Chu vi đường tròn là \(2\pi r = x \Leftrightarrow r = \frac{x}{{2\pi }}\).
b) Đúng. Chu vi hình vuông là 6 – x, suy ra độ dài cạnh là \(\frac{{6 - x}}{4}\).
Diện tích hình vuông là \({\left( {\frac{{6 - x}}{4}} \right)^2}\).
c) Đúng. Diện tích hình tròn là \({S_{tron}} = \pi {\left( {\frac{x}{{2\pi }}} \right)^2} = \frac{{{x^2}}}{{4\pi }}\).
Diện tích hình vuông là \({S_{vuong}} = {\left( {\frac{{6 - x}}{4}} \right)^2} = \frac{{36 - 12x + {x^2}}}{{16}}\).
Tổng diện tích hai hình là \(S = {S_{tron}} + {S_{vuong}} = \frac{{4{x^2} + 36\pi - 12\pi x + \pi {x^2}}}{{16\pi }} = \frac{{(4 + \pi ){x^2} - 12\pi x + 36\pi }}{{16\pi }}\).
d) Sai. Ta có
\(S' = \frac{{2(4 + \pi )x - 12\pi }}{{16\pi }} = 0 \Leftrightarrow 2(4 + \pi )x - 12\pi = 0 \Leftrightarrow x = \frac{{6\pi }}{{4 + \pi }}\).
Bảng biến thiên:
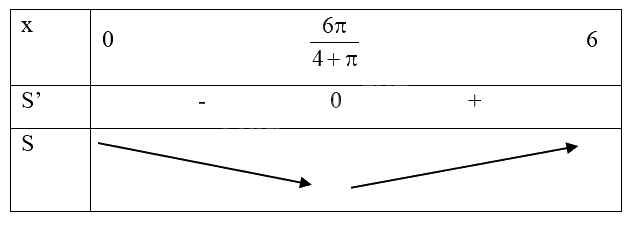
Vậy khi \(x = \frac{{6\pi }}{{4 + \pi }}\) thì tổng diện tích hai hình nhỏ nhất.
Cho hàm số f(x) = sin2x – x.
a) \(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( {\frac{\pi }{2}} \right) = - \frac{\pi }{2}\).
b) Đạo hàm của hàm số đã cho là f’(x) = cos2x – 1.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{6}\) hoặc \(\frac{\pi }{6}\).
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{2}\).
a) \(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( {\frac{\pi }{2}} \right) = - \frac{\pi }{2}\).
b) Đạo hàm của hàm số đã cho là f’(x) = cos2x – 1.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{6}\) hoặc \(\frac{\pi }{6}\).
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{2}\).
a) Thay \( - \frac{\pi }{2}\), \(\frac{\pi }{2}\) vào x của phương trình rồi tính.
b) Áp dụng công thức đạo hàm của hàm hợp lượng giác: (sinu)’ = u’.cosu.
c) Nếu \(\cos \alpha = m\) thì \(\cos x = m \Leftrightarrow \cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
Dựa vào khoảng hoặc đoạn đề bài cho, tìm các giá trị k thỏa mãn rồi thay vào công thức nghiệm và kết luận.
d) Thay giá trị hai đầu mút của đoạn và các giá trị sao cho f’(x) = 0 vào f(x) và tìm giá trị nhỏ nhất.
a) Đúng. \(f\left( { - \frac{\pi }{2}} \right) = \sin ( - \pi ) - \left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\) và \(f\left( {\frac{\pi }{2}} \right) = \sin (\pi ) - \frac{\pi }{2} = - \frac{\pi }{2}\).
b) Sai. f’(x) = 2cos2x – 1.
c) Đúng. \(2\cos 2x - 1 = 0 \Leftrightarrow \cos 2x = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = - \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{6} + k\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
+) \( - \frac{\pi }{2} \le x \le \frac{\pi }{2} \Leftrightarrow - \frac{\pi }{2} \le \frac{\pi }{6} + k\pi \le \frac{\pi }{2} \Leftrightarrow - \frac{{2\pi }}{3} \le k\pi \le \frac{\pi }{3} \Leftrightarrow - \frac{2}{3} \le k \le \frac{1}{3} \Rightarrow k = 0\) (vì \(k \in \mathbb{Z}\)).
Suy ra \(x = \frac{\pi }{6} + 0.\pi = \frac{\pi }{6}\).
+) \( - \frac{\pi }{2} \le x \le \frac{\pi }{2} \Rightarrow - \frac{\pi }{2} \le - \frac{\pi }{6} + k\pi \le \frac{\pi }{2} \Leftrightarrow - \frac{\pi }{3} \le k\pi \le \frac{{2\pi }}{3} \Leftrightarrow - \frac{1}{3} \le k \le \frac{2}{3} \Rightarrow k = 0\) (vì \(k \in \mathbb{Z}\)).
Suy ra \(x = - \frac{\pi }{6} + 0.\pi = - \frac{\pi }{6}\).
Vậy trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thì f’(x) = 0 có hai nghiệm là \(x = \frac{\pi }{6}\); \(x = - \frac{\pi }{6}\).
d) Đúng. f(x) = sin2x – x;
f’(x) = 2cos2x – 1 có nghiệm \(x = \pm \frac{\pi }{6} \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
\(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( {\frac{\pi }{2}} \right) = - \frac{\pi }{2}\); \(f\left( { - \frac{\pi }{6}} \right) = \sin \left( { - \frac{\pi }{3}} \right) - \left( { - \frac{\pi }{6}} \right) = - \frac{{\sqrt 3 }}{2} + \frac{\pi }{6}\); \(f\left( {\frac{\pi }{6}} \right) = \sin \frac{\pi }{3} - \frac{\pi }{6} = \frac{{\sqrt 3 }}{2} - \frac{\pi }{6}\).
Vậy giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \( - \frac{\pi }{2}\).
Cho hàm số \(y = {x^3} - 3{x^2} + 4\).
a) Hàm số y = f(x) nghịch biến trên khoảng (0;2).
b) Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
c) Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số y = f(x). Khi đó độ dài AB bằng \(\sqrt 5 \).
d) Đồ thị hàm số \(y = \frac{{x + 1}}{{f(x)}}\) có đúng hai đường tiệm cận đứng.
a) Hàm số y = f(x) nghịch biến trên khoảng (0;2).
b) Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
c) Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số y = f(x). Khi đó độ dài AB bằng \(\sqrt 5 \).
d) Đồ thị hàm số \(y = \frac{{x + 1}}{{f(x)}}\) có đúng hai đường tiệm cận đứng.
Tính đạo hàm, lập bảng biến thiên và nhận xét.
\(f'(x) = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).
Ta có bảng biến thiên:
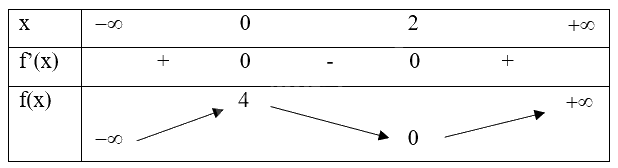
a) Đúng. Hàm số y = f(x) nghịch biến trên khoảng (0;2).
b) Đúng. Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
c) Sai. Giả sử A(0;4), B(2;0). Ta có \(AB = \sqrt {{{(2 - 0)}^2} + {{(0 - 4)}^2}} = 2\sqrt 5 \).
d) Sai. Ta có \(y = \frac{{x + 1}}{{f(x)}} = \frac{{x + 1}}{{{x^3} - 3{x^2} + 4}} = \frac{{x + 1}}{{(x + 1){{(x - 2)}^2}}} = \frac{1}{{{{(x - 2)}^2}}}\).
Có \(\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{{{(x - 2)}^2}}} = + \infty \) nên đồ thị hàm số \(y = \frac{{x + 1}}{{f(x)}}\) có một đường tiệm cận đứng là x = 2.
Hai bạn Bảo và Nam của lớp 12A cùng tham gia giải bóng bàn đơn nam do nhà trường tổ chức. Hai bạn đó không cùng thuộc một bảng đấu vòng loại và mỗi bảng đấu vòng loại chỉ chọn một người vào vòng chung kết. Xác suất lọt qua vòng loại để vào vòng chung kết của bạn Bảo và bạn Nam lần lượt là 0,8 và 0,6.
Gọi A là biến cố “Có ít nhất một bạn lọt vào vòng chung kết".
Gọi B là biến cố “Chỉ có bạn Bảo lọt vào vòng chung kết".
a) Xác suất để bạn Nam không lọt vào vòng chung kết là 0,4.
b) Xác suất để cả hai bạn lọt vào vòng chung kết là 0,8.
c) Xác suất của biến cố A là 0,48.
d) Xác suất của biến cố B là 0,32.
a) Xác suất để bạn Nam không lọt vào vòng chung kết là 0,4.
b) Xác suất để cả hai bạn lọt vào vòng chung kết là 0,8.
c) Xác suất của biến cố A là 0,48.
d) Xác suất của biến cố B là 0,32.
Áp dụng phương pháp tính xác suất của biến cố đối và quy tắc nhân xác suất.
a) Đúng. Xác suất bạn Nam lọt vào vòng chung kết là 0,6 nên xác suất bạn Nam không lọt vào vòng chung kết là 1 – 0,6 = 0,4.
b) Sai. Xác suất để cả hai bạn lọt vào vòng chung kết là 0,8.0,6 = 0,48.
c) Sai. Xác suất bạn Bảo không lọt vào vòng chung kết là 1 – 0,8 = 0,2.
\(\overline A \): “Không có bạn nào lọt vào vòng chung kết”. \(P\left( {\overline A } \right) = 0,2.0,4 = 0,08\).
\(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - 0,08 = 0,92\).
d) Đúng. \(P\left( B \right) = 0,8.0,4 = 0,32\).
Một máy bay không người lái bay lên tại một điểm. Sau một thời gian bay, máy bay cách điểm xuất phát về phía Bắc 50 (km) và về phía Tây 20 (km), đồng thời cách mặt đất 1 (km). Lúc đó máy bay cách vị trí tại điểm xuất phát của nó là a (km), giá trị của a là bao nhiêu (kết quả làm tròn đến hàng phần mười)?
Đáp án:
Đáp án:
Đặt hệ trục tọa độ ở vị trí phù hợp. Áp dụng công thức tính khoảng cách giữa hai điểm \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
Đặt hệ trục tọa độ Oxyz sao cho gốc tọa độ trùng với vị trí xuất phát, mặt đất là mặt phẳng (Oxy), trục Ox hướng về phía Bắc, trục Oy hướng về phía Tây, trục Oz hướng lên trời.
Khi đó, vị trí của máy bay sau một thời gian bay là A(50;20;1).
Khoảng cách của máy bay tới điểm xuất phát là \(OA = \sqrt {{{50}^2} + {{20}^2} + {1^2}} \approx 53,9\) (km).
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng 2, cạnh bên bằng \(2\sqrt 2 \). Tính khoảng cách giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần mười).
Đáp án:
Đáp án:
Đưa về tính khoảng cách từ điểm tới mặt phẳng.
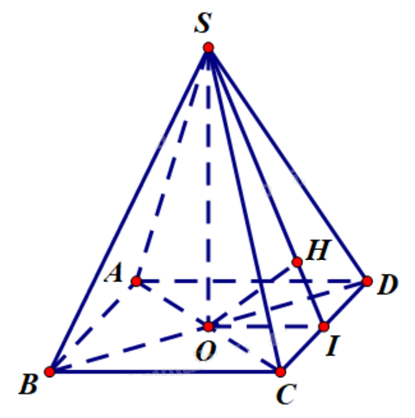
Gọi O là tâm tứ giác ABCD, I là trung điểm của CD. Trong mặt phẳng (SOI), kẻ \(OH \bot SI\), H thuộc SI.
Vì S.ABCD là chóp tứ giác đều nên ABCD là hình vuông, có AB // CD nên AB // (ACD).
Khi đó \(d\left( {AB,SD} \right) = d\left( {AB,(SCD)} \right) = d\left( {A,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\) vì AC = 2AO.
Vì S.ABCD là chóp tứ giác đều nên \(SO \bot (ABCD) \Rightarrow SO \bot CD\).
Có OI là đường trung bình của tam giác ACD nên OI // AD, suy ra \(OI \bot CD\).
Ta có \(\left\{ \begin{array}{l}SO \bot CD\\OI \bot CD\end{array} \right. \Rightarrow CD \bot (SOI) \Rightarrow CD \bot OH\).
Mặt khác \(\left\{ \begin{array}{l}OH \bot CD\\OH \bot SI\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O,(SCD)} \right) = OH\).
\(AC = 2\sqrt 2 \Rightarrow OC = \sqrt 2 \Rightarrow SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - {{\left( {\sqrt 2 } \right)}^2}} = \sqrt {6} \); \(OI = \frac{{AD}}{2} = \frac{2}{2} = 1\).
Xét tam giác SOI vuông tại O có đường cao OH:
\(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{I^2}}} = \frac{1}{{6}} + \frac{1}{1} = \frac{{7}}{{6}} \Rightarrow OH = \frac{{\sqrt {42} }}{{7}}\).
Vậy \(d\left( {AB,SD} \right) = 2d\left( {O,(SCD)} \right) = 2OH = \frac{{2\sqrt {42} }}{{7}} \approx 1,9\).
Cho f(x) là hàm số liên tục trên \(\mathbb{R}\), biết \(f(x) = 16{x^3} - 15{x^2} + 2x\int\limits_1^2 {f(t)dt} - 21\). Giá trị của f(2) bằng bao nhiêu?
Đáp án:
Đáp án:
Đặt \(\int\limits_1^2 {f(t)dt} = \int\limits_1^2 {f(x)dx} = A\) và lấy tích phân hai vế của \(f(x) = 16{x^3} - 15{x^2} + 2x\int\limits_1^2 {f(t)dt} - 21\).
Đặt \(\int\limits_1^2 {f(t)dt} = \int\limits_1^2 {f(x)dx} = A\) (hằng số). Khi đó \(f(x) = 16{x^3} - 15{x^2} + 2x.A - 21\).
\(\int\limits_1^2 {f(x)dx} = \int\limits_1^2 {\left( {16{x^3} - 15{x^2} + 2Ax - 21} \right)dx} = \left( {4{x^4} - 5{x^3} + A{x^2} - 21x} \right)\left| {\begin{array}{*{20}{c}}{^2}\\{_1}\end{array}} \right.\)
\( = \left( {{{4.2}^4} - {{5.2}^3} + A{{.2}^2} - 21.2} \right) - \left( {{{4.1}^4} - {{5.1}^3} + A{{.1}^2} - 21.1} \right)\)
\(= - 18 + 4A - ( - 22 + A) = 4 + 3A\).
Suy ra \(A = 4 + 3A \Leftrightarrow A = - 2\).
Do đó \(f(x) = 16{x^3} - 15{x^2} - 4x - 21 \Rightarrow f(2) = 39\).
Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hình vẽ bên dưới). Chi phí di chuyển giữa các thành phố được mô tả trên hình. Xe giao hàng của công ty xuất phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố ban đầu. Tìm chi phí thấp nhất của xe giao hàng.
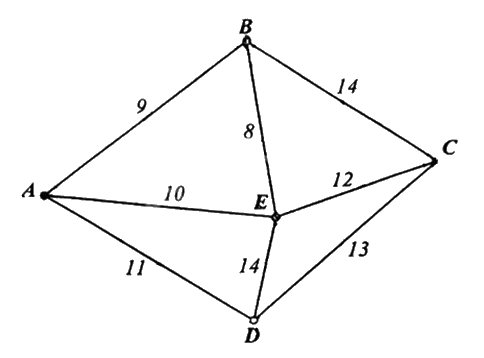
Đáp án:
Đáp án:
Liệt kê và so sánh.
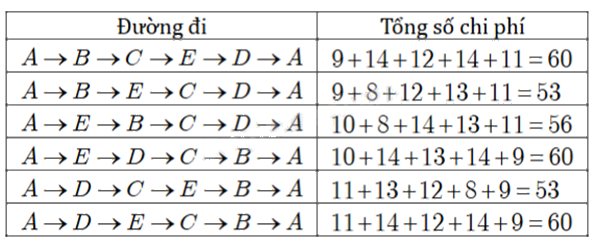
Do đó, chi phí nhỏ nhất của xe giao hàng là 53.
Người ta muốn lắp một ống dẫn dầu từ nhà máy lọc dầu ở vị trí A đến kho chứa dầu đặt ở vị trí B qua một con sông rộng 2 km, dài 6 km. Chi phí lắp đặt đường ống dẫn dầu trên mặt đất để nối từ nhà máy lọc dầu đến trạm trung chuyển tại vị trí P là 4 tỷ VNĐ/km và chi phí lắp đặt ống dẫn dầu dưới dòng sông để nối từ P đến kho chứa dầu tại vị trí B là 8 tỷ VNĐ/km (như hình vẽ dưới). Hỏi để chi phí lắp đặt ít nhất, cần đặt vị trí P cách nhà máy lọc dầu là bao nhiêu kilômét (làm tròn kết quả đến hàng phần trăm)?
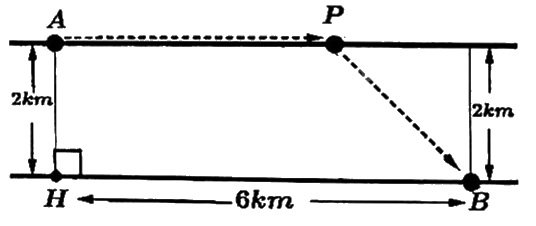
Đáp án:
Đáp án:
Đặt ẩn, lập hàm chi phí lắp đặt ống dẫn rồi ứng dụng đạo hàm để tìm giá trị nhỏ nhất.
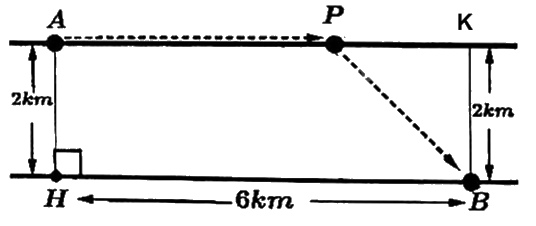
Đặt điểm K ở vị trí như hình. Gọi x = PK (km; \(0 \le x \le 6\)).
Khi đó AP = 6 – x (km), \(PB = \sqrt {{x^2} + 4} \) (km).
Chi phí lắp đặt ống dẫn là \(C(x) = 4(6 - x) + 8\sqrt {{x^2} + 4} \) (tỷ đồng).
\(C'(x) = 4(6 - x) + 8\sqrt {{x^2} + 4} = - 4 + \frac{{8x}}{{\sqrt {{x^2} + 4} }} = 0\)
\( \Leftrightarrow \frac{{8x}}{{\sqrt {{x^2} + 4} }} = 4 \Leftrightarrow 2x = \sqrt {{x^2} + 4} \Leftrightarrow {x^2} + 4 = 4{x^2} \Leftrightarrow 3{x^2} = 4 \Rightarrow x = \frac{{2\sqrt 3 }}{3}\) (km).
Bảng biến thiên:
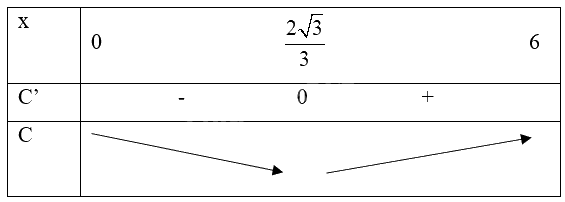
Để chi phí lắp đặt ít nhất, cần đặt vị trí P cách nhà máy lọc dầu A một khoảng \(6 - \frac{{2\sqrt 3 }}{3} \approx 4,85\) (km).
Trong đợt ủng hộ sách giáo khoa cho những học sinh bị ảnh hưởng do trận lũ lụt vừa qua, lớp 12A nhận được 20 cuốn gồm 5 cuốn sách Toán học, 7 cuốn sách Vật lí, 8 cuốn sách Hóa học, các sách cùng môn học là giống nhau. Số sách này được chia đều cho 10 học sinh, mỗi học sinh chỉ được nhận đúng 2 cuốn sách khác môn học. Trong số 10 học sinh nhận sách đợt này có bạn Hưng và bạn Thành. Tính xác suất để 2 cuốn sách mà bạn Hưng nhận được giống 2 cuốn sách của bạn Thành (làm tròn kết quả đến hàng phần trăm).
Đáp án:
Đáp án:
Chia từng trường hợp và áp dụng quy tắc tổ hợp.
Từ số sách trên, ta chia được 10 bộ 2 cuốn sách khác nhau để chia cho 10 học sinh:
- 2 bộ Toán – Lí.
- 5 bộ Lí – Hóa.
- 3 bộ Toán – Hóa.
Không gian mẫu: \(C_{10}^5.C_5^3.C_2^2 = 2520\).
A: “Hưng và Thành nhận được cùng loại bộ sách”.
- Nhận 2 bộ Toán – Lí: \(1.C_8^5.C_3^3 = 56\).
- Nhận 2 bộ Lí – Hóa: \(1.C_8^3.C_5^3.C_2^2 = 560\).
- Nhận 2 bộ Toán – Hóa: \(1.C_8^1.C_7^5.C_2^2 = 168\).
\(P(A) = \frac{{56 + 560 + 168}}{{2520}} = \frac{{14}}{{45}} \approx 0,31\).
Kỳ thi THPT Quốc gia là một bước ngoặt quan trọng trong cuộc đời học sinh, quyết định con đường học vấn và tương lai của mỗi người. Môn Toán, với vai trò là một trong những môn thi chính, đòi hỏi sự chuẩn bị kỹ lưỡng và phương pháp ôn tập hiệu quả. Đề thi thử THPT môn Toán năm 2025 do Sở GD Quảng Bình biên soạn đóng vai trò then chốt trong quá trình chuẩn bị này.
Đề thi thử THPT môn Toán năm 2025 Sở GD Quảng Bình thường có cấu trúc tương tự như đề thi chính thức, bao gồm các phần:
Nội dung đề thi bao phủ đầy đủ các chủ đề quan trọng trong chương trình Toán THPT, bao gồm:
Việc luyện tập với đề thi thử THPT môn Toán năm 2025 Sở GD Quảng Bình mang lại nhiều lợi ích:
Để đạt hiệu quả cao nhất khi luyện đề thi thử, học sinh nên:
Giaitoan.edu.vn cung cấp đầy đủ các đề thi thử THPT môn Toán năm 2025 Sở GD Quảng Bình, cùng với lời giải chi tiết và các bài giảng chất lượng cao. Chúng tôi cam kết đồng hành cùng bạn trên con đường chinh phục môn Toán, giúp bạn đạt kết quả tốt nhất trong kỳ thi THPT Quốc gia.
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi thử THPT môn Toán năm 2025 Sở GD Quảng Bình:
| Dạng bài tập | Ví dụ |
|---|---|
| Hàm số bậc ba | Tìm cực trị, điểm uốn, khoảng đơn điệu của hàm số. |
| Phương trình lượng giác | Giải phương trình lượng giác cơ bản và nâng cao. |
| Hình không gian | Tính khoảng cách, góc giữa hai đường thẳng, hai mặt phẳng. |
| Tích phân | Tính tích phân xác định, ứng dụng tích phân để tính diện tích. |
Hãy luôn giữ vững tinh thần lạc quan, tự tin và nỗ lực hết mình trong quá trình ôn tập. Chúc các em thành công trong kỳ thi THPT Quốc gia 2025!