Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 11 Chân trời sáng tạo - Đề số 6, được biên soạn theo chuẩn chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ đầy đủ các kiến thức trọng tâm của chương trình học kì 2 Toán 11 Chân trời sáng tạo.
Mệnh đề nào sau đây đúng?
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({180^o}\)
Số đo của góc nhị diện nhận giá trị từ \({90^o}\) đến \({180^o}\)
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({90^o}\)
Hai mặt phẳng cắt nhau tạo thành hai góc nhị diện
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mệnh đề nào sau đây đúng?
(SB,CD) = (SB,AD)
(SB,CD) = (SC,CD)
(SB,CD) = (SD,CD)
(SB,CD) = (SB,AB)
Trong không gian, cho 3 đường thẳng a, b, c phân biệt và mặt phẳng (P). Mệnh đề nào sau đâyđúng?
Nếu \(a \bot c\) và \(b \bot c\) thì a // b
Nếu \(a \bot b\) và \(b \bot c\) thì \(a \bot c\)
Nếu \(a \bot b\) thì a và b cắt nhau hoặc chéo nhau
Nếu \(a \bot c\) và \((P) \bot c\) thì a // (P)
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách giữa hai mặt phẳng (ABCD) và (A’B’C’D’) bằng
\(a\sqrt 2 \)
\(\frac{a}{3}\)
\(a\)
\(\frac{a}{2}\)
Thể tích khối chóp có diện tích đáy bằng B và chiều cao bằng h là
\(V = \frac{1}{3}\pi {B^2}h\)
\(V = \frac{1}{3}Bh\)
\(V = \frac{\pi }{3}Bh\)
\(V = Bh\)
Với a là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
\({a^{\frac{5}{2}}}\)
\(a\)
\({a^{\frac{3}{2}}}\)
\({a^{\frac{1}{4}}}\)
Đặt \(a = {\log _2}5\). Khi đó \({\log _{25}}32\) bằng
\(\frac{5}{{2a}}\)
\(\frac{{5a}}{2}\)
\(\frac{2}{{5a}}\)
\(\frac{{2a}}{5}\)
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
\(y = {\left( {\frac{1}{e}} \right)^x}\)
\(y = {\left( {\sqrt {\frac{1}{\pi }} } \right)^x}\)
\(y = {\left( {\frac{1}{3}} \right)^x}\)
\(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\)
Tập nghiệm S của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{125}}} \right)^{ - x}}\) là
\(S = \left( { - \infty ;1} \right)\)
\(S = \left( { - \infty ;2} \right)\)
\(S = \left( {2; + \infty } \right)\)
\(S = \left( {1; + \infty } \right)\)
Tìm tập xác định D của hàm số \({\log _2}\left( {{x^2} - 2x - 3} \right)\).
\(D = \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
\(D = \left[ { - 1;3} \right]\)
(D = \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
\(D = \left( { - 1;3} \right)\)
Rút gọn biểu thức \(P = {x^2}.\sqrt[3]{x}\), x > 0.
\(P = {x^{\frac{4}{3}}}\)
\(P = {x^{\frac{5}{3}}}\)
\(P = {x^{\frac{7}{3}}}\)
\(P = {x^{\frac{8}{3}}}\)
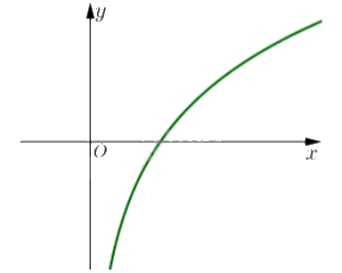
Hàm số nào sau đây có đồ thị như hình bên?
\(y = {\log _{\frac{1}{2}}}x\)
\(y = {\log _2}x\)
\(y = {2^x}\)
\(y = {\left( {\frac{1}{2}} \right)^x}\)
Cho phương trình \({\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + 1\) (*).
a) Điều kiện: x > 1.
b) Gọi x = a là nghiệm của phương trình (*), khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x - 3} \right) = \frac{5}{2}\).
c) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng \({d_1}\): 2x – y – 8 = 0 với \({d_2}\): y = 0.
d) Phương trình (*) có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và \(SA \bot (ABCD)\). Gọi M và N lần lượt là hình chiếu của điểm A trên các đường thẳng SB và SD.
a) \(SA \bot AO\).
b) \(AC \bot (SBD)\).
c) Đường thẳng AM không vuông góc với mặt phẳng (SBC).
d) Gọi K là giao điểm của SC với mặt phẳng (AMN). Khi đó tứ giác AMNK có hai đường chéo vuông góc với nhau.
Năng lượng giải tỏa E của một trận động đất tại tâm địa chấn ở M độ Richte được xác định bởicông thức log(E) = 11,4 + 1,5M. Vào năm 1995, Thành phố X xảy ra một trận động đất 8 độ Richte và năng lượng giải tỏa tại tâm địa chấn của nó gấp 14 lần trận động đất xảy ra tại thành phố Y vào năm 1997. Hỏi khi đó độ lớn của trận động đất tại thành phố Y là bao nhiêu độ Richte (kết quả làm tròn đến hàng phần trăm).
Đáp án:
Kim tự tháp có hình dạng là một khối chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 230 m, độ dài cạnh bên bằng 214 m. Tính khoảng cách từ tâm của đáy đến mặt bên của kim tự tháp (kết quả làm tròn đến hàng đơn vị).
Đáp án:
Số lượng loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức \(s(t) = s(0){.2^t}\), trong đó s(0) là số lượng vi khuẩn A lúc ban đầu, s(t) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu kể từ lúc ban đầu, số lượng loại vi khuẩn A là 20 triệu con?
Đáp án:
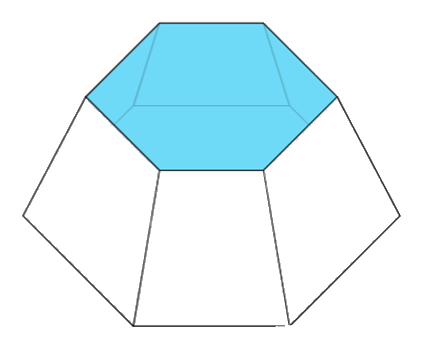
Cho một chậu nước hình chóp cụt đều (hình vẽ) có chiều cao bằng 3 dm, đáy là lục giác đều, độ dài cạnh đáy lớn bằng 2 dm và độ dài cạnh đáy nhỏ bằng 1 dm. Tính thể tích của chậu nước (tính chính xác đến hàng phần mười của \(d{m^3}\)).
Đáp án:
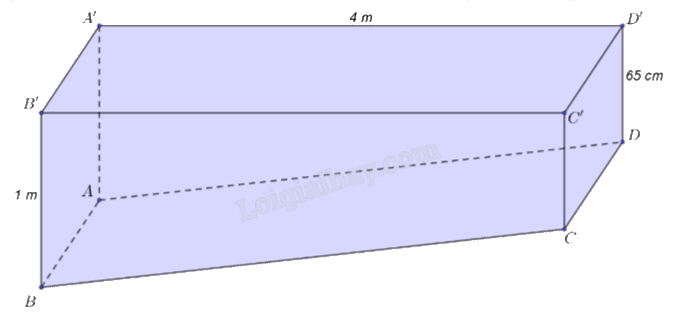
Bác Minh có một khối gỗ có kích thước như hình vẽ. Biết ABCD, A’B’C’D’, A’B’BA, CDD’C’ là các hình chữ nhật, A’D’DA, B’C’CB là các hình thang vuông. Bác Minh muốn làm đẹp khối gỗ đó bằng cách cắt khối gỗ theo mặt phẳng (P) đi qua C và song song với mặt phẳng (A’B’C’D’). Khi đó, bác Minh cần đặt mép BC của khối gỗ tạo với lưỡi cắt của máy cắt một góc bao nhiêu độ?
Một người gửi tiết kiệm theo thể thức lãi suất kép với lãi suất 8,4%/năm. Giả sử lãi suất không thay đổi, hỏi sau ít nhất bao nhiêu năm người đó thu được số tiền gấp đôi số tiền ban đầu?
Cho \(x = {a^2}\), \({\log _b}x = 8\) với a, b là các số thực lớn hơn 1. Tính \({\log _{\frac{a}{{{b^2}}}}}x\).
Mệnh đề nào sau đây đúng?
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({180^o}\)
Số đo của góc nhị diện nhận giá trị từ \({90^o}\) đến \({180^o}\)
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({90^o}\)
Hai mặt phẳng cắt nhau tạo thành hai góc nhị diện
Đáp án : A
Dựa vào lý thuyết góc nhị diện.
Số đo của góc nhị diện nhận giá trị từ \({0^o}\) đến \({180^o}\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mệnh đề nào sau đây đúng?
(SB,CD) = (SB,AD)
(SB,CD) = (SC,CD)
(SB,CD) = (SD,CD)
(SB,CD) = (SB,AB)
Đáp án : D
Nếu a // b thì (a,c) = (b,c).
Vì AB // CD nên (SB,CD) = (SB,AB).
Trong không gian, cho 3 đường thẳng a, b, c phân biệt và mặt phẳng (P). Mệnh đề nào sau đâyđúng?
Nếu \(a \bot c\) và \(b \bot c\) thì a // b
Nếu \(a \bot b\) và \(b \bot c\) thì \(a \bot c\)
Nếu \(a \bot b\) thì a và b cắt nhau hoặc chéo nhau
Nếu \(a \bot c\) và \((P) \bot c\) thì a // (P)
Đáp án : C
Dựa vào quan hệ song song và vuông góc trong không gian.
Xét phương án A: Nếu \(a \bot c\) và \(b \bot c\) thì a, b có thể vuông góc, cắt nhau hoặc chéo nhau hoặc song song. Vậy A sai.
Xét phương án B: Nếu \(a \bot b\) và \(b \bot c\) thì a, b có thể vuông góc, cắt nhau hoặc chéo nhau hoặc song song. Vậy B sai.
Xét phương án C: Nếu \(a \bot b\) thì a và b cắt nhau hoặc chéo nhau. Vậy C đúng.
Xét phương án D: Nếu \(a \bot c\) và \((P) \bot c\) thì a // (P) hoặc \(a \subset (P)\). Vậy A sai.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách giữa hai mặt phẳng (ABCD) và (A’B’C’D’) bằng
\(a\sqrt 2 \)
\(\frac{a}{3}\)
\(a\)
\(\frac{a}{2}\)
Đáp án : C
Đưa về tính khoảng cách từ một điểm đến một mặt phẳng.
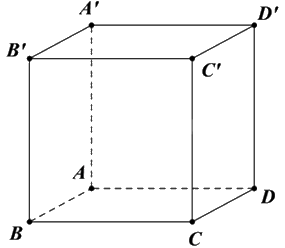
Vì (ABCD) // (A’B’C’D’) nên \(d\left( {(ABCD),(A'B'C'D')} \right) = d\left( {A,(A'B'C'D')} \right)\).
Mặt khác, A’ là hình chiếu vuông góc của A lên (A’B’C’D’) nên \(d\left( {A,(A'B'C'D')} \right) = AA'\).
Vậy \(d\left( {(ABCD),(A'B'C'D')} \right) = AA' = a\).
Thể tích khối chóp có diện tích đáy bằng B và chiều cao bằng h là
\(V = \frac{1}{3}\pi {B^2}h\)
\(V = \frac{1}{3}Bh\)
\(V = \frac{\pi }{3}Bh\)
\(V = Bh\)
Đáp án : B
Áp dụng công thức tính thể tích khối chóp.
Thể tích khối chóp có diện tích đáy bằng B và chiều cao bằng h là \(V = \frac{1}{3}Bh\).
Với a là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
\({a^{\frac{5}{2}}}\)
\(a\)
\({a^{\frac{3}{2}}}\)
\({a^{\frac{1}{4}}}\)
Đáp án : A
Áp dụng tính chất của lũy thừa \({a^m}.{a^n} = {a^{m + n}}\).
\({a^2}.{a^{\frac{1}{2}}} = {a^{2 + \frac{1}{2}}} = {a^{\frac{5}{2}}}\).
Đặt \(a = {\log _2}5\). Khi đó \({\log _{25}}32\) bằng
\(\frac{5}{{2a}}\)
\(\frac{{5a}}{2}\)
\(\frac{2}{{5a}}\)
\(\frac{{2a}}{5}\)
Đáp án : A
Áp dụng công thức \({\log _{{a^m}}}b = \frac{1}{m}{\log _a}b\) và \({\log _a}{b^m} = m{\log _a}b\).
\({\log _{25}}32 = {\log _{{5^2}}}{2^5} = \frac{5}{2}{\log _5}2 = \frac{5}{{2{{\log }_2}5}} = \frac{5}{{2a}}\).
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
\(y = {\left( {\frac{1}{e}} \right)^x}\)
\(y = {\left( {\sqrt {\frac{1}{\pi }} } \right)^x}\)
\(y = {\left( {\frac{1}{3}} \right)^x}\)
\(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\)
Đáp án : D
Hàm số \(y = {a^x}\) đồng biến khi a > 1.
Vì \(\sqrt[{2024}]{\pi } > 1\) nên \(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\) đồng biến trên tập xác định.
Tập nghiệm S của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{125}}} \right)^{ - x}}\) là
\(S = \left( { - \infty ;1} \right)\)
\(S = \left( { - \infty ;2} \right)\)
\(S = \left( {2; + \infty } \right)\)
\(S = \left( {1; + \infty } \right)\)
Đáp án : D
Đưa hai vế của bất phương trình về cùng cơ số.
\({5^{x + 2}} < {\left( {\frac{1}{{125}}} \right)^{ - x}} \Leftrightarrow {5^{x + 2}} < {\left( {{5^{ - 3}}} \right)^{ - x}} \Leftrightarrow {5^{x + 2}} < {5^{3x}} \Leftrightarrow x + 2 < 3x \Leftrightarrow x > 1\).
Tìm tập xác định D của hàm số \({\log _2}\left( {{x^2} - 2x - 3} \right)\).
\(D = \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
\(D = \left[ { - 1;3} \right]\)
(D = \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
\(D = \left( { - 1;3} \right)\)
Đáp án : C
Điều kiện xác định của hàm \({\log _a}x\) là x > 0.
ĐKXĐ: \({x^2} - 2x - 3 > 0 \Leftrightarrow \left[ \begin{array}{l}x > 3\\x < - 1\end{array} \right.\). Vậy \(D = \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\).
Rút gọn biểu thức \(P = {x^2}.\sqrt[3]{x}\), x > 0.
\(P = {x^{\frac{4}{3}}}\)
\(P = {x^{\frac{5}{3}}}\)
\(P = {x^{\frac{7}{3}}}\)
\(P = {x^{\frac{8}{3}}}\)
Đáp án : C
Áp dụng công thức \({x^m}.{x^n} = {x^{m + n}}\), \(\sqrt[b]{{{x^a}}} = {x^{\frac{a}{b}}}\).
\(P = {x^2}.\sqrt[3]{x} = {x^2}.{x^{\frac{1}{3}}} = {x^{2 + \frac{1}{3}}} = {x^{\frac{7}{3}}}\).
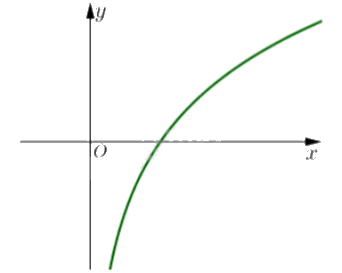
Hàm số nào sau đây có đồ thị như hình bên?
\(y = {\log _{\frac{1}{2}}}x\)
\(y = {\log _2}x\)
\(y = {2^x}\)
\(y = {\left( {\frac{1}{2}} \right)^x}\)
Đáp án : B
Dựa vào điểm đồ thị đi qua và xét sự đồng biến, nghịch biến.
Vì đồ thị hàm số đi qua điểm có tọa độ (1;0) và x > 0 nên đây là hàm số logarit có dạng \(y = {\log _a}x\).
Đồ thị đi lên từ trái sang nên hàm số đồng biến trên \((0; + \infty )\). Do đó, a > 1.
Cho phương trình \({\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + 1\) (*).
a) Điều kiện: x > 1.
b) Gọi x = a là nghiệm của phương trình (*), khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x - 3} \right) = \frac{5}{2}\).
c) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng \({d_1}\): 2x – y – 8 = 0 với \({d_2}\): y = 0.
d) Phương trình (*) có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
a) Điều kiện: x > 1.
b) Gọi x = a là nghiệm của phương trình (*), khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x - 3} \right) = \frac{5}{2}\).
c) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng \({d_1}\): 2x – y – 8 = 0 với \({d_2}\): y = 0.
d) Phương trình (*) có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
Giải các phương trình rồi so sánh tập nghiệm.
a)Đúng. Điều kiện: \(\left\{ \begin{array}{l}x + 6 > 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 6\\x > 1\end{array} \right. \Leftrightarrow x > 1\).
b) Sai. \({\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + 1 \Leftrightarrow {\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + {\log _3}3\)
\( \Leftrightarrow {\log _3}\left( {x + 6} \right) = {\log _3}3\left( {x - 1} \right) \Leftrightarrow x + 6 = 3\left( {x - 1} \right) \Leftrightarrow x = \frac{9}{2}\) (TMĐK).
Ta có \(\mathop {\lim }\limits_{x \to \frac{9}{2}} \left( {x - 3} \right) = \frac{9}{2} - 3 = \frac{3}{2}\).
c) Sai. Hoành độ giao điểm của \({d_1}\) và \({d_2}\) là nghiệm của phương trình \(2x - 8 = 0 \Leftrightarrow x = 4\).
Vậy hoành độ giao điểm của \({d_1}\) và \({d_2}\) không là nghiệm của (*).
d) Sai. \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0 \Leftrightarrow {x^2} - 11x + 9 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{11 + \sqrt {85} }}{2}\\x = \frac{{11 - \sqrt {85} }}{2}\end{array} \right.\).
Vậy phương trình (*) không có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và \(SA \bot (ABCD)\). Gọi M và N lần lượt là hình chiếu của điểm A trên các đường thẳng SB và SD.
a) \(SA \bot AO\).
b) \(AC \bot (SBD)\).
c) Đường thẳng AM không vuông góc với mặt phẳng (SBC).
d) Gọi K là giao điểm của SC với mặt phẳng (AMN). Khi đó tứ giác AMNK có hai đường chéo vuông góc với nhau.
a) \(SA \bot AO\).
b) \(AC \bot (SBD)\).
c) Đường thẳng AM không vuông góc với mặt phẳng (SBC).
d) Gọi K là giao điểm của SC với mặt phẳng (AMN). Khi đó tứ giác AMNK có hai đường chéo vuông góc với nhau.
Áp dụng điều kiện để đường thẳng vuông góc với mặt phẳng; quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.
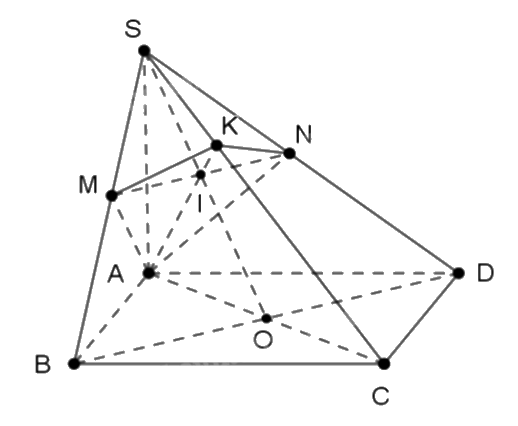
a) Đúng. Vì \(SA \bot (ABCD)\), mà \(AO \subset (ABCD)\) nên \(SA \bot AO\).
b) Sai. Giả sử \(AC \bot (SBD)\), khi đó \(AC \bot SO\). Điều đó vô lí vì \(AC \bot SA\).
c) Sai. Vì \(SA \bot (ABCD)\) nên \(SA \bot BC\). Mặt khác, vì ABCD là hình vuông nên \(AB \bot BC\).
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AM\).
Lại có \(\left\{ \begin{array}{l}BC \bot AM\\SB \bot AM\end{array} \right. \Rightarrow AM \bot (SBC)\).
d) Đúng. Hai tam giác vuông SAB và SAD bằng nhau có các đường cao tương ứng là AM và AN nên BM = DN.Mặt khác tam giác SBD cân tại đỉnh S nên MN // BD.
Do ABCD là hình vuông nên \(AC \bot BD\), mà \(SA \bot BD\) nên \(BD \bot (SAC)\).Vì MN // BD nên \(MN \bot (SAC) \Rightarrow MN \bot AK\).
Năng lượng giải tỏa E của một trận động đất tại tâm địa chấn ở M độ Richte được xác định bởicông thức log(E) = 11,4 + 1,5M. Vào năm 1995, Thành phố X xảy ra một trận động đất 8 độ Richte và năng lượng giải tỏa tại tâm địa chấn của nó gấp 14 lần trận động đất xảy ra tại thành phố Y vào năm 1997. Hỏi khi đó độ lớn của trận động đất tại thành phố Y là bao nhiêu độ Richte (kết quả làm tròn đến hàng phần trăm).
Đáp án:
Đáp án:
Thay các giá trị từ đề bài vào công thức đã cho. Áp dụng quy tắc biến đổi phương trình logarit.
Năng lượng giải tỏa của trận động đất ở thành phố X là \({E_X} = {10^{11,4 + 1,5.8}} = {10^{23,4}}\).
Theo đề bài, ta có năng lượng giải tỏa của trận động đất ở thành phố Y là \({E_Y} = \frac{{{E_1}}}{{14}} = \frac{{{{10}^{23,4}}}}{{14}}\).
Độ lớn của trận động đất ở thành phố Y là:
\(\log ({E_Y}) = 11,4 + 1,5{M_Y} \Rightarrow M = \frac{{\log ({E_Y}) - 11,4}}{{1,5}} = \frac{{\log \left( {\frac{{{{10}^{23,4}}}}{{14}}} \right) - 11,4}}{{1,5}} \approx 7,2\) độ Richte.
Kim tự tháp có hình dạng là một khối chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 230 m, độ dài cạnh bên bằng 214 m. Tính khoảng cách từ tâm của đáy đến mặt bên của kim tự tháp (kết quả làm tròn đến hàng đơn vị).
Đáp án:
Đáp án:
Khoảng cách từ một điểm đến một mặt phẳng là khoảng cách từ hình chiếu vuông góc của điểm lên mặt phẳng tới điểm đó.
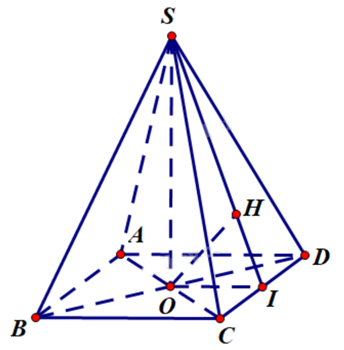
S.ABCD là chóp tứ giác đều nên ABCD là hình vuông.
Giả sử O là tâm hình vuông ABCD, khi đó \(SO \bot (ABCD) \Rightarrow SO \bot CD\).
Gọi I là trung điểm của CD. Khi đó OI // AD (tính chất đường trung bình) và \(CD \bot OI\).
Lấy H thuộc SI sao cho \(OH \bot SI\).
Ta có \(\left\{ \begin{array}{l}CD \bot OI\\CD \bot SO\end{array} \right. \Rightarrow CD \bot (SOI) \Rightarrow CD \bot OH\).
Mặt khác \(\left\{ \begin{array}{l}OH \bot SI\\OH \bot CD\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O,(SCD)} \right) = OH\) (do H thuộc (SCD).
\(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {S{A^2} - {{\left( {\frac{{AC}}{2}} \right)}^2}} = \sqrt {{{214}^2} - {{\left( {\frac{{230\sqrt 2 }}{2}} \right)}^2}} = \sqrt {19346} \) (m).
\(OH = \frac{1}{{\sqrt {\frac{1}{{S{O^2}}} + \frac{1}{{O{I^2}}}} }} = \frac{1}{{\sqrt {\frac{1}{{19346}} + \frac{1}{{{{\left( {\frac{{230}}{2}} \right)}^2}}}} }} \approx 89\) (m).
Vậy khoảng cách từ tâm của đáy đến mặt bên của kim tự tháp xấp xỉ 89 mét.
Số lượng loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức \(s(t) = s(0){.2^t}\), trong đó s(0) là số lượng vi khuẩn A lúc ban đầu, s(t) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu kể từ lúc ban đầu, số lượng loại vi khuẩn A là 20 triệu con?
Đáp án:
Đáp án:
Thay các giá trị từ đề bài vào công thức đã cho. Áp dụng quy tắc biến đổi phương trình mũ.
\(s(3) = s(0){.2^3} \Leftrightarrow 625000 = s(0){.2^3} \Leftrightarrow s(0) = 78125\).
\(20000000 = {78125.2^t} \Leftrightarrow {2^t} = 256 \Leftrightarrow t = 8\).
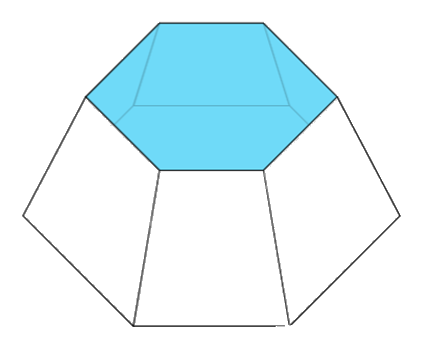
Cho một chậu nước hình chóp cụt đều (hình vẽ) có chiều cao bằng 3 dm, đáy là lục giác đều, độ dài cạnh đáy lớn bằng 2 dm và độ dài cạnh đáy nhỏ bằng 1 dm. Tính thể tích của chậu nước (tính chính xác đến hàng phần mười của \(d{m^3}\)).
Đáp án:
Đáp án:
Các đáy lục giác đều cạnh a được tạo thành từ 6 tam giác đều cạnh a. Từ đó, tính diện tích hai đáy của khối chóp và áp dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}\pi \left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right)\).
\({S_1} = \frac{{{1^2}.\sqrt 3 }}{4}.6 = \frac{{3\sqrt 3 }}{2}\); \({S_2} = \frac{{{2^2}.\sqrt 3 }}{4}.6 = 6\sqrt 3 \); \({S_1}{S_2} = \frac{{3\sqrt 3 }}{2}.6\sqrt 3 = 27\).
\(V = \frac{1}{3}h\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right) = \frac{1}{3}.3\left( {\frac{{3\sqrt 3 }}{2} + 3\sqrt 3 + 6\sqrt 3 } \right) = \frac{{21\sqrt 3 }}{2} \approx 18,2\) \((d{m^3})\).
Bác Minh có một khối gỗ có kích thước như hình vẽ. Biết ABCD, A’B’C’D’, A’B’BA, CDD’C’ là các hình chữ nhật, A’D’DA, B’C’CB là các hình thang vuông. Bác Minh muốn làm đẹp khối gỗ đó bằng cách cắt khối gỗ theo mặt phẳng (P) đi qua C và song song với mặt phẳng (A’B’C’D’). Khi đó, bác Minh cần đặt mép BC của khối gỗ tạo với lưỡi cắt của máy cắt một góc bao nhiêu độ?
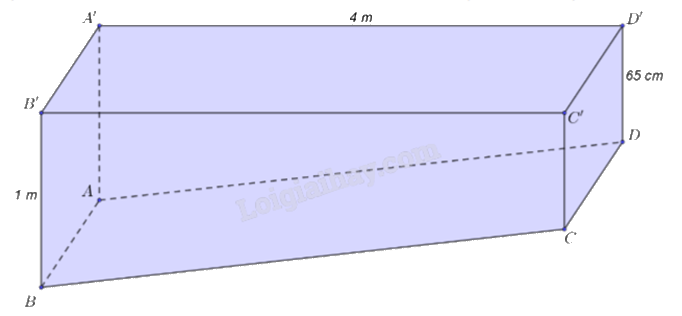
Dựng mặt phẳng (P) theo yêu cầu đề bài. Tính góc giữa (P) và (ABCD) bằng cách đưa về tính góc giữa hai đường thẳng thuộc hai mặt phẳng và vuông góc với giao tuyến của của hai mặt phẳng đó.
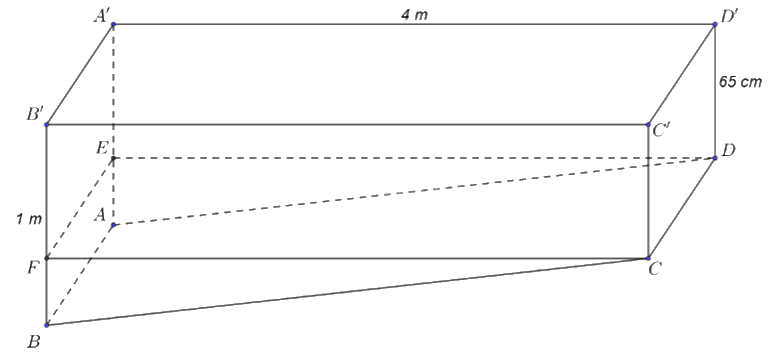
Dựng mặt phẳng hình chữ nhật (CDEF) song song với mặt phẳng (A’B’C’D’) với E thuộc AA’, F thuộc BB’.
Xét hai mặt phẳng (CDEF) và (ABCD) có giao tuyến là CD. Vì CF và CB cùng vuông góc với CD nên \(\left( {CDEF,ABCD} \right) = \left( {CF,CB} \right) = \widehat {FCB}\).
Ta có BB’ = 1 m = 100 cm; B’F = 65 cm; BF = BB’ – B’F = 100 – 65 = 35 cm; CF = 4 m = 400 cm.
Xét tam giác BCF vuông tại F, ta có \(\tan \widehat {FCB} = \frac{{FB}}{{FC}} = \frac{{35}}{{400}} = \frac{7}{{80}} \Rightarrow \widehat {FCB} \approx {5^o}\).
Vậy, bác Minh cần đặt mép BC của khối gỗ tạo với lưỡi cắt của máy cắt một góc xấp xỉ \({5^o}\).
Một người gửi tiết kiệm theo thể thức lãi suất kép với lãi suất 8,4%/năm. Giả sử lãi suất không thay đổi, hỏi sau ít nhất bao nhiêu năm người đó thu được số tiền gấp đôi số tiền ban đầu?
Áp dụng công thức tính lãi kép: \(P = A{\left( {1 + r} \right)^n}\).
Gọi A là số tiền ban đầu gửi tiết kiệm theo thể thức lãi suất kép với lãi suất 8,4%/năm.
Khi đó sau n năm số tiền thu được là \(P = A{\left( {1 + 8,4\% } \right)^n}\).
Để thu được số tiền gấp đôi số tiền ban đầu thì \(2A = A{\left( {1 + 8,4\% } \right)^n} \Leftrightarrow {\left( {1 + 8,4\% } \right)^n} = 2 \Leftrightarrow n = {\log _{1 + 8,4\% }}2 \approx 8,59\) (năm).
Vậy sau ít nhất 9 năm người đó thu được số tiền gấp đôi số tiền ban đầu.
Cho \(x = {a^2}\), \({\log _b}x = 8\) với a, b là các số thực lớn hơn 1. Tính \({\log _{\frac{a}{{{b^2}}}}}x\).
Áp dụng các công thức biến đổi logarit, tính a theo b rồi thay vào biểu thức \({\log _{\frac{a}{{{b^2}}}}}x\) và rút gọn.
\({\log _b}x = 8 \Leftrightarrow x = {b^8}\), mà \(x = {a^2}\) suy ra \({a^2} = {b^8} \Leftrightarrow a = {b^4}\) (vì a > 1).
\({\log _{\frac{a}{{{b^2}}}}}x = {\log _{\frac{{{b^4}}}{{{b^2}}}}}x = {\log _{{b^2}}}x = \frac{1}{2}{\log _b}x = \frac{1}{2}.8 = 4\).
Đề thi giữa kì 2 Toán 11 Chân trời sáng tạo - Đề số 6 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một nửa học kì. Đề thi này không chỉ kiểm tra kiến thức lý thuyết mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Việc nắm vững cấu trúc đề thi và các dạng bài tập thường gặp là yếu tố then chốt để đạt kết quả tốt.
Thông thường, đề thi giữa kì 2 Toán 11 Chân trời sáng tạo - Đề số 6 có cấu trúc bao gồm hai phần chính:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để giải phương trình lượng giác, cần nắm vững các công thức lượng giác cơ bản và các phương pháp giải phương trình lượng giác thường dùng như phương pháp đặt ẩn phụ, phương pháp biến đổi góc, phương pháp sử dụng đường tròn lượng giác.
Khi tính đạo hàm của hàm số, cần áp dụng đúng các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp. Đồng thời, cần nhớ các đạo hàm cơ bản của các hàm số thường gặp như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
Để tính tích phân xác định, cần tìm nguyên hàm của hàm số dưới dấu tích phân và áp dụng công thức tính tích phân xác định. Trong một số trường hợp, cần sử dụng phương pháp đổi biến hoặc phương pháp tích phân từng phần để tính tích phân.
Để đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 11 Chân trời sáng tạo, học sinh cần luyện tập thường xuyên và ôn tập đầy đủ các kiến thức đã học. Nên giải nhiều đề thi thử để làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán. Ngoài ra, cần tham khảo các tài liệu ôn tập, sách giáo khoa và các trang web học toán online uy tín như giaitoan.edu.vn để bổ sung kiến thức và tìm hiểu các phương pháp giải toán hiệu quả.
Việc nắm vững kiến thức nền tảng là yếu tố quyết định đến khả năng giải quyết các bài toán phức tạp trong đề thi. Do đó, học sinh cần dành thời gian ôn tập lại các khái niệm, định nghĩa, tính chất và công thức cơ bản. Đồng thời, cần hiểu rõ mối liên hệ giữa các kiến thức khác nhau để có thể vận dụng linh hoạt vào giải quyết các bài toán.
Đề thi giữa kì 2 Toán 11 Chân trời sáng tạo - Đề số 6 là cơ hội để học sinh đánh giá năng lực học tập và rèn luyện kỹ năng giải toán. Việc chuẩn bị kỹ lưỡng và luyện tập thường xuyên sẽ giúp học sinh tự tin đạt kết quả tốt nhất trong kỳ thi.