Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 4, được biên soạn theo chuẩn chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 1. Học sinh có thể sử dụng đề thi này để tự đánh giá năng lực và chuẩn bị tốt nhất cho kỳ thi sắp tới.
Nghiệm của phương trình \(\tan 2x = \tan \frac{\pi }{4}\) là:
\(x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\) là nghiệm của phương trình:
Tập giá trị của hàm số \(y = \cos x\) là:
Hàm số nào sau đây là hàm số lẻ?
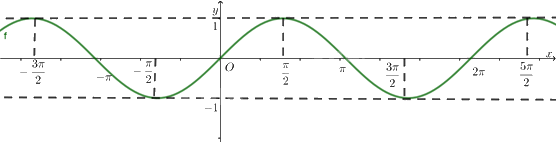
Hình vẽ dưới đây là đồ thị của hàm số nào?
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d. Số hạng tổng quát \({u_n}\) được xác định theo công thức:
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội q. Số hạng tổng quát \({u_n}\) được xác định theo công thức:
Dãy số nào dưới đây gồm các số tự nhiên chẵn nhỏ hơn 10?
Chọn đáp án đúng:
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) chứa điểm \({x_0}\). Hàm số f(x) được gọi là liên tục tại điểm \({x_0}\) nếu:
Cho hàm số f(x) thỏa mãn \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 2\). Tính giới hạn \(\mathop {\lim }\limits_{x \to 0} 3f\left( x \right)\).
Cho dãy số \(\left( {{u_n}} \right)\) có \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 6\), dãy số \(\left( {{v_n}} \right)\) có \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = 2\). Chọn khẳng định đúng:
Trong các câu sau, câu nào sai?
Cho hình chóp S. ABCD với ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Đường thẳng OE nằm trong mặt phẳng nào?
Trong các mệnh đề sau, mệnh đề nào đúng?
Chọn câu đúng:
Hình tứ diện đều có bốn mặt là hình gì?
Chọn câu đúng:
Cho hai góc nhọn a và b. Biết \(\cos a = \frac{1}{3};\cos b = \frac{1}{5}\). Giá trị \(\cos \left( {a + b} \right).\cos \left( {a - b} \right)\) bằng:
Nghiệm của phương trình \(\sin 2x - \cos x = 0\) là:
Cho \(\cos \alpha = \frac{1}{4}\) và \(0 < \alpha < \frac{\pi }{2}\) thì \(\sin 2\alpha \) bằng:
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi: \(\left\{ \begin{array}{l}{u_1} = \frac{1}{4}\\{u_n} = \frac{1}{{2 + {u_{n - 1}}}},\forall n \ge 2\end{array} \right.\). Chọn đáp án đúng
Một thửa ruộng bậc thang có thửa thấp nhất (bậc thấp nhất) nằm ở độ cao 900m so với mực nước biển và độ chênh lệch giữa thửa trên và thửa dưới (hai thửa liên tiếp) trung bình là 1,5m. Hỏi bậc thứ 19 của thửa ruộng đó có độ cao là bao nhiêu so với mực nước biển?
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 6 - 4n - 4{n^2}\). Chọn khẳng định đúng:
Với giá trị nào của m thì \(\mathop {\lim }\limits_{x \to 1} \frac{{mx + 5}}{{x + 1}} = 6\)?
Chọn đáp án đúng:
Cho hàm số \(f\left( x \right) = \frac{{{x^2} - 5}}{{{x^2} + 5x + 4}}\). Hàm số f(x) liên tục trên khoảng nào?
Cho hình chóp tứ giác S. ABCD có đáy ABCD là tứ giác lồi. Gọi M, N lần lượt là trung điểm của SA và SC. Đường thẳng MN song song với mặt phẳng nào?
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm AD và AC. Gọi G là một điểm nằm trong tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng:
Cho hình chóp S. ABC. Lấy E, F, G lần lượt thuộc các cạnh SA, BC, AC. Điểm nào dưới đây thuộc giao tuyến của hai mặt phẳng (EFG) và (SAB)?
Cho tứ diện ABCD. Gọi M là trung điểm của AD. Hình chiếu song song của điểm M theo phương AC lên mặt phẳng (BCD) là:
Bảng dưới đây là kết quả điều tra về tuổi (tính theo năm) của một số chiếc ô tô:
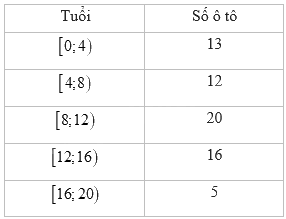
Giá trị đại diện của nhóm có tần số là 20 là:
Kết quả khảo sát cân nặng của 30 quả táo ở một lô hàng cho trong bảng sau:

Mẫu số liệu trên có bao nhiêu nhóm?
Doanh thu bán hàng trong 25 ngày được lựa chọn ngẫu nhiên của một cửa hàng được cho ở trong bảng sau (đơn vị: Triệu đồng):

Có bao nhiêu ngày có doanh thu bán hàng từ 9 triệu đồng trở lên?
Mẫu số liệu ghép nhóm dưới đây thống kê thời gian (giờ) sử dụng pin điện thoại di động của Mai từ lúc sạc đầy pin cho tới khi hết pin:

Mốt của mẫu số liệu này là:
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} + 3} - 2}}{{x - 1}}\;khi\;x \ne 1\\ - 2m + 5\;\;\;\;\;\;khi\;x = 1\end{array} \right.\). Tìm m để hàm số liên tục tại \({x_0} = 1\).
Cho hình chóp tứ giác S. ABCD có đáy ABCD là hình thang, AD//BC, \(AD = 2BC\). Gọi O là giao điểm của AC và BD. Gọi G là trọng tâm của tam giác SCD. Chứng minh rằng OG//(SBC).
Giải phương trình: \({2^{2023}}\left( {{{\sin }^{2024}}x + {{\cos }^{2024}}x} \right)\left( {\sin x + \cos x} \right)\cos x = \frac{{\cos 2x}}{{1 - \tan x}}\)
Đầu năm 2023, anh M mua một chiếc ô tô 4 chỗ giá 800 triệu đồng để chở khách. Trung bình sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 0,5% (so với tháng trước đó). Biết rằng mỗi tháng anh làm ra được 16 triệu đồng (số tiền làm ra mỗi tháng không đổi). Hỏi sau 3 năm, tổng số tiền (bao gồm giá tiền ô tô và tổng số tiền anh M làm ra) anh M có được là bao nhiêu?
Nghiệm của phương trình \(\tan 2x = \tan \frac{\pi }{4}\) là:
Đáp án : C
Sử dụng kiến thức giải phương trình lượng giác: Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) thỏa mãn \(\tan \alpha = m\). Khi đó, \(\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right)\)
Ta có: \(\tan 2x = \tan \frac{\pi }{4} \Leftrightarrow 2x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right) \Leftrightarrow x = \frac{\pi }{8} + \frac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\)
\(x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\) là nghiệm của phương trình:
Đáp án : B
Sử dụng kiến thức về nghiệm phương trình lượng giác: Phương trình \(\sin x = 1\) có nghiệm là: \(x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)
Phương trình \(\sin x = 1\) có nghiệm là: \(x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)
Tập giá trị của hàm số \(y = \cos x\) là:
Đáp án : D
Sử dụng kiến thức về tập giá trị của hàm số \(y = \cos x\): Hàm số \(y = \cos x\) có tập giá trị là: \(D = \left[ { - 1;1} \right]\)
Tập giá trị của hàm số \(y = \cos x\) là: \(D = \left[ { - 1;1} \right]\)
Hàm số nào sau đây là hàm số lẻ?
Đáp án : B
Sử dụng kiến thức về hàm số lẻ: Hàm số \(y = f\left( x \right)\) với tập xác định D được gọi là hàm số lẻ nếu với mọi \(x \in D\) ta có \( - x \in D\) và \(f\left( { - x} \right) = - f\left( x \right)\)
Vì \(\tan \left( { - x} \right) = - \tan x\) nên hàm số \(y = \tan x\) là hàm số lẻ.
Hình vẽ dưới đây là đồ thị của hàm số nào?
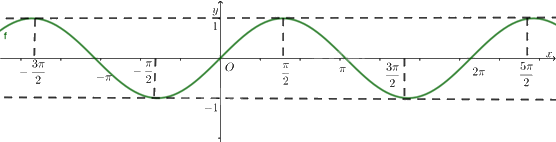
Đáp án : C
Sử kiến thức về đồ thị hàm số \(y = \sin x\).
Hình trên là đồ thị của hàm số \(y = \sin x\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d. Số hạng tổng quát \({u_n}\) được xác định theo công thức:
Đáp án : A
Sử dụng kiến thức về số hạng tổng quát của cấp số cộng: Cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d. Số hạng tổng quát \({u_n}\) được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).
Cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d. Số hạng tổng quát \({u_n}\) được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội q. Số hạng tổng quát \({u_n}\) được xác định theo công thức:
Đáp án : D
Sử dụng kiến thức về số hạng tổng quát của cấp số nhân: Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội q. Số hạng tổng quát \({u_n}\) được xác định theo công thức: \({u_n} = {u_1}.{q^{n - 1}}\) với \(n \ge 2\).
Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội q. Số hạng tổng quát \({u_n}\) được xác định theo công thức: \({u_n} = {u_1}.{q^{n - 1}}\) với \(n \ge 2\).
Dãy số nào dưới đây gồm các số tự nhiên chẵn nhỏ hơn 10?
Đáp án : D
Sử dụng kiến thức về cách cho một dãy số.
Dãy số gồm các số tự nhiên chẵn nhỏ hơn 10 là: 0; 2; 4; 6; 8.
Chọn đáp án đúng:
Đáp án : B
Sử dụng quy tắc về giới hạn hàm số: \(\mathop {\lim }\limits_{x \to - \infty } {x^k} = + \infty \) với k là số chẵn.
\(\mathop {\lim }\limits_{x \to - \infty } {x^k} = + \infty \) với k là số chẵn.
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) chứa điểm \({x_0}\). Hàm số f(x) được gọi là liên tục tại điểm \({x_0}\) nếu:
Đáp án : A
Sử dụng kiến thức hàm số liên tục: Hàm số \(y = f\left( x \right)\) được xác định trên khoảng (a; b) chứa điểm \({x_0}\). Hàm số f(x) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Hàm số \(y = f\left( x \right)\) được xác định trên khoảng (a; b) chứa điểm \({x_0}\). Hàm số f(x) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Cho hàm số f(x) thỏa mãn \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 2\). Tính giới hạn \(\mathop {\lim }\limits_{x \to 0} 3f\left( x \right)\).
Đáp án : B
Sử dụng kiến thức về giới hạn của hàm số: Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right).g\left( x \right)} \right] = L.M\)
\(\mathop {\lim }\limits_{x \to 0} 3f\left( x \right) = \mathop {\lim }\limits_{x \to 0} 3.\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 3.2 = 6\)
Cho dãy số \(\left( {{u_n}} \right)\) có \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 6\), dãy số \(\left( {{v_n}} \right)\) có \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = 2\). Chọn khẳng định đúng:
Đáp án : D
Sử dụng quy tắc tính giới hạn của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b \ne 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\).
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{6}{2} = 3\)
Trong các câu sau, câu nào sai?
Đáp án : D
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng trong không gian.
Hai đường thẳng không có điểm chung thì có thể song song hoặc chéo nhau nên đáp án D sai.
Cho hình chóp S. ABCD với ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Đường thẳng OE nằm trong mặt phẳng nào?
Đáp án : A
Sử dụng kiến thức đường thẳng nằm trong mặt phẳng: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.
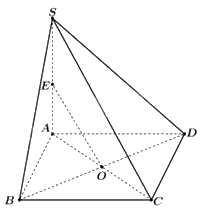
Do \(O \in AC \subset \left( {SAC} \right),E \in SA \subset \left( {SAC} \right)\) nên đường thẳng OE nằm trong mặt phẳng (SAC)
Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án : C
Sử dụng kiến thức về vị trí hai đường thẳng trong không gian.
Hai đường thẳng chéo nhau thì hai đường thẳng đó thuộc hai mặt phẳng khác nhau
Chọn câu đúng:
Đáp án : C
Sử dụng kiến thức hai mặt phẳng song song: Nếu trong mặt phẳng (P) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
Nếu trong mặt phẳng (P) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
Hình tứ diện đều có bốn mặt là hình gì?
Đáp án : A
Sử dụng kiến thức về hình tứ diện đều: Hình tứ diện có bốn mặt là các tam giác đều gọi là hình tứ diện đều.
Hình tứ diện đều có bốn mặt là các tam giác đều.
Chọn câu đúng:
Đáp án : C
Sử dụng kiến thức về phép chiếu song song: Trong không gian, phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Trong không gian, phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Cho hai góc nhọn a và b. Biết \(\cos a = \frac{1}{3};\cos b = \frac{1}{5}\). Giá trị \(\cos \left( {a + b} \right).\cos \left( {a - b} \right)\) bằng:
Đáp án : A
Sử dụng công thức: \(\cos a.\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\).
\(\cos \left( {a + b} \right).\cos \left( {a - b} \right) = \frac{1}{2}\left( {\cos 2a + \cos 2b} \right) = \frac{1}{2}\left( {2{{\cos }^2}a - 1 + 2{{\cos }^2}b - 1} \right) = {\cos ^2}a + {\cos ^2}b - 1\)
\( = {\left( {\frac{1}{3}} \right)^2} + {\left( {\frac{1}{5}} \right)^2} - 1 = \frac{{ - 191}}{{225}}\)
Nghiệm của phương trình \(\sin 2x - \cos x = 0\) là:
Đáp án : B
Phương trình \(\sin x = \sin \alpha \)có nghiệm: \(x = \alpha + k2\pi ,k \in \mathbb{Z}\) và \(x = \pi - \alpha + k2\pi ,k \in \mathbb{Z}\)
\(\sin 2x - \cos x = 0 \Leftrightarrow \sin 2x = \cos x \Leftrightarrow \sin 2x = \sin \left( {\frac{\pi }{2} - x} \right) \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{2} - x + k2\pi \\2x = \pi - \left( {\frac{\pi }{2} - x} \right) + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}3x = \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + \frac{{k2\pi }}{3}\\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Cho \(\cos \alpha = \frac{1}{4}\) và \(0 < \alpha < \frac{\pi }{2}\) thì \(\sin 2\alpha \) bằng:
Đáp án : C
Sử dụng kiến công thức: \({\sin ^2}a + {\cos ^2}a = 1,\sin 2a = 2\sin a\cos a\)
Vì \(0 < \alpha < \frac{\pi }{2}\) nên \(\sin \alpha > 0\). Ta có: \(\sin \alpha = \sqrt {1 - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt {15} }}{4}\)
Do đó, \(\sin 2\alpha = 2\sin \alpha \cos \alpha = 2.\frac{1}{4}.\frac{{\sqrt {15} }}{4} = \frac{{\sqrt {15} }}{8}\)
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi: \(\left\{ \begin{array}{l}{u_1} = \frac{1}{4}\\{u_n} = \frac{1}{{2 + {u_{n - 1}}}},\forall n \ge 2\end{array} \right.\). Chọn đáp án đúng
Đáp án : C
Sử dụng kiến thức về dãy số cho bởi công thức truy hồi.
Ta có: \({u_2} = \frac{1}{{2 + {u_1}}} = \frac{1}{{2 + \frac{1}{4}}} = \frac{4}{9},{u_3} = \frac{1}{{2 + {u_2}}} = \frac{1}{{2 + \frac{4}{9}}} = \frac{9}{{22}}\)
Một thửa ruộng bậc thang có thửa thấp nhất (bậc thấp nhất) nằm ở độ cao 900m so với mực nước biển và độ chênh lệch giữa thửa trên và thửa dưới (hai thửa liên tiếp) trung bình là 1,5m. Hỏi bậc thứ 19 của thửa ruộng đó có độ cao là bao nhiêu so với mực nước biển?
Đáp án : D
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số cộng: Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).
Gọi \({u_n}\) là chiều cao so với mực nước biển của thửa ruộng bậc thang ở bậc thứ n.
Khi đó, \(\left( {{u_n}} \right)\) là một cấp số cộng với \({u_1} = 900m\) và \(d = 1,5m\)
Ta có: \({u_{19}} = {u_1} + 18d = 900 + 18.1,5 = 927\)
Vậy bậc thứ 19 của thửa ruộng có độ cao là 927m so với mực nước biển.
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 6 - 4n - 4{n^2}\). Chọn khẳng định đúng:
Đáp án : B
Sử dụng kiến thức về dãy số bị chặn:
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn trên nếu tồn tại một số M sao cho \({u_n} \le M\) với mọi \(n \in \mathbb{N}*\)
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn dưới nếu tồn tại một số m sao cho \({u_n} \ge m\) với mọi \(n \in \mathbb{N}*\)
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới.
Ta có: \({u_n} = 6 - 4n - 4{n^2} = 7 - \left( {1 + 4n + 4{n^2}} \right) = 7 - {\left( {2n + 1} \right)^2} \le 7\) với mọi \(n \in \mathbb{N}*\).
Do đó, dãy số \(\left( {{u_n}} \right)\) bị chặn trên, không bị chặn dưới.
Với giá trị nào của m thì \(\mathop {\lim }\limits_{x \to 1} \frac{{mx + 5}}{{x + 1}} = 6\)?
Đáp án : A
Sử dụng kiến thức giới hạn hàm số: \(\mathop {\lim }\limits_{x \to {x_0}} {x^n} = x_0^n\) với \(n \in \mathbb{N}\)
\(\mathop {\lim }\limits_{x \to 1} \frac{{mx + 5}}{{x + 1}} = \frac{{m + 5}}{{1 + 1}} = \frac{{m + 5}}{2}\)
Do đó, \(\frac{{m + 5}}{2} = 6 \Leftrightarrow m + 5 = 12 \Leftrightarrow m = 7\)
Chọn đáp án đúng:
Đáp án : B
Sử dụng quy tắc về giới hạn của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b \ne 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\).
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{\sqrt {{n^2} + 2n} }}{{n - 2}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{\sqrt {\frac{{{n^2}}}{{{n^2}}} + \frac{2}{n}} }}{{\frac{n}{n} - \frac{2}{n}}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{\sqrt {1 + \frac{2}{n}} }}{{1 - \frac{2}{n}}} = 1\)
Cho hàm số \(f\left( x \right) = \frac{{{x^2} - 5}}{{{x^2} + 5x + 4}}\). Hàm số f(x) liên tục trên khoảng nào?
Đáp án : C
Sử dụng kiến thức về tính liên tục của hàm số sơ cấp cơ bản: Hàm phân thức hữu tỉ (thương là hai đa thức) liên tục trên tập xác định của chúng.
Hàm số f(x) xác định khi: \({x^2} + 5x + 4 \ne 0 \Leftrightarrow \left( {x + 4} \right)\left( {x + 1} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne - 4\\x \ne - 1\end{array} \right.\)
Do đó, hàm số f(x) liên tục trên các khoảng \(\left( { - \infty ; - 4} \right),\left( { - 4; - 1} \right),\left( { - 1; + \infty } \right)\)
Cho hình chóp tứ giác S. ABCD có đáy ABCD là tứ giác lồi. Gọi M, N lần lượt là trung điểm của SA và SC. Đường thẳng MN song song với mặt phẳng nào?
Đáp án : C
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong mặt phẳng (P) thì a song song với (P).
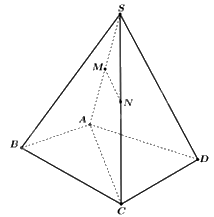
Vì \(MN \subset \left( {SAC} \right)\) nên MN không song song với (SAC)
Vì M, N lần lượt là trung điểm của SA và SC nên MN là đường trung bình của tam giác SAC. Do đó, MN//AC. Mà \(AC \subset \left( {ABCD} \right)\) nên MN// (ABCD).
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm AD và AC. Gọi G là một điểm nằm trong tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng:
Đáp án : B
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
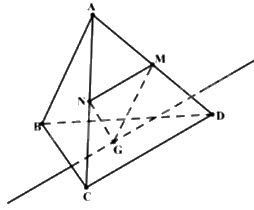
Vì M, N lần lượt là trung điểm của AD và AC nên MN là đường trung bình của tam giác CAD.
Do đó, MN//CD. Mà \(MN \subset \left( {MNG} \right),CD \subset \left( {BCD} \right)\), G là điểm chung của hai mặt phẳng (GMN) và (BCD) nên giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng qua G song song với CD.
Cho hình chóp S. ABC. Lấy E, F, G lần lượt thuộc các cạnh SA, BC, AC. Điểm nào dưới đây thuộc giao tuyến của hai mặt phẳng (EFG) và (SAB)?
Đáp án : D
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó và kí hiệu là \(d = \left( P \right) \cap \left( Q \right)\).
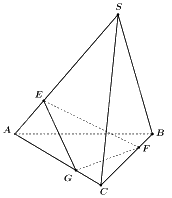
Vì hai đường thẳng GF và AB cùng nằm trong mặt phẳng (ABC) nên giao điểm GF và AB thuộc giao tuyến của hai mặt phẳng (EFG) và (SAB).
Cho tứ diện ABCD. Gọi M là trung điểm của AD. Hình chiếu song song của điểm M theo phương AC lên mặt phẳng (BCD) là:
Đáp án : C
Sử dụng kiến thức về phép chiếu song song: Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:
+ Nếu điểm M thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và \(\Delta \).
+ Nếu điểm M không thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và đường thẳng qua M song song với \(\Delta \).
Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng \(\left( \alpha \right)\) theo phương \(\Delta \).
Phép đặt tương ứng mỗi điểm M với hình chiếu M’ của nó được gọi là phép chiếu song song lên \(\left( \alpha \right)\) theo phương \(\Delta \).
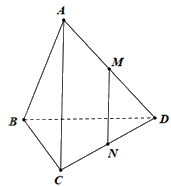
Qua M kẻ đường thẳng song song với AC cắt CD tại N.
Tam giác ACD có MN//AC, M là trung điểm của AD nên N là trung điểm của CD.
Vậy hình chiếu song song của điểm M theo phương AC lên mặt phẳng (BCD) là trung điểm của CD.
Bảng dưới đây là kết quả điều tra về tuổi (tính theo năm) của một số chiếc ô tô:
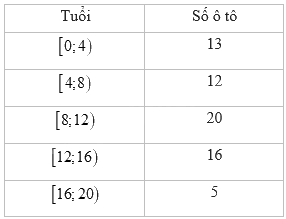
Giá trị đại diện của nhóm có tần số là 20 là:
Đáp án : B
Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm: Giá trị \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
Nhóm \(\left[ {8;12} \right)\) có tần số là 20 nên giá trị đại diện của nhóm là: \(\frac{{8 + 12}}{2} = 10\)
Kết quả khảo sát cân nặng của 30 quả táo ở một lô hàng cho trong bảng sau:

Mẫu số liệu trên có bao nhiêu nhóm?
Đáp án : C
Sử dụng kiến thức về mẫu số liệu ghép nhóm.
Mẫu số liệu trên có 5 nhóm là: \(\left[ {150;155} \right)\); \(\left[ {155;160} \right)\); \(\left[ {160;165} \right)\); \(\left[ {165;170} \right)\); \(\left[ {170;175} \right)\).
Doanh thu bán hàng trong 25 ngày được lựa chọn ngẫu nhiên của một cửa hàng được cho ở trong bảng sau (đơn vị: Triệu đồng):

Có bao nhiêu ngày có doanh thu bán hàng từ 9 triệu đồng trở lên?
Đáp án : A
Sử dụng kiến thức số tần số của mẫu số liệu ghép nhóm: Số giá trị của mẫu số liệu thuộc mỗi nhóm là tần số của nhóm đó.
Số ngày có doanh thu từ 9 triệu đồng trở lên là: \(6 + 3 = 9\) (ngày)
Mẫu số liệu ghép nhóm dưới đây thống kê thời gian (giờ) sử dụng pin điện thoại di động của Mai từ lúc sạc đầy pin cho tới khi hết pin:

Mốt của mẫu số liệu này là:
Đáp án : D
Sử dụng kiến thức về tìm mốt của mẫu số liệu ghép nhóm: Để tìm mốt của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: \(\left[ {{a_j};{a_{j + 1}}} \right)\).
Bước 2: Mốt được xác định là: \({M_o} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\).
Trong đó, \({m_j}\) là tần số của nhóm j, (quy ước \({m_o} = {m_{k + 1}} = 0\)) và h là độ dài của nhóm.
Nhóm chứa mốt của mẫu số liệu trên là \(\left[ {10;12} \right)\).
Ta có: \(j = 3;{a_3} = 10,{m_2} = 8\), \({m_1} = 5;{m_3} = 5,h = 2\). Do đó, \({M_o} = 10 + \frac{{8 - 5}}{{\left( {8 - 5} \right) + \left( {8 - 5} \right)}}.2 = 11\) (phút)
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} + 3} - 2}}{{x - 1}}\;khi\;x \ne 1\\ - 2m + 5\;\;\;\;\;\;khi\;x = 1\end{array} \right.\). Tìm m để hàm số liên tục tại \({x_0} = 1\).
Sử dụng kiến thức về hàm số liên tục: Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Ta có: \(f\left( 1 \right) = - 2m + 5\)
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {{x^2} + 3} - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {\sqrt {{x^2} + 3} - 2} \right)\left( {\sqrt {{x^2} + 3} + 2} \right)}}{{\left( {x - 1} \right)\left( {\sqrt {{x^2} + 3} + 2} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{\left( {x - 1} \right)\left( {\sqrt {{x^2} + 3} + 2} \right)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{x + 1}}{{\sqrt {{x^2} + 3} + 2}} = \frac{{1 + 1}}{{\sqrt {{1^2} + 3} + 2}} = \frac{2}{4} = \frac{1}{2}\)
Để hàm số f(x) liên tục tại \({x_0} = 1\) thì \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right) \Leftrightarrow - 2m + 5 = \frac{1}{2} \Leftrightarrow - 4m + 10 = 1 \Leftrightarrow - 4m = - 9 \Leftrightarrow m = \frac{9}{4}\)
Cho hình chóp tứ giác S. ABCD có đáy ABCD là hình thang, AD//BC, \(AD = 2BC\). Gọi O là giao điểm của AC và BD. Gọi G là trọng tâm của tam giác SCD. Chứng minh rằng OG//(SBC).
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong mặt phẳng (P) thì a song song với P.
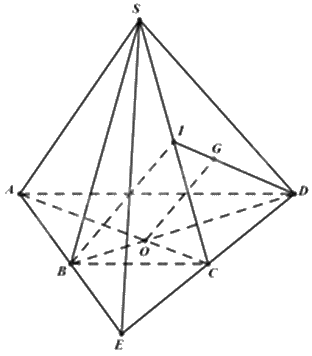
Gọi E là giao điểm của AB và CD.
Vì AD//BC nên $\Delta EBC\backsim \Delta EAD\Rightarrow \frac{EB}{EA}=\frac{EC}{ED}=\frac{BC}{AD}=\frac{1}{2}\Rightarrow EB=\frac{1}{2}EA,EC=\frac{1}{2}ED$
Do đó, B là trung điểm của AE, C là trung điểm của DE.
Suy ra, BD, AC là hai đường trung tuyến của tam giác ADE. Mà O là giao điểm của AC và BD.
Do đó, O là trọng tâm của tam giác ADE. Do đó, \(\frac{{DO}}{{DB}} = \frac{2}{3}\)
Gọi I là trung điểm của SC. Vì G là trọng tâm của tam giác SCD nên \(\frac{{DG}}{{DI}} = \frac{2}{3}\)
Tam giác DIB có: \(\frac{{DG}}{{DI}} = \frac{{DO}}{{DB}} = \frac{2}{3}\) nên OG//IB (định lý Thalès đảo). Mà \(IB \subset \left( {SBC} \right)\) nên OG//(SBC).
Giải phương trình: \({2^{2023}}\left( {{{\sin }^{2024}}x + {{\cos }^{2024}}x} \right)\left( {\sin x + \cos x} \right)\cos x = \frac{{\cos 2x}}{{1 - \tan x}}\)
Sử dụng kiến thức giải phương trình lượng giác: Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) thỏa mãn \(\tan \alpha = m\). Khi đó, \(\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right)\)
Điều kiện: \(\cos x \ne 0,\tan x \ne 1\)
Ta có: \(\frac{{\cos 2x}}{{1 - \tan x}} = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{1 - \frac{{\sin x}}{{\cos x}}}} = \cos x\left( {\cos x + \sin x} \right)\)
\({2^{2023}}\left( {{{\sin }^{2024}}x + {{\cos }^{2024}}x} \right)\left( {\sin x + \cos x} \right)\cos x = \frac{{\cos 2x}}{{1 - \tan x}}\)
\( \Leftrightarrow {2^{2023}}\left( {{{\sin }^{2024}}x + {{\cos }^{2024}}x} \right)\left( {\sin x + \cos x} \right)\cos x = \cos x\left( {\cos x + \sin x} \right)\)
\( \Leftrightarrow \left( {\sin x + \cos x} \right)\cos x\left[ {{2^{2023}}\left( {{{\sin }^{2024}}x + {{\cos }^{2024}}x} \right) - 1} \right] = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\sin x + \cos x = 0\\{2^{2023}}\left( {{{\sin }^{2024}}x + {{\cos }^{2024}}x} \right) - 1 = 0\end{array} \right.\left( {do\;\cos x \ne 0} \right) \Leftrightarrow \left[ \begin{array}{l}\tan x = - 1\\{\sin ^{2024}}x + {\cos ^{2024}}x = \frac{1}{{{2^{2023}}}}\end{array} \right.\)
+) \(\tan x = - 1 \Leftrightarrow x = - \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\)
+) \({\sin ^{2024}}x + {\cos ^{2024}}x = \frac{1}{{{2^{2023}}}}\) (*) (thỏa mãn điều kiện)
Ta có: \({\sin ^{2024}}x + {\cos ^{2024}}x = 2\left[ {\frac{{{{\left( {{{\sin }^2}x} \right)}^{1012}} + {{\left( {{{\cos }^2}x} \right)}^{1012}}}}{2}} \right] \ge 2{\left( {\frac{{{{\sin }^2}x + {{\cos }^2}x}}{2}} \right)^{1012}} = \frac{1}{{{2^{1011}}}}\)
Do đó, phương trình (*) vô nghiệm.
Đầu năm 2023, anh M mua một chiếc ô tô 4 chỗ giá 800 triệu đồng để chở khách. Trung bình sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 0,5% (so với tháng trước đó). Biết rằng mỗi tháng anh làm ra được 16 triệu đồng (số tiền làm ra mỗi tháng không đổi). Hỏi sau 3 năm, tổng số tiền (bao gồm giá tiền ô tô và tổng số tiền anh M làm ra) anh M có được là bao nhiêu?
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số nhân: Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội q thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1}.{q^{n - 1}},n \ge 2\).
Sau 1 tháng, giá trị của ô tô còn lại là: \({u_1} = 800 - 800.0,5\% = 800\left( {1 - 0,5\% } \right)\) (triệu đồng)
Sau 2 tháng, giá trị của ô tô còn lại là:
\({u_2} = 800\left( {1 - 0,5\% } \right) - 800\left( {1 - 0,5\% } \right).0,5\% = 800{\left( {1 - 0,5\% } \right)^2}\) (triệu đồng)
Sau 3 tháng, giá trị của ô tô còn lại là:
\({u_3} = 800{\left( {1 - 0,5\% } \right)^2} - 800{\left( {1 - 0,5\% } \right)^2}.0,5\% = 800{\left( {1 - 0,5\% } \right)^3}\) (triệu đồng)
Gọi \({u_n}\) là giá trị ô tô sau n tháng sử dụng.
Dãy số \(\left( {{u_n}} \right)\) tạo thành một cấp số nhân với số hạng đầu là \({u_1} = 800\left( {1 - 0,5\% } \right)\), công bội \(q = 1 - 0,5\% \)
Khi đó, công thức tổng quát của \(\left( {{u_n}} \right)\) là: \({u_n} = 800.{\left( {1 - 0,5} \right)^n}\)
Sau 3 năm, giá trị sử dụng ô tô còn lại là: \({u_{36}} = 800{\left( {1 - 0,5\% } \right)^{36}} \approx 667,91\) (triệu đồng)
Sau 3 năm, số tiền anh M làm ra là: \(16.36 = 576\) (triệu đồng)
Vậy sau 3 năm, tổng số tiền (bao gồm giá tiền ô tô và tổng số tiền anh M làm ra) anh M có được là: \(667,91 + 576 = 1234,91\) (triệu đồng)
Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 4 là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau nửa học kỳ đầu tiên. Đề thi này không chỉ kiểm tra kiến thức lý thuyết mà còn tập trung vào khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế.
Đề thi thường bao gồm hai phần chính: phần trắc nghiệm và phần tự luận. Phần trắc nghiệm thường chiếm khoảng 30-40% tổng số điểm, tập trung vào các kiến thức cơ bản và các công thức quan trọng. Phần tự luận chiếm khoảng 60-70% tổng số điểm, yêu cầu học sinh trình bày chi tiết các bước giải và giải thích rõ ràng lý do tại sao lại chọn phương pháp giải đó.
Nội dung đề thi thường bao gồm các chủ đề sau:
Dạng 1: Giải phương trình lượng giác
Để giải phương trình lượng giác, học sinh cần nắm vững các công thức lượng giác cơ bản và các phương pháp giải phương trình lượng giác thường gặp, như phương pháp đặt ẩn phụ, phương pháp biến đổi lượng giác. Ví dụ, để giải phương trình sin(x) = 0, ta có thể sử dụng công thức sin(x) = 0 khi x = kπ, với k là số nguyên.
Dạng 2: Tính đạo hàm của hàm số
Để tính đạo hàm của hàm số, học sinh cần nắm vững các quy tắc tính đạo hàm, như quy tắc đạo hàm của tổng, hiệu, tích, thương của các hàm số. Ví dụ, để tính đạo hàm của hàm số y = x2 + 2x + 1, ta sử dụng quy tắc đạo hàm của tổng và quy tắc đạo hàm của lũy thừa để được y' = 2x + 2.
Dạng 3: Tìm cực trị của hàm số
Để tìm cực trị của hàm số, học sinh cần tìm các điểm mà đạo hàm bằng 0 hoặc không tồn tại, sau đó xét dấu của đạo hàm để xác định xem đó là điểm cực đại hay cực tiểu. Ví dụ, để tìm cực trị của hàm số y = x3 - 3x2 + 2, ta tính đạo hàm y' = 3x2 - 6x, sau đó giải phương trình y' = 0 để được x = 0 và x = 2. Tiếp theo, ta xét dấu của y' trên các khoảng (0, 2) và (2, +∞) để xác định x = 0 là điểm cực đại và x = 2 là điểm cực tiểu.
Để đạt kết quả tốt nhất trong kỳ thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 4, học sinh cần:
Học sinh có thể tham khảo thêm các tài liệu sau để ôn tập và luyện thi:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 4!