Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 8, được biên soạn theo chuẩn chương trình học mới nhất. Đề thi này là tài liệu ôn tập và luyện thi vô cùng hữu ích cho học sinh trước kỳ kiểm tra.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề và nắm vững kiến thức đã học.
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
\({30^o}\)
\({45^o}\)
\({60^o}\)
\({90^o}\)
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
\(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
\(\sin \alpha = - \frac{{\sqrt {15} }}{4}\)
\(\sin \alpha = \frac{{15}}{{16}}\)
\(\sin \alpha = - \frac{{15}}{{16}}\)
Giá trị lượng giác \(\cos \left( {\frac{{37\pi }}{{12}}} \right)\) bằng?
\(\frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\(\frac{{\sqrt 6 - \sqrt 2 }}{4}\)
\( - \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\( - \frac{{\sqrt 6 - \sqrt 2 }}{4}\)
Hàm số nào sau đây là hàm số chẵn?
\(y = \left| {\sin x} \right|\)
\(y = {x^2}.\sin x\)
\(y = \frac{x}{{\cos x}}\)
\(y = x + \sin x\)
Nghiệm của phương trình \(\cos x = 0\) là?
\(x = k2\pi ,k \in \mathbb{Z}\)
\(x = k\pi ,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\)
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
5
8
28
13
Dãy số nào sau đây là cấp số cộng?
1; 4; 8; 10
2; 3; 5; 8; 9
0; 2; 4; 6; 8
1; 3; -5; -7; -9
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 12\) và công bội \(q = - 2\). Số hạng thứ sáu của cấp số nhân đã cho bằng
2
-384
-24
-34
Trên mặt phẳng cho bốn điểm A, B, C, D như hình vẽ. Ba điểm nào sau đây không xác định một mặt phẳng?
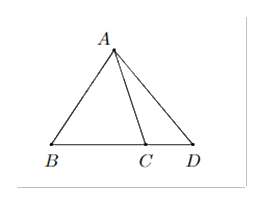
A, B, C
B, C, D
A, B, D
A, C, D
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chọn khẳng định đúng.
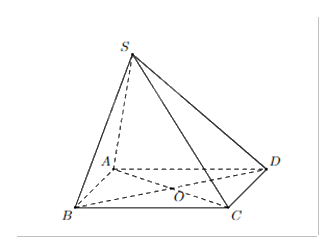
AB//(SBD)
BC//(SCD)
AD//(SBC)
BD//(SAC)
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \([0;2\pi ]\) là
3
1
2
4
Cho cấp số cộng \(({u_n})\) có \({u_5} = - 10\) và \({u_{15}} = 60\). Tổng 20 số hạng đầu tiên của cấp số cộng là
560
480
570
475
Cho phương trình lượng giác \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\). Khi đó
a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
c) \(\tan \alpha = \sqrt {15} \)
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó
a) Dãy số \(({u_n})\) là dãy số tăng
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_6} = 65\)
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Trong mặt phẳng (P), cho hình bình hành ABCD tâm O, ngoài mặt phẳng (P) cho một điểm S.
a) C là một điểm chung của hai mặt phẳng (SAB) và (SCD)
b) Giao tuyến của hai mặt phẳng (SCB) và (SCD) là đường thẳng SC
c) Đường thẳng AB song song với mặt phẳng (SCD)
d) Giao điểm của đường thẳng BC với mặt phẳng (SBD) là điểm C
Hằng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu h (m) của mực nước theo thời gian t (giờ) trong một ngày được cho bởi công thức \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) với \(0 \le t \le 24\). Tính thời điểm mực nước tại cảng cao nhất.
Đáp án:
Phương trình \(2\sin 2x + 4\cos x = 0\) có bao nhiêu nghiệm trong khoảng (0;3000)?
Đáp án:
Công ty cây xanh X trồng 496 cây hoa trong một khu vườn hình tam giác như sau: hàng thứ nhất trồng 1 cây hoa, kể từ hàng thứ hai trở đi số cây hoa trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi công ty cây xanh X trồng được bao nhiêu hàng cây trong khu vườn hình tam giác đó.
Đáp án:
Cho dãy số \(({u_n})\) biết \({u_n} = n + \frac{1}{n}\). Tìm m để dãy số \(({u_n})\) bị chặn dưới bởi m.
Đáp án:
Cho tứ diện ABCD, M thuộc đoạn AB, thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) đi qua M song song với BD và AC là hình có mấy cạnh?
Đáp án:
Cho tứ diện ABCD có N, P lần lượt là trung điểm của BC, BD. Điểm M là điểm thay đổi trên cạnh AC. Mặt phẳng (MNP) cắt AD tại Q. Giả sử AC = kAM. Tìm k để tứ giác MNPQ là hình bình hành.
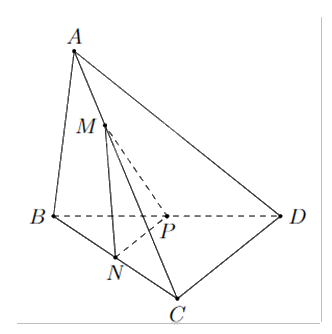
Đáp án:
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
\({30^o}\)
\({45^o}\)
\({60^o}\)
\({90^o}\)
Đáp án : A
Áp dụng quan hệ giữa radian và độ: \(1rad = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \frac{\pi }{{180}}rad\).
Ta có: \(\frac{\pi }{6}rad = \frac{\pi }{6}.\frac{{{{180}^o}}}{\pi } = {30^o}\).
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
\(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
\(\sin \alpha = - \frac{{\sqrt {15} }}{4}\)
\(\sin \alpha = \frac{{15}}{{16}}\)
\(\sin \alpha = - \frac{{15}}{{16}}\)
Đáp án : B
Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và sử dụng đường tròn lượng giác để xét dấu.
Ta có: \({\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - {\left( {\frac{1}{4}} \right)^2} = \frac{{15}}{{16}}\), suy ra \(\sin \alpha = \pm \frac{{\sqrt {15} }}{4}\).
Vì \(\pi < \alpha < \frac{{3\pi }}{2}\) nên điểm cuối của cung \(\alpha \) thuộc cung phần tư thứ III, do đó \(\sin \alpha < 0\).
Vậy \(\sin \alpha = - \frac{{\sqrt {15} }}{4}\).
Giá trị lượng giác \(\cos \left( {\frac{{37\pi }}{{12}}} \right)\) bằng?
\(\frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\(\frac{{\sqrt 6 - \sqrt 2 }}{4}\)
\( - \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\( - \frac{{\sqrt 6 - \sqrt 2 }}{4}\)
Đáp án : C
Sử dụng công thức cộng lượng giác \(\cos (a - b) = \cos a.\cos b + \sin b.\sin a\).
\(\cos \frac{{37\pi }}{{12}} = \cos \left( {3\pi + \frac{\pi }{{12}}} \right) = \cos \left( {\pi + \frac{\pi }{{12}}} \right) = - \cos \frac{\pi }{{12}} = - \cos \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right)\)
\( = - \left( {\cos \frac{\pi }{3}.\cos \frac{\pi }{4} + \sin \frac{\pi }{3}.\sin \frac{\pi }{4}} \right) = - \frac{{\sqrt 6 + \sqrt 2 }}{4}\).
Hàm số nào sau đây là hàm số chẵn?
\(y = \left| {\sin x} \right|\)
\(y = {x^2}.\sin x\)
\(y = \frac{x}{{\cos x}}\)
\(y = x + \sin x\)
Đáp án : A
Cho hàm số y = f(x) liên tục và xác định trên khoảng (đoạn) K. Với mỗi \(x \in K\) thì \( - x \in K\).
- Nếu f(x) = f(-x) thì hàm số y = f(x) là hàm số chẵn trên tập xác định.
- Nếu f(-x) = -f(x) thì hàm số y = f(x) là hàm số lẻ trên tập xác định.
Xét phương án A, hàm số \(y = \left| {\sin x} \right|\) có tập xác định D = R, suy ra có \(x \in R\) thì \( - x \in R\).
Mặt khác, \(f( - x) = \left| {\sin ( - x)} \right| = \left| { - \sin x} \right| = \sin x = f(x)\).
Vậy hàm số đáp án A là hàm số chẵn.
Nghiệm của phương trình \(\cos x = 0\) là?
\(x = k2\pi ,k \in \mathbb{Z}\)
\(x = k\pi ,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\)
Đáp án : C
Nghiệm của phương trình lượng giác cơ bản.
\(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
5
8
28
13
Đáp án : D
Tìm lần lượt \({u_2},{u_3}\) bằng cách thay n vào công thức tổng quát.
Ta có:
\({u_2} = 2{u_{2 - 1}} + 3 = 2{u_1} + 3 = 2.1 + 3 = 5\)
\({u_3} = 2{u_{3 - 1}} + 3 = 2{u_2} + 3 = 2.5 + 3 = 13\)
Dãy số nào sau đây là cấp số cộng?
1; 4; 8; 10
2; 3; 5; 8; 9
0; 2; 4; 6; 8
1; 3; -5; -7; -9
Đáp án : C
Dãy số lập thành một cấp số cộng khi và chỉ khi hai phần tử liên tiếp sai khác nhau một hằng số.
Xét hiệu các phần tử liên tiếp trong các dãy số, chỉ có dãy ở đáp án C phần tử sau hơn phần tử liền trước 2 đơn vị (8 – 6 = 6 – 4 = 4 – 2 = 2 – 0 = 2).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 12\) và công bội \(q = - 2\). Số hạng thứ sáu của cấp số nhân đã cho bằng
2
-384
-24
-34
Đáp án : B
Sử dụng công thức \({u_n} = {u_1}{q^{n - 1}}\).
Ta có: \({u_6} = {u_1}{q^{6 - 1}} = 12.{( - 2)^5} = - 384\).
Trên mặt phẳng cho bốn điểm A, B, C, D như hình vẽ. Ba điểm nào sau đây không xác định một mặt phẳng?
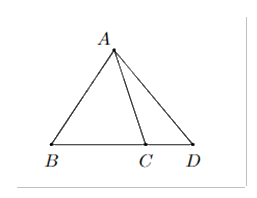
A, B, C
B, C, D
A, B, D
A, C, D
Đáp án : B
Một mặt phẳng được xác định nếu nó đi qua:
- Ba điểm không thẳng hàng.
- Một điểm và một đường thẳng không đi qua điểm đó.
- Hai đường thẳng cắt nhau.
Một mặt phẳng được xác định nếu nó đi qua:
- Ba điểm không thẳng hàng.
- Một điểm và một đường thẳng không đi qua điểm đó.
- Hai đường thẳng cắt nhau.
Vì B, C, D thẳng hàng nên ba điểm này không xác định một mặt phẳng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chọn khẳng định đúng.
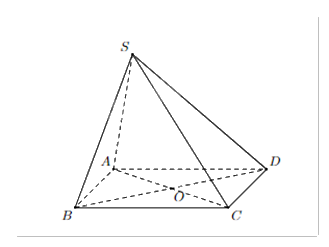
AB//(SBD)
BC//(SCD)
AD//(SBC)
BD//(SAC)
Đáp án : C
Lý thuyết đường thẳng song song với mặt phẳng.
- Xét A: AB và (SBD) chung điểm B nên AB cắt (SBD)
- Xét B: BC và (SCD) chung điểm C nên BC cắt (SCD)
- Xét C: AD//BC vì ABCD là hình bình hành nên AD//(SBC)
- Xét D: Vì BD cắt AC tại tâm O của hình bình hành nên BD cắt (SAC)
Vậy khẳng định đúng là C.
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \([0;2\pi ]\) là
3
1
2
4
Đáp án : D
Biến đổi phương trình trở thành dạng phương trình tích, đưa về giải phương trình lượng giác cơ bản.
\(\sin 2x + \cos x = 0 \Leftrightarrow 2\sin x.\cos x + \cos x = 0 \Leftrightarrow \cos x.(2\sin x + 1) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{2\sin x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{\sin x = - \frac{1}{2}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.} \right.\) với \(k \in \mathbb{Z}\).
Vì \(x \in [0;2\pi ]\) nên chỉ có 4 nghiệm thỏa mãn: \(x = \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\frac{{7\pi }}{6};\frac{{11\pi }}{6}} \right\}\).
Cho cấp số cộng \(({u_n})\) có \({u_5} = - 10\) và \({u_{15}} = 60\). Tổng 20 số hạng đầu tiên của cấp số cộng là
560
480
570
475
Đáp án : C
Tìm số hạng đầu và công sai dựa theo công thức \({u_n} = {u_1} + (n - 1)d\).
Từ đó tìm tổng 20 số hạng đầu tiên \({S_n} = \frac{{({u_1} + {u_n})n}}{2}\).
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{{u_5} = {u_1} + 4d}\\{{u_{15}} = {u_1} + 14d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 10 = {u_1} + 4d}\\{60 = {u_1} + 14d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{u_1} = - 38}\\{d = 7}\end{array}} \right.\)
Từ đó ta tính được \({u_{20}} = - 38 + (20 - 1)7 = 95\).
Vậy tổng 20 số hạng đầu của cấp số cộng là \({S_{20}} = \frac{{({u_1} + {u_{20}}).20}}{2} = \frac{{( - 38 + 95).20}}{2} = 570\).
Cho phương trình lượng giác \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\). Khi đó
a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Giải phương trình lượng giác \(\sin x = a\):
- Nếu \(\left| a \right| > 1\) thì phương trình vô nghiệm.
- Nếu \(\left| a \right| \le 1\) thì chọn cung \(\alpha \) sao cho \(\sin \alpha = a\). Khi đó phương trình trở thành:
\(\sin x = \sin \alpha \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\).
\(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - \frac{\pi }{{12}} = - \frac{\pi }{3} + k2\pi }\\{x - \frac{\pi }{{12}} = \pi + \frac{\pi }{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{4} + k2\pi }\\{x = \frac{{17\pi }}{{12}} + k2\pi }\end{array}} \right.\)
a)Sai. \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\)
b) Sai. Phương trình có nghiệm là \(x = - \frac{\pi }{4} + k2\pi \); \(x = \frac{{17\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\).
c) Đúng.
+ Xét họ nghiệm \(x = - \frac{\pi }{4} + k2\pi \):
Nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\) khi k = 0.
+ Xét họ nghiệm \(x = \frac{{17\pi }}{{12}} + k2\pi \):
Nghiệm âm lớn nhất là \(x = - \frac{{7\pi }}{{12}}\) khi k = -1.
Vì \( - \frac{\pi }{4} > - \frac{{7\pi }}{{12}}\) nên nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\).
d) Đúng.
+ Xét họ nghiệm \(x = - \frac{\pi }{4} + k2\pi \):
\( - \pi < x < \pi \Leftrightarrow - \pi < - \frac{\pi }{4} + k2\pi < \pi \)
\( \Leftrightarrow - 1 < - \frac{1}{4} + 2k < 1 \Leftrightarrow - \frac{3}{4} < 2k < \frac{5}{4} \Leftrightarrow - \frac{3}{8} < k < \frac{5}{8}\).
Vậy chỉ có k = 0 thỏa mãn. Khi đó \(x = - \frac{\pi }{4}\).
+ Xét họ nghiệm \(x = \frac{{17\pi }}{{12}} + k2\pi \):
\( - \pi < x < \pi \Leftrightarrow - \pi < \frac{{17\pi }}{{12}} + k2\pi < \pi \Leftrightarrow - 1 < \frac{{17}}{{12}} + 2k < 1\)
\( \Leftrightarrow - \frac{{29}}{{12}} < 2k < - \frac{5}{{12}} \Leftrightarrow - \frac{{29}}{{24}} < k < - \frac{5}{{24}}\).
Vậy chỉ có k = -1 thỏa mãn. Khi đó \(x = - \frac{{7\pi }}{{12}}\).
Vậy phương trình có hai nghiệm thuộc khoảng \(( - \pi ;\pi )\) là \(x = - \frac{\pi }{4}\) và \(x = - \frac{{7\pi }}{{12}}\).
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
c) \(\tan \alpha = \sqrt {15} \)
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
c) \(\tan \alpha = \sqrt {15} \)
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
a) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu.
b) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu.
c) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{1}{{\cot \alpha }}\)
d) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\tan \alpha }}\)
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( { - \frac{1}{4}} \right)^2} = \frac{{15}}{{16}} \Rightarrow \sin \alpha = \pm \frac{{\sqrt {15} }}{4}\).
Vì \(\pi < \alpha < \frac{{3\pi }}{2}\) nên điểm cuối của cung \(\alpha \) thuộc góc phần tư thứ III nên \(\sin \alpha < 0\). Vậy \(\sin \alpha = - \frac{{\sqrt {15} }}{4}\).
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - \frac{1}{4}}}{{ - \frac{{\sqrt {15} }}{4}}} = \sqrt {15} \); \(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{\sqrt {15} }}\).
a)Đúng.
b) Sai.
c) Đúng.
d) Sai.
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó
a) Dãy số \(({u_n})\) là dãy số tăng
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_6} = 65\)
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
a) Dãy số \(({u_n})\) là dãy số tăng
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_6} = 65\)
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
a) Dãy số \(({u_n})\) là dãy số giảm nếu \({u_n} > {u_{n + 1}}\). Dãy số \(({u_n})\) là dãy số tăng nếu \({u_n} < {u_{n + 1}}\).
b) Dãy số \(({u_n})\) là dãy số bị chặn nếu \(({u_n})\) vừa bị chặn trên vừa bị chặn dưới, tức tồn tại hai số m, M sao cho \(m \le {u_n} \le M\) \(\forall n \in \mathbb{N}*\).
c) Tính \({u_6}\) bằng công thức \({u_n} = {2^n} + 1\).
d) Thay n + 2 vào n trong công thức số hạng tổng quát \({u_n} = {2^n} + 1\).
a) Đúng. \({u_{n + 1}} - {u_n} = {2^{n + 1}} + 1 - ({2^n} + 1) = {2^{n + 1}} - {2^n} = {2^n}(2 - 1) = {2^n} > 0\) với mọi n. Vậy dãy số là dãy tăng.
b) Sai. Dãy không bị chặn trên vì không có giá trị M nào để \({2^n} < M\) với mọi n. Vậy dãy số không bị chặn.
c) Đúng. \({u_6} = {2^6} + 1 = 64 + 1 = 65\).
d) Sai. \({u_{n + 2}} = {2^{n + 2}} + 1 = {4.2^n} + 1\).
Trong mặt phẳng (P), cho hình bình hành ABCD tâm O, ngoài mặt phẳng (P) cho một điểm S.
a) C là một điểm chung của hai mặt phẳng (SAB) và (SCD)
b) Giao tuyến của hai mặt phẳng (SCB) và (SCD) là đường thẳng SC
c) Đường thẳng AB song song với mặt phẳng (SCD)
d) Giao điểm của đường thẳng BC với mặt phẳng (SBD) là điểm C
a) C là một điểm chung của hai mặt phẳng (SAB) và (SCD)
b) Giao tuyến của hai mặt phẳng (SCB) và (SCD) là đường thẳng SC
c) Đường thẳng AB song song với mặt phẳng (SCD)
d) Giao điểm của đường thẳng BC với mặt phẳng (SBD) là điểm C
Sử dụng các định lý về đường thẳng song song với mặt phẳng, cách tìm giao tuyến của hai mặt phẳng.
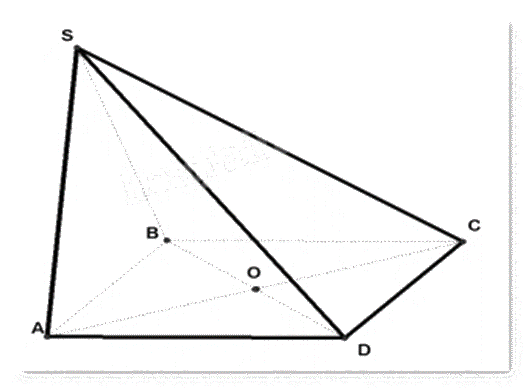
a) Sai. C không thuộc mặt phẳng (SAB).
b) Đúng. Giao tuyến của hai mặt phẳng (SCB) và (SCD) là đường thẳng SC.
c) Đúng. Vì ABCD là hình bình hành nên AB//CD, khi đó AB//(SCD).
d) Sai. Giao điểm của đường thẳng BC với mặt phẳng (SBD) là điểm B.
Hằng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu h (m) của mực nước theo thời gian t (giờ) trong một ngày được cho bởi công thức \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) với \(0 \le t \le 24\). Tính thời điểm mực nước tại cảng cao nhất.
Đáp án:
Đáp án:
Tìm t sao cho hàm số \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) đạt giá trị lớn nhất.
\(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) đạt giá trị lớn nhất khi \(\sin \left( {\frac{\pi }{{12}}t} \right) = 1 \Leftrightarrow \frac{\pi }{{12}}t = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 6 + 24k\) (giờ).
Vì \(0 \le t \le 24\) nên chỉ có giá trị t = 6 thỏa mãn.
Vậy thời điểm mực nước tại cảng cao nhất là lúc 6 giờ.
Phương trình \(2\sin 2x + 4\cos x = 0\) có bao nhiêu nghiệm trong khoảng (0;3000)?
Đáp án:
Đáp án:
Giải phương trình lượng giác bằng cách biến đổi về dạng phương trình tích. Xét họ nghiệm trong khoảng (0;3000) để tìm số giá trị k nguyên thỏa mãn.
Ta có: \(2\sin 2x + 4\cos x = 0 \Rightarrow 4\sin x.\cos x + 4\cos x = 0 \Rightarrow 4\cos x.(\sin x + 1) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{\sin x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = \frac{{3\pi }}{2} + k2\pi }\end{array}} \right. \Leftrightarrow x = \frac{\pi }{2} + k\pi \) với \(k \in \mathbb{Z}\).
Xét họ nghiệm \(x = \frac{\pi }{2} + k\pi \), ta có:
\(0 < \frac{\pi }{2} + k\pi < 3000 \Leftrightarrow - \frac{\pi }{2} < k\pi < 3000 - \frac{\pi }{2} \Leftrightarrow - \frac{1}{2} < k < \frac{{3000}}{\pi } - \frac{1}{2} \Leftrightarrow - 0,5 < k < 954,43\).
Mà \(k \in \mathbb{Z}\) nên \(k \in \{ 0;1;2;3;...;954\} \), tức có 955 giá trị k thỏa mãn.
Vậy phương trình có 955 nghiệm thuộc khoảng (0;3000).
Công ty cây xanh X trồng 496 cây hoa trong một khu vườn hình tam giác như sau: hàng thứ nhất trồng 1 cây hoa, kể từ hàng thứ hai trở đi số cây hoa trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi công ty cây xanh X trồng được bao nhiêu hàng cây trong khu vườn hình tam giác đó.
Đáp án:
Đáp án:
Số cây mỗi hàng lập thành một cấp số cộng với tổng n số hạng là 496, số hạng đầu \({u_1} = 1\) công sai d = 1. Tìm n.
Số cây mỗi hàng lập thành một cấp số cộng với tổng n số hạng là 496, số hạng đầu \({u_1} = 1\) công sai d = 1.
Ta có: \(496 = \frac{{2.1 + (n - 1).1}}{2}.n \Leftrightarrow 992 = (2 + n - 1).n = {n^2} + n - 992 = 0\).
Ta tính được n = 31 hoặc n = -32 (loại).
Vậy số hàng cây trồng được là 31 hàng.
Cho dãy số \(({u_n})\) biết \({u_n} = n + \frac{1}{n}\). Tìm m để dãy số \(({u_n})\) bị chặn dưới bởi m.
Đáp án:
Đáp án:
Chứng minh dãy số tăng và bị chặn dưới tại \(m = {u_1}\).
Xét \({u_{n + 1}} - {u_n} = \left( {n + 1 + \frac{1}{{n + 1}}} \right) - \left( {n + \frac{1}{n}} \right) = 1 + \frac{1}{{n + 1}} - \frac{1}{n} = \left( {1 - \frac{1}{n}} \right) + \frac{1}{{n + 1}}\).
Ta có: \(n \ge 1 \Leftrightarrow \frac{1}{n} < 1 \Leftrightarrow 1 - \frac{1}{n} > 0\); \(n \ge 1 \Rightarrow \frac{1}{{n + 1}} > 0\).
Vậy \({u_{n + 1}} - {u_n} > 0\), tức dãy số tăng.
Khi đó, dãy bị chặn dưới bởi \({u_1} = 1 + \frac{1}{1} = 2 = m\).
Cho tứ diện ABCD, M thuộc đoạn AB, thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) đi qua M song song với BD và AC là hình có mấy cạnh?
Đáp án:
Đáp án:
Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’ để xác định thiết diện.
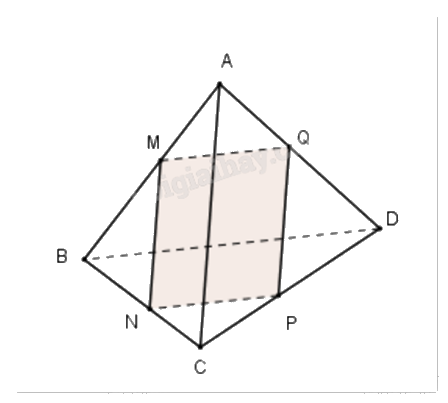
\(\left\{ \begin{array}{l}M \in (\alpha ) \cap (ABC)\\(\alpha )//AC \subset (ABC)\end{array} \right.\) nên giao tuyến của \(\left( \alpha \right)\) và (ABC) là đường thẳng qua M và song song với AB, cắt BC tại N, suy ra MN//AC.
\(\left\{ \begin{array}{l}N \in (\alpha ) \cap (BCD)\\(\alpha )//BD \subset (BCD)\end{array} \right.\) nên giao tuyến của \(\left( \alpha \right)\) và (BCD) là đường thẳng qua N và song song với BD, cắt CD tại P, suy ra NP//BD.
\(\left\{ \begin{array}{l}P \in (\alpha ) \cap (ACD)\\(\alpha )//AC \subset (ACD)\end{array} \right.\) nên giao tuyến của \(\left( \alpha \right)\) và (ACD) là đường thẳng qua P và song song với AC, cắt AD tại Q, suy ra PQ//AC.
\(\left\{ \begin{array}{l}P \in (\alpha ) \cap (ACD)\\(\alpha )//AC \subset (ACD)\end{array} \right.\) nên giao tuyến của \(\left( \alpha \right)\) và (ACD) là đường thẳng qua P và song song với AC, cắt AD tại Q, suy ra PQ//AC.
\(\left\{ {\begin{array}{*{20}{c}}{(\alpha ) \cap (ABD) = MQ}\\{(\alpha )//BD \subset (ABD)}\end{array}} \right.\) nên MQ//BD.
Có: MN//PQ (cùng song song với AC), NP//MQ (cùng song song với BD) nên MNPQ là hình bình hành.
Vậy thiết diện cần tìm có 4 cạnh.
Cho tứ diện ABCD có N, P lần lượt là trung điểm của BC, BD. Điểm M là điểm thay đổi trên cạnh AC. Mặt phẳng (MNP) cắt AD tại Q. Giả sử AC = kAM. Tìm k để tứ giác MNPQ là hình bình hành.
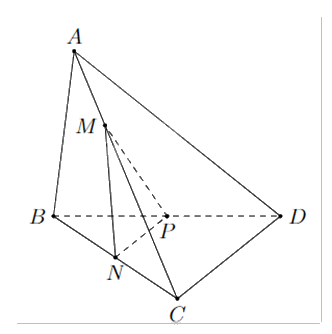
Đáp án:
Đáp án:
- Định lý Thales.
- Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song là đường thẳng song song với hai đường thẳng đó.
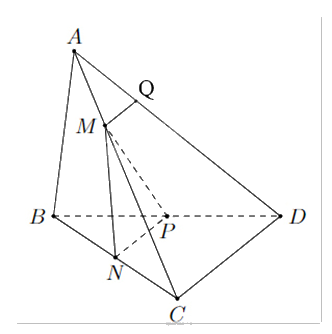
Xét tam giác BCD có N là trung điểm của BC, P là trung điểm của BD.
Khi đó, NP là đường trung bình của tam giác BCD, suy ra NP//CD.
Ta có \(\left\{ {\begin{array}{*{20}{c}}{(MNP) \cap (ACD) = \{ M\} }\\\begin{array}{l}NP//CD\\NP \subset (MNP)\\CD \subset (ACD)\end{array}\end{array}} \right.\) nên giao tuyến của (MNP) và (ACD) là đường thẳng qua M song song với NP và CD. Gọi giao tuyến đó là d.
Mà \(\left\{ {\begin{array}{*{20}{c}}{Q \in (MNP)}\\{Q \in AD \subset (ACD)}\end{array}} \right.\) nên \(Q \in d\) và MQ//NP, MQ//CD.
Vì đã có MQ//NP nên để MNPQ là hình bình hành thì cần điều kiện MQ = NP.
Mà \(NP = \frac{1}{2}CD\) nên cần \(MQ = \frac{1}{2}CD\).
Xét tam giác ACD có \(M \in AC\), \(Q \in AD\) và MQ//CD.
Khi đó, \(\frac{{AM}}{{AC}} = \frac{{MQ}}{{CD}}\) (định lý Thales đảo).
Vậy để MNPQ là hình bình hành thì \(\frac{{AM}}{{AC}} = \frac{{MQ}}{{CD}} = \frac{1}{2} \Leftrightarrow AC = 2AM\).
Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 8 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kỳ đầu tiên. Đề thi này bao gồm các chủ đề chính như hàm số bậc hai, hàm số lượng giác, và các kiến thức về vector trong mặt phẳng. Việc ôn tập kỹ lưỡng và làm quen với các dạng bài tập trong đề thi là rất cần thiết để đạt kết quả tốt.
Đề thi thường được chia thành hai phần chính: trắc nghiệm và tự luận. Phần trắc nghiệm thường chiếm khoảng 40-50% tổng số điểm, tập trung vào việc kiểm tra khả năng hiểu và vận dụng kiến thức cơ bản. Phần tự luận chiếm khoảng 50-60% tổng số điểm, yêu cầu học sinh trình bày chi tiết lời giải và chứng minh các kết quả.
Để giải đề thi một cách hiệu quả, học sinh cần:
Để chuẩn bị tốt nhất cho kỳ thi giữa kì 1, học sinh nên tham khảo các tài liệu sau:
Hãy dành thời gian ôn tập đều đặn và làm nhiều bài tập để nắm vững kiến thức. Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 11 Chân trời sáng tạo!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số bậc hai | Cao |
| Hàm số lượng giác | Trung bình |
| Vector trong mặt phẳng | Trung bình |
| Nguồn: Giaitoan.edu.vn | |