Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 7, được biên soạn theo chuẩn chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 1. Học sinh có thể sử dụng đề thi này để tự đánh giá năng lực và chuẩn bị tốt nhất cho kỳ thi sắp tới.
Số nào dưới đây là một nghiệm của phương trình \(\sin x = \frac{{\sqrt 2 }}{2}\)?
\(\frac{\pi }{2}\)
\(\frac{\pi }{4}\)
\( - \frac{{3\pi }}{4}\)
\( - \frac{\pi }{4}\)
Đồ thị của hàm số y = cosx có tính chất nào dưới đây?
Đối xứng qua gốc tọa độ
Đối xứng qua trục hoành
Đối xứng qua trục tung
Đối xứng qua điểm I(0;1)
Cho dãy số vô hạn \(\left( {{u_n}} \right)\), biết \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = 2{u_n} + 3,n \in {\mathbb{N}^*}\end{array} \right.\). Tìm số hạng thứ 4 của dãy số.
21
29
11
13
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 1\) và \({u_2} = 3\). Giá trị của \({u_3}\) bằng
6
9
4
5
Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu \({u_1} = 3\), công bội q = 2. Giá trị của \({u_2}\) bằng
8
9
6
4
Trong các dãy số sau, dãy số nào có giới hạn bằng 0?
Dãy \(\left( {{v_n}} \right)\) với \({v_n} = \frac{{n + 1}}{n}\)
Dãy \(\left( {{v_n}} \right)\) với \({v_n} = \frac{1}{n}\)
Dãy \(\left( {{v_n}} \right)\) với \({v_n} = 2023\)
Dãy \(\left( {{v_n}} \right)\) với \({v_n} = \frac{{2n + 3}}{n}\)
Cho hàm số \(f(x) = \frac{{x - 3}}{{x - 2}}\). Khẳng định nào sau đây sai?
f(x) liên tục tại \({x_0} = 3\)
f(x) liên tục tại \({x_0} = - 2\)
f(x) liên tục tại \({x_0} = 2\)
f(x) liên tục tại \({x_0} = - 3\)
Điều kiện để hai đường thẳng trong không gian song song với nhau là
Không có điểm chung
Đồng phẳng hoặc không có điểm chung
Đồng phẳng
Đồng phẳng và không có điểm chung
Trong không gian, mệnh đề nào sau đây đúng?
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng song song
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng trùng nhau
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC. Chọn khẳng định đúng?
MN//(BCD)
MN//(ACD)
MN//(ABD)
MN//(ABC)
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
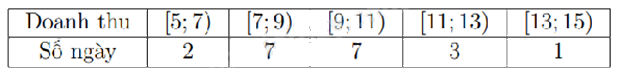
Giá trị đại diện của nhóm thứ hai là
8
7
9
2
Thống kê chiều cao của học sinh lớp 11A ta có bảng số liệu sau:

Hỏi lớp có bao nhiêu học sinh có chiều cao từ 168 cm trở lên?
11
20
31
8
Cho góc \(\alpha \in \left( {\frac{{3\pi }}{2};2\pi } \right)\).
a) \(\cot \alpha < 0\).
b) \(\tan \left( {\pi - \alpha } \right) = \tan \alpha < 0\).
c) Nếu \(\sin \alpha = - \frac{3}{5}\) thì \(\cos \alpha = \frac{4}{5}\).
d) Nếu \(\sin 2\alpha = \frac{{ - \sqrt 3 }}{2}\) thì \({\left( {\sin \alpha + \cos \alpha } \right)^2} = \frac{{2 - \sqrt 3 }}{2}\).
Cho \({u_n} = \frac{{{7^n} + {2^{2n - 1}} + {3^{n + 1}}}}{{{7^{n + 1}} + {5^{n - 1}}}}\). Biết \(\lim {u_n} = \frac{a}{b}\) với \(a,b \in \mathbb{Z}\), \(\frac{a}{b}\) tối giản. Khi đó:
a) a + b = 8.
b) a – b = -7.
c) Bộ ba số a; b; 13 tạo thành một cấp số cộng có công sai d = 7.
d) Bộ ba số a; b; 49 tạo thành một cấp số nhân có công bội q = 7.
Cho hình chóp S.ABCD có ABCD là hình thang với hai cạnh đáy là AD và BC, đáy lớn là AD. Gọi M, N là lần lượt là trung điểm của SA và SD.
a) MN//BC.
b) Giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song với AD.
c) Gọi \(AB \cap CD = \{ E\} \), \(\{ F\} = SB \cap ME\). Khi đó \(SB \cap (MCD) = \{ F\} \).
d) Giao tuyến của (SAB) và (SCD) là đường thẳng qua S và song song với AB.
Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:

a) Cỡ mẫu là n = 50.
b) Nhóm chứa mốt của mẫu số liệu là [8;8,5).
c) Mốt của mẫu số liệu bằng \({M_o} = 8,12\).
d) Số trung bình của mẫu số liệu làm tròn đến hàng phần nghìn là \(\overline x = 8,122\).
Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày \((0 \le t < 24)\) cho bởi công thức \(h = \cos \left( {\frac{{\pi t}}{6} + 2\pi } \right) + 5\). Hỏi trong ngày mực nước xuống thấp nhất trễ nhất là mấy giờ?
Đáp án:
Người ta thiết kế số ghế ngồi trên khán đài một sân vận động bóng đá như sau. Hàng ghế đầu tiên gần sân bóng đá nhất có 1600 ghế. Kể từ hàng thứ hai trở đi, mỗi hàng liên sau hơn hàng liên trước 400 ghế. Muốn sức chứa trên khán đài có ít nhất 222000 ghế thì cần phải thiết kế ít nhất bao nhiêu hàng ghế?
Đáp án:
Tìm công bội của cấp số nhân thỏa \(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 135\\{u_4} + {u_5} + {u_6} = 40\end{array} \right.\) là \(\frac{a}{b}\) là phân số tối giản. Giá trị a + b là bao nhiêu?
Đáp án:
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{a(x + 2)}}{{{x^3} + 8}}\\2x + b\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x > - 2\\x \le - 2\end{array}\). Với a, b là các số thực. Để hàm số đã cho liên tục tại x = -2 thì a – 12b bằng bao nhiêu?
Đáp án:
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB và BC. P là điểm thuộc CD sao cho PD = 2PC. Gọi Q là giao diểm của đường thẳng AD và mặt phẳng (MNP). Tính tỉ số \(\frac{{AQ}}{{AD}}\) (làm tròn đến hàng phần trăm).
Đáp án:
Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần ở bảng sau:
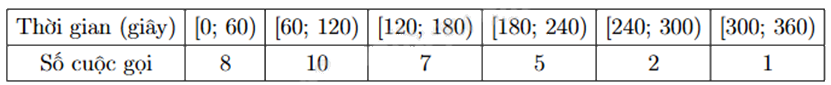
Tứ phân vị thứ ba của mẫu số liệu bằng bao nhiêu?
Đáp án:
Số nào dưới đây là một nghiệm của phương trình \(\sin x = \frac{{\sqrt 2 }}{2}\)?
\(\frac{\pi }{2}\)
\(\frac{\pi }{4}\)
\( - \frac{{3\pi }}{4}\)
\( - \frac{\pi }{4}\)
Đáp án : B
Tra bảng giá trị lượng giác hoặc sử dụng máy tính cá nhân.
Ta có \(\sin \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\).
Đồ thị của hàm số y = cosx có tính chất nào dưới đây?
Đối xứng qua gốc tọa độ
Đối xứng qua trục hoành
Đối xứng qua trục tung
Đối xứng qua điểm I(0;1)
Đáp án : C
Sử dụng tính chất của hàm số và đồ thị hàm số y = cosx.
Hàm số y = cosx là hàm số chẵn nên đồ thị đối xứng qua trục tung.
Cho dãy số vô hạn \(\left( {{u_n}} \right)\), biết \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = 2{u_n} + 3,n \in {\mathbb{N}^*}\end{array} \right.\). Tìm số hạng thứ 4 của dãy số.
21
29
11
13
Đáp án : B
Tìm lần lượt 4 số hạng đầu của dãy số.
Ta có: \({u_1} = 1\); \({u_2} = 2.1 + 3 = 5\);
\({u_3} = 2.5 + 3 = 13\); \({u_4} = 2.13 + 3 = 29\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 1\) và \({u_2} = 3\). Giá trị của \({u_3}\) bằng
6
9
4
5
Đáp án : D
\({u_{n + 1}} = {u_n} + d\).
Ta có \({u_2} = {u_1} + d \Leftrightarrow 3 = 1 + d \Leftrightarrow d = 2\).
Suy ra \({u_3} = {u_2} + d = 3 + 2 = 5\).
Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu \({u_1} = 3\), công bội q = 2. Giá trị của \({u_2}\) bằng
8
9
6
4
Đáp án : C
\({u_n} = {u_1}{q^{n - 1}}\).
\({u_2} = {u_1}q = 3.2 = 6\).
Trong các dãy số sau, dãy số nào có giới hạn bằng 0?
Dãy \(\left( {{v_n}} \right)\) với \({v_n} = \frac{{n + 1}}{n}\)
Dãy \(\left( {{v_n}} \right)\) với \({v_n} = \frac{1}{n}\)
Dãy \(\left( {{v_n}} \right)\) với \({v_n} = 2023\)
Dãy \(\left( {{v_n}} \right)\) với \({v_n} = \frac{{2n + 3}}{n}\)
Đáp án : B
Theo định nghĩa giới hạn hữu hạn của dãy số.
Ta có: \(\lim \frac{{n + 1}}{n} = 1\); \(\lim \frac{1}{n} = 0\); \(\lim 2023 = 2023\); \(\lim \frac{{2n + 3}}{n} = 2\).
Cho hàm số \(f(x) = \frac{{x - 3}}{{x - 2}}\). Khẳng định nào sau đây sai?
f(x) liên tục tại \({x_0} = 3\)
f(x) liên tục tại \({x_0} = - 2\)
f(x) liên tục tại \({x_0} = 2\)
f(x) liên tục tại \({x_0} = - 3\)
Đáp án : C
f(x) không liên tục tại điểm hàm số không xác định.
Hàm số có tập xác định là \(D = \mathbb{R}\backslash \{ 2\} \), do đó hàm số không liên tục tại \({x_0} = 2\).
Điều kiện để hai đường thẳng trong không gian song song với nhau là
Không có điểm chung
Đồng phẳng hoặc không có điểm chung
Đồng phẳng
Đồng phẳng và không có điểm chung
Đáp án : D
Sử dụng kiến thức về điều kiện để hai đường thẳng trong không gian song song với nhau.
Điều kiện để hai đường thẳng trong không gian song song với nhau là đồng phẳng và không có điểm chung.
Trong không gian, mệnh đề nào sau đây đúng?
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng song song
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng trùng nhau
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau
Đáp án : C
Sử dụng tính chất của phép chiếu song song.
Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC. Chọn khẳng định đúng?
MN//(BCD)
MN//(ACD)
MN//(ABD)
MN//(ABC)
Đáp án : A
Đường thẳng song song với mặt phẳng nếu nó song song với một đường thẳng trong mặt phẳng đó.
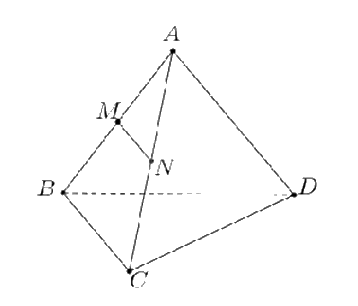
Xét tam giác ABC có MN là đường trung bình, suy ra MN//BC.
Mà \(MN\not{ \subset }(BCD)\), \(BC \subset (BCD)\).
Suy ra MN//(BCD).
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
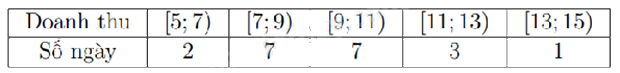
Giá trị đại diện của nhóm thứ hai là
8
7
9
2
Đáp án : A
Giá trị đại diện của nhóm là trung bình cộng của đầu mút trái và đầu mút phải nhóm đó.
Giá trị đại diện của nhóm thứ hai là \(\frac{{7 + 9}}{2} = 8\).
Thống kê chiều cao của học sinh lớp 11A ta có bảng số liệu sau:

Hỏi lớp có bao nhiêu học sinh có chiều cao từ 168 cm trở lên?
11
20
31
8
Đáp án : A
Số học sinh cần tìm là tổng tần số của các nhóm chứa giá trị từ 168 cm trở lên
Số học sinh có chiều cao từ 168 cm trở lên là 8 + 3 = 11.
Cho góc \(\alpha \in \left( {\frac{{3\pi }}{2};2\pi } \right)\).
a) \(\cot \alpha < 0\).
b) \(\tan \left( {\pi - \alpha } \right) = \tan \alpha < 0\).
c) Nếu \(\sin \alpha = - \frac{3}{5}\) thì \(\cos \alpha = \frac{4}{5}\).
d) Nếu \(\sin 2\alpha = \frac{{ - \sqrt 3 }}{2}\) thì \({\left( {\sin \alpha + \cos \alpha } \right)^2} = \frac{{2 - \sqrt 3 }}{2}\).
a) \(\cot \alpha < 0\).
b) \(\tan \left( {\pi - \alpha } \right) = \tan \alpha < 0\).
c) Nếu \(\sin \alpha = - \frac{3}{5}\) thì \(\cos \alpha = \frac{4}{5}\).
d) Nếu \(\sin 2\alpha = \frac{{ - \sqrt 3 }}{2}\) thì \({\left( {\sin \alpha + \cos \alpha } \right)^2} = \frac{{2 - \sqrt 3 }}{2}\).
a) Dựa vào vị trí tia cuối của góc lượng giác để nhận xét dấu của giá trị lượng giác.
b) Sử dụng công thức \(\tan (\pi - \alpha ) = - \tan \alpha \).
c) Sử dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha \) và dựa vào vị trí tia cuối của góc lượng giác để nhận xét dấu của giá trị lượng giác.
d) Sử dụng công thức nhân đôi \(\sin 2\alpha = 2\sin \alpha \cos \alpha \).
a) Đúng. \(\alpha \in \left( {\frac{{3\pi }}{2};2\pi } \right)\) nên tia cuối của góc lượng giác nằm ở góc phần tư thứ IV.
Khi đó: \(\sin \alpha < 0\), \(\cos \alpha > 0\). Suy ra \(\cot \alpha < 0\).
b) Sai. \(\tan (\pi - \alpha ) = - \tan \alpha \).
c) Đúng. Ta có \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{{ - 3}}{5}} \right)^2} = \frac{{16}}{{25}}\).
Vì \(\cos \alpha > 0\) nên \(\cos \alpha = \sqrt {\frac{{16}}{{25}}} = \frac{4}{5}\).
d) Đúng. Ta có: \({\left( {\sin \alpha + \cos \alpha } \right)^2} = {\sin ^2}\alpha + {\cos ^2}\alpha + 2\sin \alpha \cos \alpha \)
\( = 1 + \sin 2\alpha = 1 + \left( {\frac{{ - \sqrt 3 }}{2}} \right) = \frac{{2 - \sqrt 3 }}{2}\).
Cho \({u_n} = \frac{{{7^n} + {2^{2n - 1}} + {3^{n + 1}}}}{{{7^{n + 1}} + {5^{n - 1}}}}\). Biết \(\lim {u_n} = \frac{a}{b}\) với \(a,b \in \mathbb{Z}\), \(\frac{a}{b}\) tối giản. Khi đó:
a) a + b = 8.
b) a – b = -7.
c) Bộ ba số a; b; 13 tạo thành một cấp số cộng có công sai d = 7.
d) Bộ ba số a; b; 49 tạo thành một cấp số nhân có công bội q = 7.
a) a + b = 8.
b) a – b = -7.
c) Bộ ba số a; b; 13 tạo thành một cấp số cộng có công sai d = 7.
d) Bộ ba số a; b; 49 tạo thành một cấp số nhân có công bội q = 7.
Chia cả tử và mẫu của \({u_n}\) cho \({7^n}\).
Áp dụng công thức \(\lim {q^n} = 0\) khi \(\left| q \right| < 1\).
Ta có \(\lim {u_n} = \lim \frac{{{7^n} + {2^{2n - 1}} + {3^{n + 1}}}}{{{7^{n + 1}} + {5^{n - 1}}}} = \lim \frac{{{7^n} + {4^n}{{.2}^{ - 1}} + {3^n}.3}}{{{7^n}.7 + {5^n}{{.5}^{ - 1}}}}\)
\( = \lim \frac{{1 + {{\left( {\frac{4}{7}} \right)}^n}{{.2}^{ - 1}} + {{\left( {\frac{3}{7}} \right)}^n}.3}}{{1.7 + {{\left( {\frac{5}{7}} \right)}^n}{{.5}^{ - 1}}}} = \frac{{1 + 0 + 0}}{{7 + 0}} = \frac{1}{7}\).
Vậy \(\frac{a}{b} = \frac{1}{7}\) hay a = 1, b = 7.
a) Đúng. a + b = 1 + 7 = 8.
b) Sai. a – b = 1 – 6 = -6.
c) Sai. 1; 7; 13 tạo thành cấp số cộng có công sai bằng d = 6.
d) Đúng. 1; 7; 49 tạo thành cấp số nhân có công bội q = 7.
Cho hình chóp S.ABCD có ABCD là hình thang với hai cạnh đáy là AD và BC, đáy lớn là AD. Gọi M, N là lần lượt là trung điểm của SA và SD.
a) MN//BC.
b) Giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song với AD.
c) Gọi \(AB \cap CD = \{ E\} \), \(\{ F\} = SB \cap ME\). Khi đó \(SB \cap (MCD) = \{ F\} \).
d) Giao tuyến của (SAB) và (SCD) là đường thẳng qua S và song song với AB.
a) MN//BC.
b) Giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song với AD.
c) Gọi \(AB \cap CD = \{ E\} \), \(\{ F\} = SB \cap ME\). Khi đó \(SB \cap (MCD) = \{ F\} \).
d) Giao tuyến của (SAB) và (SCD) là đường thẳng qua S và song song với AB.
Sử dụng các điều kiện, tính chất của đường thẳng và mặt phẳng song song.
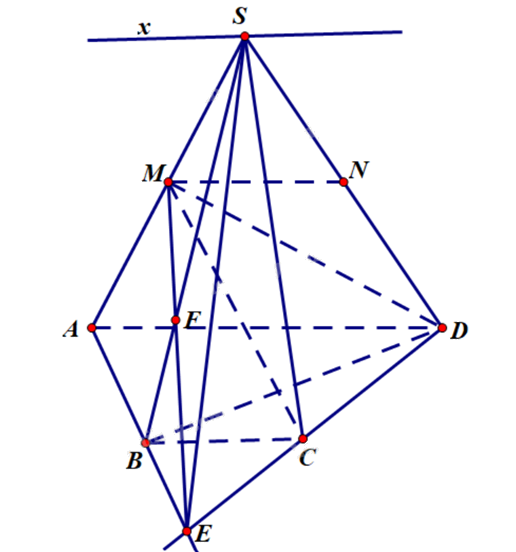
a) Đúng. Ta có MN là đường trung bình của tam giác SAD nên MN//AD.
Mà AD//BC vì ABCD là hình thang có hai đáy AD, BC.
Suy ra MN//BC.
b) Đúng. Ta có \(\left\{ \begin{array}{l}AD//BC\\AD \subset (SAD)\\BC \subset (SBC)\\S \in (SAD) \cap (SBC)\end{array} \right.\) suy ra giao tuyến của (SAD) và (SBC) là đường thẳng qua S, song song với AD, BC.
c) Đúng. Vì \(E \in AB \subset (SAB)\) suy ra \(ME \subset (SAB)\).
Xét trong mặt phẳng (SAB) có \(\{ F\} = SB \cap ME\) (giả thiết) nên \(F \in SB\) (1)
Vì \(E \in CD \subset (MCD)\) nên \(ME \subset (MCD)\).
Mà \(F \in ME\) suy ra \(F \in (MCD)\) (2)
Từ (1), (2) suy ra \(SB \cap (MCD) = \{ F\} \).
d) Sai. Ta có \(S \in (SAB) \cap (SCD)\).
Mặt khác \(\left\{ \begin{array}{l}E \in AB \subset (SAB)\\E \in CD \subset (SCD)\end{array} \right.\) suy ra \(E \in (SAB) \cap (SCD)\).
Vậy SE là giao tuyến của (SAB) và (SCD).
Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:

a) Cỡ mẫu là n = 50.
b) Nhóm chứa mốt của mẫu số liệu là [8;8,5).
c) Mốt của mẫu số liệu bằng \({M_o} = 8,12\).
d) Số trung bình của mẫu số liệu làm tròn đến hàng phần nghìn là \(\overline x = 8,122\).
a) Cỡ mẫu là n = 50.
b) Nhóm chứa mốt của mẫu số liệu là [8;8,5).
c) Mốt của mẫu số liệu bằng \({M_o} = 8,12\).
d) Số trung bình của mẫu số liệu làm tròn đến hàng phần nghìn là \(\overline x = 8,122\).
a) Cỡ mẫu bằng tổng tần số trong bảng số liệu.
b) Nhóm chứa mốt có tần số lớn nhất trong bảng số liệu.
c) Công thức tính mốt thuộc nhóm \([{u_m};{u_{m + 1}})\):
\({M_o} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right)\left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\); trong đó \({n_m}\) là tần số nhóm thứ m.
d) Công thức tính số trung bình: \(\overline x = \frac{{{c_1}{n_1} + {c_2}{n_2}... + {c_n}{n_k}}}{N}\); trong đó N là kích thước của bảng tần số k nhóm, \({n_i}\) là tần số nhóm i, \({c_i}\) là giá trị đại diện nhóm i \((1 \le i \le k)\).
a) Sai. n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82.
b) Đúng. Nhóm chứa mốt là [8;8,5).
c) Sai. \({M_o} = 8 + \frac{{24 - 16}}{{\left( {24 - 16} \right)\left( {24 - 13} \right)}}.\left( {8,5 - 8} \right) = \frac{{177}}{{22}} = 8,0(45)\).
d) Đúng. \(\overline x = \frac{{6,75.8 + 7,25.10 + 7,75.16 + 8,25.24 + 8,75.13 + 9,25.7 + 9,75.4}}{{82}} = \frac{{333}}{{41}} \approx 8,122\).
Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày \((0 \le t < 24)\) cho bởi công thức \(h = \cos \left( {\frac{{\pi t}}{6} + 2\pi } \right) + 5\). Hỏi trong ngày mực nước xuống thấp nhất trễ nhất là mấy giờ?
Đáp án:
Đáp án:
Mực nước thấp nhất khi \(\cos \left( {\frac{{\pi t}}{6} + 2\pi } \right)\) nhỏ nhất.
Sử dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
Mực nước thấp nhất khi \(h = \cos \left( {\frac{{\pi t}}{6} + 2\pi } \right) + 5\) nhỏ nhất, hay \(\cos \left( {\frac{{\pi t}}{6} + 2\pi } \right)\) nhỏ nhất.
Khi đó \(\cos \left( {\frac{{\pi t}}{6} + 2\pi } \right) = - 1 \Leftrightarrow \cos \left( {\frac{{\pi t}}{6}} \right) = - 1 \Leftrightarrow \frac{{\pi t}}{6} = \pi + k2\pi \)
\( \Leftrightarrow \frac{t}{6} = 1 + 12k \Leftrightarrow t = 6 + 12k\).
Ta có \(0 \le t < 24 \Leftrightarrow 0 \le 6 + 12k < 24 \Leftrightarrow - 6 \le 12k < 18 \Leftrightarrow - 2 \le k < \frac{3}{2}\).
Vậy k = 0 hoặc k = 1.
Với k = 0 thì t = 6 + 12.0 = 6.
Với k = 1 thì t = 6 + 12.1 = 18.
Vậy mực nước của kênh thấp nhất trễ nhất vào thời điểm t = 18 (giờ).
Người ta thiết kế số ghế ngồi trên khán đài một sân vận động bóng đá như sau. Hàng ghế đầu tiên gần sân bóng đá nhất có 1600 ghế. Kể từ hàng thứ hai trở đi, mỗi hàng liên sau hơn hàng liên trước 400 ghế. Muốn sức chứa trên khán đài có ít nhất 222000 ghế thì cần phải thiết kế ít nhất bao nhiêu hàng ghế?
Đáp án:
Đáp án:
Sử dụng công thức tổng n số hạng đầu của cấp số cộng: \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2}\).
Số ghế mỗi hàng lập thành một cấp số cộng với \({u_1} = 1600\) và d = 400.
Tổng số ghế trong rạp là:
\(222000 = \frac{{n\left[ {2.1600 + (n - 1).400} \right]}}{2} \Leftrightarrow 444000 = n\left( {2800 + 400n} \right) \Leftrightarrow \left[ \begin{array}{l}n = 30\\n = - 37\end{array} \right.\)
Giá trị n thỏa mãn là n = 30.
Vậy cần thiết kế ít nhất 30 hàng ghế.
Tìm công bội của cấp số nhân thỏa \(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 135\\{u_4} + {u_5} + {u_6} = 40\end{array} \right.\) là \(\frac{a}{b}\) là phân số tối giản. Giá trị a + b là bao nhiêu?
Đáp án:
Đáp án:
Sử dụng công thức số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\).
\(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 135\\{u_4} + {u_5} + {u_6} = 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} + {u_1}q + {u_1}{q^2} = 135\\{u_1}{q^3} + {u_1}{q^4} + {u_1}{q^5} = 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}(1 + q + {q^2}) = 135\\{u_1}{q^3}(1 + q + {q^2}) = 40\end{array} \right.\)
\( \Leftrightarrow {q^3} = \frac{{40}}{{135}} \Leftrightarrow q = \frac{2}{3}\).
Suy ra a = 2, b = 3. Vậy a + b = 2 + 3 = 5.
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{a(x + 2)}}{{{x^3} + 8}}\\2x + b\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x > - 2\\x \le - 2\end{array}\). Với a, b là các số thực. Để hàm số đã cho liên tục tại x = -2 thì a – 12b bằng bao nhiêu?
Đáp án:
Đáp án:
Hàm số liên tục tại \({x_0}\) khi \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = f({x_0})\).
Ta có:
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = f( - 2) = b - 4\).
\(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{a(x + 2)}}{{{x^3} + 8}} = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{a(x + 2)}}{{(x + 2)({x^2} - 2x + 4)}}\)
\( = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{a}{{{x^2} - 2x + 4}} = \frac{a}{{{{( - 2)}^2} - 2.( - 2) + 4}} = \frac{a}{{12}}\).
Để hàm số liên tục tại x = -2 thì \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} f(x) = f( - 2)\).
Suy ra \(\frac{a}{{12}} = b - 4 \Leftrightarrow a = 12b - 48 \Leftrightarrow a - 12b = - 48\).
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB và BC. P là điểm thuộc CD sao cho PD = 2PC. Gọi Q là giao diểm của đường thẳng AD và mặt phẳng (MNP). Tính tỉ số \(\frac{{AQ}}{{AD}}\) (làm tròn đến hàng phần trăm).
Đáp án:
Đáp án:
Sử dụng tính chất đường trung bình, định lí Thales, tính chất các giao tuyến của ba mặt phẳng cắt nhau.
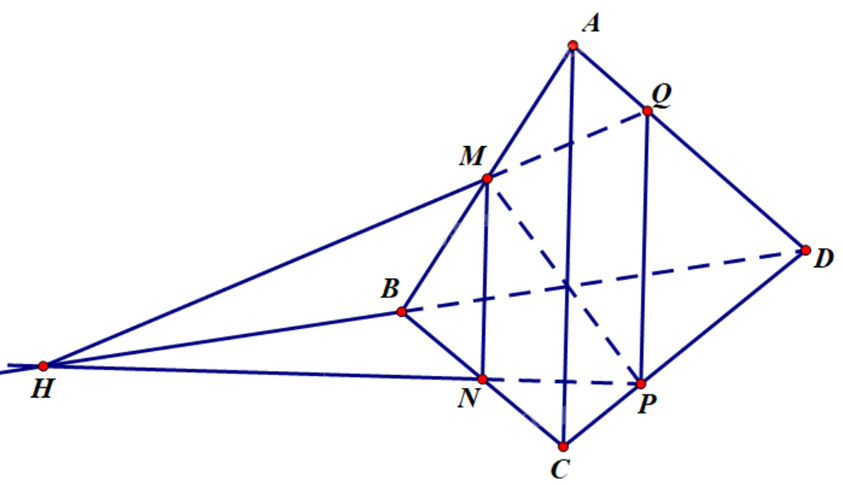
Vì PD = 2PC nên \(\frac{{CP}}{{CD}} = \frac{1}{3}\).
Xét trong mặt phẳng (BCD) có NP không song song với BD do \(\frac{{CN}}{{CB}} \ne \frac{{CP}}{{CD}}\) \(\left( {\frac{1}{2} \ne \frac{1}{3}} \right)\).
Giả sử NP cắt BD tại H. Khi đó \(\left\{ \begin{array}{l}H \in NP \subset (MNP)\\H \in BD \subset (ABD)\end{array} \right.\) suy ra \(H \in (MNP) \cap (ABD)\) (1)
Mặt khác \(\left\{ \begin{array}{l}M \in (MNP)\\H \in AB \subset (ABD)\end{array} \right.\) suy ra \(M \in (MNP) \cap (ABD)\) (2)
Từ (1) và (2) suy ra MH là giao tuyến của hai mặt phẳng (MNP) và (ABD).
Xét trong mặt phẳng (ABD), giả sử MH cắt AD tại Q’.
Khi đó \(\left\{ \begin{array}{l}Q' \in MH \subset (MNP)\\Q' \in AD\end{array} \right.\), suy ra Q’ là giao điểm của AD và mặt phẳng (MNP).
Do đó Q’ trùng Q.
Xét tam giác ABC có MN là đường trung bình, suy ra MN//AC.
Ta có \(\left\{ \begin{array}{l}(ABC) \cap (ACD) = AC\\(ABC) \cap (MNP) = MN\\(ACD) \cap (MNP) = PQ\\MN//AC\end{array} \right.\) suy ra PQ//MN//AC.
Xét tam giác ACD có PQ//AC: \(\frac{{AQ}}{{AD}} = \frac{{CP}}{{CD}} = \frac{1}{3} \approx 0,33\).
Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần ở bảng sau:
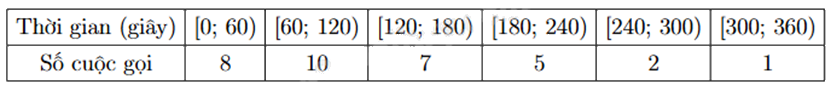
Tứ phân vị thứ ba của mẫu số liệu bằng bao nhiêu?
Đáp án:
Đáp án:
Tính \({Q_3}\).
Cỡ mẫu: n = 8 + 10 + 7 + 5 + 2 + 1 = 33.
Gọi \({x_1};{x_2};...;{x_{33}}\) là số thời gian thực hiện cuộc gọi sắp xếp theo thứ tự không giảm.
\({Q_3} = \frac{{{x_{25}} + {x_{26}}}}{2}\).
Vì \({x_{25}} \in [120;180)\) và \({x_{26}} \in [180;240)\) nên \({Q_3} = 180\).
Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 7 là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau nửa học kỳ đầu tiên. Đề thi này không chỉ kiểm tra kiến thức lý thuyết mà còn yêu cầu học sinh vận dụng kiến thức vào giải quyết các bài toán thực tế.
Đề thi thường bao gồm hai phần chính: phần trắc nghiệm và phần tự luận. Phần trắc nghiệm thường chiếm khoảng 30-40% tổng số điểm, tập trung vào các kiến thức cơ bản và các công thức quan trọng. Phần tự luận chiếm khoảng 60-70% tổng số điểm, yêu cầu học sinh trình bày chi tiết các bước giải và giải thích rõ ràng lý do tại sao lại chọn phương pháp giải đó.
Nội dung đề thi thường bao gồm các chủ đề sau:
Bài 1: Giải phương trình lượng giác
Ví dụ: Giải phương trình sin(2x) = 1
Hướng dẫn: Phương trình sin(2x) = 1 tương đương với 2x = π/2 + k2π (k ∈ Z). Suy ra x = π/4 + kπ (k ∈ Z).
Bài 2: Tính đạo hàm của hàm số
Ví dụ: Tính đạo hàm của hàm số y = x3 + 2x2 - 5x + 1
Hướng dẫn: Sử dụng các quy tắc tính đạo hàm, ta có y' = 3x2 + 4x - 5.
Bài 3: Tìm cực trị của hàm số
Ví dụ: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Hướng dẫn: Tính đạo hàm y' = 3x2 - 6x. Giải phương trình y' = 0, ta được x = 0 hoặc x = 2. Lập bảng biến thiên để xác định cực trị của hàm số.
Để chuẩn bị tốt nhất cho kỳ thi học kì 1, học sinh nên tham khảo các tài liệu sau:
Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 7 là một cơ hội tốt để học sinh đánh giá năng lực và chuẩn bị tốt nhất cho kỳ thi sắp tới. Hy vọng với những phân tích chi tiết và hướng dẫn giải trên, các em học sinh sẽ tự tin hơn khi làm bài thi.