Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 3, được biên soạn theo chuẩn chương trình học mới nhất của Bộ Giáo dục và Đào tạo. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi thực tế và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 1 Toán 9 Kết nối tri thức. Đi kèm với đề thi là đáp án chi tiết và hướng dẫn giải, giúp học sinh tự đánh giá năng lực và khắc phục những điểm còn yếu.
Phương trình \(x - 3y = 0\) có nghiệm tổng quát là:
\(x \in \mathbb{R},y = 3x\).
\(x = 3y,y \in \mathbb{R}\).
\(x \in \mathbb{R},y = 3\).
\(y \in \mathbb{R},x = 0\).
Nghiệm của phương trình \(\left( {2x - 3} \right)\left( {x + 2} \right) = 0\) là
\(x = \frac{3}{2};x = - 2\).
\(x = - \frac{3}{2};x = - 2\).
\(x = \frac{3}{2};x = 2\).
\(x = - \frac{3}{2};x = 2\).
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
\( - 2{x^2} + 5 > 0\).
\(3x - y \le 0\).
\( - 4x - 2 < 0\).
\(5 + 0x \ge - 7\).
Căn bậc hai số học của 25 là
5.
-5.
5 và -5.
625 và - 625.
Biểu thức \(\sqrt {2x - 1} \) xác định khi
\(x \le \frac{1}{2}\).
\(x \ge \frac{1}{2}\).
\(x < \frac{1}{2}\).
\(x > \frac{1}{2}\).
Rút gọn biểu thức \(\frac{2}{{\sqrt 7 - 3}} - \frac{2}{{\sqrt 7 + 3}}\) ta được
\(\sqrt 7 + 3\).
\(\sqrt 7 - 3\).
\( - 6\).
\(0\).
Kết quả của \(\sqrt[3]{{{{\left( {x - 1} \right)}^3}}}\) là
\(\frac{{x - 1}}{3}\).
\(1 - x\).
\(3\left( {x - 1} \right)\).
\(x - 1\).
Cho tam giác ABC có AB = 9cm, AC = 12cm, BC = 15cm. Độ dài đường cao AH (H \( \in \) BC) của tam giác ABC là
8,4cm.
7,2cm.
6,8cm.
4,2cm.
Đường tròn là hình
không có trục đối xứng.
có một trục đối xứng.
có hai trục đối xứng.
có vô số trục đối xứng.
Hình nào dưới đây biểu diễn góc ở tâm?
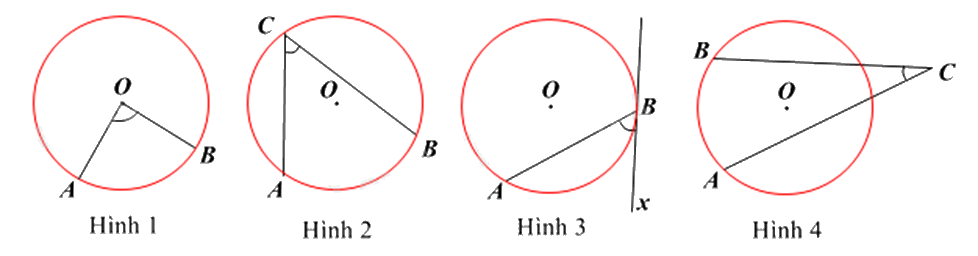
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho đường tròn (O) đường kính 8cm và đường tròn \((O';2cm)\). OA là một bán kính của (O) (A \( \in \) (O)) và \(O'\) là trung điểm của đoạn \(OA\). Vị trí tương đối của hai đường tròn trên là
Tiếp xúc ngoài.
Cắt nhau.
Ở ngoài nhau.
Tiếp xúc trong.
Hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài. Số tiếp tuyến chung của chúng là
1.
2.
3.
4.
Cho \(A = \left( {\frac{1}{{\sqrt x {\rm{\;}} + 1}} - \frac{{2\sqrt x {\rm{\;}} - 2}}{{x\sqrt x {\rm{\;}} - \sqrt x {\rm{\;}} + x - 1}}} \right):\left( {\frac{1}{{\sqrt x {\rm{\;}} - 1}} - \frac{2}{{x - 1}}} \right)\) với \(x \ge 0,x \ne 1.\)
a) Rút gọn A.
b) Tìm\(x \in \mathbb{Z}\) để \(A \in \mathbb{Z}\).
c) Tìm x để A đạt GTNN.
Ngày chủ nhật hai bạn Tâm và Hiếu được bố mẹ chở đi siêu thị để mua sắm. Khi đến quầy thức ăn Tâm mua \(6\) chiếc bánh và \(3\) ly nước, Hiếu mua \(5\) chiếc bánh và \(3\) ly nước. Tổng số tiền ăn uống của cả hai bạn là 252 nghìn đồng. Biết giá tiền của một ly nước cao hơn giá tiền của một chiếc bánh là \(8\) nghìn đồng. Hỏi giá tiền của một cái bánh và một ly nước là bao nhiêu?
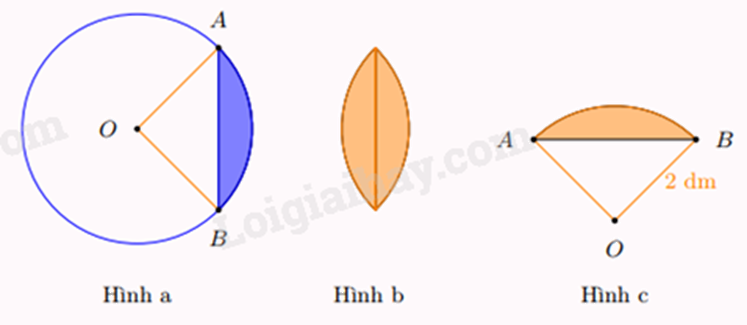
Hình viên phân là hình giới hạn bởi một cung tròn và dây cung (tương ứng) của đường tròn (minh họa bởi phần tô đậm ở hình a). Người ta làm một họa tiết trang trí bằng cách ghép hai hình viên phân bằng nhau (hình b), mỗi hình viên phân đó có góc ở tâm tương ứng là \(90^\circ \) và bán kính đường tròn tương ứng là \(2{\rm{dm}}\) (hình c). Tính diện tích của họa tiết trang trí đó (lấy \(\pi \approx 3,14\))
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn, \(D \in \left( O \right)\) và \(E \in \left( {O'} \right)\). Gọi M là giao điểm của BD và CE.
a) Tính số đo của \(\widehat {DAE}\).
b) Tứ giác ADME là hình gì?
c) Chứng minh MA là tiếp tuyến chung của hai đường tròn.
Một bánh xe có dạng hình tròn bán kính 20cm lăn đến bức tường hợp với mặt đất một góc \(60^\circ \). Hãy tính khoảng cách ngắn nhất từ tâm bánh xe đến góc tường.

Phương trình \(x - 3y = 0\) có nghiệm tổng quát là:
\(x \in \mathbb{R},y = 3x\).
\(x = 3y,y \in \mathbb{R}\).
\(x \in \mathbb{R},y = 3\).
\(y \in \mathbb{R},x = 0\).
Đáp án : B
Tìm nghiệm tổng quát bằng cách rút, ta cần rút y theo x (\(by = c - ax\)), từ đó ta giải được \(y = \frac{{c - ax}}{b}\) với \(b \ne 0\). Đối với trường hợp \(b = 0\) thì ta làm ngược lại (rút x theo y ). Thì nghiệm tổng quát có dạng \(\left( {x;\frac{{c - ax}}{b}} \right)\) với \(x \in \mathbb{R}\) tuỳ ý.
Vì \(x - 3y = 0\) nên \(x = 3y\).
Vậy nghiệm của phương trình \(x - 3y = 0\) là \(x = 3y,y \in \mathbb{R}\).
Đáp án B
Nghiệm của phương trình \(\left( {2x - 3} \right)\left( {x + 2} \right) = 0\) là
\(x = \frac{3}{2};x = - 2\).
\(x = - \frac{3}{2};x = - 2\).
\(x = \frac{3}{2};x = 2\).
\(x = - \frac{3}{2};x = 2\).
Đáp án : A
Để giải phương trình tích \(A\left( x \right).B\left( x \right) = 0\) thì ta giải hai phương trình \(A\left( x \right) = 0\) và \(B\left( x \right) = 0\).
Ta có: \(\left( {2x - 3} \right)\left( {x + 2} \right) = 0\)
+) \(2x - 3 = 0\) suy ra \(2x = 3\) nên \(x = \frac{3}{2}\).
+) \(x + 2 = 0\) suy ra \(x = - 2\).
Vậy nghiệm của phương trình là \(x = \frac{3}{2}\); \(x = - 2\).
Đáp án A
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
\( - 2{x^2} + 5 > 0\).
\(3x - y \le 0\).
\( - 4x - 2 < 0\).
\(5 + 0x \ge - 7\).
Đáp án : C
Bất phương trình dạng \(ax + b < c\) (hoặc \(ax + b > c;ax + b \le 0;ax + b \ge 0\)) trong đó a, b là hai số đã cho, \(a \ne 0\) được gọi là bất phương trình bậc nhất một ẩn x.
Bất phương trình \( - 4x - 2 < 0\) là bất phương trình bậc nhất một ẩn.
Đáp án C
Căn bậc hai số học của 25 là
5.
-5.
5 và -5.
625 và - 625.
Đáp án : A
Căn bậc hai số học của số dương a là \(\sqrt a \).
\(\sqrt {25} = 5\).
Đáp án A
Biểu thức \(\sqrt {2x - 1} \) xác định khi
\(x \le \frac{1}{2}\).
\(x \ge \frac{1}{2}\).
\(x < \frac{1}{2}\).
\(x > \frac{1}{2}\).
Đáp án : B
Biểu thức \(\sqrt A \) xác định khi \(A \ge 0\).
Điều kiện xác định của \(\sqrt {2x - 1} \) là \(2x - 1 \ge 0\) hay \(x \ge \frac{1}{2}\).
Đáp án B
Rút gọn biểu thức \(\frac{2}{{\sqrt 7 - 3}} - \frac{2}{{\sqrt 7 + 3}}\) ta được
\(\sqrt 7 + 3\).
\(\sqrt 7 - 3\).
\( - 6\).
\(0\).
Đáp án : C
Quy đồng và thực hiện phép tính với phân thức để rút gọn.
\(\begin{array}{l}\frac{2}{{\sqrt 7 - 3}} - \frac{2}{{\sqrt 7 + 3}}\\ = \frac{{2\left( {\sqrt 7 + 3} \right)}}{{\left( {\sqrt 7 - 3} \right)\left( {\sqrt 7 + 3} \right)}} - \frac{{2\left( {\sqrt 7 - 3} \right)}}{{\left( {\sqrt 7 - 3} \right)\left( {\sqrt 7 + 3} \right)}}\\ = \frac{{2\left( {\sqrt 7 + 3} \right) - 2\left( {\sqrt 7 - 3} \right)}}{{\left( {\sqrt 7 - 3} \right)\left( {\sqrt 7 + 3} \right)}}\\ = \frac{{2\sqrt 7 + 6 - 2\sqrt 7 + 6}}{{7 - 9}}\\ = \frac{{12}}{{ - 2}} = - 6\end{array}\)
Đáp án C
Kết quả của \(\sqrt[3]{{{{\left( {x - 1} \right)}^3}}}\) là
\(\frac{{x - 1}}{3}\).
\(1 - x\).
\(3\left( {x - 1} \right)\).
\(x - 1\).
Đáp án : D
Sử dụng kiến thức về căn thức bậc ba: \(\sqrt[3]{{{A^3}}} = A\).
\(\sqrt[3]{{{{\left( {x - 1} \right)}^3}}} = x - 1\).
Đáp án D
Cho tam giác ABC có AB = 9cm, AC = 12cm, BC = 15cm. Độ dài đường cao AH (H \( \in \) BC) của tam giác ABC là
8,4cm.
7,2cm.
6,8cm.
4,2cm.
Đáp án : B
Chứng minh tam giác ABC vuông. Sử dụng tính chất của tỉ số lượng giác để tính AH.
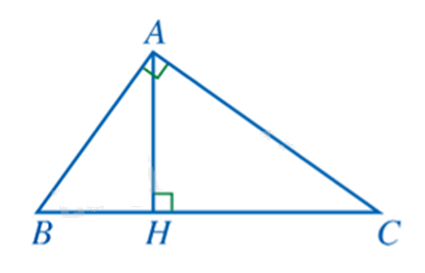
Vì \(A{B^2} + A{C^2} = {9^2} + {12^2} = 225 = {15^2} = B{C^2}\) nên tam giác ABC vuông tại A.
Khi đó \(\sin B = \frac{{AC}}{{BC}} = \frac{{12}}{{15}} = \frac{4}{5}\).
Mà tam giác ABH vuông tại H nên \(\sin B = \frac{{AH}}{{AB}} = \frac{{AH}}{9}\).
Suy ra \(\frac{{AH}}{9} = \frac{4}{5}\).
Do đó \(AH = 9.\frac{4}{5} = \frac{{36}}{5} = 7,2\left( {cm} \right)\).
Đáp án B
Đường tròn là hình
không có trục đối xứng.
có một trục đối xứng.
có hai trục đối xứng.
có vô số trục đối xứng.
Đáp án : D
Dựa vào kiến thức về trục đối xứng của đường tròn.
Đường tròn có vô số trục đối xứng.
Đáp án D
Hình nào dưới đây biểu diễn góc ở tâm?
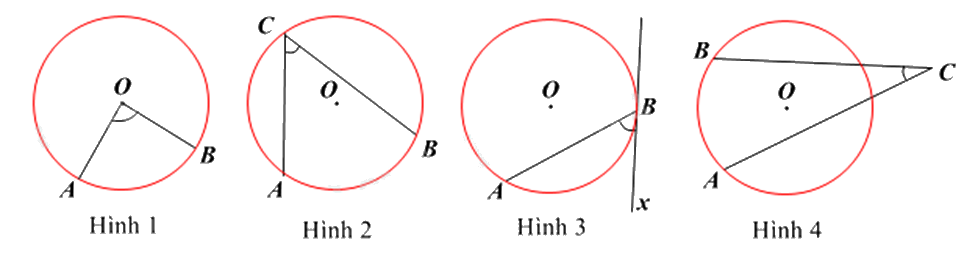
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đáp án : A
Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.
Hình biểu diễn góc ở tâm là Hình 1.
Đáp án A
Cho đường tròn (O) đường kính 8cm và đường tròn \((O';2cm)\). OA là một bán kính của (O) (A \( \in \) (O)) và \(O'\) là trung điểm của đoạn \(OA\). Vị trí tương đối của hai đường tròn trên là
Tiếp xúc ngoài.
Cắt nhau.
Ở ngoài nhau.
Tiếp xúc trong.
Đáp án : D
Cách 1. Vẽ hai đường tròn. Quan sát hình vẽ để xác định.
Cách 2. Dựa vào mối liên hệ giữa khoảng cách hai tâm và bán kính.
Đường tròn (O) có đường kính 8cm nên bán kính là \(8:2 = 4cm\).
Cách 1. Vẽ đường tròn (O) và (O’) theo đề bài, ta được hình vẽ sau:
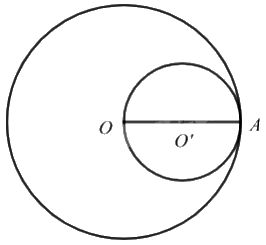
Quan sát hình vẽ ta thấy hai đường tròn tiếp xúc trong.
Cách 2. Vì O’ là trung điểm của OA nên OO’ = 4 : 2 = 2(cm).
Do đó hai đường tròn này tiếp xúc trong với nhau vì \(OO' = OA - O'A = 4 - 2 = 2cm\).
Đáp án D
Hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài. Số tiếp tuyến chung của chúng là
1.
2.
3.
4.
Đáp án : C
Dựa vào kiến thức về tiếp tuyến của đường tròn.
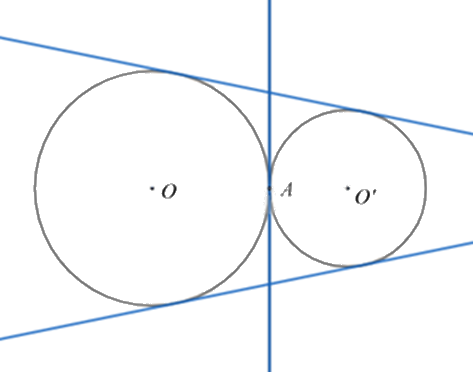
Hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài thì có 3 tiếp tuyến chung.
Đáp án C
Cho \(A = \left( {\frac{1}{{\sqrt x {\rm{\;}} + 1}} - \frac{{2\sqrt x {\rm{\;}} - 2}}{{x\sqrt x {\rm{\;}} - \sqrt x {\rm{\;}} + x - 1}}} \right):\left( {\frac{1}{{\sqrt x {\rm{\;}} - 1}} - \frac{2}{{x - 1}}} \right)\) với \(x \ge 0,x \ne 1.\)
a) Rút gọn A.
b) Tìm\(x \in \mathbb{Z}\) để \(A \in \mathbb{Z}\).
c) Tìm x để A đạt GTNN.
a) Quy đồng và rút gọn phân thức
b) Tính và đưa A về dạng \(A = a + \frac{b}{c}\) với a, b là các số nguyên, c là biểu thức chứa x.
c) Từ điều kiện của x để tìm giá trị lớn nhất của A.
a) Với \(x \ge 0,x \ne 1\) ta có:
\(A = \left( {\frac{1}{{\sqrt x {\rm{\;}} + 1}} - \frac{{2\sqrt x {\rm{\;}} - 2}}{{x\sqrt x {\rm{\;}} - \sqrt x {\rm{\;}} + x - 1}}} \right):\left( {\frac{1}{{\sqrt x {\rm{\;}} - 1}} - \frac{2}{{x - 1}}} \right)\)\(A = \left( {\frac{1}{{\sqrt x {\rm{\;}} + 1}} - \frac{{2\sqrt x {\rm{\;}} - 2}}{{\left( {x - 1} \right)\left( {\sqrt x {\rm{\;}} + 1} \right)}}} \right):\left( {\frac{1}{{\sqrt x {\rm{\;}} - 1}} - \frac{2}{{\left( {\sqrt x {\rm{\;}} - 1} \right)\left( {\sqrt x {\rm{\;}} + 1} \right)}}} \right)\)
\(A = \frac{{x - 1 - 2\sqrt x {\rm{\;}} + 2}}{{\left( {x - 1} \right)\left( {\sqrt x {\rm{\;}} + 1} \right)}}:\frac{{\sqrt x {\rm{\;}} + 1 - 2}}{{\left( {\sqrt x {\rm{\;}} - 1} \right)\left( {\sqrt x {\rm{\;}} + 1} \right)}}\)
\(A = \frac{{x - 2\sqrt x {\rm{\;}} + 1}}{{\left( {x - 1} \right)\left( {\sqrt x {\rm{\;}} + 1} \right)}}:\frac{{\sqrt x {\rm{\;}} - 1}}{{\left( {\sqrt x {\rm{ \;}} - 1} \right)\left( {\sqrt x {\rm{\;}} + 1} \right)}}\)
\(A = \frac{{{{\left( {\sqrt x {\rm{\;}} - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {\sqrt x {\rm{\;}} + 1} \right)}}.\left( {\sqrt x {\rm{\;}} + 1} \right)\)
\(A = \frac{{{{\left( {\sqrt x {\rm{\;}} - 1} \right)}^2}}}{{\left( {\sqrt x {\rm{\;}} - 1} \right)\left( {\sqrt x {\rm{\;}} + 1} \right)}}\)
\(A = \frac{{\sqrt x {\rm{\;}} - 1}}{{\sqrt x {\rm{\;}} + 1}}\).
b) Ta có \(A = \frac{{\sqrt x {\rm{\;}} - 1}}{{\sqrt x {\rm{\;}} + 1}} = \frac{{\sqrt x {\rm{\;}} + 1 - 2}}{{\sqrt x {\rm{\;}} + 1}} = 1 - \frac{2}{{\sqrt x {\rm{\;}} + 1}},{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {x \ge 0} \right).\)
Đặt \(B = \sqrt x {\rm{\;}} + 1\), để A nguyên khi x nguyên thì B là ước nguyên của 2.
Vì \(x \ge 0\) nên \(B > 0{\mkern 1mu} {\mkern 1mu} \), suy ra B là ước nguyên dương của 2.
Ư\(\left( 2 \right) = \left\{ {1;2} \right\}\)
TH1: \(\sqrt x {\rm{\;}} + 1 = 1\) suy ra \(x = 0{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)\)
TH2: \(\sqrt x {\rm{\;}} + 1 = 2\) suy ra \(x = 1{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)\)
Vậy \(x = 0\) thì A nguyên.
c) Ta có \(A = \frac{{\sqrt x {\rm{\;}} - 1}}{{\sqrt x {\rm{\;}} + 1}} = 1 - \frac{2}{{\sqrt x {\rm{\;}} + 1}}\).
Vì \(\sqrt x {\rm{\;}} + 1 \ge 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} \sqrt x {\rm{\;}} \ge 0} \right)\) nên \(\frac{2}{{\sqrt x {\rm{\;}} + 1}} \le \frac{2}{1}\)
Suy ra \( - \frac{2}{{\sqrt x {\rm{\;}} + 1}} \ge {\rm{\;}} - 2\)
Do đó \(1 - \frac{2}{{\sqrt x {\rm{\;}} + 1}} \ge {\rm{\;}} - 1\) hay \(A \ge {\rm{\;}} - 1\).
Dấu “=” xảy ra khi \(x = 0.\)
Vậy \(\min A = {\rm{\;}} - 1\) khi \(x = 0\).
Ngày chủ nhật hai bạn Tâm và Hiếu được bố mẹ chở đi siêu thị để mua sắm. Khi đến quầy thức ăn Tâm mua \(6\) chiếc bánh và \(3\) ly nước, Hiếu mua \(5\) chiếc bánh và \(3\) ly nước. Tổng số tiền ăn uống của cả hai bạn là 252 nghìn đồng. Biết giá tiền của một ly nước cao hơn giá tiền của một chiếc bánh là \(8\) nghìn đồng. Hỏi giá tiền của một cái bánh và một ly nước là bao nhiêu?
Gọi giá tiền một chiếc bánh và một ly nước lần lượt là \(x,y\) nghìn đồng (\(x,y \in {\mathbb{N}^*};y > 8\))
Lập hệ phương trình theo x, y.
Giải hệ phương trình đó.
Gọi giá tiền một chiếc bánh và một ly nước lần lượt là \(x,y\) nghìn đồng (\(x,y \in {\mathbb{N}^*};y > 8\))
Vì Tâm mua \(6\) chiếc bánh và \(3\) ly nước, Hiếu mua \(5\) chiếc bánh và \(3\) ly nước nên tổng số bánh và nước hai bạn mua là 11 chiếc bánh và 6 ly nước. Tổng số tiền ăn uống của hai bạn là 252 nghìn đồng nên ta có phương trình: \(11x + 6y = 252\).
Vì giá tiền của một ly nước cao hơn giá tiền của một chiếc bánh là \(8\) nghìn đồng nên \(y - x = 8\) hay \( - x + y = 8\).
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ - x + y = 8}\\{11x + 6y = 252}\end{array}} \right.\)
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{y = 8 + x}\\{11x + 6\left( {8 + x} \right) = 252}\end{array}} \right.\\\left\{ \begin{array}{l}y = 8 + x\\17x = 204\end{array} \right.\\\left\{ \begin{array}{l}x = 12\\y = 8 + 12\end{array} \right.\\\left\{ \begin{array}{l}x = 12(TM)\\y = 20(TM)\end{array} \right.\end{array}\)
Vậy giá một chiếc bánh là \(12\) nghìn đồng, giá một ly nước là \(20\) nghìn đồng.
Hình viên phân là hình giới hạn bởi một cung tròn và dây cung (tương ứng) của đường tròn (minh họa bởi phần tô đậm ở hình a). Người ta làm một họa tiết trang trí bằng cách ghép hai hình viên phân bằng nhau (hình b), mỗi hình viên phân đó có góc ở tâm tương ứng là \(90^\circ \) và bán kính đường tròn tương ứng là \(2{\rm{dm}}\) (hình c). Tính diện tích của họa tiết trang trí đó (lấy \(\pi \approx 3,14\))
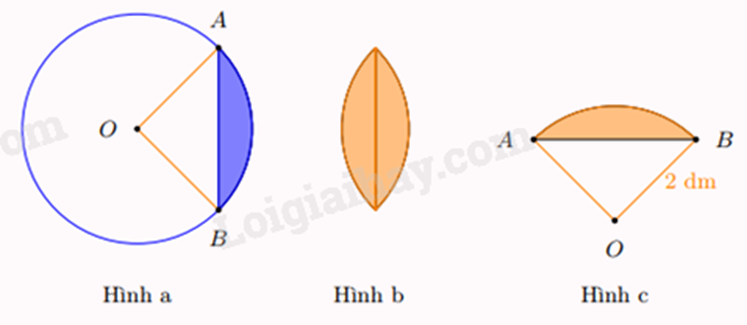
+) Sử dụng công thức tính diện tích tam giác: S = \(\frac{1}{2}\). chiều cao. đáy tương ứng.
+) Sử dụng công thức tính diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).
+) Diện tích hình viên phân = diện tích hình quạt tròn – diện tích hình tam giác.
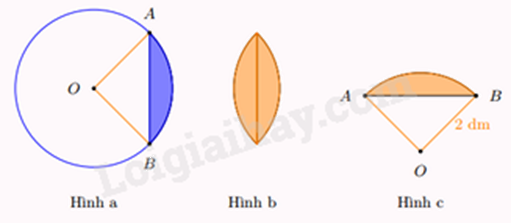
Vì góc ở tâm \(AOB\) bằng \(90^\circ \) nên tam giác OAB vuông tại O.
+ Diện tích tam giác \(OAB\) là:
\({S_1} = \frac{1}{2}OA \cdot OB = \frac{1}{2} \cdot 2 \cdot 2 = 2\left( {{\rm{d}}{{\rm{m}}^2}} \right)\)
+ Do sđ\(\overset\frown{AB}=\widehat{AOB}=90{}^\circ \) nên diện tích hình quạt tròn \(OAB\) tương ứng là:
\({S_2} = \frac{{\pi \cdot {2^2} \cdot 90}}{{360}} = \pi \left( {{\rm{d}}{{\rm{m}}^2}} \right)\)
Suy ra diện tích hình viên phân là:
\({S_3} = {S_2} - {S_1} = \pi - 2\,\left( {{\rm{d}}{{\rm{m}}^2}} \right)\)
Diện tích của họa tiết trang trí đó là:
\(S = 2{S_3} = 2\left( {\pi - 2} \right) \approx 2,28\left( {{\rm{d}}{{\rm{m}}^2}} \right)\).
Vậy diện tích của họa tiết trang trí đó khoảng \(2,28d{m^2}\).
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn, \(D \in \left( O \right)\) và \(E \in \left( {O'} \right)\). Gọi M là giao điểm của BD và CE.
a) Tính số đo của \(\widehat {DAE}\).
b) Tứ giác ADME là hình gì?
c) Chứng minh MA là tiếp tuyến chung của hai đường tròn.
Vận dụng kiến thức về vị trí tương đối của hai đường tròn liên quan đến trường hợp hai đường tròn không cắt nhau.
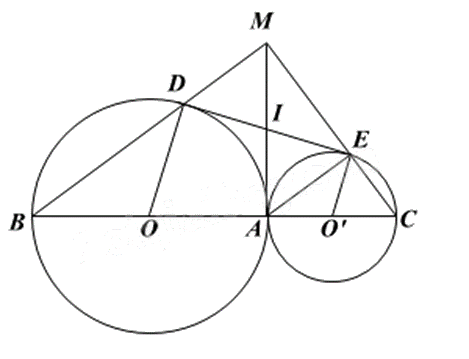
Từ A kẻ tiếp tuyến chung của hai đường tròn, tiếp tuyến này cắt DE tại I.
Theo tính chất hai tiếp tuyến cắt nhau, ta có ID = IA = IE nên \(\Delta DAE\) vuông tại A. Suy ra \(\widehat {DAE} = 90^\circ \).
b) Vì AB và AC là các đường kính của (O) và (O’) nên \(\widehat {ADB} = \widehat {AEC} = 90^\circ \).
Suy ra \(\widehat {ADM} = \widehat {AEM} = 90^\circ \).
Mà \(\widehat {DAE} = 90^\circ \) nên tứ giác ADME là hình chữ nhật.
c) Vì tứ giác ADME là hình chữ nhật nên 3 điểm M, I, A thẳng hàng.
Do vậy MA là tiếp tuyến chung của hai đường trong (O); (O’).
Một bánh xe có dạng hình tròn bán kính 20cm lăn đến bức tường hợp với mặt đất một góc \(60^\circ \). Hãy tính khoảng cách ngắn nhất từ tâm bánh xe đến góc tường.

Giải thích đề bài: Khi bánh xe chạm tới bức tường thì không thể di chuyển vào thêm được nữa. Điều này có nghĩa khoảng cách của tâm bánh xe đến góc tường ngắn nhất là khi bánh xe tiếp xúc với bức tường và mặt đất.
Khi đó mặt tường và mặt đất là hai tiếp tuyến cắt nhau của đường tròn biểu diễn bánh xe.
Sử dụng tính chất hai tiếp tuyến cắt nhau để tính số đo góc OAB.
Sử dụng tỉ số lượng giác trong tam giác vuông để tính khoảng cách ngắn nhất từ tâm bánh xe đến góc tường.
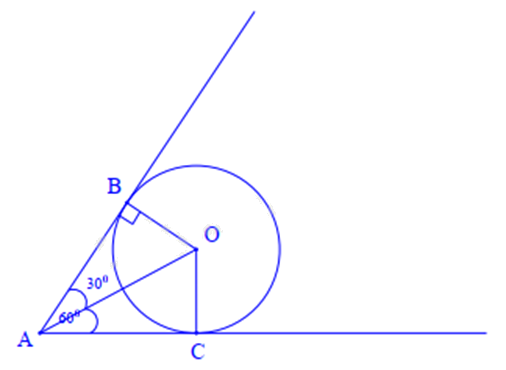
Ta có: OA = OC = 20cm.
Khi bánh xe chạm tới bức tường thì không thể di chuyển vào thêm được nữa. Điều này có nghĩa khoảng cách của tâm bánh xe đến góc tường ngắn nhất là khi bánh xe tiếp xúc với bức tường và mặt đất.
Gọi AB và AC là hai đoạn biểu diễn mặt tường và mặt đất tiếp xúc với đường tròn (O), khi đó AB và AC là hai tiếp tuyến cắt nhau tại A của đường tròn (O).
Vì \(\widehat {BAC} = 60^\circ \) nên \(\widehat {BAO} = \widehat {CAO} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.60^\circ = 30^\circ \) (tính chất hai tiếp tuyến cắt nhau).
Xét tam giác ABO vuông tại B (vì AB là tiếp tuyến của (O) nên \(AB \bot OB\)), ta có:
\(\sin BAO = \frac{{OB}}{{AO}}\) (tỉ số lượng giác trong tam giác vuông)
Suy ra \(AO = \frac{{OB}}{{\sin BAO}} = \frac{{20}}{{\sin 30^\circ }} = 40\left( {cm} \right)\)
Vậy khoảng cách ngắn nhất từ bánh xe đến góc tường là 40cm.
Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 3 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một học kì. Việc nắm vững kiến thức và kỹ năng giải toán là yếu tố then chốt để đạt kết quả tốt trong kỳ thi này. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp, và hướng dẫn ôn tập hiệu quả.
Đề thi thường bao gồm hai phần chính: phần trắc nghiệm và phần tự luận. Phần trắc nghiệm thường chiếm khoảng 30-40% tổng số điểm, tập trung vào các kiến thức cơ bản và khả năng vận dụng nhanh. Phần tự luận chiếm khoảng 60-70% tổng số điểm, đòi hỏi học sinh phải trình bày lời giải chi tiết và logic.
Để giúp học sinh ôn tập hiệu quả, chúng ta sẽ phân tích chi tiết Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 3. Đề thi này bao gồm các câu hỏi sau:
| STT | Nội dung câu hỏi | Điểm |
|---|---|---|
| 1 | Giải phương trình: 2x + 5 = 11 | 1.0 |
| 2 | Tìm x để biểu thức P = (x - 3)(x + 3) đạt giá trị nhỏ nhất. | 1.5 |
| 3 | Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính BC và diện tích tam giác ABC. | 2.0 |
| 4 | Vẽ đồ thị hàm số y = 2x - 1. | 1.5 |
| 5 | Tính trung bình cộng của các số liệu: 5, 7, 9, 11, 13. | 1.0 |
Hướng dẫn giải:
1. Giải phương trình: 2x + 5 = 11 => 2x = 6 => x = 3
2. P = (x - 3)(x + 3) = x2 - 9. P đạt giá trị nhỏ nhất khi x = 0, P = -9
3. BC = √(AB2 + AC2) = √(32 + 42) = 5cm. Diện tích tam giác ABC = (1/2) * AB * AC = (1/2) * 3 * 4 = 6cm2
4. Vẽ đồ thị hàm số y = 2x - 1 bằng cách xác định hai điểm thuộc đồ thị, ví dụ (0, -1) và (1, 1).
5. Trung bình cộng = (5 + 7 + 9 + 11 + 13) / 5 = 9
Hãy chuẩn bị kỹ lưỡng cho kỳ thi học kì 1 Toán 9 Kết nối tri thức - Đề số 3 bằng cách ôn tập đầy đủ kiến thức, luyện tập thường xuyên, và làm đề thi thử. Chúc các em học sinh đạt kết quả tốt nhất!