Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 9 - Đề số 3, một công cụ hữu ích giúp các em học sinh ôn luyện và củng cố kiến thức Toán 9. Đề thi được biên soạn theo chuẩn chương trình học, bao gồm các dạng bài tập thường gặp trong đề thi thực tế.
Với đáp án chi tiết đi kèm, các em có thể tự đánh giá năng lực và tìm ra những điểm cần cải thiện. Hãy cùng giaitoan.edu.vn chinh phục kỳ thi giữa kì 2 Toán 9 một cách tự tin nhất!
Cho đồ thị hàm số \(y = 8{x^2}\), điểm thuộc đồ thị hàm số có tung độ bằng \(4\) là
\(\left( {\frac{{\sqrt 2 }}{2};4} \right)\) và \(\left( { - \frac{{\sqrt 2 }}{2};4} \right)\).
\(\left( {1;4} \right)\) và \(\left( { - 1;4} \right)\).
\(\left( {\frac{{\sqrt 2 }}{2};4} \right)\) và \(\left( { - 1;4} \right)\).
\(\left( {1;4} \right)\) và \(\left( { - \frac{{\sqrt 2 }}{2};4} \right)\).
Phương trình bậc hai một ẩn \(3{x^2} - 8x - 2 = 0\) có hệ số \(a,b,c\) lần lượt là:
\(a = - 2,b = - 8,c = 3\).
\(a = - 8,b = 3,c = - 2\).
\(a = 3,b = - 8,c = - 2\).
\(a = 3,b = - 2,c = - 8\).
Phương trình \(\left( {\sqrt 3 - 2} \right){x^2} + 2x - \sqrt 3 = 0\) có nghiệm là
\({x_1} = - 1;{x_2} = \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\).
\({x_1} = - 1;{x_2} = - \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\).
\({x_1} = 1;{x_2} = \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\).
\({x_1} = 1;{x_2} = - \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\).
Các số liệu thống kê kích thước (đơn vị: cm) của 24 con mực được nuôi cấy thử nghiệm của trung tâm A được ghi lại như sau:
12, 11, 11, 12, 8, 11, 12, 7, 7, 10, 11, 12, 9, 12, 5, 9, 9, 12, 8, 9, 7, 10, 12, 10.
Trong 24 số liệu trên có bao nhiêu giá trị khác nhau?
Có 5 giá trị khác nhau.
Có 6 giá trị khác nhau.
Có 7 giá trị khác nhau.
Có 8 giá trị khác nhau.
Cho tứ giác \(BEGH\) nội tiếp đường tròn tâm \((I)\), biết \(\widehat B = 116^\circ \), \(\widehat E = 92^\circ \), tính số đo \(\widehat G\).
\(\widehat G = 78^\circ \).
\(\widehat G = 64^\circ \).
\(\widehat G = 88^\circ \).
\(\widehat G = 84^\circ \).
Cho tam giác ABC nội tiếp đường tròn (O). Biết \(\widehat {BOC} = 120^\circ \) và \(\widehat {OCA} = 40^\circ \). Tính số đo góc BAO.
\(40^\circ \).
\(60^\circ \).
\(20^\circ \).
\(80^\circ \).
Lớp 9A định tổ chức một trò chơi dân gian khi đi dã ngoại. Lớp trưởng đã yêu cầu mỗi bạn đề xuất một trò chơi bằng cách ghi vào phiếu. Sau khi thu phiếu và tổng hợp kết quả, lớp trưởng thu được biểu đồ cột như sau:
a) Số học sinh lớp 9A là 40 học sinh.
b) Bảng tần số của biểu đồ tần số trên là:

c) Tần số tương đối của trò Nhảy bao bố là 15%.
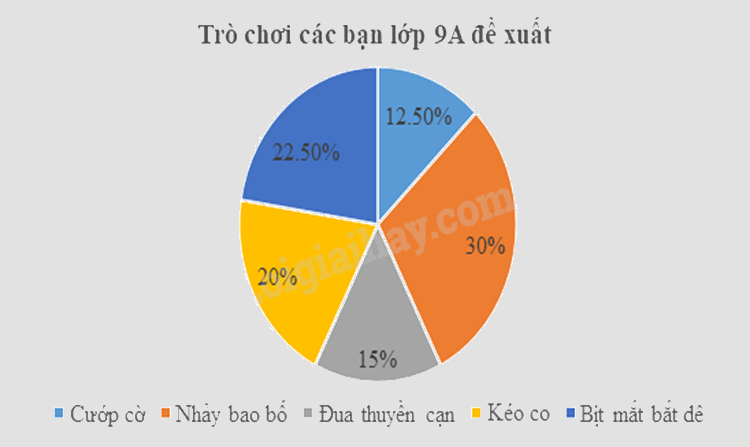
d) Biểu đồ hình quạt biểu diễn tần số tương đối của trò chơi các bạn lớp 9A đề xuất là:
Cho tứ giác ABCD có \(\widehat A = \widehat C = 90^\circ \) nội tiếp đường tròn tâm O.
a) \(\widehat {ABD} = \widehat {ACD}\).
b) Đường tròn \(\left( O \right)\) là đường tròn nội tiếp tam giác ABC.
c) Nếu \(\widehat {ABC} = 80^\circ \) thì \(\widehat {ADC} = 100^\circ \).
d) Bán kính đường tròn ngoại tiếp tam giác ACD bằng \(\frac{{BD}}{2}\).
Biết rằng đường cong trong hình sau là một parabol \(y = a{x^2}\). Hệ số \(a\) của hàm số là:
Đáp án:
Biết rằng phương trình \({x^2} - 2\left( {3m + 2} \right)x + 2{m^2} - 3m - 10 = 0\) có một nghiệm bằng \( - 1\). Tìm nghiệm còn lại với m > 0.
Đáp án:
Biểu đồ tranh thể hiện số ti vi (TV) bán được qua các năm của 1 siêu thị điện máy như sau:

Tần số tương đối của số ti vi bán được trong năm 2022 là: …. (không điền dấu %)
Đáp án:
Cho tứ giác ABCD nội tiếp đường tròn (O;R) có AB = BC = R. Số đo \(\widehat {ABC}\) bằng bao nhiêu độ? (không cần ghi độ)
Đáp án:
Một ca nô chạy xuôi dòng quãng đường AB dài 80km, sau đó ngược dòng đến địa điểm C cách B là 72km. Thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút. Tính vận tốc thực của ca nô, biết vận tốc dòng nước là 4km/h.
Một bức ảnh hình tròn có bán kính 40 cm, người ta làm một khung gỗ hình tam giác đều bao bên ngoài bức ảnh sao cho bức ảnh hình tròn tiếp xúc với các cạnh của khung gỗ. Tính độ dài cạnh khung gỗ (làm tròn đến số thập phân thứ nhất).
Biết rằng phương trình bậc hai \({x^2} + x + m = 0\) có hai nghiệm là \({x_1} = \frac{{\sqrt 2 + 1}}{{\sqrt 2 - 1}}\) và \({x_2}\). Tính giá trị của biểu thức \(A = 2024{x_1} + 2025{x_2}\)
Cho đồ thị hàm số \(y = 8{x^2}\), điểm thuộc đồ thị hàm số có tung độ bằng \(4\) là
\(\left( {\frac{{\sqrt 2 }}{2};4} \right)\) và \(\left( { - \frac{{\sqrt 2 }}{2};4} \right)\).
\(\left( {1;4} \right)\) và \(\left( { - 1;4} \right)\).
\(\left( {\frac{{\sqrt 2 }}{2};4} \right)\) và \(\left( { - 1;4} \right)\).
\(\left( {1;4} \right)\) và \(\left( { - \frac{{\sqrt 2 }}{2};4} \right)\).
Đáp án : A
Thay tung độ \(y = 4\) vào hàm số, ta tính được giá trị của \(x\) tương ứng.
Thay \(y = 4\) vào hàm số \(y = 8{x^2}\) ta được \(4 = 8{x^2}\) suy ra \({x^2} = \frac{1}{2}\) suy ra \(x = \frac{{\sqrt 2 }}{2}\) hoặc \(x = - \frac{{\sqrt 2 }}{2}\)
Các điểm thuộc đồ thị hàm số có tung độ bằng \(4\) là \(\left( {\frac{{\sqrt 2 }}{2};4} \right)\) và \(\left( { - \frac{{\sqrt 2 }}{2};4} \right)\).
Đáp án A
Phương trình bậc hai một ẩn \(3{x^2} - 8x - 2 = 0\) có hệ số \(a,b,c\) lần lượt là:
\(a = - 2,b = - 8,c = 3\).
\(a = - 8,b = 3,c = - 2\).
\(a = 3,b = - 8,c = - 2\).
\(a = 3,b = - 2,c = - 8\).
Đáp án : C
Phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hệ số a, b, c.
Hệ số a, b, c của phương trình \(3{x^2} - 8x - 2 = 0\) lần lượt là: \(a = 3,b = - 8,c = - 2\).
Đáp án C
Phương trình \(\left( {\sqrt 3 - 2} \right){x^2} + 2x - \sqrt 3 = 0\) có nghiệm là
\({x_1} = - 1;{x_2} = \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\).
\({x_1} = - 1;{x_2} = - \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\).
\({x_1} = 1;{x_2} = \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\).
\({x_1} = 1;{x_2} = - \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\).
Đáp án : D
Phương trình \(a{x^2} + bx + c = 0\) có \(a + b + c = 0\) thì phương trình có nghiệm là \({x_1} = 1;{x_2} = \frac{c}{a}\).
Vì \(a + b + c = \left( {\sqrt 3 - 2} \right) + 2 - \sqrt 3 = 0\) nên phương trình \(\left( {\sqrt 3 - 2} \right){x^2} + 2x - \sqrt 3 = 0\) có nghiệm là \({x_1} = 1;{x_2} = \frac{c}{a} = - \frac{{\sqrt 3 }}{{\sqrt 3 - 2}}\)
Đáp án D
Các số liệu thống kê kích thước (đơn vị: cm) của 24 con mực được nuôi cấy thử nghiệm của trung tâm A được ghi lại như sau:
12, 11, 11, 12, 8, 11, 12, 7, 7, 10, 11, 12, 9, 12, 5, 9, 9, 12, 8, 9, 7, 10, 12, 10.
Trong 24 số liệu trên có bao nhiêu giá trị khác nhau?
Có 5 giá trị khác nhau.
Có 6 giá trị khác nhau.
Có 7 giá trị khác nhau.
Có 8 giá trị khác nhau.
Đáp án : C
Lập bảng tần số, xác định các giá trị khác nhau và tần số xuất hiện của các giá trị.
Ta có bảng tần số:

Có 7 giá trị khác nhau.
Đáp án C
Cho tứ giác \(BEGH\) nội tiếp đường tròn tâm \((I)\), biết \(\widehat B = 116^\circ \), \(\widehat E = 92^\circ \), tính số đo \(\widehat G\).
\(\widehat G = 78^\circ \).
\(\widehat G = 64^\circ \).
\(\widehat G = 88^\circ \).
\(\widehat G = 84^\circ \).
Đáp án : B
Sử dụng tổng hai góc đối của tứ giác nội tiếp bằng \(180^\circ \).
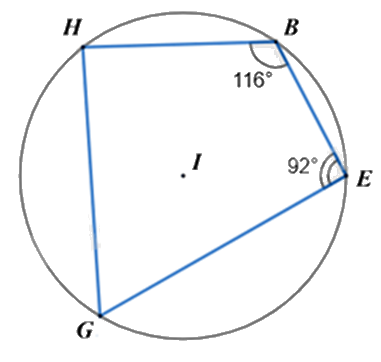
Tứ giác BEGH nội tiếp đường tròn (I) nên ta có:
\(\widehat G + \widehat B = 180^\circ \)
Suy ra \(\widehat G = 180^\circ - \widehat B = 180^\circ - 116^\circ = 64^\circ \)
Đáp án B
Cho tam giác ABC nội tiếp đường tròn (O). Biết \(\widehat {BOC} = 120^\circ \) và \(\widehat {OCA} = 40^\circ \). Tính số đo góc BAO.
\(40^\circ \).
\(60^\circ \).
\(20^\circ \).
\(80^\circ \).
Đáp án : C
Từ tam giác cân OAC, tính góc OAC.
Tính góc nội tiếp BAC = \(\frac{1}{2}\) góc ở tâm chắn cung đó.
Ta tính được số đo góc BAO.
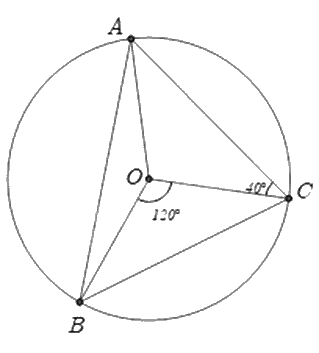
Vì tam giác AOC cân nên \(\widehat {OAC} = \widehat {OCA} = 40^\circ \)
Vì tam giác ABC nội tiếp đường tròn (O) nên \(\widehat {BAC}\) là góc nội tiếp chắn cung BC. Mà \(\widehat {BOC}\) là góc ở tâm chắn cung BC nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}.120^\circ = 60^\circ \).
Mà \(\widehat {BAO} + \widehat {OAC} = \widehat {BAC}\) nên ta có:
\(\widehat {BAO} = \widehat {BAC} - \widehat {OAC} = 60^\circ - 40^\circ = 20^\circ \).
Đáp án C
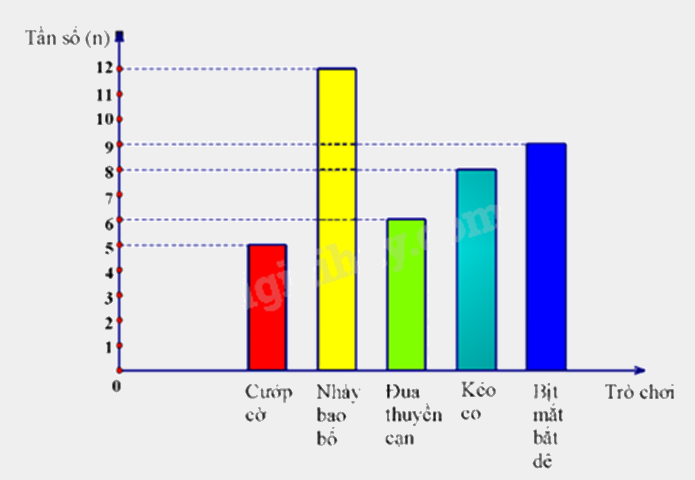
Lớp 9A định tổ chức một trò chơi dân gian khi đi dã ngoại. Lớp trưởng đã yêu cầu mỗi bạn đề xuất một trò chơi bằng cách ghi vào phiếu. Sau khi thu phiếu và tổng hợp kết quả, lớp trưởng thu được biểu đồ cột như sau:
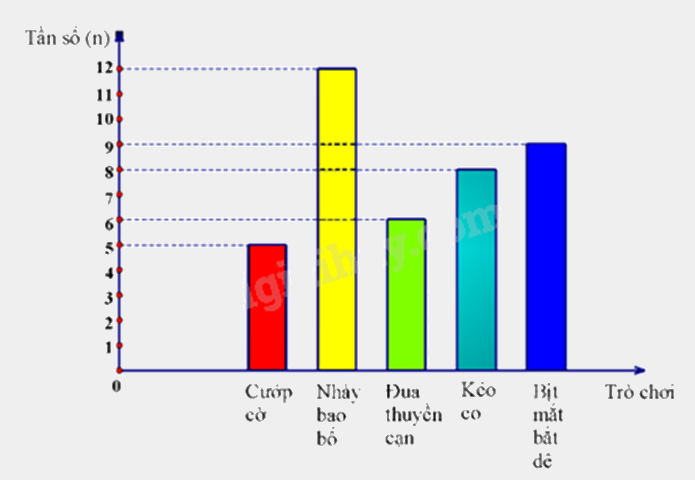
a) Số học sinh lớp 9A là 40 học sinh.
b) Bảng tần số của biểu đồ tần số trên là:

c) Tần số tương đối của trò Nhảy bao bố là 15%.
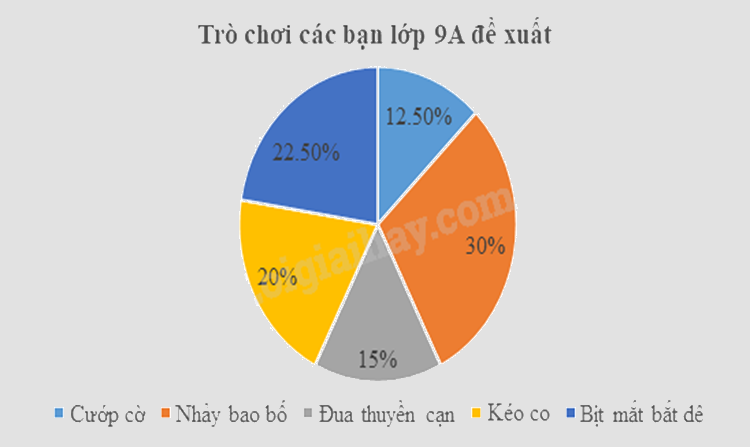
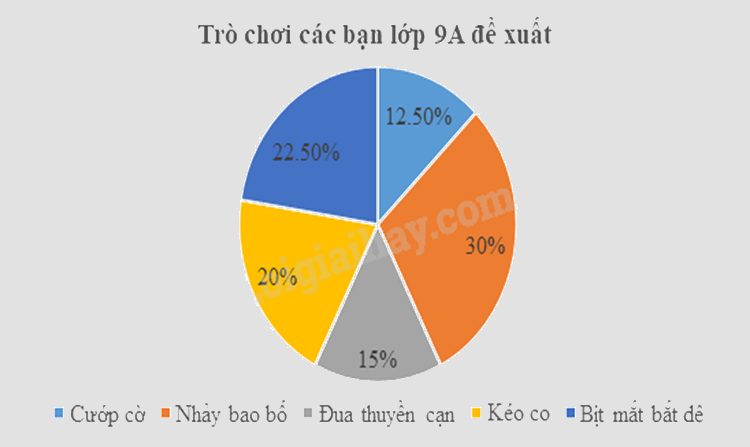
d) Biểu đồ hình quạt biểu diễn tần số tương đối của trò chơi các bạn lớp 9A đề xuất là:
a) Số học sinh lớp 9A là 40 học sinh.
b) Bảng tần số của biểu đồ tần số trên là:

c) Tần số tương đối của trò Nhảy bao bố là 15%.
d) Biểu đồ hình quạt biểu diễn tần số tương đối của trò chơi các bạn lớp 9A đề xuất là:
a) Tính tổng số học sinh cả lớp dựa vào tần số các giá trị.
b) Quan sát biểu đồ tần số để xác định tần số của các giá trị và lập bảng tần số.
c) Tần số tương đối của giá trị bằng tần số của giá trị với tổng tần số.
d) Tính tần số tương đối của các giá trị để vẽ biểu đồ tần số tương đối.
a) Đúng
Lớp 9A có số học sinh là:
5 + 12 + 6 + 8 + 9 = 40 (học sinh)
Vậy a) đúng.
b) Sai
Quan sát biểu đồ, ta lập được bảng tần số:

Vậy b) sai.
c) Sai
Tần số tương đối của trò Nhảy bao bố là: \(\frac{{12}}{{40}}.100\% = 30\% \).
Vậy c) sai.
d) Đúng
Tần số tương đối của trò chơi Cướp cờ; Nhảy bao bố; Đua thuyền cạn; Kéo co; Bịt mắt bắt dê lần lượt là:
\({f_1} = \frac{{5.100}}{{40}}\% = 12,5\% \); \({f_2} = \frac{{12.100}}{{40}} = 30\% \); \({f_3} = \frac{{6.100}}{{40}}\% = 15\% \); \({f_4} = \frac{{8.100}}{{40}}\% = 20\% \); \({f_5} = \frac{{9.100}}{{40}}\% = 22,5\% \).
Ta có bảng tần số tương đối là:

Vậy biểu đồ hình quạt tròn biểu diễn tần số tương đối của trò chơi các bạn lớp 9A đề xuất là:
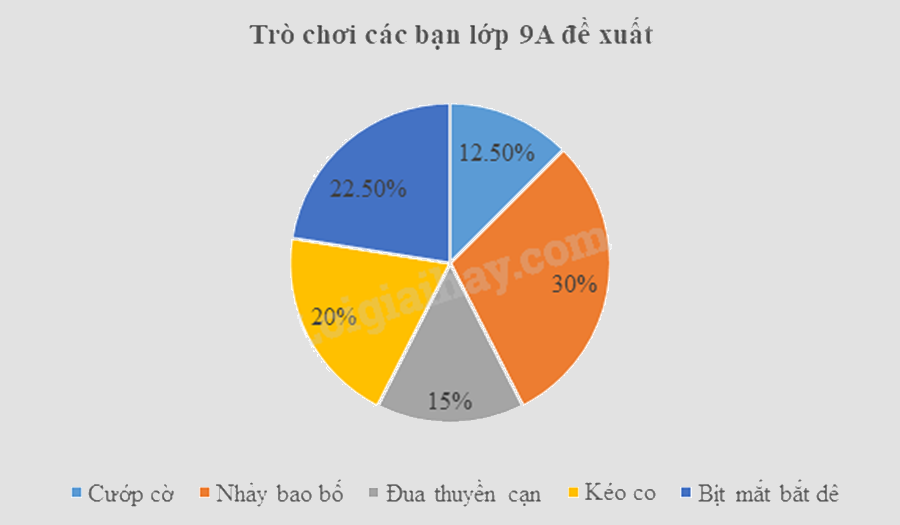
Đáp án: ĐSSĐ
Cho tứ giác ABCD có \(\widehat A = \widehat C = 90^\circ \) nội tiếp đường tròn tâm O.
a) \(\widehat {ABD} = \widehat {ACD}\).
b) Đường tròn \(\left( O \right)\) là đường tròn nội tiếp tam giác ABC.
c) Nếu \(\widehat {ABC} = 80^\circ \) thì \(\widehat {ADC} = 100^\circ \).
d) Bán kính đường tròn ngoại tiếp tam giác ACD bằng \(\frac{{BD}}{2}\).
a) \(\widehat {ABD} = \widehat {ACD}\).
b) Đường tròn \(\left( O \right)\) là đường tròn nội tiếp tam giác ABC.
c) Nếu \(\widehat {ABC} = 80^\circ \) thì \(\widehat {ADC} = 100^\circ \).
d) Bán kính đường tròn ngoại tiếp tam giác ACD bằng \(\frac{{BD}}{2}\).
a) Sử dụng hai góc nội tiếp chắn cùng một cung thì bằng nhau.
b) Đường tròn đi qua ba đỉnh của một tam giác là đường tròn ngoại tiếp tam giác đó.
c) Dựa vào tổng hai góc đối của tứ giác nội tiếp bằng \(180^\circ \).
d) Bán kính đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền.
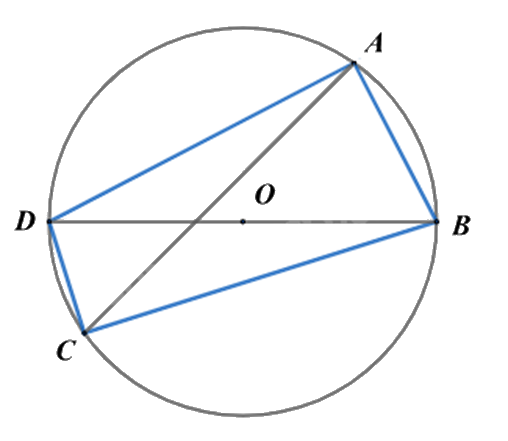
a) Đúng
Vì \(\widehat {ABD}\) và \(\widehat {ACD}\) là hai góc nội tiếp cùng chắn cung AD nên \(\widehat {ABD} = \widehat {ACD}\).
b) Sai
Đường tròn \(\left( O \right)\) đi qua ba đỉnh của tam giác ABC nên là đường tròn ngoại tiếp tam giác ABC.
c) Đúng
Vì tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat {ABC} + \widehat {ADC} = 180^\circ \).
Suy ra \(\widehat {ADC} = 180^\circ - \widehat {ABC} = 180^\circ - 80^\circ = 100^\circ \).
d) Đúng
Xét tam giác ABD nội tiếp đường tròn (O) (vì ABCD là tứ giác nội tiếp) có \(\widehat A = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên tam giác ABD vuông tại A.
Do đó bán kính đường tròn ngoại tiếp tam giác ABD bằng \(\frac{{BD}}{2}\), hay bán kính đường tròn (O) bằng \(\frac{{BD}}{2}\).
Đường tròn \(\left( O \right)\) đi qua ba đỉnh của tam giác ACD nên là đường tròn ngoại tiếp tam giác ACD.
Vậy bán kính đường tròn ngoại tiếp tam giác ACD bằng \(\frac{{BD}}{2}\).
Đáp án: ĐSĐĐ
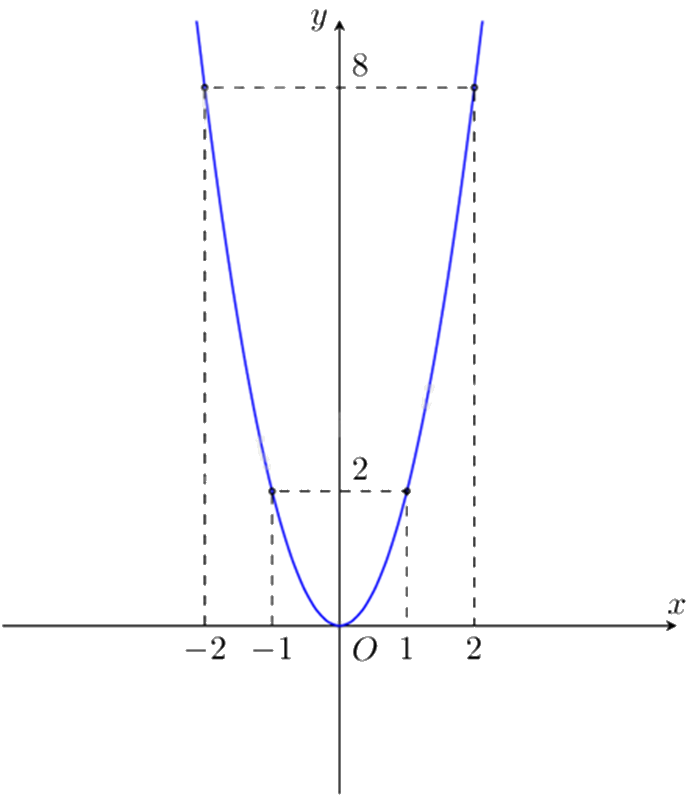
Biết rằng đường cong trong hình sau là một parabol \(y = a{x^2}\). Hệ số \(a\) của hàm số là:
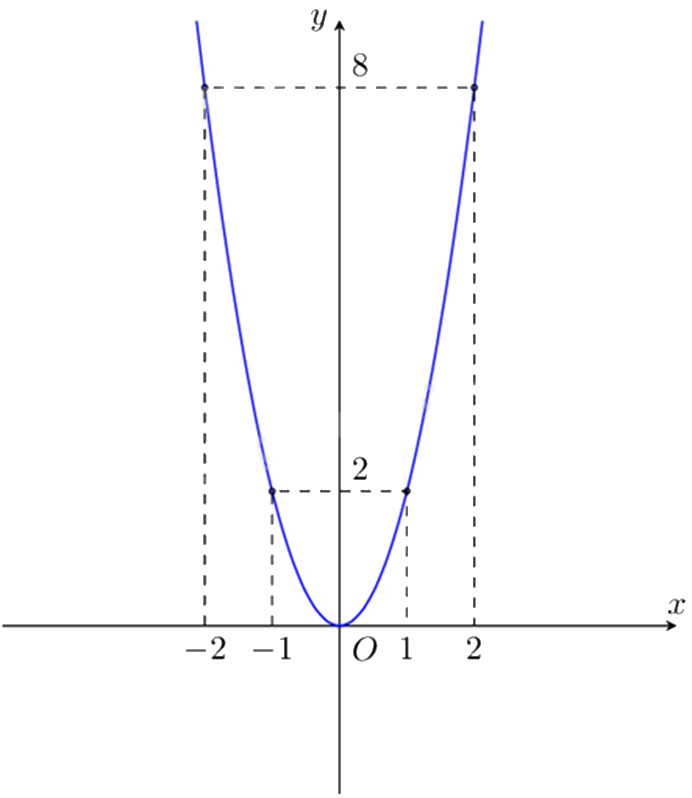
Đáp án:
Đáp án:
Xác định một điểm \(\left( {{x_0};{y_0}} \right)\) thuộc parabol, khi đó thay \(\left( {{x_0};{y_0}} \right)\) vào hàm số \(y = a{x^2}\) thì \({y_0} = a{x_0}^2\) nên \(a = \frac{{{y_0}}}{{{x_0}^2}}\) với \({x_0} \ne 0\).
Từ đồ thị ta có điểm \(\left( {1;2} \right)\) thuộc parabol \(y = a{x^2}\) nên ta có: \(2 = a{.1^2}\)
suy ra \(a = \frac{2}{{{1^2}}} = 2\).
Vậy a = 2.
Đáp án: 2
Biết rằng phương trình \({x^2} - 2\left( {3m + 2} \right)x + 2{m^2} - 3m - 10 = 0\) có một nghiệm bằng \( - 1\). Tìm nghiệm còn lại với m > 0.
Đáp án:
Đáp án:
Thay \(x = - 1\) vào phương trình để tìm m.
Với m vừa tìm được, giải phương trình để tìm nghiệm còn lại.
Thay \(x = - 1\) vào phương trình \({x^2} - 2\left( {3m + 2} \right)x + 2{m^2} - 3m - 10 = 0\), ta được:
\(\begin{array}{l}{\left( { - 1} \right)^2} - 2\left( {3m + 2} \right).\left( { - 1} \right) + 2{m^2} - 3m - 10 = 0\\1 + 6m + 4 + 2{m^2} - 3m - 10 = 0\\2{m^2} + 3m - 5 = 0\\2{m^2} - 2m + 5m - 5 = 0\\2m\left( {m - 1} \right) + 5\left( {m - 1} \right) = 0\\\left( {2m + 5} \right)\left( {m - 1} \right) = 0\end{array}\)
2m + 5 = 0 hoặc m – 1 = 0
2m = -5 hoặc m = 1
\(m = - \frac{5}{2}\) (loại) hoặc m = 1 (TM)
Với m = 1, phương trình trở thành: \({x^2} - 10x - 11 = 0\)
Giải phương trình:
\(\begin{array}{l}{x^2} - 10x - 11 = 0\\{x^2} - 11x + x - 11 = 0\\x\left( {x - 11} \right) + \left( {x - 11} \right) = 0\\\left( {x + 1} \right)\left( {x - 11} \right) = 0\end{array}\)
\(x + 1 = 0\) hoặc \(x - 11 = 0\)
\(x = - 1\) hoặc \(x = 11\)
Vậy nghiệm còn lại của phương trình là \(x = 11\)
Đáp án: 11
Biểu đồ tranh thể hiện số ti vi (TV) bán được qua các năm của 1 siêu thị điện máy như sau:

Tần số tương đối của số ti vi bán được trong năm 2022 là: …. (không điền dấu %)
Đáp án:
Đáp án:
Từ biểu đồ tranh, tính tổng số ti vi bán được từ năm 2018 đến năm 2022 và số ti vi bán được trong năm 2022.
Tần số tương đối của số ti vi bán được trong năm 2022 bằng tỉ số phần trăm giữa số ti vi bán được năm 2022 với tổng số ti vi bán được.
Từ biểu đồ tranh, ta thấy số ti vi bán được của các năm 2018; 2019; 2020; 2021; 2022 lần lượt là: 500; 600; 250; 300; 350.
Tổng số ti vi bán được từ năm 2018 đến 2022 là: 500 + 600 + 250 + 300 + 350 = 2000 (chiếc)
Tần số tương đối của số ti vi bán được trong năm 2022 là: \(\frac{{350}}{{2000}}.100\% = 17,5\% \)
Đáp án: 17,5
Cho tứ giác ABCD nội tiếp đường tròn (O;R) có AB = BC = R. Số đo \(\widehat {ABC}\) bằng bao nhiêu độ? (không cần ghi độ)
Đáp án:
Đáp án:
Chứng minh tam giác BCO, BAO đều nên tính được số đo góc BOC, BOA.
Ta tính được số đo góc AOC, từ đó suy ra số đo góc ADC (liên hệ giữa góc ở tâm và góc nội tiếp cùng một cung).
Kết hợp với tính chất hai góc đối của tứ giác nội tiếp, ta có số đo góc ABC.
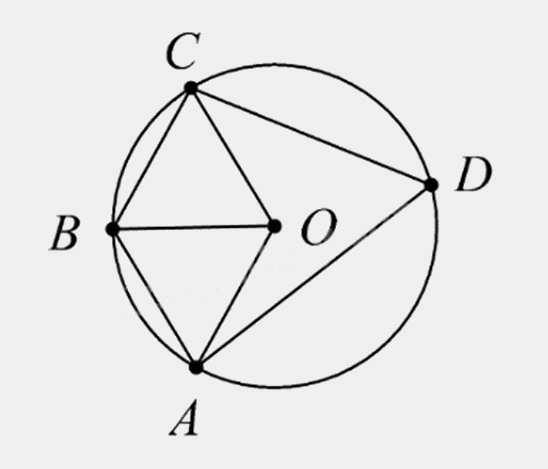
Xét tam giác BCO có: BC = CO = BO = R nên tam giác BCO đều, do đó \(\widehat {BOC} = 60^\circ \).
Xét tam giác BAO có: BA = AO = BO = R nên tam giác BAO đều, do đó \(\widehat {BAC} = 60^\circ \).
\(\widehat {AOC} = \widehat {AOB} + \widehat {BOC} = 60^\circ + 60^\circ = 120^\circ \)
Mà \(\widehat {AOC}\) là góc ở tâm chắn cung AC, \(\widehat {ADC}\) là góc nội tiếp chắn cung AC nên \(\widehat {ADC} = \frac{1}{2}\widehat {AOC} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì tứ giác ABCD nội tiếp đường tròn nên \(\widehat {ABC} + \widehat {ADC} = 180^\circ \)
Suy ra \(\widehat {ABC} = 180^\circ - \widehat {ADC} = 180^\circ - 60^\circ = 120^\circ \)
Đáp án: 120
Một ca nô chạy xuôi dòng quãng đường AB dài 80km, sau đó ngược dòng đến địa điểm C cách B là 72km. Thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút. Tính vận tốc thực của ca nô, biết vận tốc dòng nước là 4km/h.
Gọi vận tốc thực của ca nô là \(x\left( {x > 0,km/h} \right)\)
Biểu diện vận tốc xuôi dòng, vận tốc ngược dòng, thời gian xuôi dòng, thời gian ngược dòng của ca nô.
Từ đó lập phương trình bậc hai ẩn \(x\) biểu diễn hiệu thời gian xuôi dòng và ngược dòng của ca nô.
Giải phương trình, kết hợp điều kiện ban đầu của \(x\) để xác định.
Gọi vận tốc thực của ca nô là \(x\left( {x > 0,km/h} \right)\)
Khi đó vận tốc xuôi dòng của ca nô là: \(x + 4\left( {km/h} \right)\), thời gian xuôi dòng của ca nô là: \(\frac{{80}}{{x + 4}}\) (h)
Vận tốc ngược dòng của ca nô là: \(x - 4\left( {km/h} \right)\), thời gian ngược dòng của ca nô là: \(\frac{{72}}{{x - 4}}\) (h)
Đổi 15 phút \( = \frac{1}{4}\)h.
Vì thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút nên ta có phương trình:
\(\frac{{72}}{{x - 4}} - \frac{{80}}{{x + 4}} = \frac{1}{4}\)
\(\begin{array}{l}\frac{{288\left( {x + 4} \right) - 320\left( {x - 4} \right)}}{{4\left( {x - 4} \right)\left( {x + 4} \right)}} = \frac{{{x^2} - 16}}{{4\left( {x - 4} \right)\left( {x + 4} \right)}}\\288x + 1152 - 320x + 1280 = {x^2} - 16\\{x^2} + 32x - 2448 = 0\end{array}\)
Ta có:
\(\Delta ' = {16^2} - \left( { - 2448} \right) = 2704\) suy ra \(\sqrt {\Delta '} = 52\)
Khi đó phương trình có hai nghiệm là \({x_1} = - 16 + 52 = 36\) (thỏa mãn); \({x_2} = - 16 - 52 = - 68\) (không thỏa mãn)
Vậy vận tốc thực của ca nô là 36km/h.
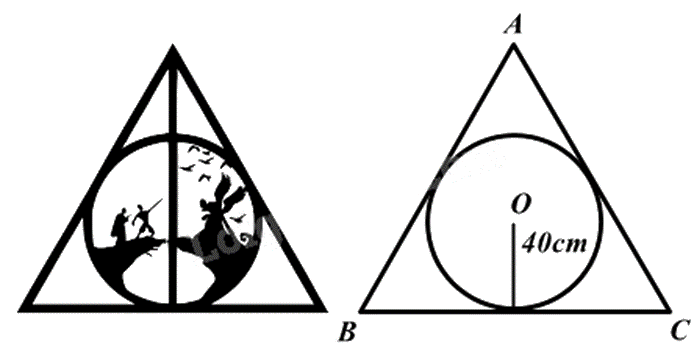
Một bức ảnh hình tròn có bán kính 40 cm, người ta làm một khung gỗ hình tam giác đều bao bên ngoài bức ảnh sao cho bức ảnh hình tròn tiếp xúc với các cạnh của khung gỗ. Tính độ dài cạnh khung gỗ (làm tròn đến số thập phân thứ nhất).
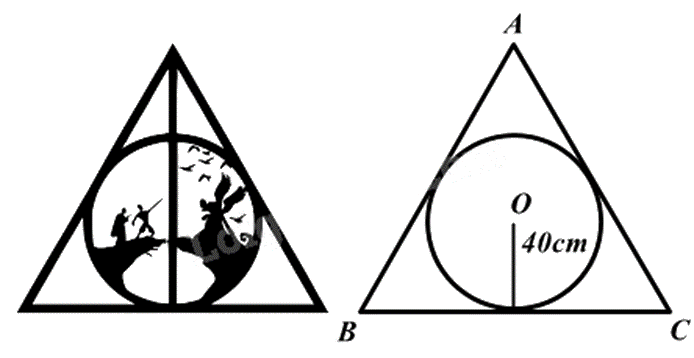
Tính độ dài cạnh khung gỗ chính là tính cạnh của tam giác đều ngoại tiếp đường tròn.
Từ công thức tính bán kính đường tròn nội tiếp tam giác đều cạnh a bằng \(\frac{{\sqrt 3 }}{3}a\), ta tính cạnh a theo bán kính đường tròn nội tiếp.
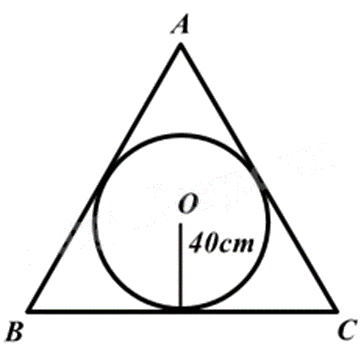
Vì khung ảnh hình tròn tiếp xúc với các cạnh của tam giác đều nên ta có đường tròn nội tiếp tam giác đều.
Vì bán kính đường tròn nội tiếp tam giác đều là \(R = \frac{{a\sqrt 3 }}{6}\) với a là độ dài cạnh tam giác đều nên ta có:
\(\begin{array}{l}40 = \frac{{a\sqrt 3 }}{6}\\a\sqrt 3 = 240\\a = \frac{{240}}{{\sqrt 3 }} \approx 138,6\left( {cm} \right)\end{array}\)
Vậy độ dài cạnh khung gỗ khoảng 138,6cm.
Biết rằng phương trình bậc hai \({x^2} + x + m = 0\) có hai nghiệm là \({x_1} = \frac{{\sqrt 2 + 1}}{{\sqrt 2 - 1}}\) và \({x_2}\). Tính giá trị của biểu thức \(A = 2024{x_1} + 2025{x_2}\)
Trục căn thức nghiệm \({x_1}\): \(\frac{C}{{\sqrt A + B}} = \frac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}\)
Sử dụng định lí Viète để tìm \({x_2}\): \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}.{x_2} = \frac{c}{a}\end{array} \right.\)
Thay \({x_1};{x_2}\) vào A.
Ta có: \({x_1} = \frac{{\sqrt 2 + 1}}{{\sqrt 2 - 1}} = \frac{{{{\left( {\sqrt 2 + 1} \right)}^2}}}{{\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}} = \frac{{2 + 2\sqrt 2 + 1}}{{2 - 1}} = 3 + 2\sqrt 2 \).
Áp dụng định lí Viète vào phương trình \({x^2} + x + m = 0\), ta có:
\({x_1} + {x_2} = \frac{{ - b}}{a} = - 1\)
\(\begin{array}{l}3 + 2\sqrt 2 + {x_2} = - 1\\{x_2} = - 1 - 3 - 2\sqrt 2 \\{x_2} = - 4 - 2\sqrt 2 \end{array}\)
Ta có:
\(\begin{array}{l}A = 2024{x_1} + 2025{x_2}\\ = 2024\left( {3 + 2\sqrt 2 } \right) + 2025\left( { - 4 - 2\sqrt 2 } \right)\\ = 6072 + 4048\sqrt 2 - 8100 - 4050\sqrt 2 \\ = - 2028 - 2\sqrt 2 \end{array}\)
Vậy \(A = - 2028 - 2\sqrt 2 \).
Kỳ thi giữa học kỳ 2 Toán 9 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh. Việc làm quen với cấu trúc đề thi và các dạng bài tập thường gặp là vô cùng cần thiết. Đề thi giữa kì 2 Toán 9 - Đề số 3 mà giaitoan.edu.vn cung cấp là một tài liệu ôn tập lý tưởng, giúp học sinh tự tin bước vào kỳ thi.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi:
Để giải hệ phương trình bậc hai, học sinh cần nắm vững các phương pháp như phương pháp thế, phương pháp cộng đại số, và phương pháp đặt ẩn phụ. Việc kiểm tra lại nghiệm sau khi giải là rất quan trọng để đảm bảo tính chính xác.
Hàm số bậc nhất có dạng y = ax + b. Để hiểu rõ về hàm số này, học sinh cần biết cách xác định hệ số a, b, vẽ đồ thị hàm số, và tìm giao điểm của đồ thị với các trục tọa độ.
Phương trình bậc hai một ẩn có dạng ax2 + bx + c = 0. Học sinh có thể giải phương trình này bằng công thức nghiệm tổng quát hoặc bằng cách phân tích thành nhân tử.
Trong phần hình học, học sinh cần nắm vững các định lý về đường tròn, tam giác đồng dạng, và tam giác vuông. Việc vẽ hình chính xác và trình bày lời giải logic là yếu tố quan trọng để đạt điểm cao.
Ngoài Đề thi giữa kì 2 Toán 9 - Đề số 3, giaitoan.edu.vn còn cung cấp nhiều đề thi khác với các mức độ khó khác nhau. Việc luyện tập thường xuyên với nhiều đề thi sẽ giúp học sinh làm quen với các dạng bài tập và nâng cao kỹ năng giải toán.
Học toán online mang lại nhiều lợi ích cho học sinh, bao gồm:
Đề thi giữa kì 2 Toán 9 - Đề số 3 của giaitoan.edu.vn là một tài liệu ôn tập hữu ích, giúp học sinh chuẩn bị tốt nhất cho kỳ thi. Hãy tận dụng tối đa tài liệu này và luyện tập thường xuyên để đạt kết quả cao nhất!