Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 9 - Đề số 2, một công cụ hữu ích giúp các em học sinh ôn luyện và củng cố kiến thức đã học. Đề thi được biên soạn theo chuẩn chương trình Toán 9, bao gồm các dạng bài tập thường gặp trong đề thi chính thức.
Với đáp án chi tiết đi kèm, các em có thể tự đánh giá năng lực của mình và tìm ra những điểm cần cải thiện. Hãy cùng Giaitoan.edu.vn chinh phục kỳ thi giữa kì 2 Toán 9 một cách tự tin nhất!
Điểm nào sau đây thuộc đồ thị hàm số \(y = 3{x^2}\)?
\(\left( {1;3} \right)\).
\(\left( {3;12} \right)\).
\(\left( {2; - 4} \right)\).
\(\left( { - 1; - 3} \right)\).
Phương trình \({x^2} - 7x + 12 = 0\) có tổng hai nghiệm là:
-4.
7.
-3.
-7.
Gọi S và P lần lượt là tổng và tích hai nghiệm của phương trình \({x^2} - 7x + 11 = 0\). Khi đó \(S + P\) bằng:
18.
7.
11.
4.
Bảng dưới đây thể hiện vé xuất ra trong 1 ngày của VinWonders Cửa Hội tại Cửa Lò. Bảng thống kê này được gọi là loại bảng thống kê nào?
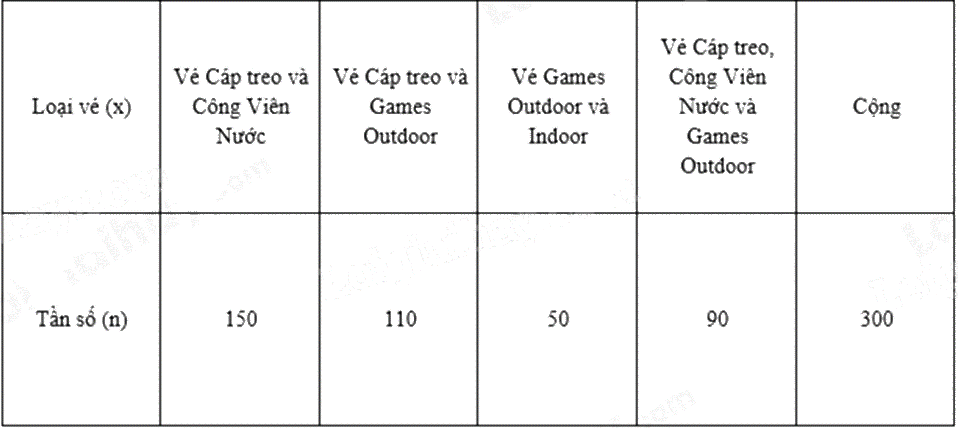
Bảng tần số.
Bảng tần số tương đối.
Bảng thống kê.
Bảng tần suất.
Có bao nhiêu tứ giác nội tiếp trong hình sau:
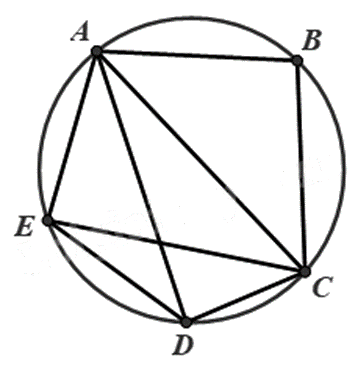
1.
2.
3.
4.
Cho tam giác ABC, gọi G là giao điểm ba đường phân giác của tam giác đó. Từ G kẻ GH, GI, GK lần lượt vuông góc với AB, AC, BC (\(H \in AB,I \in AC,K \in BC\)). So sánh độ dài GH, GI, GK.
GH < GI < GK.
GH = GI = GK.
GH > GI > GK.
GH = GI > GK.
Kết quả điểm kiểm tra môn Toán cuối học kì 1 của học sinh lớp 9A được biểu diễn bằng biểu đồ cột dưới đây.
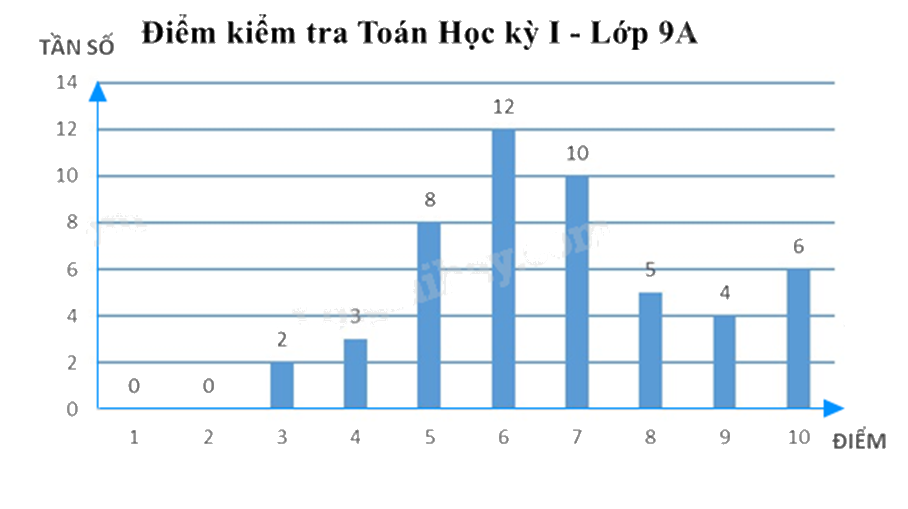
a) Bảng tần số biểu thị mẫu dữ liệu trong biểu đồ cột là:

b) Tổng số học sinh lớp 9A tham gia làm bài kiểm tra môn toán là 48.
c) Tần số tương đối của số học sinh đạt 8 điểm là 10%.
d) Số học sinh đạt điểm giỏi (điểm 8; 9; 10) bằng 50% số học sinh đạt điểm trung bình và khá (điểm 5; 6; 7).
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O), đường cao BD của tam giác cắt (O) tại điểm thứ hai là \(E\) (\(E\) khác \(B\)), vẽ EF vuông góc với BC (\(F\) thuộc BC).
a) DFCE là tứ giác nội tiếp.
b) Số đo của \(\widehat {ABD} = \widehat {ECF}\).
c) Gọi I là trung điểm của EC thì EC vuông góc OI.
d) \(BD.BE = BF.BC\).
Hệ số \(a\) của hàm số \(y = a{x^2}\) đi qua điểm \(A\left( {1;3} \right)\) là …
Đáp án:
Cho phương trình bậc hai \({x^2} - 5x + m = 0\) (\(m\) là tham số). Tìm m để phương trình có hai nghiệm phân biệt sao cho tổng bình phương của hai nghiệm bằng 13.
Đáp án:
Một cửa hàng khảo sát mức độ hài lòng của khách hàng thông qua việc khách hàng đánh giá từ ★ đến ★★★★★. Kết quả được thống kê bởi bảng số liệu sau:

Tần số tương đối của mức độ ★★★★★ là …
(không điền dấu %)
Đáp án:
Cho tam giác ABC vuông tại A có AB = 5cm, AC = 7cm. Tính bán kính đường tròn đi qua 3 điểm A, B, C (làm tròn đơn vị đến hàng phần mười của cm).
Đáp án:
Bác An vay 200 triệu đồng của ngân hàng để kinh doanh trong thời hạn 1 năm. Lẽ ra, cuối năm bác phải trả cả vốn lẫn lãi. Tuy nhiên bác được ngân hàng cho kéo dài thời hạn thêm năm nữa, số lãi của năm đầu được gộp vào vốn để tính lãi năm sau và lãi suất như cũ. Hết 2 năm, bác phải trả tất cả 242 triệu đồng. Hỏi lãi suất cho vay của ngân hàng là bao nhiêu phần trăm?
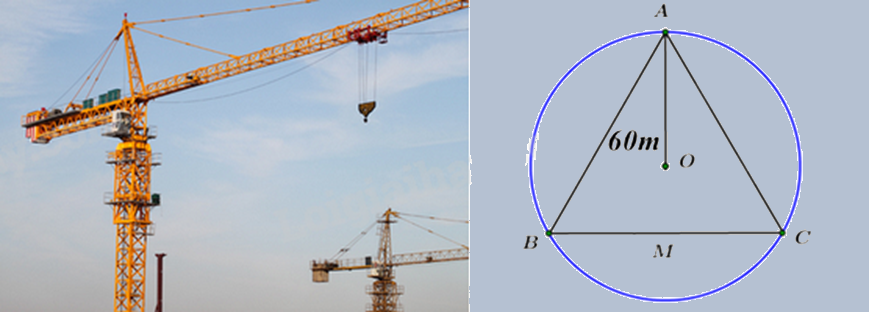
Cẩu tháp là một loại thiết bị nâng hạ được thiết kế để nâng, hạ và di chuyền vật liệu xây dựng tại các công trường, đặc biệt là trong xây dựng các công trình cao tầng. Có khả năng hoạt động ở độ cao lớn và với tải trọng nặng, cẩu tháp được lắp đặt cố định hoặc có thể di chuyển trên ray tại công trường, giúp tăng hiệu quả công việc và đảm bảo an toàn lao động. Ba vị trí A, B, C của một công trình là ba đỉnh của một tam giác đều. Trên công trình, người ta muốn đặt cẩu tháp tại điểm O sao cho bán kính quay của cẩu tháp đến các vị trí điểm A, B, C bằng nhau và bằng 60 m (hình bên). Tính khoảng cách từ A đến B (làm tròn đến số hàng đơn vị).
Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \({x^2} - 3x - 7 = 0\). Không giải phương trình, hãy tính giá trị của biểu thức \(N = \left( {3{x_1} + {x_2}} \right)\left( {3{x_2} + {x_1}} \right)\).
Điểm nào sau đây thuộc đồ thị hàm số \(y = 3{x^2}\)?
\(\left( {1;3} \right)\).
\(\left( {3;12} \right)\).
\(\left( {2; - 4} \right)\).
\(\left( { - 1; - 3} \right)\).
Đáp án : A
Thay từng điểm xem điểm \(\left( {{x_0};{y_0}} \right)\) xem điểm nào thỏa mãn \({y_0} = 3{x_0}^2\).
Vì hàm số \(y = 3{x^2}\) nên các điểm thuộc đồ thị hàm số có tung độ dương, loại đáp án C, D.
Thay \(x = 1\) vào hàm số, ta được: \(y = {3.1^2} = 3\) nên điểm \(\left( {1;3} \right)\) thuộc đồ thị hàm số.
Thay \(x = 3\) vào hàm số, ta được: \(y = {3.3^2} = 27 \ne 12\) nên điểm \(\left( {3;12} \right)\) không thuộc đồ thị hàm số.
Đáp án A
Phương trình \({x^2} - 7x + 12 = 0\) có tổng hai nghiệm là:
-4.
7.
-3.
-7.
Đáp án : B
Xác định \(\Delta = {b^2} - 4ac\) để xác định nghiệm của phương trình.
(Ta cũng có thể sử dụng máy tính cầm tay để xác định nghiệm)
Phương trình \({x^2} - 7x + 12 = 0\) có hai nghiệm là \({x_1} = 4;{x_2} = 3\) nên tổng hai nghiệm là \(4 + 3 = 7\).
Đáp án B
Gọi S và P lần lượt là tổng và tích hai nghiệm của phương trình \({x^2} - 7x + 11 = 0\). Khi đó \(S + P\) bằng:
18.
7.
11.
4.
Đáp án : A
Sử dụng định lí Viète để tìm S, P:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},{x_2}\) thì \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - b}}{a}\\P = {x_1}.{x_2} = \frac{c}{a}\end{array} \right.\).
Ta có: \(\Delta = {\left( { - 7} \right)^2} - 4.11 = 49 - 44 = 5 > 0\) nên phương trình có hai nghiệm phân biệt.
Áp dụng định lí Viète, ta được: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - b}}{a} = 7\\P = {x_1}.{x_2} = \frac{c}{a} = 11\end{array} \right.\)
Vậy S + P = 7 + 11 = 18.
Đáp án A
Bảng dưới đây thể hiện vé xuất ra trong 1 ngày của VinWonders Cửa Hội tại Cửa Lò. Bảng thống kê này được gọi là loại bảng thống kê nào?
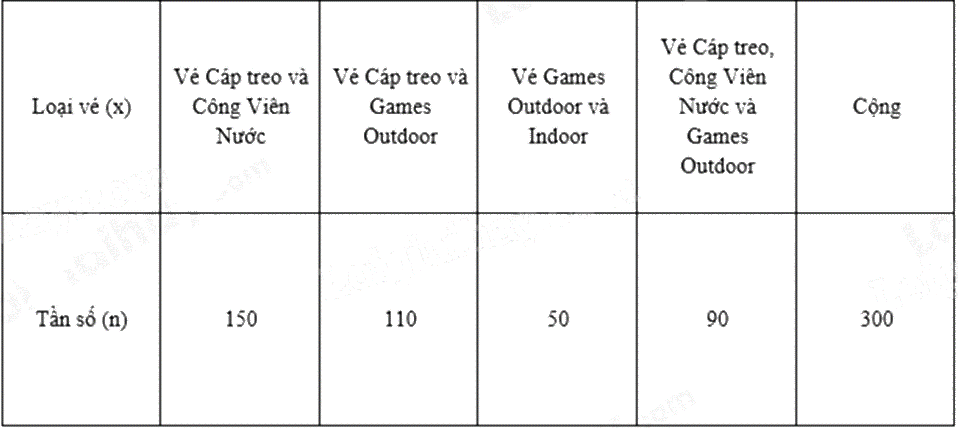
Bảng tần số.
Bảng tần số tương đối.
Bảng thống kê.
Bảng tần suất.
Đáp án : A
Dựa vào khái niệm các loại bảng đã học.
Bảng trên là bảng tần số.
Đáp án A
Có bao nhiêu tứ giác nội tiếp trong hình sau:
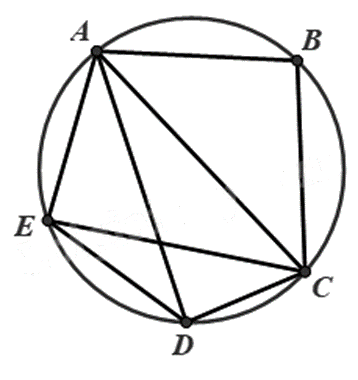
1.
2.
3.
4.
Đáp án : C
Quan sát hình vẽ để xác định các tứ giác nội tiếp.
Hình trên có 3 tứ giác nội tiếp, đó là: ABCD, ABCE, ACDE.
Đáp án C
Cho tam giác ABC, gọi G là giao điểm ba đường phân giác của tam giác đó. Từ G kẻ GH, GI, GK lần lượt vuông góc với AB, AC, BC (\(H \in AB,I \in AC,K \in BC\)). So sánh độ dài GH, GI, GK.
GH < GI < GK.
GH = GI = GK.
GH > GI > GK.
GH = GI > GK.
Đáp án : B
Giao điểm của ba đường phân giác của tam giác chính là tâm đường tròn nội tiếp tam giác và GH, GI, GK chính là giao của đường tròn với ba cạnh của tam giác.
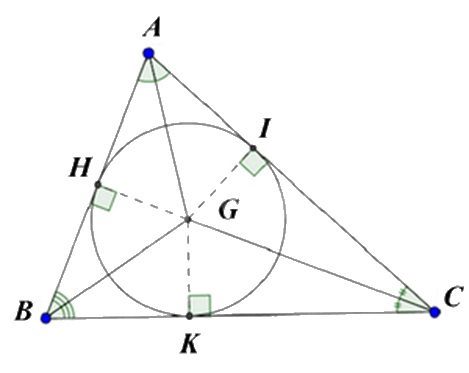
Vì G là giao điểm ba đường phân giác của tam giác nên G là tâm đường tròn nội tiếp tam giác.
GH, GI, GK lần lượt vuông góc với AB, AC, BC tại H, I, K nên GH = GI = GK = bán kính đường tròn nội tiếp tam giác ABC.
Đáp án B
Kết quả điểm kiểm tra môn Toán cuối học kì 1 của học sinh lớp 9A được biểu diễn bằng biểu đồ cột dưới đây.
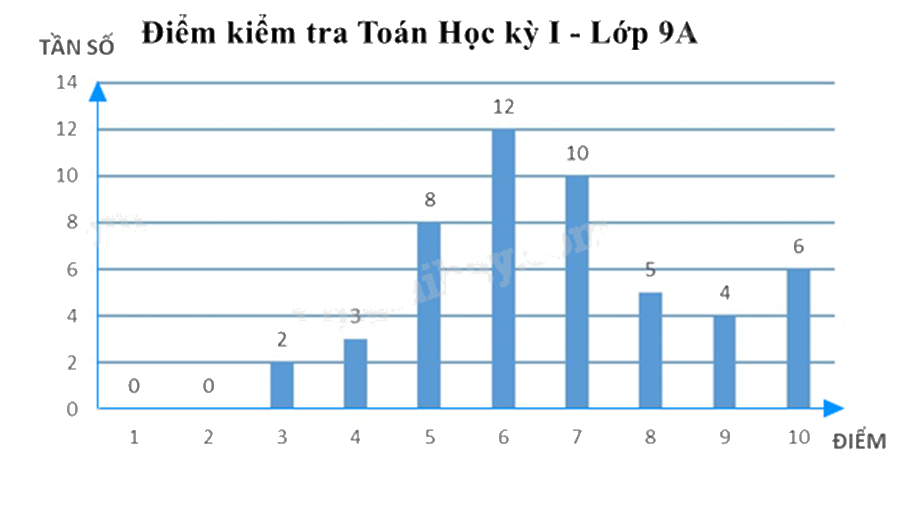
a) Bảng tần số biểu thị mẫu dữ liệu trong biểu đồ cột là:

b) Tổng số học sinh lớp 9A tham gia làm bài kiểm tra môn toán là 48.
c) Tần số tương đối của số học sinh đạt 8 điểm là 10%.
d) Số học sinh đạt điểm giỏi (điểm 8; 9; 10) bằng 50% số học sinh đạt điểm trung bình và khá (điểm 5; 6; 7).
a) Bảng tần số biểu thị mẫu dữ liệu trong biểu đồ cột là:

b) Tổng số học sinh lớp 9A tham gia làm bài kiểm tra môn toán là 48.
c) Tần số tương đối của số học sinh đạt 8 điểm là 10%.
d) Số học sinh đạt điểm giỏi (điểm 8; 9; 10) bằng 50% số học sinh đạt điểm trung bình và khá (điểm 5; 6; 7).
a) Quan sát biểu đồ tần số để xác định tần số của các giá trị và lập bảng tần số.
b) Tổng số học sinh tham gia làm bài kiểm tra bằng tổng tần số của các điểm.
c) Tần số tương đối của giá trị bằng tần số của giá trị với tổng tần số.
d) Xác định số học sinh đạt điểm giỏi, điểm trung bình và khá.
Tính tỉ số phần trăm giữa số học sinh đạt điểm giỏi với số học sinh đạt điểm trung bình và khá.
a) Đúng
Bảng tần số biểu thị mẫu dữ liệu trong biểu đồ cột là:
Vậy a) đúng.
b) Sai
Tổng số các tần số trong bảng là:
\(2 + 3 + 8 + 12 + 10 + 5 + 4 + 6 = 50\) (học sinh)
Vậy b) sai.
c) Đúng
Tần số tương đối của số học sinh đạt điểm 8 là: \(\frac{5}{{50}}.100\% = 10\% \).
Vậy c) đúng.
d) Đúng
Tổng số học sinh đạt điểm giỏi (điểm 8; 9; 10) là: \(5 + 4 + 6 = 15\) (học sinh)
Tổng số HS đạt điểm trung bình và khá (điểm 5; 6; 7) là: \(8 + 12 + 10 = 30\) (học sinh)
Vậy số học sinh đạt điểm giỏi (điểm 8; 9; 10) bằng:
\(\frac{{15}}{{30}} = 50\% \) số học sinh đạt điểm trung bình và khá (điểm 5; 6; 7).
Vậy d) đúng.
Đáp án ĐSĐĐ
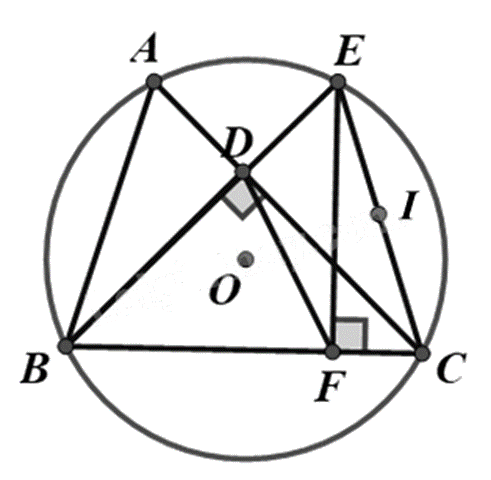
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O), đường cao BD của tam giác cắt (O) tại điểm thứ hai là \(E\) (\(E\) khác \(B\)), vẽ EF vuông góc với BC (\(F\) thuộc BC).
a) DFCE là tứ giác nội tiếp.
b) Số đo của \(\widehat {ABD} = \widehat {ECF}\).
c) Gọi I là trung điểm của EC thì EC vuông góc OI.
d) \(BD.BE = BF.BC\).
a) DFCE là tứ giác nội tiếp.
b) Số đo của \(\widehat {ABD} = \widehat {ECF}\).
c) Gọi I là trung điểm của EC thì EC vuông góc OI.
d) \(BD.BE = BF.BC\).
a) Chứng minh tam giác DEC và tam giác EFC cùng nội tiếp một đường tròn nên DFCE là tứ giác nội tiếp.
b) Xác định cung chắn hai góc trên để kiểm tra.
c) Dựa vào tính chất đường trung trực của đoạn thẳng để kiểm tra.
d) Dựa vào 2 tam giác đồng dạng tam giác \(BDC\) và tam giác \(BFE\) suy tỉ số và dựa tính chất tỉ lệ thức.
a) Đúng
Xét tam giác DEC có \(\widehat {CDE} = 90^\circ \) nên nội tiếp đường tròn đường kính EC.
Xét tam giác EFC có \(\widehat {EFC} = 90^\circ \) nên nội tiếp đường tròn đường kính EC.
Do đó 4 điểm D, F, C, E cùng thuộc đường tròn đường kính EC hay DFCE là tứ giác nội tiếp.
b) Sai
Ta có: \(\widehat {ABD}\) hay \(\widehat {ABE}\) chắn cung AE, \(\widehat {ECF}\) hay \(\widehat {ECB}\) chắn cung BE.
Mà cung BE và cung AE không bằng nhau nên \(\widehat {ABD} \ne \widehat {ECF}\).
c) Đúng
Vì E, C thuộc đường tròn (O) nên OE = OC hay O cách đều hai điểm E, C.
Vì I là trung điểm của EC nên IE = IC hay I cách đều hai điểm E, C.
Suy ra OI là đường trung trực của EC nên \(EC \bot OI\).
d) Đúng
Xét tam giác BDC và tam giác BFE có:
\(\widehat {BDC} = \widehat {BFE}\left( { = 90^\circ } \right)\)
\(\widehat B\) chung
Suy ra $\Delta BDC\backsim \Delta BFE\left( g.g \right)$
Do đó \(\frac{{BD}}{{BC}} = \frac{{BF}}{{BE}}\) nên \(BD.BE = BF.BC\).
Đáp án: ĐSĐĐ
Hệ số \(a\) của hàm số \(y = a{x^2}\) đi qua điểm \(A\left( {1;3} \right)\) là …
Đáp án:
Đáp án:
Nếu hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(\left( {{x_0};{y_0}} \right)\) thì \({y_0} = a{x_0}^2\) nên \(a = \frac{{{y_0}}}{{{x_0}^2}}\) với \({x_0} \ne 0\).
Vì hàm số \(y = a{x^2}\) đi qua điểm \(A\left( {1;3} \right)\) nên \(3 = a{.1^2}\), suy ra:
\(a = \frac{3}{{{1^2}}} = 3\).
Vậy a = 3.
Đáp án: 3
Cho phương trình bậc hai \({x^2} - 5x + m = 0\) (\(m\) là tham số). Tìm m để phương trình có hai nghiệm phân biệt sao cho tổng bình phương của hai nghiệm bằng 13.
Đáp án:
Đáp án:
- Sử dụng công thức nghiệm Delta để tìm điều kiện của m sao cho phương trình có hai nghiệm phân biệt.
\(\Delta = {b^2} - 4ac > 0\) thì phương trình có hai nghiệm phân biệt.
- Biến đổi tổng bình phương của hai nghiệm sao cho xuất hiện tổng/tích của hai nghiệm để sử dụng định li Viète để tìm m.
Định lí Viète: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}.{x_2} = \frac{c}{a}\end{array} \right.\).
Xét phương trình \({x^2} - 5x + m = 0\) (\(m\) là tham số) có \(a = 1;b = - 5;c = m\) nên ta có:
\(\Delta = {\left( { - 5} \right)^2} - 4.1.m = 25 - 4m\).
Để phương trình có hai nghiệm phân biệt thì \(\Delta > 0\) nên ta có:
\(\begin{array}{l}25 - 4m > 0\\ - 4m > - 25\\m < \frac{{25}}{4}\end{array}\)
Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 5\\{x_1}.{x_2} = \frac{c}{a} = m\end{array} \right.\)
Mặt khác, \({x_1}^2 + {x_2}^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\).
Vì tổng bình phương của hai nghiệm bằng 13 nên ta có:
\(\begin{array}{l}{5^2} - 2.m = 13\\2m = 25 - 13\\2m = 12\\m = 6\left( {TM} \right)\end{array}\)
Vậy với \(m = 6\) thì phương trình có hai nghiệm phân biệt thỏa mãn tổng các bình phương của hai nghiệm bằng 13.
Đáp án: 6
Một cửa hàng khảo sát mức độ hài lòng của khách hàng thông qua việc khách hàng đánh giá từ ★ đến ★★★★★. Kết quả được thống kê bởi bảng số liệu sau:

Tần số tương đối của mức độ ★★★★★ là …
(không điền dấu %)
Đáp án:
Đáp án:
Tần số tương đối của một giá trị bằng tỉ số phần trăm giữa tần số của giá trị đó với tổng tần số.
Tần số tương đối của mức độ ★★★★★ là: \(\frac{{312}}{{500}}.100\% = 62,4\% \).
Đáp án: 62,4
Cho tam giác ABC vuông tại A có AB = 5cm, AC = 7cm. Tính bán kính đường tròn đi qua 3 điểm A, B, C (làm tròn đơn vị đến hàng phần mười của cm).
Đáp án:
Đáp án:
Áp dụng định lí Pythagore vào tam giác vuông để tính BC.
Đường tròn ngoại tiếp tam giác vuông có bán kính bằng một nửa cạnh huyền của tam giác vuông.
Áp dụng định lí Pythagore vào tam giác ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {7^2} = 74\)
Suy ra \(BC = \sqrt {74} \) (cm).
Đường tròn đi qua 3 điểm A, B, C là đường tròn ngoại tiếp tam giác ABC.
Vì tam giác ABC vuông tại A nên đường tròn ngoại tiếp tam giác ABC có đường kính là cạnh huyền BC.
Bán kính đường tròn ngoại tiếp tam giác ABC là: \(\frac{{\sqrt {74} }}{2} \approx 4,3\) (cm).
Đáp án: 4,3
Bác An vay 200 triệu đồng của ngân hàng để kinh doanh trong thời hạn 1 năm. Lẽ ra, cuối năm bác phải trả cả vốn lẫn lãi. Tuy nhiên bác được ngân hàng cho kéo dài thời hạn thêm năm nữa, số lãi của năm đầu được gộp vào vốn để tính lãi năm sau và lãi suất như cũ. Hết 2 năm, bác phải trả tất cả 242 triệu đồng. Hỏi lãi suất cho vay của ngân hàng là bao nhiêu phần trăm?
Gọi lãi suất cho vay của ngân hàng là \(x\left( \% \right),x > 0\).
Lập các biểu thức biểu diễn số tiền lãi sau 1 năm, số tiền lãi sau 2 năm và số tiền bác An phải trả sau hai năm
Từ đó lập phương trình bậc hai ẩn \(x\) biểu diễn số tiền bác phải trả.
Giải phương trình, kết hợp điều kiện ban đầu của \(x\) để xác định.
Gọi lãi suất cho vay của ngân hàng là \(x\left( \% \right),x > 0\).
Số tiền lãi sau 1 năm là:
\(200.x\% = 2x\) (triệu đồng)
Sau 1 năm, số tiền cả gốc lẫn lãi là:
\(200 + 2x\) (triệu đồng)
Số tiền lãi sau 2 năm là:
\(\left( {200 + 2x} \right).x\% = 2x + 0,02{x^2}\) (triệu đồng)
Số tiền bác An phải trả sau 2 năm là:
\(200 + 2x + 2x + 0,02{x^2} = 0,02{x^2} + 4x + 200\) (triệu đồng)
Vì sau 2 năm, bác phải trả tất cả 242 triệu đồng nên ta có phương trình:
\(\begin{array}{l}0,02{x^2} + 4x + 200 = 242\\0,02{x^2} + 4x - 42 = 0\\{x^2} + 200x - 2100 = 0\end{array}\)
Giải phương trình, ta được: \({x_1} = 10\) (TM), \({x_2} = - 210\) (không thỏa mãn)
Vậy lãi suất cho vay của ngân hàng là 10%.
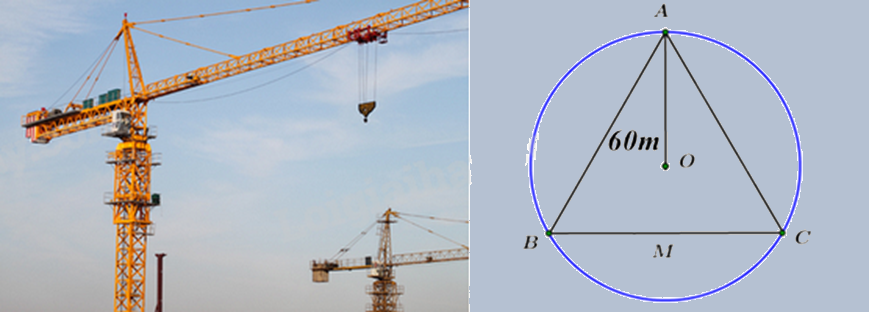
Cẩu tháp là một loại thiết bị nâng hạ được thiết kế để nâng, hạ và di chuyền vật liệu xây dựng tại các công trường, đặc biệt là trong xây dựng các công trình cao tầng. Có khả năng hoạt động ở độ cao lớn và với tải trọng nặng, cẩu tháp được lắp đặt cố định hoặc có thể di chuyển trên ray tại công trường, giúp tăng hiệu quả công việc và đảm bảo an toàn lao động. Ba vị trí A, B, C của một công trình là ba đỉnh của một tam giác đều. Trên công trình, người ta muốn đặt cẩu tháp tại điểm O sao cho bán kính quay của cẩu tháp đến các vị trí điểm A, B, C bằng nhau và bằng 60 m (hình bên). Tính khoảng cách từ A đến B (làm tròn đến số hàng đơn vị).
Tính khoảng cách giữa hai vị trí A và B chính là tìm cạnh của tam giác đều ABC khi biết bán kính đường tròn ngoại tiếp tam giác.
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).
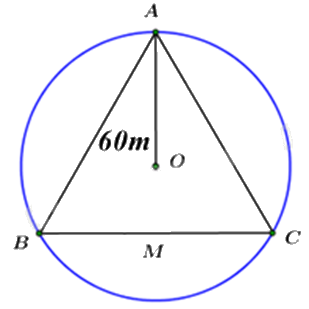
Vì O cách đều 3 đỉnh của tam giác ABC nên O là tâm đường tròn ngoại tiếp tam giác đều ABC.
Gọi a (m) là độ dài cạnh của tam giác đều ABC (a > 0)
Ta có bán kính đường tròn ngoại tiếp tam giác đều là 60m nên \(R = \frac{{a\sqrt 3 }}{3}\), suy ra \(60 = \frac{{a\sqrt 3 }}{3}\)
Do đó\(\begin{array}{l}a\sqrt 3 = 60.3 = 180\\a = 180:\sqrt 3 \approx 104\left( {TM} \right)\end{array}\)
Vậy khoảng cách từ A đến B khoảng 104 m.
Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \({x^2} - 3x - 7 = 0\). Không giải phương trình, hãy tính giá trị của biểu thức \(N = \left( {3{x_1} + {x_2}} \right)\left( {3{x_2} + {x_1}} \right)\).
Xác định số nghiệm của phương trình bằng tích a.c.
Áp dụng định lí Viète để biểu diễn tổng và tích của hai nghiệm.
Biến đổi N sao cho xuất hiện tổng (tích) của hai nghiệm để tính giá trị biểu thức.
Vì phương trình \({x^2} - 3x - 7 = 0\) có \(a.c = 1.\left( { - 7} \right) = - 7 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\).
Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 3\\{x_1}.{x_2} = \frac{c}{a} = - 7\end{array} \right.\).
Ta có:
\(N = \left( {3{x_1} + {x_2}} \right)\left( {3{x_2} + {x_1}} \right)\\ = 9{x_1}{x_2} + 3{x_2}^2 + 3{x_1}^2 + {x_1}{x_2}\\ = 3{x_1}^2 + 3{x_2}^2 + 10{x_1}{x_2}\\ = 3{x_1}^2 + 3{x_2}^2 + 6{x_1}{x_2} + 4{x_1}{x_2}\\ = 3\left( {{x_1}^2 + 2{x_1}{x_2} + {x_2}^2} \right) + 4{x_1}{x_2}\\ = 3{\left( {{x_1} + {x_2}} \right)^2} + 4{x_1}{x_2}\\ = {3.3^2} + 4.\left( { - 7} \right)\\ = 27 - 28\\ = - 1\)
Đề thi giữa kì 2 Toán 9 - Đề số 2 là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau nửa học kỳ. Đề thi thường bao gồm các chủ đề chính như đại số, hình học và các ứng dụng thực tế của toán học.
Cấu trúc đề thi có thể thay đổi tùy theo từng trường và từng giáo viên, nhưng nhìn chung, đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi giữa kì 2 Toán 9 - Đề số 2 bao gồm:
Dưới đây là hướng dẫn giải một số dạng bài tập thường gặp trong đề thi giữa kì 2 Toán 9 - Đề số 2:
Để giải phương trình bậc nhất một ẩn, ta thực hiện các bước sau:
Để giải hệ phương trình bậc nhất hai ẩn, ta có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số.
Để giải bất phương trình bậc nhất một ẩn, ta thực hiện các bước tương tự như giải phương trình, nhưng cần chú ý đến việc đổi dấu bất phương trình khi nhân hoặc chia cả hai vế cho một số âm.
Hy vọng với những thông tin và hướng dẫn trên, các em học sinh sẽ tự tin hơn khi làm bài thi giữa kì 2 Toán 9 - Đề số 2. Chúc các em đạt kết quả tốt nhất!