Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 12 - Đề số 5, một công cụ hữu ích giúp các em học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo cấu trúc chuẩn của Bộ Giáo dục và Đào tạo, bao gồm nhiều dạng bài tập khác nhau, từ cơ bản đến nâng cao.
Với đáp án chi tiết đi kèm, các em có thể tự kiểm tra và rút kinh nghiệm sau khi làm bài. Đây là cơ hội tuyệt vời để các em củng cố kiến thức, rèn luyện kỹ năng giải đề và tự tin bước vào kỳ thi giữa kì 1 Toán 12.
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:
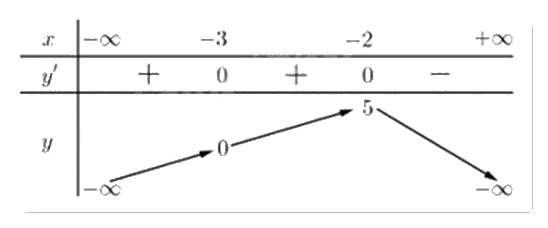
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
i) Hàm số đã cho đồng biến trên các khoảng (-∞;-5) và (-3;-2).
ii) Hàm số đã cho đồng biến trên khoảng (-∞;5).
iii) Hàm số đã cho nghịch biến trên khoảng (-2;+∞).
iv) Hàm số đã cho đồng biến trên khoảng (-∞;-2).
1
2
3
4
Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
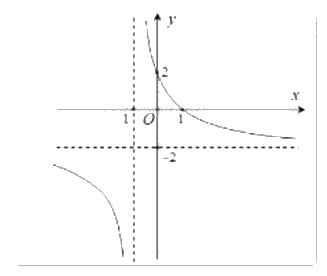
\(y = \frac{{2 - 2x}}{{x + 1}}\)
\(y = 2{x^3} - x + 1\)
\(y = \frac{{ - 2x + 1}}{{x + 2}}\)
\(y = {x^4} + 2{x^2} + 2\)
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
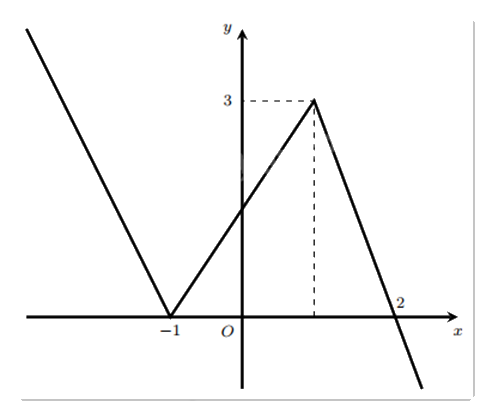
Tìm giá trị lớn nhất của hàm số g(x) = 2f(x) – 1trên đoạn [–1;2].
3
4
5
6
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
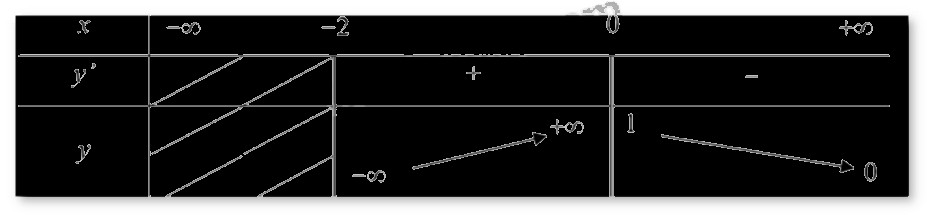
1
3
2
4
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 9x + 3}}{{x + 2}}\) là:
y = 2x + 13
y = -2x + 13
y = 2x - 13
y = -2x - 13
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) là:
(2;1)
(-1;3)
(3;2)
(1;2)
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Khẳng định nào sau đây là đúng?
\(\overrightarrow {AB} = \overrightarrow {CD} \)
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \)
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {A'C} \)
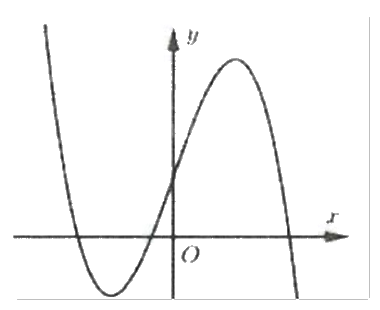
Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
\(y = - {x^3} + 3{x^2} + 1\)
\(y = - {x^3} + 3x + 1\)
\(y = {x^3} - 3x + 1\)
\(y = - {x^3} - 3x + 1\)
Giá trị nhỏ nhất của hàm số \(y = 2\sin x + \sin 2x\) trên đoạn \(\left[ {0;\frac{{3\pi }}{2}} \right]\) là:
-2
2
0
\(\frac{{3\sqrt 3 }}{2}\)
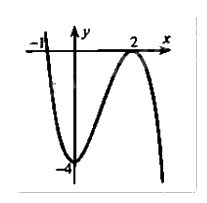
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ sau:
\(y = {x^3} + 3{x^2} - 4\)
\(y = - {x^3} + 3{x^2} + 4\)
\(y = {x^3} + 3{x^2} + 4\)
\(y = - {x^3} + 3{x^2} - 4\)
Trong không gian Oxyz, cho hai điểm M(2;3;1), N(3;1;5). Tọa độ của vecto \(\overrightarrow {MN} \) là
(-5;-4;-6)
(5;4;6)
(-1;2;-4)
(1;-2;4)
Trong mặt phẳng tọa độ Oxyz, cho hai vecto \(\overrightarrow u = \overrightarrow i + 3\overrightarrow j + 2\overrightarrow k \), \(\overrightarrow v = 2\overrightarrow i + \overrightarrow j + 5\overrightarrow k \). Tích \(\overrightarrow u .\overrightarrow v \) bằng:
0
6
15
3
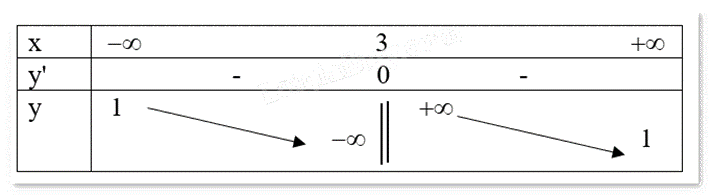
Cho hàm số f(x) xác định trên R\{3} có bảng biến thiên như sau:
a) Hàm số f(x) đồng biến trên mỗi khoảng xác định
b) Số điểm cực trị của hàm số đã cho là 1
c) Hàm số f(x) có giá trị lớn nhất bằng 1
d) Đồ thị hàm số f(x) có hai đường tiệm cận
Cho hàm số \(f(x) = {x^4} - 10{x^2} - 4\).
a) Hàm số f(x) nghịch biến trên khoảng
b) Hàm số có 3 điểm cực trị
c) Hàm số f(x) có giá trị lớn nhất trên đoạn [0;9] bằng -4
d) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [2;19] bằng -29
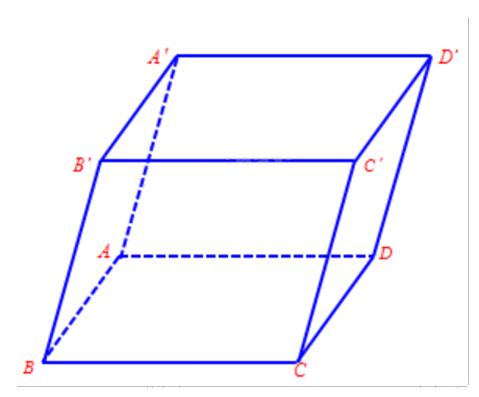
Cho hình hộp ABCD.A’B’C’D’.
a) \(\overrightarrow {A'A} = - \overrightarrow {CC'} \)
b) \(\overrightarrow {BA'} = \overrightarrow {CD'} \)
c) \(\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} = \overrightarrow {A'C} \)
d) \(\overrightarrow {C'C} + \overrightarrow {AB} + \overrightarrow {B'C'} = 2\overrightarrow {A'C} \)
Trong không gian Oxyz, cho vecto \(\overrightarrow a = (2;1; - 2)\), \(\overrightarrow b = (0; - 1;1)\).
a) \(\left| {\overrightarrow a } \right| = 3\)
b) \(\overrightarrow a + \overrightarrow b = (2;0; - 1)\)
c) \(\overrightarrow a .\overrightarrow b = - 1\)
d) Góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng \({60^o}\)
Giá trị lớn nhất của hàm số \(y = \sqrt {3 - 2x - {x^2}} \) bằng bao nhiêu?
Đáp án:
Biết rằng đồ thị hàm số \(y = \frac{{(n - 3)x + n - 2017}}{{x + m + 3}}\) nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cận đứng. Khi đó, giá trị của m + n bằng bao nhiêu?
Đáp án:
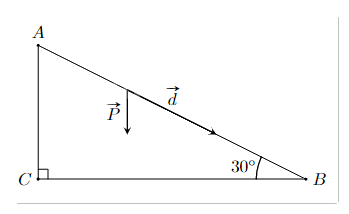
Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5 m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \({30^o}\). Độ lớn của trọng lực \(\overrightarrow P = m\overrightarrow g \) tác dụng lên em nhỏ, cho biết vecto gia tốc rơi tự do \(\overrightarrow g \) có độ lớn là 9,8 \(m/{s^2}\). Công A (J) sinh bởi một lực \(\overrightarrow F \) có độ dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trong lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt (làm tròn đến hàng đơn vị).
Đáp án:
Một tấm kẽm hình vuông ABCD có cạnh bằng 30 cm. Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau (như hình) để được một lăng trụ khuyết hai đáy.
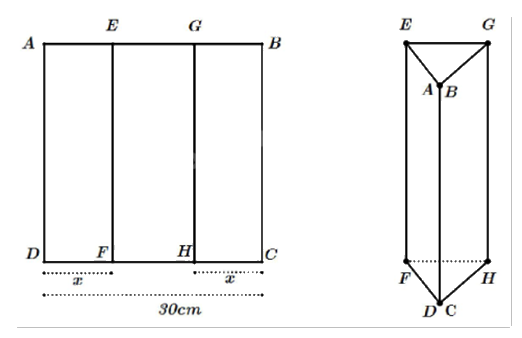
Tìm giá trị của x để thể tích khối lăng trụ lớn nhất.
Đáp án:
Giả sử không gian ngoài vũ trụ được xét theo hệ tọa độ Oxyz, một phi thuyền ở ngoài không gian đang ở vị trí gốc tọa độ. Có 3 vệ tinh nhân tạo lần lượt ở 3 vị trí A(2500; 4700; -3600), B(3700; 1100; 2900), C(-5000; -4000; -7100), phi thuyền cần đến vị trí trọng tâm của 3 vệ tinh A, B, C để nhận và truyền tín hiệu đến các vệ tinh. Quãng đường mà phi thuyền cần di chuyển để đến được trọng tâm của 3 vệ tinh là bao nhiêu (làm tròn đến hàng đơn vị)?
Đáp án:
Dân số của một quốc gia sau t năm kể từ năm 2023 được ước tính bởi công thức \(N(t) = 100{e^{0,012t}}\) (N(t) được tính bằng triệu người), \(0 \le t \le 50\)). Đạo hàm của hàm số N(t) biểu thị tốc độ tăng trưởng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm nào tốc độ tăng trưởng dân số của quốc gia đó là 1,5 triệu người/năm?
Đáp án:
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:
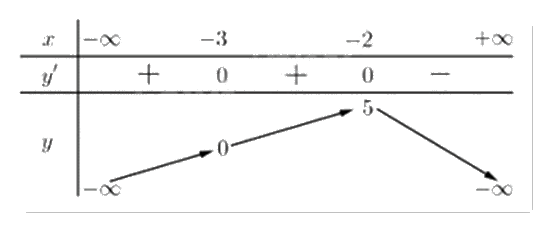
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
i) Hàm số đã cho đồng biến trên các khoảng (-∞;-5) và (-3;-2).
ii) Hàm số đã cho đồng biến trên khoảng (-∞;5).
iii) Hàm số đã cho nghịch biến trên khoảng (-2;+∞).
iv) Hàm số đã cho đồng biến trên khoảng (-∞;-2).
1
2
3
4
Đáp án : A
Quan sát bảng biến thiên và nhận xét.
Nhìn vào bảng biến thiên ta thấy đồ thị hàm số đã cho đồng biến trên khoảng (-∞;-2); nghịch biến trên khoảng (-2;+∞).
Suy ra ii) Sai; iii) Đúng; iv) Đúng.
Ta thấy khoảng (-∞;-3) chứa khoảng (-∞;-5) nên i) Đúng.
Vậy chỉ có ii) sai.
Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
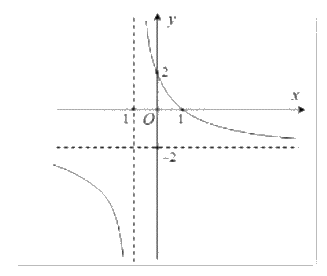
\(y = \frac{{2 - 2x}}{{x + 1}}\)
\(y = 2{x^3} - x + 1\)
\(y = \frac{{ - 2x + 1}}{{x + 2}}\)
\(y = {x^4} + 2{x^2} + 2\)
Đáp án : A
Quan sát đồ thị và nhận xét.
Ta có đây là đồ thị hàm số dạng \(y = \frac{{ax + b}}{{cx + d}}\).
Mặt khác, đồ thị có tiệm cận đứng x = -1.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
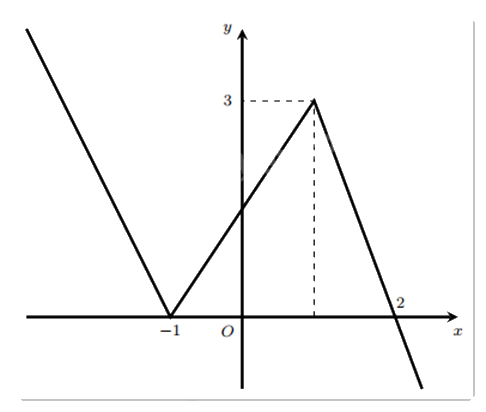
Tìm giá trị lớn nhất của hàm số g(x) = 2f(x) – 1trên đoạn [–1;2].
3
4
5
6
Đáp án : C
Quan sát đồ thị và nhận xét.
Dựa vào đồ thị ta thấy:
\(\mathop {\max }\limits_{[ - 1;2]} f(x) = 3\).
Do đó, \(\mathop {\max }\limits_{[ - 1;2]} g(x) = 2\mathop {\max }\limits_{[ - 1;2]} f(x) - 1 = 2.3 - 1 = 5\).
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
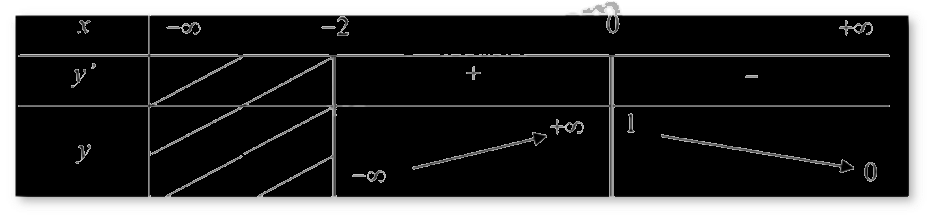
1
3
2
4
Đáp án : B
Quan sát bảng biến thiên và nhận xét.
Dựa vào bảng biến thiên ta có: \(\mathop {\lim }\limits_{x \to {0^ - }} f(x) = + \infty \), \(\mathop {\lim }\limits_{x \to {{( - 2)}^ + }} f(x) = - \infty \) nên x = 0, x = -2 là tiệm cận đứng của đồ thị hàm số.
Mặt khác: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 0\) nên y = 0 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị có ba tiệm cận.
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 9x + 3}}{{x + 2}}\) là:
y = 2x + 13
y = -2x + 13
y = 2x - 13
y = -2x - 13
Đáp án : C
Thực hiện phép chia đa thức (ở tử) cho đa thức (ở mẫu) ta được \(y = ax + b + \frac{M}{{cx + d}}\)(a≠0) với M là hằng số.
Đường thẳng y = ax + b (a≠0) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
Kết luận đường thẳng y = ax +b là đường tiệm cận xiên của đồ thị hàm số.
Ta có: \(y = \frac{{2{x^2} - 9x + 3}}{{x + 2}} = 2x - 13 + \frac{{29}}{{x + 2}} = f(x)\).
Từ đó: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (2x - 13)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{29}}{{x + 2}} = 0\).
Vậy đường thẳng y = 2x - 13 là đường tiệm cận xiên của đồ thị hàm số đã cho.
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) là:
(2;1)
(-1;3)
(3;2)
(1;2)
Đáp án : D
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị và tìm giao điểm của chúng.
Tiệm cận ngang của đồ thị là y = 2, tiệm cận đứng của đồ thị là x = 1 nên tâm đối xứng có tọa độ (1;2).
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Khẳng định nào sau đây là đúng?
\(\overrightarrow {AB} = \overrightarrow {CD} \)
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \)
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {A'C} \)
Đáp án : B
Dựa vào quy tắc ba điểm, khái niệm hai vecto bằng nhau và quy tắc hình hộp.
A sai vì \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng.
B đúng (theo quy tắc hình hộp).
C sai (theo quy tắc ba điểm).
D sai (theo quy tắc hình hộp).
Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
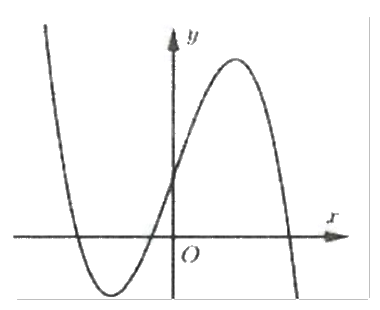
\(y = - {x^3} + 3{x^2} + 1\)
\(y = - {x^3} + 3x + 1\)
\(y = {x^3} - 3x + 1\)
\(y = - {x^3} - 3x + 1\)
Đáp án : B
Quan sát đồ thị và nhận xét.
Dựa vào đồ thị ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) nên hệ số a < 0. Loại đáp án C.
Hàm số có hai điểm cực trị \({x_1} < 0 < {x_2}\) nên y’ = 0 có hai nghiệm trái dấu.
Xét đáp án A, có \(y' = - 3{x^2} + 6x = 0 \Leftrightarrow \) x = 0 hoặc x = 2 (loại).
Xét đáp án D, có \(y' = - 3{x^2} - 3x < 0\) \((\forall x \in \mathbb{R})\) (loại).
Giá trị nhỏ nhất của hàm số \(y = 2\sin x + \sin 2x\) trên đoạn \(\left[ {0;\frac{{3\pi }}{2}} \right]\) là:
-2
2
0
\(\frac{{3\sqrt 3 }}{2}\)
Đáp án : C
Tìm đạo hàm của hàm số sau đó tính các giá trị f(x).
\(f'(x) = 2\cos x + 2\cos 2x = 4\cos \frac{x}{2}\cos \frac{{3x}}{2}\).
Vì \(x \in \left[ {0;\frac{{3\pi }}{2}} \right]\) nên \(f'(x) = 0 \Leftrightarrow x = 0,x = \frac{\pi }{3}\).
Ta có: \(f\left( 0 \right) = 0\); \(f\left( {\frac{\pi }{3}} \right) = \frac{{3\sqrt 3 }}{2}\); \(f\left( {\frac{{5\pi }}{6}} \right) = \frac{{2 - \sqrt 3 }}{2}\).
Vậy giá trị nhỏ nhất của hàm số \(y = 2\sin x + \sin 2x\) trên đoạn \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\) bằng 0.
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ sau:
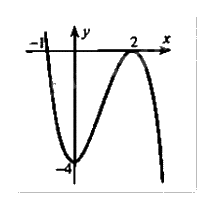
\(y = {x^3} + 3{x^2} - 4\)
\(y = - {x^3} + 3{x^2} + 4\)
\(y = {x^3} + 3{x^2} + 4\)
\(y = - {x^3} + 3{x^2} - 4\)
Đáp án : D
Dựa vào sự biến thiên, cực trị và các điểm hàm số đi qua để lập hệ phương trình tìm hệ số.
Ta có: \(f'(x) = 3a{x^2} + 2bx + c\).
Đồ thị hàm số đạt cực trị tại điểm (0;-4) và (2;0) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{f'(0) = 0}\\{f(0) = - 4}\\{f'(2) = 0}\\{f(2) = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = - 4}\\{12a + 4b + c = 0}\\{8a + 4b + 2c + d = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3a + b = 0}\\{2a + b = 1}\\{c = 0}\\{d = - 4}\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = 3}\\{c = 0}\\{d = - 4}\end{array}} \right.\)
Vậy hàm số cần tìm là \(y = - {x^3} + 3{x^2} - 4\).
Trong không gian Oxyz, cho hai điểm M(2;3;1), N(3;1;5). Tọa độ của vecto \(\overrightarrow {MN} \) là
(-5;-4;-6)
(5;4;6)
(-1;2;-4)
(1;-2;4)
Đáp án : A
\(\overrightarrow {MN} = ({x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M})\).
\(\overrightarrow {MN} = ({x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}) = (3 - 2;1 - 3;5 - 1) = (1; - 2;4)\).
Trong mặt phẳng tọa độ Oxyz, cho hai vecto \(\overrightarrow u = \overrightarrow i + 3\overrightarrow j + 2\overrightarrow k \), \(\overrightarrow v = 2\overrightarrow i + \overrightarrow j + 5\overrightarrow k \). Tích \(\overrightarrow u .\overrightarrow v \) bằng:
0
6
15
3
Đáp án : C
Sử dụng công thức tính tọa độ tích vô hướng của hai vecto.
Theo giả thiết, ta có: \(\overrightarrow u = (1;3;2)\), \(\overrightarrow v = (2;1;5)\).
Khi đó: \(\overrightarrow u .\overrightarrow v = 1.2 + 3.1 + 2.5 = 15\).
Cho hàm số f(x) xác định trên R\{3} có bảng biến thiên như sau:
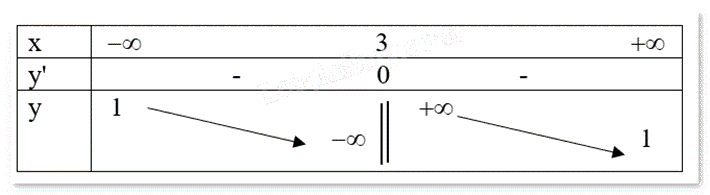
a) Hàm số f(x) đồng biến trên mỗi khoảng xác định
b) Số điểm cực trị của hàm số đã cho là 1
c) Hàm số f(x) có giá trị lớn nhất bằng 1
d) Đồ thị hàm số f(x) có hai đường tiệm cận
a) Hàm số f(x) đồng biến trên mỗi khoảng xác định
b) Số điểm cực trị của hàm số đã cho là 1
c) Hàm số f(x) có giá trị lớn nhất bằng 1
d) Đồ thị hàm số f(x) có hai đường tiệm cận
Quan sát bảng biến thiên và nhận xét.
a) Sai. Hàm số f(x) nghịch biến trên mỗi khoảng xác định.
b) Sai. Hàm số không có điểm cực trị.
c) Sai. Hàm số f(x) không có giá trị lớn nhất.
d) Đúng. Đồ thị hàm số f(x) có hai đường tiệm cận là x = 3, y = 1.
Cho hàm số \(f(x) = {x^4} - 10{x^2} - 4\).
a) Hàm số f(x) nghịch biến trên khoảng
b) Hàm số có 3 điểm cực trị
c) Hàm số f(x) có giá trị lớn nhất trên đoạn [0;9] bằng -4
d) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [2;19] bằng -29
a) Hàm số f(x) nghịch biến trên khoảng
b) Hàm số có 3 điểm cực trị
c) Hàm số f(x) có giá trị lớn nhất trên đoạn [0;9] bằng -4
d) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [2;19] bằng -29
Lập bảng biến thiên và nhận xét.
\(f'(x) = 4{x^3} - 20x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \sqrt 5 }\\{x = - \sqrt 5 \notin [0;9]}\end{array}} \right.\)

Ta có: f(0) = -4; \(f(\sqrt 5 ) = - 29\); f(9) = 5747.
a) Sai. Hàm số f(x) nghịch biến trên khoảng \((0;\sqrt 5 )\) và đồng biến trên khoảng \((\sqrt 5 ; + \infty )\).
b) Đúng. Hàm số có 3 điểm cực trị (\(x = - \sqrt 5 \), x = 0, \(x = \sqrt 5 \)).
c) Sai. Hàm số f(x) có giá trị lớn nhất trên đoạn [0;9] bằng 5747.
d) Đúng. Hàm số f(x) có giá trị nhỏ nhất trên đoạn [2;19] bằng -29.
Cho hình hộp ABCD.A’B’C’D’.
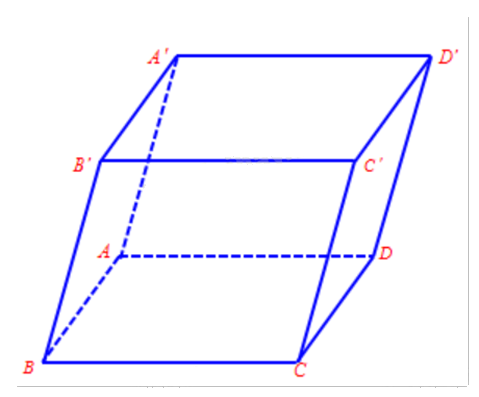
a) \(\overrightarrow {A'A} = - \overrightarrow {CC'} \)
b) \(\overrightarrow {BA'} = \overrightarrow {CD'} \)
c) \(\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} = \overrightarrow {A'C} \)
d) \(\overrightarrow {C'C} + \overrightarrow {AB} + \overrightarrow {B'C'} = 2\overrightarrow {A'C} \)
a) \(\overrightarrow {A'A} = - \overrightarrow {CC'} \)
b) \(\overrightarrow {BA'} = \overrightarrow {CD'} \)
c) \(\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} = \overrightarrow {A'C} \)
d) \(\overrightarrow {C'C} + \overrightarrow {AB} + \overrightarrow {B'C'} = 2\overrightarrow {A'C} \)
Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, quy tắc hình hộp.
a) Đúng. Vì hai vecto \(\overrightarrow {A'A} \), \(\overrightarrow {CC'} \) ngược hướng và cùng độ dài.
b) Đúng. Vì hai vecto \(\overrightarrow {BA'} \), \(\overrightarrow {CD'} \) ngược hướng và cùng độ dài.
c) Đúng. Vì \(\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} = \overrightarrow {A'C} \) theo quy tắc hình hộp).
d) Sai. Vì \(\overrightarrow {C'C} + \overrightarrow {AB} + \overrightarrow {B'C'} = \overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} = \overrightarrow {A'C} \) theo quy tắc hình hộp).
Trong không gian Oxyz, cho vecto \(\overrightarrow a = (2;1; - 2)\), \(\overrightarrow b = (0; - 1;1)\).
a) \(\left| {\overrightarrow a } \right| = 3\)
b) \(\overrightarrow a + \overrightarrow b = (2;0; - 1)\)
c) \(\overrightarrow a .\overrightarrow b = - 1\)
d) Góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng \({60^o}\)
a) \(\left| {\overrightarrow a } \right| = 3\)
b) \(\overrightarrow a + \overrightarrow b = (2;0; - 1)\)
c) \(\overrightarrow a .\overrightarrow b = - 1\)
d) Góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng \({60^o}\)
Sử dụng các quy tắc cộng vecto, công thức tính tích vô hướng của hai vecto, độ dài vecto, góc giữa hai vecto.
a) Đúng. Vì \(\left| {\overrightarrow a } \right| = \sqrt {{2^2} + {1^2} + {{( - 2)}^2}} = 3\).
b) Đúng. Vì \(\overrightarrow a + \overrightarrow b = (2 + 0;1 - 1; - 2 + 1) = (2;0; - 1)\).
c) Sai. Vì \(\overrightarrow a .\overrightarrow b = 2.0 + 1.( - 1) - 2.1 = - 3\).
d) Sai. Vì \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 3}}{{\sqrt {{2^2} + {1^2} + {{( - 2)}^2}} .\sqrt {{0^2} + {{( - 1)}^2} + {1^2}} }} = \frac{{ - \sqrt 2 }}{2}\) nên góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng \({135^o}\).
Giá trị lớn nhất của hàm số \(y = \sqrt {3 - 2x - {x^2}} \) bằng bao nhiêu?
Đáp án:
Đáp án:
- Tính y’, tìm các nghiệm của y’ = 0
- Tìm giá trị y tại các điểm cực trị của hàm số và hai đầu mút của đoạn.
Tập xác định: [-3;1].
Ta có: \(f'(x) = \frac{{ - 2 - 2x}}{{2\sqrt {3 - 2x - {x^2}} }} = \frac{{x + 1}}{{\sqrt {3 - 2x - {x^2}} }} = 0 \Leftrightarrow x = - 1\).
f(-3) = 0; f(-1) = 2; f(1) = 0.
Vậy giá trị lớn nhất của hàm số là 2.
Biết rằng đồ thị hàm số \(y = \frac{{(n - 3)x + n - 2017}}{{x + m + 3}}\) nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cận đứng. Khi đó, giá trị của m + n bằng bao nhiêu?
Đáp án:
Đáp án:
Sử dụng quy tắc tìm đường tiệm cận của hàm phân thức.
Đồ thị nhận trục hoành làm tiệm cận ngang, tức \(n - 3 = 0 \Leftrightarrow n = 3\).
Đồ thị nhận trục tung làm tiệm cận đứng, tức \( - m - 3 = 0 \Leftrightarrow m = - 3\).
Vậy m + n = -3 + 3 = 0.
Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5 m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \({30^o}\). Độ lớn của trọng lực \(\overrightarrow P = m\overrightarrow g \) tác dụng lên em nhỏ, cho biết vecto gia tốc rơi tự do \(\overrightarrow g \) có độ lớn là 9,8 \(m/{s^2}\). Công A (J) sinh bởi một lực \(\overrightarrow F \) có độ dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trong lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt (làm tròn đến hàng đơn vị).
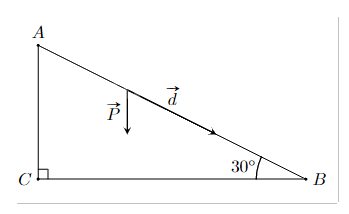
Đáp án:
Đáp án:
Sử dụng công thức tính tích vô hướng của hai vecto trong không gian.
Độ lớn trọng lực tác dụng lên em nhỏ là: P = m.g = 25.9,8 = 245 (N).
Góc giữa hai vecto \(\overrightarrow P \) và \(\overrightarrow d \) là: \(\widehat {CAB} = {90^o} - \widehat {ABC} = {90^o} - {30^o} = {60^o}\).
Ta có: \(A = \overrightarrow F .\overrightarrow d = \overrightarrow P .\overrightarrow d = Pd\cos \left( {\overrightarrow P ,\overrightarrow d } \right) = 245.3,5.\cos {60^o} = 428,75 \approx 429\) (J).
Một tấm kẽm hình vuông ABCD có cạnh bằng 30 cm. Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau (như hình) để được một lăng trụ khuyết hai đáy.
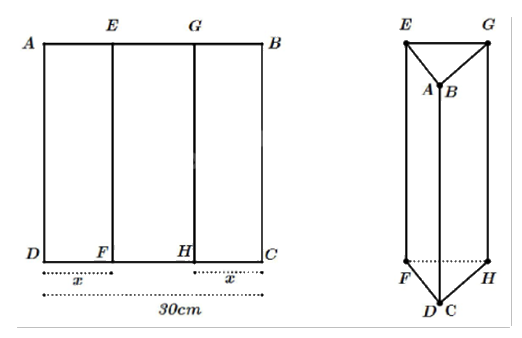
Tìm giá trị của x để thể tích khối lăng trụ lớn nhất.
Đáp án:
Đáp án:
Thiết lập hàm số biểu diễn thể tích lăng trụ theo x. Lập bảng biến thiên và tìm giá trị lớn nhất của hàm số đó.
Ta có: DF = CH = x, FH = 30 – 2x. Suy ra chu vi tam giác DHF là p = 15.
Thể tích khối lăng trụ là: \(V = {S_{DHF}}.EF = 30\sqrt {15(15 - x)(15 - x)(15 - 30 + 2x)} \)
\( = 30\sqrt {15{{(15 - x)}^2}(2x - 15)} \), \(x \in \left( {\frac{{15}}{2};15} \right)\).
Xét hàm số \(f(x) = {(15 - x)^2}(2x - 15)\).
\(f'(x) = - 2(15 - x)(2x - 15) + 2{(15 - x)^2} = - 2(15 - x)(3x - 30)\)
\(f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 10}\\{x = 15}\end{array}} \right.\)
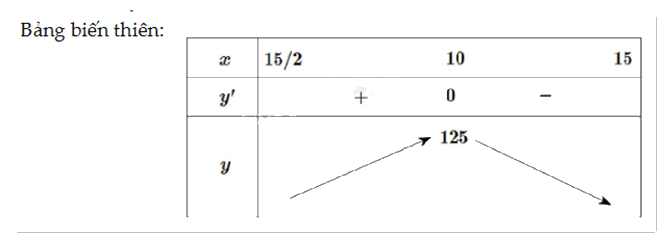
Dựa vào bảng biến thiên, thể tích lăng trụ lớn nhất khi x = 10 (cm).
Giả sử không gian ngoài vũ trụ được xét theo hệ tọa độ Oxyz, một phi thuyền ở ngoài không gian đang ở vị trí gốc tọa độ. Có 3 vệ tinh nhân tạo lần lượt ở 3 vị trí A(2500; 4700; -3600), B(3700; 1100; 2900), C(-5000; -4000; -7100), phi thuyền cần đến vị trí trọng tâm của 3 vệ tinh A, B, C để nhận và truyền tín hiệu đến các vệ tinh. Quãng đường mà phi thuyền cần di chuyển để đến được trọng tâm của 3 vệ tinh là bao nhiêu (làm tròn đến hàng đơn vị)?
Đáp án:
Đáp án:
Gọi điểm G là trọng tâm của tam giác ABC. Tính khoảng cách OG.
Gọi điểm G là trọng tâm của tam giác ABC.
Khi đó:
\(G\left( {\frac{{2500 + 3700 - 5000}}{3};\frac{{4700 + 1100 - 4000}}{3};\frac{{ - 3600 + 2900 - 7100}}{3}} \right) = \left( {400;600; - 2600} \right)\).
Phi thuyền đang ở vị trí gốc tọa độ, cần di chuyển đến vị trí trọng tâm G của 3 vệ tinh A, B, C nên quãng đường cần di chuyển bằng độ dài vecto \(\overrightarrow {OG} = \left( {400;600; - 2600} \right)\).
Độ dài vecto \(\overrightarrow {OG} \) là \(\sqrt {{{400}^2} + {{600}^2} + {{( - 2600)}^2}} \approx 2698\).
Dân số của một quốc gia sau t năm kể từ năm 2023 được ước tính bởi công thức \(N(t) = 100{e^{0,012t}}\) (N(t) được tính bằng triệu người), \(0 \le t \le 50\)). Đạo hàm của hàm số N(t) biểu thị tốc độ tăng trưởng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm nào tốc độ tăng trưởng dân số của quốc gia đó là 1,5 triệu người/năm?
Đáp án:
Đáp án:
Tìm N’(t) và giải phương trình N’(t) = 1,5.
Ta có: \(N'(t) = 100.0,012{e^{0,012t}} = 1,2{e^{0,012t}}\).
Tốc độ tăng trưởng dân số đạt 1,5 triệu người/năm tức là \(N'(t) = 1,5 \Leftrightarrow 1,2{e^{0,012t}} = 1,5 \Leftrightarrow t \approx 18,6\).
Vậy, vào năm 2023 + 18 = 2041, tốc độ tăng trưởng dân số của quốc gia đó là 1,5 triệu người/năm.
Đề thi giữa kì 1 Toán 12 - Đề số 5 là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau một nửa học kỳ. Đề thi thường bao gồm các chủ đề chính như hàm số, đạo hàm, tích phân, số phức, và hình học không gian. Việc làm quen với cấu trúc đề thi và các dạng bài tập thường gặp là yếu tố then chốt để đạt kết quả tốt.
Thông thường, đề thi giữa kì 1 Toán 12 - Đề số 5 có cấu trúc gồm hai phần chính:
Để tìm cực trị của hàm số y = f(x), ta thực hiện các bước sau:
Để tính tích phân xác định ∫ab f(x) dx, ta thực hiện các bước sau:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 12, các em cần luyện tập thường xuyên với các đề thi thử, đặc biệt là Đề thi giữa kì 1 Toán 12 - Đề số 5. Việc làm đề thi sẽ giúp các em làm quen với cấu trúc đề thi, các dạng bài tập thường gặp, và rèn luyện kỹ năng giải đề. Sau khi làm bài, các em nên tự kiểm tra và rút kinh nghiệm từ những sai lầm của mình.
Hãy dành thời gian ôn tập kiến thức một cách hệ thống, luyện tập giải đề thường xuyên, và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 12!