Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề số 3, được biên soạn theo chuẩn chương trình học mới nhất của Bộ Giáo dục và Đào tạo.
Đề thi này là tài liệu ôn tập lý tưởng, giúp các em học sinh làm quen với cấu trúc đề thi thực tế và rèn luyện kỹ năng giải toán. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 2.
Họ các nguyên hàm của hàm số \(f(x) = 5{x^4} - 6{x^2} + 1\) là
\(20{x^3} - 12x + C\)
\({x^5} - 2{x^3} + x + C\)
\(20{x^5} - 12{x^3} + x + C\)
\(\frac{{{x^4}}}{4} + 2{x^2} - 2x + C\)
Hàm số F(x) là một nguyên hàm của hàm số f(x) trên khoảng K nếu
F’(x) = -f(x), \(\forall x \in K\)
f’(x) = F(x), \(\forall x \in K\)
F’(x) = f(x), \(\forall x \in K\)
f’(x) = -F(x), \(\forall x \in K\)
Họ nguyên hàm của hàm số \(f(x) = \frac{1}{{3\sqrt[3]{{{x^2}}}}} + \frac{1}{{\sqrt x }} + \frac{3}{2}\sqrt x \) là
\(3\sqrt[3]{x} + 2\sqrt x + x\sqrt x + C\)
\(\frac{{\sqrt[3]{x}}}{9} + 2\sqrt x + \frac{{9x\sqrt x }}{4} + C\)
\(\sqrt[3]{x} + 2\sqrt x + x\sqrt x + C\)
\(\sqrt[3]{x} + \sqrt x + x\sqrt x + C\)
Cho f(x) là hàm số liên tục trên đoạn [a;b] và F(x) là một nguyên hàm của hàm số f(x). Tích phân từ a đến b của hàm số f (x) được kí hiệu là
\(\int\limits_a^b {F(x)dx} = f(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = f(a) - f(b)\)
\(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(a) - F(b)\)
\(\int\limits_a^b {F(x)dx} = f(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = f(b) - f(a)\)
\(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(b) - F(a)\)
Tính \(\int\limits_{ - 1}^3 {{x^2}dx} \) được kết quả là
\(\frac{{28}}{3}\)
\(\frac{{26}}{3}\)
\(\frac{{25}}{3}\)
\(\frac{{29}}{3}\)
Cho \(I = \int\limits_{ - 1}^3 {\left| {2x - 4} \right|dx} \). Chọn khẳng định đúng.
\(I = \left| {\int\limits_{ - 1}^3 {\left( {2x - 4} \right)dx} } \right|\)
\(I = - \int\limits_{ - 1}^2 {\left( {2x - 4} \right)dx} + \int\limits_2^3 {\left( {2x - 4} \right)dx} \)
\(I = \int\limits_{ - 1}^2 {\left( {2x - 4} \right)dx} + \int\limits_2^3 {\left( {2x - 4} \right)dx} \)
\(I = \int\limits_{ - 1}^2 {\left( {2x - 4} \right)dx} - \int\limits_2^3 {\left( {2x - 4} \right)dx} \)
Cho mặt phẳng \(\left( \alpha \right)\) vuông góc với giá của \(\overrightarrow a = ( - 4;2;6)\). Vecto nào dưới đây là một vecto pháp tuyến của \(\left( \alpha \right)\)?
\(\overrightarrow {{n_1}} = (2;1;3)\)
\(\overrightarrow {{n_2}} = ( - 2;1;3)\)
\(\overrightarrow {{n_3}} = (4; - 2;6)\)
\(\overrightarrow {{n_4}} = (4;2; - 6)\)
Trong không gian Oxyz, cho hai điểm A(1;2;3) và B(1;-4;1). Mặt phẳng qua A và vuông góc với đường thẳng AB có phương trình là
\( - 6y - 2z - 18 = 0\)
\(3y + z + 1 = 0\)
\( - 6y - 2z - 22 = 0\)
\(3y + z - 9 = 0\)
Trong không gian Oxyz, cho mặt phẳng (P): x + y – 3z – 4 = 0. Điểm nào sau đây không thuộc mặt phẳng (P)?
A(0;4;0)
B(1;-6;-3)
C(2;2;0)
D(2;2;1)
Trong không gian Oxyz, đường thẳng d đi qua điểm M(1;1;1) có vecto chỉ phương \(\overrightarrow u = (1;2;3)\) có phương trình là
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 1 - 3t\end{array} \right.\) \((t \in \mathbb{R})\)
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 2t\\z = 1 + t\end{array} \right.\) \((t \in \mathbb{R})\)
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 3t\\z = 1 + 2t\end{array} \right.\) \((t \in \mathbb{R})\)
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 1 + 3t\end{array} \right.\) \((t \in \mathbb{R})\)
Trong không gian Oxyz, khoảng cách từ điểm M(1;4;-7) đến (P): 2x – y + 2z + 7 = 0 là
3
5
7
12
Góc giữa hai mặt phẳng (P): x + 2y + z – 1 = 0 và (Q): -x + y + 2z + 2 = 0 bằng
\({30^o}\)
\({45^o}\)
\({60^o}\)
\({90^o}\)
Cho hàm số \(f(x) = {x^2} - 4x\).
a) Hoành độ giao điểm của đồ thị hàm số y = f(x) và Ox là nghiệm của phương trình f(x) = 0.
b) \({x^2} - 4x \ge 0\), \(\forall x \in [0;4]\).
c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và Ox được tính theo công thức \(\int\limits_4^0 {\left| {{x^2} - 4x} \right|dx} \).
d) Hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và Ox có diện tích là 32.
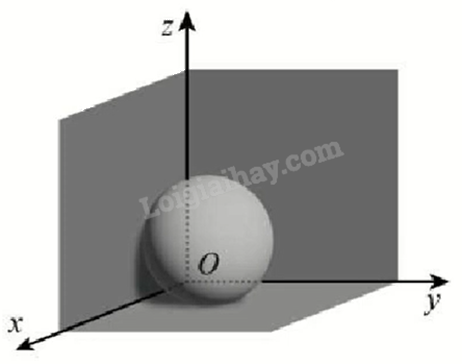
Đặt một quả bóng ở góc nhà, biết trên quả bóng có một điểm M cách hai bức tường 5 cm và cách sàn nhà 6 cm. Chọn hệ trục tọa độ Oxyz sao cho góc nhà là góc phần tư thứ nhất và sàn nhà là mặt phẳng Oxy.
a) M(5;5;6).
b) Mặt phẳng chứa hai bức tường có phương trình lần lượt là y = 0 và x = 0.
c) Chỉ có một quả bóng thỏa mãn yêu cầu bài toán.
d) Bán kính của quả bóng thuộc (5;11) cm).
Một ô tô đang chạy với vận tốc 18 m/s thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với vận tốc v(t) = -36t + 18 (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
Đáp án:
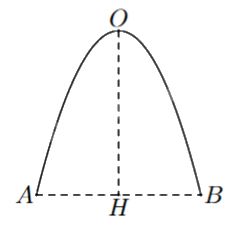
Mặt cắt đứng của một cái cổng có dạng một đường parabol với chiều cao OH = 4 m và khoảng cách giữa hai chân cổng là AB = 4 m (hình bên). Diện tích hình phẳng giới hạn bởi đường parabol và đoạn thẳng AB bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Đáp án:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;4;1); B(−1;1;3) và mặt phẳng (P): x – 3y + 2z – 5 = 0. Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có dạng ax + by + cz – 11 = 0. Tính a + b + c.
Đáp án:
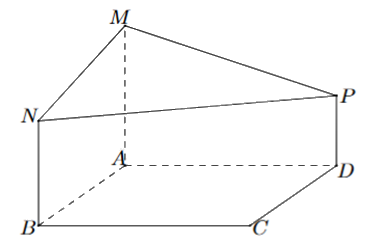
Một phần thiết kế của một công trình đang xây dựng có dạng như hình bên, trong đó ABCD là hình vuông cạnh 6 m, AM, BN, DP cùng vuông góc với (ABCD), AM = 4 m, BN = 3 m và DP = 2 m. Góc giữa hai mặt phẳng (ABCD) và (MNP) là \({n^o}\) (làm tròn kết quả đến hàng đơn vị của độ, n là số nguyên dương). Giá trị của n là bao nhiêu?
Đáp án:
Giá trị dương của tham số m sao cho diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 2x + 3 và các đường thẳng y = 0, x = 0, x = m bằng 10 là bao nhiêu?
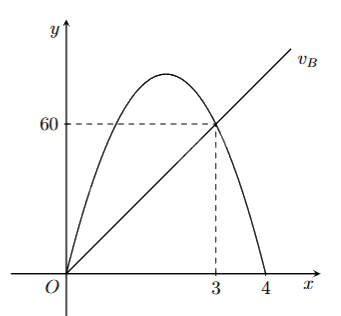
Cho đồ thị biểu diễn vận tốc của hai xe A và B khởi hành cùng một lúc và cùng vạch xuất phát, đi cùng chiều trên một con đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường parabol và đồ thị biểu diễn vận tốc của xe B là một đường thẳng như hình vẽ bên. Hỏi sau 5 giây kể từ lúc xuất phát thì khoảng cách giữa hai xe là bao nhiêu mét (làm tròn đến hàng phần chục và biết rằng xe A sẽ dừng lại khi vận tốc bằng 0)?
Trong không gian Oxyz, cho (P): x − y + z − 3 = 0 và A(5;6;7). Gọi H(a;b;c) là hình chiếu vuông góc của A trên (P). Tính a + 2b + c.
Họ các nguyên hàm của hàm số \(f(x) = 5{x^4} - 6{x^2} + 1\) là
\(20{x^3} - 12x + C\)
\({x^5} - 2{x^3} + x + C\)
\(20{x^5} - 12{x^3} + x + C\)
\(\frac{{{x^4}}}{4} + 2{x^2} - 2x + C\)
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lũy thừa: \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int {\left( {5{x^4} - 6{x^2} + 1} \right)dx} = 5.\frac{{{x^5}}}{5} - 6.\frac{{{x^3}}}{3} + x + C = {x^5} - 2{x^3} + x + C\).
Hàm số F(x) là một nguyên hàm của hàm số f(x) trên khoảng K nếu
F’(x) = -f(x), \(\forall x \in K\)
f’(x) = F(x), \(\forall x \in K\)
F’(x) = f(x), \(\forall x \in K\)
f’(x) = -F(x), \(\forall x \in K\)
Đáp án : C
Áp dụng định nghĩa nguyên hàm.
Hàm số F(x) là một nguyên hàm của hàm số f(x) trên khoảng K nếu F’(x) = f(x), \(\forall x \in K\).
Họ nguyên hàm của hàm số \(f(x) = \frac{1}{{3\sqrt[3]{{{x^2}}}}} + \frac{1}{{\sqrt x }} + \frac{3}{2}\sqrt x \) là
\(3\sqrt[3]{x} + 2\sqrt x + x\sqrt x + C\)
\(\frac{{\sqrt[3]{x}}}{9} + 2\sqrt x + \frac{{9x\sqrt x }}{4} + C\)
\(\sqrt[3]{x} + 2\sqrt x + x\sqrt x + C\)
\(\sqrt[3]{x} + \sqrt x + x\sqrt x + C\)
Đáp án : C
Áp dụng công thức nguyên hàm của hàm số lũy thừa: \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(f(x) = \frac{1}{{3\sqrt[3]{{{x^2}}}}} + \frac{1}{{\sqrt x }} + \frac{3}{2}\sqrt x = \frac{1}{3}{x^{ - \frac{2}{3}}} + {x^{ - \frac{1}{2}}} + \frac{3}{2}{x^{ - \frac{1}{2}}}\).
\(\int {f(x)dx} = \int {\left( {\frac{1}{3}{x^{ - \frac{2}{3}}} + {x^{ - \frac{1}{2}}} + \frac{3}{2}{x^{\frac{1}{2}}}} \right)dx} = \frac{1}{3}.3{x^{\frac{1}{3}}} + 2{x^{\frac{1}{2}}} + \frac{3}{2}.\frac{2}{3}{x^{\frac{3}{2}}} + C = \sqrt[3]{x} + 2\sqrt x + {\left( {{x^{\frac{1}{2}}}} \right)^3} + C\)
\( = \sqrt[3]{x} + 2\sqrt x + {\left( {\sqrt x } \right)^3} + C = \sqrt[3]{x} + 2\sqrt x + x\sqrt x + C\).
Cho f(x) là hàm số liên tục trên đoạn [a;b] và F(x) là một nguyên hàm của hàm số f(x). Tích phân từ a đến b của hàm số f (x) được kí hiệu là
\(\int\limits_a^b {F(x)dx} = f(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = f(a) - f(b)\)
\(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(a) - F(b)\)
\(\int\limits_a^b {F(x)dx} = f(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = f(b) - f(a)\)
\(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(b) - F(a)\)
Đáp án : D
Dựa vào định nghĩa tích phân.
Cho f(x) là hàm số liên tục trên đoạn [a;b] và F(x) là một nguyên hàm của hàm số f(x). Tích phân từ a đến b của hàm số f (x) được kí hiệu là \(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(b) - F(a)\).
Tính \(\int\limits_{ - 1}^3 {{x^2}dx} \) được kết quả là
\(\frac{{28}}{3}\)
\(\frac{{26}}{3}\)
\(\frac{{25}}{3}\)
\(\frac{{29}}{3}\)
Đáp án : A
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
Áp dụng định nghĩa tích phân \(\int\limits_a^b {f(x)dx} = F(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = F(b) - F(a)\).
\(\int\limits_{ - 1}^3 {{x^2}dx} = \frac{{{x^3}}}{3}\left| {\begin{array}{*{20}{c}}{^3}\\{_{ - 1}}\end{array}} \right. = \frac{{{3^3}}}{3} - \frac{{{{( - 1)}^3}}}{3} = 9 + \frac{1}{3} = \frac{{28}}{3}\).
Cho \(I = \int\limits_{ - 1}^3 {\left| {2x - 4} \right|dx} \). Chọn khẳng định đúng.
\(I = \left| {\int\limits_{ - 1}^3 {\left( {2x - 4} \right)dx} } \right|\)
\(I = - \int\limits_{ - 1}^2 {\left( {2x - 4} \right)dx} + \int\limits_2^3 {\left( {2x - 4} \right)dx} \)
\(I = \int\limits_{ - 1}^2 {\left( {2x - 4} \right)dx} + \int\limits_2^3 {\left( {2x - 4} \right)dx} \)
\(I = \int\limits_{ - 1}^2 {\left( {2x - 4} \right)dx} - \int\limits_2^3 {\left( {2x - 4} \right)dx} \)
Đáp án : B
Khi f(x) < 0 thì |f(x)| = -f(x).
Khi f(x) > 0 thì |f(x)| = f(x).
\(2x - 4 = 0 \Leftrightarrow x = 2\).
Khi \(x < 2 \Leftrightarrow 2x - 4 < 0 \Rightarrow \left| {2x - 4} \right| = - (2x - 4)\).
Khi \(x > 2 \Leftrightarrow 2x - 4 > 0 \Rightarrow \left| {2x - 4} \right| = 2x - 4\).
\(I = \int\limits_{ - 1}^3 {\left| {2x - 4} \right|dx} = \int\limits_{ - 1}^2 {\left| {2x - 4} \right|dx} + \int\limits_2^3 {\left| {2x - 4} \right|dx} = - \int\limits_{ - 1}^2 {\left( {2x - 4} \right)dx} + \int\limits_2^3 {\left( {2x - 4} \right)dx} \).
Cho mặt phẳng \(\left( \alpha \right)\) vuông góc với giá của \(\overrightarrow a = ( - 4;2;6)\). Vecto nào dưới đây là một vecto pháp tuyến của \(\left( \alpha \right)\)?
\(\overrightarrow {{n_1}} = (2;1;3)\)
\(\overrightarrow {{n_2}} = ( - 2;1;3)\)
\(\overrightarrow {{n_3}} = (4; - 2;6)\)
\(\overrightarrow {{n_4}} = (4;2; - 6)\)
Đáp án : B
Áp dụng điều kiện để hai vecto cùng phương: \(\overrightarrow a = k\overrightarrow b \).
Vecto pháp tuyến của \(\left( \alpha \right)\) cùng phương với \(\overrightarrow a = ( - 4;2;6)\).
Mà \(\overrightarrow {{n_2}} = ( - 2;1;3) = \frac{1}{2}\overrightarrow a \) nên \(\overrightarrow {{n_2}} = ( - 2;1;3)\) là một vecto pháp tuyến của \(\left( \alpha \right)\).
Trong không gian Oxyz, cho hai điểm A(1;2;3) và B(1;-4;1). Mặt phẳng qua A và vuông góc với đường thẳng AB có phương trình là
\( - 6y - 2z - 18 = 0\)
\(3y + z + 1 = 0\)
\( - 6y - 2z - 22 = 0\)
\(3y + z - 9 = 0\)
Đáp án : D
Mặt phẳng qua A và vuông góc với đường thẳng AB nhận \(\overrightarrow {AB} \) làm vecto pháp tuyến.
Mặt phẳng qua A(1;2;3) và vuông góc với đường thẳng AB nhận \(\overrightarrow {AB} = (1 - 1; - 4 - 2;1 - 3) = (0; - 6; - 2)\) làm vecto pháp tuyến có phương trình là:
\(0(x - 1) - 6(y - 2) - 2(z - 3) = 0 \Leftrightarrow - 6y - 2z + 18 = 0 \Leftrightarrow 3y + z - 9 = 0\).
Trong không gian Oxyz, cho mặt phẳng (P): x + y – 3z – 4 = 0. Điểm nào sau đây không thuộc mặt phẳng (P)?
A(0;4;0)
B(1;-6;-3)
C(2;2;0)
D(2;2;1)
Đáp án : D
Thay tọa độ các điểm vào phương trình, nếu thỏa mãn thì điểm đó thuộc mặt phẳng.
Thay tọa độ các điểm vào phương trình mặt phẳng:
Xét đáp án A: 1.0 + 1.4 – 3.0 – 4 = 0. Vậy A(0;4;0) thuộc (P).
Xét đáp án B: 1.1 + 1.(-6) – 3.(-3) – 4 = 0. Vậy B(1;-6;-3) thuộc (P).
Xét đáp án C: 1.2 + 1.2 – 3.0 – 4 = 0. Vậy C(2;2;0) thuộc (P).
Xét đáp án D: 1.2 + 1.2 – 3.1 – 4 = -3. Vậy D(2;2;0) không thuộc (P).
Trong không gian Oxyz, đường thẳng d đi qua điểm M(1;1;1) có vecto chỉ phương \(\overrightarrow u = (1;2;3)\) có phương trình là
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 1 - 3t\end{array} \right.\) \((t \in \mathbb{R})\)
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 1 + 2t\\z = 1 + t\end{array} \right.\) \((t \in \mathbb{R})\)
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 3t\\z = 1 + 2t\end{array} \right.\) \((t \in \mathbb{R})\)
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 1 + 3t\end{array} \right.\) \((t \in \mathbb{R})\)
Đáp án : D
Đường thẳng đi qua điểm \(M({x_0};{y_0};{z_0})\) có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) có phương trình là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\).
d đi qua điểm M(1;1;1) có vecto chỉ phương \(\overrightarrow u = (1;2;3)\) có phương trình là \(\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 1 + 3t\end{array} \right.\) \((t \in \mathbb{R})\).
Trong không gian Oxyz, khoảng cách từ điểm M(1;4;-7) đến (P): 2x – y + 2z + 7 = 0 là
3
5
7
12
Đáp án : A
Áp dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng.
\(d\left( {M,(P)} \right) = \frac{{\left| {2.1 - 1.4 + 2.( - 7) + 7} \right|}}{{\sqrt {{2^2} + {{( - 1)}^2} + {2^2}} }} = \frac{9}{3} = 3\).
Góc giữa hai mặt phẳng (P): x + 2y + z – 1 = 0 và (Q): -x + y + 2z + 2 = 0 bằng
\({30^o}\)
\({45^o}\)
\({60^o}\)
\({90^o}\)
Đáp án : C
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\vec n{\rm{\;}} = \left( {A;B;C} \right),\vec n'{\rm{\;}} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {(P),(Q)} \right) = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\).
\(\cos \left( {(P),(Q)} \right) = \frac{{\left| {1.( - 1) + 2.1 + 1.2} \right|}}{{\sqrt {{1^2} + {2^2} + {1^2}} .\sqrt {{{( - 1)}^2} + {1^2} + {2^2}} }} = \frac{1}{2} \Rightarrow \left( {(P),(Q)} \right) = {60^o}\).
Cho hàm số \(f(x) = {x^2} - 4x\).
a) Hoành độ giao điểm của đồ thị hàm số y = f(x) và Ox là nghiệm của phương trình f(x) = 0.
b) \({x^2} - 4x \ge 0\), \(\forall x \in [0;4]\).
c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và Ox được tính theo công thức \(\int\limits_4^0 {\left| {{x^2} - 4x} \right|dx} \).
d) Hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và Ox có diện tích là 32.
a) Hoành độ giao điểm của đồ thị hàm số y = f(x) và Ox là nghiệm của phương trình f(x) = 0.
b) \({x^2} - 4x \ge 0\), \(\forall x \in [0;4]\).
c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và Ox được tính theo công thức \(\int\limits_4^0 {\left| {{x^2} - 4x} \right|dx} \).
d) Hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và Ox có diện tích là 32.
a) Hoành độ giao điểm của đồ thị y = f(x) với đồ thị y = g(x) là nghiệm của phương trình f(x) = g(x).
b) Áp dụng định lí về dấu của tam thức bậc hai.
c, d) Áp dụng công thức tính diện tích của hình phẳng \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
a)Đúng. Trục Ox có phương trình y = 0 nên hoành độ giao điểm của đồ thị y = f(x) với trục hoành là nghiệm của phương trình y = f(x).
b) Sai. \({x^2} - 4x \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le 0\\x \ge 4\end{array} \right.\) và \({x^2} - 4x \le 0 \Leftrightarrow 0 \le x \le 4\).
c) Sai. Phần diện tích giới hạn bởi đồ thị y = f(x) với trục Ox có hoành độ thuộc đoạn [0;4], được tính bởi công thức \(\int\limits_0^4 {\left| {{x^2} - 4x} \right|dx} \).
d) Sai. Trên đoạn [0;4], ta có \({x^2} - 4x \le 0\) nên \(\left| {{x^2} - 4x} \right| = 4x - {x^2}\).
Diện tích hình phẳng đó là \(\int\limits_0^4 {\left| {{x^2} - 4x} \right|dx} = \int\limits_0^4 {\left( {4x - {x^2}} \right)dx} = \left( {2{x^2} - \frac{{{x^3}}}{3}} \right)\left| {\begin{array}{*{20}{c}}{^4}\\{_0}\end{array} = } \right.{2.4^2} - \frac{{{4^3}}}{3} = \frac{{32}}{3}\).
Đặt một quả bóng ở góc nhà, biết trên quả bóng có một điểm M cách hai bức tường 5 cm và cách sàn nhà 6 cm. Chọn hệ trục tọa độ Oxyz sao cho góc nhà là góc phần tư thứ nhất và sàn nhà là mặt phẳng Oxy.
a) M(5;5;6).
b) Mặt phẳng chứa hai bức tường có phương trình lần lượt là y = 0 và x = 0.
c) Chỉ có một quả bóng thỏa mãn yêu cầu bài toán.
d) Bán kính của quả bóng thuộc (5;11) cm).
a) M(5;5;6).
b) Mặt phẳng chứa hai bức tường có phương trình lần lượt là y = 0 và x = 0.
c) Chỉ có một quả bóng thỏa mãn yêu cầu bài toán.
d) Bán kính của quả bóng thuộc (5;11) cm).
Áp dụng quy tắc xác định tọa độ điểm và công thức tính khoảng cách giữa hai điểm trong không gian.
a)Đúng. M(5;5;6).
b) Đúng. Mặt phẳng chứa hai bức tường có phương trình lần lượt là x = 0 và y = 0.
c) Sai. Gọi I là tâm của quả bóng. Vì bóng được đặt ở góc nhà (tiếp xúc với hai mặt tường và sàn nhà) nên I cách ba mặt phẳng trên đúng một khoảng bằng bán kính r. Khi đó I(r;r;r).
Vì M là một điểm trên bề mặt quả bóng nên \(IM = r \Leftrightarrow {\left( {5 - r} \right)^2} + {\left( {5 - r} \right)^2} + {\left( {6 - r} \right)^2} = {r^2}\)
\( \Leftrightarrow 86 - 32r + 2{r^2} = 0 \Leftrightarrow \left[ \begin{array}{l}{r_1} = 8 + \sqrt {21} \approx 12,58\\{r_2} = 8 - \sqrt {21} \approx 3,42\end{array} \right.\).
Vậy có hai quả bóng thỏa mãn yêu cầu bài toán.
d) Sai. Bán kính của quả bóng có thể là \({r_1} \approx 12,58\) (cm) hoặc \({r_2} \approx 3,42\) (cm) nên không thuộc (5;11) (cm).
Một ô tô đang chạy với vận tốc 18 m/s thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với vận tốc v(t) = -36t + 18 (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
Đáp án:
Đáp án:
Tìm thời gian \({t_0}\) để xe dừng hẳn từ lúc hãm phanh.
Tính \(\int\limits_0^{{t_0}} {v(t)dt} \).
Khi ô tô dừng hẳn thì \(v(t) = 0 \Leftrightarrow - 36.t + 18 = 0 \Leftrightarrow t = 0,5\) (s).
Quãng đường ô tô di chuyển được từ lúc bắt đầu hãm phanh đến khi dừng hẳn là:
\(s(0,5) = \int\limits_0^{0,5} {v(t)dt} = \int\limits_0^{0,5} {( - 36t + 18)dt} = \left( { - 18{t^2} + 18t} \right)\left| {\begin{array}{*{20}{c}}{^{0,5}}\\{_0}\end{array}} \right. = - 18.0,{5^2} + 18.0,5 = 4,5\) (m).
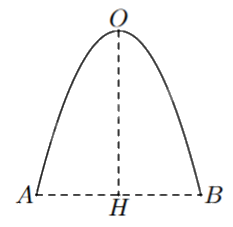
Mặt cắt đứng của một cái cổng có dạng một đường parabol với chiều cao OH = 4 m và khoảng cách giữa hai chân cổng là AB = 4 m (hình bên). Diện tích hình phẳng giới hạn bởi đường parabol và đoạn thẳng AB bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Đáp án:
Đáp án:
Chọn hệ trục tọa độ phù hợp. Dựa vào tọa độ các điểm thuộc parabol để tìm phương trình của parabol. Từ đó ứng dụng tích phân để tính diện tích hình phẳng.
Chọn hệ trục tọa độ sao cho H trùng với gốc tọa độ, A và B nằm trên trục hoành và B có hoành độ dương. O nằm trên trục tung.
Cổng parabol có phương trình dạng \(y = a{x^2} + bx + c\) với a < 0 vì bề lõm hướng xuống dưới.
Khi đó H(0;0), A(-2;0), B(2;0) và O(0;4).
Vì A, B, H thuộc parabol nên ta có hệ:
\(\left\{ \begin{array}{l}0 = a{.2^2} + b.2 + c\\0 = a.{( - 2)^2} + b.( - 2) + c\\4 = a{.0^2} + b.0 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4 = 4a + 2b\\ - 4 = 4a - 2b\\4 = c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 0\end{array} \right. \Rightarrow y = - {x^2} + 4\).
Trên đoạn [-2;2], ta thấy parabol nằm phía trên trục hoành nên \( - {x^2} + 4 \ge 0 \Leftrightarrow \left| { - {x^2} + 4} \right| = - {x^2} + 4\).
Diện tích hình phẳng giới hạn bởi parabol và đoạn AB là:
\(\int\limits_{ - 2}^2 {\left| { - {x^2} + 4} \right|dx} = \int\limits_{ - 2}^2 {\left( { - {x^2} + 4} \right)dx} = \left( { - \frac{{{x^3}}}{3} + 4x} \right)\)
\(\left| {\begin{array}{*{20}{c}}{^2}\\{_{ - 2}}\end{array} = \left( { - \frac{{{2^3}}}{3} + 4.2} \right)} \right. - \left[ { - \frac{{{{( - 2)}^3}}}{3} + 4.( - 2)} \right] = \frac{{16}}{3} - \left( { - \frac{{16}}{3}} \right) = \frac{{32}}{3} \approx 10,7\) \(({m^2})\).
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;4;1); B(−1;1;3) và mặt phẳng (P): x – 3y + 2z – 5 = 0. Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có dạng ax + by + cz – 11 = 0. Tính a + b + c.
Đáp án:
Đáp án:
Cặp vecto chỉ phương của (Q) là vecto pháp tuyến của (P) và \(\overrightarrow {AB} \).
Áp dụng biểu thức tọa độ của tích có hướng để tìm vecto pháp tuyến của (Q) rồi lập phương trình.
Vecto pháp tuyến của (P) là \(\overrightarrow {{n_P}} = (1; - 3;2)\).
Ta có \(\overrightarrow {{n_P}} = (1; - 3;2)\) và \(\overrightarrow {AB} = ( - 1 - 2;1 - 4;3 - 1) = ( - 3; - 3;2)\) là cặp vecto chỉ phương của (Q).
\(\overrightarrow {AB} = ( - 1 - 2;1 - 4;3 - 1) = ( - 3; - 3;2)\)
Vecto pháp tuyến của (Q) là \(\overrightarrow {{n_Q}} = \left[ {\overrightarrow {{n_P}} ,\overrightarrow {AB} } \right] = (0; - 8; - 12)\).
Mặt phẳng (Q) có vecto pháp tuyến \(\overrightarrow {{n_Q}} = (0; - 8; - 12)\) và đi qua A(2;4;1) có phương trình là:
\(0(x - 2) - 8(y - 4) - 12(z - 1) = 0 \Leftrightarrow - 8y - 12z + 44 = 0 \Leftrightarrow 2y + 3z - 11 = 0\).
Vậy a + b + c = 0 + 2 + 3 = 5.
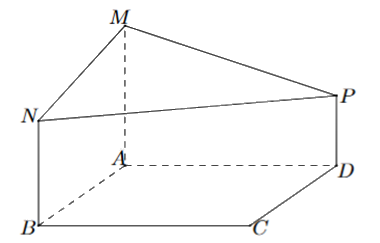
Một phần thiết kế của một công trình đang xây dựng có dạng như hình bên, trong đó ABCD là hình vuông cạnh 6 m, AM, BN, DP cùng vuông góc với (ABCD), AM = 4 m, BN = 3 m và DP = 2 m. Góc giữa hai mặt phẳng (ABCD) và (MNP) là \({n^o}\) (làm tròn kết quả đến hàng đơn vị của độ, n là số nguyên dương). Giá trị của n là bao nhiêu?
Đáp án:
Đáp án:
Chọn hệ trục tọa độ phù hợp. Lập phương trình mặt phẳng (ABCD) và (MNP) rồi áp dụng công thức tính góc giữa hai mặt phẳng.
Chọn hệ trục tọa độ Oxyz sao cho A trùng với gốc tọa độ, B thuộc tia Ox, D thuộc tia Oy và M thuộc tia Oz.
Khi đó: A(0;0;0), M(0;0;4), N(6;0;3), P(0;6;2) và mặt phẳng (ABCD) trùng với mặt phẳng (Oxy), hay (ABCD) có phương trình tổng quát z = 0.
\(\overrightarrow {MN} = (6;0; - 1)\); \(\overrightarrow {MP} = (0;6; - 2)\).
Vecto pháp tuyến của (MNP) là \(\overrightarrow n = \left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = (6;12;36)\).
Phương trình mặt phẳng (MNP) là:
\(6(x - 0) + 12(y - 0) + 36(z - 0) = 0 \Leftrightarrow 6x + 12y + 36z = 0 \Leftrightarrow x + 2y + 6z = 0\).
Góc giữa hai mặt phẳng (ABCD) và (MNP) là:
\(\cos \left( {(ABCD),(MNP)} \right) = \frac{{\left| {1.0 + 2.0 + 6.1} \right|}}{{\sqrt {{1^2} + {2^2} + {6^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{6\sqrt {41} }}{{41}} \Rightarrow \left( {(ABCD),(MNP)} \right) \approx {20^o}\).
Giá trị dương của tham số m sao cho diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 2x + 3 và các đường thẳng y = 0, x = 0, x = m bằng 10 là bao nhiêu?
Áp dụng công thức tính diện tích của hình phẳng \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
Với m > 0, diện tích hình phẳng là \(\int\limits_0^m {\left| {2x + 3} \right|dx} = 10 \Leftrightarrow \int\limits_0^m {\left( {2x + 3} \right)dx} = 10 \Leftrightarrow \left( {{x^2} + 3x} \right)\left| {\begin{array}{*{20}{c}}{^m}\\{_0}\end{array} = 10} \right.\)
\( \Leftrightarrow {m^2} + 3m = 10 \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 5\end{array} \right.\).
Vì m dương nên loại m = -5. Vậy m = 2 là giá trị thỏa mãn yêu cầu đề bài.
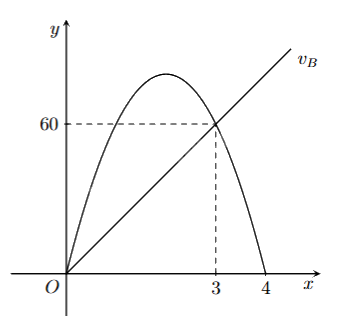
Cho đồ thị biểu diễn vận tốc của hai xe A và B khởi hành cùng một lúc và cùng vạch xuất phát, đi cùng chiều trên một con đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường parabol và đồ thị biểu diễn vận tốc của xe B là một đường thẳng như hình vẽ bên. Hỏi sau 5 giây kể từ lúc xuất phát thì khoảng cách giữa hai xe là bao nhiêu mét (làm tròn đến hàng phần chục và biết rằng xe A sẽ dừng lại khi vận tốc bằng 0)?
Lập phương trình parabol và đường thẳng biểu diễn vận tốc. Áp dụng tích phân để tính quãng đường từ các hàm vận tốc vừa tìm.
Gọi parabol \({v_A}\) biểu diễn vận tốc xe A có phương trình \(y = {a_A}{x^2} + {b_A}x + c\) và đường thẳng \({v_B}\) biểu diễn vận tốc xe B có phương trình \(y = {a_B}x + {b_B}\).
Parabol \({v_A}\) di qua ba điểm O(0;0), M(3;60) và N(4;0) nên ta có:
\(\left\{ \begin{array}{l}0 = {a_A}{.0^2} + {b_A}.0 + c\\60 = {a_A}{.3^2} + {b_A}.3 + c\\0 = {a_A}{.4^2} + {b_A}.4 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a_A} = - 20\\{b_A} = 80\\c = 0\end{array} \right. \Rightarrow y = - 20{x^2} + 80x\).
\({v_B}\) là đường thẳng đi qua hai điểm O(0;0) và M(3;60) nên \(\left\{ \begin{array}{l}0 = {a_B}.0 + {b_B}\\60 = {a_B}.3 + {b_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b_B} = 0\\{a_B} = 20\end{array} \right. \Rightarrow y = 20x\).
Quãng đường xe A đi được sau 4 giây là \(\int\limits_0^4 {\left( { - 20{x^2} + 80x} \right)dx} = \frac{{640}}{3}\). Khi x = 4 thì \({v_A} = 0\) nên xe dừng sau 4 giây, đi được quãng đường bằng \(\frac{{640}}{3}\).
Quãng đường xe B đi được sau 5 giây là \(\int\limits_0^5 {20xdx} = 250\).
Khoảng cách giữa hai xe sau 5 giây là \(250 - \frac{{640}}{3} = \frac{{110}}{3} \approx 36,7\).
Trong không gian Oxyz, cho (P): x − y + z − 3 = 0 và A(5;6;7). Gọi H(a;b;c) là hình chiếu vuông góc của A trên (P). Tính a + 2b + c.
Lập phương trình đường thẳng đi qua A và vuông góc với (P).
H là giao điểm của d và (P).
Gọi d là đường thẳng qua A và vuông góc với (P). Khi đó, d giao (P) tại H.
d là đường thẳng đi qua A(5;6;7) và nhận \(\overrightarrow u = (1; - 1;1)\) làm vecto chỉ phương nên phương trình tham số của d là \(\left\{ \begin{array}{l}x = 5 + t\\y = 6 - t\\z = 7 + t\end{array} \right.\) \((t \in \mathbb{R})\).
H là giao điểm của d và (P) nên ta có \(5 + t - (6 - t) + 7 + t - 3 = 0 \Leftrightarrow 3 + 3t = 0 \Leftrightarrow t = - 1\).
Vậy H(4;7;6), suy ra a + 2b + c = 4 + 7.2 + 6 = 24.
Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề số 3 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một học kì ôn luyện. Việc nắm vững kiến thức và kỹ năng giải đề là yếu tố then chốt để đạt kết quả tốt. Bài viết này sẽ cung cấp phân tích chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp, và hướng dẫn giải chi tiết từng câu hỏi.
Đề thi thường bao gồm hai phần chính: Phần trắc nghiệm và phần tự luận. Phần trắc nghiệm thường chiếm khoảng 40-50% tổng số điểm, tập trung vào các kiến thức cơ bản và khả năng vận dụng nhanh. Phần tự luận chiếm khoảng 50-60% tổng số điểm, đòi hỏi học sinh phải trình bày bài giải một cách logic, rõ ràng và chính xác.
Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm đạo hàm f'(x).
Giải:
f'(x) = 3x2 - 6x
Giải phương trình: log2(x + 1) = 3
Giải:
x + 1 = 23
x + 1 = 8
x = 7
Để chuẩn bị tốt nhất cho kỳ thi giữa kì 2 Toán 12 Kết nối tri thức, bạn nên tham khảo các tài liệu sau:
Hãy luôn tự tin vào khả năng của mình và cố gắng hết sức trong kỳ thi. Chúc các em học sinh đạt kết quả tốt nhất!
| Chủ đề | Nội dung chính |
|---|---|
| Hàm số | Khái niệm hàm số, các loại hàm số, đồ thị hàm số, ứng dụng của hàm số. |
| Phương trình | Phương trình bậc nhất, bậc hai, bậc ba, phương trình vô tỉ, phương trình lượng giác. |
| Hình học | Vectơ, đường thẳng, mặt phẳng, đường tròn, đường conic. |