Chào mừng các em học sinh lớp 10 đến với đề thi giữa kì 1 môn Toán chương trình Cánh diều - Đề số 5.
Đề thi này được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán!
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai? A. (P(2)) B. (P(4)). C. (P(3)). D. (P(7))
I. PHẦN TRẮC NGHIỆM
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai?
A. \(P(2)\) B. \(P(4)\). C. \(P(3)\). D. \(P(7)\)
Câu 2. Cặp số \((1; - 1)\) là nghiệm của bất phương trình nào sau đây?
A. \(x + y - 3 > 0\) B. \( - x - y < 0\). C. \(x + 3y + 1 < 0\). D. \( - x - 3y - 1 < 0\)
Câu 3. Mệnh đề phủ định của mệnh đề “Có một số thực sao cho bình phương của nó không là số nguyên dương”
A. \(\exists x \in \mathbb{R},{x^2} > 0\) B. \(\exists x \in \mathbb{R},{x^2} \le 0\). C. \(\forall x \in \mathbb{R},{x^2} \le 0\). D. \(\forall x \in \mathbb{R},{x^2} > 0\)
Câu 4. Tập xác định của hàm số \(y = \frac{{x + 2}}{{{x^2} - 4x + 3}} + \sqrt {{x^2} - 9} \)
A. \((3; + \infty )\). B. \(\mathbb{R}{\rm{\backslash }}\{ 1;3\} \) C. \(\mathbb{R}{\rm{\backslash }}( - 3;3]\). D. \(\mathbb{R}{\rm{\backslash }}[ - 3;3]\).
Câu 5. Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
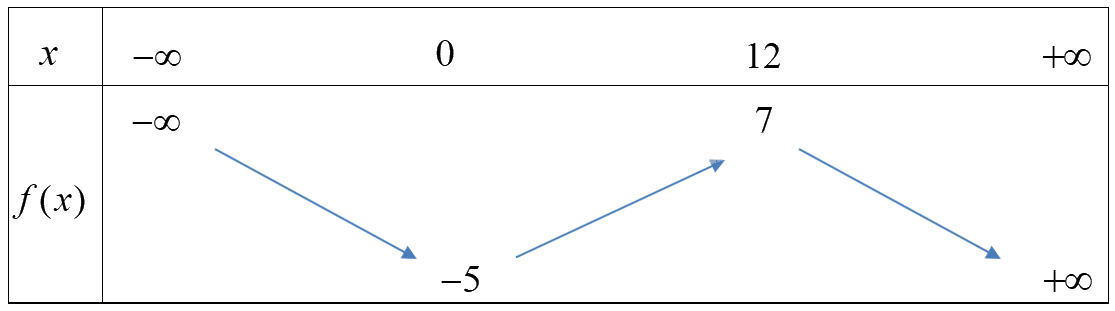
Khẳng định nào sau đây đúng?
A. \(f( - 5) < f( - 1)\) B. \(f(7) < f(11)\) C. \(f(1) > f(6)\) D. \(f(2022) > f(20)\)
Câu 6. Cho hai tập hợp \(X = \{ 1;3;5;8\} ,Y = \{ 3;5;7;9\} \). Tập hợp \(X \cup Y\) bằng tập hợp nào sau đây?
A. \(\{ 3;5\} \) B. \(\{ 1;3;5;7;8;9\} \). C. \(\{ 1;7;9\} \). D. \(\{ 1;3;5\} \)
Câu 7. Biết rằng \({C_\mathbb{R}}A = [ - 3;11)\) và \({C_\mathbb{R}}B = ( - 8;1]\). Khi đó, \({C_\mathbb{R}}\left( {A \cap B} \right)\) bằng?
A. \(( - 8;11)\) B. \([3;1]\). C. \(( - \infty ; - 8] \cup [11; + \infty )\). D. \(( - \infty ; - 3) \cup (1; + \infty )\)
Câu 8. Cho mệnh đề: “Có học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:
A. Mọi học sinh trong lớp 10A đều thích học môn Văn.
B. Mọi học sinh trong lớp 10A đều không thích học môn Toán.
C. Có học sinh trong lớp 10A thích học môn Toán.
D. Mọi học sinh trong lớp 10A đều thích học môn Toán.
Câu 9. Cho hàm số \(f(x) = - {x^2} + 2x - 5\). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên \(( - \infty ;1)\), nghịch biến trên\((1; + \infty )\).
B. Hàm số đồng biến trên \((1; + \infty )\), nghịch biến trên\(( - \infty ;1)\).
C. Hàm số nghịch biến trên\(\mathbb{R}\).
D. Hàm số đồng biến trên\(\mathbb{R}\).
Câu 10. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\sqrt {x - 2} + 5\quad (x \ge 2)\\3{x^2} - x + 1\quad (x < 2)\end{array} \right.\). Giá trị của \(2.f(3) - 4.f(1)\) là:
A. \(38\) B. \(12\) C. \(0\). D. \( - 4\).
Câu 11. Trong mặt phẳng Oxy, phần nửa mặt phẳng không tô màu (không kể bờ) trong hình dưới đây biểu diễn tập nghiệm của bất phương trình nào?
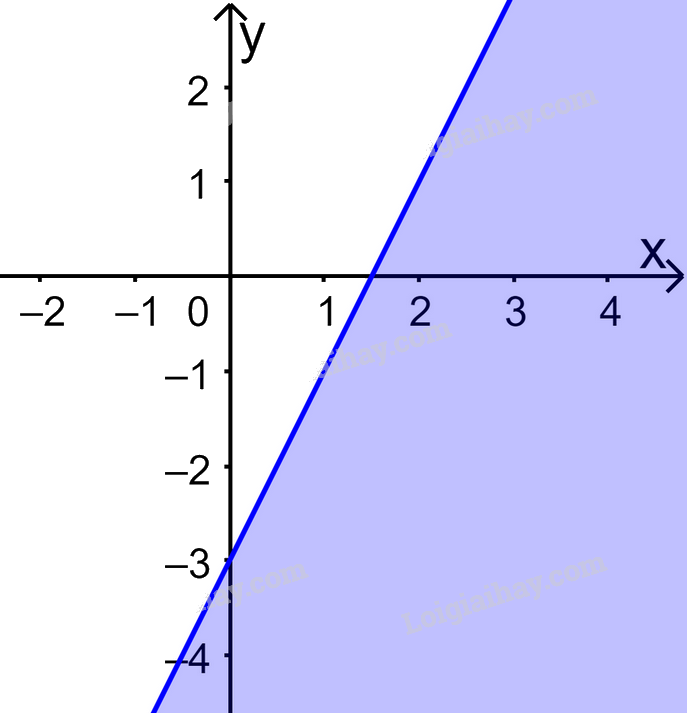
A.\(2x - y > 3\). B. \(2x - y < 3\). C. \(x - 2y > 3\). D. \(x - 2y < 3\).
Câu 12. Cho \(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} \), \(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} \), \(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} \), \(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} \). Khẳng định nào dưới đây đúng?
A.\(M \subset N\). B. \(Q \subset P\). C.\(M \cap N = N\). D. \(P \cap Q = Q\).
Câu 13. Cặp số \((2;3)\) không là nghiệm của bất phương trình nào sau đây?
A.\(2x - 3y - 1 < 0\). B. \(x - y > 0\). C.\(4x - 3y < 0\). D. \(x + 3y - 7 \ge 0\).
Câu 14. Cho hàm số \(y = {x^2} - 2x + 108\), mệnh đề nào sai?
A. Đồ thị hàm số nhận \(I(1;107)\) làm đỉnh
B. Hàm số đồng biến trên \((1; + \infty )\).
C. Hàm số nghịch biến trên\(( - 5;0)\).
D. Đồ thị hàm số có trục đối xứng \(x = - 1\).
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
II. PHẦN TỰ LUẬN
Câu 1.
a) Cho hai tập hợp \(A = \{ x \in \mathbb{Z}|(2x + 1)({x^2} - 9) = 0\} \) và \(B = \{ x \in \mathbb{N}|x < 4\} \). Xác định các tập hợp \(A \cap B,A \cup B,A{\rm{\backslash }}B\)
b) Cho hai tập hợp \(M = (0;3)\) và \(N = [m;m + 1)\). Tìm \(m \in \mathbb{Z}\) để \(M \cap N = N\)
Câu 2. Trong một đợt quảng cáo và bán khuyến mãi sản phẩm mới, công ty X cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, mỗi chiếc chở được tối đa 20 người và 0,6 tấn hàng, giá thuê là 4 triệu; xe loại B có 9 chiếc, mỗi chiếc chở được tối đa 10 người và 1,5 tấn hàng, giá thuê là 3 triệu. Hỏi công ty cần thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất?
Câu 3.
a) Xác định parabol (P) biết \((P):y = a{x^2} + bx + c\) đi qua A(2;-2) và có đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
b) Xét sự biến thiên và vẽ đồ thị hàm số trên.
Câu 4. Tìm giá trị lớn nhất, nhỏ nhất (nếu có) của hàm số: \(y = 3{x^2} - 6x + 7\) trên đoạn [0;8].
I. PHẦN TRẮC NGHIỆM
1. B | 2. C | 3. D | 4. C | 5. B |
6. B | 7. A | 8. D | 9. A | 10. C |
11. B | 12. C | 13. B | 14. D | 15. A |
Câu 1.
Cách giải:
Ta có: \(P(2) = 5,P(4) = 17,P(3) = 10,P(7) = 50\)
Chọn B
Câu 2.
Cách giải:
Thay \(x = 1,y = - 1\) vào từng bất phương trình, ta được:
\(1 + ( - 1) - 3 = 3 < 0\) => Lọai A
\( - 1 - ( - 1) = 0\) => Loại B
\(1 + 3.( - 1) + 1 = - 1 < 0\) => Chọn C
\( - 1 - 3.( - 1) - 1 = 1 > 0\) => Loại D
Chọn C
Câu 3.
Cách giải:
Viết lại mệnh đề đã cho: P: “\(\exists x \in \mathbb{R},{x^2} \le 0\)”
Suy ra \(\overline P :\) “\(\forall x \in \mathbb{R},{x^2} > 0\)”
Chọn D
Câu 4.
Cách giải:
Hàm số \(y = \frac{{x + 2}}{{{x^2} - 4x + 3}} + \sqrt {{x^2} - 9} \) xác định khi \(\left\{ \begin{array}{l}{x^2} - 4x + 3 \ne 0\\{x^2} - 9 \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}(x - 1)(x - 3) \ne 0\\{x^2} \ge 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left\{ \begin{array}{l}x \ne 1\\x \ne 3\end{array} \right.\\\left[ \begin{array}{l}x \ge 3\\x \le - 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 3\\x \le - 3\end{array} \right.\)
Vậy tập xác định \(D = ( - \infty ; - 3] \cup (3; + \infty ) = \mathbb{R}{\rm{\backslash }}( - 3;3]\)
Chọn C
Câu 5.
Cách giải:
Từ đồ thị hàm số ta thấy:
Hàm số đồng biến trên (0;12) và nghịch biến trên các khoảng \(( - \infty ;0)\) và \((12; + \infty )\)
Vì \( - 5 < - 1\) nên \(f( - 5) > f( - 1)\) => Loại A.
Vì \(7 < 11\) nên \(f(7) < f(11)\) => Chọn B.
Vì \(1 < 6\) nên \(f(1) < f(6)\) => Loại C.
Vì \(2022 > 20\) nên \(f(2022) < f(20)\) => Loại D.
Chọn B
Câu 6.
Cách giải:
Ta có: \(X \cup Y = \{ 1;3;5;7;8;9\} \)
Chọn B
Câu 7.
Cách giải:
Ta có: \({C_\mathbb{R}}A = [ - 3;11) \Rightarrow A = ( - \infty ; - 3) \cup [11; + \infty )\)
\({C_\mathbb{R}}B = ( - 8;1] \Rightarrow B = ( - \infty ; - 8] \cup (1; + \infty )\)
\(\begin{array}{l} \Rightarrow A \cap B = ( - \infty ; - 8] \cup [11; + \infty )\\ \Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = ( - 8;11)\end{array}\)
Chọn A
Câu 8.
Cách giải:
Phủ định của mệnh đề đó là: “Mọi học sinh trong lớp 10A đều thích học môn Toán”.
Chọn D
Câu 9.
Cách giải:
Hàm số \(f(x) = - {x^2} + 2x - 5\) có \(a = - 1 < 0,b = 2, - \frac{b}{{2a}} = 1\) và \(f(1) = - 4\)
Ta có bảng biến thiên:
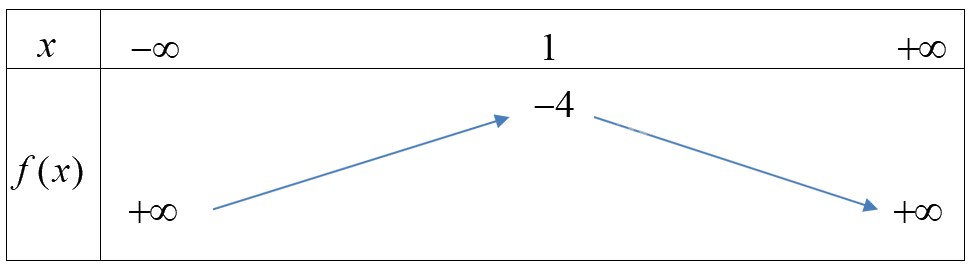
Hàm số đồng biến trên \(( - \infty ;1)\)và nghịch biến trên\((1; + \infty )\).
Chọn A
Câu 10.
Cách giải:
Tại \(x = 3 \ge 2\) thì \(f(3) = \sqrt {3 - 2} + 5 = 6\)
Tại \(x = 1 < 2\) thì \(f(1) = {3.1^2} - 1 + 1 = 3\)
\( \Rightarrow 2.f(3) - 4.f(1) = 2.6 - 4.3 = 0\)
Chọn C
Câu 11.
Cách giải:
+ Xác định đường thẳng là bở của miền nghiệm:
Đường thẳng d đi qua \(A(\frac{3}{2};0)\) và \(B(0; - 3)\) \( \Rightarrow d:2x - y = 3\)
+ Điểm O(0;0) thuộc miền nghiệm và \(2.0 - 0 = 0 < 3\)
Do đó BPT cần tìm là \(2x - y < 3\)
Chọn B
Câu 12.
Cách giải:
\(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} = \{ 0;2;4;6;8;...\} \)
\(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} = \{ 0;6;12;18;24;...\} \)
\(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} = \{ 1;2\} \)
\(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} = \{ 1;2;3;6\} \)
Ta có: \(N \subset M\) và \(P \subset Q\)
Do đó: \(M \cap N = N\) và \(P \cap Q = P\)
Chọn C
Câu 13.
Cách giải:
Thay \(x = 2,y = 3\) vào từng bất phương trình, ta được:
\(2.2 - 3.3 - 1 = - 6 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(2x - 3y - 1 < 0\)
\(2 - 3 = - 1 < 0 \Rightarrow A(2;3)\) không là nghiệm của BPT \(x - y > 0\)
\(4.2 - 3.3 = - 1 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(4x - 3y < 0\)
\(2 + 3.3 - 7 = 4 \ge 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(x + 3y - 7 \ge 0\)
Chọn B
Câu 14.
Cách giải:
Hàm số \(y = {x^2} - 2x + 108\) có \(a = 1 > 0,b = - 2,c = 108\)
\( \Rightarrow - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1;f(1) = 107\)
\( \Rightarrow \)Đồ thị hàm số có đỉnh \(I(1;107)\) và trục đối xứng \(x = 1\)
Hàm số đồng biến trên \((1; + \infty )\)và nghịch biến trên\(( - \infty ;1) \supset ( - 5;0)\).
Chọn D
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
Cách giải:
\(B \subset A \Leftrightarrow (m; + \infty ) \subset (2; + \infty ) \Leftrightarrow m \ge 2\)
Chọn A
II. PHẦN TỰ LUẬN
Câu 1:
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Ta có: \((2x + 1)({x^2} - 9) = 0 \Leftrightarrow (2x + 1)(x - 3)(x + 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - 3 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = 3\\x = - 3\end{array} \right.\)
Mà \( - \frac{1}{2} \notin \mathbb{Z}\)\( \Rightarrow A = \{ - 3;3\} \)
\(B = \{ x \in \mathbb{N}|x < 4\} = \{ 0;1;2;3\} \)
Do đó \(A \cap B = \{ 3\} ,A \cup B = \{ - 3;0;1;2;3\} ,A{\rm{\backslash }}B = \{ - 3\} \)
b) \(M = (0;3)\) và. Để \(M \cap N = N \Leftrightarrow N \subset M\)
\(\begin{array}{l} \Leftrightarrow [m;m + 1) \subset (0;3)\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m + 1 \le 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m \le 2\end{array} \right. \Leftrightarrow 0 < m \le 2\end{array}\)
Mà \(m \in \mathbb{Z}\) nên \(m = 1\) hoặc \(m = 2\).
Vậy \(m = 1\) hoặc \(m = 2\) thì \(M \cap N = N.\)
Câu 2:
Cách giải:
Gọi x là số xe loại A, y là số xe loại B mà công ty cần thuê (đơn vị: chiếc). \((x,y \in \mathbb{N})\)
Theo đề bài ta có: \(0 \le x \le 10\) và \(0 \le y \le 9\)
Tổng chi phí thuê xe là \(F(x;y) = 4x + 3y\) (triệu đồng)
Số người cần chở là 140 mà mỗi xe A chở tối đa 20 người, mỗi xe B chở tối đa 10 người nên ta có \(20x + 10y \ge 140\) hay \(2x + y \ge 14\)
Số hàng cần chở là 9 tấn mà mỗi xe A chở được 0,6 tấn, mỗi xe B chở được 1,5 tấn nên ta có \(0,6x + 1,5y \ge 9\) hay \(2x + 5y \ge 30\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\2x + y \ge 14\\2x + 5y \ge 30\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
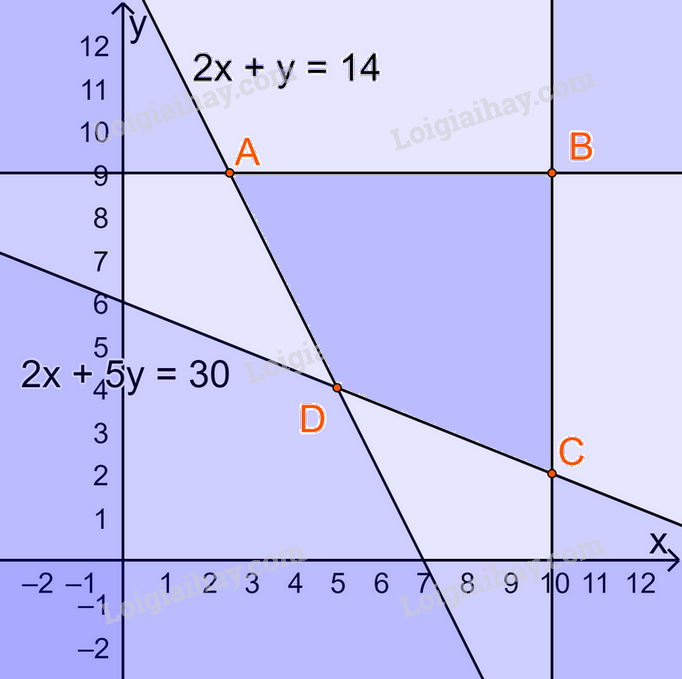
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(\frac{5}{2};9),B(10;9),C(10;2),D(5;4)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 4x + 3y\) ta được:
\(\begin{array}{l}F(\frac{5}{2};9) = 4.\frac{5}{2} + 3.9 = 37\\F(10;9) = 4.10 + 3.9 = 67\\F(10;2) = 4.10 + 3.2 = 46\\F(5;4) = 4.5 + 3.4 = 32\end{array}\)
Do đó F đạt giá trị nhỏ nhất bằng 32 tại \(x = 5;y = 4\)
Vậy công ty đó cần thuê 5 xe loại A và 4 xe loại B.
Câu 3
Cách giải:
a) Parabol \((P):y = a{x^2} + bx + c\) đi qua A(2;-2) nên \( - 2 = a{.2^2} + b.2 + c \Leftrightarrow 4a + 2b + c = - 2\)
Lại có: (P) có đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = \frac{5}{2}\\a.{\left( {\frac{5}{2}} \right)^2} + b.\left( {\frac{5}{2}} \right) + c = \frac{{ - 9}}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5a + b = 0\\25a + 10b + 4c = - 9\end{array} \right.\)
Thay \(b = - 5a\) ta được \(\left\{ \begin{array}{l}4a + 2.( - 5a) + c = - 2\\25a + 10.( - 5b) + 4c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6a + c = - 2\\ - 25a + 4c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = 4\end{array} \right.\)
Suy ra \(b = - 5a = - 5\)
Vậy parabol đó là \((P):y = {x^2} - 5x + 4\)
b) Parabol \((P):y = {x^2} - 5x + 4\) có \(a = 1 > 0,b = - 5\)
Bảng biến thiên
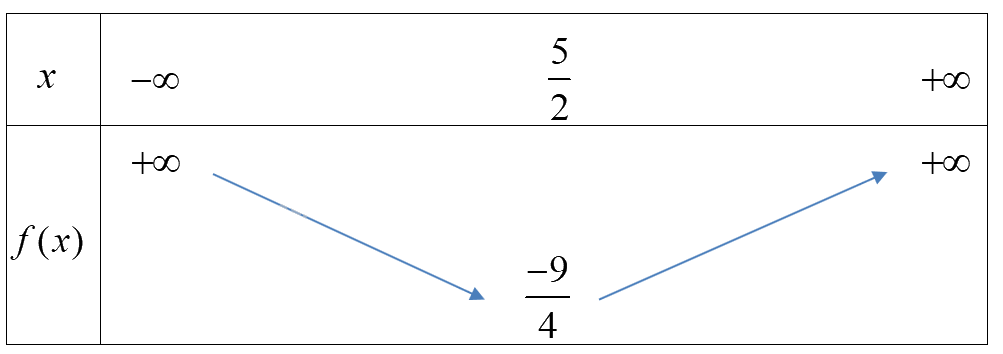
Hàm số đồng biến trên \((\frac{5}{2}; + \infty )\)và nghịch biến trên\(( - \infty ;\frac{5}{2})\).
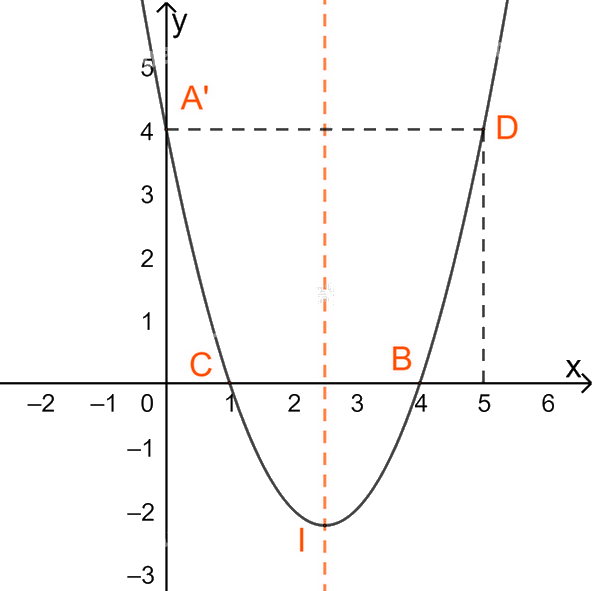
+ Vẽ đồ thị
Đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
(P) giao Oy tại điểm \(A'\left( {0;4} \right)\)
(P) giao Ox tại \(B(4;0)\) và \(C(1;0)\)
Điểm \(D(5;4)\) đối xứng với \(A'\left( {0;4} \right)\) qua trục đối xứng.
Câu 4.
Cách giải:
Hàm số \(y = 3{x^2} - 6x + 7\) có \(a = 3 > 0,b = - 6 \Rightarrow - \frac{b}{{2a}} = 1;\;y(1) = 4\).
Ta có bảng biến thiên
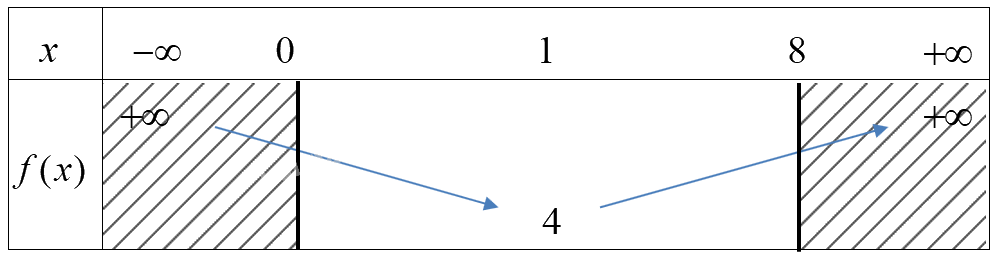
Mà \(f(0) = 7,f(8) = 151,f(1) = 4\)
\( \Rightarrow \) Trên [0;8]
Hàm số đạt GTLN bằng 151 tại \(x = 8\), đạt GTNN bằng 4 tại \(x = 1\).
Tải về
I. PHẦN TRẮC NGHIỆM
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai?
A. \(P(2)\) B. \(P(4)\). C. \(P(3)\). D. \(P(7)\)
Câu 2. Cặp số \((1; - 1)\) là nghiệm của bất phương trình nào sau đây?
A. \(x + y - 3 > 0\) B. \( - x - y < 0\). C. \(x + 3y + 1 < 0\). D. \( - x - 3y - 1 < 0\)
Câu 3. Mệnh đề phủ định của mệnh đề “Có một số thực sao cho bình phương của nó không là số nguyên dương”
A. \(\exists x \in \mathbb{R},{x^2} > 0\) B. \(\exists x \in \mathbb{R},{x^2} \le 0\). C. \(\forall x \in \mathbb{R},{x^2} \le 0\). D. \(\forall x \in \mathbb{R},{x^2} > 0\)
Câu 4. Tập xác định của hàm số \(y = \frac{{x + 2}}{{{x^2} - 4x + 3}} + \sqrt {{x^2} - 9} \)
A. \((3; + \infty )\). B. \(\mathbb{R}{\rm{\backslash }}\{ 1;3\} \) C. \(\mathbb{R}{\rm{\backslash }}( - 3;3]\). D. \(\mathbb{R}{\rm{\backslash }}[ - 3;3]\).
Câu 5. Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
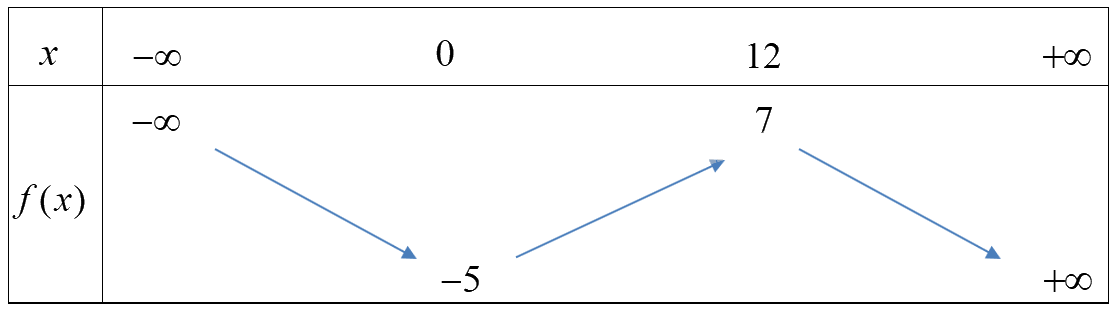
Khẳng định nào sau đây đúng?
A. \(f( - 5) < f( - 1)\) B. \(f(7) < f(11)\) C. \(f(1) > f(6)\) D. \(f(2022) > f(20)\)
Câu 6. Cho hai tập hợp \(X = \{ 1;3;5;8\} ,Y = \{ 3;5;7;9\} \). Tập hợp \(X \cup Y\) bằng tập hợp nào sau đây?
A. \(\{ 3;5\} \) B. \(\{ 1;3;5;7;8;9\} \). C. \(\{ 1;7;9\} \). D. \(\{ 1;3;5\} \)
Câu 7. Biết rằng \({C_\mathbb{R}}A = [ - 3;11)\) và \({C_\mathbb{R}}B = ( - 8;1]\). Khi đó, \({C_\mathbb{R}}\left( {A \cap B} \right)\) bằng?
A. \(( - 8;11)\) B. \([3;1]\). C. \(( - \infty ; - 8] \cup [11; + \infty )\). D. \(( - \infty ; - 3) \cup (1; + \infty )\)
Câu 8. Cho mệnh đề: “Có học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:
A. Mọi học sinh trong lớp 10A đều thích học môn Văn.
B. Mọi học sinh trong lớp 10A đều không thích học môn Toán.
C. Có học sinh trong lớp 10A thích học môn Toán.
D. Mọi học sinh trong lớp 10A đều thích học môn Toán.
Câu 9. Cho hàm số \(f(x) = - {x^2} + 2x - 5\). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên \(( - \infty ;1)\), nghịch biến trên\((1; + \infty )\).
B. Hàm số đồng biến trên \((1; + \infty )\), nghịch biến trên\(( - \infty ;1)\).
C. Hàm số nghịch biến trên\(\mathbb{R}\).
D. Hàm số đồng biến trên\(\mathbb{R}\).
Câu 10. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\sqrt {x - 2} + 5\quad (x \ge 2)\\3{x^2} - x + 1\quad (x < 2)\end{array} \right.\). Giá trị của \(2.f(3) - 4.f(1)\) là:
A. \(38\) B. \(12\) C. \(0\). D. \( - 4\).
Câu 11. Trong mặt phẳng Oxy, phần nửa mặt phẳng không tô màu (không kể bờ) trong hình dưới đây biểu diễn tập nghiệm của bất phương trình nào?
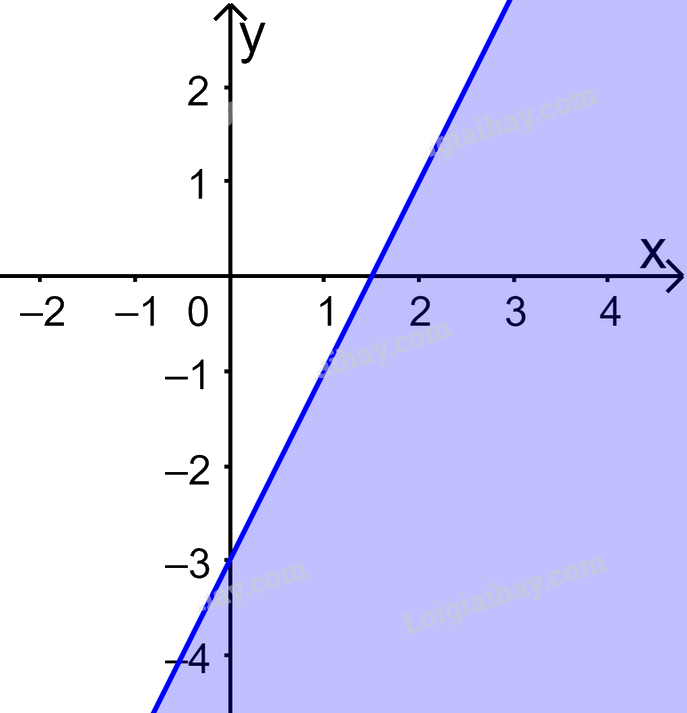
A.\(2x - y > 3\). B. \(2x - y < 3\). C. \(x - 2y > 3\). D. \(x - 2y < 3\).
Câu 12. Cho \(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} \), \(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} \), \(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} \), \(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} \). Khẳng định nào dưới đây đúng?
A.\(M \subset N\). B. \(Q \subset P\). C.\(M \cap N = N\). D. \(P \cap Q = Q\).
Câu 13. Cặp số \((2;3)\) không là nghiệm của bất phương trình nào sau đây?
A.\(2x - 3y - 1 < 0\). B. \(x - y > 0\). C.\(4x - 3y < 0\). D. \(x + 3y - 7 \ge 0\).
Câu 14. Cho hàm số \(y = {x^2} - 2x + 108\), mệnh đề nào sai?
A. Đồ thị hàm số nhận \(I(1;107)\) làm đỉnh
B. Hàm số đồng biến trên \((1; + \infty )\).
C. Hàm số nghịch biến trên\(( - 5;0)\).
D. Đồ thị hàm số có trục đối xứng \(x = - 1\).
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
II. PHẦN TỰ LUẬN
Câu 1.
a) Cho hai tập hợp \(A = \{ x \in \mathbb{Z}|(2x + 1)({x^2} - 9) = 0\} \) và \(B = \{ x \in \mathbb{N}|x < 4\} \). Xác định các tập hợp \(A \cap B,A \cup B,A{\rm{\backslash }}B\)
b) Cho hai tập hợp \(M = (0;3)\) và \(N = [m;m + 1)\). Tìm \(m \in \mathbb{Z}\) để \(M \cap N = N\)
Câu 2. Trong một đợt quảng cáo và bán khuyến mãi sản phẩm mới, công ty X cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, mỗi chiếc chở được tối đa 20 người và 0,6 tấn hàng, giá thuê là 4 triệu; xe loại B có 9 chiếc, mỗi chiếc chở được tối đa 10 người và 1,5 tấn hàng, giá thuê là 3 triệu. Hỏi công ty cần thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất?
Câu 3.
a) Xác định parabol (P) biết \((P):y = a{x^2} + bx + c\) đi qua A(2;-2) và có đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
b) Xét sự biến thiên và vẽ đồ thị hàm số trên.
Câu 4. Tìm giá trị lớn nhất, nhỏ nhất (nếu có) của hàm số: \(y = 3{x^2} - 6x + 7\) trên đoạn [0;8].
I. PHẦN TRẮC NGHIỆM
1. B | 2. C | 3. D | 4. C | 5. B |
6. B | 7. A | 8. D | 9. A | 10. C |
11. B | 12. C | 13. B | 14. D | 15. A |
Câu 1.
Cách giải:
Ta có: \(P(2) = 5,P(4) = 17,P(3) = 10,P(7) = 50\)
Chọn B
Câu 2.
Cách giải:
Thay \(x = 1,y = - 1\) vào từng bất phương trình, ta được:
\(1 + ( - 1) - 3 = 3 < 0\) => Lọai A
\( - 1 - ( - 1) = 0\) => Loại B
\(1 + 3.( - 1) + 1 = - 1 < 0\) => Chọn C
\( - 1 - 3.( - 1) - 1 = 1 > 0\) => Loại D
Chọn C
Câu 3.
Cách giải:
Viết lại mệnh đề đã cho: P: “\(\exists x \in \mathbb{R},{x^2} \le 0\)”
Suy ra \(\overline P :\) “\(\forall x \in \mathbb{R},{x^2} > 0\)”
Chọn D
Câu 4.
Cách giải:
Hàm số \(y = \frac{{x + 2}}{{{x^2} - 4x + 3}} + \sqrt {{x^2} - 9} \) xác định khi \(\left\{ \begin{array}{l}{x^2} - 4x + 3 \ne 0\\{x^2} - 9 \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}(x - 1)(x - 3) \ne 0\\{x^2} \ge 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left\{ \begin{array}{l}x \ne 1\\x \ne 3\end{array} \right.\\\left[ \begin{array}{l}x \ge 3\\x \le - 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 3\\x \le - 3\end{array} \right.\)
Vậy tập xác định \(D = ( - \infty ; - 3] \cup (3; + \infty ) = \mathbb{R}{\rm{\backslash }}( - 3;3]\)
Chọn C
Câu 5.
Cách giải:
Từ đồ thị hàm số ta thấy:
Hàm số đồng biến trên (0;12) và nghịch biến trên các khoảng \(( - \infty ;0)\) và \((12; + \infty )\)
Vì \( - 5 < - 1\) nên \(f( - 5) > f( - 1)\) => Loại A.
Vì \(7 < 11\) nên \(f(7) < f(11)\) => Chọn B.
Vì \(1 < 6\) nên \(f(1) < f(6)\) => Loại C.
Vì \(2022 > 20\) nên \(f(2022) < f(20)\) => Loại D.
Chọn B
Câu 6.
Cách giải:
Ta có: \(X \cup Y = \{ 1;3;5;7;8;9\} \)
Chọn B
Câu 7.
Cách giải:
Ta có: \({C_\mathbb{R}}A = [ - 3;11) \Rightarrow A = ( - \infty ; - 3) \cup [11; + \infty )\)
\({C_\mathbb{R}}B = ( - 8;1] \Rightarrow B = ( - \infty ; - 8] \cup (1; + \infty )\)
\(\begin{array}{l} \Rightarrow A \cap B = ( - \infty ; - 8] \cup [11; + \infty )\\ \Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = ( - 8;11)\end{array}\)
Chọn A
Câu 8.
Cách giải:
Phủ định của mệnh đề đó là: “Mọi học sinh trong lớp 10A đều thích học môn Toán”.
Chọn D
Câu 9.
Cách giải:
Hàm số \(f(x) = - {x^2} + 2x - 5\) có \(a = - 1 < 0,b = 2, - \frac{b}{{2a}} = 1\) và \(f(1) = - 4\)
Ta có bảng biến thiên:
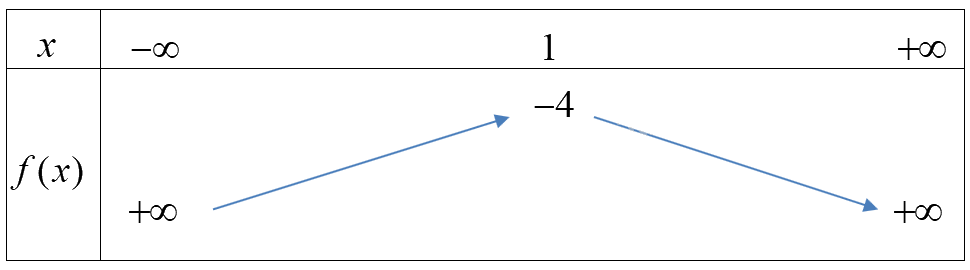
Hàm số đồng biến trên \(( - \infty ;1)\)và nghịch biến trên\((1; + \infty )\).
Chọn A
Câu 10.
Cách giải:
Tại \(x = 3 \ge 2\) thì \(f(3) = \sqrt {3 - 2} + 5 = 6\)
Tại \(x = 1 < 2\) thì \(f(1) = {3.1^2} - 1 + 1 = 3\)
\( \Rightarrow 2.f(3) - 4.f(1) = 2.6 - 4.3 = 0\)
Chọn C
Câu 11.
Cách giải:
+ Xác định đường thẳng là bở của miền nghiệm:
Đường thẳng d đi qua \(A(\frac{3}{2};0)\) và \(B(0; - 3)\) \( \Rightarrow d:2x - y = 3\)
+ Điểm O(0;0) thuộc miền nghiệm và \(2.0 - 0 = 0 < 3\)
Do đó BPT cần tìm là \(2x - y < 3\)
Chọn B
Câu 12.
Cách giải:
\(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} = \{ 0;2;4;6;8;...\} \)
\(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} = \{ 0;6;12;18;24;...\} \)
\(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} = \{ 1;2\} \)
\(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} = \{ 1;2;3;6\} \)
Ta có: \(N \subset M\) và \(P \subset Q\)
Do đó: \(M \cap N = N\) và \(P \cap Q = P\)
Chọn C
Câu 13.
Cách giải:
Thay \(x = 2,y = 3\) vào từng bất phương trình, ta được:
\(2.2 - 3.3 - 1 = - 6 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(2x - 3y - 1 < 0\)
\(2 - 3 = - 1 < 0 \Rightarrow A(2;3)\) không là nghiệm của BPT \(x - y > 0\)
\(4.2 - 3.3 = - 1 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(4x - 3y < 0\)
\(2 + 3.3 - 7 = 4 \ge 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(x + 3y - 7 \ge 0\)
Chọn B
Câu 14.
Cách giải:
Hàm số \(y = {x^2} - 2x + 108\) có \(a = 1 > 0,b = - 2,c = 108\)
\( \Rightarrow - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1;f(1) = 107\)
\( \Rightarrow \)Đồ thị hàm số có đỉnh \(I(1;107)\) và trục đối xứng \(x = 1\)
Hàm số đồng biến trên \((1; + \infty )\)và nghịch biến trên\(( - \infty ;1) \supset ( - 5;0)\).
Chọn D
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
Cách giải:
\(B \subset A \Leftrightarrow (m; + \infty ) \subset (2; + \infty ) \Leftrightarrow m \ge 2\)
Chọn A
II. PHẦN TỰ LUẬN
Câu 1:
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Ta có: \((2x + 1)({x^2} - 9) = 0 \Leftrightarrow (2x + 1)(x - 3)(x + 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - 3 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = 3\\x = - 3\end{array} \right.\)
Mà \( - \frac{1}{2} \notin \mathbb{Z}\)\( \Rightarrow A = \{ - 3;3\} \)
\(B = \{ x \in \mathbb{N}|x < 4\} = \{ 0;1;2;3\} \)
Do đó \(A \cap B = \{ 3\} ,A \cup B = \{ - 3;0;1;2;3\} ,A{\rm{\backslash }}B = \{ - 3\} \)
b) \(M = (0;3)\) và. Để \(M \cap N = N \Leftrightarrow N \subset M\)
\(\begin{array}{l} \Leftrightarrow [m;m + 1) \subset (0;3)\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m + 1 \le 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m \le 2\end{array} \right. \Leftrightarrow 0 < m \le 2\end{array}\)
Mà \(m \in \mathbb{Z}\) nên \(m = 1\) hoặc \(m = 2\).
Vậy \(m = 1\) hoặc \(m = 2\) thì \(M \cap N = N.\)
Câu 2:
Cách giải:
Gọi x là số xe loại A, y là số xe loại B mà công ty cần thuê (đơn vị: chiếc). \((x,y \in \mathbb{N})\)
Theo đề bài ta có: \(0 \le x \le 10\) và \(0 \le y \le 9\)
Tổng chi phí thuê xe là \(F(x;y) = 4x + 3y\) (triệu đồng)
Số người cần chở là 140 mà mỗi xe A chở tối đa 20 người, mỗi xe B chở tối đa 10 người nên ta có \(20x + 10y \ge 140\) hay \(2x + y \ge 14\)
Số hàng cần chở là 9 tấn mà mỗi xe A chở được 0,6 tấn, mỗi xe B chở được 1,5 tấn nên ta có \(0,6x + 1,5y \ge 9\) hay \(2x + 5y \ge 30\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\2x + y \ge 14\\2x + 5y \ge 30\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
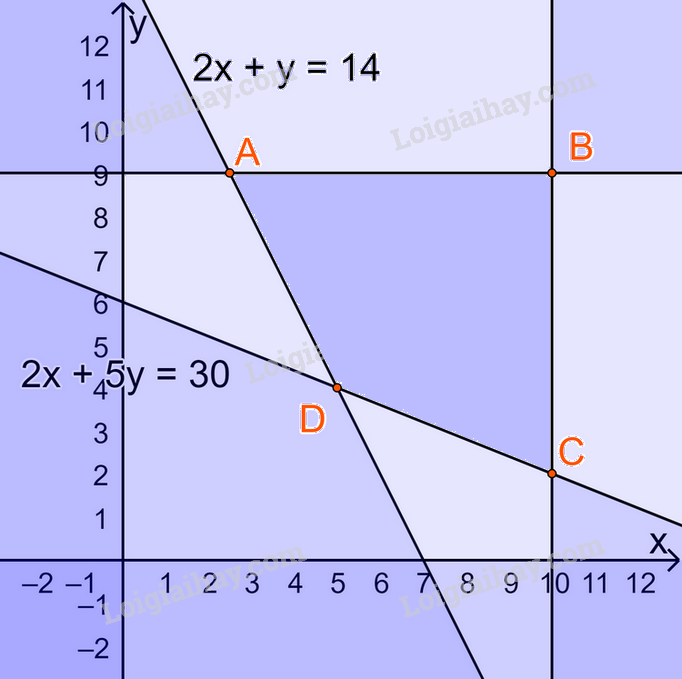
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(\frac{5}{2};9),B(10;9),C(10;2),D(5;4)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 4x + 3y\) ta được:
\(\begin{array}{l}F(\frac{5}{2};9) = 4.\frac{5}{2} + 3.9 = 37\\F(10;9) = 4.10 + 3.9 = 67\\F(10;2) = 4.10 + 3.2 = 46\\F(5;4) = 4.5 + 3.4 = 32\end{array}\)
Do đó F đạt giá trị nhỏ nhất bằng 32 tại \(x = 5;y = 4\)
Vậy công ty đó cần thuê 5 xe loại A và 4 xe loại B.
Câu 3
Cách giải:
a) Parabol \((P):y = a{x^2} + bx + c\) đi qua A(2;-2) nên \( - 2 = a{.2^2} + b.2 + c \Leftrightarrow 4a + 2b + c = - 2\)
Lại có: (P) có đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = \frac{5}{2}\\a.{\left( {\frac{5}{2}} \right)^2} + b.\left( {\frac{5}{2}} \right) + c = \frac{{ - 9}}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5a + b = 0\\25a + 10b + 4c = - 9\end{array} \right.\)
Thay \(b = - 5a\) ta được \(\left\{ \begin{array}{l}4a + 2.( - 5a) + c = - 2\\25a + 10.( - 5b) + 4c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6a + c = - 2\\ - 25a + 4c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = 4\end{array} \right.\)
Suy ra \(b = - 5a = - 5\)
Vậy parabol đó là \((P):y = {x^2} - 5x + 4\)
b) Parabol \((P):y = {x^2} - 5x + 4\) có \(a = 1 > 0,b = - 5\)
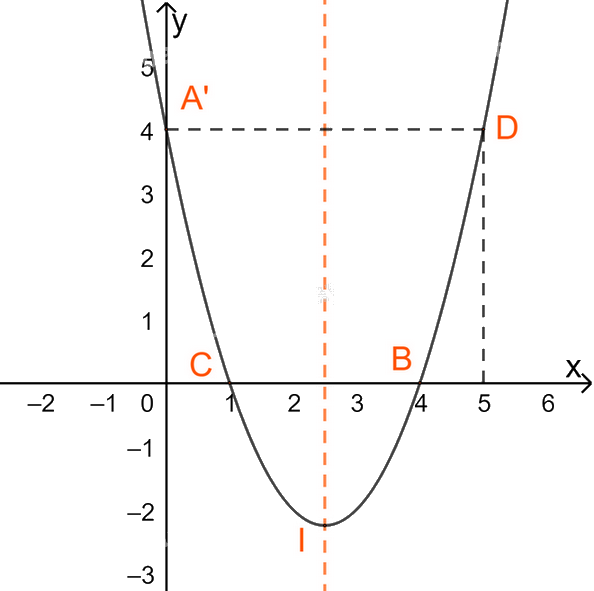
Bảng biến thiên
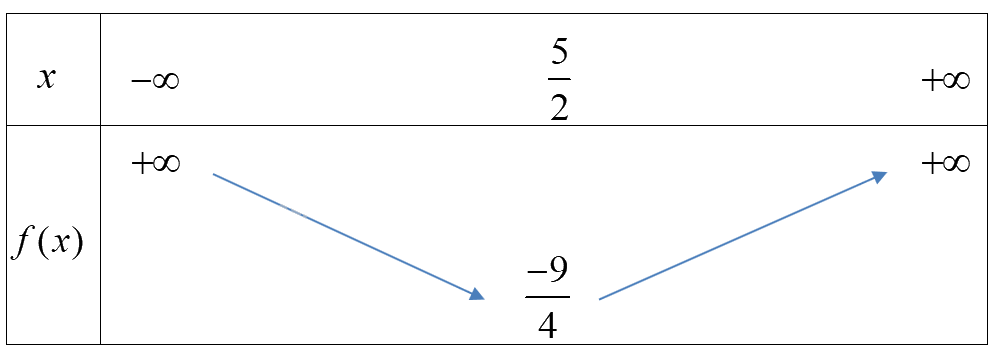
Hàm số đồng biến trên \((\frac{5}{2}; + \infty )\)và nghịch biến trên\(( - \infty ;\frac{5}{2})\).
+ Vẽ đồ thị
Đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
(P) giao Oy tại điểm \(A'\left( {0;4} \right)\)
(P) giao Ox tại \(B(4;0)\) và \(C(1;0)\)
Điểm \(D(5;4)\) đối xứng với \(A'\left( {0;4} \right)\) qua trục đối xứng.
Câu 4.
Cách giải:
Hàm số \(y = 3{x^2} - 6x + 7\) có \(a = 3 > 0,b = - 6 \Rightarrow - \frac{b}{{2a}} = 1;\;y(1) = 4\).
Ta có bảng biến thiên
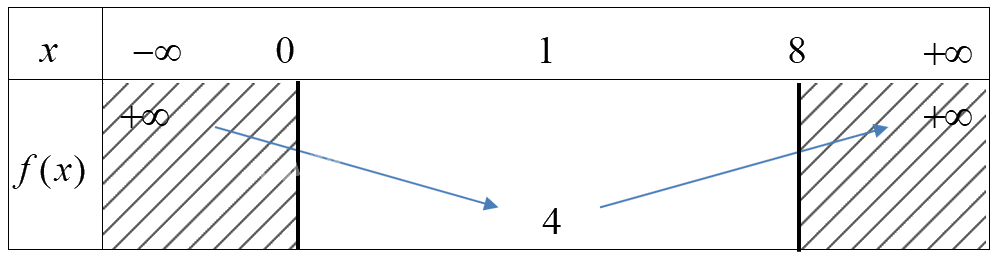
Mà \(f(0) = 7,f(8) = 151,f(1) = 4\)
\( \Rightarrow \) Trên [0;8]
Hàm số đạt GTLN bằng 151 tại \(x = 8\), đạt GTNN bằng 4 tại \(x = 1\).
Đề thi giữa kì 1 Toán 10 Cánh diều - Đề số 5 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập thuộc chương trình đại số và hình học, đòi hỏi học sinh phải có khả năng vận dụng linh hoạt các công thức, định lý và kỹ năng giải toán cơ bản.
Thông thường, đề thi giữa kì 1 Toán 10 Cánh diều - Đề số 5 có cấu trúc tương tự như sau:
Để đạt kết quả tốt trong đề thi giữa kì 1 Toán 10 Cánh diều - Đề số 5, học sinh cần nắm vững các kiến thức sau:
1. Giải phương trình bậc hai: Sử dụng công thức nghiệm tổng quát hoặc phương pháp phân tích thành nhân tử.
2. Giải hệ phương trình tuyến tính: Sử dụng phương pháp thế hoặc phương pháp cộng đại số.
3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: Sử dụng phương pháp hoàn thiện bình phương hoặc phương pháp khảo sát hàm số.
4. Chứng minh bất đẳng thức: Sử dụng các tính chất của bất đẳng thức, các bất đẳng thức quen thuộc (Cauchy-Schwarz, AM-GM).
5. Tính góc trong tam giác: Sử dụng định lý tổng ba góc trong một tam giác.
Để chuẩn bị tốt nhất cho đề thi giữa kì 1 Toán 10 Cánh diều - Đề số 5, học sinh nên:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu học tập, bài giảng, đề thi và đáp án chi tiết môn Toán lớp 10, giúp học sinh học tập hiệu quả và đạt kết quả cao trong các kỳ thi. Truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu hữu ích khác!
Bài tập: Giải phương trình 2x2 - 5x + 2 = 0
Lời giải:
Phương trình có dạng ax2 + bx + c = 0 với a = 2, b = -5, c = 2.
Tính delta: Δ = b2 - 4ac = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + 3) / (2 * 2) = 2
x2 = (-b - √Δ) / 2a = (5 - 3) / (2 * 2) = 0.5
Vậy phương trình có hai nghiệm x1 = 2 và x2 = 0.5