Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 10 Cánh diều - Đề số 1, được biên soạn theo chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 2. Đi kèm với đề thi là đáp án chi tiết, giúp học sinh tự đánh giá kết quả và rút kinh nghiệm.
Phần trắc nghiệm (7 điểm) Câu 1: Nam muốn tô màu cho một hình vuông và một hình tròn. Biết rằng chỉ có thể tô màu xanh, màu đỏ hoặc màu vàng cho hình vuông, và chỉ có thể tô màu hồng hoặc màu tím cho hình tròn. Hỏi Nam có bao nhiêu cách tô màu cho hai hình?
Phần trắc nghiệm
Câu 1. D | Câu 2. B | Câu 3. C | Câu 4. C | Câu 5. C | Câu 6. B | Câu 7. B |
Câu 8. C | Câu 9. B | Câu 10. C | Câu 11. B | Câu 12. C | Câu 13. A | Câu 14. B |
Câu 15. B | Câu 16. D | Câu 17. D | Câu 18. A | Câu 19. A | Câu 20. C | Câu 21. A |
Câu 22. B | Câu 23. C | Câu 24. C | Câu 25. A | Câu 26. B | Câu 27. B | Câu 28. A |
Câu 29. D | Câu 30. A | Câu 31. C | Câu 32. D | Câu 33. D | Câu 34. D | Câu 35. B |
Câu 1: Nam muốn tô màu cho một hình vuông và một hình tròn. Biết rằng chỉ có thể tô màu xanh, màu
đỏ hoặc màu vàng cho hình vuông, và chỉ có thể tô màu hồng hoặc màu tím cho hình tròn. Hỏi Nam có bao nhiêu cách tô màu cho hai hình?
A. 2 cách.
B. 3 cách.
C. 5 cách.
D. 6 cách.
Lời giải
Đáp án D.
Câu 2: Từ Hà Nội bay vào Đà Nẵng có các chuyến bay trực tiếp của ba hãng máy bay. Hãng thứ nhất cung cấp 4 chuyến bay mỗi ngày. Hãng thứ hai cung cấp 3 chuyến bay mỗi ngày. Hãng thứ ba cung cấp 1 chuyến bay mỗi ngày. Hỏi mỗi ngày có bao nhiêu cách bay trực tiếp từ Hà Nội vào Đà Nẵng?
A. 3 cách.
B. 8 cách.
C. 12 cách.
D. 16 cách.
Lời giải
Đáp án B.
Câu 3: Lớp \(10\;A\) có 21 bạn nam và 18 bạn nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
A. 168 cách.
B. 29 cách.
C. 39 cách.
D. 158 cách.
Lời giải
Đáp án C.
Câu 4: Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?
A. 5 cách.
B. 7 cách.
C. 10 cách.
D. 3 cách.
Lời giải
Đáp án C.
Câu 5: Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?
A. 5 cách.
B. 7 cách.
C. 10 cách.
D. 3 cách.
Lời giải
Đáp án C.
Câu 6: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 10 học sinh?
A. \(A_{10}^2\).
B. \(C_{10}^2\).
C. \({10^2}\).
D. \({2^{10}}\).
Lời giải
Đáp án B.
Câu 7: Có 5 con ngựa chạy đua. Hỏi có bao nhiêu kết quả có thể xảy ra? Biết rằng không có hai con ngựa nào vể đích cùng lúc.
A. 2!.
B. 5!.
C. \(C_5^2\).
D. \(A_5^2\).
Lời giải
Đáp án B.
Câu 8: Đội tuyển toán có 5 bạn nam và 7 bạn nữ. Giáo viên phải chọn ra một nhóm bốn bạn. Hỏi giáo viên có bao nhiêu cách chọn?
A. \(\frac{{12!}}{{4!}}\).
B. 12!.
C. \(C_{12}^4\).
D. \(A_{12}^4\).
Lời giải
Đáp án C.
Câu 9: Một lớp có 34 học sinh. Hỏi có bao nhiêu cách chọn ra 10 học sinh để tham gia hoạt động trồng cây của trường?
A. \(A_{34}^{10}\).
B. \(C_{34}^{10}\).
C. \(\frac{{34!}}{{10!}}\).
D. \(\frac{{10!}}{{(34 - 10)!}}\).
Lời giải
Đáp án B.
Câu 10: Cho tập hợp \(A = \{ 1;2;3;4;5;6;7\} \). Hỏi có bao nhiêu cách lập được số có ba chữ số khác nhau từ các chữ số thuộc tập hợp \(A\)?
A. \(C_7^3\).
B. \(C_7^4\).
C. \(A_7^3\).
D. \(A_7^4\).
Lời giải
Đáp án C.
Câu 11: Số cách chia 10 học sinh thành ba nhóm lần lượt có \(2,3,5\) học sinh là:
A. \(C_{10}^2 + C_{10}^3 + C_{10}^5\).
B. \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\).
C. \(C_{10}^2 + C_8^3 + C_5^5\).
D. \(C_{10}^5 + C_5^3 + C_2^2\).
Lời giải
Chọn 2 trong 10 học sinh vào nhóm thứ nhất: có \(C_{10}^2\) cách.
Chọn 3 trong 8 học sinh còn lại vào nhóm thứ hai: có \(C_8^3\) cách.
Chọn 5 trong 5 học sinh cuối cùng vào nhóm thứ ba: có \(C_5^5\) cách.
Vậy có \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\) cách chọn thỏa mãn đề bài.
Đáp án B.
Câu 12: Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
A. 5!.7!.
B. \(2.5!.7!\).
C. \(5!.8!\).
D. \(12!\).
Lời giải
Sắp xếp 5 quyển Văn chung một nhóm ngang (nhóm \(V)\): có 5! cách.
Sắp xếp 7 quyển Toán với \(V\) (ta xem như sắp xếp 8 phần tử): có \(8!\) cách. Vậy có tất cả \(5!.8!\) cách sắp xếp thỏa mãn đề bài.
Đáp án C.
Câu 13: Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:
A. \(\frac{{5!}}{{2!}}\).
B. 8.
C. \(\frac{{5!}}{{3!2!}}\).
D. \({5^3}\).
Lời giải
Chọn 3 trong 5 màu để tô vào 3 nước khác nhau: có \(A_5^3 = \frac{{5!}}{{2!}}\) cách.
Đáp án A.
Câu 14: Trong mặt phẳng cho 2010 điểm phân biệt. Hỏi có bao nhiêu vectơ khác \(\vec 0\) có điểm đầu và điểm cuối lấy từ 2010 điểm đã cho?
A. 4039137.
B. 4038090.
C. 4167114.
D. 167541284.
Lời giải
Số vectơ thỏa mãn là \(A_{2010}^2 = 4038090\).
Đáp án B.
Câu 15: Khai triển của \({(x + 1)^4}\) là:
A. \({x^4} + 2{x^2} + 1\).
B. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).
C. \({x^4} + 5{x^3} + 10{x^2} + 5x + 1\).
D. \({x^4} + 3{x^3} + 4{x^2} + 3x + 1\).
Lời giải
Đáp án B.
Câu 16: Hệ số của \({x^3}\) trong khai triển của \({(2x + 1)^4}\) là:
A. 4.
B. 6.
C. 10.
D. 32.
Lời giải
Đáp án D.
Câu 17: Tổng các hệ số trong khai triển của \({(x + 2)^4}\) là:
A. 14.
B. 16.
C. 79.
D. 81.
Lời giải
Đáp án D.
Câu 18: Hệ số của \({x^2}\) trong khai triển của \({(2x - 3)^4}\) là:
A. 216.
B. 16.
C. \( - 16\).
D. \( - 216\).
Lời giải
Đáp án A.
Câu 19: Giả sử có khai triển \({(1 - 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\). Tìm \({a_4}\) biết \({a_0} + {a_1} + {a_2} = 31\).
A. 80.
B. \( - 80\).
C. 40.
D. \( - 40\).
Lời giải
Ta có:
\({(1 - 2x)^n} = C_n^0{1^n}{( - 2x)^0} + C_n^1{n^{n - 1}}( - 2x) + C_n^2{n^{n - 2}}{( - 2x)^2} + \ldots = 1 - 2C_n^1x + 4C_n^2{x^2} + \ldots \)
Vậy \({a_0} = 1;{a_1} = - 2C_n^1;{a_2} = 4C_n^2\). Theo bài ra \({a_0} + {a_1} + {a_2} = 31\) nên ta có:
\(1 - 2C_n^1 + 4C_n^2 = 31 \Leftrightarrow 1 - 2\frac{{n!}}{{1!(n - 1)!}} + 4\frac{{n!}}{{2!(n - 2)!}} = 31 \Leftrightarrow 1 - 2n + 2n(n - 1) = 31\)
\( \Leftrightarrow 2{n^2} - 4n - 30 = 0 \Leftrightarrow {n^2} - 2n - 15 = 0 \Rightarrow n = 5\). Từ đó ta có \({a_4} = C_5^4{( - 2)^4} = 80\).
Đáp án A.
Câu 20: Trong mặt phẳng toạ độ \(Oxy\), toạ độ của vectơ \(2\vec i - 7\vec j\) là:
A. \((2;7)\).
B. \(( - 2;7)\).
C. \((2; - 7)\).
D. \(( - 7;2)\).
Lời giải
Đáp án C.
Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(3; - 2)\). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. \((3; - 2)\).
B. \(( - 3;2)\).
C. \(( - 2;3)\).
D. \((2; - 3)\).
Lời giải
Đáp án A.
Câu 22: Trong mặt phẳng toạ độ \(Oxy\), cho \(A( - 3;2),B(5; - 1)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \((2;1)\).
B. \((8; - 3)\).
C. \(( - 8;3)\).
D. \(( - 2; - 1)\).
Lời giải
Đáp án B.
Câu 23: Trong mặt phẳng toạ độ \(Oxy\) cho các vectơ \(\vec a,\vec b,\vec c,\vec d\) được vẽ ở hình bên. Ta có các khẳng định sau:
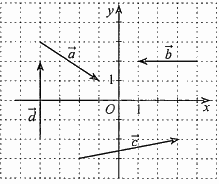
a) \(\vec a = (2; - 3)\);
b) \(\vec b = ( - 3;0)\);
c) \(\vec c = (5;1)\);
d) \(\vec d = (4;0)\).
A. 0.
B. 1.
C. 2.
D. 3.
Lời giải
Đáp án C.
Câu 24: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (2; - 3),\vec b = ( - 2;5)\). Toạ độ của vectơ \( - \vec a + 3\vec b\) là:
A. \((8;18)\).
B. \(( - 8; - 18)\).
C. \(( - 8;18)\).
D. \((8; - 18)\).
Lời giải
Ta có: \( - \vec a = ( - 2;3)\) và \(3\vec b = ( - 6;15)\). Suy ra \( - \vec a + 3\vec b = ( - 8;18)\).
Đáp án C.
Câu 25: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (1;2),\vec b = (3; - 3)\). Toạ độ của vectơ \(\vec c = 3\vec a - 2\vec b\) là:
A. \(( - 3;12)\).
B. \((3;12)\).
C. \((9;0)\).
D. \(( - 3;0)\).
Lời giải
Ta có: \(3\vec a = (3;6)\) và \( - 2\vec b = ( - 6;6)\). Suy ra \(3\vec a - 2\vec b = ( - 3;12)\).
Đáp án A.
Câu 26: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( - 1;2),B(2; - 2),C(3;1)\). Toạ độ của vectơ \(\overrightarrow {AB} + \overrightarrow {BC} \) là:
A. \(( - 4; - 1)\).
B. \((4; - 1)\).
C. \(( - 4;1)\).
D. \((4;1)\).
Lời giải
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} = (4; - 1)\).
Đáp án B.
Câu 27: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( - 1;2),B(0; - 2),C(3;3)\). Toạ độ của vectơ \(2\overrightarrow {AB} - 4\overrightarrow {BC} \) là:
A. \((14;12)\).
B. \(( - 10; - 28)\).
C. \(( - 14; - 12)\).
D. \((10;28)\).
Lời giải
Ta có: \(\overrightarrow {AB} = (1; - 4) \Rightarrow 2\overrightarrow {AB} = (2; - 8)\); \(\overrightarrow {BC} = (3;5) \Rightarrow 4\overrightarrow {BC} = (12;20).\)
Suy ra \(2\overrightarrow {AB} - 4\overrightarrow {BC} = ( - 10; - 28)\).
Đáp án B.
Câu 28: Trong mặt phẳng toạ độ \(Oxy\), cặp vectơ nào sau đây có cùng phương?
A. \(\vec a = \left( { - \frac{2}{3};2} \right)\) và \(\vec b = (2; - 6)\).
B. \(\vec u = (2;1)\) và \(\vec v = (2; - 6)\).
C. \(\vec c = (\sqrt 2 ;2\sqrt 2 )\) và \(\vec d = (2;2)\).
D. \(\vec e = (1; - 1)\) và \(\vec f = (3;3)\).
Lời giải
Đáp án A.
Câu 29: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải
Đáp án D.
Câu 30: Một vectơ pháp tuyến của đường thẳng \(\Delta :y = 2x + 1\) là:
A. \(\overrightarrow {{n_\Delta }} (2; - 1)\).
B. \(\overrightarrow {{n_\Delta }} (1; - 1)\).
C. \(\overrightarrow {{n_\Delta }} ( - 2; - 1)\).
D. \(\overrightarrow {{n_\Delta }} (1;1)\).
Lời giải
Đáp án A.
Câu 31: Đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow {{u_\Delta }} (12; - 13)\). Vectơ nào sau đây là vectơ pháp tuyến của \(\Delta \)?
A. \(\overrightarrow {{n_\Delta }} ( - 13;12)\).
B. \(\overrightarrow {{n_\Delta }} (12;13)\).
C. \(\overrightarrow {{n_\Delta }} (13;12)\).
D. \(\overrightarrow {{n_\Delta }} ( - 12; - 13)\).
Lời giải
Đáp án C.
Câu 32: Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:
A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).
B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).
C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).
D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Lời giải
Đáp án D.
Câu 33: Trong mặt phẳng toạ độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\), \({\Delta _2}:3x - y + 7 = 0\). Nhận định nào sau đây là đúng?
A. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
B. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
C. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trùng nhau.
D. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
Lời giải
Đáp án D.
Câu 34: Người ta quy ước góc giữa hai đường thẳng song song hoặc trùng nhau là:
A. \({180^0}\).
B. \({120^0}\).
C. \({90^0}\).
D. \({0^0}\).
Lời giải
Đáp án D.
Câu 35: Cho \(\alpha \) là góc tạo bởi hai đường thẳng \({\Delta _1}:2x - 3y + 5 = 0\) và \({\Delta _2}:3x + y - 14 = 0\). Giá trị của cosa là:
A. \(\frac{{ - 3}}{{130}}\).
B. \(\frac{3}{{\sqrt {130} }}\).
C. \(\frac{{\sqrt 3 }}{{130}}\).
D. \(\frac{{ - 3}}{{\sqrt {130} }}\)
Lời giải
Đáp án B.
Phần tự luận (3 điểm)
Bài 1. Từ một nhóm 30 học sinh lớp 12 gồm 15 học sinh khối \(A,10\) học sinh khối \(B\) và 5 học sinh khối \(C\), cần chọn ra 15 học sinh, hỏi có bao nhiêu cách chọn sao cho:
a) Số học sinh mỗi khối là bằng nhau?
b) Có ít nhất 5 học sinh khối \(A\) và có đúng 2 học sinh khối \(C\)?
Lời giải
a) Số cách chọn 5 học sinh mỗi khối \((A,B,C)\) lần lượt là: \(C_{15}^5,C_{10}^5,C_5^5\).
Vậy số cách chọn thỏa mãn là \(C_{15}^5 \times C_{10}^5 \times C_5^5 = 756756\) (cách).
b) Ta sử dụng quy tắc loại trừ như Lời giải sau:
Xét bài toán 1: Chọn 2 học sinh khối \(C,13\) học sinh khối \(B\) hoặc khối \(A\): có \(C_5^2C_{25}^{13}\) cách.
Xét bài toán 2: Chọn 2 học sinh khối \(C,13\) học sinh khối \(B\) và khối \(A\) không thỏa mãn yêu cầu.
- Trường hợp 1: Chọn 2 học sinh khối \(C,10\) học sinh khối \(B\) và 3 học sinh khối A có \(C_5^2C_{10}^{10}C_{15}^3\) cách.
- Trường hợp 2: Chọn 2 học sinh khối \(C,9\) học sinh khối \(B\) và 4 học sinh khối A có \(C_5^2C_{10}^9C_{15}^4\) cách.
Vậy số cách chọn thỏa mãn là \(C_5^2C_{25}^{13} - C_{10}^{10}C_{15}^3 - C_{10}^9C_{15}^4 = 51861950\) (cách).
Bài 2. Cho biểu thức \(Q = {(xy - 1)^5}\).
a) Viết khai triển biểu thức \(Q\) bằng nhị thức Newton.
b) Tìm số hạng có chứa \({x^2}{y^2}\) trong khai triển trên.
Lời giải
a) Ta có: \(Q = {(xy - 1)^5} = C_5^0{(xy)^5} + C_5^1{(xy)^4}( - 1) + C_5^2{(xy)^3}{( - 1)^2}\)
\(\begin{array}{l} + C_5^3{(xy)^2}{( - 1)^3} + C_5^4(xy){( - 1)^4} + C_5^5{( - 1)^5}\\ = {x^5}{y^5} - 5{x^4}{y^4} + 10{x^3}{y^3} - 10{x^2}{y^2} + 5xy - 1.\end{array}\)
b) Số hạng có chứa \({x^2}{y^2}\) trong khai triển là \( - 10{x^2}{y^2}\).
Bài 3. Cho các vectơ \(\vec a = (2;0),\vec b = \left( { - 1;\frac{1}{2}} \right),\vec c = (4; - 6)\).
a) Tìm tọa độ của vectơ \(\vec d = 2\vec a - 3\vec b + 5\vec c\).
b) Biểu diễn vectơ \(\vec c\) theo cặp vectơ không cùng phương \(\vec a,\vec b\).
Lời giải
a) Ta có: \(\left\{ {\begin{array}{*{20}{l}}{2\vec a = (4;0)}\\{ - 3\vec b = \left( {3; - \frac{3}{2}} \right) \Rightarrow \vec d = 2\vec a - 3\vec b + 5\vec c = \left( {27; - \frac{{63}}{2}} \right)}\\{5\vec c = (20; - 30)}\end{array}} \right.\)
b) Gọi: \(\vec c = x\vec a + y\vec b(x,y \in \mathbb{R})\). Ta có: \(\left\{ {\begin{array}{*{20}{l}}{4 = x \cdot 2 + y( - 1)}\\{ - 6 = x \cdot 0 + y \cdot \frac{1}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 4}\\{y = - 12}\end{array}} \right.} \right.\) Vậy \(\vec c = - 4\vec a - 12\vec b\).
Bài 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x - y + 4 = 0\).
a) Viết phương trình đường cao \(AH\) của tam giác.
b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.
Lời giải
a) Đường cao \(AH\) vuông góc với \(BC\) nên nhận \(\vec u = (1; - 1)\) làm vectơ chỉ phương, suy ra \(AH\) có một vectơ pháp tuyến là \(\vec n = (1;1)\).
Phương trình tổng quát \(AH:1(x + 1) + 1(y + 2) = 0\) hay \(x + y + 3 = 0\).
b) Chọn điểm \(K(0;4)\) thuộc \(BC\), gọi \(E\) là trung điểm đoạn \(AK\) nên \(E\left( { - \frac{1}{2};1} \right)\). Gọi \(d\) là đường trung bình ứng với cạnh đáy \(BC\) của tam giác \(ABC\), suy ra \(d\) qua \(E\) và có một vectơ pháp tuyến .
Phương trình tổng quát \(d:1\left( {x + \frac{1}{2}} \right) - 1(y - 1) = 0\) hay \(2x - 2y + 3 = 0\).
Phần trắc nghiệm (7 điểm)
Câu 1: Nam muốn tô màu cho một hình vuông và một hình tròn. Biết rằng chỉ có thể tô màu xanh, màu
đỏ hoặc màu vàng cho hình vuông, và chỉ có thể tô màu hồng hoặc màu tím cho hình tròn. Hỏi Nam có bao nhiêu cách tô màu cho hai hình?
A. 2 cách.
B. 3 cách.
C. 5 cách.
D. 6 cách.
Câu 2: Từ Hà Nội bay vào Đà Nẵng có các chuyến bay trực tiếp của ba hãng máy bay. Hãng thứ nhất cung cấp 4 chuyến bay mỗi ngày. Hãng thứ hai cung cấp 3 chuyến bay mỗi ngày. Hãng thứ ba cung cấp 1 chuyến bay mỗi ngày. Hỏi mỗi ngày có bao nhiêu cách bay trực tiếp từ Hà Nội vào Đà Nẵng?
A. 3 cách.
B. 8 cách.
C. 12 cách.
D. 16 cách.
Câu 3: Lớp \(10\;A\) có 21 bạn nam và 18 bạn nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
A. 168 cách.
B. 29 cách.
C. 39 cách.
D. 158 cách.
Câu 4: Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?
A. 5 cách.
B. 7 cách.
C. 10 cách.
D. 3 cách.
Câu 5: Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?
A. 5 cách.
B. 7 cách.
C. 10 cách.
D. 3 cách.
Câu 6: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 10 học sinh?
A. \(A_{10}^2\).
B. \(C_{10}^2\).
C. \({10^2}\).
D. \({2^{10}}\).
Câu 7: Có 5 con ngựa chạy đua. Hỏi có bao nhiêu kết quả có thể xảy ra? Biết rằng không có hai con ngựa nào vể đích cùng lúc.
A. 2!.
B. 5!.
C. \(C_5^2\).
D. \(A_5^2\).
Câu 8: Đội tuyển toán có 5 bạn nam và 7 bạn nữ. Giáo viên phải chọn ra một nhóm bốn bạn. Hỏi giáo viên có bao nhiêu cách chọn?
A. \(\frac{{12!}}{{4!}}\).
B. 12!.
C. \(C_{12}^4\).
D. \(A_{12}^4\).
Câu 9: Một lớp có 34 học sinh. Hỏi có bao nhiêu cách chọn ra 10 học sinh để tham gia hoạt động trồng cây của trường?
A. \(A_{34}^{10}\).
B. \(C_{34}^{10}\).
C. \(\frac{{34!}}{{10!}}\).
D. \(\frac{{10!}}{{(34 - 10)!}}\).
Câu 10: Cho tập hợp \(A = \{ 1;2;3;4;5;6;7\} \). Hỏi có bao nhiêu cách lập được số có ba chữ số khác nhau từ các chữ số thuộc tập hợp \(A\)?
A. \(C_7^3\).
B. \(C_7^4\).
C. \(A_7^3\).
D. \(A_7^4\).
Câu 11: Số cách chia 10 học sinh thành ba nhóm lần lượt có \(2,3,5\) học sinh là:
A. \(C_{10}^2 + C_{10}^3 + C_{10}^5\).
B. \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\).
C. \(C_{10}^2 + C_8^3 + C_5^5\).
D. \(C_{10}^5 + C_5^3 + C_2^2\).
Câu 12: Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
A. 5!.7!.
B. \(2.5!.7!\).
C. \(5!.8!\).
D. \(12!\).
Câu 13: Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:
A. \(\frac{{5!}}{{2!}}\).
B. 8.
C. \(\frac{{5!}}{{3!2!}}\).
D. \({5^3}\).
Câu 14: Trong mặt phẳng cho 2010 điểm phân biệt. Hỏi có bao nhiêu vectơ khác \(\vec 0\) có điểm đầu và điểm cuối lấy từ 2010 điểm đã cho?
A. 4039137.
B. 4038090.
C. 4167114.
D. 167541284.
Câu 15: Khai triển của \({(x + 1)^4}\) là:
A. \({x^4} + 2{x^2} + 1\).
B. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).
C. \({x^4} + 5{x^3} + 10{x^2} + 5x + 1\).
D. \({x^4} + 3{x^3} + 4{x^2} + 3x + 1\).
Câu 16: Hệ số của \({x^3}\) trong khai triển của \({(2x + 1)^4}\) là:
A. 4.
B. 6.
C. 10.
D. 32.
Câu 17: Tổng các hệ số trong khai triển của \({(x + 2)^4}\) là:
A. 14.
B. 16.
C. 79.
D. 81.
Câu 18: Hệ số của \({x^2}\) trong khai triển của \({(2x - 3)^4}\) là:
A. 216.
B. 16.
C. \( - 16\).
D. \( - 216\).
Câu 19: Giả sử có khai triển \({(1 - 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\). Tìm \({a_4}\) biết \({a_0} + {a_1} + {a_2} = 31\).
A. 80.
B. \( - 80\).
C. 40.
D. \( - 40\).
Câu 20: Trong mặt phẳng toạ độ \(Oxy\), toạ độ của vectơ \(2\vec i - 7\vec j\) là:
A. \((2;7)\).
B. \(( - 2;7)\).
C. \((2; - 7)\).
D. \(( - 7;2)\).
Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(3; - 2)\). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. \((3; - 2)\).
B. \(( - 3;2)\).
C. \(( - 2;3)\).
D. \((2; - 3)\).
Câu 22: Trong mặt phẳng toạ độ \(Oxy\), cho \(A( - 3;2),B(5; - 1)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \((2;1)\).
B. \((8; - 3)\).
C. \(( - 8;3)\).
D. \(( - 2; - 1)\).
Câu 23: Trong mặt phẳng toạ độ \(Oxy\) cho các vectơ \(\vec a,\vec b,\vec c,\vec d\) được vẽ ở hình bên. Ta có các khẳng định sau:
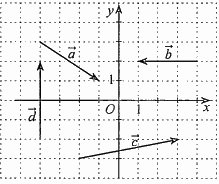
a) \(\vec a = (2; - 3)\);
b) \(\vec b = ( - 3;0)\);
c) \(\vec c = (5;1)\);
d) \(\vec d = (4;0)\).
A. 0.
B. 1.
C. 2.
D. 3.
Câu 24: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (2; - 3),\vec b = ( - 2;5)\). Toạ độ của vectơ \( - \vec a + 3\vec b\) là:
A. \((8;18)\).
B. \(( - 8; - 18)\).
C. \(( - 8;18)\).
D. \((8; - 18)\).
Câu 25: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (1;2),\vec b = (3; - 3)\). Toạ độ của vectơ \(\vec c = 3\vec a - 2\vec b\) là:
A. \(( - 3;12)\).
B. \((3;12)\).
C. \((9;0)\).
D. \(( - 3;0)\).
Câu 26: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( - 1;2),B(2; - 2),C(3;1)\). Toạ độ của vectơ \(\overrightarrow {AB} + \overrightarrow {BC} \) là:
A. \(( - 4; - 1)\).
B. \((4; - 1)\).
C. \(( - 4;1)\).
D. \((4;1)\).
Câu 27: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( - 1;2),B(0; - 2),C(3;3)\). Toạ độ của vectơ \(2\overrightarrow {AB} - 4\overrightarrow {BC} \) là:
A. \((14;12)\).
B. \(( - 10; - 28)\).
C. \(( - 14; - 12)\).
D. \((10;28)\).
Câu 28: Trong mặt phẳng toạ độ \(Oxy\), cặp vectơ nào sau đây có cùng phương?
A. \(\vec a = \left( { - \frac{2}{3};2} \right)\) và \(\vec b = (2; - 6)\).
B. \(\vec u = (2;1)\) và \(\vec v = (2; - 6)\).
C. \(\vec c = (\sqrt 2 ;2\sqrt 2 )\) và \(\vec d = (2;2)\).
D. \(\vec e = (1; - 1)\) và \(\vec f = (3;3)\).
Câu 29: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 0.
B. 1.
C. 2.
D. Vô số.
Câu 30: Một vectơ pháp tuyến của đường thẳng \(\Delta :y = 2x + 1\) là:
A. \(\overrightarrow {{n_\Delta }} (2; - 1)\).
B. \(\overrightarrow {{n_\Delta }} (1; - 1)\).
C. \(\overrightarrow {{n_\Delta }} ( - 2; - 1)\).
D. \(\overrightarrow {{n_\Delta }} (1;1)\).
Câu 31: Đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow {{u_\Delta }} (12; - 13)\). Vectơ nào sau đây là vectơ pháp tuyến của \(\Delta \)?
A. \(\overrightarrow {{n_\Delta }} ( - 13;12)\).
B. \(\overrightarrow {{n_\Delta }} (12;13)\).
C. \(\overrightarrow {{n_\Delta }} (13;12)\).
D. \(\overrightarrow {{n_\Delta }} ( - 12; - 13)\).
Câu 32: Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:
A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).
B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).
C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).
D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Câu 33: Trong mặt phẳng toạ độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\), \({\Delta _2}:3x - y + 7 = 0\). Nhận định nào sau đây là đúng?
A. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
B. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
C. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trùng nhau.
D. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
Câu 34: Người ta quy ước góc giữa hai đường thẳng song song hoặc trùng nhau là:
A. \({180^0}\).
B. \({120^0}\).
C. \({90^0}\).
D. \({0^0}\).
Câu 35: Cho \(\alpha \) là góc tạo bởi hai đường thẳng \({\Delta _1}:2x - 3y + 5 = 0\) và \({\Delta _2}:3x + y - 14 = 0\). Giá trị của cosa là:
A. \(\frac{{ - 3}}{{130}}\).
B. \(\frac{3}{{\sqrt {130} }}\).
C. \(\frac{{\sqrt 3 }}{{130}}\).
D. \(\frac{{ - 3}}{{\sqrt {130} }}\)
Phần tự luận (3 điểm)
Bài 1. Từ một nhóm 30 học sinh lớp 12 gồm 15 học sinh khối \(A,10\) học sinh khối \(B\) và 5 học sinh khối \(C\), cần chọn ra 15 học sinh, hỏi có bao nhiêu cách chọn sao cho:
a) Số học sinh mỗi khối là bằng nhau?
b) Có ít nhất 5 học sinh khối \(A\) và có đúng 2 học sinh khối \(C\)?
Bài 2. Cho biểu thức \(Q = {(xy - 1)^5}\).
a) Viết khai triển biểu thức \(Q\) bằng nhị thức Newton.
b) Tìm số hạng có chứa \({x^2}{y^2}\) trong khai triển trên.
Bài 3. Cho các vectơ \(\vec a = (2;0),\vec b = \left( { - 1;\frac{1}{2}} \right),\vec c = (4; - 6)\).
a) Tìm tọa độ của vectơ \(\vec d = 2\vec a - 3\vec b + 5\vec c\).
b) Biểu diễn vectơ \(\vec c\) theo cặp vectơ không cùng phương \(\vec a,\vec b\).
Bài 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x - y + 4 = 0\).
a) Viết phương trình đường cao \(AH\) của tam giác.
b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.
-------- Hết --------
Tải về
Phần trắc nghiệm (7 điểm)
Câu 1: Nam muốn tô màu cho một hình vuông và một hình tròn. Biết rằng chỉ có thể tô màu xanh, màu
đỏ hoặc màu vàng cho hình vuông, và chỉ có thể tô màu hồng hoặc màu tím cho hình tròn. Hỏi Nam có bao nhiêu cách tô màu cho hai hình?
A. 2 cách.
B. 3 cách.
C. 5 cách.
D. 6 cách.
Câu 2: Từ Hà Nội bay vào Đà Nẵng có các chuyến bay trực tiếp của ba hãng máy bay. Hãng thứ nhất cung cấp 4 chuyến bay mỗi ngày. Hãng thứ hai cung cấp 3 chuyến bay mỗi ngày. Hãng thứ ba cung cấp 1 chuyến bay mỗi ngày. Hỏi mỗi ngày có bao nhiêu cách bay trực tiếp từ Hà Nội vào Đà Nẵng?
A. 3 cách.
B. 8 cách.
C. 12 cách.
D. 16 cách.
Câu 3: Lớp \(10\;A\) có 21 bạn nam và 18 bạn nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
A. 168 cách.
B. 29 cách.
C. 39 cách.
D. 158 cách.
Câu 4: Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?
A. 5 cách.
B. 7 cách.
C. 10 cách.
D. 3 cách.
Câu 5: Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?
A. 5 cách.
B. 7 cách.
C. 10 cách.
D. 3 cách.
Câu 6: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 10 học sinh?
A. \(A_{10}^2\).
B. \(C_{10}^2\).
C. \({10^2}\).
D. \({2^{10}}\).
Câu 7: Có 5 con ngựa chạy đua. Hỏi có bao nhiêu kết quả có thể xảy ra? Biết rằng không có hai con ngựa nào vể đích cùng lúc.
A. 2!.
B. 5!.
C. \(C_5^2\).
D. \(A_5^2\).
Câu 8: Đội tuyển toán có 5 bạn nam và 7 bạn nữ. Giáo viên phải chọn ra một nhóm bốn bạn. Hỏi giáo viên có bao nhiêu cách chọn?
A. \(\frac{{12!}}{{4!}}\).
B. 12!.
C. \(C_{12}^4\).
D. \(A_{12}^4\).
Câu 9: Một lớp có 34 học sinh. Hỏi có bao nhiêu cách chọn ra 10 học sinh để tham gia hoạt động trồng cây của trường?
A. \(A_{34}^{10}\).
B. \(C_{34}^{10}\).
C. \(\frac{{34!}}{{10!}}\).
D. \(\frac{{10!}}{{(34 - 10)!}}\).
Câu 10: Cho tập hợp \(A = \{ 1;2;3;4;5;6;7\} \). Hỏi có bao nhiêu cách lập được số có ba chữ số khác nhau từ các chữ số thuộc tập hợp \(A\)?
A. \(C_7^3\).
B. \(C_7^4\).
C. \(A_7^3\).
D. \(A_7^4\).
Câu 11: Số cách chia 10 học sinh thành ba nhóm lần lượt có \(2,3,5\) học sinh là:
A. \(C_{10}^2 + C_{10}^3 + C_{10}^5\).
B. \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\).
C. \(C_{10}^2 + C_8^3 + C_5^5\).
D. \(C_{10}^5 + C_5^3 + C_2^2\).
Câu 12: Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
A. 5!.7!.
B. \(2.5!.7!\).
C. \(5!.8!\).
D. \(12!\).
Câu 13: Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:
A. \(\frac{{5!}}{{2!}}\).
B. 8.
C. \(\frac{{5!}}{{3!2!}}\).
D. \({5^3}\).
Câu 14: Trong mặt phẳng cho 2010 điểm phân biệt. Hỏi có bao nhiêu vectơ khác \(\vec 0\) có điểm đầu và điểm cuối lấy từ 2010 điểm đã cho?
A. 4039137.
B. 4038090.
C. 4167114.
D. 167541284.
Câu 15: Khai triển của \({(x + 1)^4}\) là:
A. \({x^4} + 2{x^2} + 1\).
B. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).
C. \({x^4} + 5{x^3} + 10{x^2} + 5x + 1\).
D. \({x^4} + 3{x^3} + 4{x^2} + 3x + 1\).
Câu 16: Hệ số của \({x^3}\) trong khai triển của \({(2x + 1)^4}\) là:
A. 4.
B. 6.
C. 10.
D. 32.
Câu 17: Tổng các hệ số trong khai triển của \({(x + 2)^4}\) là:
A. 14.
B. 16.
C. 79.
D. 81.
Câu 18: Hệ số của \({x^2}\) trong khai triển của \({(2x - 3)^4}\) là:
A. 216.
B. 16.
C. \( - 16\).
D. \( - 216\).
Câu 19: Giả sử có khai triển \({(1 - 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\). Tìm \({a_4}\) biết \({a_0} + {a_1} + {a_2} = 31\).
A. 80.
B. \( - 80\).
C. 40.
D. \( - 40\).
Câu 20: Trong mặt phẳng toạ độ \(Oxy\), toạ độ của vectơ \(2\vec i - 7\vec j\) là:
A. \((2;7)\).
B. \(( - 2;7)\).
C. \((2; - 7)\).
D. \(( - 7;2)\).
Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(3; - 2)\). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. \((3; - 2)\).
B. \(( - 3;2)\).
C. \(( - 2;3)\).
D. \((2; - 3)\).
Câu 22: Trong mặt phẳng toạ độ \(Oxy\), cho \(A( - 3;2),B(5; - 1)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \((2;1)\).
B. \((8; - 3)\).
C. \(( - 8;3)\).
D. \(( - 2; - 1)\).
Câu 23: Trong mặt phẳng toạ độ \(Oxy\) cho các vectơ \(\vec a,\vec b,\vec c,\vec d\) được vẽ ở hình bên. Ta có các khẳng định sau:
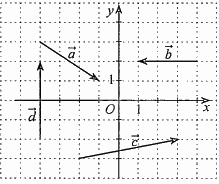
a) \(\vec a = (2; - 3)\);
b) \(\vec b = ( - 3;0)\);
c) \(\vec c = (5;1)\);
d) \(\vec d = (4;0)\).
A. 0.
B. 1.
C. 2.
D. 3.
Câu 24: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (2; - 3),\vec b = ( - 2;5)\). Toạ độ của vectơ \( - \vec a + 3\vec b\) là:
A. \((8;18)\).
B. \(( - 8; - 18)\).
C. \(( - 8;18)\).
D. \((8; - 18)\).
Câu 25: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (1;2),\vec b = (3; - 3)\). Toạ độ của vectơ \(\vec c = 3\vec a - 2\vec b\) là:
A. \(( - 3;12)\).
B. \((3;12)\).
C. \((9;0)\).
D. \(( - 3;0)\).
Câu 26: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( - 1;2),B(2; - 2),C(3;1)\). Toạ độ của vectơ \(\overrightarrow {AB} + \overrightarrow {BC} \) là:
A. \(( - 4; - 1)\).
B. \((4; - 1)\).
C. \(( - 4;1)\).
D. \((4;1)\).
Câu 27: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( - 1;2),B(0; - 2),C(3;3)\). Toạ độ của vectơ \(2\overrightarrow {AB} - 4\overrightarrow {BC} \) là:
A. \((14;12)\).
B. \(( - 10; - 28)\).
C. \(( - 14; - 12)\).
D. \((10;28)\).
Câu 28: Trong mặt phẳng toạ độ \(Oxy\), cặp vectơ nào sau đây có cùng phương?
A. \(\vec a = \left( { - \frac{2}{3};2} \right)\) và \(\vec b = (2; - 6)\).
B. \(\vec u = (2;1)\) và \(\vec v = (2; - 6)\).
C. \(\vec c = (\sqrt 2 ;2\sqrt 2 )\) và \(\vec d = (2;2)\).
D. \(\vec e = (1; - 1)\) và \(\vec f = (3;3)\).
Câu 29: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 0.
B. 1.
C. 2.
D. Vô số.
Câu 30: Một vectơ pháp tuyến của đường thẳng \(\Delta :y = 2x + 1\) là:
A. \(\overrightarrow {{n_\Delta }} (2; - 1)\).
B. \(\overrightarrow {{n_\Delta }} (1; - 1)\).
C. \(\overrightarrow {{n_\Delta }} ( - 2; - 1)\).
D. \(\overrightarrow {{n_\Delta }} (1;1)\).
Câu 31: Đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow {{u_\Delta }} (12; - 13)\). Vectơ nào sau đây là vectơ pháp tuyến của \(\Delta \)?
A. \(\overrightarrow {{n_\Delta }} ( - 13;12)\).
B. \(\overrightarrow {{n_\Delta }} (12;13)\).
C. \(\overrightarrow {{n_\Delta }} (13;12)\).
D. \(\overrightarrow {{n_\Delta }} ( - 12; - 13)\).
Câu 32: Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:
A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).
B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).
C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).
D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Câu 33: Trong mặt phẳng toạ độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\), \({\Delta _2}:3x - y + 7 = 0\). Nhận định nào sau đây là đúng?
A. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
B. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
C. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trùng nhau.
D. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
Câu 34: Người ta quy ước góc giữa hai đường thẳng song song hoặc trùng nhau là:
A. \({180^0}\).
B. \({120^0}\).
C. \({90^0}\).
D. \({0^0}\).
Câu 35: Cho \(\alpha \) là góc tạo bởi hai đường thẳng \({\Delta _1}:2x - 3y + 5 = 0\) và \({\Delta _2}:3x + y - 14 = 0\). Giá trị của cosa là:
A. \(\frac{{ - 3}}{{130}}\).
B. \(\frac{3}{{\sqrt {130} }}\).
C. \(\frac{{\sqrt 3 }}{{130}}\).
D. \(\frac{{ - 3}}{{\sqrt {130} }}\)
Phần tự luận (3 điểm)
Bài 1. Từ một nhóm 30 học sinh lớp 12 gồm 15 học sinh khối \(A,10\) học sinh khối \(B\) và 5 học sinh khối \(C\), cần chọn ra 15 học sinh, hỏi có bao nhiêu cách chọn sao cho:
a) Số học sinh mỗi khối là bằng nhau?
b) Có ít nhất 5 học sinh khối \(A\) và có đúng 2 học sinh khối \(C\)?
Bài 2. Cho biểu thức \(Q = {(xy - 1)^5}\).
a) Viết khai triển biểu thức \(Q\) bằng nhị thức Newton.
b) Tìm số hạng có chứa \({x^2}{y^2}\) trong khai triển trên.
Bài 3. Cho các vectơ \(\vec a = (2;0),\vec b = \left( { - 1;\frac{1}{2}} \right),\vec c = (4; - 6)\).
a) Tìm tọa độ của vectơ \(\vec d = 2\vec a - 3\vec b + 5\vec c\).
b) Biểu diễn vectơ \(\vec c\) theo cặp vectơ không cùng phương \(\vec a,\vec b\).
Bài 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x - y + 4 = 0\).
a) Viết phương trình đường cao \(AH\) của tam giác.
b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.
-------- Hết --------
Phần trắc nghiệm
Câu 1. D | Câu 2. B | Câu 3. C | Câu 4. C | Câu 5. C | Câu 6. B | Câu 7. B |
Câu 8. C | Câu 9. B | Câu 10. C | Câu 11. B | Câu 12. C | Câu 13. A | Câu 14. B |
Câu 15. B | Câu 16. D | Câu 17. D | Câu 18. A | Câu 19. A | Câu 20. C | Câu 21. A |
Câu 22. B | Câu 23. C | Câu 24. C | Câu 25. A | Câu 26. B | Câu 27. B | Câu 28. A |
Câu 29. D | Câu 30. A | Câu 31. C | Câu 32. D | Câu 33. D | Câu 34. D | Câu 35. B |
Câu 1: Nam muốn tô màu cho một hình vuông và một hình tròn. Biết rằng chỉ có thể tô màu xanh, màu
đỏ hoặc màu vàng cho hình vuông, và chỉ có thể tô màu hồng hoặc màu tím cho hình tròn. Hỏi Nam có bao nhiêu cách tô màu cho hai hình?
A. 2 cách.
B. 3 cách.
C. 5 cách.
D. 6 cách.
Lời giải
Đáp án D.
Câu 2: Từ Hà Nội bay vào Đà Nẵng có các chuyến bay trực tiếp của ba hãng máy bay. Hãng thứ nhất cung cấp 4 chuyến bay mỗi ngày. Hãng thứ hai cung cấp 3 chuyến bay mỗi ngày. Hãng thứ ba cung cấp 1 chuyến bay mỗi ngày. Hỏi mỗi ngày có bao nhiêu cách bay trực tiếp từ Hà Nội vào Đà Nẵng?
A. 3 cách.
B. 8 cách.
C. 12 cách.
D. 16 cách.
Lời giải
Đáp án B.
Câu 3: Lớp \(10\;A\) có 21 bạn nam và 18 bạn nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
A. 168 cách.
B. 29 cách.
C. 39 cách.
D. 158 cách.
Lời giải
Đáp án C.
Câu 4: Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?
A. 5 cách.
B. 7 cách.
C. 10 cách.
D. 3 cách.
Lời giải
Đáp án C.
Câu 5: Một quán ăn phục vụ 5 món ăn vặt và 2 loại nước uống. Hỏi bạn Mai có bao nhiêu cách để gọi một món ăn và một loại nước uống?
A. 5 cách.
B. 7 cách.
C. 10 cách.
D. 3 cách.
Lời giải
Đáp án C.
Câu 6: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 10 học sinh?
A. \(A_{10}^2\).
B. \(C_{10}^2\).
C. \({10^2}\).
D. \({2^{10}}\).
Lời giải
Đáp án B.
Câu 7: Có 5 con ngựa chạy đua. Hỏi có bao nhiêu kết quả có thể xảy ra? Biết rằng không có hai con ngựa nào vể đích cùng lúc.
A. 2!.
B. 5!.
C. \(C_5^2\).
D. \(A_5^2\).
Lời giải
Đáp án B.
Câu 8: Đội tuyển toán có 5 bạn nam và 7 bạn nữ. Giáo viên phải chọn ra một nhóm bốn bạn. Hỏi giáo viên có bao nhiêu cách chọn?
A. \(\frac{{12!}}{{4!}}\).
B. 12!.
C. \(C_{12}^4\).
D. \(A_{12}^4\).
Lời giải
Đáp án C.
Câu 9: Một lớp có 34 học sinh. Hỏi có bao nhiêu cách chọn ra 10 học sinh để tham gia hoạt động trồng cây của trường?
A. \(A_{34}^{10}\).
B. \(C_{34}^{10}\).
C. \(\frac{{34!}}{{10!}}\).
D. \(\frac{{10!}}{{(34 - 10)!}}\).
Lời giải
Đáp án B.
Câu 10: Cho tập hợp \(A = \{ 1;2;3;4;5;6;7\} \). Hỏi có bao nhiêu cách lập được số có ba chữ số khác nhau từ các chữ số thuộc tập hợp \(A\)?
A. \(C_7^3\).
B. \(C_7^4\).
C. \(A_7^3\).
D. \(A_7^4\).
Lời giải
Đáp án C.
Câu 11: Số cách chia 10 học sinh thành ba nhóm lần lượt có \(2,3,5\) học sinh là:
A. \(C_{10}^2 + C_{10}^3 + C_{10}^5\).
B. \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\).
C. \(C_{10}^2 + C_8^3 + C_5^5\).
D. \(C_{10}^5 + C_5^3 + C_2^2\).
Lời giải
Chọn 2 trong 10 học sinh vào nhóm thứ nhất: có \(C_{10}^2\) cách.
Chọn 3 trong 8 học sinh còn lại vào nhóm thứ hai: có \(C_8^3\) cách.
Chọn 5 trong 5 học sinh cuối cùng vào nhóm thứ ba: có \(C_5^5\) cách.
Vậy có \(C_{10}^2 \cdot C_8^3 \cdot C_5^5\) cách chọn thỏa mãn đề bài.
Đáp án B.
Câu 12: Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
A. 5!.7!.
B. \(2.5!.7!\).
C. \(5!.8!\).
D. \(12!\).
Lời giải
Sắp xếp 5 quyển Văn chung một nhóm ngang (nhóm \(V)\): có 5! cách.
Sắp xếp 7 quyển Toán với \(V\) (ta xem như sắp xếp 8 phần tử): có \(8!\) cách. Vậy có tất cả \(5!.8!\) cách sắp xếp thỏa mãn đề bài.
Đáp án C.
Câu 13: Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:
A. \(\frac{{5!}}{{2!}}\).
B. 8.
C. \(\frac{{5!}}{{3!2!}}\).
D. \({5^3}\).
Lời giải
Chọn 3 trong 5 màu để tô vào 3 nước khác nhau: có \(A_5^3 = \frac{{5!}}{{2!}}\) cách.
Đáp án A.
Câu 14: Trong mặt phẳng cho 2010 điểm phân biệt. Hỏi có bao nhiêu vectơ khác \(\vec 0\) có điểm đầu và điểm cuối lấy từ 2010 điểm đã cho?
A. 4039137.
B. 4038090.
C. 4167114.
D. 167541284.
Lời giải
Số vectơ thỏa mãn là \(A_{2010}^2 = 4038090\).
Đáp án B.
Câu 15: Khai triển của \({(x + 1)^4}\) là:
A. \({x^4} + 2{x^2} + 1\).
B. \({x^4} + 4{x^3} + 6{x^2} + 4x + 1\).
C. \({x^4} + 5{x^3} + 10{x^2} + 5x + 1\).
D. \({x^4} + 3{x^3} + 4{x^2} + 3x + 1\).
Lời giải
Đáp án B.
Câu 16: Hệ số của \({x^3}\) trong khai triển của \({(2x + 1)^4}\) là:
A. 4.
B. 6.
C. 10.
D. 32.
Lời giải
Đáp án D.
Câu 17: Tổng các hệ số trong khai triển của \({(x + 2)^4}\) là:
A. 14.
B. 16.
C. 79.
D. 81.
Lời giải
Đáp án D.
Câu 18: Hệ số của \({x^2}\) trong khai triển của \({(2x - 3)^4}\) là:
A. 216.
B. 16.
C. \( - 16\).
D. \( - 216\).
Lời giải
Đáp án A.
Câu 19: Giả sử có khai triển \({(1 - 2x)^n} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_n}{x^n}\). Tìm \({a_4}\) biết \({a_0} + {a_1} + {a_2} = 31\).
A. 80.
B. \( - 80\).
C. 40.
D. \( - 40\).
Lời giải
Ta có:
\({(1 - 2x)^n} = C_n^0{1^n}{( - 2x)^0} + C_n^1{n^{n - 1}}( - 2x) + C_n^2{n^{n - 2}}{( - 2x)^2} + \ldots = 1 - 2C_n^1x + 4C_n^2{x^2} + \ldots \)
Vậy \({a_0} = 1;{a_1} = - 2C_n^1;{a_2} = 4C_n^2\). Theo bài ra \({a_0} + {a_1} + {a_2} = 31\) nên ta có:
\(1 - 2C_n^1 + 4C_n^2 = 31 \Leftrightarrow 1 - 2\frac{{n!}}{{1!(n - 1)!}} + 4\frac{{n!}}{{2!(n - 2)!}} = 31 \Leftrightarrow 1 - 2n + 2n(n - 1) = 31\)
\( \Leftrightarrow 2{n^2} - 4n - 30 = 0 \Leftrightarrow {n^2} - 2n - 15 = 0 \Rightarrow n = 5\). Từ đó ta có \({a_4} = C_5^4{( - 2)^4} = 80\).
Đáp án A.
Câu 20: Trong mặt phẳng toạ độ \(Oxy\), toạ độ của vectơ \(2\vec i - 7\vec j\) là:
A. \((2;7)\).
B. \(( - 2;7)\).
C. \((2; - 7)\).
D. \(( - 7;2)\).
Lời giải
Đáp án C.
Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(3; - 2)\). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. \((3; - 2)\).
B. \(( - 3;2)\).
C. \(( - 2;3)\).
D. \((2; - 3)\).
Lời giải
Đáp án A.
Câu 22: Trong mặt phẳng toạ độ \(Oxy\), cho \(A( - 3;2),B(5; - 1)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \((2;1)\).
B. \((8; - 3)\).
C. \(( - 8;3)\).
D. \(( - 2; - 1)\).
Lời giải
Đáp án B.
Câu 23: Trong mặt phẳng toạ độ \(Oxy\) cho các vectơ \(\vec a,\vec b,\vec c,\vec d\) được vẽ ở hình bên. Ta có các khẳng định sau:
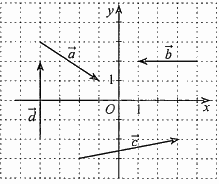
a) \(\vec a = (2; - 3)\);
b) \(\vec b = ( - 3;0)\);
c) \(\vec c = (5;1)\);
d) \(\vec d = (4;0)\).
A. 0.
B. 1.
C. 2.
D. 3.
Lời giải
Đáp án C.
Câu 24: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (2; - 3),\vec b = ( - 2;5)\). Toạ độ của vectơ \( - \vec a + 3\vec b\) là:
A. \((8;18)\).
B. \(( - 8; - 18)\).
C. \(( - 8;18)\).
D. \((8; - 18)\).
Lời giải
Ta có: \( - \vec a = ( - 2;3)\) và \(3\vec b = ( - 6;15)\). Suy ra \( - \vec a + 3\vec b = ( - 8;18)\).
Đáp án C.
Câu 25: Trong mặt phẳng toạ độ \(Oxy\), cho \(\vec a = (1;2),\vec b = (3; - 3)\). Toạ độ của vectơ \(\vec c = 3\vec a - 2\vec b\) là:
A. \(( - 3;12)\).
B. \((3;12)\).
C. \((9;0)\).
D. \(( - 3;0)\).
Lời giải
Ta có: \(3\vec a = (3;6)\) và \( - 2\vec b = ( - 6;6)\). Suy ra \(3\vec a - 2\vec b = ( - 3;12)\).
Đáp án A.
Câu 26: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( - 1;2),B(2; - 2),C(3;1)\). Toạ độ của vectơ \(\overrightarrow {AB} + \overrightarrow {BC} \) là:
A. \(( - 4; - 1)\).
B. \((4; - 1)\).
C. \(( - 4;1)\).
D. \((4;1)\).
Lời giải
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} = (4; - 1)\).
Đáp án B.
Câu 27: Trong mặt phẳng toạ độ \(Oxy\), cho ba điểm \(A( - 1;2),B(0; - 2),C(3;3)\). Toạ độ của vectơ \(2\overrightarrow {AB} - 4\overrightarrow {BC} \) là:
A. \((14;12)\).
B. \(( - 10; - 28)\).
C. \(( - 14; - 12)\).
D. \((10;28)\).
Lời giải
Ta có: \(\overrightarrow {AB} = (1; - 4) \Rightarrow 2\overrightarrow {AB} = (2; - 8)\); \(\overrightarrow {BC} = (3;5) \Rightarrow 4\overrightarrow {BC} = (12;20).\)
Suy ra \(2\overrightarrow {AB} - 4\overrightarrow {BC} = ( - 10; - 28)\).
Đáp án B.
Câu 28: Trong mặt phẳng toạ độ \(Oxy\), cặp vectơ nào sau đây có cùng phương?
A. \(\vec a = \left( { - \frac{2}{3};2} \right)\) và \(\vec b = (2; - 6)\).
B. \(\vec u = (2;1)\) và \(\vec v = (2; - 6)\).
C. \(\vec c = (\sqrt 2 ;2\sqrt 2 )\) và \(\vec d = (2;2)\).
D. \(\vec e = (1; - 1)\) và \(\vec f = (3;3)\).
Lời giải
Đáp án A.
Câu 29: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải
Đáp án D.
Câu 30: Một vectơ pháp tuyến của đường thẳng \(\Delta :y = 2x + 1\) là:
A. \(\overrightarrow {{n_\Delta }} (2; - 1)\).
B. \(\overrightarrow {{n_\Delta }} (1; - 1)\).
C. \(\overrightarrow {{n_\Delta }} ( - 2; - 1)\).
D. \(\overrightarrow {{n_\Delta }} (1;1)\).
Lời giải
Đáp án A.
Câu 31: Đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow {{u_\Delta }} (12; - 13)\). Vectơ nào sau đây là vectơ pháp tuyến của \(\Delta \)?
A. \(\overrightarrow {{n_\Delta }} ( - 13;12)\).
B. \(\overrightarrow {{n_\Delta }} (12;13)\).
C. \(\overrightarrow {{n_\Delta }} (13;12)\).
D. \(\overrightarrow {{n_\Delta }} ( - 12; - 13)\).
Lời giải
Đáp án C.
Câu 32: Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:
A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).
B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).
C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).
D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Lời giải
Đáp án D.
Câu 33: Trong mặt phẳng toạ độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\), \({\Delta _2}:3x - y + 7 = 0\). Nhận định nào sau đây là đúng?
A. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
B. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
C. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trùng nhau.
D. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
Lời giải
Đáp án D.
Câu 34: Người ta quy ước góc giữa hai đường thẳng song song hoặc trùng nhau là:
A. \({180^0}\).
B. \({120^0}\).
C. \({90^0}\).
D. \({0^0}\).
Lời giải
Đáp án D.
Câu 35: Cho \(\alpha \) là góc tạo bởi hai đường thẳng \({\Delta _1}:2x - 3y + 5 = 0\) và \({\Delta _2}:3x + y - 14 = 0\). Giá trị của cosa là:
A. \(\frac{{ - 3}}{{130}}\).
B. \(\frac{3}{{\sqrt {130} }}\).
C. \(\frac{{\sqrt 3 }}{{130}}\).
D. \(\frac{{ - 3}}{{\sqrt {130} }}\)
Lời giải
Đáp án B.
Phần tự luận (3 điểm)
Bài 1. Từ một nhóm 30 học sinh lớp 12 gồm 15 học sinh khối \(A,10\) học sinh khối \(B\) và 5 học sinh khối \(C\), cần chọn ra 15 học sinh, hỏi có bao nhiêu cách chọn sao cho:
a) Số học sinh mỗi khối là bằng nhau?
b) Có ít nhất 5 học sinh khối \(A\) và có đúng 2 học sinh khối \(C\)?
Lời giải
a) Số cách chọn 5 học sinh mỗi khối \((A,B,C)\) lần lượt là: \(C_{15}^5,C_{10}^5,C_5^5\).
Vậy số cách chọn thỏa mãn là \(C_{15}^5 \times C_{10}^5 \times C_5^5 = 756756\) (cách).
b) Ta sử dụng quy tắc loại trừ như Lời giải sau:
Xét bài toán 1: Chọn 2 học sinh khối \(C,13\) học sinh khối \(B\) hoặc khối \(A\): có \(C_5^2C_{25}^{13}\) cách.
Xét bài toán 2: Chọn 2 học sinh khối \(C,13\) học sinh khối \(B\) và khối \(A\) không thỏa mãn yêu cầu.
- Trường hợp 1: Chọn 2 học sinh khối \(C,10\) học sinh khối \(B\) và 3 học sinh khối A có \(C_5^2C_{10}^{10}C_{15}^3\) cách.
- Trường hợp 2: Chọn 2 học sinh khối \(C,9\) học sinh khối \(B\) và 4 học sinh khối A có \(C_5^2C_{10}^9C_{15}^4\) cách.
Vậy số cách chọn thỏa mãn là \(C_5^2C_{25}^{13} - C_{10}^{10}C_{15}^3 - C_{10}^9C_{15}^4 = 51861950\) (cách).
Bài 2. Cho biểu thức \(Q = {(xy - 1)^5}\).
a) Viết khai triển biểu thức \(Q\) bằng nhị thức Newton.
b) Tìm số hạng có chứa \({x^2}{y^2}\) trong khai triển trên.
Lời giải
a) Ta có: \(Q = {(xy - 1)^5} = C_5^0{(xy)^5} + C_5^1{(xy)^4}( - 1) + C_5^2{(xy)^3}{( - 1)^2}\)
\(\begin{array}{l} + C_5^3{(xy)^2}{( - 1)^3} + C_5^4(xy){( - 1)^4} + C_5^5{( - 1)^5}\\ = {x^5}{y^5} - 5{x^4}{y^4} + 10{x^3}{y^3} - 10{x^2}{y^2} + 5xy - 1.\end{array}\)
b) Số hạng có chứa \({x^2}{y^2}\) trong khai triển là \( - 10{x^2}{y^2}\).
Bài 3. Cho các vectơ \(\vec a = (2;0),\vec b = \left( { - 1;\frac{1}{2}} \right),\vec c = (4; - 6)\).
a) Tìm tọa độ của vectơ \(\vec d = 2\vec a - 3\vec b + 5\vec c\).
b) Biểu diễn vectơ \(\vec c\) theo cặp vectơ không cùng phương \(\vec a,\vec b\).
Lời giải
a) Ta có: \(\left\{ {\begin{array}{*{20}{l}}{2\vec a = (4;0)}\\{ - 3\vec b = \left( {3; - \frac{3}{2}} \right) \Rightarrow \vec d = 2\vec a - 3\vec b + 5\vec c = \left( {27; - \frac{{63}}{2}} \right)}\\{5\vec c = (20; - 30)}\end{array}} \right.\)
b) Gọi: \(\vec c = x\vec a + y\vec b(x,y \in \mathbb{R})\). Ta có: \(\left\{ {\begin{array}{*{20}{l}}{4 = x \cdot 2 + y( - 1)}\\{ - 6 = x \cdot 0 + y \cdot \frac{1}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 4}\\{y = - 12}\end{array}} \right.} \right.\) Vậy \(\vec c = - 4\vec a - 12\vec b\).
Bài 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x - y + 4 = 0\).
a) Viết phương trình đường cao \(AH\) của tam giác.
b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.
Lời giải
a) Đường cao \(AH\) vuông góc với \(BC\) nên nhận \(\vec u = (1; - 1)\) làm vectơ chỉ phương, suy ra \(AH\) có một vectơ pháp tuyến là \(\vec n = (1;1)\).
Phương trình tổng quát \(AH:1(x + 1) + 1(y + 2) = 0\) hay \(x + y + 3 = 0\).
b) Chọn điểm \(K(0;4)\) thuộc \(BC\), gọi \(E\) là trung điểm đoạn \(AK\) nên \(E\left( { - \frac{1}{2};1} \right)\). Gọi \(d\) là đường trung bình ứng với cạnh đáy \(BC\) của tam giác \(ABC\), suy ra \(d\) qua \(E\) và có một vectơ pháp tuyến .
Phương trình tổng quát \(d:1\left( {x + \frac{1}{2}} \right) - 1(y - 1) = 0\) hay \(2x - 2y + 3 = 0\).
Đề thi giữa kì 2 Toán 10 Cánh diều - Đề số 1 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một học kì. Đề thi này không chỉ kiểm tra kiến thức mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Dưới đây là phân tích chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết.
Thông thường, đề thi giữa kì 2 Toán 10 Cánh diều - Đề số 1 sẽ bao gồm hai phần chính:
Dưới đây là một số dạng bài tập thường gặp trong đề thi giữa kì 2 Toán 10 Cánh diều - Đề số 1:
Ví dụ 1: Giải bất phương trình 2x + 3 > 5
Giải:
2x + 3 > 5
2x > 2
x > 1
Vậy, nghiệm của bất phương trình là x > 1.
Ví dụ 2: Tìm tập xác định của hàm số y = √(x - 2)
Giải:
Hàm số y = √(x - 2) xác định khi và chỉ khi x - 2 ≥ 0
Suy ra x ≥ 2
Vậy, tập xác định của hàm số là [2, +∞).
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu ôn thi sau:
Chúc các bạn học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi giữa kì 2 Toán 10 Cánh diều - Đề số 1!