Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 10 Cánh diều - Đề số 9, một công cụ ôn luyện hiệu quả giúp học sinh nắm vững kiến thức và tự tin bước vào kỳ thi. Đề thi được biên soạn theo chương trình học mới, bám sát nội dung sách giáo khoa Cánh diều.
Đề thi này bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề và áp dụng kiến thức vào thực tế.
Câu 1: Tìm tập xác định ({rm{D}}) của hàm số (y = sqrt {6 - 3x} + frac{1}{{sqrt {x - 1} }}.) A. ({rm{D}} = left[ {1;2} right].) B. ({rm{D}} = left( {1;2} right).) C. ({rm{D}} = (1;2].) D. ({rm{D}} = left[ { - 1;2} right].)
I. Trắc nghiệm (6 điểm)
Câu 1: Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \sqrt {6 - 3x} + \frac{1}{{\sqrt {x - 1} }}.\)
A.\({\rm{D}} = \left[ {1;2} \right].\) B. \({\rm{D}} = \left( {1;2} \right).\) C. \({\rm{D}} = (1;2].\)D. \({\rm{D}} = \left[ { - 1;2} \right].\)
Câu 2: Cho mệnh đề P(x): “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)”. Mệnh đề phủ định của mệnh đề P(x) là
A. “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 < 0\)”. B. “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”.
C. “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”. D. “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)”.
Câu 3: Cho hàm số \(.y = \frac{{\sqrt {x - 2} - 2}}{{x - 6}}\). Điểm nào sau đây thuộc đồ thị hàm số:
A.\((6;0)\).B.\((2; - 0,5)\).C.\((2;0,5)\).D.\((0;6)\).
Câu 4: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng:
A. \(A = \left\{ {x \in \mathbb{R}|\left| x \right| < 1} \right\}\) B. \(A = \left\{ {x \in \mathbb{Z}|6{x^2} - 7x + 1 = 0} \right\}\) C. \(A = \left\{ {x \in \mathbb{Z}|{x^2} - 4x + 2 = 0} \right\}\) D. \(A = \left\{ {x \in \mathbb{N}|{x^2} - 4x + 3 = 0} \right\}\)
Câu 5: Cho hai tập hợp \(A = \left( { - \infty ;2} \right]\) và \(B = \left( { - 3;5} \right]\). Tìm mệnh đề sai.
A. \(A \cap B = \left( { - 3;2} \right].\) B. \(A\backslash B = \left( { - \infty ; - 3} \right)\). C. \(A \cup B = \left( { - \infty ;5} \right]\). D. \(B\backslash A = \left( {2;5} \right]\).
Câu 6: Cho tập hợp: \(B = \left\{ {x;{\mkern 1mu} {\mkern 1mu} y;{\mkern 1mu} {\mkern 1mu} z;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 5} \right\}.\) Số tập hợp con của tập hợp \(B\) là
A. 29 B. 30 C. 31 D. 32
Câu 7: Hàm số \(y = a{x^2} + bx + c\), \((a > 0)\) nghịch biến trong khoảng nào sau đậy?
A. \(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\) B. \(\left( { - \frac{b}{{2a}};\, + \infty } \right).\)C. \(\left( { - \frac{\Delta }{{4a}};\, + \infty } \right).\)D. \(\left( { - \infty ;\, - \frac{\Delta }{{4a}}} \right).\)
Câu 8: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. \(2{x^2} + 3y > 0\) B. \({x^2} + {y^2} < 2\) C. \(x + {y^2} \ge 0\) D. \(x + y \ge 0\)
Câu 9: Miền nghiệm của bất phương trình \(\left( {1 + \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y \ge 2\) chứa điểm nào sau đây?
A. A(1;-1) B. B(-1;-1) C. C(-1;1) D. \(D\left( { - \sqrt 3 ;\sqrt 3 } \right)\)
Câu 10: (ID: 590544) Trong tam giác EFG, chọn mệnh đề đúng.
A. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos G.\) B. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos E.\)
C. \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos E.\) D. \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos G.\)
Câu 11: Cho hình chữ nhật ABCD có \(AB = a\) và \(AD = a\sqrt 2 \). Gọi K là trung điểm của cạnh AD. Tính \(\overrightarrow {BK} .\overrightarrow {AC} \)
A. \(\overrightarrow {BK} .\overrightarrow {AC} = \overrightarrow 0 \) B. \(\overrightarrow {BK} .\overrightarrow {AC} = - {a^2}\sqrt 2 \) C. \(\overrightarrow {BK} .\overrightarrow {AC} = {a^2}\sqrt 2 \) D. \(\overrightarrow {BK} .\overrightarrow {AC} = 2{a^2}\)
Câu 12: (ID: 590546) Cho tam giác ABC có b = 7, c = 5, \(\cos A = \frac{3}{5}.\) Độ dài đường cao \({h_a}\) của tam giác ABC là:
A. \(8.\) B. \(8\sqrt 3 .\) C. \(\frac{{7\sqrt 2 }}{2}.\) D. \(7\sqrt 2 .\)
Câu 13: Hàm số bậc hai nào sau đây có đồ thị là parabol có đỉnh là \(S\left( {\frac{5}{2};\frac{1}{2}} \right)\)và đi qua \(A\left( {1; - 4} \right)\)?
A. \(y = - {x^2} + 5x - 8\). B. \(y = - 2{x^2} + 10x - 12\).
C. \(y = {x^2} - 5x\). D. \(y = - 2{x^2} + 5x + \frac{1}{2}\).
Câu 14: Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
A. \(O\left( {0;0} \right)\) B. \(M\left( {1;0} \right)\) C. \(N\left( {0; - 2} \right)\) D. \(P\left( {0;2} \right)\)
Câu 15: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau
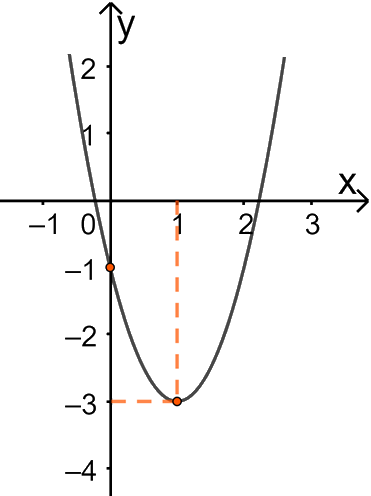
Phương trình của parabol này là
A. \(y = - {x^2} + x - 1\).B. \(y = 2{x^2} + 4x + 1\).C. \(y = {x^2} - 2x - 1\). D. \(y = 2{x^2} - 4x - 1\).
Câu 16: Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a.
A. \(r = \frac{{a\sqrt 3 }}{4}\) B. \(r = \frac{{a\sqrt 2 }}{5}\) C. \(r = \frac{{a\sqrt 3 }}{6}\) D. \(r = \frac{{a\sqrt 5 }}{7}\)
Câu 17: Tam giác ABC có \(AB = \sqrt 2 ,\,\,AC = \sqrt 3 \) và \(C = {45^0}\). Tính độ dài cạnh BC.
A. \(BC = \sqrt 5 \) B. \(BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\) C. \(BC = \frac{{\sqrt 6 - \sqrt 2 }}{2}\) D. \(BC = \sqrt 6 \)
Câu 18: Bảng biến thiên của hàm số \(y = - {x^2} + 2x - 1\) là:
A. 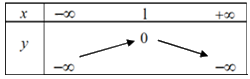 B.
B. 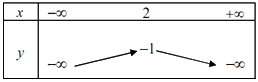
C. 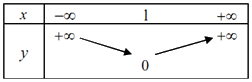 D.
D. 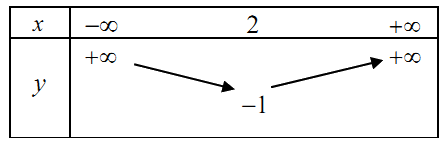
Câu 19: Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?

A. \(\left( { - 3; + \infty } \right).\) B. \(\left( {5; + \infty } \right).\) C. \(\{ - 3;5\} \) D. \(\left( { - 3;5} \right].\)
Câu 20: Giá trị lớn nhất của hàm số \(y = - 3{x^2} + 2x + 1\) trên đoạn \(\left[ {1;3} \right]\) là:
A. \(\frac{4}{5}\) B. 0 C. \(\frac{1}{3}\)D. \( - 20\)
Câu 21: Cho hai vectơ \(\vec a\) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 3,\) \(\left| {\overrightarrow b } \right| = 2\) và \(\vec a.\vec b = - 3.\) Xác định góc \(\alpha \) giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b .\)
A. \(\alpha = {30^0}.\) B. \(\alpha = {45^0}.\) C. \(\alpha = {60^0}.\) D. \(\alpha = {120^0}.\)
Câu 22: Cho tam giác cân \(ABC\) có\(\widehat A = {120^0}\)và \(AB = AC = a\). Lấy điểm \(M\)trên cạnh \(BC\) sao cho \(BM = \frac{{2BC}}{5}\). Tính độ dài \(AM.\)
A. \(\frac{{a\sqrt 3 }}{3}\)B. \(\frac{{11a}}{5}\)C. \(\frac{{a\sqrt 7 }}{5}\)D. \(\frac{{a\sqrt 6 }}{4}\)
Câu 23: Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
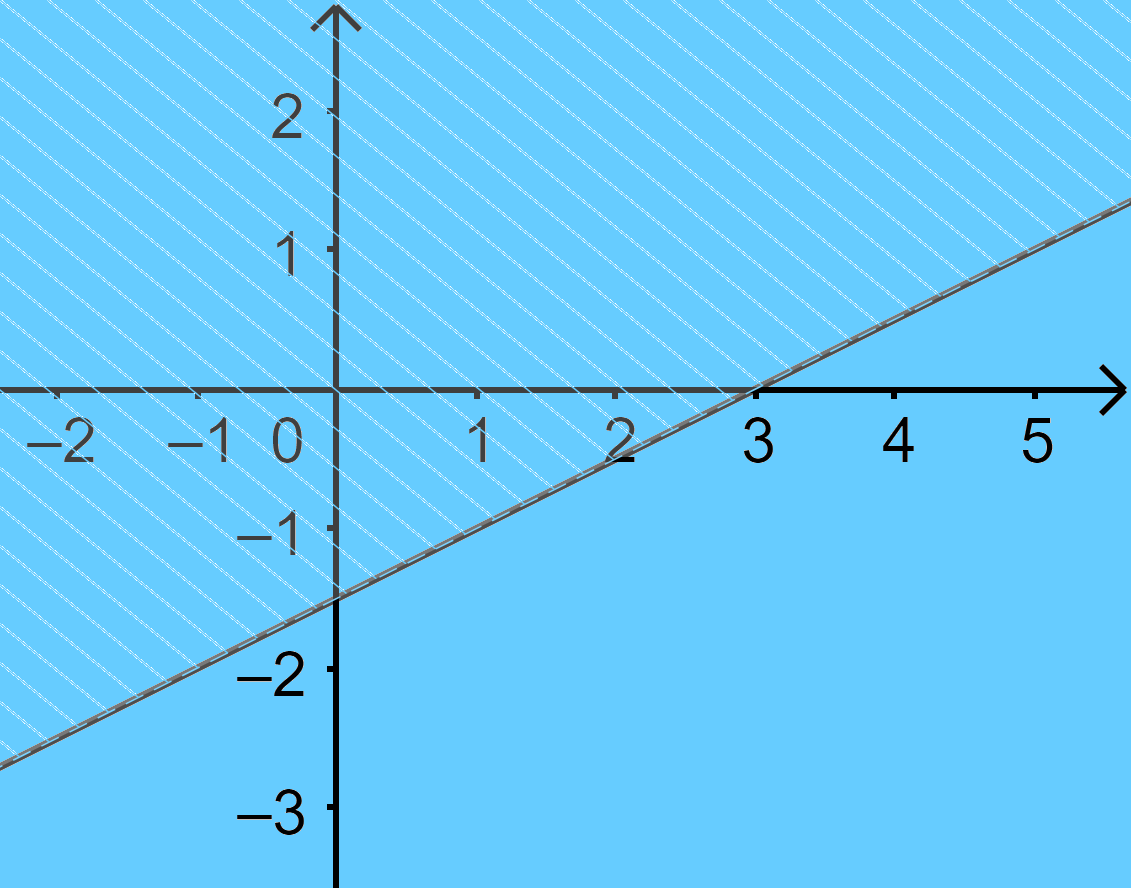
A. \(2x - y < 3\) B. \(2x - y > 3\) C. \(x - 2y < 3\) D. \(x - 2y > 3\)
Câu 24: Cho góc \(\alpha \) với \({0^0} < \alpha < {180^0}\). Tính giá trị của \(\cos \alpha \), biết \(\tan \alpha = - 2\sqrt 2 \).
A. \( - \frac{1}{3}.\) B. \(\frac{1}{3}.\) C. \(\frac{{2\sqrt 2 }}{3}.\) D. \(\frac{{\sqrt 2 }}{3}.\)
Câu 25: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn cùng một điểm trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40cm, \(\angle CAB = {45^0}\), \(\angle CBA = {70^0}\). Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây?
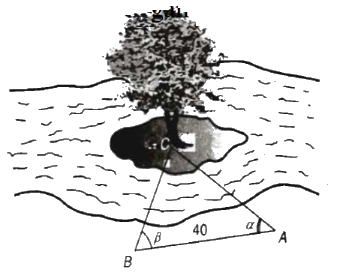
A. 53 m B. 30 m C. 41,5 m D. 41 m
Câu 26: Cho hình vuông ABCD cạnh \(a\), \(M\) là điểm thay đổi. Độ dài véctơ \(\vec u = \overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} {\rm{\;}} - 3\overrightarrow {MD} \) là:
A. \(4a\sqrt 2 \) B. \(a\sqrt 2 \) C. \(3a\sqrt 2 \) D. \(2a\sqrt 2 \)
Câu 27: Cho tam giác ABC đều cạnh a, G là trọng tâm. Mệnh đề nào sau đây sai?
A. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}{a^2}.\) B. \(\overrightarrow {AC} .\overrightarrow {CB} = - \frac{1}{2}{a^2}.\) C. \(\overrightarrow {GA} .\overrightarrow {GB} = \frac{1}{6}{a^2}.\) D. \(\overrightarrow {AB} .\overrightarrow {AG} = \frac{1}{2}{a^2}.\)
Câu 28: Cho bốn điểm A,B,C,Dphân biệt. Khi đó, \(\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} - \overrightarrow {AD} \) bằng véctơ nào sau đây?
A. \(\vec 0\) B. \(\overrightarrow {BD} \) C. \(\overrightarrow {AC} \) D. \(2\overrightarrow {DC} \)
Câu 29: Cho hình chữ nhật ABCD. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AC} {\rm{ \;}} = \overrightarrow {BD} \) B. \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \vec 0\)
C. \(\left| {\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AD} } \right|\) D. \(\left| {\overrightarrow {BC} {\rm{ \;}} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AC} {\rm{ \;}} - \overrightarrow {AB} } \right|\)
Câu 30: Cho tam giác ABC có trung tuyến BM và trọng tâm \(G\). Đặt \(\overrightarrow {BC} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BA} {\rm{\;}} = b\). Hãy phân tích vectơ \(\overrightarrow {BG} \) theo \(\vec a\) và \(\vec b\).
A. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\) B. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{2}{3}\vec b\) C. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{2}{3}\vec b\) D. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{1}{3}\vec b\)
II. Tự luận (4 điểm)
Câu 1: Cho ba lực \(\overrightarrow {{F_1}} {\rm{\;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{\;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{\;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ lực \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M. Tìm hướng và cường độ lực \(\overrightarrow {{F_3}} \)
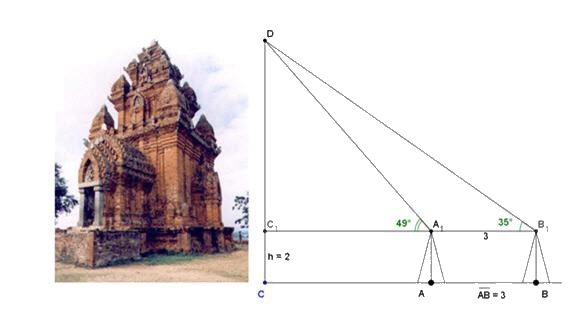
Câu 2: Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách \(AB = 12m\) , cùng thẳng hàng với chân C của tháp để đặt giác kế. Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm \({A_1},{B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao CD của tháp. Người ta đo được \(\widehat {D{A_1}{C_1}} = {49^ \circ }\) và \(\widehat {D{B_1}{C_1}} = {35^ \circ }\). Tính chiều cao CD của tháp đó.
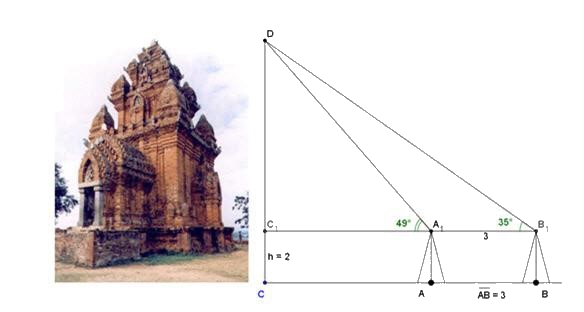
Câu 3: Tìm parabol (P) \(y = a{x^2} + bx + c\) biết (P) có đỉnh \(I(2;3)\) và giao với Oy tại điểm có tung độ bằng -1. Vẽ đồ thị hàm số tìm được.
-----HẾT-----
I. Trắc nghiệm (6 điểm)
1. C | 2. C | 3. C | 4. C | 5. B | 6. D | 7.A | 8. D |
9. A | 10. D | 11. A | 12. C | 13. B | 14. C | 15. D | 16. C |
17. B | 18. A | 19. D | 20. B | 21. D | 22. C | 23. D | 24. C |
25. C | 26. D | 27. C | 28. A | 29.A | 30. A |
Câu 1 (NB):
Phương pháp:
Cách giải:
Hàm số \(y = \sqrt {6 - 3x} + \frac{1}{{\sqrt {x - 1} }}\) xác định khi \(\left\{ \begin{array}{l}6 - 3x \ge 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\x > 1\end{array} \right. \Leftrightarrow 1 < x \le 2\)
Vậy tập xác định \(D = (1;2]\)
Chọn C.
Câu 2 (TH):
Phương pháp:
Phủ định của mệnh đề “\(\forall x \in K,\,\,P\left( x \right)\)” là mệnh đề “\(\exists x \in K,\,\,\overline {P\left( x \right)} \)”.
Cách giải:
Mệnh đề phủ định của mệnh đề P(x): “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)” là “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”.
Chọn C.
Câu 3 (TH):
Phương pháp:
Thay tọa độ các điểm vào hàm số
Cách giải:
Với \(x = 6,x = 0\)thì \(y = \frac{{\sqrt {x - 2} - 2}}{{x - 6}}\) không xác định. Suy ra điểm \((6;0)\) và \((0;6)\)không thuộc đồ thị hàm số
Với \(x = 2\) thì \(y = \frac{{\sqrt {2 - 2} - 2}}{{2 - 6}} = 0,5 \ne - 0,5\). Suy ra điểm \((2; - 0,5)\)không thuộc đồ thị hàm số, điểm \((2;0,5)\) thuộc đồ thị hàm số
Chọn C.
Câu 4 (TH):
Phương pháp:
Tập hợp rỗng không chứa phần tử nào.
Cách giải:
+) Xét đáp án A: \(\left\{ {\begin{array}{*{20}{l}}{x \in \mathbb{R}}\\{\left| x \right| < 1}\end{array}} \right. \Rightarrow {\rm{\;}} - 1 < x < 1\) \( \Rightarrow A = \left( { - 1;{\mkern 1mu} {\mkern 1mu} 1} \right) \ne \emptyset \)
\( \Rightarrow \) Loại đáp án A.
+) Xét đáp án B: \(6{x^2} - 7x + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = \frac{1}{6}}\end{array}} \right.\) \( \Rightarrow A = \left\{ 1 \right\} \ne \emptyset \)
\( \Rightarrow \) Loại đáp án B.
+) Xét đáp án C: \({x^2} - 4x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2 + \sqrt 2 }\\{x = 2 - \sqrt 2 }\end{array}} \right.\) \( \Rightarrow A = \emptyset \)
Chọn C.
Câu 5 (VD):
Phương pháp:
Thực hiện các phép toán trên tập hợp. Sử dụng trục số.
Cách giải:
+) \(A \cap B = \left( { - 3;2} \right]\)
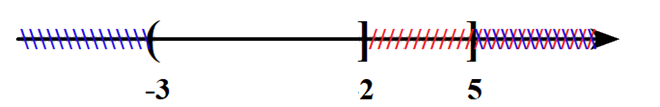
=> A đúng.
+) \(A\backslash B = \left( { - \infty ; - 3} \right]\)

=> B sai.
+) \(A \cup B = \left( { - \infty ;5} \right]\)
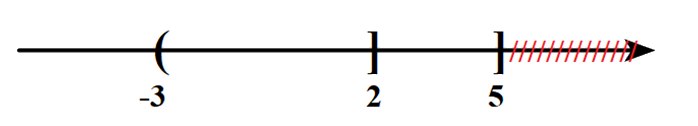
=> C đúng.
+) \(B\backslash A = \left( {2;5} \right]\).
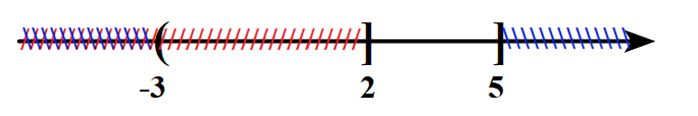
=> D đúng.
Chọn B.
Câu 6 (TH):
Phương pháp:
Cho tập hợp B có n phần tử. Số tập hợp con của B là \({2^n}\)
Cách giải:
Tập hợp \(B = \left\{ {x;{\mkern 1mu} {\mkern 1mu} y;{\mkern 1mu} {\mkern 1mu} z;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 5} \right\}\) có 5 phần tử.
Số tập hợp con của tập B là: \({2^5} = 32\)
Chọn D.
Câu 7 (NB):
Cách giải:
Với \(a > 0\), ta có bảng biến thiên
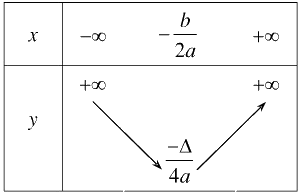
Hàm số nghịch biến trên \(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\)
Chọn A.
Câu 8 (TH):
Phương pháp:
Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là \(ax + by + c < 0\), \(ax + by + c > 0\), \(ax + by + c \le 0\), \(ax + by + c \ge 0\), trong đó a, b, c là các số cho trước sao cho \({a^2} + {b^2} \ne 0\).
Cách giải:
Bất phương trình bậc nhất hai ẩn là \(x + y \ge 0\).
Chọn D.
Câu 9 (TH):
Phương pháp:
Thay tọa độ các điểm ở các đáp án vào bất phương trình.
Cách giải:
Thay tọa độ điểm A(1;-1) ta có: \(\left( {1 + \sqrt 3 } \right) + \left( {1 - \sqrt 3 } \right) = 2 \ge 2\) (Đúng).
Vậy điểm A thuộc miền nghiệm của bất phương trình.
Chọn A.
Câu 10 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác: \({a^2} = {b^2} + {c^2} - 2bc.\cos A.\)
Cách giải:
\(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos G\) là mệnh đề đúng.
Chọn D.
Câu 11 (VD):
Cách giải:
Ta có:
\(AC = BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \)
Lại có:
\(\left\{ \begin{array}{l}\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{1}{2}\overrightarrow {AD} \\\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \end{array} \right.\)
\(\begin{array}{l} \Rightarrow \overrightarrow {BK} .\overrightarrow {AC} = \left( {\overrightarrow {BA} + \frac{1}{2}\overrightarrow {AD} } \right).\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\\ = \overrightarrow {BA} .\overrightarrow {AB} + \overrightarrow {BA} .\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AD} .\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} .\overrightarrow {AD} \\ = - {a^2} + 0 + 0 + \frac{1}{2}{\left( {a\sqrt 2 } \right)^2}\\ = 0\end{array}\)
Chọn A.
Câu 12 (VD):
Phương pháp:
Tính sinA.
Tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)
Sử dụng định lí cosin trong tam giác tính a: \({a^2} = {b^2} + {c^2} - 2bc.\cos A.\)
Sử dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}a{h_a}\), từ đó tính \({h_a}\).
Cách giải:
Ta có:
\(\begin{array}{l}{\sin ^2}A + {\cos ^2}A = 1\\ \Leftrightarrow {\sin ^2}A + {\left( {\frac{3}{5}} \right)^2} = 1\\ \Leftrightarrow {\sin ^2}A = \frac{{16}}{{25}}\end{array}\)
Vì \({0^0} < A < {180^0}\) nên sinA > 0 \( \Rightarrow \sin A = \frac{4}{5}.\)
Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A. = \frac{1}{2}.7.5.\frac{4}{5} = 14.\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A.\\\,\,\,\,\,\, = {7^2} + {5^2} - 2.7.5.\frac{3}{5}\\\,\,\,\,\,\, = 32\\ \Rightarrow a = 4\sqrt 2 .\end{array}\)
Lại có: \(S = \frac{1}{2}a{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}.\)
Chọn C.
Câu 13 (TH):
Cách giải:
Hàm số bậc hai cần tìm có phương trình: \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Hàm số bậc hai có đồ thị là parabol có đỉnh là \(S\left( {\frac{5}{2};\frac{1}{2}} \right)\)và đi qua \(A\left( {1; - 4} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = \frac{5}{2}\\a.\frac{{25}}{4} + b.\frac{5}{2} + c = \frac{1}{2}\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{ - b}}{a} = 5\\25a + 10b + 2c = 2\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5{\rm{a + b = 0}}\\25a + 10b + 2c = 2\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 10\\c = - 12\end{array} \right.\)
Chọn B.
Câu 14 (TH):
Phương pháp:
Thay tọa độ các điểm vào hệ bất phương trình.
Cách giải:
Dễ thấy các điểm \(O\left( {0;0} \right)\), \(M\left( {1;0} \right)\), \(P\left( {0;2} \right)\) không thỏa mãn bất phương trình \(x + y + 1 < 0\) nên không thỏa mãn cả hệ bất phương trình.
Chọn C.
Câu 15 (TH):
Cách giải:
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, - 1} \right)\) nên \(c = - 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, - 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 1\\a{.1^2} + b.1 - 1 = - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 4\end{array} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} - 4x - 1\).
Chọn D.
Câu 16 (TH):
Phương pháp:
Sử dụng công thức tính diện tích tam giác \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = pr\).
Cách giải:
Nửa chu vi tam giác đều cạnh a là \(p = \frac{{a + a + a}}{2} = \frac{{3a}}{2}\).
Tam giác đều cạnh a có diện tích \(S = \sqrt {\frac{{3a}}{2}\left( {\frac{{3a}}{2} - a} \right)\left( {\frac{{3a}}{2} - a} \right)\left( {\frac{{3a}}{2} - a} \right)} = \frac{{{a^2}\sqrt 3 }}{4}\).
Lại có \(S = pr \Leftrightarrow r = \frac{S}{p} = \frac{{{a^2}\sqrt 3 }}{4}:\frac{{3a}}{2} = \frac{{a\sqrt 3 }}{6}\).
Chọn C.
Câu 17 (NB):
Phương pháp:
Sử dụng hệ quả định lí Cosin trong tam giác: \(\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}}\).
Cách giải:
Áp dụng hệ quả định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{l}\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}}\\ \Leftrightarrow \cos {45^0} = \frac{{{{\left( {\sqrt 3 } \right)}^2} + B{C^2} - {{\left( {\sqrt 2 } \right)}^2}}}{{2.\sqrt 3 .BC}}\\ \Leftrightarrow \sqrt 6 BC = B{C^2} + 1\\ \Leftrightarrow B{C^2} - \sqrt 6 BC + 1 = 0\\ \Leftrightarrow BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\end{array}\).
Chọn B.
Câu 18 (TH):
Phương pháp:
Số chính phương có các chữ số tận cùng là \(0,{\rm{ }}1,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}9\). Dùng loại trừ để đưa ra đáp án đúng.
Cách giải:
Hàm số \(y = - {x^2} + 2x - 1\) có \(a = - 1 < 0\), nên loại C,D.
Hoành độ đỉnh \({x_I} = - \frac{b}{{2a}} = - \frac{2}{{2.( - 1)}} = 1\)
Chọn A.
Câu 19 (NB):
Phương pháp:
Biểu diễn tập hợp trên trục số.
Cách giải:
Hình vẽ đã cho là minh họa cho tập hợp \(( - 3;5]\)
Chọn D.
Câu 20 (VD):
Cách giải:
Ta có \( - \frac{b}{{2a}} = \frac{1}{3}\) và \(a = - 3 < 0\). Suy ra hàm số đã cho nghịch biến trên khoảng \(\left( {\frac{1}{3}; + \infty } \right)\).
Mà \(\left[ {1;3} \right] \subset \left( {\frac{1}{3}; + \infty } \right)\).
Do đó trên đoạn \(\left[ {1;3} \right]\) hàm số đạt giá trị lớn nhất tại \(x = 1\), tức là \(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = f\left( 1 \right) = 0\).
Chọn B.
Câu 21 (TH):
Phương pháp:
Áp dụng công thức \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)
Cách giải:
Ta có \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 3}}{{3.2}} = - \frac{1}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {120^o}\)
Chọn D.
Câu 22 (VD):
Phương pháp:
- Tính BC dựa vào định lí côsin trong tam giác cân ABC.
- Tính BM.
- Tính AM dựa vào định lí côsin trong tam giác ABM.
Cách giải:
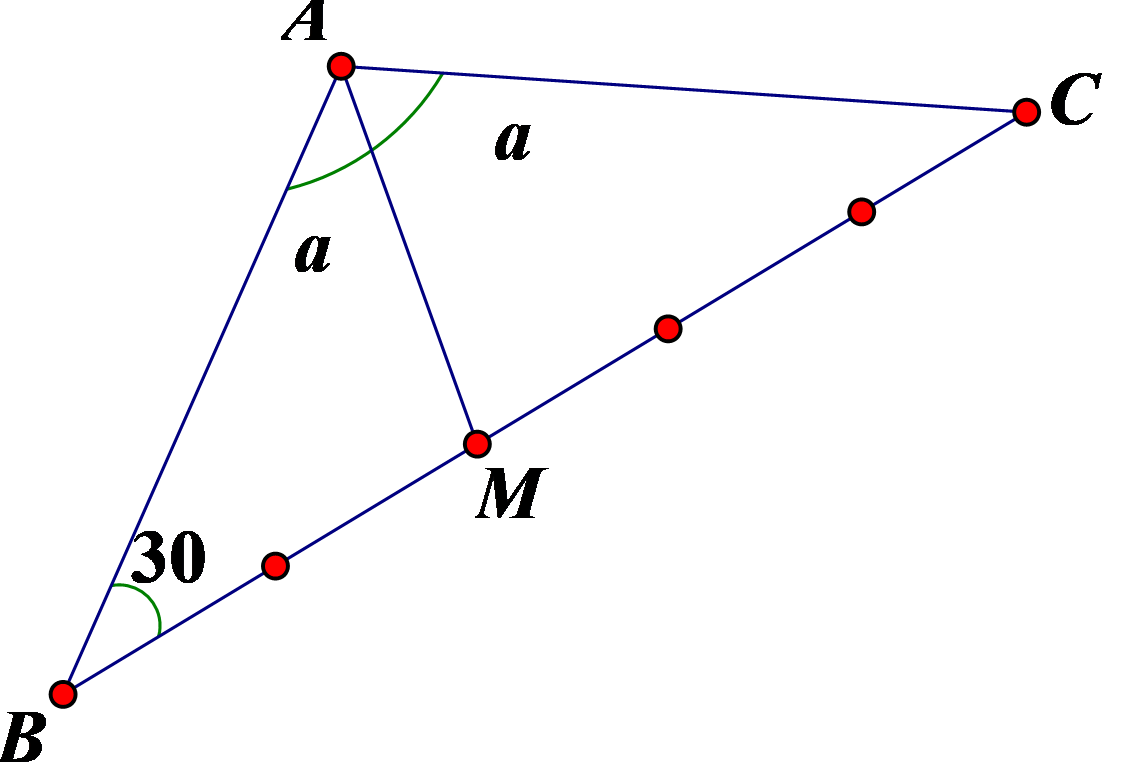
\(BC = \sqrt {A{B^2} + A{C^2} - 2ABAC\cos {{120}^0}} = \sqrt {{a^2} + {a^2} - 2a.a.\left( { - \frac{1}{2}} \right)} = a\sqrt 3 {\rm{ }} \Rightarrow BM = \frac{{2a\sqrt 3 }}{5}\)
\(AM = \sqrt {A{B^2} + B{M^2} - 2AB.BM.cos{{30}^0}} = \sqrt {{a^2} + {{\left( {\frac{{2a\sqrt 3 }}{5}} \right)}^2} - 2a.\frac{{2a\sqrt 3 }}{5}.\frac{{\sqrt 3 }}{2}} = \frac{{a\sqrt 7 }}{5}\).
Chọn C.
Câu 23 (TH):
Phương pháp:
Tìm phương trình đường thẳng d. Loại đáp án.
Thay tọa độ điểm O(0;0) vào các bất phương trình chưa bị loại ở các đáp án, tiếp tục loại đáp án.
Cách giải:
Đường thẳng d đi qua điểm (3;0) nên loại đáp án A, B.
Ta thấy điểm O(0;0) không thuộc miền nghiệm của bất phương trình.
+ Thay tọa độ điểm O(0;0) vào biểu thức \(x - 2y\) ta có: \(0 - 2.0 = 0 < 3\)
Do đó bất phươn trình cần tìm là \(x - 2y > 3\)
Chọn D.
Câu 24 (TH):
Phương pháp:
Sử dụng công thức: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}.\)
Cách giải:
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow 1 + {\left( { - 2\sqrt 2 } \right)^2} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\cos ^2}\alpha = \frac{1}{9}\\ \Leftrightarrow {\sin ^2}\alpha = 1 - \frac{1}{9} = \frac{8}{9}\\ \Leftrightarrow \sin \alpha = \pm \frac{{2\sqrt 2 }}{3}\end{array}\)
Vì \({0^0} < \alpha < {180^0}\) \( \Rightarrow \sin \alpha > 0\).
Vậy \(\sin \alpha = \frac{{2\sqrt 2 }}{3}.\)
Chọn C.
Câu 25 (VD):
Phương pháp:
Áp dụng hệ quả định lí Sin trong tam giác ABC.
Cách giải:
Ta có: \(\angle ACB = {180^0} - {45^0} - {70^0} = {65^0}\)
Áp dụng hệ quả định lí Sin trong tam giác ABC ta có:
\(\begin{array}{l}\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{AC}}{{\sin {{70}^0}}} = \frac{{40}}{{\sin {{65}^0}}}\\ \Rightarrow AC = \frac{{40}}{{\sin {{65}^0}}}.\sin {70^0} \approx 41,47\,\,\left( m \right)\end{array}\)
Chọn C.
Câu 26 (VD):
Phương pháp:
Áp dụng quy tắc cộng vecto để tìm được vecto \(\vec u\).
Cách giải:
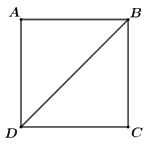
Vì ABCD là hình vuông nên ta có: \(AB = BC = CD = DA = 2\); \(AC = BD = a\sqrt 2 \).
Ta có:
\(\vec u = \overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} {\rm{\;}} - 3\overrightarrow {MD} \)
\({\mkern 1mu} = \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DA} } \right) + \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DB} } \right) + \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DC} } \right) - 3\overrightarrow {MD} \)
\({\mkern 1mu} = \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DA} {\rm{\;}} + \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DB} {\rm{\;}} + \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DC} {\rm{\;}} - 3\overrightarrow {MD} \)
\( = \overrightarrow {DA} {\rm{\;}} + \overrightarrow {DB} {\rm{\;}} + \overrightarrow {DC} \)
\( = \left( {\overrightarrow {DA} {\rm{\;}} + \overrightarrow {DC} } \right) + \overrightarrow {DB} \)
\( = \overrightarrow {DB} {\rm{\;}} + \overrightarrow {DB} \)
\( = 2\overrightarrow {DB} \)
\( \Rightarrow \vec u = 2\overrightarrow {DB} \)
\( \Rightarrow \left| {\vec u} \right| = \left| {2.\overrightarrow {DB} } \right| = 2.a.\sqrt 2 {\rm{\;}} = 2\sqrt 2 a\)
Chọn D.
Câu 27 (VD):
Phương pháp:
Áp dụng tích vô hướng \(\overrightarrow a .\overrightarrow b = a.b.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
Cách giải:
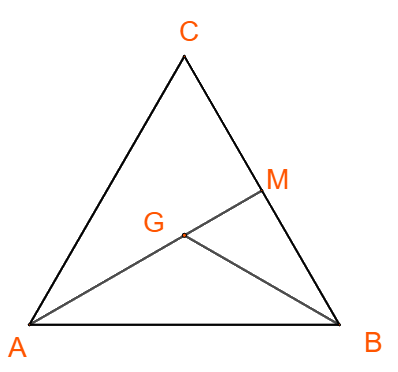
Ta có:
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a.\cos A = {a^2}\cos {60^ \circ } = \frac{1}{2}{a^2}\) => A đúng
\(\overrightarrow {AC} .\overrightarrow {CB} = AC.CB.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a.a.\cos {120^ \circ } = - \frac{1}{2}{a^2}\) => B đúng
+ \(AG = \frac{2}{3}AM;AM = AC.\sin C = a.\sin {60^ \circ } = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AG = BG = \frac{{a\sqrt 3 }}{3}\)
\(\overrightarrow {GA} .\overrightarrow {GB} = GA.GB.\cos \left( {\overrightarrow {GA} ,\overrightarrow {GB} } \right) = \frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt 3 }}{3}.\cos {120^ \circ } = - \frac{1}{6}{a^2}\) => C sai.
\(\overrightarrow {AB} .\overrightarrow {AG} = AB.AG.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AG} } \right) = a.\frac{{a\sqrt 3 }}{3}.\cos {30^ \circ } = \frac{1}{2}{a^2}\) => D đúng.
Chọn C.
Câu 28 (NB):
Phương pháp:
Nhóm \(\overrightarrow {AB} ,\overrightarrow {BC} \); \(\overrightarrow {DC} ,\overrightarrow {AD} \), áp dụng quy tắc cộng vectơ.
Cách giải:
Ta có: \(\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} - \overrightarrow {AD} {\rm{ \;}} = \left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right) - \left( {\overrightarrow {AD} {\rm{ \;}} + \overrightarrow {DC} } \right) = \overrightarrow {AC} {\rm{ \;}} - \overrightarrow {AC} {\rm{ \;}} = \vec 0\).
Chọn A.
Câu 29 (NB):
Phương pháp:
Sử dụng quy tắc hình bình hành tính \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} \).
Tính độ dài vectơ vừa tìm được.
Cách giải:
Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\).
Chọn A.
Câu 30 (TH):
Phương pháp:
Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để biểu diễn véctơ.
Cách giải:
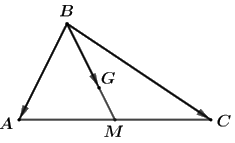
\(\overrightarrow {BM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {BC} } \right) = \frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\overrightarrow {BM} {\rm{\;}} = \frac{2}{3} \cdot \left( {\frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} } \right) = \frac{1}{3}\overrightarrow {BA} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
Mặt khác, \(\overrightarrow {BA} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BC} {\rm{\;}} = \vec b\) nên ta có: \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\)
Vậy \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\).
Chọn A.
II. Tự luận (3 điểm)
Câu 1 (VD):
Phương pháp:
Áp dụng quy tắc hình bình hành.
Vật đứng yên khi tổng các lực tác động lên điểm bằng 0.
Cách giải:
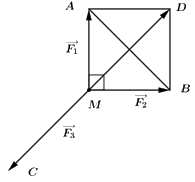
Có cường độ lực \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M
\( \Rightarrow \) Tam giác MAB vuông cân tại M
Lấy điểm D sao cho MADB là hình vuông
\( \Rightarrow MD = \sqrt {M{A^2} + A{D^2}} {\rm{\;}} = \sqrt {M{A^2} + M{B^2}} {\rm{\;}} = 50\sqrt 2 {\mkern 1mu} {\mkern 1mu} N\)
Vì vật đứng yên nên tổng các lực tác động lên điểm bằng 0
\( \Rightarrow \overrightarrow {{F_1}} {\rm{\;}} + \overrightarrow {{F_2}} {\rm{\;}} + \overrightarrow {{F_3}} {\rm{\;}} = \vec 0\) hay \(\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {{F_3}} {\rm{\;}} = \vec 0\)
\( \Rightarrow \overrightarrow {{F_3}} {\rm{\;}} = {\rm{\;}} - \left( {\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} } \right) = {\rm{\;}} - \overrightarrow {MD} \)
Vậy lực \(\overrightarrow {{F_3}} \) có hướng ngược với \(\overrightarrow {MD} \) và có cường độ bằng \(50\sqrt 2 {\mkern 1mu} {\mkern 1mu} N \approx 70,71{\mkern 1mu} {\mkern 1mu} N\)
Câu 2 (VD):
Cách giải:
Ta có: \(\widehat {D{A_1}B} = {180^ \circ } - {49^ \circ } = {131^ \circ };\widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lý sin trong tam giác \(D{A_1}{B_1}\) ta có:
\(\begin{array}{l}\frac{{{A_1}{B_1}}}{{\sin \widehat {{A_1}D{B_1}}}} = \frac{{D{B_1}}}{{\sin \widehat {D{A_1}{B_1}}}} \Leftrightarrow \frac{3}{{\sin {{14}^ \circ }}} = \frac{{D{B_1}}}{{\sin {{131}^ \circ }}}\\ \Rightarrow D{B_1} = \sin {131^ \circ }.\frac{3}{{\sin {{14}^ \circ }}}\end{array}\)
Lại có: \(\Delta D{C_1}{B_1}\) vuông tại \({C_1}\) nên \(D{C_1} = D{B_1}.\sin {B_1} = D{B_1}.\sin {35^ \circ }\)
\( \Rightarrow D{C_1} = \sin {131^ \circ }.\frac{3}{{\sin {{14}^ \circ }}}.\sin {35^ \circ } \approx 5,37\)
Chiều cao CD của tháp là \(5,37 + 2 = 7,37(m)\)
Vậy tháp cao khoảng 7,37m.
Câu 3 (VD):
Cách giải:
Parabol (P) \(y = a{x^2} + bx + c\) giao với Oy tại điểm có tọa độ \((0;c)\), do đó \(c = - 1\)
(P) có hoành độ đỉnh \({x_I} = - \frac{b}{{2a}} = 2 \Rightarrow b = - 4a\)
Điểm \(I(2;3)\) thuộc (P) nên \(a{.2^2} + b.2 - 1 = 3\) hay \(4a + 2b = 4\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}4a + 2b = 4\\b = - 4a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = - 1\end{array} \right.\)
Vậy parabol cần tìm là \(y = - {x^2} + 4x - 1\)
* Vẽ parabol
Đỉnh \(I(2;3)\)
Trục đối xứng \(x = 2\)
Giao với Oy tại A(0;-1), lấy điểm B(4;-1) đối xứng với A qua trục đối xứng
Lấy điểm C(1;2) và D(3;2) thuộc đồ thị.
Tải về
I. Trắc nghiệm (6 điểm)
Câu 1: Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \sqrt {6 - 3x} + \frac{1}{{\sqrt {x - 1} }}.\)
A.\({\rm{D}} = \left[ {1;2} \right].\) B. \({\rm{D}} = \left( {1;2} \right).\) C. \({\rm{D}} = (1;2].\)D. \({\rm{D}} = \left[ { - 1;2} \right].\)
Câu 2: Cho mệnh đề P(x): “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)”. Mệnh đề phủ định của mệnh đề P(x) là
A. “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 < 0\)”. B. “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”.
C. “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”. D. “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)”.
Câu 3: Cho hàm số \(.y = \frac{{\sqrt {x - 2} - 2}}{{x - 6}}\). Điểm nào sau đây thuộc đồ thị hàm số:
A.\((6;0)\).B.\((2; - 0,5)\).C.\((2;0,5)\).D.\((0;6)\).
Câu 4: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng:
A. \(A = \left\{ {x \in \mathbb{R}|\left| x \right| < 1} \right\}\) B. \(A = \left\{ {x \in \mathbb{Z}|6{x^2} - 7x + 1 = 0} \right\}\) C. \(A = \left\{ {x \in \mathbb{Z}|{x^2} - 4x + 2 = 0} \right\}\) D. \(A = \left\{ {x \in \mathbb{N}|{x^2} - 4x + 3 = 0} \right\}\)
Câu 5: Cho hai tập hợp \(A = \left( { - \infty ;2} \right]\) và \(B = \left( { - 3;5} \right]\). Tìm mệnh đề sai.
A. \(A \cap B = \left( { - 3;2} \right].\) B. \(A\backslash B = \left( { - \infty ; - 3} \right)\). C. \(A \cup B = \left( { - \infty ;5} \right]\). D. \(B\backslash A = \left( {2;5} \right]\).
Câu 6: Cho tập hợp: \(B = \left\{ {x;{\mkern 1mu} {\mkern 1mu} y;{\mkern 1mu} {\mkern 1mu} z;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 5} \right\}.\) Số tập hợp con của tập hợp \(B\) là
A. 29 B. 30 C. 31 D. 32
Câu 7: Hàm số \(y = a{x^2} + bx + c\), \((a > 0)\) nghịch biến trong khoảng nào sau đậy?
A. \(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\) B. \(\left( { - \frac{b}{{2a}};\, + \infty } \right).\)C. \(\left( { - \frac{\Delta }{{4a}};\, + \infty } \right).\)D. \(\left( { - \infty ;\, - \frac{\Delta }{{4a}}} \right).\)
Câu 8: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. \(2{x^2} + 3y > 0\) B. \({x^2} + {y^2} < 2\) C. \(x + {y^2} \ge 0\) D. \(x + y \ge 0\)
Câu 9: Miền nghiệm của bất phương trình \(\left( {1 + \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y \ge 2\) chứa điểm nào sau đây?
A. A(1;-1) B. B(-1;-1) C. C(-1;1) D. \(D\left( { - \sqrt 3 ;\sqrt 3 } \right)\)
Câu 10: (ID: 590544) Trong tam giác EFG, chọn mệnh đề đúng.
A. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos G.\) B. \(E{F^2} = E{G^2} + F{G^2} + 2EG.FG.\cos E.\)
C. \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos E.\) D. \(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos G.\)
Câu 11: Cho hình chữ nhật ABCD có \(AB = a\) và \(AD = a\sqrt 2 \). Gọi K là trung điểm của cạnh AD. Tính \(\overrightarrow {BK} .\overrightarrow {AC} \)
A. \(\overrightarrow {BK} .\overrightarrow {AC} = \overrightarrow 0 \) B. \(\overrightarrow {BK} .\overrightarrow {AC} = - {a^2}\sqrt 2 \) C. \(\overrightarrow {BK} .\overrightarrow {AC} = {a^2}\sqrt 2 \) D. \(\overrightarrow {BK} .\overrightarrow {AC} = 2{a^2}\)
Câu 12: (ID: 590546) Cho tam giác ABC có b = 7, c = 5, \(\cos A = \frac{3}{5}.\) Độ dài đường cao \({h_a}\) của tam giác ABC là:
A. \(8.\) B. \(8\sqrt 3 .\) C. \(\frac{{7\sqrt 2 }}{2}.\) D. \(7\sqrt 2 .\)
Câu 13: Hàm số bậc hai nào sau đây có đồ thị là parabol có đỉnh là \(S\left( {\frac{5}{2};\frac{1}{2}} \right)\)và đi qua \(A\left( {1; - 4} \right)\)?
A. \(y = - {x^2} + 5x - 8\). B. \(y = - 2{x^2} + 10x - 12\).
C. \(y = {x^2} - 5x\). D. \(y = - 2{x^2} + 5x + \frac{1}{2}\).
Câu 14: Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
A. \(O\left( {0;0} \right)\) B. \(M\left( {1;0} \right)\) C. \(N\left( {0; - 2} \right)\) D. \(P\left( {0;2} \right)\)
Câu 15: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau
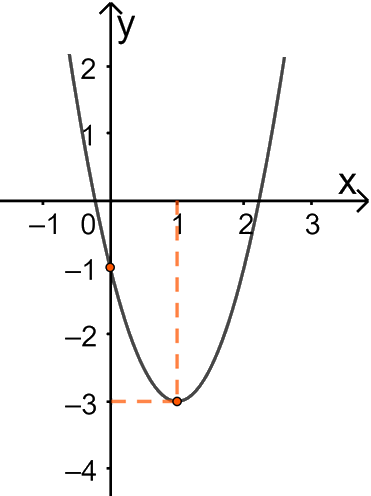
Phương trình của parabol này là
A. \(y = - {x^2} + x - 1\).B. \(y = 2{x^2} + 4x + 1\).C. \(y = {x^2} - 2x - 1\). D. \(y = 2{x^2} - 4x - 1\).
Câu 16: Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a.
A. \(r = \frac{{a\sqrt 3 }}{4}\) B. \(r = \frac{{a\sqrt 2 }}{5}\) C. \(r = \frac{{a\sqrt 3 }}{6}\) D. \(r = \frac{{a\sqrt 5 }}{7}\)
Câu 17: Tam giác ABC có \(AB = \sqrt 2 ,\,\,AC = \sqrt 3 \) và \(C = {45^0}\). Tính độ dài cạnh BC.
A. \(BC = \sqrt 5 \) B. \(BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\) C. \(BC = \frac{{\sqrt 6 - \sqrt 2 }}{2}\) D. \(BC = \sqrt 6 \)
Câu 18: Bảng biến thiên của hàm số \(y = - {x^2} + 2x - 1\) là:
A. 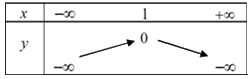 B.
B. 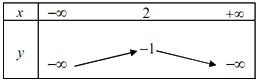
C. 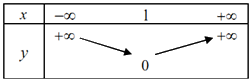 D.
D. 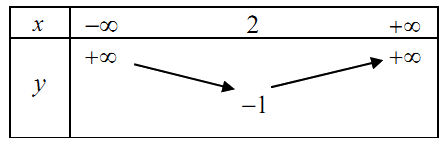
Câu 19: Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?

A. \(\left( { - 3; + \infty } \right).\) B. \(\left( {5; + \infty } \right).\) C. \(\{ - 3;5\} \) D. \(\left( { - 3;5} \right].\)
Câu 20: Giá trị lớn nhất của hàm số \(y = - 3{x^2} + 2x + 1\) trên đoạn \(\left[ {1;3} \right]\) là:
A. \(\frac{4}{5}\) B. 0 C. \(\frac{1}{3}\)D. \( - 20\)
Câu 21: Cho hai vectơ \(\vec a\) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 3,\) \(\left| {\overrightarrow b } \right| = 2\) và \(\vec a.\vec b = - 3.\) Xác định góc \(\alpha \) giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b .\)
A. \(\alpha = {30^0}.\) B. \(\alpha = {45^0}.\) C. \(\alpha = {60^0}.\) D. \(\alpha = {120^0}.\)
Câu 22: Cho tam giác cân \(ABC\) có\(\widehat A = {120^0}\)và \(AB = AC = a\). Lấy điểm \(M\)trên cạnh \(BC\) sao cho \(BM = \frac{{2BC}}{5}\). Tính độ dài \(AM.\)
A. \(\frac{{a\sqrt 3 }}{3}\)B. \(\frac{{11a}}{5}\)C. \(\frac{{a\sqrt 7 }}{5}\)D. \(\frac{{a\sqrt 6 }}{4}\)
Câu 23: Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
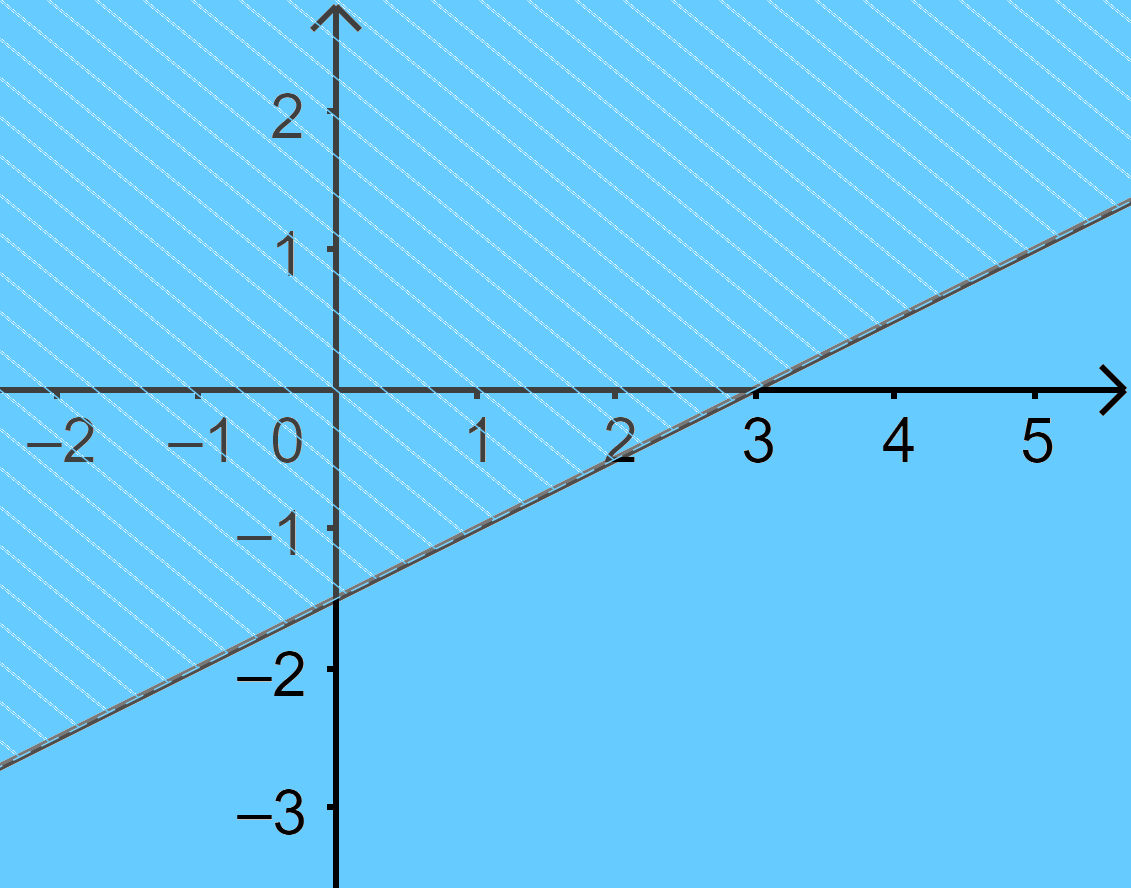
A. \(2x - y < 3\) B. \(2x - y > 3\) C. \(x - 2y < 3\) D. \(x - 2y > 3\)
Câu 24: Cho góc \(\alpha \) với \({0^0} < \alpha < {180^0}\). Tính giá trị của \(\cos \alpha \), biết \(\tan \alpha = - 2\sqrt 2 \).
A. \( - \frac{1}{3}.\) B. \(\frac{1}{3}.\) C. \(\frac{{2\sqrt 2 }}{3}.\) D. \(\frac{{\sqrt 2 }}{3}.\)
Câu 25: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn cùng một điểm trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40cm, \(\angle CAB = {45^0}\), \(\angle CBA = {70^0}\). Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây?
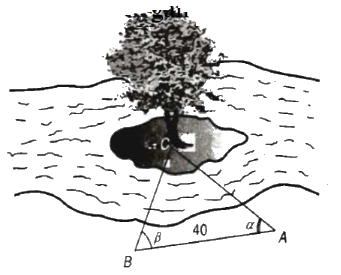
A. 53 m B. 30 m C. 41,5 m D. 41 m
Câu 26: Cho hình vuông ABCD cạnh \(a\), \(M\) là điểm thay đổi. Độ dài véctơ \(\vec u = \overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} {\rm{\;}} - 3\overrightarrow {MD} \) là:
A. \(4a\sqrt 2 \) B. \(a\sqrt 2 \) C. \(3a\sqrt 2 \) D. \(2a\sqrt 2 \)
Câu 27: Cho tam giác ABC đều cạnh a, G là trọng tâm. Mệnh đề nào sau đây sai?
A. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}{a^2}.\) B. \(\overrightarrow {AC} .\overrightarrow {CB} = - \frac{1}{2}{a^2}.\) C. \(\overrightarrow {GA} .\overrightarrow {GB} = \frac{1}{6}{a^2}.\) D. \(\overrightarrow {AB} .\overrightarrow {AG} = \frac{1}{2}{a^2}.\)
Câu 28: Cho bốn điểm A,B,C,Dphân biệt. Khi đó, \(\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} - \overrightarrow {AD} \) bằng véctơ nào sau đây?
A. \(\vec 0\) B. \(\overrightarrow {BD} \) C. \(\overrightarrow {AC} \) D. \(2\overrightarrow {DC} \)
Câu 29: Cho hình chữ nhật ABCD. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AC} {\rm{ \;}} = \overrightarrow {BD} \) B. \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} {\rm{ \;}} + \overrightarrow {AD} {\rm{ \;}} = \vec 0\)
C. \(\left| {\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AD} } \right|\) D. \(\left| {\overrightarrow {BC} {\rm{ \;}} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AC} {\rm{ \;}} - \overrightarrow {AB} } \right|\)
Câu 30: Cho tam giác ABC có trung tuyến BM và trọng tâm \(G\). Đặt \(\overrightarrow {BC} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BA} {\rm{\;}} = b\). Hãy phân tích vectơ \(\overrightarrow {BG} \) theo \(\vec a\) và \(\vec b\).
A. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\) B. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{2}{3}\vec b\) C. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{2}{3}\vec b\) D. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{1}{3}\vec b\)
II. Tự luận (4 điểm)
Câu 1: Cho ba lực \(\overrightarrow {{F_1}} {\rm{\;}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} {\rm{\;}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} {\rm{\;}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ lực \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M. Tìm hướng và cường độ lực \(\overrightarrow {{F_3}} \)
Câu 2: Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách \(AB = 12m\) , cùng thẳng hàng với chân C của tháp để đặt giác kế. Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm \({A_1},{B_1}\) cùng thẳng hàng với \({C_1}\) thuộc chiều cao CD của tháp. Người ta đo được \(\widehat {D{A_1}{C_1}} = {49^ \circ }\) và \(\widehat {D{B_1}{C_1}} = {35^ \circ }\). Tính chiều cao CD của tháp đó.
Câu 3: Tìm parabol (P) \(y = a{x^2} + bx + c\) biết (P) có đỉnh \(I(2;3)\) và giao với Oy tại điểm có tung độ bằng -1. Vẽ đồ thị hàm số tìm được.
-----HẾT-----
I. Trắc nghiệm (6 điểm)
1. C | 2. C | 3. C | 4. C | 5. B | 6. D | 7.A | 8. D |
9. A | 10. D | 11. A | 12. C | 13. B | 14. C | 15. D | 16. C |
17. B | 18. A | 19. D | 20. B | 21. D | 22. C | 23. D | 24. C |
25. C | 26. D | 27. C | 28. A | 29.A | 30. A |
Câu 1 (NB):
Phương pháp:
Cách giải:
Hàm số \(y = \sqrt {6 - 3x} + \frac{1}{{\sqrt {x - 1} }}\) xác định khi \(\left\{ \begin{array}{l}6 - 3x \ge 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\x > 1\end{array} \right. \Leftrightarrow 1 < x \le 2\)
Vậy tập xác định \(D = (1;2]\)
Chọn C.
Câu 2 (TH):
Phương pháp:
Phủ định của mệnh đề “\(\forall x \in K,\,\,P\left( x \right)\)” là mệnh đề “\(\exists x \in K,\,\,\overline {P\left( x \right)} \)”.
Cách giải:
Mệnh đề phủ định của mệnh đề P(x): “\(\forall x \in \mathbb{R}\), \({x^2} + x + 1 > 0\)” là “\(\exists x \in \mathbb{R}\), \({x^2} + x + 1 \le 0\)”.
Chọn C.
Câu 3 (TH):
Phương pháp:
Thay tọa độ các điểm vào hàm số
Cách giải:
Với \(x = 6,x = 0\)thì \(y = \frac{{\sqrt {x - 2} - 2}}{{x - 6}}\) không xác định. Suy ra điểm \((6;0)\) và \((0;6)\)không thuộc đồ thị hàm số
Với \(x = 2\) thì \(y = \frac{{\sqrt {2 - 2} - 2}}{{2 - 6}} = 0,5 \ne - 0,5\). Suy ra điểm \((2; - 0,5)\)không thuộc đồ thị hàm số, điểm \((2;0,5)\) thuộc đồ thị hàm số
Chọn C.
Câu 4 (TH):
Phương pháp:
Tập hợp rỗng không chứa phần tử nào.
Cách giải:
+) Xét đáp án A: \(\left\{ {\begin{array}{*{20}{l}}{x \in \mathbb{R}}\\{\left| x \right| < 1}\end{array}} \right. \Rightarrow {\rm{\;}} - 1 < x < 1\) \( \Rightarrow A = \left( { - 1;{\mkern 1mu} {\mkern 1mu} 1} \right) \ne \emptyset \)
\( \Rightarrow \) Loại đáp án A.
+) Xét đáp án B: \(6{x^2} - 7x + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = \frac{1}{6}}\end{array}} \right.\) \( \Rightarrow A = \left\{ 1 \right\} \ne \emptyset \)
\( \Rightarrow \) Loại đáp án B.
+) Xét đáp án C: \({x^2} - 4x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2 + \sqrt 2 }\\{x = 2 - \sqrt 2 }\end{array}} \right.\) \( \Rightarrow A = \emptyset \)
Chọn C.
Câu 5 (VD):
Phương pháp:
Thực hiện các phép toán trên tập hợp. Sử dụng trục số.
Cách giải:
+) \(A \cap B = \left( { - 3;2} \right]\)
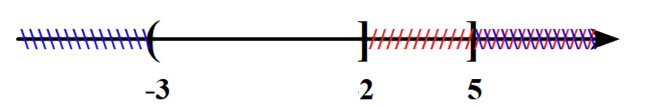
=> A đúng.
+) \(A\backslash B = \left( { - \infty ; - 3} \right]\)

=> B sai.
+) \(A \cup B = \left( { - \infty ;5} \right]\)
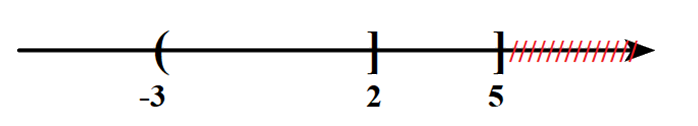
=> C đúng.
+) \(B\backslash A = \left( {2;5} \right]\).
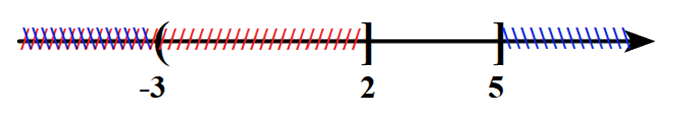
=> D đúng.
Chọn B.
Câu 6 (TH):
Phương pháp:
Cho tập hợp B có n phần tử. Số tập hợp con của B là \({2^n}\)
Cách giải:
Tập hợp \(B = \left\{ {x;{\mkern 1mu} {\mkern 1mu} y;{\mkern 1mu} {\mkern 1mu} z;{\mkern 1mu} {\mkern 1mu} 1;{\mkern 1mu} {\mkern 1mu} 5} \right\}\) có 5 phần tử.
Số tập hợp con của tập B là: \({2^5} = 32\)
Chọn D.
Câu 7 (NB):
Cách giải:
Với \(a > 0\), ta có bảng biến thiên
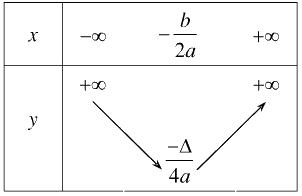
Hàm số nghịch biến trên \(\left( { - \infty ;\, - \frac{b}{{2a}}} \right).\)
Chọn A.
Câu 8 (TH):
Phương pháp:
Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là \(ax + by + c < 0\), \(ax + by + c > 0\), \(ax + by + c \le 0\), \(ax + by + c \ge 0\), trong đó a, b, c là các số cho trước sao cho \({a^2} + {b^2} \ne 0\).
Cách giải:
Bất phương trình bậc nhất hai ẩn là \(x + y \ge 0\).
Chọn D.
Câu 9 (TH):
Phương pháp:
Thay tọa độ các điểm ở các đáp án vào bất phương trình.
Cách giải:
Thay tọa độ điểm A(1;-1) ta có: \(\left( {1 + \sqrt 3 } \right) + \left( {1 - \sqrt 3 } \right) = 2 \ge 2\) (Đúng).
Vậy điểm A thuộc miền nghiệm của bất phương trình.
Chọn A.
Câu 10 (NB):
Phương pháp:
Sử dụng định lí cosin trong tam giác: \({a^2} = {b^2} + {c^2} - 2bc.\cos A.\)
Cách giải:
\(E{F^2} = E{G^2} + F{G^2} - 2EG.FG.\cos G\) là mệnh đề đúng.
Chọn D.
Câu 11 (VD):
Cách giải:
Ta có:
\(AC = BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \)
Lại có:
\(\left\{ \begin{array}{l}\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{1}{2}\overrightarrow {AD} \\\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \end{array} \right.\)
\(\begin{array}{l} \Rightarrow \overrightarrow {BK} .\overrightarrow {AC} = \left( {\overrightarrow {BA} + \frac{1}{2}\overrightarrow {AD} } \right).\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\\ = \overrightarrow {BA} .\overrightarrow {AB} + \overrightarrow {BA} .\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AD} .\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} .\overrightarrow {AD} \\ = - {a^2} + 0 + 0 + \frac{1}{2}{\left( {a\sqrt 2 } \right)^2}\\ = 0\end{array}\)
Chọn A.
Câu 12 (VD):
Phương pháp:
Tính sinA.
Tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)
Sử dụng định lí cosin trong tam giác tính a: \({a^2} = {b^2} + {c^2} - 2bc.\cos A.\)
Sử dụng công thức tính diện tích tam giác: \(S = \frac{1}{2}a{h_a}\), từ đó tính \({h_a}\).
Cách giải:
Ta có:
\(\begin{array}{l}{\sin ^2}A + {\cos ^2}A = 1\\ \Leftrightarrow {\sin ^2}A + {\left( {\frac{3}{5}} \right)^2} = 1\\ \Leftrightarrow {\sin ^2}A = \frac{{16}}{{25}}\end{array}\)
Vì \({0^0} < A < {180^0}\) nên sinA > 0 \( \Rightarrow \sin A = \frac{4}{5}.\)
Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A. = \frac{1}{2}.7.5.\frac{4}{5} = 14.\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A.\\\,\,\,\,\,\, = {7^2} + {5^2} - 2.7.5.\frac{3}{5}\\\,\,\,\,\,\, = 32\\ \Rightarrow a = 4\sqrt 2 .\end{array}\)
Lại có: \(S = \frac{1}{2}a{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}.\)
Chọn C.
Câu 13 (TH):
Cách giải:
Hàm số bậc hai cần tìm có phương trình: \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Hàm số bậc hai có đồ thị là parabol có đỉnh là \(S\left( {\frac{5}{2};\frac{1}{2}} \right)\)và đi qua \(A\left( {1; - 4} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = \frac{5}{2}\\a.\frac{{25}}{4} + b.\frac{5}{2} + c = \frac{1}{2}\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{ - b}}{a} = 5\\25a + 10b + 2c = 2\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5{\rm{a + b = 0}}\\25a + 10b + 2c = 2\\a + b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = 10\\c = - 12\end{array} \right.\)
Chọn B.
Câu 14 (TH):
Phương pháp:
Thay tọa độ các điểm vào hệ bất phương trình.
Cách giải:
Dễ thấy các điểm \(O\left( {0;0} \right)\), \(M\left( {1;0} \right)\), \(P\left( {0;2} \right)\) không thỏa mãn bất phương trình \(x + y + 1 < 0\) nên không thỏa mãn cả hệ bất phương trình.
Chọn C.
Câu 15 (TH):
Cách giải:
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, - 1} \right)\) nên \(c = - 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, - 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 1\\a{.1^2} + b.1 - 1 = - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 4\end{array} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} - 4x - 1\).
Chọn D.
Câu 16 (TH):
Phương pháp:
Sử dụng công thức tính diện tích tam giác \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = pr\).
Cách giải:
Nửa chu vi tam giác đều cạnh a là \(p = \frac{{a + a + a}}{2} = \frac{{3a}}{2}\).
Tam giác đều cạnh a có diện tích \(S = \sqrt {\frac{{3a}}{2}\left( {\frac{{3a}}{2} - a} \right)\left( {\frac{{3a}}{2} - a} \right)\left( {\frac{{3a}}{2} - a} \right)} = \frac{{{a^2}\sqrt 3 }}{4}\).
Lại có \(S = pr \Leftrightarrow r = \frac{S}{p} = \frac{{{a^2}\sqrt 3 }}{4}:\frac{{3a}}{2} = \frac{{a\sqrt 3 }}{6}\).
Chọn C.
Câu 17 (NB):
Phương pháp:
Sử dụng hệ quả định lí Cosin trong tam giác: \(\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}}\).
Cách giải:
Áp dụng hệ quả định lí Cosin trong tam giác ABC ta có:
\(\begin{array}{l}\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}}\\ \Leftrightarrow \cos {45^0} = \frac{{{{\left( {\sqrt 3 } \right)}^2} + B{C^2} - {{\left( {\sqrt 2 } \right)}^2}}}{{2.\sqrt 3 .BC}}\\ \Leftrightarrow \sqrt 6 BC = B{C^2} + 1\\ \Leftrightarrow B{C^2} - \sqrt 6 BC + 1 = 0\\ \Leftrightarrow BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}\end{array}\).
Chọn B.
Câu 18 (TH):
Phương pháp:
Số chính phương có các chữ số tận cùng là \(0,{\rm{ }}1,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}9\). Dùng loại trừ để đưa ra đáp án đúng.
Cách giải:
Hàm số \(y = - {x^2} + 2x - 1\) có \(a = - 1 < 0\), nên loại C,D.
Hoành độ đỉnh \({x_I} = - \frac{b}{{2a}} = - \frac{2}{{2.( - 1)}} = 1\)
Chọn A.
Câu 19 (NB):
Phương pháp:
Biểu diễn tập hợp trên trục số.
Cách giải:
Hình vẽ đã cho là minh họa cho tập hợp \(( - 3;5]\)
Chọn D.
Câu 20 (VD):
Cách giải:
Ta có \( - \frac{b}{{2a}} = \frac{1}{3}\) và \(a = - 3 < 0\). Suy ra hàm số đã cho nghịch biến trên khoảng \(\left( {\frac{1}{3}; + \infty } \right)\).
Mà \(\left[ {1;3} \right] \subset \left( {\frac{1}{3}; + \infty } \right)\).
Do đó trên đoạn \(\left[ {1;3} \right]\) hàm số đạt giá trị lớn nhất tại \(x = 1\), tức là \(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = f\left( 1 \right) = 0\).
Chọn B.
Câu 21 (TH):
Phương pháp:
Áp dụng công thức \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)
Cách giải:
Ta có \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 3}}{{3.2}} = - \frac{1}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {120^o}\)
Chọn D.
Câu 22 (VD):
Phương pháp:
- Tính BC dựa vào định lí côsin trong tam giác cân ABC.
- Tính BM.
- Tính AM dựa vào định lí côsin trong tam giác ABM.
Cách giải:
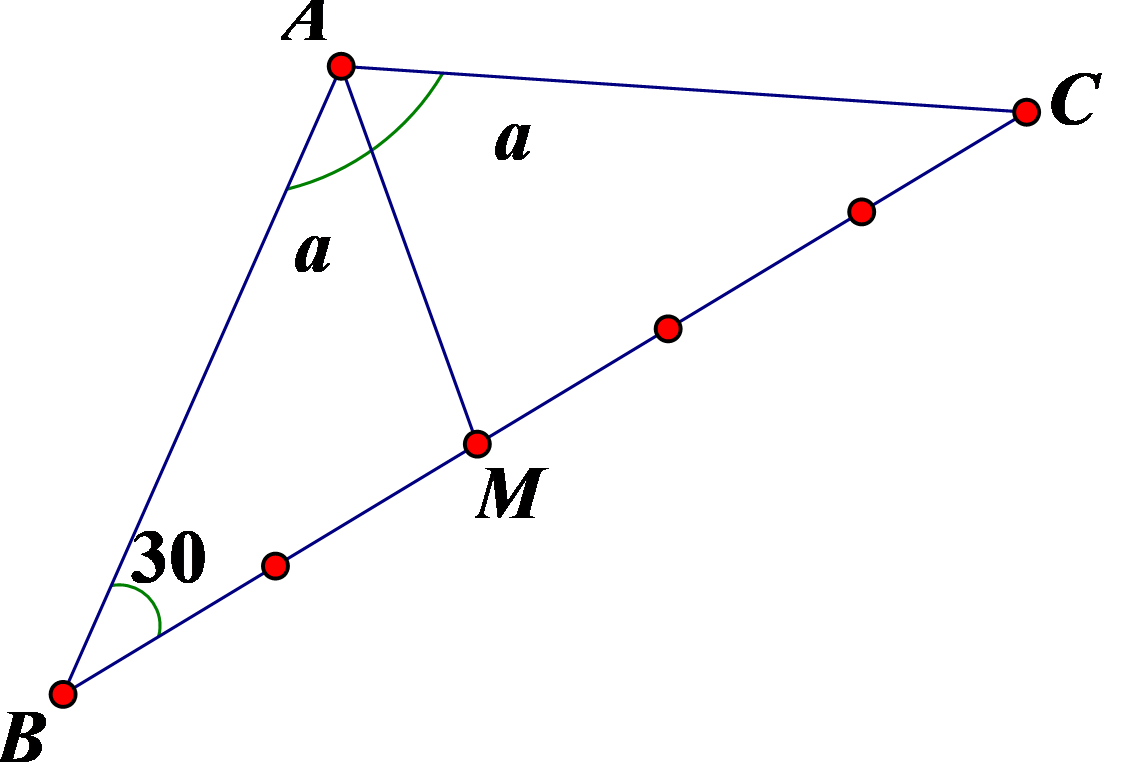
\(BC = \sqrt {A{B^2} + A{C^2} - 2ABAC\cos {{120}^0}} = \sqrt {{a^2} + {a^2} - 2a.a.\left( { - \frac{1}{2}} \right)} = a\sqrt 3 {\rm{ }} \Rightarrow BM = \frac{{2a\sqrt 3 }}{5}\)
\(AM = \sqrt {A{B^2} + B{M^2} - 2AB.BM.cos{{30}^0}} = \sqrt {{a^2} + {{\left( {\frac{{2a\sqrt 3 }}{5}} \right)}^2} - 2a.\frac{{2a\sqrt 3 }}{5}.\frac{{\sqrt 3 }}{2}} = \frac{{a\sqrt 7 }}{5}\).
Chọn C.
Câu 23 (TH):
Phương pháp:
Tìm phương trình đường thẳng d. Loại đáp án.
Thay tọa độ điểm O(0;0) vào các bất phương trình chưa bị loại ở các đáp án, tiếp tục loại đáp án.
Cách giải:
Đường thẳng d đi qua điểm (3;0) nên loại đáp án A, B.
Ta thấy điểm O(0;0) không thuộc miền nghiệm của bất phương trình.
+ Thay tọa độ điểm O(0;0) vào biểu thức \(x - 2y\) ta có: \(0 - 2.0 = 0 < 3\)
Do đó bất phươn trình cần tìm là \(x - 2y > 3\)
Chọn D.
Câu 24 (TH):
Phương pháp:
Sử dụng công thức: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}.\)
Cách giải:
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow 1 + {\left( { - 2\sqrt 2 } \right)^2} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\cos ^2}\alpha = \frac{1}{9}\\ \Leftrightarrow {\sin ^2}\alpha = 1 - \frac{1}{9} = \frac{8}{9}\\ \Leftrightarrow \sin \alpha = \pm \frac{{2\sqrt 2 }}{3}\end{array}\)
Vì \({0^0} < \alpha < {180^0}\) \( \Rightarrow \sin \alpha > 0\).
Vậy \(\sin \alpha = \frac{{2\sqrt 2 }}{3}.\)
Chọn C.
Câu 25 (VD):
Phương pháp:
Áp dụng hệ quả định lí Sin trong tam giác ABC.
Cách giải:
Ta có: \(\angle ACB = {180^0} - {45^0} - {70^0} = {65^0}\)
Áp dụng hệ quả định lí Sin trong tam giác ABC ta có:
\(\begin{array}{l}\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow \frac{{AC}}{{\sin {{70}^0}}} = \frac{{40}}{{\sin {{65}^0}}}\\ \Rightarrow AC = \frac{{40}}{{\sin {{65}^0}}}.\sin {70^0} \approx 41,47\,\,\left( m \right)\end{array}\)
Chọn C.
Câu 26 (VD):
Phương pháp:
Áp dụng quy tắc cộng vecto để tìm được vecto \(\vec u\).
Cách giải:
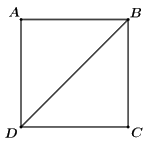
Vì ABCD là hình vuông nên ta có: \(AB = BC = CD = DA = 2\); \(AC = BD = a\sqrt 2 \).
Ta có:
\(\vec u = \overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} {\rm{\;}} - 3\overrightarrow {MD} \)
\({\mkern 1mu} = \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DA} } \right) + \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DB} } \right) + \left( {\overrightarrow {MD} {\rm{\;}} + \overrightarrow {DC} } \right) - 3\overrightarrow {MD} \)
\({\mkern 1mu} = \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DA} {\rm{\;}} + \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DB} {\rm{\;}} + \overrightarrow {MD} {\rm{\;}} + \overrightarrow {DC} {\rm{\;}} - 3\overrightarrow {MD} \)
\( = \overrightarrow {DA} {\rm{\;}} + \overrightarrow {DB} {\rm{\;}} + \overrightarrow {DC} \)
\( = \left( {\overrightarrow {DA} {\rm{\;}} + \overrightarrow {DC} } \right) + \overrightarrow {DB} \)
\( = \overrightarrow {DB} {\rm{\;}} + \overrightarrow {DB} \)
\( = 2\overrightarrow {DB} \)
\( \Rightarrow \vec u = 2\overrightarrow {DB} \)
\( \Rightarrow \left| {\vec u} \right| = \left| {2.\overrightarrow {DB} } \right| = 2.a.\sqrt 2 {\rm{\;}} = 2\sqrt 2 a\)
Chọn D.
Câu 27 (VD):
Phương pháp:
Áp dụng tích vô hướng \(\overrightarrow a .\overrightarrow b = a.b.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
Cách giải:
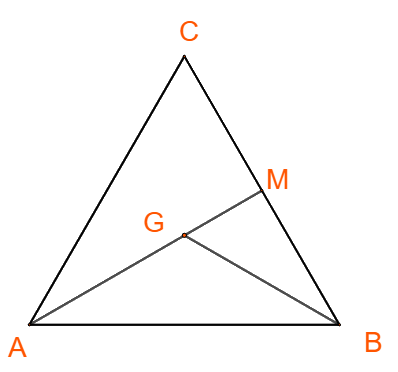
Ta có:
\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a.\cos A = {a^2}\cos {60^ \circ } = \frac{1}{2}{a^2}\) => A đúng
\(\overrightarrow {AC} .\overrightarrow {CB} = AC.CB.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a.a.\cos {120^ \circ } = - \frac{1}{2}{a^2}\) => B đúng
+ \(AG = \frac{2}{3}AM;AM = AC.\sin C = a.\sin {60^ \circ } = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AG = BG = \frac{{a\sqrt 3 }}{3}\)
\(\overrightarrow {GA} .\overrightarrow {GB} = GA.GB.\cos \left( {\overrightarrow {GA} ,\overrightarrow {GB} } \right) = \frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt 3 }}{3}.\cos {120^ \circ } = - \frac{1}{6}{a^2}\) => C sai.
\(\overrightarrow {AB} .\overrightarrow {AG} = AB.AG.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AG} } \right) = a.\frac{{a\sqrt 3 }}{3}.\cos {30^ \circ } = \frac{1}{2}{a^2}\) => D đúng.
Chọn C.
Câu 28 (NB):
Phương pháp:
Nhóm \(\overrightarrow {AB} ,\overrightarrow {BC} \); \(\overrightarrow {DC} ,\overrightarrow {AD} \), áp dụng quy tắc cộng vectơ.
Cách giải:
Ta có: \(\overrightarrow {AB} {\rm{ \;}} - \overrightarrow {DC} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} - \overrightarrow {AD} {\rm{ \;}} = \left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right) - \left( {\overrightarrow {AD} {\rm{ \;}} + \overrightarrow {DC} } \right) = \overrightarrow {AC} {\rm{ \;}} - \overrightarrow {AC} {\rm{ \;}} = \vec 0\).
Chọn A.
Câu 29 (NB):
Phương pháp:
Sử dụng quy tắc hình bình hành tính \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} \).
Tính độ dài vectơ vừa tìm được.
Cách giải:
Ta có: \(\left| {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\).
Chọn A.
Câu 30 (TH):
Phương pháp:
Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để biểu diễn véctơ.
Cách giải:
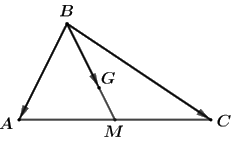
\(\overrightarrow {BM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {BC} } \right) = \frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\overrightarrow {BM} {\rm{\;}} = \frac{2}{3} \cdot \left( {\frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} } \right) = \frac{1}{3}\overrightarrow {BA} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
Mặt khác, \(\overrightarrow {BA} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BC} {\rm{\;}} = \vec b\) nên ta có: \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\)
Vậy \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\).
Chọn A.
II. Tự luận (3 điểm)
Câu 1 (VD):
Phương pháp:
Áp dụng quy tắc hình bình hành.
Vật đứng yên khi tổng các lực tác động lên điểm bằng 0.
Cách giải:
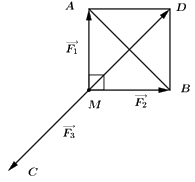
Có cường độ lực \(\overrightarrow {{F_1}} ,{\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M
\( \Rightarrow \) Tam giác MAB vuông cân tại M
Lấy điểm D sao cho MADB là hình vuông
\( \Rightarrow MD = \sqrt {M{A^2} + A{D^2}} {\rm{\;}} = \sqrt {M{A^2} + M{B^2}} {\rm{\;}} = 50\sqrt 2 {\mkern 1mu} {\mkern 1mu} N\)
Vì vật đứng yên nên tổng các lực tác động lên điểm bằng 0
\( \Rightarrow \overrightarrow {{F_1}} {\rm{\;}} + \overrightarrow {{F_2}} {\rm{\;}} + \overrightarrow {{F_3}} {\rm{\;}} = \vec 0\) hay \(\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {{F_3}} {\rm{\;}} = \vec 0\)
\( \Rightarrow \overrightarrow {{F_3}} {\rm{\;}} = {\rm{\;}} - \left( {\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} } \right) = {\rm{\;}} - \overrightarrow {MD} \)
Vậy lực \(\overrightarrow {{F_3}} \) có hướng ngược với \(\overrightarrow {MD} \) và có cường độ bằng \(50\sqrt 2 {\mkern 1mu} {\mkern 1mu} N \approx 70,71{\mkern 1mu} {\mkern 1mu} N\)
Câu 2 (VD):
Cách giải:
Ta có: \(\widehat {D{A_1}B} = {180^ \circ } - {49^ \circ } = {131^ \circ };\widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lý sin trong tam giác \(D{A_1}{B_1}\) ta có:
\(\begin{array}{l}\frac{{{A_1}{B_1}}}{{\sin \widehat {{A_1}D{B_1}}}} = \frac{{D{B_1}}}{{\sin \widehat {D{A_1}{B_1}}}} \Leftrightarrow \frac{3}{{\sin {{14}^ \circ }}} = \frac{{D{B_1}}}{{\sin {{131}^ \circ }}}\\ \Rightarrow D{B_1} = \sin {131^ \circ }.\frac{3}{{\sin {{14}^ \circ }}}\end{array}\)
Lại có: \(\Delta D{C_1}{B_1}\) vuông tại \({C_1}\) nên \(D{C_1} = D{B_1}.\sin {B_1} = D{B_1}.\sin {35^ \circ }\)
\( \Rightarrow D{C_1} = \sin {131^ \circ }.\frac{3}{{\sin {{14}^ \circ }}}.\sin {35^ \circ } \approx 5,37\)
Chiều cao CD của tháp là \(5,37 + 2 = 7,37(m)\)
Vậy tháp cao khoảng 7,37m.
Câu 3 (VD):
Cách giải:
Parabol (P) \(y = a{x^2} + bx + c\) giao với Oy tại điểm có tọa độ \((0;c)\), do đó \(c = - 1\)
(P) có hoành độ đỉnh \({x_I} = - \frac{b}{{2a}} = 2 \Rightarrow b = - 4a\)
Điểm \(I(2;3)\) thuộc (P) nên \(a{.2^2} + b.2 - 1 = 3\) hay \(4a + 2b = 4\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}4a + 2b = 4\\b = - 4a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = - 1\end{array} \right.\)
Vậy parabol cần tìm là \(y = - {x^2} + 4x - 1\)
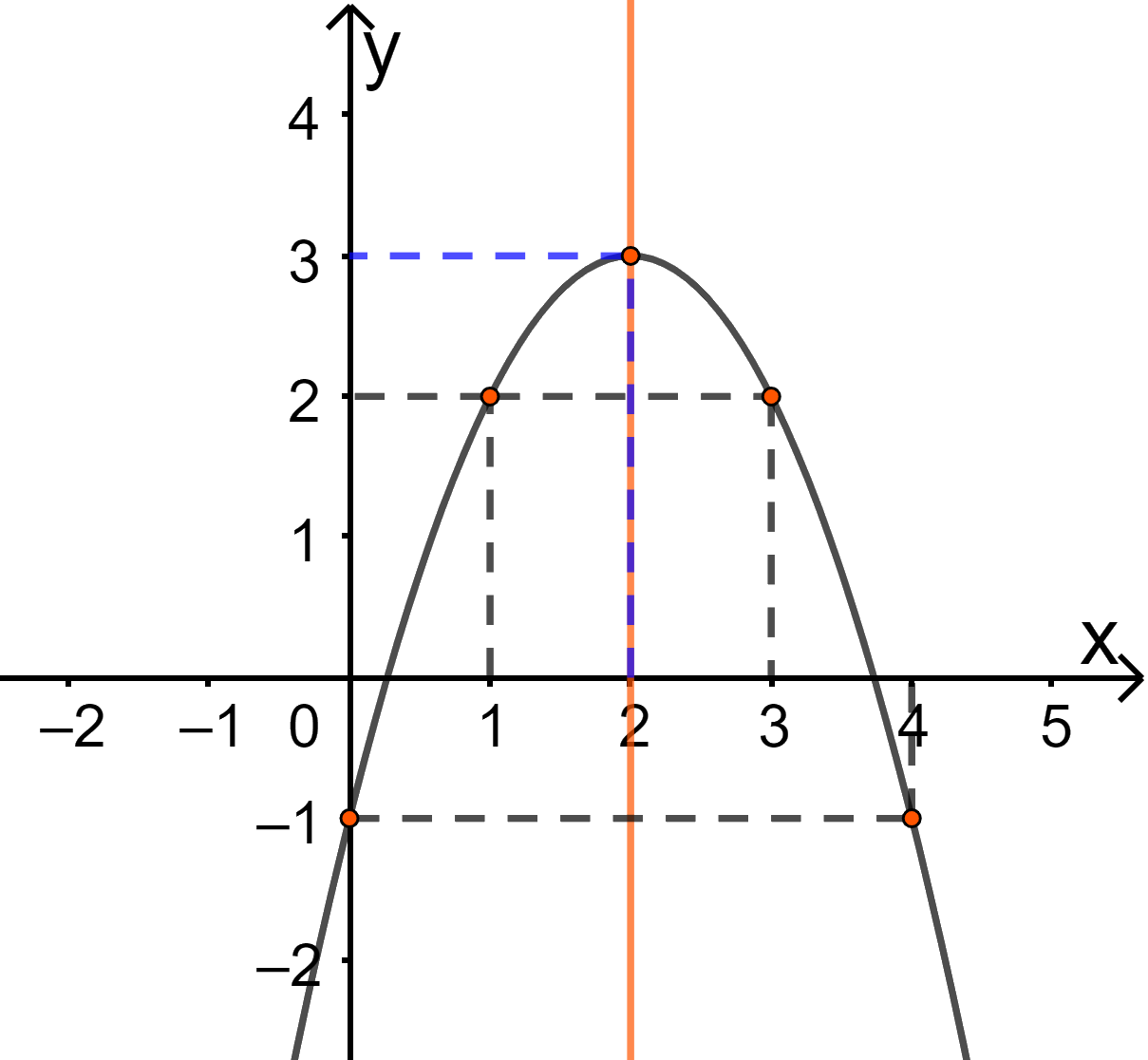
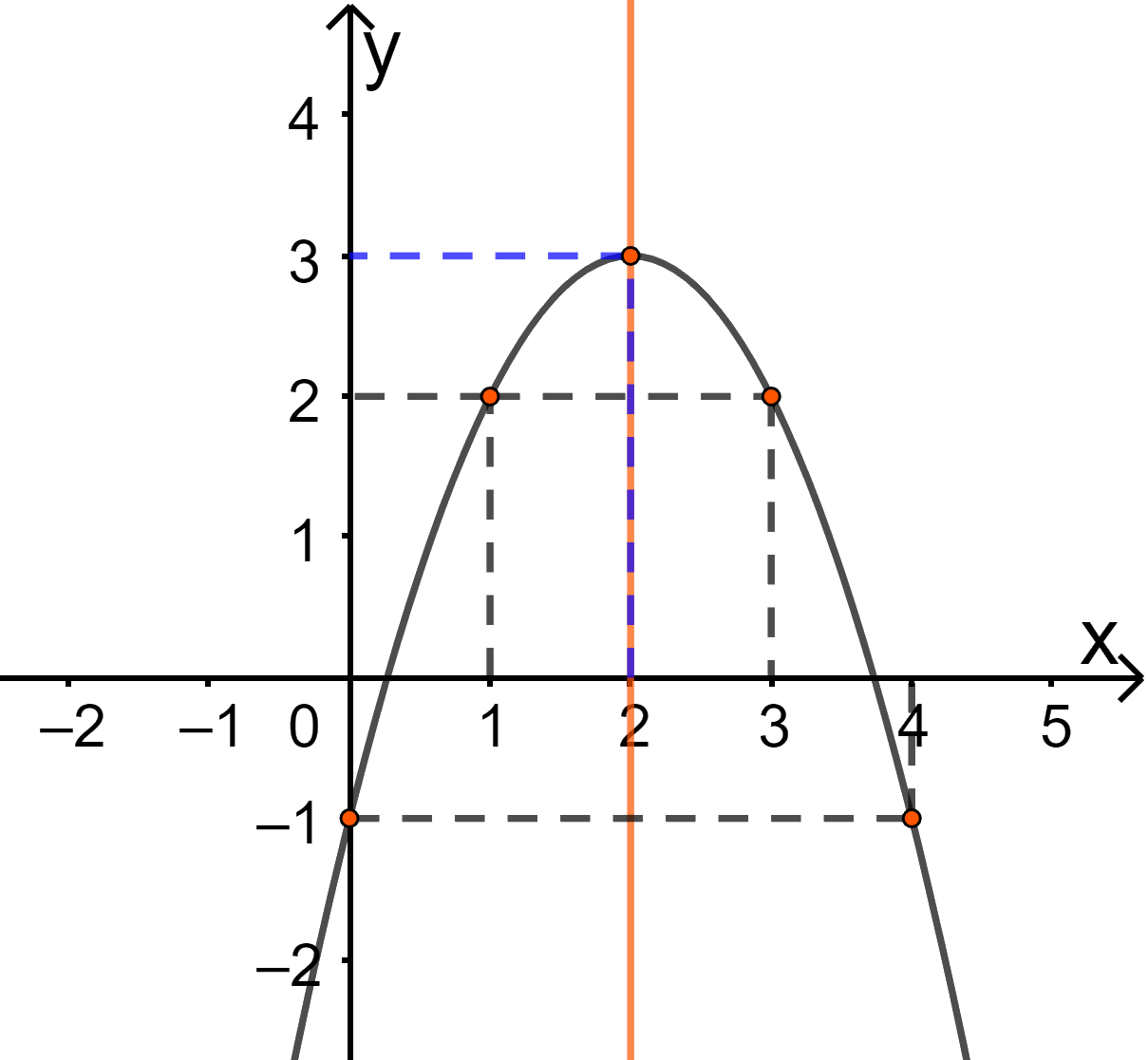
* Vẽ parabol
Đỉnh \(I(2;3)\)
Trục đối xứng \(x = 2\)
Giao với Oy tại A(0;-1), lấy điểm B(4;-1) đối xứng với A qua trục đối xứng
Lấy điểm C(1;2) và D(3;2) thuộc đồ thị.
Đề thi học kì 1 Toán 10 Cánh diều - Đề số 9 là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức của học sinh sau một học kỳ học tập. Đề thi bao gồm các chủ đề chính như tập hợp, hàm số, phương trình, bất phương trình, hệ phương trình và các ứng dụng của chúng.
Đề thi thường được chia thành hai phần chính: phần trắc nghiệm và phần tự luận. Phần trắc nghiệm thường chiếm khoảng 30-40% tổng số điểm, tập trung vào việc kiểm tra khả năng hiểu và vận dụng kiến thức cơ bản. Phần tự luận chiếm khoảng 60-70% tổng số điểm, yêu cầu học sinh trình bày chi tiết lời giải và chứng minh các kết quả.
Các dạng bài tập thường xuất hiện trong đề thi bao gồm:
Để giải tốt đề thi học kì 1 Toán 10 Cánh diều - Đề số 9, học sinh cần:
Bài 1: Giải phương trình x2 - 5x + 6 = 0
Lời giải:
Phương trình x2 - 5x + 6 = 0 là một phương trình bậc hai. Ta có thể giải phương trình này bằng cách sử dụng công thức nghiệm của phương trình bậc hai:
x = (-b ± √(b2 - 4ac)) / 2a
Trong trường hợp này, a = 1, b = -5, c = 6. Thay các giá trị này vào công thức, ta được:
x = (5 ± √((-5)2 - 4 * 1 * 6)) / (2 * 1)
x = (5 ± √(25 - 24)) / 2
x = (5 ± √1) / 2
x = (5 ± 1) / 2
Vậy, phương trình có hai nghiệm là:
x1 = (5 + 1) / 2 = 3
x2 = (5 - 1) / 2 = 2
Để ôn tập và luyện thi hiệu quả, học sinh có thể tham khảo các tài liệu sau:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi học kì 1 Toán 10 Cánh diều - Đề số 9!