Chào mừng các em học sinh đến với đề kiểm tra học kì 2 môn Toán 10, đề số 3, thuộc chương trình Cánh diều. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học hiệu quả và tự tin hơn trong kỳ thi sắp tới.
I. PHẦN TRẮC NGHIỆM ( 35 câu - 7,0 điểm ).
I. PHẦN TRẮC NGHIỆM (7 Điểm)
Câu 1. Lớp 10A có 20 bạn nữ và 18 bạn nam. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
A. \(38\) cách. B. \(20\)cách. C. \(18\) cách. D. \(360\).
Câu 2. Mã khoá số của chiếc Vali du lịch là một dãy số gồm ba chữ số. Mỗi chữ số có thể là một chữ số bất kì từ 0 đến 9. Hỏi có thể có bao nhiêu mã mở khoá khác nhau?
A. \({10^3}\). B. \(720.\) C. \(900.\) D. \(30.\)
Câu 3. Trong kì thi THPT Quốc gia năm 2022 tại một điểm thi có \(5\) sinh viên tình nguyện được phân công trực hướng dẫn thi sinh ở \(5\)vị trí khác nhau. Yêu cầu mỗi vị trí có đúng \(1\) sinh viên. Hỏi có bao nhiêu cách phân công vị trí trực cho 5 sinh viên đó?
A.\(625\). B.\(3125\). C.\(120\). D.\(80\).
Câu 4. Có thể tạo thành bao nhiêu véc-tơ khác vectơ không từ hai mươi điểm phân biệt trên mặt phẳng?
A. \(20!\) B. \(C_{20}^2\) C. \(20\) D. \(A_{20}^2\)
Câu 5. Một hộp đựng \(8\) quả cầu trắng và \(5\) quả cầu đỏ. Lấy ngẫu nhiên \(5\) quả. Có bao nhiêu cách để lấy ra được \(3\) quả đỏ?
A. \(40\). B. \(13\). C. \(38\). D. \(280\).
Câu 6. Một đề kiểm tra trắc nghiệm có 10 câu hỏi, mỗi câu hỏi chỉ có 1 đáp án đúng trong 4 đáp án. Giả sử các đáp án được chọn ngẫu nhiên. Số khả năng để bạn Uyên làm đúng 5 câu trong 10 câu hỏi của đề thi đó là:
A. \(C_{10}^5\). B. \(A_{10}^5\). C. \({3^5}.C_{10}^5\). D. \(5.C_{10}^5\).
Câu 7. Viết khai triển theo công thức nhị thức Niu-tơn của biểu thức \({\left( {x + 2} \right)^5}\).
A. \({x^5} + 10{x^4} + 40{x^3} + 80{x^2} + 80x + 32\).
B. \({x^5} - 10{x^4} + 40{x^3} - 80{x^2} + 80x - 32\).
C. \({x^5} - 10{x^4} - 40{x^3} - 80{x^2} - 80x + 32\).
D. \({x^5} + 10{x^4} - 40{x^3} + 80{x^2} - 80x + 32\).
Câu 8. Hệ số của \({x^3}\) trong khai triển biểu thức \({\left( {1 - 3x} \right)^8}\) là:
A. \(1512\). B.\( - 1512\). C.\(56\). D. \(1215\).
Câu 9. Tìm tổng \(T = C_n^1 + 3C_n^2 + {3^2}C_n^3 + ... + {3^{n - 1}}C_n^n\)
A. \({4^n}\). B. \({4^n} + 1\). C. \({4^n} - 1\). D. \(\frac{{{4^n} - 1}}{3}\).
Câu 10. Cho số gần đúng \(a = 23748023\) với độ chính xác \(d = 101\). Hãy viết số quy tròn của số a
A. \(23749000\). B. \(23748000\). C. \(23746000.\) D. \(23747000\).
Câu 11. Điểm trung bình thi học kỳ II môn Toán của một nhóm gồm \(N\) học sinh lớp 12A6 là \(8,1\). Biết rằng tổng điểm môn toán của nhóm này là \(72,9\). Tìm số học sinh của nhóm.
A. \(20\). B. \(9\). C. \(8\). D. \(15\).
Câu 12. Thống kê điểm kiểm tra \(15'\) môn Toán của lớp 10A1 trường THPT Chu Văn An được ghi lại như sau:

Số trung vị của mẫu số liệu trên là
A. \(8\). B. \(6\). C. \(7\). D. \(9\).
Câu 13. Theo kết quả thống kê điểm thi học kỳ 1 môn toán khối 10 của trường THPT Chu Văn An, người ta tính được phương sai của bảng thống kê đó là \(s_x^2 = 0,679\). Độ lệch chuẩn của bảng thống kê đó bằng:
A. \(0,812\). B. \(0,824\). C. \(0,936\). D. \(0,657\).
Câu 14. Tính phương sai của dãy số liệu: \(1,3,3,5,7,9,10,11,11,11.\)
A. \(\frac{{71}}{{10}}\).
B. \(\frac{{1329}}{{10}}\).
C. \(\frac{{710}}{{10}}\).
D. \(\frac{{1329}}{{100}}\).
Câu 15. Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:
163 159 172 167 165 168 170 161.
Khoảng biến thiên của mẫu số liệu trên là:
A. \(10\). B. \(13\). C. \(12\). D. \(14\).
Câu 16. Gieo một đồng xu cân đối và đồng chất liên tiếp \(3\) lần thì \(n(\Omega )\) là bao nhiêu?
A. \(6\). B. \(8\). C. \(32\). D. \(16\).
Câu 17. Gieo một con súc sắc. Xác suất để mặt lẻ chẵn xuất hiện là:
A.0,2 B. 0,3 C.0,4. D. 0,5
Câu 18. Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 5 là:
A. \(\frac{2}{9}\). B.\(\frac{1}{6}\). C. \(\frac{1}{9}\). D. \(\frac{5}{36}\).
Câu 19. Gieo hai con xúc xắc một cách vô tư. Tính xác suất của biến cố “Các mặt xuất hiện có số chấm bằng nhau”.
A. \(\frac{2}{9}\). B.\(\frac{1}{6}\). C. \(\frac{1}{9}\). D. \(\frac{5}{36}\).
Câu 20. Gieo một con súc xắc cân đối và đồng chất hai lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm là
A. \(\frac{{12}}{{36}}\). B. \(\frac{{11}}{{36}}\). C. \(\frac{6}{{36}}\). D. \(\frac{8}{{36}}\).
Câu 21. Cho tập hợp \(X = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\). Chọn ngẫu nhiên từ \(X\) ra ba số tự nhiên. Xác suất để chọn được ba số có tích là một số chẵn là:
A. \(P = 1 - \frac{{C_4^3}}{{C_{10}^3}}\).
B. \(P = 1 - \frac{{C_6^3}}{{C_{10}^3}}\).
C. \(P = 1 - \frac{{C_5^3}}{{C_9^3}}\).
D. \(P = \frac{{C_5^3}}{{C_9^3}}\).
Câu 22. Trường THPT Cao Bá Quát có 23 lớp, trong đó khối 10 có 8 lớp, khối 11 có 8 lớp, khối 12 có 7 lớp, mỗi lớp có một chi đoàn, mỗi chi đoàn có một em làm bí thư. Các em bí thư đều giỏi và rất năng động nên Ban chấp hành Đoàn trường chọn ngẫu nhiên 9 em bí thư đi thi cán bộ đoàn giỏi cấp thành phố. Tính xác suất để 9 em được chọn có đủ cả ba khối?
A. \(\frac{{7345}}{{7429}}\).
B. \(\frac{{7012}}{{7429}}\).
C. \(\frac{{7234}}{{7429}}\).
D. \(\frac{{7123}}{{7429}}\).
Câu 23. Trong mặt phẳng toạ độ \(Oxy\) cho hai điểm \(A\left( { - 1;3} \right),B\left( {2; - 5} \right)\).Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \(\left( {3;8} \right)\)
B. \(\left( {1; - 8} \right)\)
C. \(\left( {3; - 8} \right)\)
D. \(\left( {3;1} \right)\)
Câu 24. Trong mặt phẳng toạ độ \(Oxy\) cho \(\overrightarrow a = \left( {2;3} \right),\overrightarrow b = \left( {1; - 2} \right)\).Toạ độ của vectơ \(\overrightarrow u = 2\overrightarrow a + 3\overrightarrow b \) là:
A. \(\left( {7;0} \right)\)
B. \(\left( {7;12} \right)\)
C. \(\left( {1;0} \right)\)
D. \(\left( {3;1} \right)\)
Câu 25. Cho tam giác \(ABC\) với \(A\left( {2;3} \right),B\left( { - 4;5} \right),C\left( {4; - 3} \right)\). Tìm toạ độ điểm \(M\)thuộc trục \(Oy\)để \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất.
A. \(M\left( {0;\frac{1}{3}} \right)\)
B. \(M\left( {0; - \frac{5}{3}} \right)\)
C. \(M\left( {0;\frac{2}{3}} \right)\)
D. \(M\left( {0;\frac{5}{3}} \right)\)
Câu 26. Vectơ nào dưới đây là một vectơ pháp tuyến của \(d:x - 2y + 2023 = 0\)?
A.\(\overrightarrow {{n_1}} = \left( {0; - 2} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {1; - 2} \right)\).
C. \(\overrightarrow {{n_3}} = \left( { - 2;0} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {2;1} \right)\).
Câu 27. Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;3} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {3;5} \right)\) có phương trình tham số là:
A. \(d:\left\{ \begin{array}{l}x = 3 - 2t\\y = 5 + 3t\end{array} \right.\).
B. \(d:\left\{ \begin{array}{l}x = - 2 + 3t\\y = 3 + 5t\end{array} \right.\).
C. \(d:\left\{ \begin{array}{l}x = - 2 + 5t\\y = 3 - 3t\end{array} \right.\).
D. \(d:\left\{ \begin{array}{l}x = 3 + 2t\\y = 5 + 3t\end{array} \right.\).
Câu 28. Trong mặt phẳng với hệ tọa độ cho đường thẳng \({d_1}:3x + 4y - 5 = 0\)và đường thẳng \({d_2}:3x - 4y - 1 = 0\).Nêu vị trí tương đối của \({d_1}\) và \({d_2}\)
A. Cắt nhau và không vuông góc.
B. Vuông góc với nhau.
C. Song song với nhau.
D. Trùng nhau.
Câu 29. Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( {2; - 3} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(\sqrt 2 \).
A. \(m = 2.\) B. \(m = - 1\). C. \(m = - \frac{1}{2}\). D. \(m = 1\).
Câu 30. Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) có phương trình \({x^2} + {y^2} - 2x + 6y - 4 = 0\). Gọi \(I\left( {a;b} \right)\)là tâm của đường tròn \(\left( C \right)\). Tính tổng \(S = a + b\)
A. \(S = 4\). B. \(S = 1\). C. \(S = - 2\). D. \(S = 2\).
Câu 31. Trong mặt phẳng với hệ trục tọa độ \(Oxy\) cho điểm \(I\left( { - 1;2} \right)\). Viết phương trình đường tròn tâm \(I\), bán kính \(R = 3\).
A. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
B. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
C. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
Câu 32. Trong mặt phẳng với hệ tọa độ \(Oxy\) cho đường tròn \(\left( C \right)\) tâm \(I\left( {2;3} \right)\) tiếp xúc với đường thẳng \(\left( d \right):4x - 3y + 11 = 0\). Viết phương trình đường tròn \(\left( C \right)\).
A. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 9\).
B. \({\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} = 4\).
C. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 3\).
D. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\).
Câu 33. Trong mặt phẳng \(Oxy\) cho elip \(\left( E \right)\) có độ dài trục lớn bằng 10, độ dài tiêu cự bằng 8. Viết phương trình chính tắc của \(\left( E \right)\).
A. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
B. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
C. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
D. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{36}} = 1\)
Câu 34. Trong mặt phẳng \(Oxy\), Hyperbol \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) có một tiêu điểm là điểm nào dưới đây?
A. \(\left( { - 5;0} \right)\)
B. \(\left( {0;\sqrt 7 } \right)\)
C. \(\left( {\sqrt 7 ;0} \right)\)
D. \(\left( {0;5} \right)\)
Câu 35. Cho Parabol \(\left( P \right):\)\({y^2} = 64x\) và đường thẳng \(\left( \Delta \right):4x + 3y + 46 = 0\). Tìm điểm \(M \in (P)\) sao cho khoảng cách từ \(M\) đến \(\left( \Delta \right)\)là ngắn nhất.
A. \(M\left( {9; - 24} \right)\)
B. \(M\left( {9;24} \right)\)
C. \(M\left( {24;9} \right)\)
D. \(M\left( {9;2} \right)\)
II. PHẦN TỰ LUẬN (3 Điểm)
Câu 36. (1 điểm) Bạn An đo chiều dài của một sân bóng ghi được \(250 \pm 0,2m\). Bạn Bình đo chiều cao của một cột cờ được \(15 \pm 0,1m\). Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong phép đo của bạn đó là bao nhiêu?
Câu 37. (1 điểm) Tìm tất cả các giá trị của tham số \(m\) sao cho hai đường thẳng \({d_1}:x - y + 3 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = - 2 + \left( {m + 1} \right)t\\y = 1 - 2t\end{array} \right.\) hợp với nhau một góc \(45^\circ \).
Câu 38. (0,5 điểm) Cho đa giác đều \({A_1}{A_2}...{A_{2n}}\) nội tiếp trong đường tròn tâm \(O\). Biết rằng số tam giác có đỉnh là \(3\) trong \(2n\) điểm \({A_1};\,{A_2};\,...;\,{A_{2n}}\) gấp \(20\) lần so với số hình chữ nhật có đỉnh là \(4\) trong \(2n\) điểm \({A_1};\,{A_2};\,...;\,{A_{2n}}\). Tìm \(n\)?
Câu 39. (0,5 điểm) Trong mặt phẳng với hệ toạ độ \(Oxy\), cho điểm \(M\left( {3;1} \right)\). Viết phương trình đường thẳng \(d\) đi qua \(M\) cắt các tia \(Ox,Oy\) tại \(A\) và \(B\) sao cho \(\left( {OA + 3OB} \right)\) nhỏ nhất.
-----------------------------------------------------
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
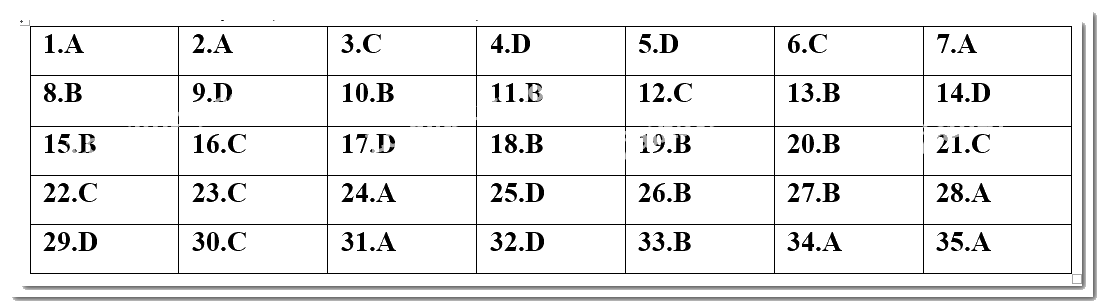
Câu 1. Lớp 10A có 20 bạn nữ và 18 bạn nam. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
A. \(38\) cách. B. \(20\)cách. C. \(18\) cách. D. \(360\).
Phương pháp
Áp dụng quy tắc cộng
Lời giải:
ChọnA
Chọn một học sinh trong số 20 hs nữ và 18 học sinh nam có: \(20 + 18 = 38\) cách.
Câu 2. Mã khoá số của chiếc Vali du lịch là một dãy số gồm ba chữ số. Mỗi chữ số có thể là một chữ số bất kì từ 0 đến 9. Hỏi có thể có bao nhiêu mã mở khoá khác nhau?
A. \({10^3}\). B. \(720.\) C. \(900.\) D. \(30.\)
Phương pháp
Áp dụng quy tắc nhân
Lời giải:
ChọnA
Chữ số thứ nhất có 10 cách chọn
Chữ số thứ hai có 10 cách chọn
Chữ số thứ ba có 10 cách chọn
Vậy có: \(10.10.10 = {10^3}\) (mã).
Câu 3. Trong kì thi THPT Quốc gia năm 2022 tại một điểm thi có \(5\) sinh viên tình nguyện được phân công trực hướng dẫn thi sinh ở \(5\)vị trí khác nhau. Yêu cầu mỗi vị trí có đúng \(1\) sinh viên. Hỏi có bao nhiêu cách phân công vị trí trực cho 5 sinh viên đó?
A.\(625\). B.\(3125\). C.\(120\). D.\(80\).
Phương pháp
Áp dụng công thức hoán vị
Lời giải:
Chọn C
Mỗi cách phân công \(5\) sinh viên trực ở \(5\)vị trí khác nhau là\(1\) hoán vị của\(5\)phần tử.
Vậy có tất cả là \(5! = 120\).
Câu 4. Có thể tạo thành bao nhiêu véc-tơ khác vectơ không từ hai mươi điểm phân biệt trên mặt phẳng?
A. \(20!\) B. \(C_{20}^2\) C. \(20\) D. \(A_{20}^2\)
Phương pháp
Áp dụng công thức chỉnh hợp
Lời giải:
Chọn D
Mỗi vectơ khác vectơ không được tạo thành bằng cách lấy hai điểm từ hai mươi điểm đã cho và phân biệt thứ tự điểm đầu và điểm cuối. Như vậy, mỗi vectơ là một chỉnh hợp chập 2 của 20. Vậy số các vectơ tạo thành là: \(A_{20}^2\).
Câu 5. Một hộp đựng \(8\) quả cầu trắng và \(5\) quả cầu đỏ. Lấy ngẫu nhiên \(5\) quả. Có bao nhiêu cách để lấy ra được \(3\) quả đỏ?
A. \(40\). B. \(13\). C. \(38\). D. \(280\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải:
Chọn D
Lấy \(5\) quả gồm \(3\) quả đỏ và \(2\) quả trắng,
Với \(5\) quả cầu đỏ lấy \(3\) quả, ta có \(C_5^3\) cách.
Với \(8\) quả cầu trắng lấy \(2\) quả, ta có \(C_8^2\) cách.
Vậy có \(C_5^3.C_8^2 = 280\) cách.
Câu 6. Một đề kiểm tra trắc nghiệm có 10 câu hỏi, mỗi câu hỏi chỉ có 1 đáp án đúng trong 4 đáp án. Giả sử các đáp án được chọn ngẫu nhiên. Số khả năng để bạn Uyên làm đúng 5 câu trong 10 câu hỏi của đề thi đó là:
A. \(C_{10}^5\). B. \(A_{10}^5\). C. \({3^5}.C_{10}^5\). D. \(5.C_{10}^5\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải:
Chọn C
Mỗi cách chọn 5 câu làm đúng trong 10 câu là một tổ hợp chập 5 của 10 phần tử nên có \(C_{10}^5\)
Vì 5 câu còn lại làm sai, mỗi câu có 3 đáp án sai nên có \(3.3.3.3.3 = {3^5}\)
Vậy có \({3^5}.C_{10}^5\)
Câu 7. Viết khai triển theo công thức nhị thức Niu-tơn của biểu thức \({\left( {x + 2} \right)^5}\).
A. \({x^5} + 10{x^4} + 40{x^3} + 80{x^2} + 80x + 32\).
B. \({x^5} - 10{x^4} + 40{x^3} - 80{x^2} + 80x - 32\).
C. \({x^5} - 10{x^4} - 40{x^3} - 80{x^2} - 80x + 32\).
D. \({x^5} + 10{x^4} - 40{x^3} + 80{x^2} - 80x + 32\).
Phương pháp
Áp dụng công thức nhị thức Newton
Lời giải:
Chọn A
\({\left( {x + 2} \right)^5} = {x^5} + 10{x^4} + 40{x^3} + 80{x^2} + 80x + 32\)
Câu 8. Hệ số của \({x^3}\) trong khai triển biểu thức \({\left( {1 - 3x} \right)^8}\) là:
A. \(1512\). B.\( - 1512\). C.\(56\). D. \(1215\).
Phương pháp
Áp dụng công thức nhị thức Newton
Lời giải:
Chọn B
Ta có \({\left( {1 - 3x} \right)^8} = \sum\limits_{k = 0}^8 {C_8^k} {\left( { - 3} \right)^k}{x^k}\).
\( \Rightarrow \) Hệ số của \({x^3}\) là \(C_8^3{\left( { - 3} \right)^3} = - 1512\).
Câu 9. Tìm tổng \(T = C_n^1 + 3C_n^2 + {3^2}C_n^3 + ... + {3^{n - 1}}C_n^n\)
A. \({4^n}\).
B. \({4^n} + 1\).
C. \({4^n} - 1\).
D. \(\frac{{{4^n} - 1}}{3}\).
Phương pháp
Áp dụng công thức nhị thức Newton
Lời giải:
Chọn D
Xét khai triển \({\left( {1 + x} \right)^n} = C_n^0 + xC_n^1 + {x^2}C_n^2 + {x^3}C_n^3 + ... + {x^n}C_n^n\)
Cho \(x = 3\) ta có: \({4^n} = C_n^0 + 3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^n\)
\( \Rightarrow {4^n} - C_n^0 = 3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^n\)
\( \Leftrightarrow {4^n} - 1 = 3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^n\)
\( \Leftrightarrow \frac{{{4^n} - 1}}{3} = C_n^1 + 3C_n^2 + {3^2}C_n^3 + ... + {3^{n - 1}}C_n^n\)
\( \Rightarrow T = \frac{{{4^n} - 1}}{3}\)
Câu 10. Cho số gần đúng \(a = 23748023\) với độ chính xác \(d = 101\). Hãy viết số quy tròn của số a
A. \(23749000\). B. \(23748000\). C. \(23746000.\) D. \(23747000\).
Phương pháp
Khi thay số đúng bởi số quy tròn đến một hàng nào đó thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng quy tròn. Như vậy, độ chính sác của số quy tròn bằng nửa đơn vị của hàng quy tròn.
Lời giải:
Chọn B
Số quy tròn của số \(a = 23748023\) là \(23748000\)
Câu 11. Điểm trung bình thi học kỳ II môn Toán của một nhóm gồm \(N\) học sinh lớp 12A6 là \(8,1\). Biết rằng tổng điểm môn toán của nhóm này là \(72,9\). Tìm số học sinh của nhóm.
A. \(20\). B. \(9\). C. \(8\). D. \(15\).
Phương pháp
Số trung bình cộng \(\overline x \) của mẫu số liệu \({x_1},{x_2},...,{x_n}\) là:
\(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}.\)
Lời giải:
Chọn B
Ta có giá giá trị \(N = \frac{{72,9}}{{8,1}} = 9\) (học sinh).
Câu 12. Thống kê điểm kiểm tra \(15'\) môn Toán của lớp 10A1 trường THPT Chu Văn An được ghi lại như sau:

Số trung vị của mẫu số liệu trên là
A. \(8\). B. \(6\). C. \(7\). D. \(9\).
Phương pháp
Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm ( hoặc không tăng).
- Nếu n là lẻ thì số liệu đứng ở vị trí thứ \(\frac{{n + 1}}{2}\) ( số đứng chính giữa) gọi là trung vị
- Nếu n là chẵn thì số trung bình cộng của hai số liệu đứng ở vị trí thứ \(\frac{n}{2}\) và \(\frac{n}{2} + 1\) gọi là trung vị
Lời giải
Chọn C
Các số liệu đã được xếp theo thức tự tăng dần.
Tổng số có 35 số liệu nên số trung vị là giá trị ở vị trí 18.
Vậy số trung vị là 7.
Câu 13. Theo kết quả thống kê điểm thi học kỳ 1 môn toán khối 10 của trường THPT Chu Văn An, người ta tính được phương sai của bảng thống kê đó là \(s_x^2 = 0,679\). Độ lệch chuẩn của bảng thống kê đó bằng:
A. \(0,812\). B. \(0,824\). C. \(0,936\). D. \(0,657\).
Phương pháp
Căn bậc hai của phương sai gọi là Độ lệch chuẩn của mẫu số liệu thống kê
Lời giải
Chọn B
Ta có công thức tính độ lệch chuẩn là \({s_x} = \sqrt {s_x^2} = \sqrt {0,679} \approx 0,824\).
Câu 14. Tính phương sai của dãy số liệu: \(1,3,3,5,7,9,10,11,11,11.\)
A. \(\frac{{71}}{{10}}\).
B. \(\frac{{1329}}{{10}}\).
C. \(\frac{{710}}{{10}}\).
D. \(\frac{{1329}}{{100}}\).
Phương sai
Cho mẫu số liêu thống kê có n giá trị \({x_1},{x_2},...,{x_n}\) và số trung bình cộng \(\overline x \).
Ta gọi số \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n}\) là phương sai của mẫu số liệu
Lời giải
Chọn D
Bảng phân bố tần số của dãy số liệu:

Ta có \(\overline x = \frac{1}{{10}}\left( {1.1 + 3.2 + 5.1 + 7.1 + 9.1 + 10.1 + 11.3} \right) = \frac{{71}}{{10}}\).
Phương sai là:
\({S^2} = \frac{1}{{10}}\left[ {1.{{\left( {1 - \frac{{71}}{{10}}} \right)}^2} + 2.{{\left( {3 - \frac{{71}}{{10}}} \right)}^2} + 1.{{\left( {5 - \frac{{71}}{{10}}} \right)}^2} + 1.{{\left( {7 - \frac{{71}}{{10}}} \right)}^2} + 1.{{\left( {9 - \frac{{71}}{{10}}} \right)}^2} + 1.{{\left( {10 - \frac{{71}}{{10}}} \right)}^2}} \right.\)
\(\left. { + 3.{{\left( {11 - \frac{{71}}{{10}}} \right)}^2}} \right] = 13,29\)
Câu 15. Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:
163 159 172 167 165 168 170 161.
Khoảng biến thiên của mẫu số liệu trên là:
A. \(10\). B. \(13\). C. \(12\). D. \(14\).
Phương pháp
Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.
Ta có thể tính khoảng bến thiên R của mẫu số liệu theo công thức \(R = {x_{\max }} - {x_{\min }}\), trong đó \({x_{\max }}\) là giá trị lớn nhất, \({x_{\min }}\)là giá trị nhỏ nhất của mẫu số liệu đó.
Lời giải
Chọn B
Chiều cao thấp nhất, cao nhất tương ứng là 159; 172.
Do đó, khoảng biến thiên là: \(R = 172 - 159 = 13\).
Câu 16. Gieo một đồng xu cân đối và đồng chất liên tiếp \(3\) lần thì \(n(\Omega )\) là bao nhiêu?
A. \(6\). B. \(8\). C. \(32\). D. \(16\).
Phương pháp
Sử dụng các quy tắc đếm
Lời giải
Chọn C
\(n(\Omega ) = {2^3} = 8\).
Câu 17. Gieo một con súc sắc. Xác suất để mặt lẻ chẵn xuất hiện là:
A.0,2. B. 0,3. C.0,4. D.0,5.
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn D
Không gian mẫu: \(\Omega = \left\{ {1;2;3;4;5;6} \right\} \Rightarrow n\left( \Omega \right) = 6\)
Biến cố xuất hiện mặt chẵn: \(A = \left\{ {1;3;5} \right\} \Rightarrow n\left( A \right) = 3\)
Suy ra \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{1}{2}\)
Câu 18. Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 5 là:
A. \(\frac{2}{9}\). B.\(\frac{1}{6}\). C. \(\frac{1}{9}\). D. \(\frac{5}{36}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn C
Gọi A:”tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 5”.
\(A = \left\{ {\left( {1;4} \right),\left( {4;1} \right),\left( {2;3} \right),\left( {3;2} \right)} \right\} \Rightarrow n\left( A \right) = 4\)
Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{{36}} = \frac{1}{9}\)
Câu 19. Gieo hai con xúc xắc một cách vô tư. Tính xác suất của biến cố “Các mặt xuất hiện có số chấm bằng nhau”.
A. \(\frac{2}{9}\). B.\(\frac{1}{6}\). C. \(\frac{7}{36}\). D. \(\frac{5}{36}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn B
Ta có: \(n(\Omega ) = 6.6 = 36\).
Số cách xuất hiện các mặt có số chấm bằng nhau là: \(\left( {1,1} \right)\left( {2,2} \right)\left( {3,3} \right)\left( {4,4} \right)\left( {5,5} \right)\left( {6,6} \right)\)
Vậy \(n(A) = 6 \Rightarrow P\left( A \right) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}\)
Câu 20. Gieo một con súc xắc cân đối và đồng chất hai lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm là
A. \(\frac{{12}}{{36}}\).
B. \(\frac{{11}}{{36}}\).
C. \(\frac{6}{{36}}\).
D. \(\frac{8}{{36}}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn B
\(n(\Omega ) = 6.6 = 36\). Gọi \(A\):”ít nhất một lần xuất hiện mặt sáu chấm”.
Khi đó \(\overline A \):”không có lần nào xuất hiện mặt sáu chấm”.
Ta có\(n(\overline A ) = 5.5 = 25\). Vậy \(P(A) = 1 - P(\overline A ) = 1 - \frac{{25}}{{36}} = \frac{{11}}{{36}}\).
Câu 21. Cho tập hợp \(X = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\). Chọn ngẫu nhiên từ \(X\) ra ba số tự nhiên. Xác suất để chọn được ba số có tích là một số chẵn là:
A. \(P = 1 - \frac{{C_4^3}}{{C_{10}^3}}\).
B. \(P = 1 - \frac{{C_6^3}}{{C_{10}^3}}\).
C. \(P = 1 - \frac{{C_5^3}}{{C_9^3}}\).
D. \(P = \frac{{C_5^3}}{{C_9^3}}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn C
Mỗi phần tử của không gian mẫu ứng với một tổ hợp chập 3 của 9 phần tử
Ta có: \(n\left( \Omega \right) = C_9^3\) cách chọn.
Tích ba số là một số chẵn thì ít nhất 1 trong 3 số phải là số chẵn.
Gọi \(A\) là biến cố: 3 số được chọn có ít nhất một số chẵn;
\(\overline A \) là biến cố: 3 số được chọn là 3 số lẻ. Suy ra \(n\left( {\overline A } \right) = C_5^3\) cách chọn.
Vậy xác suất để chọn được ba số có tích là một số chẵn là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{C_5^3}}{{C_9^3}}\).
Câu 22. Trường THPT Cao Bá Quát có 23 lớp, trong đó khối 10 có 8 lớp, khối 11 có 8 lớp, khối 12 có 7 lớp, mỗi lớp có một chi đoàn, mỗi chi đoàn có một em làm bí thư. Các em bí thư đều giỏi và rất năng động nên Ban chấp hành Đoàn trường chọn ngẫu nhiên 9 em bí thư đi thi cán bộ đoàn giỏi cấp thành phố. Tính xác suất để 9 em được chọn có đủ cả ba khối?
A. \(\frac{{7345}}{{7429}}\).
B. \(\frac{{7012}}{{7429}}\).
C. \(\frac{{7234}}{{7429}}\).
D. \(\frac{{7123}}{{7429}}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn C
Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{23}^9 = 817190\)
Gọi A là biến cố “9 em được chọn có đủ cả ba khối”
\( \Rightarrow \overline A \) “9 em được chọn không có đủ ba khối”
Vì mỗi khối số bí thư đều nhỏ hơn 9 nên có các khả năng sau:
TH1: Chỉ có học sinh ở khối 10 và 11. Có \(C_{16}^9\) cách.
TH2: Chỉ có học sinh ở khối 11 và 12. Có \(C_{15}^9\) cách.
TH3: Chỉ có học sinh ở khối 10 và 12. Có \(C_{15}^9\) cách.
Số phần tử của biến cố \(\overline A \) là: \(n\left( {\overline A } \right) = C_{16}^9 + C_{15}^9 + C_{15}^9 = 21450\)
Xác suất của biến cố \(\overline A \) là: \(P\left( {\overline A } \right) = \frac{{21450}}{{817190}} = \frac{{195}}{{7429}}\).
Xác suất của biến cố A là: \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{195}}{{7429}} = \frac{{7234}}{{7429}}\).
Câu 23. Trong mặt phẳng toạ độ \(Oxy\) cho hai điểm \(A\left( { - 1;3} \right),B\left( {2; - 5} \right)\).Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \(\left( {3;8} \right)\)
B. \(\left( {1; - 8} \right)\)
C. \(\left( {3; - 8} \right)\)
D. \(\left( {3;1} \right)\)
Phương pháp
Với \(A({x_A};{y_A});B({x_B};{y_B})\) thì \(\overrightarrow {AB} = \left( {({x_B} - {x_A});({y_B} - {y_A})} \right)\)
Lời giải
Chọn C
\(\overrightarrow {AB} = \left( {3; - 8} \right)\)
Câu 24. Trong mặt phẳng toạ độ \(Oxy\) cho \(\overrightarrow a = \left( {2;3} \right),\overrightarrow b = \left( {1; - 2} \right)\).Toạ độ của vectơ \(\overrightarrow u = 2\overrightarrow a + 3\overrightarrow b \) là:
A. \(\left( {7;0} \right)\)
B. \(\left( {7;12} \right)\)
C. \(\left( {1;0} \right)\)
D. \(\left( {3;1} \right)\)
Phương pháp
Trong mặt phẳng \(Oxy\), cho \(\vec a = \left( {{a_1}\,;\,{a_2}} \right)\); \(\vec b = \left( {{b_1}\,;\,{b_2}} \right)\). Tọa độ vectơ \(k\overrightarrow a + t\overrightarrow b = (k{a_1} + t{b_1};k{a_2} + t{b_2})\)
Lời giải
Chọn A
Ta có \(\overrightarrow a = \left( {2;3} \right) \Rightarrow 2\overrightarrow a = \left( {4;6} \right)\)
\(\overrightarrow b = \left( {1; - 2} \right) \Rightarrow 3\overrightarrow b = \left( {3; - 6} \right)\)
Vậy \(\overrightarrow u = 2\overrightarrow a + 3\overrightarrow b = \left( {7;0} \right)\)
Câu 25. Cho tam giác \(ABC\) với \(A\left( {2;3} \right),B\left( { - 4;5} \right),C\left( {4; - 3} \right)\). Tìm toạ độ điểm \(M\)thuộc trục \(Oy\)để \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất.
A. \(M\left( {0;\frac{1}{3}} \right)\)
B. \(M\left( {0; - \frac{5}{3}} \right)\)
C. \(M\left( {0;\frac{2}{3}} \right)\)
D. \(M\left( {0;\frac{5}{3}} \right)\)
Phương pháp
M là hình chiếu vuông góc của \(G\) lên \(Oy\) với \(G\) là trọng tâm tam giác \(ABC\)
Lời giải
Chọn D
Gọi \(G\) là trọng tâm tam giác \(ABC \Rightarrow G\left( {\frac{2}{3};\frac{5}{3}} \right)\)
Ta có \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
\( \Rightarrow \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {3\overrightarrow {MG} } \right| = 3MG\)
\( \Rightarrow \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất khi \(MG\) nhỏ nhất
mà \(M \in Oy \Rightarrow M\) là hình chiếu vuông góc của \(G\) lên \(Oy \Rightarrow M\left( {0;\frac{5}{3}} \right)\)
Câu 26. Vectơ nào dưới đây là một vectơ pháp tuyến của \(d:x - 2y + 2023 = 0\)?
A.\(\overrightarrow {{n_1}} = \left( {0; - 2} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {1; - 2} \right)\).
C. \(\overrightarrow {{n_3}} = \left( { - 2;0} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {2;1} \right)\).
Phương pháp
Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)
Lời giải
Chọn B
(d:x - 2y + 2023 = 0 \Rightarrow VTPT\overrightarrow {{n_d}} = \left( {1; - 2} \right)\)
Câu 27. Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;3} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {3;5} \right)\) có phương trình tham số là:
A. \(d:\left\{ \begin{array}{l}x = 3 - 2t\\y = 5 + 3t\end{array} \right.\).
B. \(d:\left\{ \begin{array}{l}x = - 2 + 3t\\y = 3 + 5t\end{array} \right.\).
C. \(d:\left\{ \begin{array}{l}x = - 2 + 5t\\y = 3 - 3t\end{array} \right.\).
D. \(d:\left\{ \begin{array}{l}x = 3 + 2t\\y = 5 + 3t\end{array} \right.\).
Phương pháp
Phương trình tham số đường thẳng \(d\) đi qua điểm \(A({x_0},{y_0})\) và có VTCP \(\overrightarrow u = \left( {a;b} \right)\)là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)
Lời giải
Chọn B
PTTS đường thẳng \(d\) đi qua điểm \(M\left( { - 2;3} \right)\) và có VTCP \(\overrightarrow u = \left( {3;5} \right)\)là \(\left\{ \begin{array}{l}x = - 2 + 3t\\y = 3 + 5t\end{array} \right.\)
Câu 28. Trong mặt phẳng với hệ tọa độ cho đường thẳng \({d_1}:3x + 4y - 5 = 0\)và đường thẳng \({d_2}:3x - 4y - 1 = 0\).Nêu vị trí tương đối của \({d_1}\) và \({d_2}\)
A. Cắt nhau và không vuông góc.
B. Vuông góc với nhau.
C. Song song với nhau.
D. Trùng nhau.
Phương pháp
Vị trí tương đối giữa hai đường thẳng
Lời giải
Chọn A
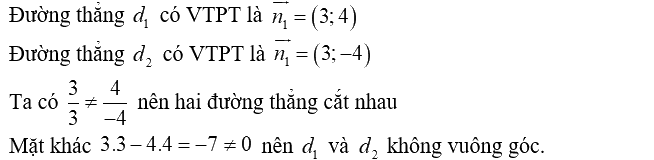
Câu 29. Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( {2; - 3} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(\sqrt 2 \).
A. \(m = 2.\)
B. \(m = - 1\).
C. \(m = - \frac{1}{2}\).
D. \(m = 1\).
Phương pháp
Khoảng cách từ điểm \(A({x_0},{y_0})\) đến đường thẳng \(d:ax + by + c = 0\) là \(d\left( {A,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn D
\(d\left( {A,\Delta } \right) = \frac{{\left| {2m - 3 - m + 4} \right|}}{{\sqrt {{m^2} + 1} }} \Leftrightarrow \frac{{\left| {m + 1} \right|}}{{\sqrt {{m^2} + 1} }} = \sqrt 2 \Leftrightarrow \left| {m + 1} \right| = \sqrt 2 .\sqrt {{m^2} + 1} \)
\( \Leftrightarrow {m^2} + 2m + 1 = 2\left( {{m^2} + 1} \right) \Leftrightarrow {m^2} - 2m + 1 = 0 \Leftrightarrow m = 1\)
Câu 30. Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) có phương trình \({x^2} + {y^2} - 2x + 6y - 4 = 0\). Gọi \(I\left( {a;b} \right)\)là tâm của đường tròn \(\left( C \right)\). Tính tổng \(S = a + b\)
A. \(S = 4\). B. \(S = 1\). C. \(S = - 2\). D. \(S = 2\).
Phương pháp
Phương trình đường tròn có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\,\,\left( {{a^2} + {b^2} - c > 0} \right)\). và tọa độ tâm \(I(a,b)\), bán kính \(\,R = \sqrt {{a^2} + {b^2} - c} \)
Lời giải
Chọn C
Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 3} \right)\) và bán kính \(R = \sqrt {1 + 9 + 4} = \sqrt {14} \)
\(a = 1,b = - 3 \Rightarrow S = a + b = - 2\)
Câu 31. Trong mặt phẳng với hệ trục tọa độ \(Oxy\) cho điểm \(I\left( { - 1;2} \right)\). Viết phương trình đường tròn tâm \(I\), bán kính \(R = 3\).
A. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
B. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
C. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn A
Đường tròn có tâm \(I\left( { - 1;2} \right)\) và bán kính \(R = 3\) có phương trình là: \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
Câu 32. Trong mặt phẳng với hệ tọa độ \(Oxy\) cho đường tròn \(\left( C \right)\) tâm \(I\left( {2;3} \right)\) tiếp xúc với đường thẳng \(\left( d \right):4x - 3y + 11 = 0\). Viết phương trình đường tròn \(\left( C \right)\).
A. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 9\).
B. \({\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} = 4\).
C. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 3\).
D. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn D
Do \(\left( C \right)\) tiếp xúc với \(\left( d \right)\) nên \(\left( C \right)\) có bán kính \(R = d\left( {I,d} \right) = \frac{{\left| {4.2 - 3.3 + 11} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 2\) .
\( \Rightarrow \left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\).
Câu 33. Trong mặt phẳng \(Oxy\) cho elip \(\left( E \right)\) có độ dài trục lớn bằng 10, độ dài tiêu cự bằng 8. Viết phương trình chính tắc của \(\left( E \right)\).
A. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
B. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
C. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
D. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{36}} = 1\)
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có hai tiêu điểm \({F_1} = \left( {c\,;\,0} \right)\); \({F_2} = \left( { - c\,;\,0} \right)\) với \(c = \sqrt {{a^2} - {b^2}} \)
Lời giải
Chọn D
Ta có: \(2a = 10 \Rightarrow a = 5;2c = 8 \Rightarrow c = 4\). Độ dài trục bé: \(b = \sqrt {{a^2} - {c^2}} = 3\).
Phương trình chính tắc của Elíp là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
Câu 34. Trong mặt phẳng \(Oxy\), Hyperbol \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) có một tiêu điểm là điểm nào dưới đây?
A. \(\left( { - 5;0} \right)\)
B. \(\left( {0;\sqrt 7 } \right)\)
C. \(\left( {\sqrt 7 ;0} \right)\)
D. \(\left( {0;5} \right)\)
Phương pháp
Phương trình Hypebol \(\left( H \right):\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) có hai tiêu điểm \({F_1} = \left( {c\,;\,0} \right)\); \({F_2} = \left( { - c\,;\,0} \right)\) với \(c = \sqrt {{a^2} + {b^2}} \)
Lời giải
Chọn A
Ta có: \({a^2} = 16;{b^2} = 9 \Rightarrow {c^2} = {a^2} + {b^2} = 16 + 9 = 25\)
Vậy hai tiêu điểm của hyperbol là \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\).
Câu 35. Cho Parabol \(\left( P \right):\)\({y^2} = 64x\) và đường thẳng \(\left( \Delta \right):4x + 3y + 46 = 0\). Tìm điểm \(M \in (P)\) sao cho khoảng cách từ \(M\) đến \(\left( \Delta \right)\)là ngắn nhất.
A. \(M\left( {9; - 24} \right)\)
B. \(M\left( {9;24} \right)\)
C. \(M\left( {24;9} \right)\)
D. \(M\left( {9;2} \right)\)
Phương pháp
Khoảng cách từ điểm \(A({x_0},{y_0})\) đến đường thẳng \(d:ax + by + c = 0\) là \(d\left( {A,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn A
Gọi \(M\left( {\frac{{{m^2}}}{{64}};m} \right) \in (P)\)
Ta có \(d\left( {M,d} \right) = \frac{{\left| {4.\frac{{{m^2}}}{{64}} + 3m + 46} \right|}}{{\sqrt {{4^2} + {3^3}} }} = \frac{{\left| {{m^2} + 48m + 736} \right|}}{{80}} = \frac{1}{{80}}\left| {{{\left( {m + 24} \right)}^2} + 160} \right| \ge 2\)
\( \Rightarrow Min\,\,d(M,d) = 2 \Leftrightarrow m = - 24 \Rightarrow M\left( {9; - 24} \right)\)
II. PHẦN TỰ LUẬN (3 Điểm)
Câu 36. (1 điểm) Bạn An đo chiều dài của một sân bóng ghi được \(250 \pm 0,2m\). Bạn Bình đo chiều cao của một cột cờ được \(15 \pm 0,1m\). Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong phép đo của bạn đó là bao nhiêu?
Phương pháp
Ta nói a là số gần đúng của số đúng \(\overline a \) với độ chính xác d nếu \({\Delta _a} = \left| {\overline a - a} \right| \le d\) và quy ước viết gọn là \(\overline a = a \pm d\)
Tỉ số \({\delta _a} = \frac{{{\Delta _a}}}{{\left| a \right|}}\) được gọi là sai số tương đối của số gần đúng a.
Lời giải:
Phép đo của bạn An có sai số tương đối \({\delta _1} \le \frac{{0,2}}{{250}} = 0,0008 = 0,08\% \)
Phép đo của bạn Bình có sai số tương đối \({\delta _2} \le \frac{{0,1}}{{15}} = 0,0066 = 0,66\% \)
Như vậy phép đo của bạn An có độ chính xác cao hơn.
Câu 37. (1 điểm) Tìm tất cả các giá trị của tham số \(m\) sao cho hai đường thẳng \({d_1}:x - y + 3 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = - 2 + \left( {m + 1} \right)t\\y = 1 - 2t\end{array} \right.\) hợp với nhau một góc \(45^\circ \).
Phương pháp
Sử dụng công thức tính góc giữa hai đường thẳng
Lời giải:
\(\left( {{d_1}} \right)\) có VTPT \(\overrightarrow {{n_1}} = \left( {1; - 1} \right)\)
\(\left( {{d_1}} \right)\) có VTCP \(\overrightarrow {{u_2}} = \left( {m + 1; - 2} \right)\)\( \Rightarrow \)VTPT \(\overrightarrow {{n_2}} = \left( {2;m + 1} \right)\)
\(\cos \left( {{d_1},{d_2}} \right) = \cos {45^ \circ } \Leftrightarrow \frac{{\left| {2 - m - 1} \right|}}{{\sqrt 2 .\sqrt {{{\left( {m + 1} \right)}^2} + 4} }} = \frac{1}{{\sqrt 2 }} \Leftrightarrow \frac{1}{{\sqrt 2 }} = \frac{{\left| {1 - m} \right|}}{{\sqrt 2 .\sqrt {{m^2} + 2m + 5} }}\)
\( \Leftrightarrow {m^2} + 2m + 5 = 1 - 2m + {m^2} \Leftrightarrow m = - 1\)
Câu 38. (0,5 điểm) Cho đa giác đều \({A_1}{A_2}...{A_{2n}}\) nội tiếp trong đường tròn tâm \(O\). Biết rằng số tam giác có đỉnh là \(3\) trong \(2n\) điểm \({A_1};\,{A_2};\,...;\,{A_{2n}}\) gấp \(20\) lần so với số hình chữ nhật có đỉnh là \(4\) trong \(2n\) điểm \({A_1};\,{A_2};\,...;\,{A_{2n}}\). Tìm \(n\)?
Phương pháp
Sử dụng các quy tắc đếm
Lời giải:
Số tam giác có 3 đỉnh là \(3\) trong \(2n\) điểm \({A_1};{A_2};...;{A_{2n}}\) là \(C_{2n}^3\).
Ứng với hai đường chéo đi qua tâm của đa giác \({A_1}{A_2}...{A_{2n}}\)cho tương ứng một hình chữ nhật có 4 đỉnh
là \(4\) điểm trong \(2n\) điểm \({A_1};{A_2};...;{A_{2n}}\)và ngược lại mỗi hình chữ nhật như vậy sẽ cho ra \(2\) đường chéo đi qua tâm\(O\) của đa giác.
Mà số đường chéo đi qua tâm của đa giác đều \(2n\) đỉnh là \(n\) nên số hình chữ nhật có đỉnh là \(4\) trong \(2n\) điểm là \(C_n^2\)
Theo đề bài ta có: \(C_{2n}^3 = 20C_n^2 \Leftrightarrow \frac{{2n\left( {2n - 1} \right)\left( {2n - 2} \right)}}{{3!}} = \frac{{20n\left( {n - 1} \right)}}{2} \Leftrightarrow n = 8\).
Câu 39. (0,5 điểm) Trong mặt phẳng với hệ toạ độ \(Oxy\), cho điểm \(M\left( {3;1} \right)\). Viết phương trình đường thẳng \(d\) đi qua \(M\) cắt các tia \(Ox,Oy\) tại \(A\) và \(B\) sao cho \(\left( {OA + 3OB} \right)\) nhỏ nhất.
Phương pháp
PT đường thẳng \(d\) cắt tia \(Ox\) tại \(A\left( {a;0} \right)\), tia \(Oy\) tại \(B\left( {0;b} \right)\) có dạng: \(\frac{x}{a} + \frac{y}{b} = 1\)\(\left( {a,b > 0} \right)\)
Lời giải:
PT đường thẳng \(d\) cắt tia \(Ox\) tại \(A\left( {a;0} \right)\), tia \(Oy\) tại \(B\left( {0;b} \right)\) có dạng: \(\frac{x}{a} + \frac{y}{b} = 1\)\(\left( {a,b > 0} \right)\)
\(M\left( {3;1} \right) \in d\) nên \(\frac{3}{a} + \frac{1}{b} = 1\).
Mà \(1 = \frac{3}{a} + \frac{1}{b}\mathop \ge \limits^{Cô-si} 2\sqrt {\frac{3}{a}.\frac{1}{b}} \Rightarrow ab \ge 12\)
Mà \(OA + 3OB = a + 3b \ge 2\sqrt {3ab} = 12\) \( \Rightarrow Min\left( {OA + 3OB} \right) = 12 \Leftrightarrow \left\{ \begin{array}{l}a = 3b\\\frac{3}{a} = \frac{1}{b} = \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 2\end{array} \right.\)
Vậy phương trình đường thẳng \(d\) là: \(\frac{x}{6} + \frac{y}{2} = 1 \Leftrightarrow x + 3y - 6 = 0\)
------------------------------------------------
Tải về
I. PHẦN TRẮC NGHIỆM (7 Điểm)
Câu 1. Lớp 10A có 20 bạn nữ và 18 bạn nam. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
A. \(38\) cách. B. \(20\)cách. C. \(18\) cách. D. \(360\).
Câu 2. Mã khoá số của chiếc Vali du lịch là một dãy số gồm ba chữ số. Mỗi chữ số có thể là một chữ số bất kì từ 0 đến 9. Hỏi có thể có bao nhiêu mã mở khoá khác nhau?
A. \({10^3}\). B. \(720.\) C. \(900.\) D. \(30.\)
Câu 3. Trong kì thi THPT Quốc gia năm 2022 tại một điểm thi có \(5\) sinh viên tình nguyện được phân công trực hướng dẫn thi sinh ở \(5\)vị trí khác nhau. Yêu cầu mỗi vị trí có đúng \(1\) sinh viên. Hỏi có bao nhiêu cách phân công vị trí trực cho 5 sinh viên đó?
A.\(625\). B.\(3125\). C.\(120\). D.\(80\).
Câu 4. Có thể tạo thành bao nhiêu véc-tơ khác vectơ không từ hai mươi điểm phân biệt trên mặt phẳng?
A. \(20!\) B. \(C_{20}^2\) C. \(20\) D. \(A_{20}^2\)
Câu 5. Một hộp đựng \(8\) quả cầu trắng và \(5\) quả cầu đỏ. Lấy ngẫu nhiên \(5\) quả. Có bao nhiêu cách để lấy ra được \(3\) quả đỏ?
A. \(40\). B. \(13\). C. \(38\). D. \(280\).
Câu 6. Một đề kiểm tra trắc nghiệm có 10 câu hỏi, mỗi câu hỏi chỉ có 1 đáp án đúng trong 4 đáp án. Giả sử các đáp án được chọn ngẫu nhiên. Số khả năng để bạn Uyên làm đúng 5 câu trong 10 câu hỏi của đề thi đó là:
A. \(C_{10}^5\). B. \(A_{10}^5\). C. \({3^5}.C_{10}^5\). D. \(5.C_{10}^5\).
Câu 7. Viết khai triển theo công thức nhị thức Niu-tơn của biểu thức \({\left( {x + 2} \right)^5}\).
A. \({x^5} + 10{x^4} + 40{x^3} + 80{x^2} + 80x + 32\).
B. \({x^5} - 10{x^4} + 40{x^3} - 80{x^2} + 80x - 32\).
C. \({x^5} - 10{x^4} - 40{x^3} - 80{x^2} - 80x + 32\).
D. \({x^5} + 10{x^4} - 40{x^3} + 80{x^2} - 80x + 32\).
Câu 8. Hệ số của \({x^3}\) trong khai triển biểu thức \({\left( {1 - 3x} \right)^8}\) là:
A. \(1512\). B.\( - 1512\). C.\(56\). D. \(1215\).
Câu 9. Tìm tổng \(T = C_n^1 + 3C_n^2 + {3^2}C_n^3 + ... + {3^{n - 1}}C_n^n\)
A. \({4^n}\). B. \({4^n} + 1\). C. \({4^n} - 1\). D. \(\frac{{{4^n} - 1}}{3}\).
Câu 10. Cho số gần đúng \(a = 23748023\) với độ chính xác \(d = 101\). Hãy viết số quy tròn của số a
A. \(23749000\). B. \(23748000\). C. \(23746000.\) D. \(23747000\).
Câu 11. Điểm trung bình thi học kỳ II môn Toán của một nhóm gồm \(N\) học sinh lớp 12A6 là \(8,1\). Biết rằng tổng điểm môn toán của nhóm này là \(72,9\). Tìm số học sinh của nhóm.
A. \(20\). B. \(9\). C. \(8\). D. \(15\).
Câu 12. Thống kê điểm kiểm tra \(15'\) môn Toán của lớp 10A1 trường THPT Chu Văn An được ghi lại như sau:

Số trung vị của mẫu số liệu trên là
A. \(8\). B. \(6\). C. \(7\). D. \(9\).
Câu 13. Theo kết quả thống kê điểm thi học kỳ 1 môn toán khối 10 của trường THPT Chu Văn An, người ta tính được phương sai của bảng thống kê đó là \(s_x^2 = 0,679\). Độ lệch chuẩn của bảng thống kê đó bằng:
A. \(0,812\). B. \(0,824\). C. \(0,936\). D. \(0,657\).
Câu 14. Tính phương sai của dãy số liệu: \(1,3,3,5,7,9,10,11,11,11.\)
A. \(\frac{{71}}{{10}}\).
B. \(\frac{{1329}}{{10}}\).
C. \(\frac{{710}}{{10}}\).
D. \(\frac{{1329}}{{100}}\).
Câu 15. Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:
163 159 172 167 165 168 170 161.
Khoảng biến thiên của mẫu số liệu trên là:
A. \(10\). B. \(13\). C. \(12\). D. \(14\).
Câu 16. Gieo một đồng xu cân đối và đồng chất liên tiếp \(3\) lần thì \(n(\Omega )\) là bao nhiêu?
A. \(6\). B. \(8\). C. \(32\). D. \(16\).
Câu 17. Gieo một con súc sắc. Xác suất để mặt lẻ chẵn xuất hiện là:
A.0,2 B. 0,3 C.0,4. D. 0,5
Câu 18. Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 5 là:
A. \(\frac{2}{9}\). B.\(\frac{1}{6}\). C. \(\frac{1}{9}\). D. \(\frac{5}{36}\).
Câu 19. Gieo hai con xúc xắc một cách vô tư. Tính xác suất của biến cố “Các mặt xuất hiện có số chấm bằng nhau”.
A. \(\frac{2}{9}\). B.\(\frac{1}{6}\). C. \(\frac{1}{9}\). D. \(\frac{5}{36}\).
Câu 20. Gieo một con súc xắc cân đối và đồng chất hai lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm là
A. \(\frac{{12}}{{36}}\). B. \(\frac{{11}}{{36}}\). C. \(\frac{6}{{36}}\). D. \(\frac{8}{{36}}\).
Câu 21. Cho tập hợp \(X = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\). Chọn ngẫu nhiên từ \(X\) ra ba số tự nhiên. Xác suất để chọn được ba số có tích là một số chẵn là:
A. \(P = 1 - \frac{{C_4^3}}{{C_{10}^3}}\).
B. \(P = 1 - \frac{{C_6^3}}{{C_{10}^3}}\).
C. \(P = 1 - \frac{{C_5^3}}{{C_9^3}}\).
D. \(P = \frac{{C_5^3}}{{C_9^3}}\).
Câu 22. Trường THPT Cao Bá Quát có 23 lớp, trong đó khối 10 có 8 lớp, khối 11 có 8 lớp, khối 12 có 7 lớp, mỗi lớp có một chi đoàn, mỗi chi đoàn có một em làm bí thư. Các em bí thư đều giỏi và rất năng động nên Ban chấp hành Đoàn trường chọn ngẫu nhiên 9 em bí thư đi thi cán bộ đoàn giỏi cấp thành phố. Tính xác suất để 9 em được chọn có đủ cả ba khối?
A. \(\frac{{7345}}{{7429}}\).
B. \(\frac{{7012}}{{7429}}\).
C. \(\frac{{7234}}{{7429}}\).
D. \(\frac{{7123}}{{7429}}\).
Câu 23. Trong mặt phẳng toạ độ \(Oxy\) cho hai điểm \(A\left( { - 1;3} \right),B\left( {2; - 5} \right)\).Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \(\left( {3;8} \right)\)
B. \(\left( {1; - 8} \right)\)
C. \(\left( {3; - 8} \right)\)
D. \(\left( {3;1} \right)\)
Câu 24. Trong mặt phẳng toạ độ \(Oxy\) cho \(\overrightarrow a = \left( {2;3} \right),\overrightarrow b = \left( {1; - 2} \right)\).Toạ độ của vectơ \(\overrightarrow u = 2\overrightarrow a + 3\overrightarrow b \) là:
A. \(\left( {7;0} \right)\)
B. \(\left( {7;12} \right)\)
C. \(\left( {1;0} \right)\)
D. \(\left( {3;1} \right)\)
Câu 25. Cho tam giác \(ABC\) với \(A\left( {2;3} \right),B\left( { - 4;5} \right),C\left( {4; - 3} \right)\). Tìm toạ độ điểm \(M\)thuộc trục \(Oy\)để \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất.
A. \(M\left( {0;\frac{1}{3}} \right)\)
B. \(M\left( {0; - \frac{5}{3}} \right)\)
C. \(M\left( {0;\frac{2}{3}} \right)\)
D. \(M\left( {0;\frac{5}{3}} \right)\)
Câu 26. Vectơ nào dưới đây là một vectơ pháp tuyến của \(d:x - 2y + 2023 = 0\)?
A.\(\overrightarrow {{n_1}} = \left( {0; - 2} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {1; - 2} \right)\).
C. \(\overrightarrow {{n_3}} = \left( { - 2;0} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {2;1} \right)\).
Câu 27. Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;3} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {3;5} \right)\) có phương trình tham số là:
A. \(d:\left\{ \begin{array}{l}x = 3 - 2t\\y = 5 + 3t\end{array} \right.\).
B. \(d:\left\{ \begin{array}{l}x = - 2 + 3t\\y = 3 + 5t\end{array} \right.\).
C. \(d:\left\{ \begin{array}{l}x = - 2 + 5t\\y = 3 - 3t\end{array} \right.\).
D. \(d:\left\{ \begin{array}{l}x = 3 + 2t\\y = 5 + 3t\end{array} \right.\).
Câu 28. Trong mặt phẳng với hệ tọa độ cho đường thẳng \({d_1}:3x + 4y - 5 = 0\)và đường thẳng \({d_2}:3x - 4y - 1 = 0\).Nêu vị trí tương đối của \({d_1}\) và \({d_2}\)
A. Cắt nhau và không vuông góc.
B. Vuông góc với nhau.
C. Song song với nhau.
D. Trùng nhau.
Câu 29. Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( {2; - 3} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(\sqrt 2 \).
A. \(m = 2.\) B. \(m = - 1\). C. \(m = - \frac{1}{2}\). D. \(m = 1\).
Câu 30. Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) có phương trình \({x^2} + {y^2} - 2x + 6y - 4 = 0\). Gọi \(I\left( {a;b} \right)\)là tâm của đường tròn \(\left( C \right)\). Tính tổng \(S = a + b\)
A. \(S = 4\). B. \(S = 1\). C. \(S = - 2\). D. \(S = 2\).
Câu 31. Trong mặt phẳng với hệ trục tọa độ \(Oxy\) cho điểm \(I\left( { - 1;2} \right)\). Viết phương trình đường tròn tâm \(I\), bán kính \(R = 3\).
A. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
B. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
C. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
Câu 32. Trong mặt phẳng với hệ tọa độ \(Oxy\) cho đường tròn \(\left( C \right)\) tâm \(I\left( {2;3} \right)\) tiếp xúc với đường thẳng \(\left( d \right):4x - 3y + 11 = 0\). Viết phương trình đường tròn \(\left( C \right)\).
A. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 9\).
B. \({\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} = 4\).
C. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 3\).
D. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\).
Câu 33. Trong mặt phẳng \(Oxy\) cho elip \(\left( E \right)\) có độ dài trục lớn bằng 10, độ dài tiêu cự bằng 8. Viết phương trình chính tắc của \(\left( E \right)\).
A. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
B. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
C. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
D. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{36}} = 1\)
Câu 34. Trong mặt phẳng \(Oxy\), Hyperbol \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) có một tiêu điểm là điểm nào dưới đây?
A. \(\left( { - 5;0} \right)\)
B. \(\left( {0;\sqrt 7 } \right)\)
C. \(\left( {\sqrt 7 ;0} \right)\)
D. \(\left( {0;5} \right)\)
Câu 35. Cho Parabol \(\left( P \right):\)\({y^2} = 64x\) và đường thẳng \(\left( \Delta \right):4x + 3y + 46 = 0\). Tìm điểm \(M \in (P)\) sao cho khoảng cách từ \(M\) đến \(\left( \Delta \right)\)là ngắn nhất.
A. \(M\left( {9; - 24} \right)\)
B. \(M\left( {9;24} \right)\)
C. \(M\left( {24;9} \right)\)
D. \(M\left( {9;2} \right)\)
II. PHẦN TỰ LUẬN (3 Điểm)
Câu 36. (1 điểm) Bạn An đo chiều dài của một sân bóng ghi được \(250 \pm 0,2m\). Bạn Bình đo chiều cao của một cột cờ được \(15 \pm 0,1m\). Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong phép đo của bạn đó là bao nhiêu?
Câu 37. (1 điểm) Tìm tất cả các giá trị của tham số \(m\) sao cho hai đường thẳng \({d_1}:x - y + 3 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = - 2 + \left( {m + 1} \right)t\\y = 1 - 2t\end{array} \right.\) hợp với nhau một góc \(45^\circ \).
Câu 38. (0,5 điểm) Cho đa giác đều \({A_1}{A_2}...{A_{2n}}\) nội tiếp trong đường tròn tâm \(O\). Biết rằng số tam giác có đỉnh là \(3\) trong \(2n\) điểm \({A_1};\,{A_2};\,...;\,{A_{2n}}\) gấp \(20\) lần so với số hình chữ nhật có đỉnh là \(4\) trong \(2n\) điểm \({A_1};\,{A_2};\,...;\,{A_{2n}}\). Tìm \(n\)?
Câu 39. (0,5 điểm) Trong mặt phẳng với hệ toạ độ \(Oxy\), cho điểm \(M\left( {3;1} \right)\). Viết phương trình đường thẳng \(d\) đi qua \(M\) cắt các tia \(Ox,Oy\) tại \(A\) và \(B\) sao cho \(\left( {OA + 3OB} \right)\) nhỏ nhất.
-----------------------------------------------------
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
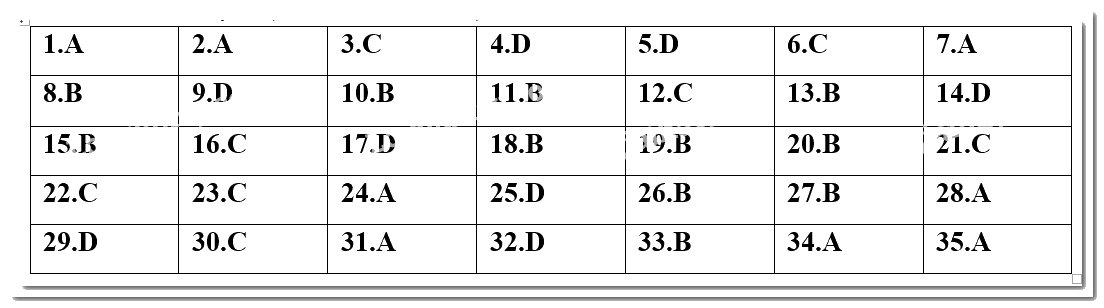
Câu 1. Lớp 10A có 20 bạn nữ và 18 bạn nam. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
A. \(38\) cách. B. \(20\)cách. C. \(18\) cách. D. \(360\).
Phương pháp
Áp dụng quy tắc cộng
Lời giải:
ChọnA
Chọn một học sinh trong số 20 hs nữ và 18 học sinh nam có: \(20 + 18 = 38\) cách.
Câu 2. Mã khoá số của chiếc Vali du lịch là một dãy số gồm ba chữ số. Mỗi chữ số có thể là một chữ số bất kì từ 0 đến 9. Hỏi có thể có bao nhiêu mã mở khoá khác nhau?
A. \({10^3}\). B. \(720.\) C. \(900.\) D. \(30.\)
Phương pháp
Áp dụng quy tắc nhân
Lời giải:
ChọnA
Chữ số thứ nhất có 10 cách chọn
Chữ số thứ hai có 10 cách chọn
Chữ số thứ ba có 10 cách chọn
Vậy có: \(10.10.10 = {10^3}\) (mã).
Câu 3. Trong kì thi THPT Quốc gia năm 2022 tại một điểm thi có \(5\) sinh viên tình nguyện được phân công trực hướng dẫn thi sinh ở \(5\)vị trí khác nhau. Yêu cầu mỗi vị trí có đúng \(1\) sinh viên. Hỏi có bao nhiêu cách phân công vị trí trực cho 5 sinh viên đó?
A.\(625\). B.\(3125\). C.\(120\). D.\(80\).
Phương pháp
Áp dụng công thức hoán vị
Lời giải:
Chọn C
Mỗi cách phân công \(5\) sinh viên trực ở \(5\)vị trí khác nhau là\(1\) hoán vị của\(5\)phần tử.
Vậy có tất cả là \(5! = 120\).
Câu 4. Có thể tạo thành bao nhiêu véc-tơ khác vectơ không từ hai mươi điểm phân biệt trên mặt phẳng?
A. \(20!\) B. \(C_{20}^2\) C. \(20\) D. \(A_{20}^2\)
Phương pháp
Áp dụng công thức chỉnh hợp
Lời giải:
Chọn D
Mỗi vectơ khác vectơ không được tạo thành bằng cách lấy hai điểm từ hai mươi điểm đã cho và phân biệt thứ tự điểm đầu và điểm cuối. Như vậy, mỗi vectơ là một chỉnh hợp chập 2 của 20. Vậy số các vectơ tạo thành là: \(A_{20}^2\).
Câu 5. Một hộp đựng \(8\) quả cầu trắng và \(5\) quả cầu đỏ. Lấy ngẫu nhiên \(5\) quả. Có bao nhiêu cách để lấy ra được \(3\) quả đỏ?
A. \(40\). B. \(13\). C. \(38\). D. \(280\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải:
Chọn D
Lấy \(5\) quả gồm \(3\) quả đỏ và \(2\) quả trắng,
Với \(5\) quả cầu đỏ lấy \(3\) quả, ta có \(C_5^3\) cách.
Với \(8\) quả cầu trắng lấy \(2\) quả, ta có \(C_8^2\) cách.
Vậy có \(C_5^3.C_8^2 = 280\) cách.
Câu 6. Một đề kiểm tra trắc nghiệm có 10 câu hỏi, mỗi câu hỏi chỉ có 1 đáp án đúng trong 4 đáp án. Giả sử các đáp án được chọn ngẫu nhiên. Số khả năng để bạn Uyên làm đúng 5 câu trong 10 câu hỏi của đề thi đó là:
A. \(C_{10}^5\). B. \(A_{10}^5\). C. \({3^5}.C_{10}^5\). D. \(5.C_{10}^5\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải:
Chọn C
Mỗi cách chọn 5 câu làm đúng trong 10 câu là một tổ hợp chập 5 của 10 phần tử nên có \(C_{10}^5\)
Vì 5 câu còn lại làm sai, mỗi câu có 3 đáp án sai nên có \(3.3.3.3.3 = {3^5}\)
Vậy có \({3^5}.C_{10}^5\)
Câu 7. Viết khai triển theo công thức nhị thức Niu-tơn của biểu thức \({\left( {x + 2} \right)^5}\).
A. \({x^5} + 10{x^4} + 40{x^3} + 80{x^2} + 80x + 32\).
B. \({x^5} - 10{x^4} + 40{x^3} - 80{x^2} + 80x - 32\).
C. \({x^5} - 10{x^4} - 40{x^3} - 80{x^2} - 80x + 32\).
D. \({x^5} + 10{x^4} - 40{x^3} + 80{x^2} - 80x + 32\).
Phương pháp
Áp dụng công thức nhị thức Newton
Lời giải:
Chọn A
\({\left( {x + 2} \right)^5} = {x^5} + 10{x^4} + 40{x^3} + 80{x^2} + 80x + 32\)
Câu 8. Hệ số của \({x^3}\) trong khai triển biểu thức \({\left( {1 - 3x} \right)^8}\) là:
A. \(1512\). B.\( - 1512\). C.\(56\). D. \(1215\).
Phương pháp
Áp dụng công thức nhị thức Newton
Lời giải:
Chọn B
Ta có \({\left( {1 - 3x} \right)^8} = \sum\limits_{k = 0}^8 {C_8^k} {\left( { - 3} \right)^k}{x^k}\).
\( \Rightarrow \) Hệ số của \({x^3}\) là \(C_8^3{\left( { - 3} \right)^3} = - 1512\).
Câu 9. Tìm tổng \(T = C_n^1 + 3C_n^2 + {3^2}C_n^3 + ... + {3^{n - 1}}C_n^n\)
A. \({4^n}\).
B. \({4^n} + 1\).
C. \({4^n} - 1\).
D. \(\frac{{{4^n} - 1}}{3}\).
Phương pháp
Áp dụng công thức nhị thức Newton
Lời giải:
Chọn D
Xét khai triển \({\left( {1 + x} \right)^n} = C_n^0 + xC_n^1 + {x^2}C_n^2 + {x^3}C_n^3 + ... + {x^n}C_n^n\)
Cho \(x = 3\) ta có: \({4^n} = C_n^0 + 3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^n\)
\( \Rightarrow {4^n} - C_n^0 = 3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^n\)
\( \Leftrightarrow {4^n} - 1 = 3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^n\)
\( \Leftrightarrow \frac{{{4^n} - 1}}{3} = C_n^1 + 3C_n^2 + {3^2}C_n^3 + ... + {3^{n - 1}}C_n^n\)
\( \Rightarrow T = \frac{{{4^n} - 1}}{3}\)
Câu 10. Cho số gần đúng \(a = 23748023\) với độ chính xác \(d = 101\). Hãy viết số quy tròn của số a
A. \(23749000\). B. \(23748000\). C. \(23746000.\) D. \(23747000\).
Phương pháp
Khi thay số đúng bởi số quy tròn đến một hàng nào đó thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng quy tròn. Như vậy, độ chính sác của số quy tròn bằng nửa đơn vị của hàng quy tròn.
Lời giải:
Chọn B
Số quy tròn của số \(a = 23748023\) là \(23748000\)
Câu 11. Điểm trung bình thi học kỳ II môn Toán của một nhóm gồm \(N\) học sinh lớp 12A6 là \(8,1\). Biết rằng tổng điểm môn toán của nhóm này là \(72,9\). Tìm số học sinh của nhóm.
A. \(20\). B. \(9\). C. \(8\). D. \(15\).
Phương pháp
Số trung bình cộng \(\overline x \) của mẫu số liệu \({x_1},{x_2},...,{x_n}\) là:
\(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}.\)
Lời giải:
Chọn B
Ta có giá giá trị \(N = \frac{{72,9}}{{8,1}} = 9\) (học sinh).
Câu 12. Thống kê điểm kiểm tra \(15'\) môn Toán của lớp 10A1 trường THPT Chu Văn An được ghi lại như sau:

Số trung vị của mẫu số liệu trên là
A. \(8\). B. \(6\). C. \(7\). D. \(9\).
Phương pháp
Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm ( hoặc không tăng).
- Nếu n là lẻ thì số liệu đứng ở vị trí thứ \(\frac{{n + 1}}{2}\) ( số đứng chính giữa) gọi là trung vị
- Nếu n là chẵn thì số trung bình cộng của hai số liệu đứng ở vị trí thứ \(\frac{n}{2}\) và \(\frac{n}{2} + 1\) gọi là trung vị
Lời giải
Chọn C
Các số liệu đã được xếp theo thức tự tăng dần.
Tổng số có 35 số liệu nên số trung vị là giá trị ở vị trí 18.
Vậy số trung vị là 7.
Câu 13. Theo kết quả thống kê điểm thi học kỳ 1 môn toán khối 10 của trường THPT Chu Văn An, người ta tính được phương sai của bảng thống kê đó là \(s_x^2 = 0,679\). Độ lệch chuẩn của bảng thống kê đó bằng:
A. \(0,812\). B. \(0,824\). C. \(0,936\). D. \(0,657\).
Phương pháp
Căn bậc hai của phương sai gọi là Độ lệch chuẩn của mẫu số liệu thống kê
Lời giải
Chọn B
Ta có công thức tính độ lệch chuẩn là \({s_x} = \sqrt {s_x^2} = \sqrt {0,679} \approx 0,824\).
Câu 14. Tính phương sai của dãy số liệu: \(1,3,3,5,7,9,10,11,11,11.\)
A. \(\frac{{71}}{{10}}\).
B. \(\frac{{1329}}{{10}}\).
C. \(\frac{{710}}{{10}}\).
D. \(\frac{{1329}}{{100}}\).
Phương sai
Cho mẫu số liêu thống kê có n giá trị \({x_1},{x_2},...,{x_n}\) và số trung bình cộng \(\overline x \).
Ta gọi số \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n}\) là phương sai của mẫu số liệu
Lời giải
Chọn D
Bảng phân bố tần số của dãy số liệu:

Ta có \(\overline x = \frac{1}{{10}}\left( {1.1 + 3.2 + 5.1 + 7.1 + 9.1 + 10.1 + 11.3} \right) = \frac{{71}}{{10}}\).
Phương sai là:
\({S^2} = \frac{1}{{10}}\left[ {1.{{\left( {1 - \frac{{71}}{{10}}} \right)}^2} + 2.{{\left( {3 - \frac{{71}}{{10}}} \right)}^2} + 1.{{\left( {5 - \frac{{71}}{{10}}} \right)}^2} + 1.{{\left( {7 - \frac{{71}}{{10}}} \right)}^2} + 1.{{\left( {9 - \frac{{71}}{{10}}} \right)}^2} + 1.{{\left( {10 - \frac{{71}}{{10}}} \right)}^2}} \right.\)
\(\left. { + 3.{{\left( {11 - \frac{{71}}{{10}}} \right)}^2}} \right] = 13,29\)
Câu 15. Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:
163 159 172 167 165 168 170 161.
Khoảng biến thiên của mẫu số liệu trên là:
A. \(10\). B. \(13\). C. \(12\). D. \(14\).
Phương pháp
Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.
Ta có thể tính khoảng bến thiên R của mẫu số liệu theo công thức \(R = {x_{\max }} - {x_{\min }}\), trong đó \({x_{\max }}\) là giá trị lớn nhất, \({x_{\min }}\)là giá trị nhỏ nhất của mẫu số liệu đó.
Lời giải
Chọn B
Chiều cao thấp nhất, cao nhất tương ứng là 159; 172.
Do đó, khoảng biến thiên là: \(R = 172 - 159 = 13\).
Câu 16. Gieo một đồng xu cân đối và đồng chất liên tiếp \(3\) lần thì \(n(\Omega )\) là bao nhiêu?
A. \(6\). B. \(8\). C. \(32\). D. \(16\).
Phương pháp
Sử dụng các quy tắc đếm
Lời giải
Chọn C
\(n(\Omega ) = {2^3} = 8\).
Câu 17. Gieo một con súc sắc. Xác suất để mặt lẻ chẵn xuất hiện là:
A.0,2. B. 0,3. C.0,4. D.0,5.
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn D
Không gian mẫu: \(\Omega = \left\{ {1;2;3;4;5;6} \right\} \Rightarrow n\left( \Omega \right) = 6\)
Biến cố xuất hiện mặt chẵn: \(A = \left\{ {1;3;5} \right\} \Rightarrow n\left( A \right) = 3\)
Suy ra \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{1}{2}\)
Câu 18. Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 5 là:
A. \(\frac{2}{9}\). B.\(\frac{1}{6}\). C. \(\frac{1}{9}\). D. \(\frac{5}{36}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn C
Gọi A:”tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 5”.
\(A = \left\{ {\left( {1;4} \right),\left( {4;1} \right),\left( {2;3} \right),\left( {3;2} \right)} \right\} \Rightarrow n\left( A \right) = 4\)
Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{{36}} = \frac{1}{9}\)
Câu 19. Gieo hai con xúc xắc một cách vô tư. Tính xác suất của biến cố “Các mặt xuất hiện có số chấm bằng nhau”.
A. \(\frac{2}{9}\). B.\(\frac{1}{6}\). C. \(\frac{7}{36}\). D. \(\frac{5}{36}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn B
Ta có: \(n(\Omega ) = 6.6 = 36\).
Số cách xuất hiện các mặt có số chấm bằng nhau là: \(\left( {1,1} \right)\left( {2,2} \right)\left( {3,3} \right)\left( {4,4} \right)\left( {5,5} \right)\left( {6,6} \right)\)
Vậy \(n(A) = 6 \Rightarrow P\left( A \right) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}\)
Câu 20. Gieo một con súc xắc cân đối và đồng chất hai lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm là
A. \(\frac{{12}}{{36}}\).
B. \(\frac{{11}}{{36}}\).
C. \(\frac{6}{{36}}\).
D. \(\frac{8}{{36}}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn B
\(n(\Omega ) = 6.6 = 36\). Gọi \(A\):”ít nhất một lần xuất hiện mặt sáu chấm”.
Khi đó \(\overline A \):”không có lần nào xuất hiện mặt sáu chấm”.
Ta có\(n(\overline A ) = 5.5 = 25\). Vậy \(P(A) = 1 - P(\overline A ) = 1 - \frac{{25}}{{36}} = \frac{{11}}{{36}}\).
Câu 21. Cho tập hợp \(X = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\). Chọn ngẫu nhiên từ \(X\) ra ba số tự nhiên. Xác suất để chọn được ba số có tích là một số chẵn là:
A. \(P = 1 - \frac{{C_4^3}}{{C_{10}^3}}\).
B. \(P = 1 - \frac{{C_6^3}}{{C_{10}^3}}\).
C. \(P = 1 - \frac{{C_5^3}}{{C_9^3}}\).
D. \(P = \frac{{C_5^3}}{{C_9^3}}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn C
Mỗi phần tử của không gian mẫu ứng với một tổ hợp chập 3 của 9 phần tử
Ta có: \(n\left( \Omega \right) = C_9^3\) cách chọn.
Tích ba số là một số chẵn thì ít nhất 1 trong 3 số phải là số chẵn.
Gọi \(A\) là biến cố: 3 số được chọn có ít nhất một số chẵn;
\(\overline A \) là biến cố: 3 số được chọn là 3 số lẻ. Suy ra \(n\left( {\overline A } \right) = C_5^3\) cách chọn.
Vậy xác suất để chọn được ba số có tích là một số chẵn là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{C_5^3}}{{C_9^3}}\).
Câu 22. Trường THPT Cao Bá Quát có 23 lớp, trong đó khối 10 có 8 lớp, khối 11 có 8 lớp, khối 12 có 7 lớp, mỗi lớp có một chi đoàn, mỗi chi đoàn có một em làm bí thư. Các em bí thư đều giỏi và rất năng động nên Ban chấp hành Đoàn trường chọn ngẫu nhiên 9 em bí thư đi thi cán bộ đoàn giỏi cấp thành phố. Tính xác suất để 9 em được chọn có đủ cả ba khối?
A. \(\frac{{7345}}{{7429}}\).
B. \(\frac{{7012}}{{7429}}\).
C. \(\frac{{7234}}{{7429}}\).
D. \(\frac{{7123}}{{7429}}\).
Phương pháp
Áp dụng công thức tính xác suất
Lời giải
Chọn C
Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{23}^9 = 817190\)
Gọi A là biến cố “9 em được chọn có đủ cả ba khối”
\( \Rightarrow \overline A \) “9 em được chọn không có đủ ba khối”
Vì mỗi khối số bí thư đều nhỏ hơn 9 nên có các khả năng sau:
TH1: Chỉ có học sinh ở khối 10 và 11. Có \(C_{16}^9\) cách.
TH2: Chỉ có học sinh ở khối 11 và 12. Có \(C_{15}^9\) cách.
TH3: Chỉ có học sinh ở khối 10 và 12. Có \(C_{15}^9\) cách.
Số phần tử của biến cố \(\overline A \) là: \(n\left( {\overline A } \right) = C_{16}^9 + C_{15}^9 + C_{15}^9 = 21450\)
Xác suất của biến cố \(\overline A \) là: \(P\left( {\overline A } \right) = \frac{{21450}}{{817190}} = \frac{{195}}{{7429}}\).
Xác suất của biến cố A là: \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{195}}{{7429}} = \frac{{7234}}{{7429}}\).
Câu 23. Trong mặt phẳng toạ độ \(Oxy\) cho hai điểm \(A\left( { - 1;3} \right),B\left( {2; - 5} \right)\).Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \(\left( {3;8} \right)\)
B. \(\left( {1; - 8} \right)\)
C. \(\left( {3; - 8} \right)\)
D. \(\left( {3;1} \right)\)
Phương pháp
Với \(A({x_A};{y_A});B({x_B};{y_B})\) thì \(\overrightarrow {AB} = \left( {({x_B} - {x_A});({y_B} - {y_A})} \right)\)
Lời giải
Chọn C
\(\overrightarrow {AB} = \left( {3; - 8} \right)\)
Câu 24. Trong mặt phẳng toạ độ \(Oxy\) cho \(\overrightarrow a = \left( {2;3} \right),\overrightarrow b = \left( {1; - 2} \right)\).Toạ độ của vectơ \(\overrightarrow u = 2\overrightarrow a + 3\overrightarrow b \) là:
A. \(\left( {7;0} \right)\)
B. \(\left( {7;12} \right)\)
C. \(\left( {1;0} \right)\)
D. \(\left( {3;1} \right)\)
Phương pháp
Trong mặt phẳng \(Oxy\), cho \(\vec a = \left( {{a_1}\,;\,{a_2}} \right)\); \(\vec b = \left( {{b_1}\,;\,{b_2}} \right)\). Tọa độ vectơ \(k\overrightarrow a + t\overrightarrow b = (k{a_1} + t{b_1};k{a_2} + t{b_2})\)
Lời giải
Chọn A
Ta có \(\overrightarrow a = \left( {2;3} \right) \Rightarrow 2\overrightarrow a = \left( {4;6} \right)\)
\(\overrightarrow b = \left( {1; - 2} \right) \Rightarrow 3\overrightarrow b = \left( {3; - 6} \right)\)
Vậy \(\overrightarrow u = 2\overrightarrow a + 3\overrightarrow b = \left( {7;0} \right)\)
Câu 25. Cho tam giác \(ABC\) với \(A\left( {2;3} \right),B\left( { - 4;5} \right),C\left( {4; - 3} \right)\). Tìm toạ độ điểm \(M\)thuộc trục \(Oy\)để \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất.
A. \(M\left( {0;\frac{1}{3}} \right)\)
B. \(M\left( {0; - \frac{5}{3}} \right)\)
C. \(M\left( {0;\frac{2}{3}} \right)\)
D. \(M\left( {0;\frac{5}{3}} \right)\)
Phương pháp
M là hình chiếu vuông góc của \(G\) lên \(Oy\) với \(G\) là trọng tâm tam giác \(ABC\)
Lời giải
Chọn D
Gọi \(G\) là trọng tâm tam giác \(ABC \Rightarrow G\left( {\frac{2}{3};\frac{5}{3}} \right)\)
Ta có \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
\( \Rightarrow \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {3\overrightarrow {MG} } \right| = 3MG\)
\( \Rightarrow \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất khi \(MG\) nhỏ nhất
mà \(M \in Oy \Rightarrow M\) là hình chiếu vuông góc của \(G\) lên \(Oy \Rightarrow M\left( {0;\frac{5}{3}} \right)\)
Câu 26. Vectơ nào dưới đây là một vectơ pháp tuyến của \(d:x - 2y + 2023 = 0\)?
A.\(\overrightarrow {{n_1}} = \left( {0; - 2} \right)\).
B. \(\overrightarrow {{n_2}} = \left( {1; - 2} \right)\).
C. \(\overrightarrow {{n_3}} = \left( { - 2;0} \right)\).
D. \(\overrightarrow {{n_4}} = \left( {2;1} \right)\).
Phương pháp
Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)
Lời giải
Chọn B
(d:x - 2y + 2023 = 0 \Rightarrow VTPT\overrightarrow {{n_d}} = \left( {1; - 2} \right)\)
Câu 27. Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;3} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {3;5} \right)\) có phương trình tham số là:
A. \(d:\left\{ \begin{array}{l}x = 3 - 2t\\y = 5 + 3t\end{array} \right.\).
B. \(d:\left\{ \begin{array}{l}x = - 2 + 3t\\y = 3 + 5t\end{array} \right.\).
C. \(d:\left\{ \begin{array}{l}x = - 2 + 5t\\y = 3 - 3t\end{array} \right.\).
D. \(d:\left\{ \begin{array}{l}x = 3 + 2t\\y = 5 + 3t\end{array} \right.\).
Phương pháp
Phương trình tham số đường thẳng \(d\) đi qua điểm \(A({x_0},{y_0})\) và có VTCP \(\overrightarrow u = \left( {a;b} \right)\)là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)
Lời giải
Chọn B
PTTS đường thẳng \(d\) đi qua điểm \(M\left( { - 2;3} \right)\) và có VTCP \(\overrightarrow u = \left( {3;5} \right)\)là \(\left\{ \begin{array}{l}x = - 2 + 3t\\y = 3 + 5t\end{array} \right.\)
Câu 28. Trong mặt phẳng với hệ tọa độ cho đường thẳng \({d_1}:3x + 4y - 5 = 0\)và đường thẳng \({d_2}:3x - 4y - 1 = 0\).Nêu vị trí tương đối của \({d_1}\) và \({d_2}\)
A. Cắt nhau và không vuông góc.
B. Vuông góc với nhau.
C. Song song với nhau.
D. Trùng nhau.
Phương pháp
Vị trí tương đối giữa hai đường thẳng
Lời giải
Chọn A
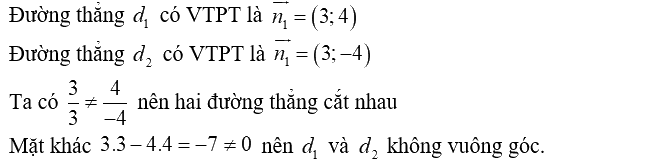
Câu 29. Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( {2; - 3} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(\sqrt 2 \).
A. \(m = 2.\)
B. \(m = - 1\).
C. \(m = - \frac{1}{2}\).
D. \(m = 1\).
Phương pháp
Khoảng cách từ điểm \(A({x_0},{y_0})\) đến đường thẳng \(d:ax + by + c = 0\) là \(d\left( {A,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn D
\(d\left( {A,\Delta } \right) = \frac{{\left| {2m - 3 - m + 4} \right|}}{{\sqrt {{m^2} + 1} }} \Leftrightarrow \frac{{\left| {m + 1} \right|}}{{\sqrt {{m^2} + 1} }} = \sqrt 2 \Leftrightarrow \left| {m + 1} \right| = \sqrt 2 .\sqrt {{m^2} + 1} \)
\( \Leftrightarrow {m^2} + 2m + 1 = 2\left( {{m^2} + 1} \right) \Leftrightarrow {m^2} - 2m + 1 = 0 \Leftrightarrow m = 1\)
Câu 30. Trong mặt phẳng với hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) có phương trình \({x^2} + {y^2} - 2x + 6y - 4 = 0\). Gọi \(I\left( {a;b} \right)\)là tâm của đường tròn \(\left( C \right)\). Tính tổng \(S = a + b\)
A. \(S = 4\). B. \(S = 1\). C. \(S = - 2\). D. \(S = 2\).
Phương pháp
Phương trình đường tròn có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\,\,\left( {{a^2} + {b^2} - c > 0} \right)\). và tọa độ tâm \(I(a,b)\), bán kính \(\,R = \sqrt {{a^2} + {b^2} - c} \)
Lời giải
Chọn C
Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 3} \right)\) và bán kính \(R = \sqrt {1 + 9 + 4} = \sqrt {14} \)
\(a = 1,b = - 3 \Rightarrow S = a + b = - 2\)
Câu 31. Trong mặt phẳng với hệ trục tọa độ \(Oxy\) cho điểm \(I\left( { - 1;2} \right)\). Viết phương trình đường tròn tâm \(I\), bán kính \(R = 3\).
A. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
B. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
C. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn A
Đường tròn có tâm \(I\left( { - 1;2} \right)\) và bán kính \(R = 3\) có phương trình là: \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
Câu 32. Trong mặt phẳng với hệ tọa độ \(Oxy\) cho đường tròn \(\left( C \right)\) tâm \(I\left( {2;3} \right)\) tiếp xúc với đường thẳng \(\left( d \right):4x - 3y + 11 = 0\). Viết phương trình đường tròn \(\left( C \right)\).
A. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 9\).
B. \({\left( {x + 2} \right)^2} + {\left( {y + 3} \right)^2} = 4\).
C. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 3\).
D. \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn D
Do \(\left( C \right)\) tiếp xúc với \(\left( d \right)\) nên \(\left( C \right)\) có bán kính \(R = d\left( {I,d} \right) = \frac{{\left| {4.2 - 3.3 + 11} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 2\) .
\( \Rightarrow \left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 4\).
Câu 33. Trong mặt phẳng \(Oxy\) cho elip \(\left( E \right)\) có độ dài trục lớn bằng 10, độ dài tiêu cự bằng 8. Viết phương trình chính tắc của \(\left( E \right)\).
A. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
B. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
C. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
D. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{36}} = 1\)
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có hai tiêu điểm \({F_1} = \left( {c\,;\,0} \right)\); \({F_2} = \left( { - c\,;\,0} \right)\) với \(c = \sqrt {{a^2} - {b^2}} \)
Lời giải
Chọn D
Ta có: \(2a = 10 \Rightarrow a = 5;2c = 8 \Rightarrow c = 4\). Độ dài trục bé: \(b = \sqrt {{a^2} - {c^2}} = 3\).
Phương trình chính tắc của Elíp là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
Câu 34. Trong mặt phẳng \(Oxy\), Hyperbol \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) có một tiêu điểm là điểm nào dưới đây?
A. \(\left( { - 5;0} \right)\)
B. \(\left( {0;\sqrt 7 } \right)\)
C. \(\left( {\sqrt 7 ;0} \right)\)
D. \(\left( {0;5} \right)\)
Phương pháp
Phương trình Hypebol \(\left( H \right):\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) có hai tiêu điểm \({F_1} = \left( {c\,;\,0} \right)\); \({F_2} = \left( { - c\,;\,0} \right)\) với \(c = \sqrt {{a^2} + {b^2}} \)
Lời giải
Chọn A
Ta có: \({a^2} = 16;{b^2} = 9 \Rightarrow {c^2} = {a^2} + {b^2} = 16 + 9 = 25\)
Vậy hai tiêu điểm của hyperbol là \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\).
Câu 35. Cho Parabol \(\left( P \right):\)\({y^2} = 64x\) và đường thẳng \(\left( \Delta \right):4x + 3y + 46 = 0\). Tìm điểm \(M \in (P)\) sao cho khoảng cách từ \(M\) đến \(\left( \Delta \right)\)là ngắn nhất.
A. \(M\left( {9; - 24} \right)\)
B. \(M\left( {9;24} \right)\)
C. \(M\left( {24;9} \right)\)
D. \(M\left( {9;2} \right)\)
Phương pháp
Khoảng cách từ điểm \(A({x_0},{y_0})\) đến đường thẳng \(d:ax + by + c = 0\) là \(d\left( {A,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn A
Gọi \(M\left( {\frac{{{m^2}}}{{64}};m} \right) \in (P)\)
Ta có \(d\left( {M,d} \right) = \frac{{\left| {4.\frac{{{m^2}}}{{64}} + 3m + 46} \right|}}{{\sqrt {{4^2} + {3^3}} }} = \frac{{\left| {{m^2} + 48m + 736} \right|}}{{80}} = \frac{1}{{80}}\left| {{{\left( {m + 24} \right)}^2} + 160} \right| \ge 2\)
\( \Rightarrow Min\,\,d(M,d) = 2 \Leftrightarrow m = - 24 \Rightarrow M\left( {9; - 24} \right)\)
II. PHẦN TỰ LUẬN (3 Điểm)
Câu 36. (1 điểm) Bạn An đo chiều dài của một sân bóng ghi được \(250 \pm 0,2m\). Bạn Bình đo chiều cao của một cột cờ được \(15 \pm 0,1m\). Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong phép đo của bạn đó là bao nhiêu?
Phương pháp
Ta nói a là số gần đúng của số đúng \(\overline a \) với độ chính xác d nếu \({\Delta _a} = \left| {\overline a - a} \right| \le d\) và quy ước viết gọn là \(\overline a = a \pm d\)
Tỉ số \({\delta _a} = \frac{{{\Delta _a}}}{{\left| a \right|}}\) được gọi là sai số tương đối của số gần đúng a.
Lời giải:
Phép đo của bạn An có sai số tương đối \({\delta _1} \le \frac{{0,2}}{{250}} = 0,0008 = 0,08\% \)
Phép đo của bạn Bình có sai số tương đối \({\delta _2} \le \frac{{0,1}}{{15}} = 0,0066 = 0,66\% \)
Như vậy phép đo của bạn An có độ chính xác cao hơn.
Câu 37. (1 điểm) Tìm tất cả các giá trị của tham số \(m\) sao cho hai đường thẳng \({d_1}:x - y + 3 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = - 2 + \left( {m + 1} \right)t\\y = 1 - 2t\end{array} \right.\) hợp với nhau một góc \(45^\circ \).
Phương pháp
Sử dụng công thức tính góc giữa hai đường thẳng
Lời giải:
\(\left( {{d_1}} \right)\) có VTPT \(\overrightarrow {{n_1}} = \left( {1; - 1} \right)\)
\(\left( {{d_1}} \right)\) có VTCP \(\overrightarrow {{u_2}} = \left( {m + 1; - 2} \right)\)\( \Rightarrow \)VTPT \(\overrightarrow {{n_2}} = \left( {2;m + 1} \right)\)
\(\cos \left( {{d_1},{d_2}} \right) = \cos {45^ \circ } \Leftrightarrow \frac{{\left| {2 - m - 1} \right|}}{{\sqrt 2 .\sqrt {{{\left( {m + 1} \right)}^2} + 4} }} = \frac{1}{{\sqrt 2 }} \Leftrightarrow \frac{1}{{\sqrt 2 }} = \frac{{\left| {1 - m} \right|}}{{\sqrt 2 .\sqrt {{m^2} + 2m + 5} }}\)
\( \Leftrightarrow {m^2} + 2m + 5 = 1 - 2m + {m^2} \Leftrightarrow m = - 1\)
Câu 38. (0,5 điểm) Cho đa giác đều \({A_1}{A_2}...{A_{2n}}\) nội tiếp trong đường tròn tâm \(O\). Biết rằng số tam giác có đỉnh là \(3\) trong \(2n\) điểm \({A_1};\,{A_2};\,...;\,{A_{2n}}\) gấp \(20\) lần so với số hình chữ nhật có đỉnh là \(4\) trong \(2n\) điểm \({A_1};\,{A_2};\,...;\,{A_{2n}}\). Tìm \(n\)?
Phương pháp
Sử dụng các quy tắc đếm
Lời giải:
Số tam giác có 3 đỉnh là \(3\) trong \(2n\) điểm \({A_1};{A_2};...;{A_{2n}}\) là \(C_{2n}^3\).
Ứng với hai đường chéo đi qua tâm của đa giác \({A_1}{A_2}...{A_{2n}}\)cho tương ứng một hình chữ nhật có 4 đỉnh
là \(4\) điểm trong \(2n\) điểm \({A_1};{A_2};...;{A_{2n}}\)và ngược lại mỗi hình chữ nhật như vậy sẽ cho ra \(2\) đường chéo đi qua tâm\(O\) của đa giác.
Mà số đường chéo đi qua tâm của đa giác đều \(2n\) đỉnh là \(n\) nên số hình chữ nhật có đỉnh là \(4\) trong \(2n\) điểm là \(C_n^2\)
Theo đề bài ta có: \(C_{2n}^3 = 20C_n^2 \Leftrightarrow \frac{{2n\left( {2n - 1} \right)\left( {2n - 2} \right)}}{{3!}} = \frac{{20n\left( {n - 1} \right)}}{2} \Leftrightarrow n = 8\).
Câu 39. (0,5 điểm) Trong mặt phẳng với hệ toạ độ \(Oxy\), cho điểm \(M\left( {3;1} \right)\). Viết phương trình đường thẳng \(d\) đi qua \(M\) cắt các tia \(Ox,Oy\) tại \(A\) và \(B\) sao cho \(\left( {OA + 3OB} \right)\) nhỏ nhất.
Phương pháp
PT đường thẳng \(d\) cắt tia \(Ox\) tại \(A\left( {a;0} \right)\), tia \(Oy\) tại \(B\left( {0;b} \right)\) có dạng: \(\frac{x}{a} + \frac{y}{b} = 1\)\(\left( {a,b > 0} \right)\)
Lời giải:
PT đường thẳng \(d\) cắt tia \(Ox\) tại \(A\left( {a;0} \right)\), tia \(Oy\) tại \(B\left( {0;b} \right)\) có dạng: \(\frac{x}{a} + \frac{y}{b} = 1\)\(\left( {a,b > 0} \right)\)
\(M\left( {3;1} \right) \in d\) nên \(\frac{3}{a} + \frac{1}{b} = 1\).
Mà \(1 = \frac{3}{a} + \frac{1}{b}\mathop \ge \limits^{Cô-si} 2\sqrt {\frac{3}{a}.\frac{1}{b}} \Rightarrow ab \ge 12\)
Mà \(OA + 3OB = a + 3b \ge 2\sqrt {3ab} = 12\) \( \Rightarrow Min\left( {OA + 3OB} \right) = 12 \Leftrightarrow \left\{ \begin{array}{l}a = 3b\\\frac{3}{a} = \frac{1}{b} = \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 2\end{array} \right.\)
Vậy phương trình đường thẳng \(d\) là: \(\frac{x}{6} + \frac{y}{2} = 1 \Leftrightarrow x + 3y - 6 = 0\)
------------------------------------------------
Đề kiểm tra học kì 2 Toán 10 - Đề số 3 - Cánh diều là một công cụ quan trọng giúp học sinh lớp 10 ôn tập và củng cố kiến thức đã học trong suốt học kì. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ các chủ đề chính trong chương trình Toán 10 như hàm số, phương trình, bất phương trình, hình học phẳng và không gian.
Đề thi thường được chia thành các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để giải đề thi hiệu quả, học sinh cần:
Bài toán: Giải phương trình 2x2 - 5x + 2 = 0
Giải:
Phương trình 2x2 - 5x + 2 = 0 có dạng ax2 + bx + c = 0 với a = 2, b = -5, c = 2.
Tính delta (Δ) = b2 - 4ac = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
x2 = (-b - √Δ) / 2a = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 0.5
Vậy, phương trình có hai nghiệm là x1 = 2 và x2 = 0.5
Việc luyện tập với đề kiểm tra học kì 2 Toán 10 - Đề số 3 - Cánh diều không chỉ giúp học sinh làm quen với cấu trúc đề thi mà còn giúp các em:
Giaitoan.edu.vn là một website cung cấp các tài liệu học tập Toán 10 chất lượng, bao gồm:
Hãy truy cập giaitoan.edu.vn để có thêm nhiều tài liệu học tập Toán 10 hữu ích và đạt kết quả tốt nhất trong kỳ thi sắp tới!