Chào mừng các em học sinh đến với đề thi học kì 2 môn Toán lớp 4 chương trình Cánh diều - Đề số 3. Đề thi này được thiết kế để giúp các em ôn luyện và củng cố kiến thức đã học trong học kì, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Giaitoan.edu.vn cung cấp đề thi với cấu trúc tương tự đề thi chính thức, bao gồm nhiều dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, giúp các em làm quen với các dạng câu hỏi thường gặp.
Số thích hợp điền vào chỗ chấm 3 m2 7 dm2 = ……. cm2 là:
Phân số thích hợp điền vào chỗ trống \(\frac{{7 \times 5 \times 11 \times 3}}{{11 \times 5 \times 9 \times 7}} = \frac{{......}}{{......}}\) là:
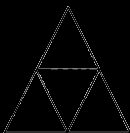
Có bao nhiêu hình thoi trong hình dưới đây:
Một hình chữ nhật có chu vi là $\frac{{35}}{4}$m, chiều dài là $\frac{{11}}{3}$m. Hỏi chiều rộng kém chiều dài bao nhiêu mét?
Một người bán được $\frac{5}{6}$tạ gạo, trong đó số gạo nếp ít hơn số gạo tẻ là $\frac{1}{3}$ tạ. Hỏi người đó bán được bao nhiêu tạ gạo nếp ?
Phân số nào không bằng phân số \(\frac{9}{{15}}\)?
Tính
a) \(\frac{5}{{24}} + \frac{3}{4}\)
b) \(4 - \frac{5}{8}\)
c) \(\frac{7}{{12}} \times \frac{9}{{14}}\)
d) \(\frac{4}{{13}}:\frac{5}{6}\)
a) Em hãy sắp xếp các phân số \(\frac{5}{2};\frac{{21}}{{18}};\frac{7}{7};\frac{{12}}{{17}};\frac{{132}}{{143}}\) theo thứ tự từ bé đến lớn.
b) Em hãy sắp xếp các phân số sau theo thứ tự từ lớn đến bé: \(\frac{1}{2};\frac{9}{{14}};\frac{1}{7};\frac{5}{{14}}\)
Hồng có 32 bông hoa, Bình có số hoa bằng $\frac{3}{4}$ của Hồng, Huệ có số hoa bằng $\frac{3}{4}$ tổng số hoa của cả Hồng và Bình. Hỏi Huệ có bao nhiêu bông hoa?
Một mảnh đất hình chữ nhật có chiều dài 96 m, chiều rộng bằng $\frac{3}{4}$chiều dài. Người ta trồng rau trên mảnh đất đó. Biết rằng cứ 1 m2, người ta thu hoạch được $\frac{2}{3}$ kg rau. Hỏi người ta thu hoạch được tất cả bao nhiêu ki-lô-gam rau trên mảnh đất đó?
Tính bằng cách thuận tiện.
a) $\frac{8}{5} + \frac{3}{6} + 2 + \frac{4}{5} + \frac{3}{2} + \frac{3}{5}$
b) $\frac{{1717}}{{3636}} \times \frac{{181818}}{{343434}}$
Số thích hợp điền vào chỗ chấm 3 m2 7 dm2 = ……. cm2 là:
Đáp án : C
1 m2 = 10 000 cm2
1 dm2 = 100 cm2
3 m2 7 dm2 = 30 700 cm2
Đáp án: C
Phân số thích hợp điền vào chỗ trống \(\frac{{7 \times 5 \times 11 \times 3}}{{11 \times 5 \times 9 \times 7}} = \frac{{......}}{{......}}\) là:
Đáp án : D
Chia nhẩm tích ở tử số và mẫu số cho các thừa số chung.
\(\frac{{7 \times 5 \times 11 \times 3}}{{11 \times 5 \times 9 \times 7}} = \frac{3}{9} = \frac{1}{3}\)
Đáp án D.
Có bao nhiêu hình thoi trong hình dưới đây:
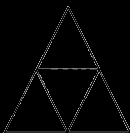
Đáp án : D
Hình thoi có hai cặp cạnh đối diện song song và độ dài bốn cạnh bằng nhau.
Vậy hình bên có 3 hình thoi.
Đáp án D.
Một hình chữ nhật có chu vi là $\frac{{35}}{4}$m, chiều dài là $\frac{{11}}{3}$m. Hỏi chiều rộng kém chiều dài bao nhiêu mét?
Đáp án : D
Nửa chu vi của hình chữ nhật = Chu vi của hình chữ nhật : 2
Chiều rộng là: Nửa chu vi - Chiều dài
Chiều rộng kém chiều dài số mét = Chiều dài - Chiều rộng
Nửa chu vi của hình chữ nhật là: $\frac{{35}}{4}$: 2 = $\frac{{35}}{8}$m
Chiều rộng là: $\frac{{35}}{8}$ - $\frac{{11}}{3}$= $\frac{{17}}{{24}}$ m
Chiều rộng kém chiều dài số mét là: $\frac{{35}}{{12}}$-$\frac{{11}}{3}$= $\frac{{17}}{{24}}$ m
Đáp án D.
Một người bán được $\frac{5}{6}$tạ gạo, trong đó số gạo nếp ít hơn số gạo tẻ là $\frac{1}{3}$ tạ. Hỏi người đó bán được bao nhiêu tạ gạo nếp ?
Đáp án : C
Số tạ gạo nếp người đó bán được = (Tổng - Hiệu) : 2
Số tạ gạo nếp người đó bán được là:
($\frac{5}{6}$- $\frac{1}{3}$) : 2 = $\frac{1}{4}$ tạ
Đáp án C.
Phân số nào không bằng phân số \(\frac{9}{{15}}\)?
Đáp án : C
Dựa vào tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
\(\frac{{21}}{{35}} = \frac{{21:7}}{{35:7}} = \frac{3}{5} = \frac{{3 \times 3}}{{5 \times 3}} = \frac{9}{{15}}\)
\(\frac{{18}}{{30}} = \frac{{18:2}}{{30:2}} = \frac{9}{{15}}\)
\(\frac{3}{5} = \frac{{3 \times 3}}{{5 \times 3}} = \frac{9}{{15}}\)
Đáp án C.
Tính
a) \(\frac{5}{{24}} + \frac{3}{4}\)
b) \(4 - \frac{5}{8}\)
c) \(\frac{7}{{12}} \times \frac{9}{{14}}\)
d) \(\frac{4}{{13}}:\frac{5}{6}\)
- Muốn cộng hoặc trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số đó, rồi cộng hoặc trừ hai phân số sau khi quy đồng.
- Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai.
a) \(\frac{5}{{24}} + \frac{3}{4} = \frac{5}{{24}} + \frac{{18}}{{24}} = \frac{{23}}{{24}}\)
b) \(4 - \frac{5}{8} = \frac{{32}}{8} - \frac{5}{8} = \frac{{27}}{8}\)
c) \(\frac{7}{{12}} \times \frac{9}{{14}} = \frac{{7 \times 9}}{{12 \times 14}} = \frac{{7 \times 3 \times 3}}{{4 \times 3 \times 7 \times 2}} = \frac{3}{8}\)
d) \(\frac{4}{{13}}:\frac{5}{6} = \frac{4}{{13}} \times \frac{6}{5} = \frac{{4 \times 6}}{{13 \times 5}} = \frac{{24}}{{65}}\)
a) Em hãy sắp xếp các phân số \(\frac{5}{2};\frac{{21}}{{18}};\frac{7}{7};\frac{{12}}{{17}};\frac{{132}}{{143}}\) theo thứ tự từ bé đến lớn.
b) Em hãy sắp xếp các phân số sau theo thứ tự từ lớn đến bé: \(\frac{1}{2};\frac{9}{{14}};\frac{1}{7};\frac{5}{{14}}\)
a) Sắp xếp các phân số theo thứ tự từ bé đến lớn
b) Sắp xếp các phân số theo thứ tự từ lớn đến bé
a)
Ta có:
+) Các phân số bé hơn 1: \(\frac{{132}}{{143}};\frac{{12}}{{17}}\)
Ta so sánh \(\frac{{132}}{{143}} và \frac{{12}}{{17}}\)
\(\frac{{132}}{{143}} = \frac{{12}}{{13}};\frac{{12}}{{17}}\) là 2 phân số có tử số giống nhau (đều là 12); có mẫu số (13<17) nên \(\frac{{12}}{{17}} < \frac{{12}}{{13}}\)hay \(\frac{{12}}{{17}} < \frac{{132}}{{143}}\)
+) \(\frac{7}{7} = 1\)
+) Các phân số lớn hơn 1: \(\frac{5}{2};\frac{{21}}{{18}}\)
\(\frac{5}{2};\frac{{27}}{{18}} = \frac{3}{2}\) là 2 phân số có mẫu số giống nhau (đều là 2); có tử số (5>3) nên\(\frac{{27}}{{18}} < \frac{5}{2}\)
Vậy sắp xếp các phân số theo thứ tự từ bé đến lớn là: \(\frac{{12}}{{17}};\frac{{132}}{{143}};\frac{7}{7};\frac{{21}}{{18}};\frac{5}{2}\)
Đáp án: \(\frac{{12}}{{17}};\frac{{132}}{{143}};\frac{7}{7};\frac{{21}}{{18}};\frac{5}{2}\)
b)
Ta có: \(\frac{1}{2} = \frac{7}{{14}};\frac{1}{7} = \frac{2}{{14}}\)
Sắp xếp các phân số theo thứ tự từ lớn đến bé là: \(\frac{9}{{14}};\frac{1}{2};\frac{5}{{14}};\frac{1}{7}\)
Đáp án:\(\frac{9}{{14}};\frac{1}{2};\frac{5}{{14}};\frac{1}{7}\)
Hồng có 32 bông hoa, Bình có số hoa bằng $\frac{3}{4}$ của Hồng, Huệ có số hoa bằng $\frac{3}{4}$ tổng số hoa của cả Hồng và Bình. Hỏi Huệ có bao nhiêu bông hoa?
Số bông hoa Bình có = Số bông hoa Hồng có x $\frac{3}{4}$
Tổng số hoa của Hồng và Bình = Số bông hoa Hồng có + Số bông hoa Bình có
Số bông hoa Huệ có = Tổng số hoa của Hồng và Bình x $\frac{3}{4}$
Bình có số bông hoa là:
32 x $\frac{3}{4}$ = 24 (bông)
Tổng số hoa của Hồng và Bình là:
32 + 24 = 56 (bông)
Huệ có số bông hoa là:
56 x $\frac{3}{4}$= 42 (bông)
Đáp số: 42 bông hoa
Một mảnh đất hình chữ nhật có chiều dài 96 m, chiều rộng bằng $\frac{3}{4}$chiều dài. Người ta trồng rau trên mảnh đất đó. Biết rằng cứ 1 m2, người ta thu hoạch được $\frac{2}{3}$ kg rau. Hỏi người ta thu hoạch được tất cả bao nhiêu ki-lô-gam rau trên mảnh đất đó?
- Tính chiều rộng của mảnh đất hình chữ nhật = Chiều dài x $\frac{3}{4}$
- Tính diện tích của mảnh đất hình chữ nhật = Chiều dài x Chiều rộng
- Tính số ki-lô-gam rau người ta thu hoạch được trên mảnh đất đó = Diện tích x $\frac{2}{3}$
Chiều rộng của mảnh đất hình chữ nhật là:
96 x $\frac{3}{4}$= 72 (m)
Diện tích của mảnh đất hình chữ nhật là:
96 x 72 = 6 912 (m2)
Người ta thu hoạch được số ki-lô-gam rau trên mảnh đất đó là:
6912 x $\frac{2}{3}$ = 4 608 (kg)
Đáp số: 4 608 kg rau
Tính bằng cách thuận tiện.
a) $\frac{8}{5} + \frac{3}{6} + 2 + \frac{4}{5} + \frac{3}{2} + \frac{3}{5}$
b) $\frac{{1717}}{{3636}} \times \frac{{181818}}{{343434}}$
- Áp dụng tính chất giao hoán, kết hợp của phép cộng
- Rút gọn phân số
$a)\frac{8}{5} + \frac{3}{6} + 2 + \frac{4}{5} + \frac{3}{2} + \frac{3}{5}$
$ = (\frac{8}{5} + \frac{4}{5} + \frac{3}{5}) + (\frac{1}{2} + \frac{3}{2}) + 2$
$ = \frac{{15}}{5} + \frac{4}{2} + 2$
= 3 + 2 + 2
= 7
\(b)\frac{{1717}}{{3636}} \times \frac{{181818}}{{343434}}\)
\( = \frac{{17 \times 101}}{{36 \times 101}} \times \frac{{18 \times 10101}}{{34 \times 10101}}\)
\( = \frac{{17}}{{36}} \times \frac{{18}}{{34}}\)
\( = \frac{{17}}{{18 \times 2}} \times \frac{{18}}{{17 \times 2}}\)
\( = \frac{{17 \times 18}}{{18 \times 2 \times 17 \times 2}}\)
\( = \frac{1}{4}\)
Kỳ thi học kì 2 Toán 4 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một học kì. Đề thi học kì 2 Toán 4 Cánh diều - Đề số 3 là một công cụ hữu ích để học sinh tự đánh giá kiến thức và kỹ năng của mình. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp, và hướng dẫn giải chi tiết từng câu hỏi.
Đề thi học kì 2 Toán 4 Cánh diều - Đề số 3 thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong đề thi:
Ví dụ 1: Tính 234 + 567
Giải:
234 + 567 = 801
Ví dụ 2: Một cửa hàng có 350 kg gạo. Buổi sáng bán được 120 kg gạo, buổi chiều bán được 150 kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Số gạo đã bán là: 120 + 150 = 270 (kg)
Số gạo còn lại là: 350 - 270 = 80 (kg)
Đáp số: 80 kg
Để đạt kết quả tốt trong kỳ thi học kì 2 Toán 4, học sinh cần:
Ngoài đề thi học kì 2 Toán 4 Cánh diều - Đề số 3, học sinh có thể tham khảo thêm các tài liệu ôn tập sau:
Đề thi học kì 2 Toán 4 Cánh diều - Đề số 3 là một công cụ quan trọng để học sinh ôn tập và củng cố kiến thức. Hy vọng rằng với những thông tin và hướng dẫn trong bài viết này, các em sẽ tự tin hơn khi bước vào kỳ thi và đạt được kết quả tốt nhất.