Bài học này sẽ hướng dẫn các em học sinh lớp 4 cách cộng các phân số một cách dễ dàng và hiệu quả. Chúng ta sẽ cùng nhau khám phá cách cộng phân số cùng mẫu số và đặc biệt là cách cộng phân số khác mẫu số thông qua phương pháp quy đồng mẫu số.
Với các ví dụ minh họa cụ thể và bài tập thực hành đa dạng, các em sẽ nắm vững kiến thức và tự tin giải các bài toán về phân số.
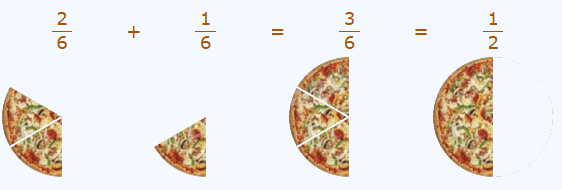
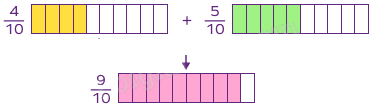
Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi cộng hai phân số đó.
Chú ý: Khi thực hiện phép cộng hai phân số, nếu phân số thu được chưa tối giản thì ta rút gọn thành phân số tối giản.
Ví dụ: $\frac{3}{8} + \frac{5}{{24}} = \frac{9}{{24}} + \frac{5}{{24}} = \frac{{14}}{{24}} = \frac{7}{{12}}$
Trong toán học, phân số là một biểu thức thể hiện một phần của một tổng thể. Phân số được viết dưới dạng a/b, trong đó a là tử số (phần được lấy) và b là mẫu số (tổng số phần).
Cộng phân số là phép toán kết hợp hai hoặc nhiều phân số để tạo ra một phân số mới, biểu thị tổng của các phần đó.
Khi cộng các phân số có cùng mẫu số, ta chỉ cần cộng các tử số lại với nhau và giữ nguyên mẫu số. Công thức tổng quát:
a/b + c/b = (a + c)/b
Ví dụ:
2/5 + 1/5 = (2 + 1)/5 = 3/5
Khi cộng các phân số có mẫu số khác nhau, ta cần thực hiện quy đồng mẫu số trước khi cộng. Quy đồng mẫu số là việc tìm một mẫu số chung nhỏ nhất (MSC) của các mẫu số và biến đổi các phân số về dạng có cùng mẫu số đó.
Các bước quy đồng mẫu số:
Ví dụ:
1/2 + 1/3
Dưới đây là một số bài tập để các em luyện tập:
Phép cộng phân số được ứng dụng rộng rãi trong cuộc sống hàng ngày, ví dụ như:
Việc nắm vững kiến thức về cộng phân số là rất quan trọng đối với học sinh lớp 4. Hy vọng rằng bài học này đã giúp các em hiểu rõ hơn về cách cộng phân số cùng mẫu số và khác mẫu số. Hãy luyện tập thường xuyên để củng cố kiến thức và tự tin giải các bài toán về phân số nhé!
| Phân Số 1 | Phân Số 2 | Kết Quả |
|---|---|---|
| 1/4 | 2/4 | 3/4 |
| 1/3 | 1/6 | 1/2 |