Bài học này sẽ giúp các em học sinh lớp 4 hiểu rõ về hai tính chất quan trọng của phép cộng: tính chất giao hoán và tính chất kết hợp. Đây là nền tảng cơ bản để giải các bài toán cộng số một cách nhanh chóng và chính xác.
Chúng ta sẽ cùng nhau khám phá định nghĩa, ví dụ minh họa và các bài tập thực hành để nắm vững kiến thức này.

Ví dụ 2. Tính bằng cách thuận tiện
a) 1 420 + 1 694 + 580 + 306
b) 1 857 + 2 557 + 443 + 143
c) 223 + 540 + 777 + 460
Hướng dẫn giải
a) 1 420 + 1 694 + 80 + 306 = (1 420 + 580) + (1 694 + 306)
= 2 000 + 2 000
= 4 000
b) 1 857 + 2 557 + 443 + 143 = (1 857 + 143) + (2 557 + 443)
= 2 000 + 3 000
= 5 000
c) 223 + 540 + 777 + 460 = (223 + 777) + (540 + 460)
= 1 000 + 1 000
= 2 000
Ví dụ 3. Điền dấu >, <, = thích hợp vào chỗ chấm
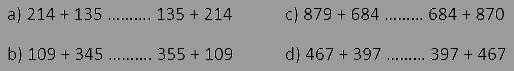
Hướng dẫn giải
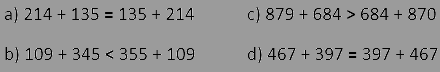
Tính chất giao hoán của phép cộng cho biết rằng thứ tự của các số hạng trong một phép cộng không ảnh hưởng đến kết quả. Nói cách khác, a + b = b + a với mọi số a và b.
Ví dụ:
Tính chất giao hoán giúp chúng ta linh hoạt hơn trong việc sắp xếp các số hạng để thực hiện phép cộng một cách dễ dàng hơn.
Tính chất kết hợp của phép cộng cho biết rằng khi cộng ba hoặc nhiều số, ta có thể nhóm các số hạng lại với nhau theo bất kỳ cách nào mà không làm thay đổi kết quả. Nói cách khác, (a + b) + c = a + (b + c) với mọi số a, b và c.
Ví dụ:
Tính chất kết hợp đặc biệt hữu ích khi chúng ta cần cộng nhiều số với nhau, giúp chúng ta chia nhỏ bài toán thành các bước nhỏ hơn và dễ quản lý hơn.
Hai tính chất này có rất nhiều ứng dụng trong thực tế, đặc biệt là trong việc giải toán và tính toán nhanh.
Ví dụ 1: Tính 25 + 18 + 32
Chúng ta có thể sử dụng tính chất giao hoán và kết hợp để tính như sau:
(25 + 32) + 18 = 57 + 18 = 75
Hoặc:
25 + (18 + 32) = 25 + 50 = 75
Hãy áp dụng tính chất giao hoán và tính chất kết hợp để tính các biểu thức sau:
Tính chất giao hoán và tính chất kết hợp chỉ áp dụng cho phép cộng (và phép nhân). Chúng không áp dụng cho phép trừ và phép chia.
Việc nắm vững tính chất giao hoán và tính chất kết hợp của phép cộng là rất quan trọng đối với học sinh lớp 4. Chúng giúp các em giải toán nhanh chóng, chính xác và hiểu sâu hơn về các phép toán cơ bản.
| Tính chất | Định nghĩa | Ví dụ |
|---|---|---|
| Giao hoán | a + b = b + a | 3 + 5 = 5 + 3 = 8 |
| Kết hợp | (a + b) + c = a + (b + c) | (2 + 3) + 4 = 2 + (3 + 4) = 9 |