Chào mừng các em học sinh đến với đề kiểm tra học kì 2 môn Toán 10 - Đề số 5, chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 2, chuẩn bị tốt nhất cho kỳ thi sắp tới.
I. PHẦN TRẮC NGHIỆM ( 35 câu - 7,0 điểm ).
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Tập xác định của hàm số \(f(x) = \frac{{x + 5}}{{x - 1}} + \frac{{x - 1}}{{x + 5}}\) là
A. \(D = \mathbb{R}\).
B. \(D = \mathbb{R}\backslash \{ 1\} .\)
C. \(D = \mathbb{R}\backslash \{ - 5\} .\)
D. \(D = \mathbb{R}\backslash \{ - 5;{\rm{ }}1\} .\)
Phương pháp
- Phân thức xác định khi mẫu thức khác 0
Lời giải
Điều kiện: \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 5 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 5\end{array} \right.\).
Vậy tập xác định của hàm số là: \(D = \mathbb{R}\backslash \left\{ {1; - 5} \right\}\).
Chọn D
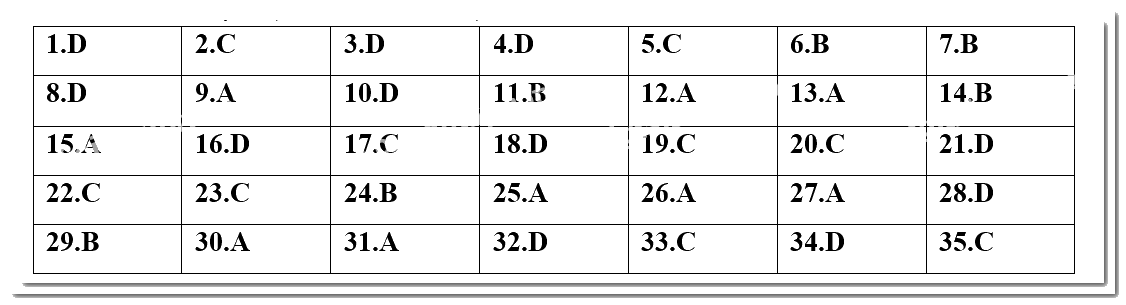
Câu 2: Cho hàm số có đồ thị như hình vẽ.
Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
Phương pháp
- Hàm số có chiều đi lên từ trái sang phải là đồng biến.
- Hàm số có chiều đi xuống từ trái sang phải là nghịch biến.
Lời giải
Từ đồ thị hàm số ta thấy:
Hàm số nghịch biến trong các khoảng: \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
Hàm số đồng biến trong các khoảng: \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Chọn C
Câu 3: Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là
A. \(\left( { - \infty ; - 2} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Phương pháp
Sử dụng công thức dấu của tam thức bậc hai.
Lờigiải
Hàm số \(y = {x^2} - 4x + 3\)có \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\).
Vì vậy hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
ChọnD
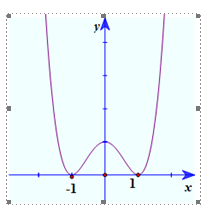
Câu 4: Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây?
A. \(y = {x^2} + 2x - 1\).
B. \(y = {x^2} + 2x - 2\).
C. \(y = 2{x^2} - 4x - 2\).
D. \(y = {x^2} - 2x - 1\).
Phương pháp
Hình dáng của đồ thị bậc hai Parabol.
Lời giải
Đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\) nên loại B và C
Hoành độ của đỉnh là \({x_I} = - \frac{b}{{2a}} = 1\) nên ta loại A và chọn D.
Chọn D
Câu 5: Cho tam thức bậc hai \(f\left( x \right) = - {x^2} - 4x + 5\). Tìm tất cả giá trị của \(x\) để \(f\left( x \right) \ge 0\).
A. \(x \in \left( { - \infty ;\, - 1} \right] \cup \left[ {5;\, + \infty } \right)\).
B. \(x \in \left[ { - 1;\,5} \right]\).
C. \(x \in \left[ { - 5;\,1} \right]\).
D. \(x \in \left( { - 5;\,1} \right)\).
Phương pháp
Sử dụng quy tắc dấu của tam thức bậc hai
Lờigiải
Ta có \(f\left( x \right) = 0\) \( \Leftrightarrow \) \( - {x^2} - 4x + 5 = 0\) \( \Leftrightarrow \) \(x = 1\), \(x = - 5\).
Mà hệ số \(a = - 1 < 0\) nên: \(f\left( x \right) \ge 0\) \( \Leftrightarrow \) \(x \in \left[ { - 5;\,1} \right]\).
ChọnC.
Câu 6: Tìm \(m\) để phương trình \( - {x^2} + 2\left( {m - 1} \right)x + m - 3 = 0\) có hai nghiệm phân biệt
A. \(\left( { - 1;2} \right)\)
B. \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)
C. \(\left[ { - 1;2} \right]\)
D. \(\left( { - \infty ; - 1} \right] \cup \left[ {2; + \infty } \right)\)
Phương pháp
Phương trình bậc hai có hai nghiệm phân biệt khi \(\Delta ' > 0\)
Lờigiải
Phương trình có hai nghiệm phân biệt
\( \Leftrightarrow \Delta ' > 0 \Leftrightarrow {\left( {m - 1} \right)^2} - \left( { - 1} \right).\left( {m - 3} \right) > 0 \Leftrightarrow {m^2} - m - 2 > 0 \Leftrightarrow \left[ \begin{array}{l}m < - 1\\m > 2\end{array} \right.\)
Vậy \(m \in \left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\).
ChọnB
Câu 7: Tập nghiệm của phương trình \(\sqrt {2{x^2} - 4x - 2} = \sqrt {{x^2} - x - 2} \) là:
A. \(S = \left\{ {0;3} \right\}.\)
B. \(S = \left\{ 3 \right\}.\)
C. \(S = \left\{ 0 \right\}.\)
D. \(S = \left\{ {2;3} \right\}.\)
Phương pháp
Thử các giá trị của x trong đáp án vào phương trình.
Lời giải
Thay các giá trị vào phương trình có \(x = 3\) vào thỏa mãn phương trình.
ChọnB
Câu 8: Phương trình \(\sqrt { - {x^2} + 4x} = 2x - 2\) có bao nhiêu nghiệm?
A. \(3\). B. \(0\). C. \(2\). D. \(1\).
Phương pháp
Bình phương hai vế của phương trình rồi giải.
Lời giải
\(\sqrt { - {x^2} + 4x} = 2x - 2\)\( \Leftrightarrow \left\{ \begin{array}{l}2x - 2 \ge 0\\ - {x^2} + 4x = {\left( {2x - 2} \right)^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\5{x^2} - 12x + 4 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}x = 2\left( n \right)\\x = \frac{2}{5}\left( l \right)\end{array} \right.\end{array} \right.\).
Vậy \(x = 2\) là nghiệm của phương trình.
ChọnD
Câu 9: Vectơ chỉ phương của đường thẳng \(d\): \(\left\{ \begin{array}{l}x = 1 - 4t\\y = - 2 + 3t\end{array} \right.\) là:
A. \(\overrightarrow u = \left( { - 4;3} \right)\).
B. \(\overrightarrow u = \left( {4;3} \right)\).
C. \(\overrightarrow u = \left( {3;4} \right)\).
D. \(\overrightarrow u = \left( {1; - 2} \right)\).
Phương pháp
Vecto chỉ phương của đường thẳng \(d:\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) là \(\overrightarrow u = \left( {a;b} \right)\)
Lời giải
Đường thẳng \(d\): \(\left\{ \begin{array}{l}x = 1 - 4t\\y = - 2 + 3t\end{array} \right.\)có vectơ chỉ phương là \(\overrightarrow u = \left( { - 4;3} \right)\).
Chọn A.
Câu 10: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\).
Phương pháp
Phương trình tham số của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {a;b} \right)\) làm vecto chỉ phương là : \(d:\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)
Lời giải
Vectơ chỉ phương \(\overrightarrow {AB} = \left( {0;6} \right)\).
Phương trình tham số của đường thẳng đi qua điểm \(A\left( {2; - 1} \right)\) và nhận \(\overrightarrow {AB} = \left( {0;6} \right)\) làm vecto chỉ phương là : \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\)
ChọnD
Câu 11: Trong mặt phẳng \(Oxy\), cho đường thẳng \(d:2x - y + 1 = 0\), một véctơ pháp tuyến của \(d\) là
A. \(\left( { - 2; - 1} \right)\).
B. \(\left( {2; - 1} \right)\).
C. \(\left( { - 1; - 2} \right)\).
D. \(\left( {1; - 2} \right)\).
Phương pháp
Vecto pháp tuyến của đường thẳng\(d:ax + by + c = 0\) là \(\overrightarrow n = \left( {a;b} \right)\)
Lời giải
ChọnB
Một véctơ pháp tuyến của đường thẳng \(d\) là \(\overrightarrow n = \left( {2; - 1} \right)\).
Câu 12: Tọa độ giao điểm của hai đường thẳng \(x - 3y - 6 = 0\) và \(3x + 4y - 1 = 0\) là
A. \(\left( {\frac{{27}}{{13}}; - \frac{{17}}{{13}}} \right)\).
B. \(\left( { - 27;17} \right)\).
C. \(\left( { - \frac{{27}}{{13}};\frac{{17}}{{13}}} \right)\).
D. \(\left( {27; - 17} \right)\).
Phương pháp
Tọa độ giao điểm của hai đường thẳng là nghiệm của cả hai phương trình đường thẳng đó
Lời giải
Ta có tọa độ giao điểm của hai đường thẳng \(x - 3y - 6 = 0\) và \(3x + 4y - 1 = 0\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - 3y - 6 = 0\\3x + 4y - 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{27}}{{13}}\\y = - \frac{{17}}{3}\end{array} \right.\).
Chọn A
Câu 13: Cho đường thẳng \({d_1}:2x + 3y + 15 = 0\) và \({d_2}:x - 2y - 3 = 0\). Khẳng định nào sau đây đúng?
A. \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau.
B. \({d_1}\) và \({d_2}\) song song với nhau.
C. \({d_1}\) và \({d_2}\) trùng nhau.
D. \({d_1}\) và \({d_2}\) vuông góc với nhau.
Phương pháp
Sử dụng công thức vị trí tương đối của hai đường thẳng.
Lời giải
Đường thẳng\({d_1}:2x + 3y + 15 = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {2;3} \right)\) và đường thẳng \({d_2}:x - 2y - 3 = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1; - 2} \right)\).
Ta thấy \(\frac{2}{1} \ne \frac{3}{{ - 2}}\) và \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 2.1 + 3.( - 2) = - 4 \ne 0\).
Vậy \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau.
Chọn A
Câu 14: Cho đường thẳng \(d:\, - 3x + y - 5 = 0\) và điểm \(M\left( { - 2;1} \right)\). Tọa độ hình chiếu vuông góc của \(M\)trên \(d\) là
A. \(\left( {\frac{7}{5}; - \frac{4}{5}} \right)\).
B. \(\left( { - \frac{7}{5};\frac{4}{5}} \right)\).
C. \(\left( { - \frac{7}{5}; - \frac{4}{5}} \right)\).
D. \(\left( { - \frac{5}{7};\frac{4}{5}} \right)\).
Phương pháp
Viết phương trình đường thẳng đi qua M và vuông góc với đường thẳng d.
Lời giải
Gọi \(\Delta \) là đường thẳng đi qua \(M\)và vuông góc với \(d\).
Ta có phương trình của \(\Delta \) là: \(x + 3y - 1 = 0\)
Tọa độ hình chiếu vuông góc của \(M\) trên \(d\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l} - 3x + y - 5 = 0\\x + 3y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{7}{5}\\y = \frac{4}{5}\end{array} \right.\).
ChọnB
Câu 15: Xác định tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9.\)
A. Tâm \(I\left( { - 1;2} \right),\) bán kính \(R = 3\).
B. Tâm \(I\left( { - 1;2} \right),\) bán kính \(R = 9\).
C. Tâm \(I\left( {1; - 2} \right),\) bán kính \(R = 3\).
D. Tâm \(I\left( {1; - 2} \right),\) bán kính \(R = 9\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lờigiải
Tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9.\) là \(I\left( { - 1;2} \right),\) bán kính \(R = 3\).
ChọnA
Câu 16: Đường tròn \(\left( C \right):{x^2} + {y^2} - 2x + 4y - 3 = 0\) có tâm \(I\), bán kính \(R\) là
A. \(I\left( { - 1;\,2} \right),\,R = \sqrt 2 \).
B. \(I\left( { - 1;\,2} \right),\,R = 2\sqrt 2 \).
C. \(I\left( {1;\, - 2} \right),\,R = \sqrt 2 \).
D. \(I\left( {1;\, - 2} \right),\,R = 2\sqrt 2 \).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lờigiải
Tâm \(I\left( {1;\, - 2} \right)\), bán kính \(\,R = \sqrt {{1^2} + {{\left( { - 2} \right)}^2} - \left( { - 3} \right)} = \sqrt 8 = 2\sqrt 2 \).
ChọnD
Câu 17: Đường tròn tâm \(I\left( {3; - 1} \right)\) và bán kính \(R = 2\) có phương trình là
A. \({\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\)
B. \({\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\)
C. \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
D. \({\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Phương trình đường tròn có tâm \(I\left( {3; - 1} \right)\), bán kính \(R = 2\) là: \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
Chọn C
Câu 18: Phương trình tiếp tuyến của đường tròn\(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\) tại điểm \(M\left( {2;1} \right)\) là:
A. \(d:\, - y + 1 = 0\)
B. \(d:\,4x + 3y + 14 = 0\)
C. \(d:\,3x - 4y - 2 = 0\)
D. \(d:\,4x + 3y - 11 = 0\)
Phương pháp
Phương trình đường thẳng nhậnvecto pháp tuyến \(\overrightarrow n = \left( {a;b} \right)\) và đi qua điểm \(A({x_0},{y_0})\) là \(d:a(x - {x_0}) + b(y - {y_0}) = 0\)
Lời giải
Đường tròn (C) có tâm \(I( - 2;2)\)nên tiếp tuyến tại M có VTPT là nên có phương trình là: \(4(x - 2) + 3(y - 1) = 0 \Leftrightarrow 4x + 3y - 11 = 0\)
Chọn D
Câu 19: Elip \(\left( E \right):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)có độ dài trục bé bằng:
A. 8 B. 10 C. 16 D. 20
Phương pháp
Độ dài trục lớp của Elip\(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) là \({B_1}{B_2} = 2b\)
Lời giải
Gọi phương trình của Elip là \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có độ dài trục bé \({B_1}{B_2} = 2b\)
Xét \(\left( E \right):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1 \Leftrightarrow \left\{ \begin{array}{l}{a^2} = 100\\{b^2} = 64\end{array} \right. \Rightarrow b = 8 \Rightarrow {B_1}{B_2} = 2.8 = 16\)
Chọn C
Câu 20: Elip có hai đỉnh là \(\left( { - 3;0} \right),\left( {3;0} \right)\) và có hai tiêu điểm là \(\left( { - 1;0} \right),\left( {1;0} \right).\) Phương trình chính tắc của elip là:
A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\)
B. \(\frac{{{x^2}}}{8} + \frac{{{y^2}}}{9} = 1\)
C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\)
D. \(\frac{{{x^2}}}{1} + \frac{{{y^2}}}{9} = 1\)
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải
Elip có hai đỉnh là \(\left( { - 3;0} \right),\left( {3;0} \right)\) suy ra a = 3
Elip có hai tiêu điểm là \(\left( { - 1;0} \right),\left( {1;0} \right).\)suy ra c = 1
Khi đó, .
Phương trình chính tắc của Elip là (E) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\).
Chọn C
Câu 21: Trong một trường THPT, khối có học sinh nam và học sinh nữ. Nhà trường cần chọn một học sinh ở khối đi dự dạ hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 45 B. 28 C. 325 D. 605
Phương pháp
Áp dụng quy tắc cộng
Lờigiải.
Nếu chọn một học sinh nam có cách.
Nếu chọn một học sinh nữ có cách.
Theo qui tắc cộng, ta có cách chọn.
Chọn D
Câu 22: Từ các số lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số lẻ
A. 360 B. 343 C. 480 D. 347
Phương pháp
Áp dụng quy tắc nhân
Lờigiải
Gọi số cần lập ; và đôi một khác nhau.
Vì số cần lập là số lẻ nên phải là số lẻ. Ta lập qua các công đoạn sau.
Bước 1: Có 4 cách chọn d
Bước 2: Có 6 cách chọn a
Bước 3: Có 5 cách chọn b
Bước 4: Có 4 cách chọn c
Vậy có 480 số thỏa yêu cầu bài toán.
Chọn C
Câu 23: Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. 4. B. 7. C. 12. D. 16.
Phương pháp
Áp dụng quy tắc nhân
Lờigiải.
Để chọn một chiếc đồng hồ, ta có:
Có 3 cách chọn mặt.
Có 4 cách chọn dây.
Vậy theo qui tắc nhân ta có cách.
Chọn C
Câu 24: Có bao nhiêu cách sắp xếp nữ sinh, nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ:
A. 6. B. 72. C. 720. D. 144.
Phương pháp
Áp dụng quy tắc nhân
Lờigiải
Chọn vị trí 3 nam và 3 nữ: cách chọn.
Xếp 3 nam có: cách xếp.
Xếp 3 nữ có: cách xếp.
Vậy có cách xếp.
Chọn B
Câu 25: Từ các chữ số \(1\), \(2\), \(3\), \(4\), \(5\) có thể lập được bao nhiêu số tự nhiên gồm \(5\) chữ số đôi một khác nhau:
A. \(120\). B. \(720\). C. \(16\). D. \(24\).
Phương pháp
Áp dụng công thức hoán vị
Lờigiải
Mỗi số tự nhiên gồm \(5\) chữ số khác nhau được lập từ các số \(1\), \(2\), \(3\), \(4\), \(5\) là một hoán vị của \(5\) phần tử đó. Nên số các số thỏa mãn yêu cầu bài toán là \({P_5} = 5!\) \( = 120\) (số).
Chọn A
Câu 26: Một câu lạc bộ có \(25\) thành viên. Số cách chọn một ban quản lí gồm \(1\) chủ tịch, \(1\) phó chủ tịch và \(1\) thư kí là:
A. \(13800\). B. \(5600\). C. 6500. D. \(6900\).
Phương pháp
Áp dụng công thức chỉnh hợp
Lờigiải
Mỗi cách chọn \(3\) người ở \(3\) vị trí là một chỉnh hợp chập \(3\) của \(25\) thành viên.
Số cách chọn là: \(A_{25}^3 = 13800\).
Chọn A
Câu 27: Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là
A. \(C_7^3\).
B. \(\frac{{7!}}{{3!}}\).
C. \(A_7^3\).
D. \(21\).
Phương pháp
Áp dụng công thức tổ hợp
Lờigiải
Số tập hợp con cần tìm là số tổ hợp chập 3 của 7 phần tử.
Vậy có \(C_7^3\) tập con cần tìm.
ChọnA
Câu 28: Trong một buổi khiêu vũ có \(20\) nam và \(18\) nữ. Hỏi có bao nhiêu cách chọn ra một đôi nam nữ để khiêu vũ?
A. \(C_{38}^2\).
B. \(A_{38}^2\).
C. \(C_{20}^2C_{18}^1\).
D. \(C_{20}^1C_{18}^1\).
Phương pháp
Áp dụng công thức tổ hợp
Lờigiải
Chọn một nam trong \(20\) nam có \(C_{20}^1\) cách.
Chọn một nữ trong \(18\) nữ có \(C_{18}^1\) cách.
Theo quy tắc nhân, số cách chọn một đôi nam nữ là \(C_{20}^1C_{18}^1\).
ChọnD
Câu 29: Tính số cách sắp xếp \(6\) nam sinh và \(4\)nữ sinh vào một dãy ghế hàng ngang có \(10\) chỗ ngồi sao cho các nữ sinh luôn ngồi cạnh nhau.
A. \(10!\).
B. \(7! \times 4!.\)
C. \(6! \times 4!.\)
D. \(6! \times 5!.\)
Phương pháp
Áp dụng công thức hoán vị
Lờigiải:
Sắp xếp \(4\) nữ sinh vào \(4\) ghế: \(4!\) cách.
Xem \(4\) nữ sinh lập thành nhóm X, sắp xếp nhóm X cùng với \(6\) nam sinh: có \(7!\) cách
vậy có \(7! \times 4!\) cách sắp xếp.
ChọnB
Câu 30: Viết khai triển theo công thức nhị thức Niu-tơn \({\left( {x - y} \right)^5}\).
A. \({x^5} - 5{x^4}y + 10{x^3}{y^2} - 10{x^2}{y^3} + 5x{y^4} - {y^5}\).
B. \({x^5} - 5{x^4}y - 10{x^3}{y^2} - 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
C. \({x^5} + 5{x^4}y + 10{x^3}{y^2} + 10{x^2}{y^3} + 5x{y^4} + {y^5}\).
D. \({x^5} + 5{x^4}y - 10{x^3}{y^2} + 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Lờigiải
Ta có:
\({\left( {x - y} \right)^5} = {\left[ {x + \left( { - y} \right)} \right]^5} = C_5^0{x^5} + C_5^1{x^4}{\left( { - y} \right)^1} + C_5^2{x^3}{\left( { - y} \right)^2} + C_5^3{x^2}{\left( { - y} \right)^3} + C_5^4{x^1}{\left( { - y} \right)^4} + C_5^5{\left( { - y} \right)^5}\)
Hay \({\left( {x - y} \right)^5} = {x^5} - 5{x^4}y + 10{x^3}{y^2} - 10{x^2}{y^3} + 5x{y^4} - {y^5}\).
ChọnA
Câu 31: Xét phép thử gieo một con súc sắc cân đối và đồng chất 6 mặt hai lần. Xét biến cố A: “Số chấm xuất hiện ở cả hai lần gieo giống nhau”. Khẳng định nào sau đây đúng?
A. \(n\left( A \right) = 6\).
B. \(n\left( A \right) = 12\).
C. \(n\left( A \right) = 16\).
D. \(n\left( A \right) = 36\).
Phương pháp
Công thức tính xác suất
Lờigiải
Gọi cặp số \(\left( {x;y} \right)\) là số chấm xuất hiện ở hai lần gieo.
Xét biến cố A: “Số chấm xuất hiện ở cả hai lần gieo giống nhau”.
Các kết quả của biến cố A là: \(\left\{ {\left( {1;1} \right);\left( {2;2} \right);\left( {3;3} \right);\left( {4;4} \right);\left( {5;5} \right);\left( {6;6} \right)} \right\}\).
Suy ra \(n\left( A \right) = 6\).
ChọnA
Câu 32: Rút ngẫu nhiên cùng lúc ba con bài từ cỗ bài tú lơ khơ \(52\) con thì \(n\left( \Omega \right)\) bằng bao nhiêu?
A. \(140608\). B. \(156\). C. \(132600\). D. \(22100\).
Phương pháp
Áp dụng công thức tổ hợp
Lờigiải
Ta có \(n\left( \Omega \right) = C_{52}^3 = 22100\).
ChọnD
Câu 33: Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất \(5\) lần. Tính số phần tử không gian mẫu.
A. \(64\). B. \(10\). C. \(32\). D. \(16\).
Phương pháp
Áp dụng quy tắc đếm
Lờigiải
Mỗi lần gieo có hai khả năng nên gieo 5 lần theo quy tắc nhân ta có \({2^5} = 32\).
Số phần tử không gian mẫu là \(n\left( \Omega \right) = 32\).
ChọnC
Câu 34: Từ một hộp chứa \(11\) quả cầu màu đỏ và \(4\) quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được \(3\) quả cầu màu xanh
A. \(\frac{{33}}{{91}}\)
B. \(\frac{{24}}{{455}}\)
C. \(\frac{4}{{165}}\)
D. \(\frac{4}{{455}}\)
Phương pháp
Công thức tính xác suất
Lờigiải
Số phần tử của không gian mẫu \(n\left( \Omega \right) = C_{15}^3\)\( = 455\).
Gọi \(A\) là biến cố "\(3\) quả cầu lấy được đều là màu xanh". Suy ra \(n\left( A \right) = C_4^3\)\( = 4\).
Vậy xác suất cần tìm là \(P\left( A \right) = \frac{4}{{455}}\).
ChọnD
Câu 35: Một tổ có \(6\) học sinh nam và \(4\) học sinh nữ. Chọn ngẫu nhiên \(4\) học sinh. Xác suất để trong \(4\) học sinh được chọn luôn có học sinh nữ là
A. \(\frac{1}{{14}}\).
B. \(\frac{1}{{210}}\).
C. \(\frac{{13}}{{14}}\).
D. \(\frac{{209}}{{210}}\).
Phương pháp
Công thức tính xác suất
Lờigiải
\(n\left( \Omega \right) = C_{10}^4 = 210\).
Gọi \(A\) là biến cố:” trong \(4\) học sinh được chọn luôn có học sinh nữ” \( \Rightarrow n\left( A \right) = C_{10}^4 - C_6^4 = 195\)
Vậy xác suất của biến cố \(A\) là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)\( = \frac{{195}}{{210}}\)\( = \frac{{13}}{{14}}\).
ChọnC
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 1. Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Bình phương hai vế của phương trình ta được
\(2{x^2} - 5x - 9 = {x^2} - 2x + 1.\)
Sau khi thu gọn ta được \({x^2} - 3x - 10 = 0\). Tử đó \(x = - 2\) hoặc \(x = 5\).
Thay lần lượt hai giá trị này của \(x\) vào phương trình đã cho, ta thấy chỉ có \(x = 5\) thoả mãn.
Vậy nghiệm của phương trình đã cho là \(x = 5\).
Câu 2. Cho điểm \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\) và \(\overrightarrow n \left( {1;2} \right)\). Viết phương trình tham số của đường thẳng D đi qua \(A\) và nhận vectơ \(\overrightarrow n \left( {1;2} \right)\) làm vectơ pháp tuyến.
Phương pháp
Phương trình tham số của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {a;b} \right)\) làm vecto chỉ phương là : \(\Delta :\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)
Lời giải
Vì \(\Delta \) nhận vectơ \(\overrightarrow n \left( {1;2} \right)\) làm vectơ pháp tuyến nên VTCP của \(\Delta \) là \(\overrightarrow u \left( { - 2;1} \right)\).
Vậy phương trình tham số của đường thẳng \(\Delta \) là \(\Delta :\left\{ \begin{array}{l}x = 1 - 2t\\y = - 3 + t\end{array} \right.\)
Câu 3. Gọi n là số nguyên dương thỏa mãn \(A_n^3 + 2A_n^2 = 48\)Tìm hệ số của \({x^3}\) trong khai triển nhị thức Niu-tơn của \({(1 - 3x)^n}\)
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Lời giải
ĐK: \(n \ge 3,n \in N\).
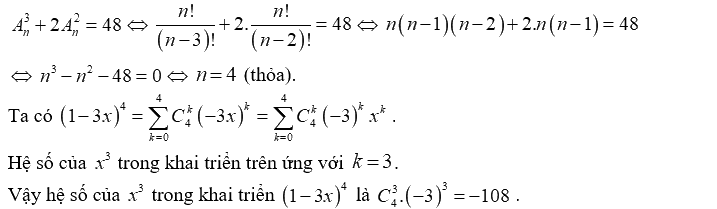
Câu 4. Viết phương trình đường tròn (C) đi qua \(A\left( {2; - 1} \right)\) và tiếp xúc với hai trục toạ độ \(Ox\) và \(Oy\)
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải:
Vì điểm A nằm ở góc phần tư thứ tư và đường tròn tiếp xúc với hai trục toạ độ nên tâm của đường tròn có dạng \(I\left( {R; - R} \right)\) trong đó R là bán kính đường tròn (C).
Ta có:\({R^2} = I{A^2} \Leftrightarrow {R^2} = {\left( {2 - R} \right)^2} + {\left( { - 1 + R} \right)^2} \Leftrightarrow {R^2} - 6R + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{R = 1}\\{R = 5}\end{array}} \right.\)
Vậy có hai đường tròn thoả mãn đầu bài là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 1\) và \({\left( {x - 5} \right)^2} + {\left( {y + 5} \right)^2} = 25\)
---------- HẾT ----------
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: T ập xác định của hàm số \(f(x) = \frac{{x + 5}}{{x - 1}} + \frac{{x - 1}}{{x + 5}}\) là
A. \(D = \mathbb{R}\).
B. \(D = \mathbb{R}\backslash \{ 1\} .\)
C. \(D = \mathbb{R}\backslash \{ - 5\} .\)
D. \(D = \mathbb{R}\backslash \{ - 5;{\rm{ }}1\} .\)
Câu 2: Cho hàm số có đồ thị như hình vẽ.
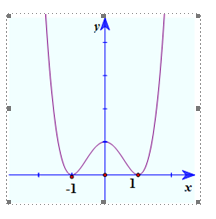
Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
Câu 3: Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là
A. \(\left( { - \infty ; - 2} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Câu 4: Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây?
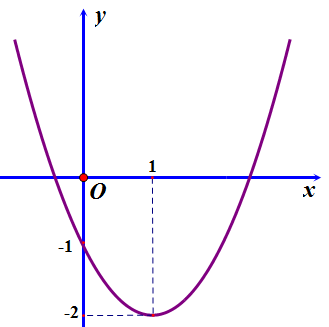
A. \(y = {x^2} + 2x - 1\). B. \(y = {x^2} + 2x - 2\). C. \(y = 2{x^2} - 4x - 2\). D. \(y = {x^2} - 2x - 1\).
Câu 5: Cho tam thức bậc hai \(f\left( x \right) = - {x^2} - 4x + 5\). Tìm tất cả giá trị của \(x\) để \(f\left( x \right) \ge 0\).
A. \(x \in \left( { - \infty ;\, - 1} \right] \cup \left[ {5;\, + \infty } \right)\).
B. \(x \in \left[ { - 1;\,5} \right]\).
C. \(x \in \left[ { - 5;\,1} \right]\).
D. \(x \in \left( { - 5;\,1} \right)\).
Câu 6: Tìm \(m\) để phương trình \( - {x^2} + 2\left( {m - 1} \right)x + m - 3 = 0\) có hai nghiệm phân biệt
A. \(\left( { - 1;2} \right)\)
B. \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)
C. \(\left[ { - 1;2} \right]\)
D. \(\left( { - \infty ; - 1} \right] \cup \left[ {2; + \infty } \right)\)
Câu 7: Tập nghiệm của phương trình \(\sqrt {2{x^2} - 4x - 2} = \sqrt {{x^2} - x - 2} \) là:
A. \(S = \left\{ {0;3} \right\}.\)
B. \(S = \left\{ 3 \right\}.\)
C. \(S = \left\{ 0 \right\}.\)
D. \(S = \left\{ {2;3} \right\}.\)
Câu 8: Phương trình \(\sqrt { - {x^2} + 4x} = 2x - 2\) có bao nhiêu nghiệm?
A. \(3\). B. \(0\). C. \(2\). D. \(1\).
Câu 9: Vectơ chỉ phương của đường thẳng \(d\): \(\left\{ \begin{array}{l}x = 1 - 4t\\y = - 2 + 3t\end{array} \right.\) là:
A. \(\overrightarrow u = \left( { - 4;3} \right)\). B. \(\overrightarrow u = \left( {4;3} \right)\). C. \(\overrightarrow u = \left( {3;4} \right)\). D. \(\overrightarrow u = \left( {1; - 2} \right)\).
Câu 10: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\).
Câu 11: Trong mặt phẳng \(Oxy\), cho đường thẳng \(d:2x - y + 1 = 0\), một véctơ pháp tuyến của \(d\) là
A. \(\left( { - 2; - 1} \right)\).
B. \(\left( {2; - 1} \right)\).
C. \(\left( { - 1; - 2} \right)\).
D. \(\left( {1; - 2} \right)\).
Câu 12: Tọa độ giao điểm của hai đường thẳng \(x - 3y - 6 = 0\) và \(3x + 4y - 1 = 0\) là
A. \(\left( {\frac{{27}}{{13}}; - \frac{{17}}{{13}}} \right)\).
B. \(\left( { - 27;17} \right)\).
C. \(\left( { - \frac{{27}}{{13}};\frac{{17}}{{13}}} \right)\).
D. \(\left( {27; - 17} \right)\).
Câu 13: Cho đường thẳng \({d_1}:2x + 3y + 15 = 0\) và \({d_2}:x - 2y - 3 = 0\). Khẳng định nào sau đây đúng?
A. \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau.
B. \({d_1}\) và \({d_2}\) song song với nhau.
C. \({d_1}\) và \({d_2}\) trùng nhau.
D. \({d_1}\) và \({d_2}\) vuông góc với nhau.
Câu 14: Cho đường thẳng \(d:\, - 3x + y - 5 = 0\) và điểm \(M\left( { - 2;1} \right)\). Tọa độ hình chiếu vuông góc của \(M\)trên \(d\) là
A. \(\left( {\frac{7}{5}; - \frac{4}{5}} \right)\).
B. \(\left( { - \frac{7}{5};\frac{4}{5}} \right)\).
C. \(\left( { - \frac{7}{5}; - \frac{4}{5}} \right)\).
D. \(\left( { - \frac{5}{7};\frac{4}{5}} \right)\).
Câu 15: Xác định tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9.\)
A. Tâm \(I\left( { - 1;2} \right),\) bán kính \(R = 3\).
B. Tâm \(I\left( { - 1;2} \right),\) bán kính \(R = 9\).
C. Tâm \(I\left( {1; - 2} \right),\) bán kính \(R = 3\).
D. Tâm \(I\left( {1; - 2} \right),\) bán kính \(R = 9\).
Câu 16: Đường tròn \(\left( C \right):{x^2} + {y^2} - 2x + 4y - 3 = 0\) có tâm \(I\), bán kính \(R\) là
A. \(I\left( { - 1;\,2} \right),\,R = \sqrt 2 \).
B. \(I\left( { - 1;\,2} \right),\,R = 2\sqrt 2 \).
C. \(I\left( {1;\, - 2} \right),\,R = \sqrt 2 \).
D. \(I\left( {1;\, - 2} \right),\,R = 2\sqrt 2 \).
Câu 17: Đường tròn tâm \(I\left( {3; - 1} \right)\) và bán kính \(R = 2\) có phương trình là
A. \({\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\) B. \({\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\)
C. \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\) D. \({\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
Câu 18: Phương trình tiếp tuyến của đường tròn\(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\) tại điểm \(M\left( {2;1} \right)\) là:
A. \(d:\, - y + 1 = 0\)
B. \(d:\,4x + 3y + 14 = 0\)
C. \(d:\,3x - 4y - 2 = 0\)
D. \(d:\,4x + 3y - 11 = 0\)
Câu 19: Elip \(\left( E \right):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)có độ dài trục bé bằng:
A. 8 B. 10 C. 16 D. 20
Câu 20: Elip có hai đỉnh là \(\left( { - 3;0} \right),\left( {3;0} \right)\) và có hai tiêu điểm là \(\left( { - 1;0} \right),\left( {1;0} \right).\) Phương trình chính tắc của elip là:
A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\)
B. \(\frac{{{x^2}}}{8} + \frac{{{y^2}}}{9} = 1\)
C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\)
D. \(\frac{{{x^2}}}{1} + \frac{{{y^2}}}{9} = 1\)
Câu 21: Trong một trường THPT, khối có học sinh nam và học sinh nữ. Nhà trường cần chọn một học sinh ở khối đi dự dạ hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 45 B. 28 C. 325 D. 605
Câu 22: Từ các số lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số lẻ
A. 360 B. 343 C. 480 D. 347
Câu 23: Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. 4. B. 7. C. 12. D. 16.
Câu 24: Có bao nhiêu cách sắp xếp nữ sinh, nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ:
A. 6. B. 72. C. 720. D. 144.
Câu 25: Từ các chữ số \(1\), \(2\), \(3\), \(4\), \(5\) có thể lập được bao nhiêu số tự nhiên gồm \(5\) chữ số đôi một khác nhau:
A. \(120\). B. \(720\). C. \(16\). D. \(24\).
Câu 26: Một câu lạc bộ có \(25\) thành viên. Số cách chọn một ban quản lí gồm \(1\) chủ tịch, \(1\) phó chủ tịch và \(1\) thư kí là:
A. \(13800\). B. \(5600\). C. 6500. D. \(6900\).
Câu 27: Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là
A. \(C_7^3\). B. \(\frac{{7!}}{{3!}}\). C. \(A_7^3\). D. \(21\).
Câu 28: Trong một buổi khiêu vũ có \(20\) nam và \(18\) nữ. Hỏi có bao nhiêu cách chọn ra một đôi nam nữ để khiêu vũ?
A. \(C_{38}^2\).
B. \(A_{38}^2\).
C. \(C_{20}^2C_{18}^1\).
D. \(C_{20}^1C_{18}^1\).
Câu 29: Tính số cách sắp xếp \(6\) nam sinh và \(4\)nữ sinh vào một dãy ghế hàng ngang có \(10\) chỗ ngồi sao cho các nữ sinh luôn ngồi cạnh nhau.
A. \(10!\).
B. \(7! \times 4!.\)
C. \(6! \times 4!.\)
D. \(6! \times 5!.\)
Câu 30: Viết khai triển theo công thức nhị thức Niu-tơn \({\left( {x - y} \right)^5}\).
A. \({x^5} - 5{x^4}y + 10{x^3}{y^2} - 10{x^2}{y^3} + 5x{y^4} - {y^5}\).
B. \({x^5} - 5{x^4}y - 10{x^3}{y^2} - 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
C. \({x^5} + 5{x^4}y + 10{x^3}{y^2} + 10{x^2}{y^3} + 5x{y^4} + {y^5}\).
D. \({x^5} + 5{x^4}y - 10{x^3}{y^2} + 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
Câu 31: Xét phép thử gieo một con súc sắc cân đối và đồng chất 6 mặt hai lần. Xét biến cố A: “Số chấm xuất hiện ở cả hai lần gieo giống nhau”. Khẳng định nào sau đây đúng?
A. \(n\left( A \right) = 6\).
B. \(n\left( A \right) = 12\).
C. \(n\left( A \right) = 16\).
D. \(n\left( A \right) = 36\).
Câu 32: Rút ngẫu nhiên cùng lúc ba con bài từ cỗ bài tú lơ khơ \(52\) con thì \(n\left( \Omega \right)\) bằng bao nhiêu?
A. \(140608\). B. \(156\). C. \(132600\). D. \(22100\).
Câu 33: Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất \(5\) lần. Tính số phần tử không gian mẫu.
A. \(64\).
B. \(10\).
C. \(32\).
D. \(16\).
Câu 34: Từ một hộp chứa \(11\) quả cầu màu đỏ và \(4\) quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được \(3\) quả cầu màu xanh
A. \(\frac{{33}}{{91}}\)
B. \(\frac{{24}}{{455}}\)
C. \(\frac{4}{{165}}\)
D. \(\frac{4}{{455}}\)
Câu 35: Một tổ có \(6\) học sinh nam và \(4\) học sinh nữ. Chọn ngẫu nhiên \(4\) học sinh. Xác suất để trong \(4\) học sinh được chọn luôn có học sinh nữ là
A. \(\frac{1}{{14}}\).
B. \(\frac{1}{{210}}\).
C. \(\frac{{13}}{{14}}\).
D. \(\frac{{209}}{{210}}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 1. Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Câu 2. Cho điểm \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\) và \(\overrightarrow n \left( {1;2} \right)\). Viết phương trình tham số của đường thẳng D đi qua \(A\) và nhận vectơ \(\overrightarrow n \left( {1;2} \right)\) làm vectơ pháp tuyến.
Câu 3. Gọi n là số nguyên dương thỏa mãn \(A_n^3 + 2A_n^2 = 48\)Tìm hệ số của \({x^3}\) trong khai triển nhị thức Niu-tơn của \({(1 - 3x)^n}\)
Câu 4. Viết phương trình đường tròn (C) đi qua \(A\left( {2; - 1} \right)\) và tiếp xúc với hai trục toạ độ \(Ox\) và \(Oy\)
Tải về
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: T ập xác định của hàm số \(f(x) = \frac{{x + 5}}{{x - 1}} + \frac{{x - 1}}{{x + 5}}\) là
A. \(D = \mathbb{R}\).
B. \(D = \mathbb{R}\backslash \{ 1\} .\)
C. \(D = \mathbb{R}\backslash \{ - 5\} .\)
D. \(D = \mathbb{R}\backslash \{ - 5;{\rm{ }}1\} .\)
Câu 2: Cho hàm số có đồ thị như hình vẽ.
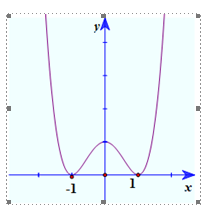
Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
Câu 3: Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là
A. \(\left( { - \infty ; - 2} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Câu 4: Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây?
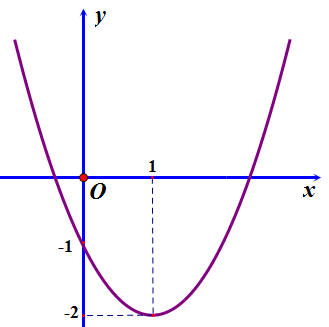
A. \(y = {x^2} + 2x - 1\). B. \(y = {x^2} + 2x - 2\). C. \(y = 2{x^2} - 4x - 2\). D. \(y = {x^2} - 2x - 1\).
Câu 5: Cho tam thức bậc hai \(f\left( x \right) = - {x^2} - 4x + 5\). Tìm tất cả giá trị của \(x\) để \(f\left( x \right) \ge 0\).
A. \(x \in \left( { - \infty ;\, - 1} \right] \cup \left[ {5;\, + \infty } \right)\).
B. \(x \in \left[ { - 1;\,5} \right]\).
C. \(x \in \left[ { - 5;\,1} \right]\).
D. \(x \in \left( { - 5;\,1} \right)\).
Câu 6: Tìm \(m\) để phương trình \( - {x^2} + 2\left( {m - 1} \right)x + m - 3 = 0\) có hai nghiệm phân biệt
A. \(\left( { - 1;2} \right)\)
B. \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)
C. \(\left[ { - 1;2} \right]\)
D. \(\left( { - \infty ; - 1} \right] \cup \left[ {2; + \infty } \right)\)
Câu 7: Tập nghiệm của phương trình \(\sqrt {2{x^2} - 4x - 2} = \sqrt {{x^2} - x - 2} \) là:
A. \(S = \left\{ {0;3} \right\}.\)
B. \(S = \left\{ 3 \right\}.\)
C. \(S = \left\{ 0 \right\}.\)
D. \(S = \left\{ {2;3} \right\}.\)
Câu 8: Phương trình \(\sqrt { - {x^2} + 4x} = 2x - 2\) có bao nhiêu nghiệm?
A. \(3\). B. \(0\). C. \(2\). D. \(1\).
Câu 9: Vectơ chỉ phương của đường thẳng \(d\): \(\left\{ \begin{array}{l}x = 1 - 4t\\y = - 2 + 3t\end{array} \right.\) là:
A. \(\overrightarrow u = \left( { - 4;3} \right)\). B. \(\overrightarrow u = \left( {4;3} \right)\). C. \(\overrightarrow u = \left( {3;4} \right)\). D. \(\overrightarrow u = \left( {1; - 2} \right)\).
Câu 10: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\).
Câu 11: Trong mặt phẳng \(Oxy\), cho đường thẳng \(d:2x - y + 1 = 0\), một véctơ pháp tuyến của \(d\) là
A. \(\left( { - 2; - 1} \right)\).
B. \(\left( {2; - 1} \right)\).
C. \(\left( { - 1; - 2} \right)\).
D. \(\left( {1; - 2} \right)\).
Câu 12: Tọa độ giao điểm của hai đường thẳng \(x - 3y - 6 = 0\) và \(3x + 4y - 1 = 0\) là
A. \(\left( {\frac{{27}}{{13}}; - \frac{{17}}{{13}}} \right)\).
B. \(\left( { - 27;17} \right)\).
C. \(\left( { - \frac{{27}}{{13}};\frac{{17}}{{13}}} \right)\).
D. \(\left( {27; - 17} \right)\).
Câu 13: Cho đường thẳng \({d_1}:2x + 3y + 15 = 0\) và \({d_2}:x - 2y - 3 = 0\). Khẳng định nào sau đây đúng?
A. \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau.
B. \({d_1}\) và \({d_2}\) song song với nhau.
C. \({d_1}\) và \({d_2}\) trùng nhau.
D. \({d_1}\) và \({d_2}\) vuông góc với nhau.
Câu 14: Cho đường thẳng \(d:\, - 3x + y - 5 = 0\) và điểm \(M\left( { - 2;1} \right)\). Tọa độ hình chiếu vuông góc của \(M\)trên \(d\) là
A. \(\left( {\frac{7}{5}; - \frac{4}{5}} \right)\).
B. \(\left( { - \frac{7}{5};\frac{4}{5}} \right)\).
C. \(\left( { - \frac{7}{5}; - \frac{4}{5}} \right)\).
D. \(\left( { - \frac{5}{7};\frac{4}{5}} \right)\).
Câu 15: Xác định tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9.\)
A. Tâm \(I\left( { - 1;2} \right),\) bán kính \(R = 3\).
B. Tâm \(I\left( { - 1;2} \right),\) bán kính \(R = 9\).
C. Tâm \(I\left( {1; - 2} \right),\) bán kính \(R = 3\).
D. Tâm \(I\left( {1; - 2} \right),\) bán kính \(R = 9\).
Câu 16: Đường tròn \(\left( C \right):{x^2} + {y^2} - 2x + 4y - 3 = 0\) có tâm \(I\), bán kính \(R\) là
A. \(I\left( { - 1;\,2} \right),\,R = \sqrt 2 \).
B. \(I\left( { - 1;\,2} \right),\,R = 2\sqrt 2 \).
C. \(I\left( {1;\, - 2} \right),\,R = \sqrt 2 \).
D. \(I\left( {1;\, - 2} \right),\,R = 2\sqrt 2 \).
Câu 17: Đường tròn tâm \(I\left( {3; - 1} \right)\) và bán kính \(R = 2\) có phương trình là
A. \({\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\) B. \({\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\)
C. \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\) D. \({\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
Câu 18: Phương trình tiếp tuyến của đường tròn\(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\) tại điểm \(M\left( {2;1} \right)\) là:
A. \(d:\, - y + 1 = 0\)
B. \(d:\,4x + 3y + 14 = 0\)
C. \(d:\,3x - 4y - 2 = 0\)
D. \(d:\,4x + 3y - 11 = 0\)
Câu 19: Elip \(\left( E \right):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)có độ dài trục bé bằng:
A. 8 B. 10 C. 16 D. 20
Câu 20: Elip có hai đỉnh là \(\left( { - 3;0} \right),\left( {3;0} \right)\) và có hai tiêu điểm là \(\left( { - 1;0} \right),\left( {1;0} \right).\) Phương trình chính tắc của elip là:
A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\)
B. \(\frac{{{x^2}}}{8} + \frac{{{y^2}}}{9} = 1\)
C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\)
D. \(\frac{{{x^2}}}{1} + \frac{{{y^2}}}{9} = 1\)
Câu 21: Trong một trường THPT, khối có học sinh nam và học sinh nữ. Nhà trường cần chọn một học sinh ở khối đi dự dạ hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 45 B. 28 C. 325 D. 605
Câu 22: Từ các số lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số lẻ
A. 360 B. 343 C. 480 D. 347
Câu 23: Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. 4. B. 7. C. 12. D. 16.
Câu 24: Có bao nhiêu cách sắp xếp nữ sinh, nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ:
A. 6. B. 72. C. 720. D. 144.
Câu 25: Từ các chữ số \(1\), \(2\), \(3\), \(4\), \(5\) có thể lập được bao nhiêu số tự nhiên gồm \(5\) chữ số đôi một khác nhau:
A. \(120\). B. \(720\). C. \(16\). D. \(24\).
Câu 26: Một câu lạc bộ có \(25\) thành viên. Số cách chọn một ban quản lí gồm \(1\) chủ tịch, \(1\) phó chủ tịch và \(1\) thư kí là:
A. \(13800\). B. \(5600\). C. 6500. D. \(6900\).
Câu 27: Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là
A. \(C_7^3\). B. \(\frac{{7!}}{{3!}}\). C. \(A_7^3\). D. \(21\).
Câu 28: Trong một buổi khiêu vũ có \(20\) nam và \(18\) nữ. Hỏi có bao nhiêu cách chọn ra một đôi nam nữ để khiêu vũ?
A. \(C_{38}^2\).
B. \(A_{38}^2\).
C. \(C_{20}^2C_{18}^1\).
D. \(C_{20}^1C_{18}^1\).
Câu 29: Tính số cách sắp xếp \(6\) nam sinh và \(4\)nữ sinh vào một dãy ghế hàng ngang có \(10\) chỗ ngồi sao cho các nữ sinh luôn ngồi cạnh nhau.
A. \(10!\).
B. \(7! \times 4!.\)
C. \(6! \times 4!.\)
D. \(6! \times 5!.\)
Câu 30: Viết khai triển theo công thức nhị thức Niu-tơn \({\left( {x - y} \right)^5}\).
A. \({x^5} - 5{x^4}y + 10{x^3}{y^2} - 10{x^2}{y^3} + 5x{y^4} - {y^5}\).
B. \({x^5} - 5{x^4}y - 10{x^3}{y^2} - 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
C. \({x^5} + 5{x^4}y + 10{x^3}{y^2} + 10{x^2}{y^3} + 5x{y^4} + {y^5}\).
D. \({x^5} + 5{x^4}y - 10{x^3}{y^2} + 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
Câu 31: Xét phép thử gieo một con súc sắc cân đối và đồng chất 6 mặt hai lần. Xét biến cố A: “Số chấm xuất hiện ở cả hai lần gieo giống nhau”. Khẳng định nào sau đây đúng?
A. \(n\left( A \right) = 6\).
B. \(n\left( A \right) = 12\).
C. \(n\left( A \right) = 16\).
D. \(n\left( A \right) = 36\).
Câu 32: Rút ngẫu nhiên cùng lúc ba con bài từ cỗ bài tú lơ khơ \(52\) con thì \(n\left( \Omega \right)\) bằng bao nhiêu?
A. \(140608\). B. \(156\). C. \(132600\). D. \(22100\).
Câu 33: Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất \(5\) lần. Tính số phần tử không gian mẫu.
A. \(64\).
B. \(10\).
C. \(32\).
D. \(16\).
Câu 34: Từ một hộp chứa \(11\) quả cầu màu đỏ và \(4\) quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được \(3\) quả cầu màu xanh
A. \(\frac{{33}}{{91}}\)
B. \(\frac{{24}}{{455}}\)
C. \(\frac{4}{{165}}\)
D. \(\frac{4}{{455}}\)
Câu 35: Một tổ có \(6\) học sinh nam và \(4\) học sinh nữ. Chọn ngẫu nhiên \(4\) học sinh. Xác suất để trong \(4\) học sinh được chọn luôn có học sinh nữ là
A. \(\frac{1}{{14}}\).
B. \(\frac{1}{{210}}\).
C. \(\frac{{13}}{{14}}\).
D. \(\frac{{209}}{{210}}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 1. Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Câu 2. Cho điểm \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\) và \(\overrightarrow n \left( {1;2} \right)\). Viết phương trình tham số của đường thẳng D đi qua \(A\) và nhận vectơ \(\overrightarrow n \left( {1;2} \right)\) làm vectơ pháp tuyến.
Câu 3. Gọi n là số nguyên dương thỏa mãn \(A_n^3 + 2A_n^2 = 48\)Tìm hệ số của \({x^3}\) trong khai triển nhị thức Niu-tơn của \({(1 - 3x)^n}\)
Câu 4. Viết phương trình đường tròn (C) đi qua \(A\left( {2; - 1} \right)\) và tiếp xúc với hai trục toạ độ \(Ox\) và \(Oy\)
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
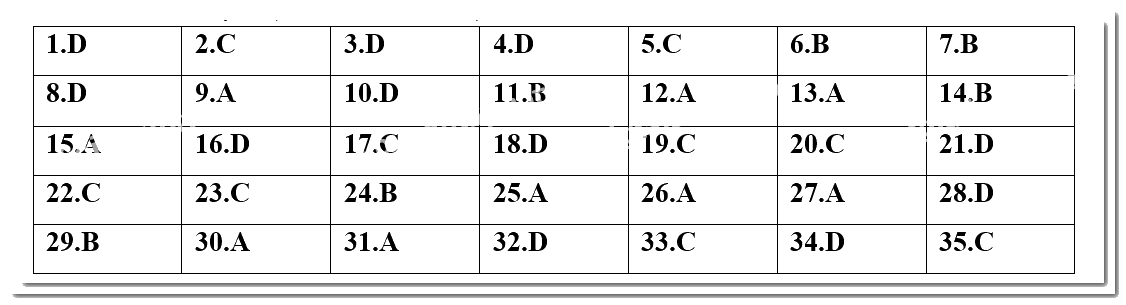
Câu 1: Tập xác định của hàm số \(f(x) = \frac{{x + 5}}{{x - 1}} + \frac{{x - 1}}{{x + 5}}\) là
A. \(D = \mathbb{R}\).
B. \(D = \mathbb{R}\backslash \{ 1\} .\)
C. \(D = \mathbb{R}\backslash \{ - 5\} .\)
D. \(D = \mathbb{R}\backslash \{ - 5;{\rm{ }}1\} .\)
Phương pháp
- Phân thức xác định khi mẫu thức khác 0
Lời giải
Điều kiện: \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 5 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 5\end{array} \right.\).
Vậy tập xác định của hàm số là: \(D = \mathbb{R}\backslash \left\{ {1; - 5} \right\}\).
Chọn D
Câu 2: Cho hàm số có đồ thị như hình vẽ.
Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
Phương pháp
- Hàm số có chiều đi lên từ trái sang phải là đồng biến.
- Hàm số có chiều đi xuống từ trái sang phải là nghịch biến.
Lời giải
Từ đồ thị hàm số ta thấy:
Hàm số nghịch biến trong các khoảng: \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
Hàm số đồng biến trong các khoảng: \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Chọn C
Câu 3: Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là
A. \(\left( { - \infty ; - 2} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Phương pháp
Sử dụng công thức dấu của tam thức bậc hai.
Lờigiải
Hàm số \(y = {x^2} - 4x + 3\)có \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\).
Vì vậy hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
ChọnD
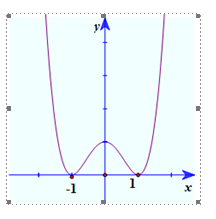
Câu 4: Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây?
A. \(y = {x^2} + 2x - 1\).
B. \(y = {x^2} + 2x - 2\).
C. \(y = 2{x^2} - 4x - 2\).
D. \(y = {x^2} - 2x - 1\).
Phương pháp
Hình dáng của đồ thị bậc hai Parabol.
Lời giải
Đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\) nên loại B và C
Hoành độ của đỉnh là \({x_I} = - \frac{b}{{2a}} = 1\) nên ta loại A và chọn D.
Chọn D
Câu 5: Cho tam thức bậc hai \(f\left( x \right) = - {x^2} - 4x + 5\). Tìm tất cả giá trị của \(x\) để \(f\left( x \right) \ge 0\).
A. \(x \in \left( { - \infty ;\, - 1} \right] \cup \left[ {5;\, + \infty } \right)\).
B. \(x \in \left[ { - 1;\,5} \right]\).
C. \(x \in \left[ { - 5;\,1} \right]\).
D. \(x \in \left( { - 5;\,1} \right)\).
Phương pháp
Sử dụng quy tắc dấu của tam thức bậc hai
Lờigiải
Ta có \(f\left( x \right) = 0\) \( \Leftrightarrow \) \( - {x^2} - 4x + 5 = 0\) \( \Leftrightarrow \) \(x = 1\), \(x = - 5\).
Mà hệ số \(a = - 1 < 0\) nên: \(f\left( x \right) \ge 0\) \( \Leftrightarrow \) \(x \in \left[ { - 5;\,1} \right]\).
ChọnC.
Câu 6: Tìm \(m\) để phương trình \( - {x^2} + 2\left( {m - 1} \right)x + m - 3 = 0\) có hai nghiệm phân biệt
A. \(\left( { - 1;2} \right)\)
B. \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)
C. \(\left[ { - 1;2} \right]\)
D. \(\left( { - \infty ; - 1} \right] \cup \left[ {2; + \infty } \right)\)
Phương pháp
Phương trình bậc hai có hai nghiệm phân biệt khi \(\Delta ' > 0\)
Lờigiải
Phương trình có hai nghiệm phân biệt
\( \Leftrightarrow \Delta ' > 0 \Leftrightarrow {\left( {m - 1} \right)^2} - \left( { - 1} \right).\left( {m - 3} \right) > 0 \Leftrightarrow {m^2} - m - 2 > 0 \Leftrightarrow \left[ \begin{array}{l}m < - 1\\m > 2\end{array} \right.\)
Vậy \(m \in \left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\).
ChọnB
Câu 7: Tập nghiệm của phương trình \(\sqrt {2{x^2} - 4x - 2} = \sqrt {{x^2} - x - 2} \) là:
A. \(S = \left\{ {0;3} \right\}.\)
B. \(S = \left\{ 3 \right\}.\)
C. \(S = \left\{ 0 \right\}.\)
D. \(S = \left\{ {2;3} \right\}.\)
Phương pháp
Thử các giá trị của x trong đáp án vào phương trình.
Lời giải
Thay các giá trị vào phương trình có \(x = 3\) vào thỏa mãn phương trình.
ChọnB
Câu 8: Phương trình \(\sqrt { - {x^2} + 4x} = 2x - 2\) có bao nhiêu nghiệm?
A. \(3\). B. \(0\). C. \(2\). D. \(1\).
Phương pháp
Bình phương hai vế của phương trình rồi giải.
Lời giải
\(\sqrt { - {x^2} + 4x} = 2x - 2\)\( \Leftrightarrow \left\{ \begin{array}{l}2x - 2 \ge 0\\ - {x^2} + 4x = {\left( {2x - 2} \right)^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\5{x^2} - 12x + 4 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}x = 2\left( n \right)\\x = \frac{2}{5}\left( l \right)\end{array} \right.\end{array} \right.\).
Vậy \(x = 2\) là nghiệm của phương trình.
ChọnD
Câu 9: Vectơ chỉ phương của đường thẳng \(d\): \(\left\{ \begin{array}{l}x = 1 - 4t\\y = - 2 + 3t\end{array} \right.\) là:
A. \(\overrightarrow u = \left( { - 4;3} \right)\).
B. \(\overrightarrow u = \left( {4;3} \right)\).
C. \(\overrightarrow u = \left( {3;4} \right)\).
D. \(\overrightarrow u = \left( {1; - 2} \right)\).
Phương pháp
Vecto chỉ phương của đường thẳng \(d:\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) là \(\overrightarrow u = \left( {a;b} \right)\)
Lời giải
Đường thẳng \(d\): \(\left\{ \begin{array}{l}x = 1 - 4t\\y = - 2 + 3t\end{array} \right.\)có vectơ chỉ phương là \(\overrightarrow u = \left( { - 4;3} \right)\).
Chọn A.
Câu 10: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\).
Phương pháp
Phương trình tham số của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {a;b} \right)\) làm vecto chỉ phương là : \(d:\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)
Lời giải
Vectơ chỉ phương \(\overrightarrow {AB} = \left( {0;6} \right)\).
Phương trình tham số của đường thẳng đi qua điểm \(A\left( {2; - 1} \right)\) và nhận \(\overrightarrow {AB} = \left( {0;6} \right)\) làm vecto chỉ phương là : \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\)
ChọnD
Câu 11: Trong mặt phẳng \(Oxy\), cho đường thẳng \(d:2x - y + 1 = 0\), một véctơ pháp tuyến của \(d\) là
A. \(\left( { - 2; - 1} \right)\).
B. \(\left( {2; - 1} \right)\).
C. \(\left( { - 1; - 2} \right)\).
D. \(\left( {1; - 2} \right)\).
Phương pháp
Vecto pháp tuyến của đường thẳng\(d:ax + by + c = 0\) là \(\overrightarrow n = \left( {a;b} \right)\)
Lời giải
ChọnB
Một véctơ pháp tuyến của đường thẳng \(d\) là \(\overrightarrow n = \left( {2; - 1} \right)\).
Câu 12: Tọa độ giao điểm của hai đường thẳng \(x - 3y - 6 = 0\) và \(3x + 4y - 1 = 0\) là
A. \(\left( {\frac{{27}}{{13}}; - \frac{{17}}{{13}}} \right)\).
B. \(\left( { - 27;17} \right)\).
C. \(\left( { - \frac{{27}}{{13}};\frac{{17}}{{13}}} \right)\).
D. \(\left( {27; - 17} \right)\).
Phương pháp
Tọa độ giao điểm của hai đường thẳng là nghiệm của cả hai phương trình đường thẳng đó
Lời giải
Ta có tọa độ giao điểm của hai đường thẳng \(x - 3y - 6 = 0\) và \(3x + 4y - 1 = 0\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - 3y - 6 = 0\\3x + 4y - 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{27}}{{13}}\\y = - \frac{{17}}{3}\end{array} \right.\).
Chọn A
Câu 13: Cho đường thẳng \({d_1}:2x + 3y + 15 = 0\) và \({d_2}:x - 2y - 3 = 0\). Khẳng định nào sau đây đúng?
A. \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau.
B. \({d_1}\) và \({d_2}\) song song với nhau.
C. \({d_1}\) và \({d_2}\) trùng nhau.
D. \({d_1}\) và \({d_2}\) vuông góc với nhau.
Phương pháp
Sử dụng công thức vị trí tương đối của hai đường thẳng.
Lời giải
Đường thẳng\({d_1}:2x + 3y + 15 = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {2;3} \right)\) và đường thẳng \({d_2}:x - 2y - 3 = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1; - 2} \right)\).
Ta thấy \(\frac{2}{1} \ne \frac{3}{{ - 2}}\) và \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 2.1 + 3.( - 2) = - 4 \ne 0\).
Vậy \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau.
Chọn A
Câu 14: Cho đường thẳng \(d:\, - 3x + y - 5 = 0\) và điểm \(M\left( { - 2;1} \right)\). Tọa độ hình chiếu vuông góc của \(M\)trên \(d\) là
A. \(\left( {\frac{7}{5}; - \frac{4}{5}} \right)\).
B. \(\left( { - \frac{7}{5};\frac{4}{5}} \right)\).
C. \(\left( { - \frac{7}{5}; - \frac{4}{5}} \right)\).
D. \(\left( { - \frac{5}{7};\frac{4}{5}} \right)\).
Phương pháp
Viết phương trình đường thẳng đi qua M và vuông góc với đường thẳng d.
Lời giải
Gọi \(\Delta \) là đường thẳng đi qua \(M\)và vuông góc với \(d\).
Ta có phương trình của \(\Delta \) là: \(x + 3y - 1 = 0\)
Tọa độ hình chiếu vuông góc của \(M\) trên \(d\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l} - 3x + y - 5 = 0\\x + 3y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{7}{5}\\y = \frac{4}{5}\end{array} \right.\).
ChọnB
Câu 15: Xác định tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9.\)
A. Tâm \(I\left( { - 1;2} \right),\) bán kính \(R = 3\).
B. Tâm \(I\left( { - 1;2} \right),\) bán kính \(R = 9\).
C. Tâm \(I\left( {1; - 2} \right),\) bán kính \(R = 3\).
D. Tâm \(I\left( {1; - 2} \right),\) bán kính \(R = 9\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lờigiải
Tâm và bán kính của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9.\) là \(I\left( { - 1;2} \right),\) bán kính \(R = 3\).
ChọnA
Câu 16: Đường tròn \(\left( C \right):{x^2} + {y^2} - 2x + 4y - 3 = 0\) có tâm \(I\), bán kính \(R\) là
A. \(I\left( { - 1;\,2} \right),\,R = \sqrt 2 \).
B. \(I\left( { - 1;\,2} \right),\,R = 2\sqrt 2 \).
C. \(I\left( {1;\, - 2} \right),\,R = \sqrt 2 \).
D. \(I\left( {1;\, - 2} \right),\,R = 2\sqrt 2 \).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lờigiải
Tâm \(I\left( {1;\, - 2} \right)\), bán kính \(\,R = \sqrt {{1^2} + {{\left( { - 2} \right)}^2} - \left( { - 3} \right)} = \sqrt 8 = 2\sqrt 2 \).
ChọnD
Câu 17: Đường tròn tâm \(I\left( {3; - 1} \right)\) và bán kính \(R = 2\) có phương trình là
A. \({\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\)
B. \({\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\)
C. \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
D. \({\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Phương trình đường tròn có tâm \(I\left( {3; - 1} \right)\), bán kính \(R = 2\) là: \({\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
Chọn C
Câu 18: Phương trình tiếp tuyến của đường tròn\(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y + 2} \right)^2} = 25\) tại điểm \(M\left( {2;1} \right)\) là:
A. \(d:\, - y + 1 = 0\)
B. \(d:\,4x + 3y + 14 = 0\)
C. \(d:\,3x - 4y - 2 = 0\)
D. \(d:\,4x + 3y - 11 = 0\)
Phương pháp
Phương trình đường thẳng nhậnvecto pháp tuyến \(\overrightarrow n = \left( {a;b} \right)\) và đi qua điểm \(A({x_0},{y_0})\) là \(d:a(x - {x_0}) + b(y - {y_0}) = 0\)
Lời giải
Đường tròn (C) có tâm \(I( - 2;2)\)nên tiếp tuyến tại M có VTPT là nên có phương trình là: \(4(x - 2) + 3(y - 1) = 0 \Leftrightarrow 4x + 3y - 11 = 0\)
Chọn D
Câu 19: Elip \(\left( E \right):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)có độ dài trục bé bằng:
A. 8 B. 10 C. 16 D. 20
Phương pháp
Độ dài trục lớp của Elip\(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) là \({B_1}{B_2} = 2b\)
Lời giải
Gọi phương trình của Elip là \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có độ dài trục bé \({B_1}{B_2} = 2b\)
Xét \(\left( E \right):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1 \Leftrightarrow \left\{ \begin{array}{l}{a^2} = 100\\{b^2} = 64\end{array} \right. \Rightarrow b = 8 \Rightarrow {B_1}{B_2} = 2.8 = 16\)
Chọn C
Câu 20: Elip có hai đỉnh là \(\left( { - 3;0} \right),\left( {3;0} \right)\) và có hai tiêu điểm là \(\left( { - 1;0} \right),\left( {1;0} \right).\) Phương trình chính tắc của elip là:
A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\)
B. \(\frac{{{x^2}}}{8} + \frac{{{y^2}}}{9} = 1\)
C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\)
D. \(\frac{{{x^2}}}{1} + \frac{{{y^2}}}{9} = 1\)
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải
Elip có hai đỉnh là \(\left( { - 3;0} \right),\left( {3;0} \right)\) suy ra a = 3
Elip có hai tiêu điểm là \(\left( { - 1;0} \right),\left( {1;0} \right).\)suy ra c = 1
Khi đó, .
Phương trình chính tắc của Elip là (E) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\).
Chọn C
Câu 21: Trong một trường THPT, khối có học sinh nam và học sinh nữ. Nhà trường cần chọn một học sinh ở khối đi dự dạ hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 45 B. 28 C. 325 D. 605
Phương pháp
Áp dụng quy tắc cộng
Lờigiải.
Nếu chọn một học sinh nam có cách.
Nếu chọn một học sinh nữ có cách.
Theo qui tắc cộng, ta có cách chọn.
Chọn D
Câu 22: Từ các số lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số lẻ
A. 360 B. 343 C. 480 D. 347
Phương pháp
Áp dụng quy tắc nhân
Lờigiải
Gọi số cần lập ; và đôi một khác nhau.
Vì số cần lập là số lẻ nên phải là số lẻ. Ta lập qua các công đoạn sau.
Bước 1: Có 4 cách chọn d
Bước 2: Có 6 cách chọn a
Bước 3: Có 5 cách chọn b
Bước 4: Có 4 cách chọn c
Vậy có 480 số thỏa yêu cầu bài toán.
Chọn C
Câu 23: Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. 4. B. 7. C. 12. D. 16.
Phương pháp
Áp dụng quy tắc nhân
Lờigiải.
Để chọn một chiếc đồng hồ, ta có:
Có 3 cách chọn mặt.
Có 4 cách chọn dây.
Vậy theo qui tắc nhân ta có cách.
Chọn C
Câu 24: Có bao nhiêu cách sắp xếp nữ sinh, nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ:
A. 6. B. 72. C. 720. D. 144.
Phương pháp
Áp dụng quy tắc nhân
Lờigiải
Chọn vị trí 3 nam và 3 nữ: cách chọn.
Xếp 3 nam có: cách xếp.
Xếp 3 nữ có: cách xếp.
Vậy có cách xếp.
Chọn B
Câu 25: Từ các chữ số \(1\), \(2\), \(3\), \(4\), \(5\) có thể lập được bao nhiêu số tự nhiên gồm \(5\) chữ số đôi một khác nhau:
A. \(120\). B. \(720\). C. \(16\). D. \(24\).
Phương pháp
Áp dụng công thức hoán vị
Lờigiải
Mỗi số tự nhiên gồm \(5\) chữ số khác nhau được lập từ các số \(1\), \(2\), \(3\), \(4\), \(5\) là một hoán vị của \(5\) phần tử đó. Nên số các số thỏa mãn yêu cầu bài toán là \({P_5} = 5!\) \( = 120\) (số).
Chọn A
Câu 26: Một câu lạc bộ có \(25\) thành viên. Số cách chọn một ban quản lí gồm \(1\) chủ tịch, \(1\) phó chủ tịch và \(1\) thư kí là:
A. \(13800\). B. \(5600\). C. 6500. D. \(6900\).
Phương pháp
Áp dụng công thức chỉnh hợp
Lờigiải
Mỗi cách chọn \(3\) người ở \(3\) vị trí là một chỉnh hợp chập \(3\) của \(25\) thành viên.
Số cách chọn là: \(A_{25}^3 = 13800\).
Chọn A
Câu 27: Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là
A. \(C_7^3\).
B. \(\frac{{7!}}{{3!}}\).
C. \(A_7^3\).
D. \(21\).
Phương pháp
Áp dụng công thức tổ hợp
Lờigiải
Số tập hợp con cần tìm là số tổ hợp chập 3 của 7 phần tử.
Vậy có \(C_7^3\) tập con cần tìm.
ChọnA
Câu 28: Trong một buổi khiêu vũ có \(20\) nam và \(18\) nữ. Hỏi có bao nhiêu cách chọn ra một đôi nam nữ để khiêu vũ?
A. \(C_{38}^2\).
B. \(A_{38}^2\).
C. \(C_{20}^2C_{18}^1\).
D. \(C_{20}^1C_{18}^1\).
Phương pháp
Áp dụng công thức tổ hợp
Lờigiải
Chọn một nam trong \(20\) nam có \(C_{20}^1\) cách.
Chọn một nữ trong \(18\) nữ có \(C_{18}^1\) cách.
Theo quy tắc nhân, số cách chọn một đôi nam nữ là \(C_{20}^1C_{18}^1\).
ChọnD
Câu 29: Tính số cách sắp xếp \(6\) nam sinh và \(4\)nữ sinh vào một dãy ghế hàng ngang có \(10\) chỗ ngồi sao cho các nữ sinh luôn ngồi cạnh nhau.
A. \(10!\).
B. \(7! \times 4!.\)
C. \(6! \times 4!.\)
D. \(6! \times 5!.\)
Phương pháp
Áp dụng công thức hoán vị
Lờigiải:
Sắp xếp \(4\) nữ sinh vào \(4\) ghế: \(4!\) cách.
Xem \(4\) nữ sinh lập thành nhóm X, sắp xếp nhóm X cùng với \(6\) nam sinh: có \(7!\) cách
vậy có \(7! \times 4!\) cách sắp xếp.
ChọnB
Câu 30: Viết khai triển theo công thức nhị thức Niu-tơn \({\left( {x - y} \right)^5}\).
A. \({x^5} - 5{x^4}y + 10{x^3}{y^2} - 10{x^2}{y^3} + 5x{y^4} - {y^5}\).
B. \({x^5} - 5{x^4}y - 10{x^3}{y^2} - 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
C. \({x^5} + 5{x^4}y + 10{x^3}{y^2} + 10{x^2}{y^3} + 5x{y^4} + {y^5}\).
D. \({x^5} + 5{x^4}y - 10{x^3}{y^2} + 10{x^2}{y^3} - 5x{y^4} + {y^5}\).
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Lờigiải
Ta có:
\({\left( {x - y} \right)^5} = {\left[ {x + \left( { - y} \right)} \right]^5} = C_5^0{x^5} + C_5^1{x^4}{\left( { - y} \right)^1} + C_5^2{x^3}{\left( { - y} \right)^2} + C_5^3{x^2}{\left( { - y} \right)^3} + C_5^4{x^1}{\left( { - y} \right)^4} + C_5^5{\left( { - y} \right)^5}\)
Hay \({\left( {x - y} \right)^5} = {x^5} - 5{x^4}y + 10{x^3}{y^2} - 10{x^2}{y^3} + 5x{y^4} - {y^5}\).
ChọnA
Câu 31: Xét phép thử gieo một con súc sắc cân đối và đồng chất 6 mặt hai lần. Xét biến cố A: “Số chấm xuất hiện ở cả hai lần gieo giống nhau”. Khẳng định nào sau đây đúng?
A. \(n\left( A \right) = 6\).
B. \(n\left( A \right) = 12\).
C. \(n\left( A \right) = 16\).
D. \(n\left( A \right) = 36\).
Phương pháp
Công thức tính xác suất
Lờigiải
Gọi cặp số \(\left( {x;y} \right)\) là số chấm xuất hiện ở hai lần gieo.
Xét biến cố A: “Số chấm xuất hiện ở cả hai lần gieo giống nhau”.
Các kết quả của biến cố A là: \(\left\{ {\left( {1;1} \right);\left( {2;2} \right);\left( {3;3} \right);\left( {4;4} \right);\left( {5;5} \right);\left( {6;6} \right)} \right\}\).
Suy ra \(n\left( A \right) = 6\).
ChọnA
Câu 32: Rút ngẫu nhiên cùng lúc ba con bài từ cỗ bài tú lơ khơ \(52\) con thì \(n\left( \Omega \right)\) bằng bao nhiêu?
A. \(140608\). B. \(156\). C. \(132600\). D. \(22100\).
Phương pháp
Áp dụng công thức tổ hợp
Lờigiải
Ta có \(n\left( \Omega \right) = C_{52}^3 = 22100\).
ChọnD
Câu 33: Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất \(5\) lần. Tính số phần tử không gian mẫu.
A. \(64\). B. \(10\). C. \(32\). D. \(16\).
Phương pháp
Áp dụng quy tắc đếm
Lờigiải
Mỗi lần gieo có hai khả năng nên gieo 5 lần theo quy tắc nhân ta có \({2^5} = 32\).
Số phần tử không gian mẫu là \(n\left( \Omega \right) = 32\).
ChọnC
Câu 34: Từ một hộp chứa \(11\) quả cầu màu đỏ và \(4\) quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được \(3\) quả cầu màu xanh
A. \(\frac{{33}}{{91}}\)
B. \(\frac{{24}}{{455}}\)
C. \(\frac{4}{{165}}\)
D. \(\frac{4}{{455}}\)
Phương pháp
Công thức tính xác suất
Lờigiải
Số phần tử của không gian mẫu \(n\left( \Omega \right) = C_{15}^3\)\( = 455\).
Gọi \(A\) là biến cố "\(3\) quả cầu lấy được đều là màu xanh". Suy ra \(n\left( A \right) = C_4^3\)\( = 4\).
Vậy xác suất cần tìm là \(P\left( A \right) = \frac{4}{{455}}\).
ChọnD
Câu 35: Một tổ có \(6\) học sinh nam và \(4\) học sinh nữ. Chọn ngẫu nhiên \(4\) học sinh. Xác suất để trong \(4\) học sinh được chọn luôn có học sinh nữ là
A. \(\frac{1}{{14}}\).
B. \(\frac{1}{{210}}\).
C. \(\frac{{13}}{{14}}\).
D. \(\frac{{209}}{{210}}\).
Phương pháp
Công thức tính xác suất
Lờigiải
\(n\left( \Omega \right) = C_{10}^4 = 210\).
Gọi \(A\) là biến cố:” trong \(4\) học sinh được chọn luôn có học sinh nữ” \( \Rightarrow n\left( A \right) = C_{10}^4 - C_6^4 = 195\)
Vậy xác suất của biến cố \(A\) là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)\( = \frac{{195}}{{210}}\)\( = \frac{{13}}{{14}}\).
ChọnC
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 1. Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Bình phương hai vế của phương trình ta được
\(2{x^2} - 5x - 9 = {x^2} - 2x + 1.\)
Sau khi thu gọn ta được \({x^2} - 3x - 10 = 0\). Tử đó \(x = - 2\) hoặc \(x = 5\).
Thay lần lượt hai giá trị này của \(x\) vào phương trình đã cho, ta thấy chỉ có \(x = 5\) thoả mãn.
Vậy nghiệm của phương trình đã cho là \(x = 5\).
Câu 2. Cho điểm \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\) và \(\overrightarrow n \left( {1;2} \right)\). Viết phương trình tham số của đường thẳng D đi qua \(A\) và nhận vectơ \(\overrightarrow n \left( {1;2} \right)\) làm vectơ pháp tuyến.
Phương pháp
Phương trình tham số của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {a;b} \right)\) làm vecto chỉ phương là : \(\Delta :\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)
Lời giải
Vì \(\Delta \) nhận vectơ \(\overrightarrow n \left( {1;2} \right)\) làm vectơ pháp tuyến nên VTCP của \(\Delta \) là \(\overrightarrow u \left( { - 2;1} \right)\).
Vậy phương trình tham số của đường thẳng \(\Delta \) là \(\Delta :\left\{ \begin{array}{l}x = 1 - 2t\\y = - 3 + t\end{array} \right.\)
Câu 3. Gọi n là số nguyên dương thỏa mãn \(A_n^3 + 2A_n^2 = 48\)Tìm hệ số của \({x^3}\) trong khai triển nhị thức Niu-tơn của \({(1 - 3x)^n}\)
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Lời giải
ĐK: \(n \ge 3,n \in N\).
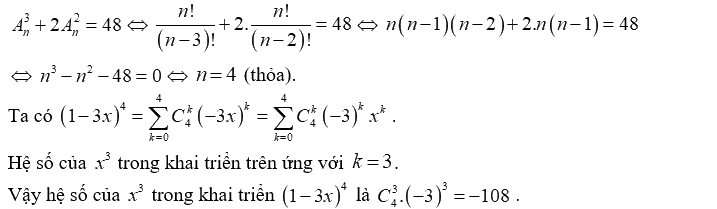
Câu 4. Viết phương trình đường tròn (C) đi qua \(A\left( {2; - 1} \right)\) và tiếp xúc với hai trục toạ độ \(Ox\) và \(Oy\)
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải:
Vì điểm A nằm ở góc phần tư thứ tư và đường tròn tiếp xúc với hai trục toạ độ nên tâm của đường tròn có dạng \(I\left( {R; - R} \right)\) trong đó R là bán kính đường tròn (C).
Ta có:\({R^2} = I{A^2} \Leftrightarrow {R^2} = {\left( {2 - R} \right)^2} + {\left( { - 1 + R} \right)^2} \Leftrightarrow {R^2} - 6R + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{R = 1}\\{R = 5}\end{array}} \right.\)
Vậy có hai đường tròn thoả mãn đầu bài là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 1\) và \({\left( {x - 5} \right)^2} + {\left( {y + 5} \right)^2} = 25\)
---------- HẾT ----------
Đề kiểm tra học kì 2 Toán 10 - Đề số 5 chương trình Kết nối tri thức là một công cụ quan trọng giúp học sinh đánh giá năng lực và kiến thức đã học trong suốt học kỳ. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như hàm số, bất phương trình, hệ phương trình, và các kiến thức hình học cơ bản.
Đề thi thường được chia thành các phần:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Bài 1: Giải phương trình bậc hai 2x2 - 5x + 3 = 0
Lời giải:
Phương trình có dạng ax2 + bx + c = 0 với a = 2, b = -5, c = 3.
Tính delta: Δ = b2 - 4ac = (-5)2 - 4 * 2 * 3 = 25 - 24 = 1
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + 1) / (2 * 2) = 3/2
x2 = (-b - √Δ) / 2a = (5 - 1) / (2 * 2) = 1
Vậy phương trình có hai nghiệm x1 = 3/2 và x2 = 1.
Để chuẩn bị tốt nhất cho kỳ thi, các em có thể tham khảo các tài liệu sau:
Đề kiểm tra học kì 2 Toán 10 - Đề số 5 - Kết nối tri thức là một cơ hội tốt để các em học sinh rèn luyện kỹ năng và kiến thức. Hãy ôn tập kỹ lưỡng và tự tin làm bài để đạt kết quả tốt nhất!