Chào mừng các em học sinh lớp 10 đến với đề thi giữa kì 1 môn Toán chương trình Kết nối tri thức - Đề số 2. Đề thi này được thiết kế để giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự đánh giá năng lực của bản thân.
Giaitoan.edu.vn cung cấp đề thi có đáp án chi tiết, giúp các em hiểu rõ phương pháp giải và tránh những sai lầm không đáng có.
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “(sqrt 2 ) không là số hữu tỉ” A. (sqrt 2 = mathbb{Q}) B. (sqrt 2 in mathbb{Q}) C. (sqrt 2 subset mathbb{Q}) D. (sqrt 2 notin mathbb{Q})
I. PHẦN TRẮC NGHIỆM
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “\(\sqrt 2 \) không là số hữu tỉ”
A. \(\sqrt 2 = \mathbb{Q}\) B. \(\sqrt 2 \in \mathbb{Q}\) C. \(\sqrt 2 \subset \mathbb{Q}\) D. \(\sqrt 2 \notin \mathbb{Q}\)
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > - 2\). B. \(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > 2\).
C. \(\forall x \in \mathbb{R},x > - 2 \Rightarrow {x^2} > 4\). D. \(\forall x \in \mathbb{R},x > 2 \Rightarrow {x^2} > 4\)
Câu 3. Cho A là tập hợp các số tự nhiên chẵn, \(B = \{ n \in \mathbb{N}|n \le 8\} \) và \(C = \{ n \in \mathbb{N}|2 \le n \le 5\} \).
Tìm tập hợp \(A \cap \left( {B \cap C} \right)\)
A. \(\{ 2;4\} \) B. \(\{ 2\} \). C. \(\{ 4\} \). D. \(\emptyset \).
Câu 4. Cho \(A = ( - 2;5]\) và \(B = (m; + \infty )\). Tìm \(m \in \mathbb{Z}\) để \(A{\rm{\backslash }}B\) chứa đúng 3 số nguyên là:
A. \(0\). B. \(1\). C. \(2\) D. \(3\)
Câu 5. Để chuẩn bị cho các tiết mục văn nghệ, lớp 10B cử ra 12 bạn tham gia tiết mục múa và 7 bạn vào tiết mục hát. Biết rằng có 3 bạn tham gia cả hai tiết mục và 22 bạn không tham gia văn nghệ. Số học sinh lớp 10B là:
A. \(36\). B. \(38\). C. \(40\). D. \(45\).
Câu 6. Miền nghiệm của bất phương trình \(x - 2y \ge 4\) là:
A.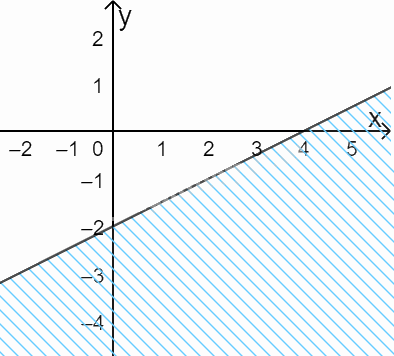 B.
B.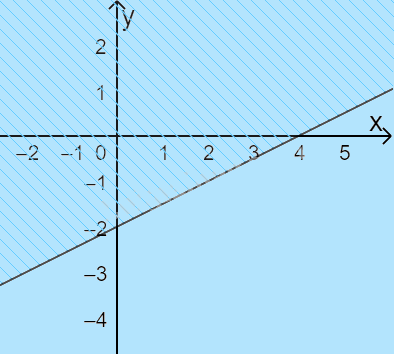
C. 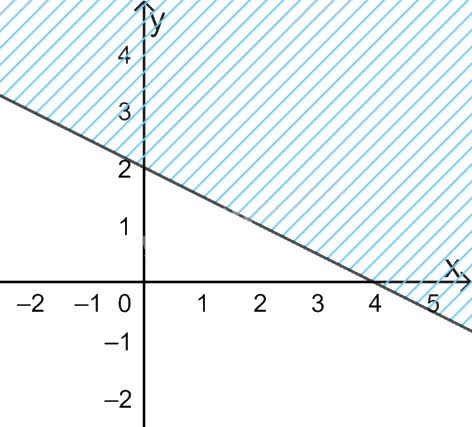 D.
D. 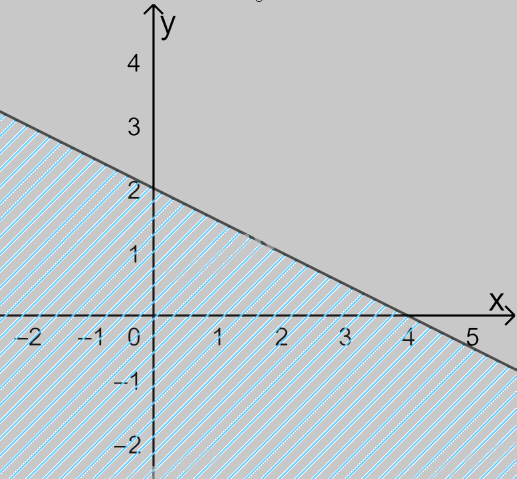
Câu 7. Giá trị lớn nhất của \(F(x;y) = x - 3y\), với điều kiện \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\)
A.\(2\) B. \( - 6\) C.\( - \frac{{34}}{3}\) D. \( - 15\)
Câu 8. Cho góc \(x\;({0^ \circ } < x < {180^ \circ })\) thỏa mãn \(\tan x = 3\). Tính biểu thức \(P = \frac{{10\sin x + 13\cos x}}{{7\sin x - 8\cos x}}\)
A. \(\frac{{10}}{7}\). B. \(\frac{{19}}{4}\). C. \(\frac{{ - 49}}{7}\). D. \(\frac{{43}}{{13}}\).
Câu 9. Rút gọn biểu thức \(A = \frac{{1 - \cos \alpha + \cos 2\alpha }}{{\sin 2\alpha - \sin \alpha }}\)
A.\(\sin \alpha \) B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \).
Câu 10. Cho tam giác ABC có góc A nhọn thỏa mãn \(\sin A\sin B = \cos C\) thì:
A. \(A{C^2} = A{B^2} + B{C^2}\) B. \(AB > AC\) C. Tam giác ABC cân tại B D. \(\cos C < 0\)
Câu 11. Cho tam giác ABC có \(a = 4,b = 5,c = 7\). Bán kính đường tròn nội tiếp r của tam giác ABC bằng:
A. \(12\) B. \(6\) C. \(\frac{{\sqrt 6 }}{2}\). D. \(\sqrt 6 \).
Câu 12. Cho tam giác \(ABC\) có \(c = 32,\widehat A = {70^o},b = 45\). Độ dài cạnh BC là:
A. \(40\) B. \(41\) C. \(42\) D. \(43\)
Câu 13. Điểm \(A(1;2)\) thuộc miền nghiệm của hệ bất phương trình nào dưới đây?
A. \(\left\{ \begin{array}{l}x + 2y > 7\\3x - y < 5\end{array} \right.\) B. \(\left\{ \begin{array}{l}2x - y > 7\\x + y \le 3\end{array} \right.\) C. \(\left\{ \begin{array}{l}3x + 4 \le 10\\4x - y > 3\end{array} \right.\) D. \(\left\{ \begin{array}{l}2x + 5y > 8\\x - 3y \le 4\end{array} \right.\)
Câu 14. Cho \({0^ \circ } < a,b < {90^ \circ }\) thỏa mãn: \(\sin {108^ \circ } = \sin ({10^ \circ } + a) = \cos (b - {10^ \circ })\). Tổng \(a + b\) là:
A. \(70\) B. \(90\) C. \(130\). D. \(170\).
Câu 15. Cho bất phương trình \(2(2x - 3y) - (2x - y + 5) > x - 3y + 1\). Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho?
A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3; - 2)\). D. \(C(0;2)\)
II. PHẦN TỰ LUẬN
Câu 1. Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - \infty ;3) \cap ( - 4; + \infty )\) b) \((1;6] \cup ( - 2;5]\) c) \([ - 3;7){\rm{\backslash }}(1; + \infty )\) d) \(\mathbb{R}{\rm{\backslash }}( - 1;8]\)
Câu 2. Nhà cô Minh có mảnh vườn rộng \(8{m^2}\). Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi \({m^2}\). Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi \({m^2}\). Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180?
Câu 3. Chứng minh rằng trong mọi tam giác ABC ta có:
a) \({b^2} - {c^2} = a(b.\cos C - c.\cos B)\)
b) \(a = r\left( {\cot \frac{B}{2} + \cot \frac{C}{2}} \right)\)
Câu 4. Cho \(\sin (a + b) = 2\cos (a - b)\). Chứng minh biểu thức \(M = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}}\) không phụ thuộc vào a,b.
I. PHẦN TRẮC NGHIỆM
1. D | 2. D | 3. A | 4. B | 5. B |
6. B | 7. A | 8. D | 9. D | 10. A |
11. C | 12. D | 13. D | 14. B | 15. C |
Câu 1:
Cách giải:
Tập hợp các số hữu tỉ: \(\mathbb{Q}\)
“\(\sqrt 2 \) không là số hữu tỉ” viết là: \(\sqrt 2 \notin \mathbb{Q}\)
Chọn D.
Câu 2:
Cách giải:
Mệnh đề “\(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > - 2\)” sai, chẳng hạn \(x = - 3\) thì \({x^2} > 4\) nhưng \(x < - 2\)
Mệnh đề “\(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > 2\)” sai, chẳng hạn \(x = - 3\) thì \({x^2} > 4\) nhưng \(x < 2\)
Mệnh đề “\(\forall x \in \mathbb{R},x > - 2 \Rightarrow {x^2} > 4\)” sai, chẳng hạn \(x = 0 > - 2\) nhưng \({x^2} < 4\)
Mệnh đề “\(\forall x \in \mathbb{R},x > 2 \Rightarrow {x^2} > 4\)” đúng
Chọn D.
Câu 3:
Phương pháp:
Cho A là tập hợp các số tự nhiên chẵn, \(B = \{ n \in \mathbb{N}|n \le 8\} \) và \(C = \{ n \in \mathbb{N}|2 \le n \le 5\} \).
Tìm tập hợp \(A \cap \left( {B \cap C} \right)\)
Cách giải:
\(A = \{ 0;2;4;6;8;...\} \)
\(B = \{ 0;1;2;3;4;5;6;7;8\} \)
\(C = \{ 2;3;4;5\} \).
Ta có: \(B \cap C = \{ 2;3;4;5\} = C \Rightarrow A \cap \left( {B \cap C} \right) = A \cap C = \{ 2;4\} \)
Chọn A.
Câu 4:
Cách giải:
+ Nếu \(m \ge 5\) thì \(A{\rm{\backslash }}B = ( - 2;5]{\rm{\backslash }}(m; + \infty ) = A = ( - 2;5]\), chứa 7 số nguyên là -1 ; 0 ;1 ;2 ;3 ;4 ;5 (nhiều hơn 3) nên ta loại trường hợp m > 5.
+ Để \(A{\rm{\backslash }}B \ne \emptyset \) thì m>-2. Xét trường hợp -2<m<5, khi đó \(A{\rm{\backslash }}B = ( - 2;5]{\rm{\backslash }}(m; + \infty ) = ( - 2;m]\)
Chứa 3 số nguyên -1 ;0 ;1 thì m=1.
Chọn B.
Câu 5:
Phương pháp:
Thay cặp số vào BPT, cặp số nào cho ta mệnh đề đúng thì cặp số đó là nghiệm của BPT đã cho.
Để chuẩn bị cho các tiết mục văn nghệ, lớp 10B cử ra 12 bạn tham gia tiết mục múa và 7 bạn vào tiết mục hát. Biết rằng có 3 bạn tham gia cả hai tiết mục và 22 bạn không tham gia văn nghệ. Số học sinh lớp 10B là:
Gọi A là tập hợp các học sinh tham gia tiết mục múa.
B là là tập hợp các học sinh tham gia tiết mục hát.
Cách giải:
Gọi A là tập hợp các học sinh tham gia tiết mục múa.
B là là tập hợp các học sinh tham gia tiết mục hát.
Suy ra : \(A \cup B\) là tập hợp các học sinh tham gia văn nghệ.
\(A \cap B\) là tập hợp các học sinh tham gia cả hai tiết mục.
Ta có : \(n(A) = 12;n(B) = 7;n(A \cap B) = 3\)
\( \Rightarrow \) Số học sinh tham gia văn nghệ là : \(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 12 + 7 - 3 = 16\) (học sinh)
Số học sinh lớp 10B (gồm học sinh tham gia văn nghệ và các học sinh không tham gia văn nghệ) là : \(16 + 22 = 38\) (học sinh)
Chọn B.
Câu 6:
Phương pháp:
Xác định đường thẳng \(x - 2y = 4\) và xét một điểm (không thuộc đường thẳng) xem có thuộc miền nghiệm hay không.
Cách giải:
Đường thẳng \(x - 2y = 4\) đi qua điểm có tọa độ (4;0) và (0; -2) => Loại C, D.
Xét điểm O(0;0), ta có: \(0 - 2.0 = 0 < 4\) nên O không thuộc miền nghiệm.
Chọn B.
Câu 7:
Phương pháp:
Bước 1: Biểu diễn miền nghiệm, xác định các đỉnh của miền nghiệm
Bước 2: Thay tọa độ các đỉnh vào \(F(x;y) = x - 3y\), kết luận giá trị nhỏ nhất.
Cách giải:
Xét hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\)
Biểu diễn miền nghiệm của hệ, ta được
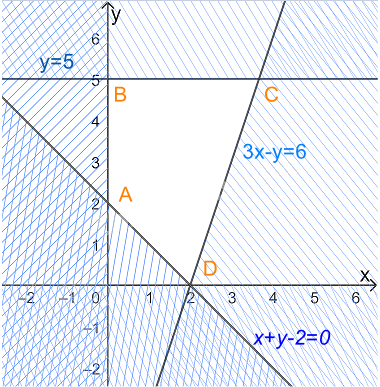
Miền nghiệm là miền tứ giác ABCD trong đó \(A\left( {0;2} \right),{\rm{ }}B\left( {0;5} \right),{\rm{ }}C\left( {\frac{{11}}{3};5} \right),D(2;0)\)
Thay tọa độ các điểm A, B, C, D vào \(F(x;y) = x - 3y\) ta được
\(F(0;2) = 0 - 3.2 = - 6\)
\(F(0;5) = 0 - 3.5 = - 15\)
\(F\left( {\frac{{11}}{3};5} \right) = \frac{{11}}{3} - 3.5 = - \frac{{34}}{3}\)
\(F(2;0) = 2 - 3.0 = 2\)
Vậy giá trị lớn nhất của F bằng 2.
Chọn A.
Câu 8:
Phương pháp:
Chia cả tử và mẫu của P cho cosx để làm xuất hiện tanx.
Cách giải:
Vì \(\tan x = 3\) nên \(\cos x \ne 0\)
Khi đó: \(P = \frac{{10\sin x + 13\cos x}}{{7\sin x - 8\cos x}} = \frac{{\frac{{10\sin x + 13\cos x}}{{\cos x}}}}{{\frac{{7\sin x - 8\cos x}}{{\cos x}}}} = \frac{{10\frac{{\sin x}}{{\cos x}} + 13}}{{7\frac{{\sin x}}{{\cos x}} - 8}}\)
\( = \frac{{10\tan x + 13}}{{7\tan x - 8}} = \frac{{10.3 + 13}}{{7.3 - 8}} = \frac{{43}}{{13}}\)
Chọn D.
Câu 9:
Phương pháp:
Áp dụng công thức: \(\cos 2\alpha = 2{\cos ^2}\alpha - 1;\sin 2\alpha = 2\sin \alpha \cos \alpha \)
Cách giải:
\(\begin{array}{l}A = \frac{{1 - \cos \alpha + \cos 2\alpha }}{{\sin 2\alpha - \sin \alpha }} = \frac{{1 - \cos \alpha + 2{{\cos }^2}\alpha - 1}}{{2\sin \alpha \cos \alpha - \sin \alpha }}\\ = \frac{{2{{\cos }^2}\alpha - \cos \alpha }}{{2\sin \alpha \cos \alpha - \sin \alpha }} = \frac{{\cos \alpha \left( {2\cos \alpha - 1} \right)}}{{\sin \alpha \left( {2\cos \alpha - 1} \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \cot \alpha \end{array}\)
Chọn D.
Câu 10:
Cách giải:
Ta có: \(\sin A\sin B = \cos C\)
Mà \(\cos C = - \cos ({180^ \circ } - C) = - \cos (A + B) = - \cos A\cos B + \sin A\sin B\)
\(\begin{array}{l} \Rightarrow \sin A\sin B = - \cos A\cos B + \sin A\sin B\\ \Leftrightarrow \cos A\cos B = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos A = 0\\\cos B = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\widehat A = {90^ \circ }\\\widehat B = {90^ \circ }\end{array} \right.\end{array}\)
Theo giải thiết, góc A nhọn nên \(\widehat B = {90^ \circ }\) hay tam giác ABC vuông tại B.
Khi đó: \(A{C^2} = A{B^2} + B{C^2}\), \(AC > AB\) (do AC là cạnh huyền), \(\cos C > 0\) (do \({0^ \circ } < \widehat C < {90^ \circ }\))
Chọn A.
Câu 11:
Phương pháp:
Bước 1: Tính diện tích \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Bước 2: Tính bán kính \(R\) dựa vào công thức \(S = \frac{{abc}}{{4R}}\)
Cách giải:
Ta có \(a = 4,b = 5,c = 7 \Rightarrow p = \frac{{4 + 5 + 7}}{2} = 8\)
Suy ra diện tích tam giác ABC là: \(S = \sqrt {8.(8 - 4)(8 - 5)(8 - 7)} = 4\sqrt 6 \)
Bán kính đường tròn nội tiếp r của tam giác ABC bằng:
\(r = \frac{S}{p} = \frac{{4\sqrt 6 }}{8} = \frac{{\sqrt 6 }}{2}\)
Chọn C.
Câu 12:
Phương pháp:
Áp dụng định lí cos: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Cách giải:
Ta có: \(c = 32,\widehat A = {70^o},b = 45\)
Áp dụng định lí cos trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
\(\begin{array}{l} \Leftrightarrow {a^2} = {45^2} + {23^2} - 2.45.23\cos {70^ \circ } \approx 1846\\ \Rightarrow a = \sqrt {1846} \approx 43\end{array}\)
Vậy độ dài cạnh AC là khoảng 43.
Chọn D.
Câu 13.
Phương pháp:
Thay tọa độ điểm A vào hệ BPT, hệ nào cho ta các mệnh đề đúng thì điểm A thuộc miền nghiệm của hệ BPT đó.
Cách giải
+ Xét hệ \(\left\{ \begin{array}{l}x + 2y > 7\\3x - y < 5\end{array} \right.\), thay \(x = 1,y = 2\) ta được: \(1 + 2.2 > 7\) sai nên A(1;2) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}2x - y > 7\\x + y \le 3\end{array} \right.\), thay \(x = 1,y = 2\) ta được: \(2.1 - 2 > 7\) sai nên A(1;2) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}3x + 4 \le 10\\4x - y > 3\end{array} \right.\), thay \(x = 1,y = 2\) ta được: \(4.1 - 2 > 3\) sai nên A(1;2) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}2x + 5y > 8\\x - 3y \le 4\end{array} \right.\), thay \(x = 1,y = 2\) ta được: \(\left\{ \begin{array}{l}2.1 + 5.2 > 8\\1 - 3.2 \le 4\end{array} \right.\) đúng nên A(1;2) thuộc miền nghiệm của hệ BPT.
Chọn D.
Câu 14. Cho \({0^ \circ } < a,b < {90^ \circ }\) thỏa mãn: \(\sin {108^ \circ } = \sin ({10^ \circ } + a) = \cos (b - {10^ \circ })\). Tổng \(a + b\) là:
A. \(70\) B. \(90\) C. \(130\). D. \(170\).
Cách giải
Ta có: \(\sin {108^ \circ } = \sin ({180^ \circ } - {108^ \circ }) = \sin {72^ \circ }\)
\( \Rightarrow \sin {72^ \circ } = \sin ({10^ \circ } + a)\)
\( \Rightarrow {72^ \circ } = {10^ \circ } + a \Leftrightarrow a = {62^ \circ }\) (do \({0^ \circ } < a < {90^ \circ }\))
Tương tự, \(\sin {72^ \circ } = \cos ({90^ \circ } - {72^ \circ }) = \cos {18^ \circ }\)
\( \Rightarrow \cos {18^ \circ } = \cos (b - {10^ \circ })\)
\( \Rightarrow {18^ \circ } = b - {10^ \circ } \Leftrightarrow b = {28^ \circ }\) (do \({0^ \circ } < b < {90^ \circ }\))
Do đó \(a + b = {62^ \circ } + {28^ \circ } = {90^ \circ }\)
Chọn B
Câu 15. Cho bất phương trình \(2(2x - 3y) - (2x - y + 5) > x - 3y + 1\). Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho?
A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3; - 2)\). D. \(C(0;2)\)
Cách giải:
Ta có: \(2(2x - 3y) - (2x - y + 5) > x - 3y + 1\)
\(\begin{array}{l} \Leftrightarrow 4x - 6y - 2x + y - 5 - x + 3y - 1 > 0\\ \Leftrightarrow x - 2y - 6 > 0\end{array}\)
Thay tọa độ các điểm vào BPT:
+ Vì \(0 - 2.0 - 6 = - 6 < 0\) nên \(O(0;0)\) không thuộc miền nghiệm
+ Vì \(1 - 2.0 - 6 = - 5 < 0\) nên \(A(1;0)\) không thuộc miền nghiệm
+ Vì \(3 - 2.( - 2) - 6 = 1 > 0\) nên \(B(3; - 2)\) thuộc miền nghiệm
+ Vì \(0 - 2.2 - 6 = - 10 < 0\) nên \(C(0;2)\) không thuộc miền nghiệm
Chọn C
II. PHẦN TỰ LUẬN
Câu 1 (TH):
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Biểu diễn hai tập \(( - \infty ;3)\) và \(( - 4; + \infty )\) trên trục số, ta được:
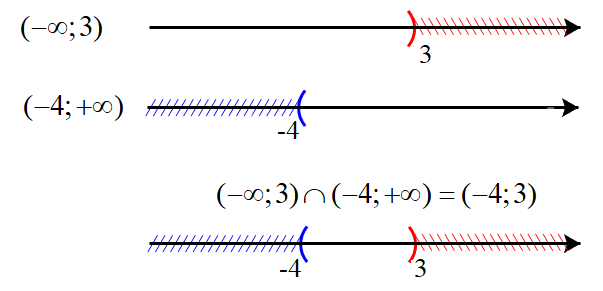
Giao của hai tập hợp: \(( - \infty ;3) \cap ( - 4; + \infty ) = ( - 4;3)\)
b) Biểu diễn hai tập \((1;6]\) và \(( - 2;5]\) trên trục số, ta được:
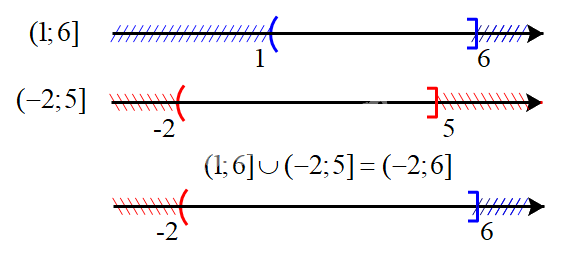
Hợp của hai tập hợp: \((1;6] \cup ( - 2;5] = ( - 2;6]\)
c) Biểu diễn hai tập \(( - 3;7]\) và \((1; + \infty )\) trên trục số, ta được:
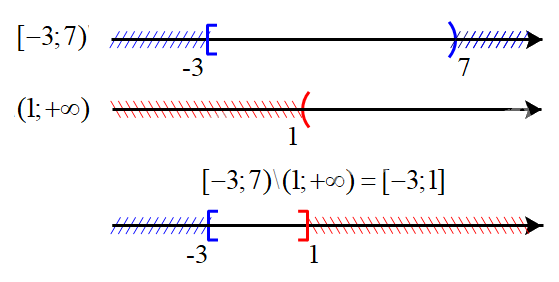
Hiệu của hai tập hợp: \([ - 3;7){\rm{\backslash }}(1; + \infty ) = [ - 3;1]\)
d) Biểu diễn tập \(( - 1;8]\) trên trục số, ta được:
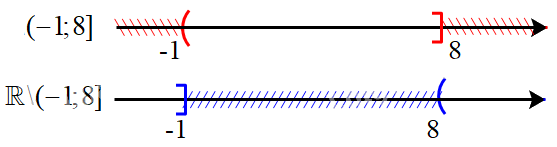
Hiệu của hai tập hợp: \(\mathbb{R}{\rm{\backslash }}( - 1;8] = ( - \infty ; - 1] \cup (8; + \infty )\)
Câu 2:
Nhà cô Minh có mảnh vườn rộng \(8{m^2}\). Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi \({m^2}\). Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi \({m^2}\). Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180?
Cách giải:
Gọi diện tích trồng cà chua và cải bắp lần lượt là x, y (đơn vị: \({m^2}\)). \((x,y \ge 0)\)
Mảnh vườn rộng \(8{m^2}\) nên ta có: \(x + y \le 8\)
Khi trồng x \({m^2}\) cà chua thì cần \(20x\) công và thu được \(300x\) nghìn đồng
Khi trồng y \({m^2}\) cải bắp thì cần \(30x\) công và thu được \(400x\) nghìn đồng
Tổng số công không quá 180 nên ta có: \(20x + 30y \le 180\) hay \(2x + 3y \le 18\)
Tổng số tiền thu được là: \(F(x;y) = 300x + 400y\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 8\\0 \le y \le 8\\x + y \le 8\\2x + 3y \le 18\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
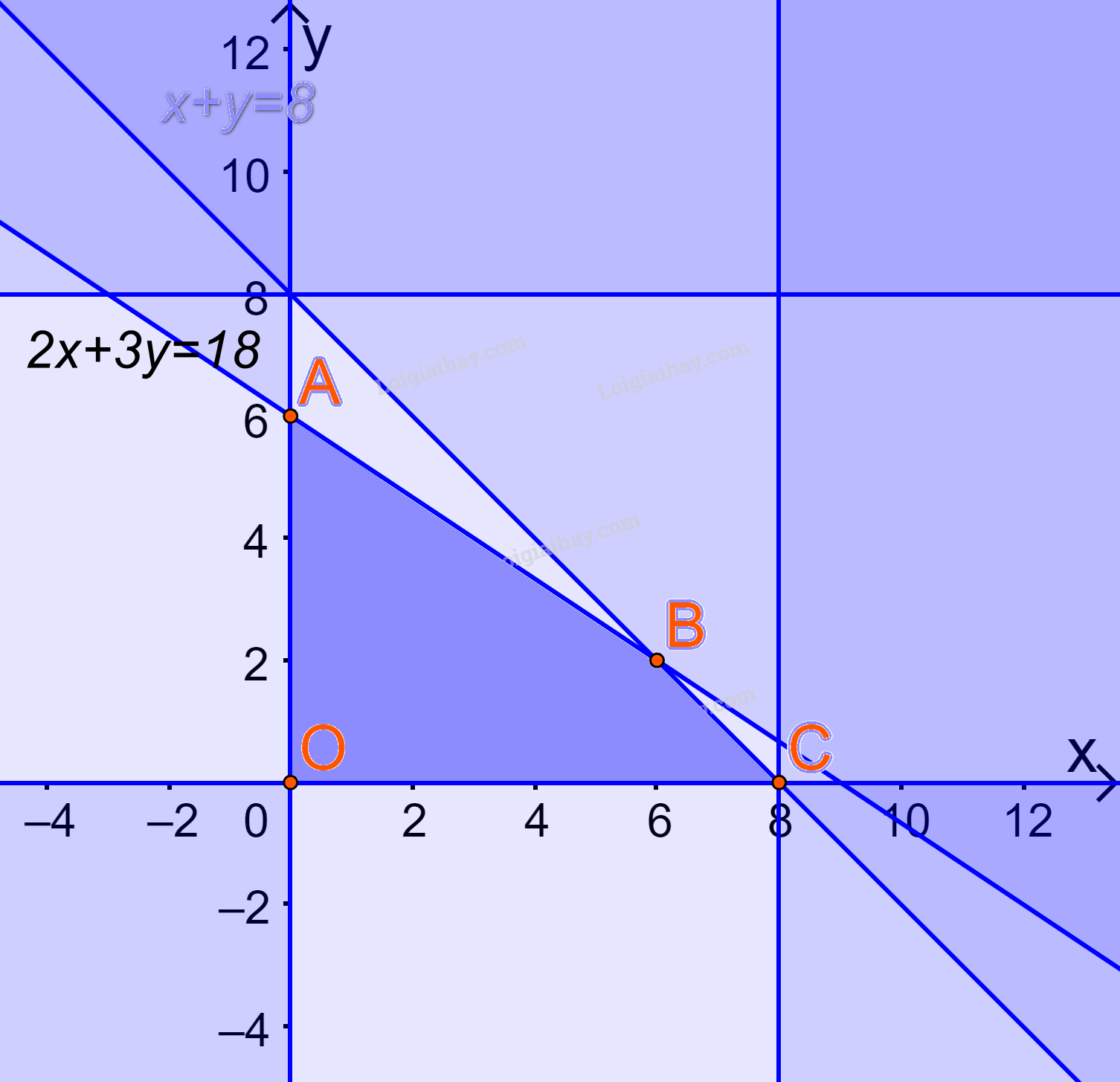
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(0;6),B(6;2),C(8;0),O(0;0)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 300x + 400y\) ta được:
\(\begin{array}{l}F(0;0) = 300.0 + 400.0 = 0\\F(0;6) = 300.0 + 400.6 = 2400\\F(2;6) = 300.2 + 400.6 = 3000\\F(8;0) = 300.8 + 400.0 = 2400\end{array}\)
Do đó F đạt giá trị lớn nhất bằng 3000 tại \(x = 2;y = 6\)
Vậy cô Minh cần mua trồng \(2{m^2}\) cà chua và \(6{m^2}\) cải bắp.
Câu 3:
Phương pháp:
a) Áp dụng hệ quả của định lí cosin: \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
b) Áp dụng các công thức tính diện tích:\(S = \frac{1}{2}a.{h_a} = \frac{{abc}}{{4R}}\)
Định lí sin: \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Cách giải:
a) Từ định lí cosin, ta suy ra:
\(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
\(\begin{array}{l} \Rightarrow a(b.\cos C - c.\cos B) = ab.\cos C - ac.\cos B)\\ = ab.\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} - ac.\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ = \frac{1}{2}\left( {{a^2} + {b^2} - {c^2}} \right) - \frac{1}{2}\left( {{a^2} + {c^2} - {b^2}} \right)\\ = \frac{1}{2}\left( {{a^2} + {b^2} - {c^2} - {a^2} - {c^2} + {b^2}} \right)\\ = \frac{1}{2}\left( {2{b^2} - 2{c^2}} \right) = {b^2} - {c^2}\end{array}\)
b) Ta có: \(S = \frac{1}{2}a.{h_a} \Rightarrow {h_a} = \frac{{2S}}{a}\)
Mà \(S = \frac{{abc}}{{4R}} \Rightarrow 2S = \frac{{abc}}{{2R}} \Rightarrow {h_a} = \frac{{bc}}{{2R}}\) (1)
Lại có: Theo định lí sin thì: \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
\( \Rightarrow \sin B = \frac{b}{{2R}};\sin C = \frac{c}{{2R}}\)
\( \Rightarrow 2R\sin B\sin C = 2R.\frac{b}{{2R}}.\frac{c}{{2R}} = \frac{{bc}}{{2R}}\) (2)
Từ (1) và (2) suy ra \({h_a} = 2R\sin B\sin C\)
Câu 4:
Cách giải:
Đặt \(2u = \sin (a + b) = 2\cos (a - b)\)
Dễ thấy \(u \ne \pm 1\) do \(\left| {2u} \right| = \left| {\sin (a + b)} \right| \le 1\).
Ta có:
\(\begin{array}{l}M = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}} = \frac{{2 - \sin 2b + 2 - \sin 2a}}{{\left( {2 - \sin 2a} \right)\left( {2 - \sin 2b} \right)}}\\ = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2\sin 2a - 2\sin 2b + \sin 2a.\sin 2b}}\\ = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2(\sin 2a + \sin 2b) + \sin 2a.\sin 2b}}\end{array}\)
Mà:
\(\sin 2a + \sin 2b = 2\sin \frac{{2a + 2b}}{2}\cos \frac{{2a - 2b}}{2}\)\( = 2\sin \left( {a + b} \right)\cos \left( {a - b} \right) = 2.2u.u = 4{u^2}\);
\(\begin{array}{l}\sin 2a.\sin 2b = - \frac{1}{2}\left[ {\cos \left( {2a + 2b} \right) - \cos \left( {2a - 2b} \right)} \right]\\ = - \frac{1}{2}\left[ {1 - 2{{\sin }^2}(a + b) - 2{{\cos }^2}(a - b) + 1} \right]\\ = {\cos ^2}(a + b) + {\sin ^2}(a - b) - 1\\ = {u^2} + {(2u)^2} - 1 = 5{u^2} - 1\end{array}\)
\( \Rightarrow M = \frac{{4 - 4{u^2}}}{{4 - 2.4{u^2} + 5{u^2} - 1}} = \frac{{4 - 4{u^2}}}{{3 - 3{u^2}}} = \frac{4}{3}\)
Vậy \(M = \frac{4}{3}\) không phụ thuộc vào a,b.
Tải về
I. PHẦN TRẮC NGHIỆM
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “\(\sqrt 2 \) không là số hữu tỉ”
A. \(\sqrt 2 = \mathbb{Q}\) B. \(\sqrt 2 \in \mathbb{Q}\) C. \(\sqrt 2 \subset \mathbb{Q}\) D. \(\sqrt 2 \notin \mathbb{Q}\)
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > - 2\). B. \(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > 2\).
C. \(\forall x \in \mathbb{R},x > - 2 \Rightarrow {x^2} > 4\). D. \(\forall x \in \mathbb{R},x > 2 \Rightarrow {x^2} > 4\)
Câu 3. Cho A là tập hợp các số tự nhiên chẵn, \(B = \{ n \in \mathbb{N}|n \le 8\} \) và \(C = \{ n \in \mathbb{N}|2 \le n \le 5\} \).
Tìm tập hợp \(A \cap \left( {B \cap C} \right)\)
A. \(\{ 2;4\} \) B. \(\{ 2\} \). C. \(\{ 4\} \). D. \(\emptyset \).
Câu 4. Cho \(A = ( - 2;5]\) và \(B = (m; + \infty )\). Tìm \(m \in \mathbb{Z}\) để \(A{\rm{\backslash }}B\) chứa đúng 3 số nguyên là:
A. \(0\). B. \(1\). C. \(2\) D. \(3\)
Câu 5. Để chuẩn bị cho các tiết mục văn nghệ, lớp 10B cử ra 12 bạn tham gia tiết mục múa và 7 bạn vào tiết mục hát. Biết rằng có 3 bạn tham gia cả hai tiết mục và 22 bạn không tham gia văn nghệ. Số học sinh lớp 10B là:
A. \(36\). B. \(38\). C. \(40\). D. \(45\).
Câu 6. Miền nghiệm của bất phương trình \(x - 2y \ge 4\) là:
A.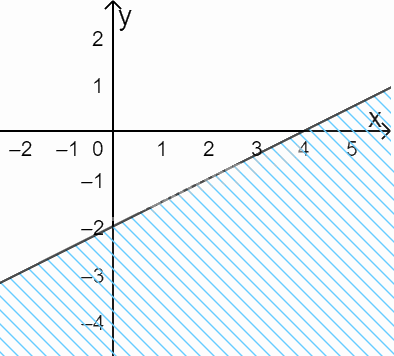 B.
B.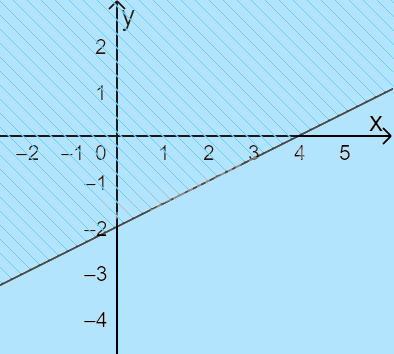
C. 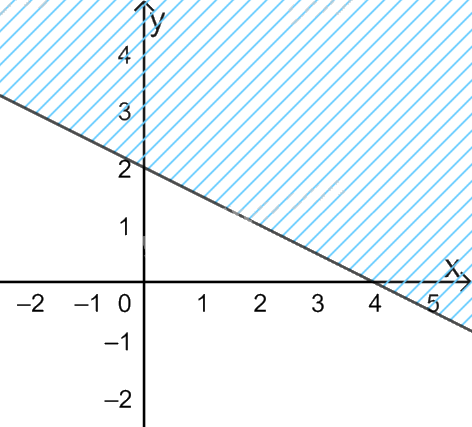 D.
D. 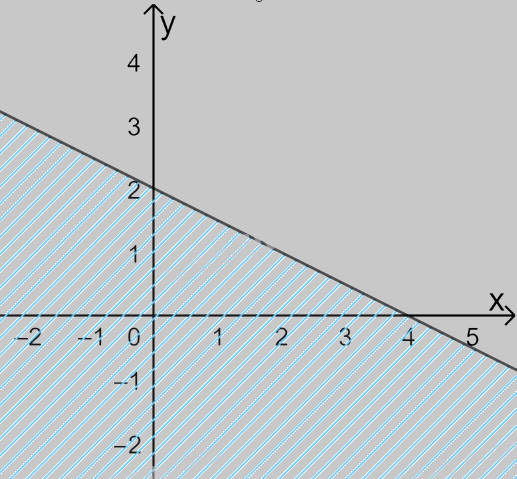
Câu 7. Giá trị lớn nhất của \(F(x;y) = x - 3y\), với điều kiện \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\)
A.\(2\) B. \( - 6\) C.\( - \frac{{34}}{3}\) D. \( - 15\)
Câu 8. Cho góc \(x\;({0^ \circ } < x < {180^ \circ })\) thỏa mãn \(\tan x = 3\). Tính biểu thức \(P = \frac{{10\sin x + 13\cos x}}{{7\sin x - 8\cos x}}\)
A. \(\frac{{10}}{7}\). B. \(\frac{{19}}{4}\). C. \(\frac{{ - 49}}{7}\). D. \(\frac{{43}}{{13}}\).
Câu 9. Rút gọn biểu thức \(A = \frac{{1 - \cos \alpha + \cos 2\alpha }}{{\sin 2\alpha - \sin \alpha }}\)
A.\(\sin \alpha \) B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \).
Câu 10. Cho tam giác ABC có góc A nhọn thỏa mãn \(\sin A\sin B = \cos C\) thì:
A. \(A{C^2} = A{B^2} + B{C^2}\) B. \(AB > AC\) C. Tam giác ABC cân tại B D. \(\cos C < 0\)
Câu 11. Cho tam giác ABC có \(a = 4,b = 5,c = 7\). Bán kính đường tròn nội tiếp r của tam giác ABC bằng:
A. \(12\) B. \(6\) C. \(\frac{{\sqrt 6 }}{2}\). D. \(\sqrt 6 \).
Câu 12. Cho tam giác \(ABC\) có \(c = 32,\widehat A = {70^o},b = 45\). Độ dài cạnh BC là:
A. \(40\) B. \(41\) C. \(42\) D. \(43\)
Câu 13. Điểm \(A(1;2)\) thuộc miền nghiệm của hệ bất phương trình nào dưới đây?
A. \(\left\{ \begin{array}{l}x + 2y > 7\\3x - y < 5\end{array} \right.\) B. \(\left\{ \begin{array}{l}2x - y > 7\\x + y \le 3\end{array} \right.\) C. \(\left\{ \begin{array}{l}3x + 4 \le 10\\4x - y > 3\end{array} \right.\) D. \(\left\{ \begin{array}{l}2x + 5y > 8\\x - 3y \le 4\end{array} \right.\)
Câu 14. Cho \({0^ \circ } < a,b < {90^ \circ }\) thỏa mãn: \(\sin {108^ \circ } = \sin ({10^ \circ } + a) = \cos (b - {10^ \circ })\). Tổng \(a + b\) là:
A. \(70\) B. \(90\) C. \(130\). D. \(170\).
Câu 15. Cho bất phương trình \(2(2x - 3y) - (2x - y + 5) > x - 3y + 1\). Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho?
A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3; - 2)\). D. \(C(0;2)\)
II. PHẦN TỰ LUẬN
Câu 1. Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - \infty ;3) \cap ( - 4; + \infty )\) b) \((1;6] \cup ( - 2;5]\) c) \([ - 3;7){\rm{\backslash }}(1; + \infty )\) d) \(\mathbb{R}{\rm{\backslash }}( - 1;8]\)
Câu 2. Nhà cô Minh có mảnh vườn rộng \(8{m^2}\). Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi \({m^2}\). Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi \({m^2}\). Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180?
Câu 3. Chứng minh rằng trong mọi tam giác ABC ta có:
a) \({b^2} - {c^2} = a(b.\cos C - c.\cos B)\)
b) \(a = r\left( {\cot \frac{B}{2} + \cot \frac{C}{2}} \right)\)
Câu 4. Cho \(\sin (a + b) = 2\cos (a - b)\). Chứng minh biểu thức \(M = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}}\) không phụ thuộc vào a,b.
I. PHẦN TRẮC NGHIỆM
1. D | 2. D | 3. A | 4. B | 5. B |
6. B | 7. A | 8. D | 9. D | 10. A |
11. C | 12. D | 13. D | 14. B | 15. C |
Câu 1:
Cách giải:
Tập hợp các số hữu tỉ: \(\mathbb{Q}\)
“\(\sqrt 2 \) không là số hữu tỉ” viết là: \(\sqrt 2 \notin \mathbb{Q}\)
Chọn D.
Câu 2:
Cách giải:
Mệnh đề “\(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > - 2\)” sai, chẳng hạn \(x = - 3\) thì \({x^2} > 4\) nhưng \(x < - 2\)
Mệnh đề “\(\forall x \in \mathbb{R},{x^2} > 4 \Rightarrow x > 2\)” sai, chẳng hạn \(x = - 3\) thì \({x^2} > 4\) nhưng \(x < 2\)
Mệnh đề “\(\forall x \in \mathbb{R},x > - 2 \Rightarrow {x^2} > 4\)” sai, chẳng hạn \(x = 0 > - 2\) nhưng \({x^2} < 4\)
Mệnh đề “\(\forall x \in \mathbb{R},x > 2 \Rightarrow {x^2} > 4\)” đúng
Chọn D.
Câu 3:
Phương pháp:
Cho A là tập hợp các số tự nhiên chẵn, \(B = \{ n \in \mathbb{N}|n \le 8\} \) và \(C = \{ n \in \mathbb{N}|2 \le n \le 5\} \).
Tìm tập hợp \(A \cap \left( {B \cap C} \right)\)
Cách giải:
\(A = \{ 0;2;4;6;8;...\} \)
\(B = \{ 0;1;2;3;4;5;6;7;8\} \)
\(C = \{ 2;3;4;5\} \).
Ta có: \(B \cap C = \{ 2;3;4;5\} = C \Rightarrow A \cap \left( {B \cap C} \right) = A \cap C = \{ 2;4\} \)
Chọn A.
Câu 4:
Cách giải:
+ Nếu \(m \ge 5\) thì \(A{\rm{\backslash }}B = ( - 2;5]{\rm{\backslash }}(m; + \infty ) = A = ( - 2;5]\), chứa 7 số nguyên là -1 ; 0 ;1 ;2 ;3 ;4 ;5 (nhiều hơn 3) nên ta loại trường hợp m > 5.
+ Để \(A{\rm{\backslash }}B \ne \emptyset \) thì m>-2. Xét trường hợp -2<m<5, khi đó \(A{\rm{\backslash }}B = ( - 2;5]{\rm{\backslash }}(m; + \infty ) = ( - 2;m]\)
Chứa 3 số nguyên -1 ;0 ;1 thì m=1.
Chọn B.
Câu 5:
Phương pháp:
Thay cặp số vào BPT, cặp số nào cho ta mệnh đề đúng thì cặp số đó là nghiệm của BPT đã cho.
Để chuẩn bị cho các tiết mục văn nghệ, lớp 10B cử ra 12 bạn tham gia tiết mục múa và 7 bạn vào tiết mục hát. Biết rằng có 3 bạn tham gia cả hai tiết mục và 22 bạn không tham gia văn nghệ. Số học sinh lớp 10B là:
Gọi A là tập hợp các học sinh tham gia tiết mục múa.
B là là tập hợp các học sinh tham gia tiết mục hát.
Cách giải:
Gọi A là tập hợp các học sinh tham gia tiết mục múa.
B là là tập hợp các học sinh tham gia tiết mục hát.
Suy ra : \(A \cup B\) là tập hợp các học sinh tham gia văn nghệ.
\(A \cap B\) là tập hợp các học sinh tham gia cả hai tiết mục.
Ta có : \(n(A) = 12;n(B) = 7;n(A \cap B) = 3\)
\( \Rightarrow \) Số học sinh tham gia văn nghệ là : \(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 12 + 7 - 3 = 16\) (học sinh)
Số học sinh lớp 10B (gồm học sinh tham gia văn nghệ và các học sinh không tham gia văn nghệ) là : \(16 + 22 = 38\) (học sinh)
Chọn B.
Câu 6:
Phương pháp:
Xác định đường thẳng \(x - 2y = 4\) và xét một điểm (không thuộc đường thẳng) xem có thuộc miền nghiệm hay không.
Cách giải:
Đường thẳng \(x - 2y = 4\) đi qua điểm có tọa độ (4;0) và (0; -2) => Loại C, D.
Xét điểm O(0;0), ta có: \(0 - 2.0 = 0 < 4\) nên O không thuộc miền nghiệm.
Chọn B.
Câu 7:
Phương pháp:
Bước 1: Biểu diễn miền nghiệm, xác định các đỉnh của miền nghiệm
Bước 2: Thay tọa độ các đỉnh vào \(F(x;y) = x - 3y\), kết luận giá trị nhỏ nhất.
Cách giải:
Xét hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\)
Biểu diễn miền nghiệm của hệ, ta được
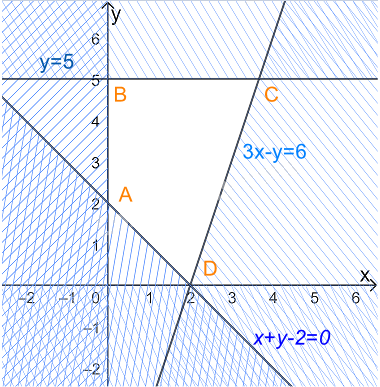
Miền nghiệm là miền tứ giác ABCD trong đó \(A\left( {0;2} \right),{\rm{ }}B\left( {0;5} \right),{\rm{ }}C\left( {\frac{{11}}{3};5} \right),D(2;0)\)
Thay tọa độ các điểm A, B, C, D vào \(F(x;y) = x - 3y\) ta được
\(F(0;2) = 0 - 3.2 = - 6\)
\(F(0;5) = 0 - 3.5 = - 15\)
\(F\left( {\frac{{11}}{3};5} \right) = \frac{{11}}{3} - 3.5 = - \frac{{34}}{3}\)
\(F(2;0) = 2 - 3.0 = 2\)
Vậy giá trị lớn nhất của F bằng 2.
Chọn A.
Câu 8:
Phương pháp:
Chia cả tử và mẫu của P cho cosx để làm xuất hiện tanx.
Cách giải:
Vì \(\tan x = 3\) nên \(\cos x \ne 0\)
Khi đó: \(P = \frac{{10\sin x + 13\cos x}}{{7\sin x - 8\cos x}} = \frac{{\frac{{10\sin x + 13\cos x}}{{\cos x}}}}{{\frac{{7\sin x - 8\cos x}}{{\cos x}}}} = \frac{{10\frac{{\sin x}}{{\cos x}} + 13}}{{7\frac{{\sin x}}{{\cos x}} - 8}}\)
\( = \frac{{10\tan x + 13}}{{7\tan x - 8}} = \frac{{10.3 + 13}}{{7.3 - 8}} = \frac{{43}}{{13}}\)
Chọn D.
Câu 9:
Phương pháp:
Áp dụng công thức: \(\cos 2\alpha = 2{\cos ^2}\alpha - 1;\sin 2\alpha = 2\sin \alpha \cos \alpha \)
Cách giải:
\(\begin{array}{l}A = \frac{{1 - \cos \alpha + \cos 2\alpha }}{{\sin 2\alpha - \sin \alpha }} = \frac{{1 - \cos \alpha + 2{{\cos }^2}\alpha - 1}}{{2\sin \alpha \cos \alpha - \sin \alpha }}\\ = \frac{{2{{\cos }^2}\alpha - \cos \alpha }}{{2\sin \alpha \cos \alpha - \sin \alpha }} = \frac{{\cos \alpha \left( {2\cos \alpha - 1} \right)}}{{\sin \alpha \left( {2\cos \alpha - 1} \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \cot \alpha \end{array}\)
Chọn D.
Câu 10:
Cách giải:
Ta có: \(\sin A\sin B = \cos C\)
Mà \(\cos C = - \cos ({180^ \circ } - C) = - \cos (A + B) = - \cos A\cos B + \sin A\sin B\)
\(\begin{array}{l} \Rightarrow \sin A\sin B = - \cos A\cos B + \sin A\sin B\\ \Leftrightarrow \cos A\cos B = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos A = 0\\\cos B = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\widehat A = {90^ \circ }\\\widehat B = {90^ \circ }\end{array} \right.\end{array}\)
Theo giải thiết, góc A nhọn nên \(\widehat B = {90^ \circ }\) hay tam giác ABC vuông tại B.
Khi đó: \(A{C^2} = A{B^2} + B{C^2}\), \(AC > AB\) (do AC là cạnh huyền), \(\cos C > 0\) (do \({0^ \circ } < \widehat C < {90^ \circ }\))
Chọn A.
Câu 11:
Phương pháp:
Bước 1: Tính diện tích \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Bước 2: Tính bán kính \(R\) dựa vào công thức \(S = \frac{{abc}}{{4R}}\)
Cách giải:
Ta có \(a = 4,b = 5,c = 7 \Rightarrow p = \frac{{4 + 5 + 7}}{2} = 8\)
Suy ra diện tích tam giác ABC là: \(S = \sqrt {8.(8 - 4)(8 - 5)(8 - 7)} = 4\sqrt 6 \)
Bán kính đường tròn nội tiếp r của tam giác ABC bằng:
\(r = \frac{S}{p} = \frac{{4\sqrt 6 }}{8} = \frac{{\sqrt 6 }}{2}\)
Chọn C.
Câu 12:
Phương pháp:
Áp dụng định lí cos: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Cách giải:
Ta có: \(c = 32,\widehat A = {70^o},b = 45\)
Áp dụng định lí cos trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
\(\begin{array}{l} \Leftrightarrow {a^2} = {45^2} + {23^2} - 2.45.23\cos {70^ \circ } \approx 1846\\ \Rightarrow a = \sqrt {1846} \approx 43\end{array}\)
Vậy độ dài cạnh AC là khoảng 43.
Chọn D.
Câu 13.
Phương pháp:
Thay tọa độ điểm A vào hệ BPT, hệ nào cho ta các mệnh đề đúng thì điểm A thuộc miền nghiệm của hệ BPT đó.
Cách giải
+ Xét hệ \(\left\{ \begin{array}{l}x + 2y > 7\\3x - y < 5\end{array} \right.\), thay \(x = 1,y = 2\) ta được: \(1 + 2.2 > 7\) sai nên A(1;2) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}2x - y > 7\\x + y \le 3\end{array} \right.\), thay \(x = 1,y = 2\) ta được: \(2.1 - 2 > 7\) sai nên A(1;2) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}3x + 4 \le 10\\4x - y > 3\end{array} \right.\), thay \(x = 1,y = 2\) ta được: \(4.1 - 2 > 3\) sai nên A(1;2) không thuộc miền nghiệm của hệ BPT.
+ Xét hệ \(\left\{ \begin{array}{l}2x + 5y > 8\\x - 3y \le 4\end{array} \right.\), thay \(x = 1,y = 2\) ta được: \(\left\{ \begin{array}{l}2.1 + 5.2 > 8\\1 - 3.2 \le 4\end{array} \right.\) đúng nên A(1;2) thuộc miền nghiệm của hệ BPT.
Chọn D.
Câu 14. Cho \({0^ \circ } < a,b < {90^ \circ }\) thỏa mãn: \(\sin {108^ \circ } = \sin ({10^ \circ } + a) = \cos (b - {10^ \circ })\). Tổng \(a + b\) là:
A. \(70\) B. \(90\) C. \(130\). D. \(170\).
Cách giải
Ta có: \(\sin {108^ \circ } = \sin ({180^ \circ } - {108^ \circ }) = \sin {72^ \circ }\)
\( \Rightarrow \sin {72^ \circ } = \sin ({10^ \circ } + a)\)
\( \Rightarrow {72^ \circ } = {10^ \circ } + a \Leftrightarrow a = {62^ \circ }\) (do \({0^ \circ } < a < {90^ \circ }\))
Tương tự, \(\sin {72^ \circ } = \cos ({90^ \circ } - {72^ \circ }) = \cos {18^ \circ }\)
\( \Rightarrow \cos {18^ \circ } = \cos (b - {10^ \circ })\)
\( \Rightarrow {18^ \circ } = b - {10^ \circ } \Leftrightarrow b = {28^ \circ }\) (do \({0^ \circ } < b < {90^ \circ }\))
Do đó \(a + b = {62^ \circ } + {28^ \circ } = {90^ \circ }\)
Chọn B
Câu 15. Cho bất phương trình \(2(2x - 3y) - (2x - y + 5) > x - 3y + 1\). Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho?
A. \(O(0;0)\) B. \(A(1;0)\). C. \(B(3; - 2)\). D. \(C(0;2)\)
Cách giải:
Ta có: \(2(2x - 3y) - (2x - y + 5) > x - 3y + 1\)
\(\begin{array}{l} \Leftrightarrow 4x - 6y - 2x + y - 5 - x + 3y - 1 > 0\\ \Leftrightarrow x - 2y - 6 > 0\end{array}\)
Thay tọa độ các điểm vào BPT:
+ Vì \(0 - 2.0 - 6 = - 6 < 0\) nên \(O(0;0)\) không thuộc miền nghiệm
+ Vì \(1 - 2.0 - 6 = - 5 < 0\) nên \(A(1;0)\) không thuộc miền nghiệm
+ Vì \(3 - 2.( - 2) - 6 = 1 > 0\) nên \(B(3; - 2)\) thuộc miền nghiệm
+ Vì \(0 - 2.2 - 6 = - 10 < 0\) nên \(C(0;2)\) không thuộc miền nghiệm
Chọn C
II. PHẦN TỰ LUẬN
Câu 1 (TH):
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Biểu diễn hai tập \(( - \infty ;3)\) và \(( - 4; + \infty )\) trên trục số, ta được:
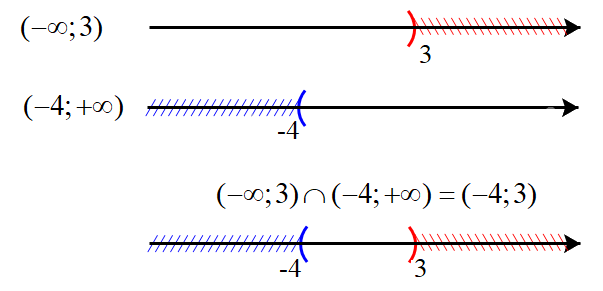
Giao của hai tập hợp: \(( - \infty ;3) \cap ( - 4; + \infty ) = ( - 4;3)\)
b) Biểu diễn hai tập \((1;6]\) và \(( - 2;5]\) trên trục số, ta được:
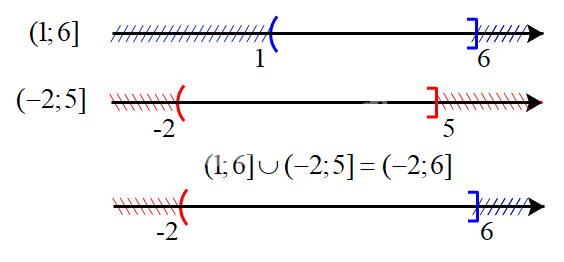
Hợp của hai tập hợp: \((1;6] \cup ( - 2;5] = ( - 2;6]\)
c) Biểu diễn hai tập \(( - 3;7]\) và \((1; + \infty )\) trên trục số, ta được:
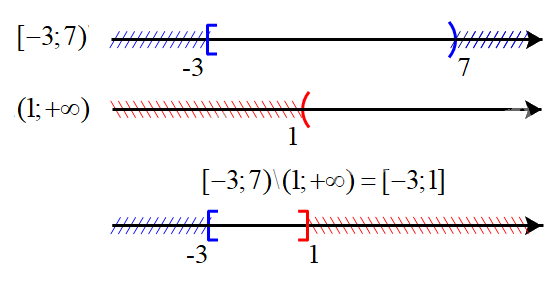
Hiệu của hai tập hợp: \([ - 3;7){\rm{\backslash }}(1; + \infty ) = [ - 3;1]\)
d) Biểu diễn tập \(( - 1;8]\) trên trục số, ta được:
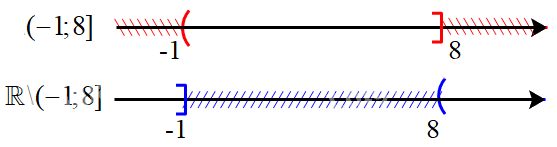
Hiệu của hai tập hợp: \(\mathbb{R}{\rm{\backslash }}( - 1;8] = ( - \infty ; - 1] \cup (8; + \infty )\)
Câu 2:
Nhà cô Minh có mảnh vườn rộng \(8{m^2}\). Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi \({m^2}\). Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi \({m^2}\). Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180?
Cách giải:
Gọi diện tích trồng cà chua và cải bắp lần lượt là x, y (đơn vị: \({m^2}\)). \((x,y \ge 0)\)
Mảnh vườn rộng \(8{m^2}\) nên ta có: \(x + y \le 8\)
Khi trồng x \({m^2}\) cà chua thì cần \(20x\) công và thu được \(300x\) nghìn đồng
Khi trồng y \({m^2}\) cải bắp thì cần \(30x\) công và thu được \(400x\) nghìn đồng
Tổng số công không quá 180 nên ta có: \(20x + 30y \le 180\) hay \(2x + 3y \le 18\)
Tổng số tiền thu được là: \(F(x;y) = 300x + 400y\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 8\\0 \le y \le 8\\x + y \le 8\\2x + 3y \le 18\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
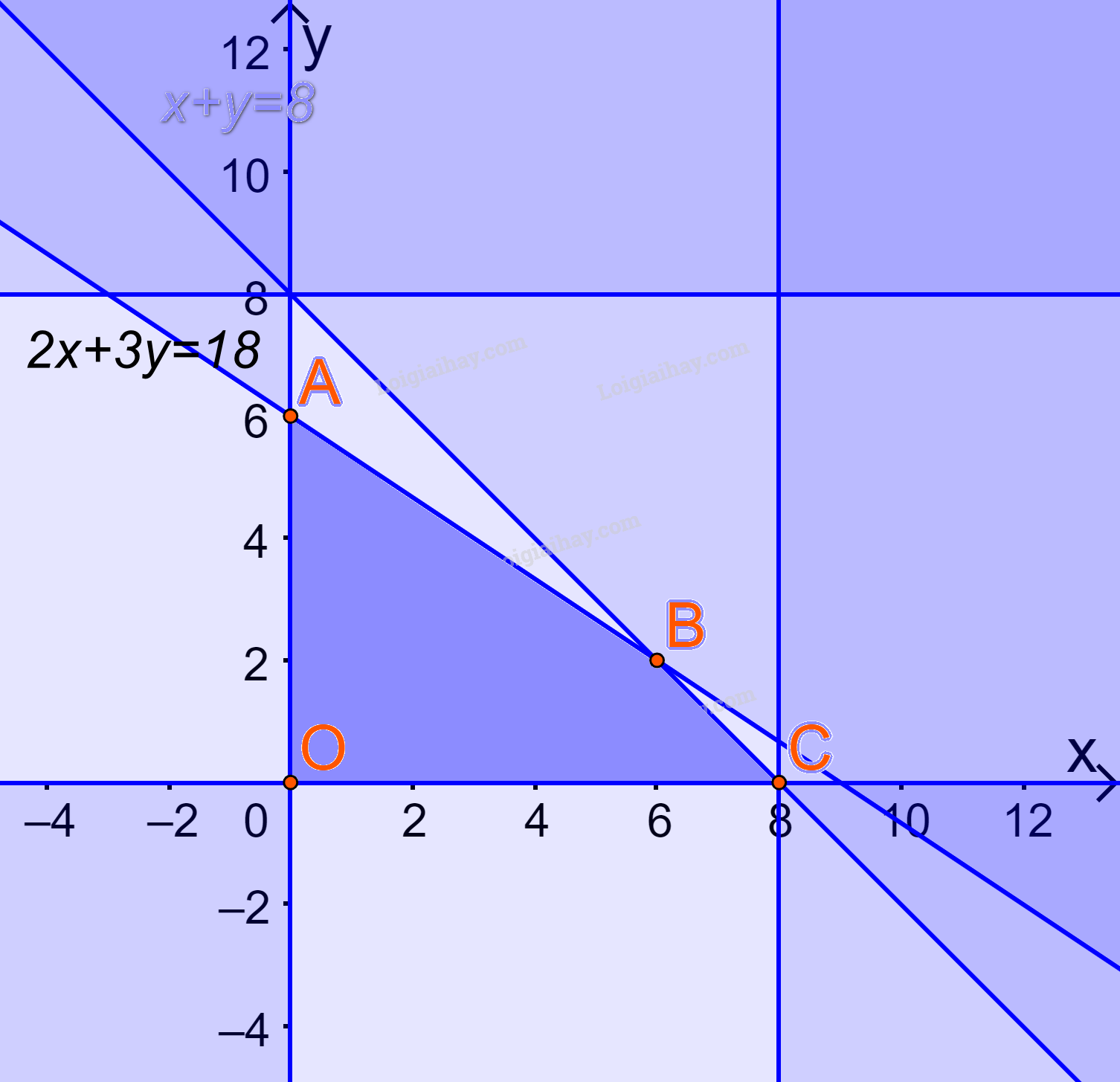
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(0;6),B(6;2),C(8;0),O(0;0)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 300x + 400y\) ta được:
\(\begin{array}{l}F(0;0) = 300.0 + 400.0 = 0\\F(0;6) = 300.0 + 400.6 = 2400\\F(2;6) = 300.2 + 400.6 = 3000\\F(8;0) = 300.8 + 400.0 = 2400\end{array}\)
Do đó F đạt giá trị lớn nhất bằng 3000 tại \(x = 2;y = 6\)
Vậy cô Minh cần mua trồng \(2{m^2}\) cà chua và \(6{m^2}\) cải bắp.
Câu 3:
Phương pháp:
a) Áp dụng hệ quả của định lí cosin: \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
b) Áp dụng các công thức tính diện tích:\(S = \frac{1}{2}a.{h_a} = \frac{{abc}}{{4R}}\)
Định lí sin: \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Cách giải:
a) Từ định lí cosin, ta suy ra:
\(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
\(\begin{array}{l} \Rightarrow a(b.\cos C - c.\cos B) = ab.\cos C - ac.\cos B)\\ = ab.\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} - ac.\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ = \frac{1}{2}\left( {{a^2} + {b^2} - {c^2}} \right) - \frac{1}{2}\left( {{a^2} + {c^2} - {b^2}} \right)\\ = \frac{1}{2}\left( {{a^2} + {b^2} - {c^2} - {a^2} - {c^2} + {b^2}} \right)\\ = \frac{1}{2}\left( {2{b^2} - 2{c^2}} \right) = {b^2} - {c^2}\end{array}\)
b) Ta có: \(S = \frac{1}{2}a.{h_a} \Rightarrow {h_a} = \frac{{2S}}{a}\)
Mà \(S = \frac{{abc}}{{4R}} \Rightarrow 2S = \frac{{abc}}{{2R}} \Rightarrow {h_a} = \frac{{bc}}{{2R}}\) (1)
Lại có: Theo định lí sin thì: \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
\( \Rightarrow \sin B = \frac{b}{{2R}};\sin C = \frac{c}{{2R}}\)
\( \Rightarrow 2R\sin B\sin C = 2R.\frac{b}{{2R}}.\frac{c}{{2R}} = \frac{{bc}}{{2R}}\) (2)
Từ (1) và (2) suy ra \({h_a} = 2R\sin B\sin C\)
Câu 4:
Cách giải:
Đặt \(2u = \sin (a + b) = 2\cos (a - b)\)
Dễ thấy \(u \ne \pm 1\) do \(\left| {2u} \right| = \left| {\sin (a + b)} \right| \le 1\).
Ta có:
\(\begin{array}{l}M = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}} = \frac{{2 - \sin 2b + 2 - \sin 2a}}{{\left( {2 - \sin 2a} \right)\left( {2 - \sin 2b} \right)}}\\ = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2\sin 2a - 2\sin 2b + \sin 2a.\sin 2b}}\\ = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2(\sin 2a + \sin 2b) + \sin 2a.\sin 2b}}\end{array}\)
Mà:
\(\sin 2a + \sin 2b = 2\sin \frac{{2a + 2b}}{2}\cos \frac{{2a - 2b}}{2}\)\( = 2\sin \left( {a + b} \right)\cos \left( {a - b} \right) = 2.2u.u = 4{u^2}\);
\(\begin{array}{l}\sin 2a.\sin 2b = - \frac{1}{2}\left[ {\cos \left( {2a + 2b} \right) - \cos \left( {2a - 2b} \right)} \right]\\ = - \frac{1}{2}\left[ {1 - 2{{\sin }^2}(a + b) - 2{{\cos }^2}(a - b) + 1} \right]\\ = {\cos ^2}(a + b) + {\sin ^2}(a - b) - 1\\ = {u^2} + {(2u)^2} - 1 = 5{u^2} - 1\end{array}\)
\( \Rightarrow M = \frac{{4 - 4{u^2}}}{{4 - 2.4{u^2} + 5{u^2} - 1}} = \frac{{4 - 4{u^2}}}{{3 - 3{u^2}}} = \frac{4}{3}\)
Vậy \(M = \frac{4}{3}\) không phụ thuộc vào a,b.
Đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 2 đóng vai trò quan trọng trong việc đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kì đầu tiên. Đề thi này thường bao gồm các dạng bài tập thuộc các chủ đề chính như tập hợp, hàm số, phương trình và bất phương trình bậc nhất, bậc hai, hệ phương trình, và các ứng dụng thực tế của đại số.
Thông thường, đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 2 có cấu trúc gồm hai phần chính:
Ví dụ 1: Giải phương trình 2x + 3 = 7
Lời giải:
Ví dụ 2: Giải bất phương trình 3x - 1 < 5
Lời giải:
Để chuẩn bị tốt nhất cho kỳ thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 2, học sinh có thể tham khảo các tài liệu sau:
Đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 2 là một cơ hội tốt để học sinh đánh giá năng lực của bản thân và chuẩn bị cho các kỳ thi tiếp theo. Hy vọng với những thông tin và hướng dẫn trên, các em sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi sắp tới.