Chào mừng các em học sinh lớp 10 đến với đề thi học kì 1 môn Toán chương trình Kết nối tri thức - Đề số 8. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi có đáp án chi tiết, giúp các em tự học và nâng cao khả năng giải quyết bài toán. Chúc các em ôn thi tốt!
Câu 1: Trong các câu sau đâu là mệnh đề chứa biến? A. 2 là số nguyên tố. B. 17 là số chẵn C. x + y > 0 D. Hình vuông có hai đường chéo vuông góc
HƯỚNG DẪN GIẢI CHI TIẾT
I. Phần trắc nghiệm (5 điểm – 25 câu)
1.C | 2.B | 3.B | 4.C | 5.B | 6.B | 7.C | 8.A | 9.A | 10.A |
11.C | 12.A | 13.B | 14.A | 15.C | 16.B | 17.D | 18.A | 19.C | 20.B |
21.B | 22.A | 23.B | 24.D | 25.C | |||||
Câu 1 (NB):
Phương pháp:
Mệnh đề chứa biến là mệnh đề có biến số
Cách giải:
x + y > 0 là mệnh đề chứa biến
Chọn C.
Câu 2 (NB):
Phương pháp:
Mệnh đề chứa biến sai khi có ít nhất 1 giá trị của biến sai.
Cách giải:
P sai, Q đúng.
Chọn B.
Câu 3 (NB):
Phương pháp:
phương trình và đối chiếu điều kiện \(x \in \mathbb{Z}\).
Cách giải:
\(9{x^2} - 8x - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \mathbb{Z}\\x = \frac{{ - 1}}{9} \notin \mathbb{Z}\end{array} \right.\). Suy ra \(X = \left\{ 1 \right\}\)
Chọn B
Câu 4 (NB):
Phương pháp:
Tìm giao 2 tập hợp ta tìm phần tử chung của hai tập hợp đó.
Cách giải:
\(X \cap Y\)=\(\left\{ {4;7} \right\}\)
Chọn C.
Câu 5 (TH):
Phương pháp:
Thể hiện các tập hợp trên trục số và tìm hợp của chúng
Cách giải:
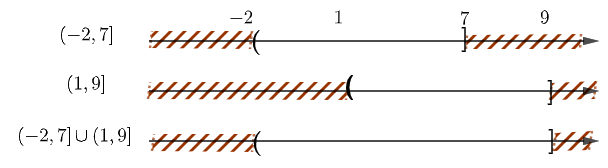
Chọn B.
Câu 6 (VD):
Phương pháp:
\(A \subset B\) khi mọi phần tử của A đều là phần tử của B.
Cách giải:
\(A \subset B \Leftrightarrow \left\{ \begin{array}{l}m \ge - 1\\m + 2 \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge - 1\\m \le 0\end{array} \right. \Leftrightarrow - 1 \le m \le 0\)
Chọn B
Câu 7 (NB):
Phương pháp:
Thay tọa độ x, y vào bât phương trình và kiểm tra tính đúng sai.
Cách giải:
Vì 2.0 + 1 = 1 không nhỏ hơn 1 nên \(\left( {0;1} \right)\)không thuộc miền nghiệm của bất phương trình.
Chọn C.
Câu 8 (NB):
Phương pháp:
Chọn 2 điểm bất kì thuộc hoặc không thuộc miền nghiệm để kiểm tra đáp án. Thông thường ta hay chọn gốc tọa độ O(0,0).
Cách giải:
Vì điểm (0,0) và (3,0) thuộc miền nghiệm nên hình vẽ A đúng.
Chọn A.
Câu 9 (NB):
Phương pháp:
Tần suất \({f_i} = \frac{n}{N} \Rightarrow n = {f_i}.N\)
Cách giải:
\(n = {f_i}.N = 2,5\% .400 = 10\)
Chọn A.
Câu 10 (NB):
Phương pháp:
Biểu đồ hình quạt thích hợp nhất để thể hiện bảng phân bố tần suất.
Cách giải:
Biểu đồ hình quạt thích hợp nhất để thể hiện bảng phân bố tần suất.
Chọn A.
Câu 11 (NB):
Phương pháp:
Số trung bình là \(\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}\)
Cách giải:
\(\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n} = \frac{{21 + 23 + 24 + 25 + 22 + 20}}{6} = 22.5\)
Chọn C.
Câu 12 (TH):
Phương pháp:
Tần suất \({f_i} = \frac{n}{N} \Rightarrow n = {f_i}.N\)
Cách giải:
Tần suất của số 4 là \(f = \frac{{10}}{{50}} = \frac{1}{5} = 20\% \)
Chọn A.
Câu 13 (TH):
Phương pháp:
Dùng MTCT để tính
Cách giải:
Chọn B.
Câu 14 (TH):
Phương pháp:
Dùng MTCT để tính
Cách giải:
Chọn A.
Câu 15 (TH):
Phương pháp:
Hai góc \(\alpha \) và \(\beta \) bù nhau thì \(\sin \alpha = \sin \beta \); \(\cos \alpha = - \cos \beta \).
Cách giải:
Giả sử \(\hat A = \alpha ;\hat B + \hat C = \beta \). Biểu thức trở thành \(P = \cos \alpha \cos \beta - \sin \alpha \sin \beta \).
Trong tam giác ABC có \(\hat A + \hat B + \hat C = {180^^\circ } \Rightarrow \alpha + \beta = {180^^\circ }\).
Do hai góc \(\alpha \) và \(\beta \) bù nhau nên \(\sin \alpha = \sin \beta \); \(\cos \alpha = - \cos \beta \).
Do đó \(P = \cos \alpha \cos \beta - \sin \alpha \sin \beta = - {\cos ^2}\alpha - {\sin ^2}\alpha = - \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = - 1\).
Chọn C.
Câu 16 (NB):
Phương pháp:
Dùng định lý sin trong tam giác.
Cách giải:
Chọn B.
Câu 17 (TH):
Phương pháp:
Dùng định lý cosin \({b^2} = {a^2} + {c^2} - 2ac.\cos B\)
Cách giải:
\({b^2} = {a^2} + {c^2} - 2ac.\cos B = {5^2} + {3^2} - 2.3.8.\cos 60 = 19 \Rightarrow b = \sqrt {19} \)
Chọn D.
Câu 18 (VD):
Phương pháp:
Chia hình thoi thành 2 tam giác bằng nhau và áp dụng công thức diện tích tam giác.
Cách giải:
\({S_{\Delta ABD}} = \frac{1}{2}.AB.AD.\sin A = \frac{1}{2}.a.a.\sin 30 = \frac{{{a^2}}}{4}\)
Chọn A.
Câu 19 (VD):
Phương pháp:
Chia cả tử và mẫu của phân thức cho cos x để xuất hiện tan x.
Cách giải:
\(E = \frac{{2\cos \alpha - 3\sin \alpha }}{{3\cos \alpha - \sin \alpha }} = \frac{{2.\frac{{\cos \alpha }}{{\cos \alpha }} - 3.\frac{{\sin \alpha }}{{\cos \alpha }}}}{{3.\frac{{\cos \alpha }}{{\cos \alpha }} - \frac{{\sin \alpha }}{{\cos \alpha }}}} = \frac{{2 - 3\tan x}}{{3 - \tan x}} = \frac{{17}}{8}\)
Chọn C.
Câu 20 (TH):
Phương pháp:
Dùng quy tắc cộng, quy tắc trừ và quy tắc hình bình hành.
Cách giải:
Theo quy tắc cộng \(\overrightarrow {MP} + \overrightarrow {NM} = \overrightarrow {NM} + \overrightarrow {MP} = \overrightarrow {NP} \)
Chọn B.
Câu 21 (NB):
Phương pháp:
Hai vecto đối nhau khi chúng cùng phương và ngược hướng.
Cách giải:
Chọn B.
Câu 22 (TH):
Phương pháp:
Hai veto bằng nhau khi chúng cùng phương và cùng hướng
Phân biệt giữa vecto và độ dài vecto
Cách giải:
\(\overrightarrow {AB} = \overrightarrow {AC} \)sai do 2 vecto này không cùng phương
Chọn A.
Câu 23 (TH):
Phương pháp:
Dùng tính chất trọng tâm tam giác
Cách giải:
Gọi \(G\) là trọng tâm tam giác \(ABC\).
Ta có \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0 \Rightarrow M \equiv G\).
Chọn B.
Câu 24 (TH):
Phương pháp:
Dùng công thức tích vô hướng của 2 vecto
Cách giải:
\(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|\cos \left( {\overrightarrow {AC} ,\,\overrightarrow {CB} } \right) = a.a.\cos 120 = \frac{{ - {a^2}}}{2}\)
Chọn D.
Câu 25 (VD):
Phương pháp:
Dùng công thức tích vô hướng của 2 vecto
Cách giải:
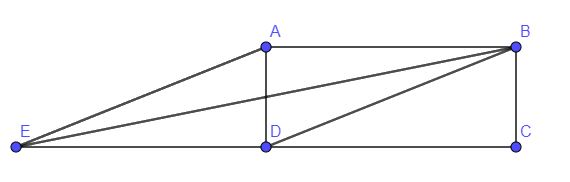
\(B{D^2} = A{B^2} + A{C^2} = {5^2} + {8^2} = 89 \Rightarrow BD = \sqrt {89} \)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {BD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BD} } \right|.\cos \left( {\overrightarrow {AB} ,\,\overrightarrow {BD} } \right) = 8.\sqrt {89} .\cos BAE\\ = 8.\sqrt {89} .\frac{{A{B^2} + A{E^2} - B{E^2}}}{{2AB.AE}} = 8.\sqrt {89} .\frac{{{8^2} + 89 - 125}}{{2.8.\sqrt {89} }} = 14\end{array}\)
Chọn C.
II. Phần tự luận (5 điểm)
Câu 1 (TH):
Phương pháp:
Dùng định nghĩa các phép toán trên tập hợp.
Cách giải:
a. \(S = \left\{ {1;2;3;4} \right\},T = \left\{ {2;4;6} \right\}\)
\(S \cap T = \left\{ {2,4} \right\},\,S \cup T = \left\{ {1,2,3,4,6} \right\},\,\,S\backslash T = \left\{ {1,3} \right\}\)
b. \(\mathop C\nolimits_\mathbb{R} B = \mathbb{R}\backslash \left[ {4 - 3m; + \infty } \right) = \left( { - \infty ,\,4 - 3m} \right)\)
Để \(\mathop C\nolimits_\mathbb{R} B \subset A\) tức là \(\left( { - \infty ,\,4 - 3m} \right) \subset \left( { - \infty ;2023} \right) \Leftrightarrow 4 - 3m \le 2023 \Leftrightarrow m \ge 673\).
Câu 2 (VD):
Phương pháp:
Dùng các hệ thức lượng trong tam giác.
Cách giải:
\(BC = DC.\tan 23,{6^0} = 200.\tan 23,{6^0} \approx 87,378\)m
\(\angle ADC = \angle ADB + \angle BDC = 15,9 + 23,6 = 39,5\)
\(AC = DC.\tan ADC = 200.\tan 39,{5^0} = 164,867m\)
Vậy chiều cao tháp là AB = AC – BC = 164,867 – 87,378 =77,489 m
Câu 3 (VD):
Phương pháp:
Dùng quy tắc cộng, chèn điểm, các vecto bằng nhau.
Cách giải:
a. \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \)
Suy ra MABC là hình bình hành.
b. Ta có \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right| \Leftrightarrow \left| {\overrightarrow {CB} } \right| = \left| {\overrightarrow {AM} } \right| \Rightarrow AM = BC\)
Mà \(A,\;B,\;C\) cố định nên tập hợp điểm \(M\) là đường tròn tâm \(A\), bán kính \(BC\).
I. Phần trắc nghiệm (5 điểm – 25 câu)
Câu 1: Trong các câu sau đâu là mệnh đề chứa biến?
A. 2 là số nguyên tố. B. 17 là số chẵn
C. x + y > 0 D. Hình vuông có hai đường chéo vuông góc
Câu 2: Cho mệnh đề P: "x + 1 < x", Q: "x + 1 > x". Xét tính đúng sai của hai mệnh đề P, Q.
A. P đúng, Q sai B. P sai, Q đúng C. P, Q đều đúng D. P, Q đều sai
Câu 3: Liệt kê các phần tử của phần tử tập hợp \(X = \left\{ {x \in \mathbb{Z}|9{x^2} - 8x - 1 = 0} \right\}\).
A. \(X = \left\{ 0 \right\}\) B. \(X = \left\{ 1 \right\}\) C. \(X = \left\{ {\frac{3}{2}} \right\}\) D. \(X = \left\{ {1;\frac{3}{2}} \right\}\)
Câu 4: Cho \(X = \left\{ {7;2;8;4;9;12} \right\}\);\(Y = \left\{ {1;3;7;4} \right\}\). Tập nào sau đây bằng tập \(X \cap Y\)?
A. \(\left\{ {1;2;3;4;8;9;7;12} \right\}\) B. \(\left\{ {2;8;9;12} \right\}\) C. \(\left\{ {4;7} \right\}\) D. \(\left\{ {1;3} \right\}\)
Câu 5: Cho hai tập hợp \(A = \left[ { - 2;7} \right),B = \left( {1;9} \right]\). Tìm \(A \cup B\).
A. \(\left( {1;7} \right)\) B. \(\left[ { - 2;9} \right]\) C. \(\left[ { - 2;1} \right)\) D. \(\left( {7;9} \right]\)
Câu 6: Cho tập hợp \(A = \left[ {m;m + 2} \right],B\left[ { - 1;2} \right]\). Tìm điều kiện của m để \(A \subset B\).
A. \(m \le - 1\) hoặc \(m \ge 0\) B. \( - 1 \le m \le 0\) C. \(1 \le m \le 2\) D. \(m < 1\) hoặc \(m > 2\)
Câu 7: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình \(2x + y < 1\)
A. \(\left( { - 2;1} \right)\) B. \(\left( {3; - 7} \right)\) C. \(\left( {0;1} \right)\) D. \(\left( {0;0} \right)\)
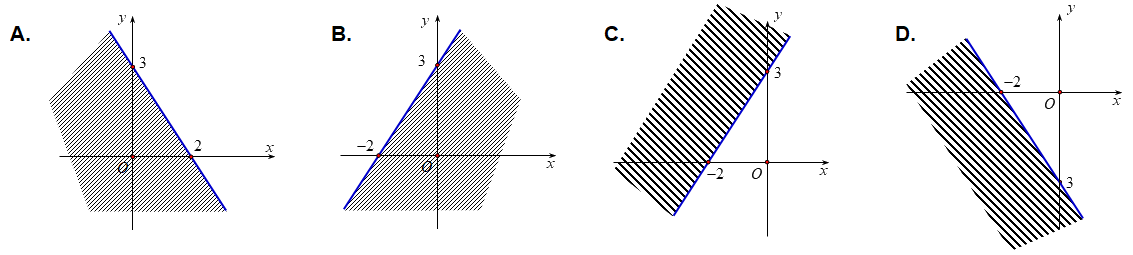
Câu 8: Miền nghiệm của bất phương trình \(3x + 2y > - 6\) là
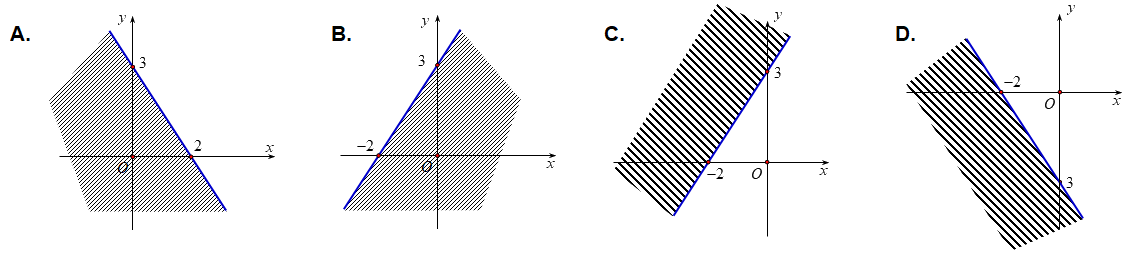
Câu 9: Thống kê điểm thi môn toán trong một kì thi của 400 em học sinh . Người ta thấy số bài được điểm 10 chiếm tỉ lệ 2,5 %. Hỏi tần số của giá trị xi = 10 là bao nhiêu?
A. 10 B. 20 C. 25 D. 5
Câu 10: Trong các loại biểu đồ sau, loại biểu đồ nào thích hợp nhất cho việc thể hiện bảng phân bố tần suất.
A. Biểu đồ hình quạt B. Biểu đồ hình cột
C. Biểu đồ hình cột kép D. Biểu đồ đa giác tần số
Câu 11: Cho dãy số liệu thống kê: 21,23,24,25,22,20. Số trung bình cộng của dãy số liệu thống kê đã cho là
A. 23.5 B. 22 C. 22.5 D. 14
Câu 12: Cho bảng phân bố tần số sau :
xi | 1 | 2 | 3 | 4 | 5 | 6 | Cộng |
ni | 10 | 5 | 15 | 10 | 5 | 5 | 50 |
Mệnh đề đúng là :
A. Tần suất của số 4 là 20% B. Tần suất của số 2 là 20%
C. Tần suất của số 5 là 45 D. Tần suất của số 5 là 90%
Câu 13: Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán
Điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Cộng |
Số học sinh | 2 | 3 | 7 | 18 | 3 | 2 | 4 | 1 | 40 |
Số trung vị là?
A. 5 B. 6 C. 6,5 D. 7
Câu 14: Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán
Điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Cộng |
Số học sinh | 2 | 3 | 7 | 18 | 3 | 2 | 4 | 1 | 40 |
Độ lệch chuẩn là:
A. 1,577 B. 2.553 C. 2,49 D. 6,1
Câu 15: Cho tam giác \(ABC\). Tính \(P = \cos A.\cos \left( {B + C} \right) - \sin A.\sin \left( {B + C} \right)\).
A. \(P = 0.\) B. \(P = 1.\) C. \(P = - 1.\) D. \(P = 2.\)
Câu 16: Cho tam giác \(ABC\). Tìm công thức sai:
A. \(\frac{a}{{\sin A}} = 2R\,.\) B. \(\sin A = \frac{a}{{2R}}\,.\) C. \(b\sin B = 2R\,.\) D. \(\sin C = \frac{{c\sin A}}{a}\,.\)
Câu 17: Tam giác \(ABC\) có \(a = 5,c = 3,\widehat B = {60^0}.\) Độ dài cạnh \(b\) bằng bao nhiêu?
A. \(\sqrt {97} \) B. \(\sqrt {61} .\) C. 7 D. \(\sqrt {19} \)
Câu 18: Cho hình thoi \(ABCD\) có cạnh bằng \(a\). Góc \(\widehat {BAD} = 30^\circ \). Diện tích hình thoi \(ABCD\) là:
A. \(\frac{{{a^2}}}{4}\) B. \(\frac{{{a^2}}}{2}\) C. \(\frac{{{a^2}\sqrt 3 }}{2}\) D. \({a^2}\)
Câu 19: Cho biết \(\tan \alpha = - 5\). Giá trị của biểu thức \(E = \frac{{2\cos \alpha - 3\sin \alpha }}{{3\cos \alpha - \sin \alpha }}\) bằng bao nhiêu?
A. \(\frac{{13}}{{16}}\) B. \( - \frac{{13}}{{16}}\) C. \(\frac{{17}}{8}\) D. \( - \frac{{17}}{8}\)
Câu 20: Cho ba điểm \(A,{\rm{ }}B,{\rm{ }}C\) phân biệt.Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} .\) B. \(\overrightarrow {MP} + \overrightarrow {NM} = \overrightarrow {NP} .\) C. \(\overrightarrow {CA} + \overrightarrow {BA} = \overrightarrow {CB} .\) D. \(\overrightarrow {AA} + \overrightarrow {BB} = \overrightarrow {AB} .\)
Câu 21: Cho \(\overrightarrow a \) và \(\overrightarrow b \) là các vectơ khác \(\overrightarrow 0 \) với \(\overrightarrow a \) là vectơ đối của \(\overrightarrow b \). Khẳng định nào sau đây sai?
A. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) cùng phương. B. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) ngược hướng.
C. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) cùng độ dài. D. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) chung điểm đầu.
Câu 22: Cho tam giác \(ABC\) cân ở \(A\), đường cao \(AH\). Khẳng định nào sau đây sai?
A. \(\overrightarrow {AB} = \overrightarrow {AC} .\) B. \(\overrightarrow {HC} = - \overrightarrow {HB} .\) C. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right|.\) D. \(\overrightarrow {BC} = 2\overrightarrow {HC} .\)
Câu 23: Cho tam giác \(ABC\) có \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \vec 0\). Xác định vị trí điểm \(M.\)
A. \(M\)thỏa mãn hình bình hành \(ACBM.\) B. \(M\)là trung điểm của đoạn thẳng \(AB.\)
C. \(M\)trùng với \(C.\) D. \(M\) là trọng tâm tam giác \(ABC.\)
Câu 24: Cho tam giác đều \(ABC\) có cạnh bằng \(a\) và chiều cao \(AH\). Mệnh đề nào sau đây là sai?
A. \(\overrightarrow {AH} .\overrightarrow {BC} = 0.\) B. \(\left( {\overrightarrow {AB} ,\overrightarrow {HA} } \right) = {150^0}.\) C. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}.\) D. \(\overrightarrow {AC} .\overrightarrow {CB} = \frac{{{a^2}}}{2}.\)
Câu 25: Cho hình chữ nhật \(ABCD\) có \(AB = 8,{\rm{ }}AD = 5.\) Tích \(\overrightarrow {AB} .\overrightarrow {BD} .\)
A. 62 B. 64 C. 14 D. -14
II. Phần tự luận (5 điểm)
Câu 1:
a. Cho hai tập hợp \(S = \left\{ {1;2;3;4} \right\},T = \left\{ {2;4;6} \right\}\). Tìm \(S \cap T,\,\,S \cup T,\,\,S\backslash T.\)
b. Cho tập hợp\(A = \left( { - \infty ;2023} \right)\), \(B = \left[ {4 - 3m; + \infty } \right)\). Tìm \(m\) để \(\mathop C\nolimits_\mathbb{R} B \subset A\).
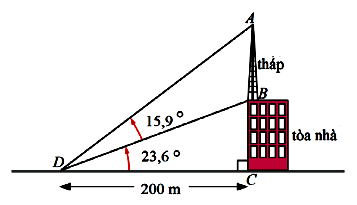
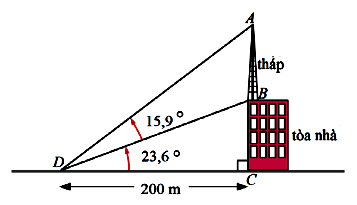
Câu 2: Một cột tháp truyền thông được xây dựng trên nóc của một tòa nhà như hình vẽ. Hãy tính chiều cao của cột tháp
Câu 3: Cho tam giác \(ABC\). Tìm điểm M thỏa mãn điều kiện:
a. \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
b. \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right|\)
----- HẾT -----
Tải về
I. Phần trắc nghiệm (5 điểm – 25 câu)
Câu 1: Trong các câu sau đâu là mệnh đề chứa biến?
A. 2 là số nguyên tố. B. 17 là số chẵn
C. x + y > 0 D. Hình vuông có hai đường chéo vuông góc
Câu 2: Cho mệnh đề P: "x + 1 < x", Q: "x + 1 > x". Xét tính đúng sai của hai mệnh đề P, Q.
A. P đúng, Q sai B. P sai, Q đúng C. P, Q đều đúng D. P, Q đều sai
Câu 3: Liệt kê các phần tử của phần tử tập hợp \(X = \left\{ {x \in \mathbb{Z}|9{x^2} - 8x - 1 = 0} \right\}\).
A. \(X = \left\{ 0 \right\}\) B. \(X = \left\{ 1 \right\}\) C. \(X = \left\{ {\frac{3}{2}} \right\}\) D. \(X = \left\{ {1;\frac{3}{2}} \right\}\)
Câu 4: Cho \(X = \left\{ {7;2;8;4;9;12} \right\}\);\(Y = \left\{ {1;3;7;4} \right\}\). Tập nào sau đây bằng tập \(X \cap Y\)?
A. \(\left\{ {1;2;3;4;8;9;7;12} \right\}\) B. \(\left\{ {2;8;9;12} \right\}\) C. \(\left\{ {4;7} \right\}\) D. \(\left\{ {1;3} \right\}\)
Câu 5: Cho hai tập hợp \(A = \left[ { - 2;7} \right),B = \left( {1;9} \right]\). Tìm \(A \cup B\).
A. \(\left( {1;7} \right)\) B. \(\left[ { - 2;9} \right]\) C. \(\left[ { - 2;1} \right)\) D. \(\left( {7;9} \right]\)
Câu 6: Cho tập hợp \(A = \left[ {m;m + 2} \right],B\left[ { - 1;2} \right]\). Tìm điều kiện của m để \(A \subset B\).
A. \(m \le - 1\) hoặc \(m \ge 0\) B. \( - 1 \le m \le 0\) C. \(1 \le m \le 2\) D. \(m < 1\) hoặc \(m > 2\)
Câu 7: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình \(2x + y < 1\)
A. \(\left( { - 2;1} \right)\) B. \(\left( {3; - 7} \right)\) C. \(\left( {0;1} \right)\) D. \(\left( {0;0} \right)\)
Câu 8: Miền nghiệm của bất phương trình \(3x + 2y > - 6\) là
Câu 9: Thống kê điểm thi môn toán trong một kì thi của 400 em học sinh . Người ta thấy số bài được điểm 10 chiếm tỉ lệ 2,5 %. Hỏi tần số của giá trị xi = 10 là bao nhiêu?
A. 10 B. 20 C. 25 D. 5
Câu 10: Trong các loại biểu đồ sau, loại biểu đồ nào thích hợp nhất cho việc thể hiện bảng phân bố tần suất.
A. Biểu đồ hình quạt B. Biểu đồ hình cột
C. Biểu đồ hình cột kép D. Biểu đồ đa giác tần số
Câu 11: Cho dãy số liệu thống kê: 21,23,24,25,22,20. Số trung bình cộng của dãy số liệu thống kê đã cho là
A. 23.5 B. 22 C. 22.5 D. 14
Câu 12: Cho bảng phân bố tần số sau :
xi | 1 | 2 | 3 | 4 | 5 | 6 | Cộng |
ni | 10 | 5 | 15 | 10 | 5 | 5 | 50 |
Mệnh đề đúng là :
A. Tần suất của số 4 là 20% B. Tần suất của số 2 là 20%
C. Tần suất của số 5 là 45 D. Tần suất của số 5 là 90%
Câu 13: Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán
Điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Cộng |
Số học sinh | 2 | 3 | 7 | 18 | 3 | 2 | 4 | 1 | 40 |
Số trung vị là?
A. 5 B. 6 C. 6,5 D. 7
Câu 14: Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán
Điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Cộng |
Số học sinh | 2 | 3 | 7 | 18 | 3 | 2 | 4 | 1 | 40 |
Độ lệch chuẩn là:
A. 1,577 B. 2.553 C. 2,49 D. 6,1
Câu 15: Cho tam giác \(ABC\). Tính \(P = \cos A.\cos \left( {B + C} \right) - \sin A.\sin \left( {B + C} \right)\).
A. \(P = 0.\) B. \(P = 1.\) C. \(P = - 1.\) D. \(P = 2.\)
Câu 16: Cho tam giác \(ABC\). Tìm công thức sai:
A. \(\frac{a}{{\sin A}} = 2R\,.\) B. \(\sin A = \frac{a}{{2R}}\,.\) C. \(b\sin B = 2R\,.\) D. \(\sin C = \frac{{c\sin A}}{a}\,.\)
Câu 17: Tam giác \(ABC\) có \(a = 5,c = 3,\widehat B = {60^0}.\) Độ dài cạnh \(b\) bằng bao nhiêu?
A. \(\sqrt {97} \) B. \(\sqrt {61} .\) C. 7 D. \(\sqrt {19} \)
Câu 18: Cho hình thoi \(ABCD\) có cạnh bằng \(a\). Góc \(\widehat {BAD} = 30^\circ \). Diện tích hình thoi \(ABCD\) là:
A. \(\frac{{{a^2}}}{4}\) B. \(\frac{{{a^2}}}{2}\) C. \(\frac{{{a^2}\sqrt 3 }}{2}\) D. \({a^2}\)
Câu 19: Cho biết \(\tan \alpha = - 5\). Giá trị của biểu thức \(E = \frac{{2\cos \alpha - 3\sin \alpha }}{{3\cos \alpha - \sin \alpha }}\) bằng bao nhiêu?
A. \(\frac{{13}}{{16}}\) B. \( - \frac{{13}}{{16}}\) C. \(\frac{{17}}{8}\) D. \( - \frac{{17}}{8}\)
Câu 20: Cho ba điểm \(A,{\rm{ }}B,{\rm{ }}C\) phân biệt.Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} .\) B. \(\overrightarrow {MP} + \overrightarrow {NM} = \overrightarrow {NP} .\) C. \(\overrightarrow {CA} + \overrightarrow {BA} = \overrightarrow {CB} .\) D. \(\overrightarrow {AA} + \overrightarrow {BB} = \overrightarrow {AB} .\)
Câu 21: Cho \(\overrightarrow a \) và \(\overrightarrow b \) là các vectơ khác \(\overrightarrow 0 \) với \(\overrightarrow a \) là vectơ đối của \(\overrightarrow b \). Khẳng định nào sau đây sai?
A. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) cùng phương. B. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) ngược hướng.
C. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) cùng độ dài. D. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) chung điểm đầu.
Câu 22: Cho tam giác \(ABC\) cân ở \(A\), đường cao \(AH\). Khẳng định nào sau đây sai?
A. \(\overrightarrow {AB} = \overrightarrow {AC} .\) B. \(\overrightarrow {HC} = - \overrightarrow {HB} .\) C. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right|.\) D. \(\overrightarrow {BC} = 2\overrightarrow {HC} .\)
Câu 23: Cho tam giác \(ABC\) có \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \vec 0\). Xác định vị trí điểm \(M.\)
A. \(M\)thỏa mãn hình bình hành \(ACBM.\) B. \(M\)là trung điểm của đoạn thẳng \(AB.\)
C. \(M\)trùng với \(C.\) D. \(M\) là trọng tâm tam giác \(ABC.\)
Câu 24: Cho tam giác đều \(ABC\) có cạnh bằng \(a\) và chiều cao \(AH\). Mệnh đề nào sau đây là sai?
A. \(\overrightarrow {AH} .\overrightarrow {BC} = 0.\) B. \(\left( {\overrightarrow {AB} ,\overrightarrow {HA} } \right) = {150^0}.\) C. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}.\) D. \(\overrightarrow {AC} .\overrightarrow {CB} = \frac{{{a^2}}}{2}.\)
Câu 25: Cho hình chữ nhật \(ABCD\) có \(AB = 8,{\rm{ }}AD = 5.\) Tích \(\overrightarrow {AB} .\overrightarrow {BD} .\)
A. 62 B. 64 C. 14 D. -14
II. Phần tự luận (5 điểm)
Câu 1:
a. Cho hai tập hợp \(S = \left\{ {1;2;3;4} \right\},T = \left\{ {2;4;6} \right\}\). Tìm \(S \cap T,\,\,S \cup T,\,\,S\backslash T.\)
b. Cho tập hợp\(A = \left( { - \infty ;2023} \right)\), \(B = \left[ {4 - 3m; + \infty } \right)\). Tìm \(m\) để \(\mathop C\nolimits_\mathbb{R} B \subset A\).
Câu 2: Một cột tháp truyền thông được xây dựng trên nóc của một tòa nhà như hình vẽ. Hãy tính chiều cao của cột tháp
Câu 3: Cho tam giác \(ABC\). Tìm điểm M thỏa mãn điều kiện:
a. \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
b. \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right|\)
----- HẾT -----
HƯỚNG DẪN GIẢI CHI TIẾT
I. Phần trắc nghiệm (5 điểm – 25 câu)
1.C | 2.B | 3.B | 4.C | 5.B | 6.B | 7.C | 8.A | 9.A | 10.A |
11.C | 12.A | 13.B | 14.A | 15.C | 16.B | 17.D | 18.A | 19.C | 20.B |
21.B | 22.A | 23.B | 24.D | 25.C | |||||
Câu 1 (NB):
Phương pháp:
Mệnh đề chứa biến là mệnh đề có biến số
Cách giải:
x + y > 0 là mệnh đề chứa biến
Chọn C.
Câu 2 (NB):
Phương pháp:
Mệnh đề chứa biến sai khi có ít nhất 1 giá trị của biến sai.
Cách giải:
P sai, Q đúng.
Chọn B.
Câu 3 (NB):
Phương pháp:
phương trình và đối chiếu điều kiện \(x \in \mathbb{Z}\).
Cách giải:
\(9{x^2} - 8x - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \mathbb{Z}\\x = \frac{{ - 1}}{9} \notin \mathbb{Z}\end{array} \right.\). Suy ra \(X = \left\{ 1 \right\}\)
Chọn B
Câu 4 (NB):
Phương pháp:
Tìm giao 2 tập hợp ta tìm phần tử chung của hai tập hợp đó.
Cách giải:
\(X \cap Y\)=\(\left\{ {4;7} \right\}\)
Chọn C.
Câu 5 (TH):
Phương pháp:
Thể hiện các tập hợp trên trục số và tìm hợp của chúng
Cách giải:
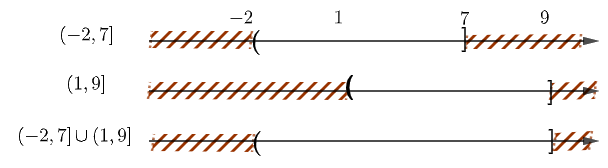
Chọn B.
Câu 6 (VD):
Phương pháp:
\(A \subset B\) khi mọi phần tử của A đều là phần tử của B.
Cách giải:
\(A \subset B \Leftrightarrow \left\{ \begin{array}{l}m \ge - 1\\m + 2 \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge - 1\\m \le 0\end{array} \right. \Leftrightarrow - 1 \le m \le 0\)
Chọn B
Câu 7 (NB):
Phương pháp:
Thay tọa độ x, y vào bât phương trình và kiểm tra tính đúng sai.
Cách giải:
Vì 2.0 + 1 = 1 không nhỏ hơn 1 nên \(\left( {0;1} \right)\)không thuộc miền nghiệm của bất phương trình.
Chọn C.
Câu 8 (NB):
Phương pháp:
Chọn 2 điểm bất kì thuộc hoặc không thuộc miền nghiệm để kiểm tra đáp án. Thông thường ta hay chọn gốc tọa độ O(0,0).
Cách giải:
Vì điểm (0,0) và (3,0) thuộc miền nghiệm nên hình vẽ A đúng.
Chọn A.
Câu 9 (NB):
Phương pháp:
Tần suất \({f_i} = \frac{n}{N} \Rightarrow n = {f_i}.N\)
Cách giải:
\(n = {f_i}.N = 2,5\% .400 = 10\)
Chọn A.
Câu 10 (NB):
Phương pháp:
Biểu đồ hình quạt thích hợp nhất để thể hiện bảng phân bố tần suất.
Cách giải:
Biểu đồ hình quạt thích hợp nhất để thể hiện bảng phân bố tần suất.
Chọn A.
Câu 11 (NB):
Phương pháp:
Số trung bình là \(\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}\)
Cách giải:
\(\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n} = \frac{{21 + 23 + 24 + 25 + 22 + 20}}{6} = 22.5\)
Chọn C.
Câu 12 (TH):
Phương pháp:
Tần suất \({f_i} = \frac{n}{N} \Rightarrow n = {f_i}.N\)
Cách giải:
Tần suất của số 4 là \(f = \frac{{10}}{{50}} = \frac{1}{5} = 20\% \)
Chọn A.
Câu 13 (TH):
Phương pháp:
Dùng MTCT để tính
Cách giải:
Chọn B.
Câu 14 (TH):
Phương pháp:
Dùng MTCT để tính
Cách giải:
Chọn A.
Câu 15 (TH):
Phương pháp:
Hai góc \(\alpha \) và \(\beta \) bù nhau thì \(\sin \alpha = \sin \beta \); \(\cos \alpha = - \cos \beta \).
Cách giải:
Giả sử \(\hat A = \alpha ;\hat B + \hat C = \beta \). Biểu thức trở thành \(P = \cos \alpha \cos \beta - \sin \alpha \sin \beta \).
Trong tam giác ABC có \(\hat A + \hat B + \hat C = {180^^\circ } \Rightarrow \alpha + \beta = {180^^\circ }\).
Do hai góc \(\alpha \) và \(\beta \) bù nhau nên \(\sin \alpha = \sin \beta \); \(\cos \alpha = - \cos \beta \).
Do đó \(P = \cos \alpha \cos \beta - \sin \alpha \sin \beta = - {\cos ^2}\alpha - {\sin ^2}\alpha = - \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = - 1\).
Chọn C.
Câu 16 (NB):
Phương pháp:
Dùng định lý sin trong tam giác.
Cách giải:
Chọn B.
Câu 17 (TH):
Phương pháp:
Dùng định lý cosin \({b^2} = {a^2} + {c^2} - 2ac.\cos B\)
Cách giải:
\({b^2} = {a^2} + {c^2} - 2ac.\cos B = {5^2} + {3^2} - 2.3.8.\cos 60 = 19 \Rightarrow b = \sqrt {19} \)
Chọn D.
Câu 18 (VD):
Phương pháp:
Chia hình thoi thành 2 tam giác bằng nhau và áp dụng công thức diện tích tam giác.
Cách giải:
\({S_{\Delta ABD}} = \frac{1}{2}.AB.AD.\sin A = \frac{1}{2}.a.a.\sin 30 = \frac{{{a^2}}}{4}\)
Chọn A.
Câu 19 (VD):
Phương pháp:
Chia cả tử và mẫu của phân thức cho cos x để xuất hiện tan x.
Cách giải:
\(E = \frac{{2\cos \alpha - 3\sin \alpha }}{{3\cos \alpha - \sin \alpha }} = \frac{{2.\frac{{\cos \alpha }}{{\cos \alpha }} - 3.\frac{{\sin \alpha }}{{\cos \alpha }}}}{{3.\frac{{\cos \alpha }}{{\cos \alpha }} - \frac{{\sin \alpha }}{{\cos \alpha }}}} = \frac{{2 - 3\tan x}}{{3 - \tan x}} = \frac{{17}}{8}\)
Chọn C.
Câu 20 (TH):
Phương pháp:
Dùng quy tắc cộng, quy tắc trừ và quy tắc hình bình hành.
Cách giải:
Theo quy tắc cộng \(\overrightarrow {MP} + \overrightarrow {NM} = \overrightarrow {NM} + \overrightarrow {MP} = \overrightarrow {NP} \)
Chọn B.
Câu 21 (NB):
Phương pháp:
Hai vecto đối nhau khi chúng cùng phương và ngược hướng.
Cách giải:
Chọn B.
Câu 22 (TH):
Phương pháp:
Hai veto bằng nhau khi chúng cùng phương và cùng hướng
Phân biệt giữa vecto và độ dài vecto
Cách giải:
\(\overrightarrow {AB} = \overrightarrow {AC} \)sai do 2 vecto này không cùng phương
Chọn A.
Câu 23 (TH):
Phương pháp:
Dùng tính chất trọng tâm tam giác
Cách giải:
Gọi \(G\) là trọng tâm tam giác \(ABC\).
Ta có \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0 \Rightarrow M \equiv G\).
Chọn B.
Câu 24 (TH):
Phương pháp:
Dùng công thức tích vô hướng của 2 vecto
Cách giải:
\(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|\cos \left( {\overrightarrow {AC} ,\,\overrightarrow {CB} } \right) = a.a.\cos 120 = \frac{{ - {a^2}}}{2}\)
Chọn D.
Câu 25 (VD):
Phương pháp:
Dùng công thức tích vô hướng của 2 vecto
Cách giải:
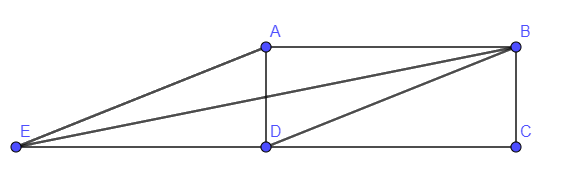
\(B{D^2} = A{B^2} + A{C^2} = {5^2} + {8^2} = 89 \Rightarrow BD = \sqrt {89} \)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {BD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BD} } \right|.\cos \left( {\overrightarrow {AB} ,\,\overrightarrow {BD} } \right) = 8.\sqrt {89} .\cos BAE\\ = 8.\sqrt {89} .\frac{{A{B^2} + A{E^2} - B{E^2}}}{{2AB.AE}} = 8.\sqrt {89} .\frac{{{8^2} + 89 - 125}}{{2.8.\sqrt {89} }} = 14\end{array}\)
Chọn C.
II. Phần tự luận (5 điểm)
Câu 1 (TH):
Phương pháp:
Dùng định nghĩa các phép toán trên tập hợp.
Cách giải:
a. \(S = \left\{ {1;2;3;4} \right\},T = \left\{ {2;4;6} \right\}\)
\(S \cap T = \left\{ {2,4} \right\},\,S \cup T = \left\{ {1,2,3,4,6} \right\},\,\,S\backslash T = \left\{ {1,3} \right\}\)
b. \(\mathop C\nolimits_\mathbb{R} B = \mathbb{R}\backslash \left[ {4 - 3m; + \infty } \right) = \left( { - \infty ,\,4 - 3m} \right)\)
Để \(\mathop C\nolimits_\mathbb{R} B \subset A\) tức là \(\left( { - \infty ,\,4 - 3m} \right) \subset \left( { - \infty ;2023} \right) \Leftrightarrow 4 - 3m \le 2023 \Leftrightarrow m \ge 673\).
Câu 2 (VD):
Phương pháp:
Dùng các hệ thức lượng trong tam giác.
Cách giải:
\(BC = DC.\tan 23,{6^0} = 200.\tan 23,{6^0} \approx 87,378\)m
\(\angle ADC = \angle ADB + \angle BDC = 15,9 + 23,6 = 39,5\)
\(AC = DC.\tan ADC = 200.\tan 39,{5^0} = 164,867m\)
Vậy chiều cao tháp là AB = AC – BC = 164,867 – 87,378 =77,489 m
Câu 3 (VD):
Phương pháp:
Dùng quy tắc cộng, chèn điểm, các vecto bằng nhau.
Cách giải:
a. \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \)
Suy ra MABC là hình bình hành.
b. Ta có \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right| \Leftrightarrow \left| {\overrightarrow {CB} } \right| = \left| {\overrightarrow {AM} } \right| \Rightarrow AM = BC\)
Mà \(A,\;B,\;C\) cố định nên tập hợp điểm \(M\) là đường tròn tâm \(A\), bán kính \(BC\).
Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 8 là một công cụ quan trọng giúp học sinh lớp 10 ôn tập và đánh giá kiến thức đã học trong nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như tập hợp, hàm số, phương trình, bất phương trình, và hình học phẳng.
Đề thi thường được chia thành các phần sau:
Các bài tập về tập hợp thường yêu cầu học sinh xác định các tập hợp, thực hiện các phép toán hợp, giao, hiệu, bù, và chứng minh các đẳng thức tập hợp.
Hàm số là một chủ đề quan trọng trong chương trình Toán 10. Đề thi thường yêu cầu học sinh xác định tập xác định, tập giá trị, vẽ đồ thị hàm số, và giải các bài toán liên quan đến hàm số.
Đây là một trong những chủ đề trọng tâm của đề thi. Học sinh cần nắm vững các phương pháp giải phương trình và bất phương trình, cũng như ứng dụng chúng vào giải các bài toán thực tế.
Các bài tập về hệ phương trình tuyến tính yêu cầu học sinh giải hệ phương trình bằng các phương pháp như phương pháp thế, phương pháp cộng đại số, và phương pháp ma trận.
Bất đẳng thức và Mệnh đề lượng giác đòi hỏi học sinh phải hiểu rõ các tính chất và quy tắc, cũng như khả năng chứng minh và so sánh các giá trị.
Các bài tập về hình học phẳng thường liên quan đến các khái niệm như tam giác, đường thẳng, đường tròn, và các tính chất của chúng. Học sinh cần nắm vững các định lý và công thức để giải các bài toán hình học.
Bài 1: Giải phương trình 2x + 3 = 7
Lời giải:
Bài 2: Tìm tập xác định của hàm số y = √(x - 1)
Lời giải:
Hàm số xác định khi và chỉ khi x - 1 ≥ 0, tức là x ≥ 1. Vậy tập xác định của hàm số là [1, +∞).
Để chuẩn bị tốt nhất cho kỳ thi học kì 1, học sinh nên tham khảo thêm các tài liệu sau:
Chúc các em học sinh đạt kết quả cao trong kỳ thi học kì 1!