Chào mừng các em học sinh đến với đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 5 của giaitoan.edu.vn. Đề thi này được biên soạn dựa trên chương trình học Toán 10 Kết nối tri thức, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ các chủ đề quan trọng trong chương trình học.
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai? A. (P(2)) B. (P(4)). C. (P(3)). D. (P(7))
I. PHẦN TRẮC NGHIỆM
1. B | 2. C | 3. D | 4. A | 5. C |
6. B | 7. A | 8. D | 9. B | 10. B |
11. B | 12. C | 13. B | 14. B | 15. A |
Câu 1.
Cách giải:
Ta có: \(P(2) = 5,P(4) = 17,P(3) = 10,P(7) = 50\)
Chọn B
Câu 2.
Cách giải:
Thay \(x = 1,y = - 1\) vào từng bất phương trình, ta được:
\(1 + ( - 1) - 3 = 3 < 0\) => Lọai A
\( - 1 - ( - 1) = 0\) => Loại B
\(1 + 3.( - 1) + 1 = - 1 < 0\) => Chọn C
\( - 1 - 3.( - 1) - 1 = 1 > 0\) => Loại D
Chọn C
Câu 3.
Cách giải:
Viết lại mệnh đề đã cho: P: “\(\exists x \in \mathbb{R},{x^2} \le 0\)”
Suy ra \(\overline P :\) “\(\forall x \in \mathbb{R},{x^2} > 0\)”
Chọn D
Câu 4.
Cách giải:
Ta có: \(b = AC = 3\sqrt 3 ,c = AB = 3,a = BC = 6\)
\(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{6^2} + {3^2} - {{\left( {3\sqrt 3 } \right)}^2}}}{{2.6.3}} = \frac{1}{2}\)
\( \Rightarrow B = {60^ \circ }\)
Chọn A
Câu 5.
Cách giải:
Ta có: \(\cos {30^o} + \sin {60^o} = \frac{{\sqrt 3 }}{2} + \frac{{\sqrt 3 }}{2} = \sqrt 3 \)
Chọn C
Câu 6.
Cách giải:
Ta có: \(X \cup Y = \{ 1;3;5;7;8;9\} \)
Chọn B
Câu 7.
Cách giải:
Ta có: \({C_\mathbb{R}}A = [ - 3;11) \Rightarrow A = ( - \infty ; - 3) \cup [11; + \infty )\)
\({C_\mathbb{R}}B = ( - 8;1] \Rightarrow B = ( - \infty ; - 8] \cup (1; + \infty )\)
\(\begin{array}{l} \Rightarrow A \cap B = ( - \infty ; - 8] \cup [11; + \infty )\\ \Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = ( - 8;11)\end{array}\)
Chọn A
Câu 8.
Cách giải:
Phủ định của mệnh đề đó là: “Mọi học sinh trong lớp 10A đều thích học môn Toán”.
Chọn D
Câu 9.
Cách giải:
Ta có
\(\begin{array}{l}A = \tan {5^o}.\tan {10^o}.\tan {15^o}...\tan {80^o}.\tan {85^o}\\ = \left( {\tan {5^o}.\tan {{85}^o}} \right).\left( {\tan {{10}^o}.\tan {{80}^o}} \right)...\left( {\tan {{40}^o}.\tan {{50}^o}} \right).\tan {45^o}\\ = \left( {\tan {5^o}.\cot {5^o}} \right).\left( {\tan {{10}^o}.\cot {{10}^o}} \right)...\left( {\tan {{40}^o}.\cot {{40}^o}} \right).\tan {45^o}\\ = \tan {45^o} = 1\end{array}\)
Chọn B
Câu 10.
Cách giải:
Theo định lí sin, ta có \(\frac{a}{{\sin A}} = 2R\)
Chọn B
Câu 11.
Cách giải:
+ Xác định đường thẳng là bở của miền nghiệm:
Đường thẳng d đi qua \(A(\frac{3}{2};0)\) và \(B(0; - 3)\) \( \Rightarrow d:2x - y = 3\)
+ Điểm O(0;0) thuộc miền nghiệm và \(2.0 - 0 = 0 < 3\)
Do đó BPT cần tìm là \(2x - y < 3\)
Chọn B
Câu 12.
Cách giải:
\(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} = \{ 0;2;4;6;8;...\} \)
\(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} = \{ 0;6;12;18;24;...\} \)
\(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} = \{ 1;2\} \)
\(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} = \{ 1;2;3;6\} \)
Ta có: \(N \subset M\) và \(P \subset Q\)
Do đó: \(M \cap N = N\) và \(P \cap Q = P\)
Chọn C
Câu 13.
Cách giải:
Thay \(x = 2,y = 3\) vào từng bất phương trình, ta được:
\(2.2 - 3.3 - 1 = - 6 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(2x - 3y - 1 < 0\)
\(2 - 3 = - 1 < 0 \Rightarrow A(2;3)\) không là nghiệm của BPT \(x - y > 0\)
\(4.2 - 3.3 = - 1 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(4x - 3y < 0\)
\(2 + 3.3 - 7 = 4 \ge 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(x + 3y - 7 \ge 0\)
Chọn B
Câu 14.
Phương pháp
Định lí “Nếu P thì Q” còn được phát biểu là:
“P là điều kiện đủ để có Q”
“Q là điều kiện cần để có P”
Cách giải:
Cách phát biểu khác là: “Một tam giác có hai góc bằng nhau là điều kiện đủ để tam giác đó là tam giác cân”
Chọn B
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
Cách giải:
\(B \subset A \Leftrightarrow (m; + \infty ) \subset (2; + \infty ) \Leftrightarrow m \ge 2\)
Chọn A
II. PHẦN TỰ LUẬN
Câu 1:
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Ta có: \((2x + 1)({x^2} - 9) = 0 \Leftrightarrow (2x + 1)(x - 3)(x + 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - 3 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = 3\\x = - 3\end{array} \right.\)
Mà \( - \frac{1}{2} \notin \mathbb{Z}\)\( \Rightarrow A = \{ - 3;3\} \)
\(B = \{ x \in \mathbb{N}|x < 4\} = \{ 0;1;2;3\} \)
Do đó \(A \cap B = \{ 3\} ,A \cup B = \{ - 3;0;1;2;3\} ,A{\rm{\backslash }}B = \{ - 3\} \)
b) \(M = (0;3)\) và. Để \(M \cap N = N \Leftrightarrow N \subset M\)
\(\begin{array}{l} \Leftrightarrow [m;m + 1) \subset (0;3)\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m + 1 \le 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m \le 2\end{array} \right. \Leftrightarrow 0 < m \le 2\end{array}\)
Mà \(m \in \mathbb{Z}\) nên \(m = 1\) hoặc \(m = 2\).
Vậy \(m = 1\) hoặc \(m = 2\) thì \(M \cap N = N.\)
Câu 2:
Cách giải:
Gọi x là số xe loại A, y là số xe loại B mà công ty cần thuê (đơn vị: chiếc). \((x,y \in \mathbb{N})\)
Theo đề bài ta có: \(0 \le x \le 10\) và \(0 \le y \le 9\)
Tổng chi phí thuê xe là \(F(x;y) = 4x + 3y\) (triệu đồng)
Số người cần chở là 140 mà mỗi xe A chở tối đa 20 người, mỗi xe B chở tối đa 10 người nên ta có \(20x + 10y \ge 140\) hay \(2x + y \ge 14\)
Số hàng cần chở là 9 tấn mà mỗi xe A chở được 0,6 tấn, mỗi xe B chở được 1,5 tấn nên ta có \(0,6x + 1,5y \ge 9\) hay \(2x + 5y \ge 30\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\2x + y \ge 14\\2x + 5y \ge 30\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
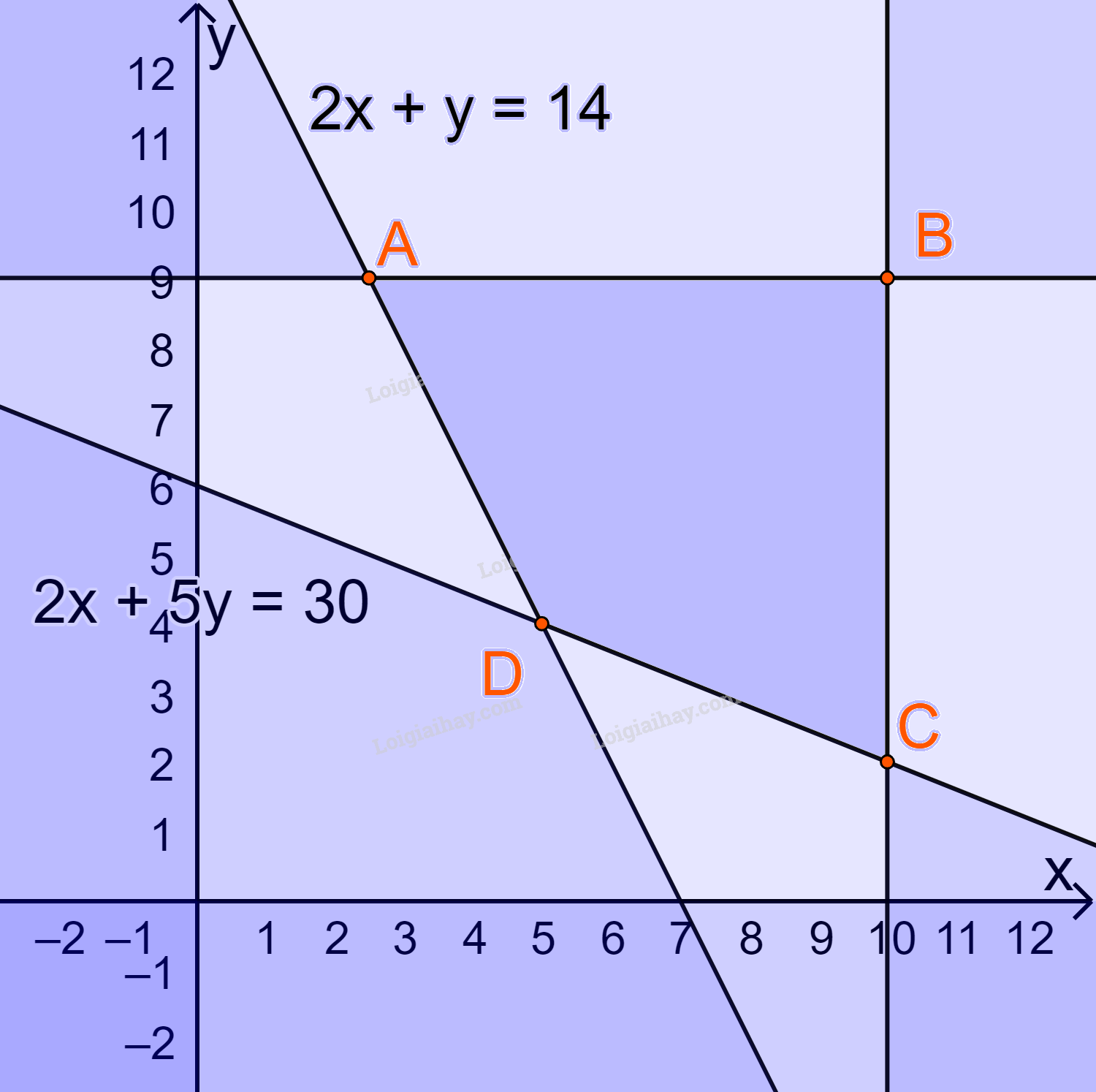
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(\frac{5}{2};9),B(10;9),C(10;2),D(5;4)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 4x + 3y\) ta được:
\(\begin{array}{l}F(\frac{5}{2};9) = 4.\frac{5}{2} + 3.9 = 37\\F(10;9) = 4.10 + 3.9 = 67\\F(10;2) = 4.10 + 3.2 = 46\\F(5;4) = 4.5 + 3.4 = 32\end{array}\)
Do đó F đạt giá trị nhỏ nhất bằng 32 tại \(x = 5;y = 4\)
Vậy công ty đó cần thuê 5 xe loại A và 4 xe loại B.
Câu 3:
Phương pháp:
Áp dụng định lí sin: \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
Cách giải:
Từ hình vẽ, ta suy ra tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} = {90^ \circ } - {30^ \circ } = {60^ \circ }\\\widehat {ABC} = {90^ \circ } + {15^ \circ }30' = {105^ \circ }30'\\AB = 70\end{array}\)
Vì \(A + B + C = {180^ \circ }\) nên \(C = {180^ \circ } - (A + B) = {180^ \circ } - \left( {{{60}^ \circ } + {{105}^ \circ }30'} \right) = {14^ \circ }30'\)
Áp dụn định lí sin trong tam giác ABC ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^ \circ }30'.\frac{{70}}{{\sin {{14}^ \circ }30'}} \approx 269,4\) (m)
Gọi CH là chiều cao ngọn núi
Tam giác ACH vuông tại H, \(\widehat {CAH} = {30^ \circ }\)
\( \Rightarrow CH = AC.\sin A = 269,4.\sin {30^ \circ } = 134,7\)(m)
Vậy ngọn núi cao khoảng 135m.
Câu 4:
Cách giải:
Đặt \(2u = \sin (a + b) = 2\cos (a - b)\)
Dễ thấy \(u \ne \pm 1\) do \(\left| {2u} \right| = \left| {\sin (a + b)} \right| \le 1\).
Ta có:
\(\begin{array}{l}M = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}} = \frac{{2 - \sin 2b + 2 - \sin 2a}}{{\left( {2 - \sin 2a} \right)\left( {2 - \sin 2b} \right)}}\\ = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2\sin 2a - 2\sin 2b + \sin 2a.\sin 2b}}\\ = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2(\sin 2a + \sin 2b) + \sin 2a.\sin 2b}}\end{array}\)
Mà:
\(\sin 2a + \sin 2b = 2\sin \frac{{2a + 2b}}{2}\cos \frac{{2a - 2b}}{2}\)\( = 2\sin \left( {a + b} \right)\cos \left( {a - b} \right) = 2.2u.u = 4{u^2}\);
\(\begin{array}{l}\sin 2a.\sin 2b = - \frac{1}{2}\left[ {\cos \left( {2a + 2b} \right) - \cos \left( {2a - 2b} \right)} \right]\\ = - \frac{1}{2}\left[ {1 - 2{{\sin }^2}(a + b) - 2{{\cos }^2}(a - b) + 1} \right]\\ = {\cos ^2}(a + b) + {\sin ^2}(a - b) - 1\\ = {u^2} + {(2u)^2} - 1 = 5{u^2} - 1\end{array}\)
\( \Rightarrow M = \frac{{4 - 4{u^2}}}{{4 - 2.4{u^2} + 5{u^2} - 1}} = \frac{{4 - 4{u^2}}}{{3 - 3{u^2}}} = \frac{4}{3}\)
Vậy \(M = \frac{4}{3}\) không phụ thuộc vào a,b.
I. PHẦN TRẮC NGHIỆM
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai?
A. \(P(2)\) B. \(P(4)\). C. \(P(3)\). D. \(P(7)\)
Câu 2. Cặp số \((1; - 1)\) là nghiệm của bất phương trình nào sau đây?
A. \(x + y - 3 > 0\) B. \( - x - y < 0\). C. \(x + 3y + 1 < 0\). D. \( - x - 3y - 1 < 0\)
Câu 3. Mệnh đề phủ định của mệnh đề “Có một số thực sao cho bình phương của nó không là số nguyên dương”
A. \(\exists x \in \mathbb{R},{x^2} > 0\) B. \(\exists x \in \mathbb{R},{x^2} \le 0\). C. \(\forall x \in \mathbb{R},{x^2} \le 0\). D. \(\forall x \in \mathbb{R},{x^2} > 0\)
Câu 4. Cho tam giác ABC có \(AC = 3\sqrt 3 ,AB = 3,BC = 6\). Tính số đo góc B?
A. \({60^o}\) B. \({45^o}\). C. \({30^o}\). D. \({120^o}\)
Câu 5. Giá trị của \(\cos {30^o} + \sin {60^o}\) bằng?
A. \(\frac{{\sqrt 3 }}{3}\) B. \(\frac{{\sqrt 3 }}{2}\). C. \(\sqrt 3 \). D. \(1\)
Câu 6. Cho hai tập hợp \(X = \{ 1;3;5;8\} ,Y = \{ 3;5;7;9\} \). Tập hợp \(X \cup Y\) bằng tập hợp nào sau đây?
A. \(\{ 3;5\} \) B. \(\{ 1;3;5;7;8;9\} \). C. \(\{ 1;7;9\} \). D. \(\{ 1;3;5\} \)
Câu 7. Biết rằng \({C_\mathbb{R}}A = [ - 3;11)\) và \({C_\mathbb{R}}B = ( - 8;1]\). Khi đó, \({C_\mathbb{R}}\left( {A \cap B} \right)\) bằng?
A. \(( - 8;11)\) B. \([3;1]\). C. \(( - \infty ; - 8] \cup [11; + \infty )\). D. \(( - \infty ; - 3) \cup (1; + \infty )\)
Câu 8. Cho mệnh đề: “Có học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:
A. Mọi học sinh trong lớp 10A đều thích học môn Văn.
B. Mọi học sinh trong lớp 10A đều không thích học môn Toán.
C. Có học sinh trong lớp 10A thích học môn Toán.
D. Mọi học sinh trong lớp 10A đều thích học môn Toán.
Câu 9. Giá trị của \(A = \tan {5^o}.\tan {10^o}.\tan {15^o}...\tan {80^o}.\tan {85^o}\)
A.\(2\). B. \(1\). C.\(0\). D.\( - 1\).
Câu 10. Cho tam giác ABC có bán kính đường tròn ngoại tiếp là R. Đẳng thức nào sau đây là đúng?
A.\(\frac{a}{{\sin A}} = R\). B. \(\frac{a}{{\sin A}} = 2R\). C. \(\frac{a}{{\sin A}} = 3R\). D. \(\frac{a}{{\sin A}} = 4R\).
Câu 11. Trong mặt phẳng Oxy, phần nửa mặt phẳng không tô màu (không kể bờ) trong hình dưới đây biểu diễn tập nghiệm của bất phương trình nào?
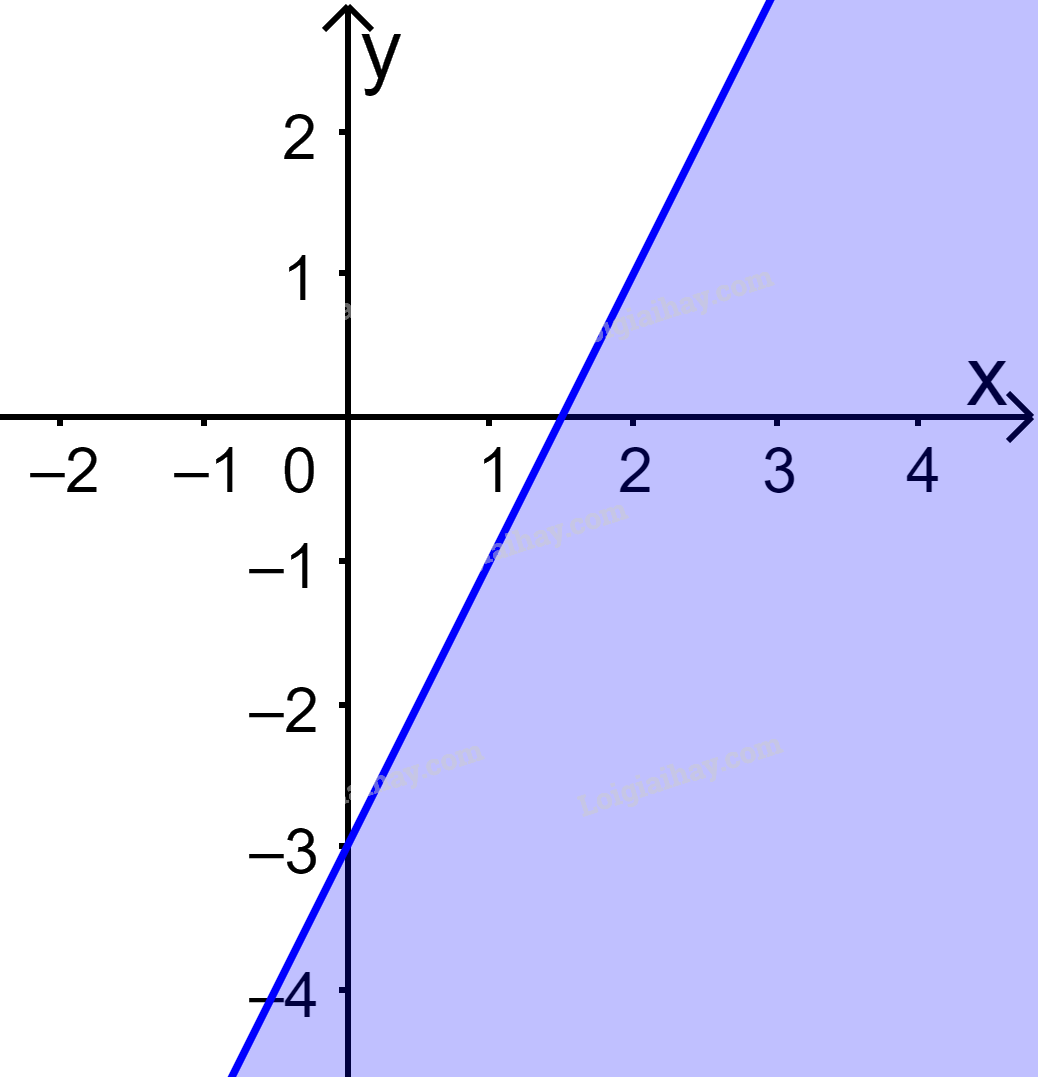
A.\(2x - y > 3\). B. \(2x - y < 3\). C. \(x - 2y > 3\). D. \(x - 2y < 3\).
Câu 12. Cho \(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} \), \(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} \), \(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} \), \(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} \). Khẳng định nào dưới đây đúng?
A.\(M \subset N\). B. \(Q \subset P\). C.\(M \cap N = N\). D. \(P \cap Q = Q\).
Câu 13. Cặp số \((2;3)\) không là nghiệm của bất phươn trình nào sau đây?
A.\(2x - 3y - 1 < 0\). B. \(x - y > 0\). C.\(4x - 3y < 0\). D. \(x + 3y - 7 \ge 0\).
Câu 14. Cách phát biểu khác của định lý “Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân”?
A. Một tam giác có hai góc bằng nhau là điều kiện cần để tam giác đó là tam giác cân.
B. Một tam giác có hai góc bằng nhau là điều kiện đủ để tam giác đó là tam giác cân.
C. Một tam giác có hai góc bằng nhau khi và chỉ khi tam giác đó là tam giác đều.
D. Nếu một tam giác là tam giác cân thì tam giác đó có hai góc bằng nhau.
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
II. PHẦN TỰ LUẬN
Câu 1.
a) Cho hai tập hợp \(A = \{ x \in \mathbb{Z}|(2x + 1)({x^2} - 9) = 0\} \) và \(B = \{ x \in \mathbb{N}|x < 4\} \). Xác định các tập hợp \(A \cap B,A \cup B,A{\rm{\backslash }}B\)
b) Cho hai tập hợp \(M = (0;3)\) và \(N = [m;m + 1)\). Tìm \(m \in \mathbb{Z}\) để \(M \cap N = N\)
Câu 2. Trong một đợt quảng cáo và bán khuyến mãi sản phẩm mới, công ty X cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, mỗi chiếc chở được tối đa 20 người và 0,6 tấn hàng, giá thuê là 4 triệu; xe loại B có 9 chiếc, mỗi chiếc chở được tối đa 10 người và 1,5 tấn hàng, giá thuê là 3 triệu. Hỏi công ty cần thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất?
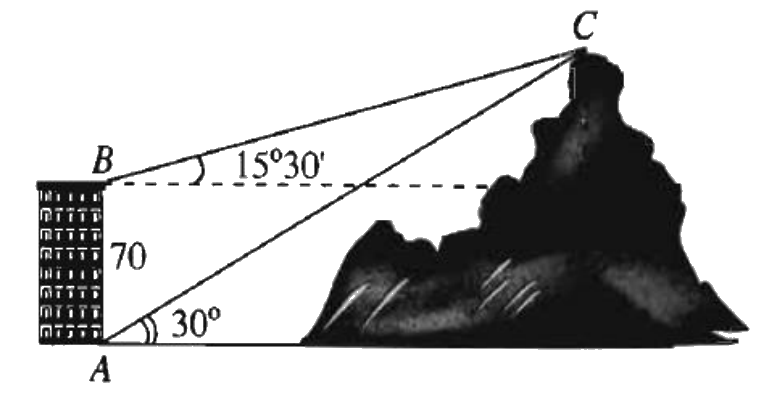
Câu 3. Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi như hình dưới. Biết rằng AB = 70m, phương nhìn AC tạo với phương nằm ngang góc \({30^o}\), phương nhìn BC tạo với phương nằm ngang góc \({15^o}30'\). Tính chiều cao của ngọn núi (làm tròn đến hàng đơn vị).
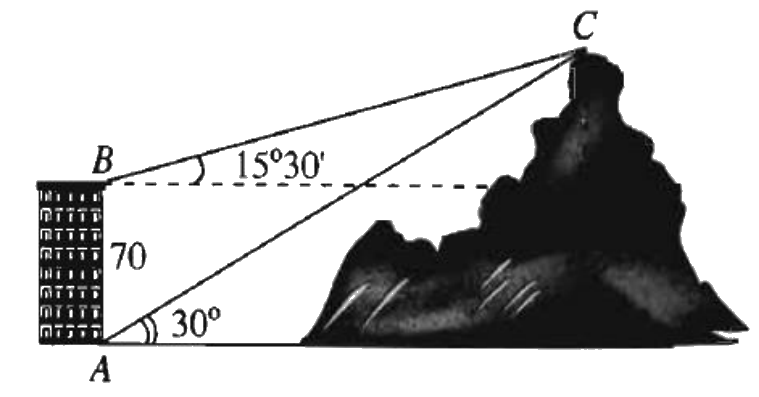
Câu 4. Cho \(\sin (a + b) = 2\cos (a - b)\). Chứng minh biểu thức \(M = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}}\) không phụ thuộc vào a,b.
Tải về
I. PHẦN TRẮC NGHIỆM
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai?
A. \(P(2)\) B. \(P(4)\). C. \(P(3)\). D. \(P(7)\)
Câu 2. Cặp số \((1; - 1)\) là nghiệm của bất phương trình nào sau đây?
A. \(x + y - 3 > 0\) B. \( - x - y < 0\). C. \(x + 3y + 1 < 0\). D. \( - x - 3y - 1 < 0\)
Câu 3. Mệnh đề phủ định của mệnh đề “Có một số thực sao cho bình phương của nó không là số nguyên dương”
A. \(\exists x \in \mathbb{R},{x^2} > 0\) B. \(\exists x \in \mathbb{R},{x^2} \le 0\). C. \(\forall x \in \mathbb{R},{x^2} \le 0\). D. \(\forall x \in \mathbb{R},{x^2} > 0\)
Câu 4. Cho tam giác ABC có \(AC = 3\sqrt 3 ,AB = 3,BC = 6\). Tính số đo góc B?
A. \({60^o}\) B. \({45^o}\). C. \({30^o}\). D. \({120^o}\)
Câu 5. Giá trị của \(\cos {30^o} + \sin {60^o}\) bằng?
A. \(\frac{{\sqrt 3 }}{3}\) B. \(\frac{{\sqrt 3 }}{2}\). C. \(\sqrt 3 \). D. \(1\)
Câu 6. Cho hai tập hợp \(X = \{ 1;3;5;8\} ,Y = \{ 3;5;7;9\} \). Tập hợp \(X \cup Y\) bằng tập hợp nào sau đây?
A. \(\{ 3;5\} \) B. \(\{ 1;3;5;7;8;9\} \). C. \(\{ 1;7;9\} \). D. \(\{ 1;3;5\} \)
Câu 7. Biết rằng \({C_\mathbb{R}}A = [ - 3;11)\) và \({C_\mathbb{R}}B = ( - 8;1]\). Khi đó, \({C_\mathbb{R}}\left( {A \cap B} \right)\) bằng?
A. \(( - 8;11)\) B. \([3;1]\). C. \(( - \infty ; - 8] \cup [11; + \infty )\). D. \(( - \infty ; - 3) \cup (1; + \infty )\)
Câu 8. Cho mệnh đề: “Có học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:
A. Mọi học sinh trong lớp 10A đều thích học môn Văn.
B. Mọi học sinh trong lớp 10A đều không thích học môn Toán.
C. Có học sinh trong lớp 10A thích học môn Toán.
D. Mọi học sinh trong lớp 10A đều thích học môn Toán.
Câu 9. Giá trị của \(A = \tan {5^o}.\tan {10^o}.\tan {15^o}...\tan {80^o}.\tan {85^o}\)
A.\(2\). B. \(1\). C.\(0\). D.\( - 1\).
Câu 10. Cho tam giác ABC có bán kính đường tròn ngoại tiếp là R. Đẳng thức nào sau đây là đúng?
A.\(\frac{a}{{\sin A}} = R\). B. \(\frac{a}{{\sin A}} = 2R\). C. \(\frac{a}{{\sin A}} = 3R\). D. \(\frac{a}{{\sin A}} = 4R\).
Câu 11. Trong mặt phẳng Oxy, phần nửa mặt phẳng không tô màu (không kể bờ) trong hình dưới đây biểu diễn tập nghiệm của bất phương trình nào?
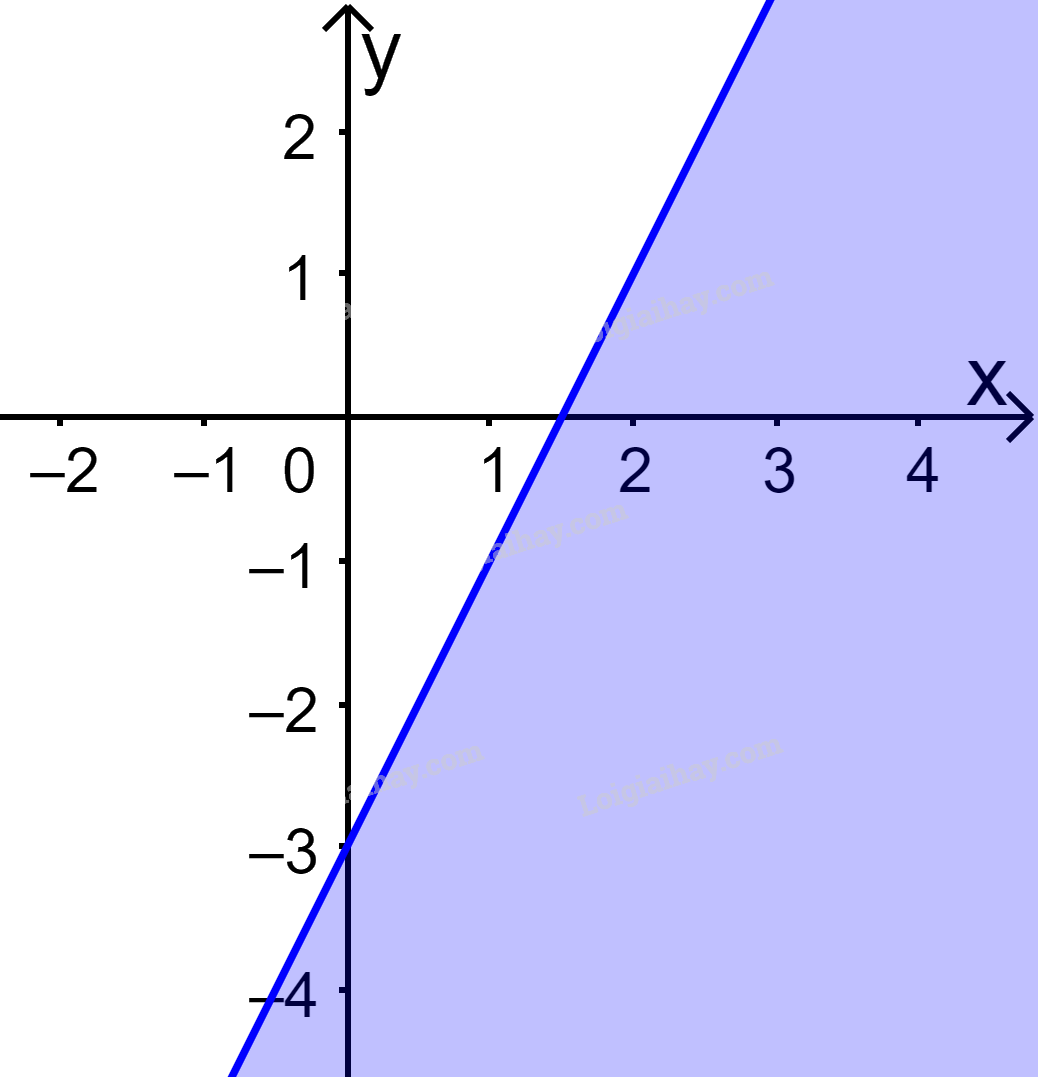
A.\(2x - y > 3\). B. \(2x - y < 3\). C. \(x - 2y > 3\). D. \(x - 2y < 3\).
Câu 12. Cho \(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} \), \(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} \), \(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} \), \(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} \). Khẳng định nào dưới đây đúng?
A.\(M \subset N\). B. \(Q \subset P\). C.\(M \cap N = N\). D. \(P \cap Q = Q\).
Câu 13. Cặp số \((2;3)\) không là nghiệm của bất phươn trình nào sau đây?
A.\(2x - 3y - 1 < 0\). B. \(x - y > 0\). C.\(4x - 3y < 0\). D. \(x + 3y - 7 \ge 0\).
Câu 14. Cách phát biểu khác của định lý “Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân”?
A. Một tam giác có hai góc bằng nhau là điều kiện cần để tam giác đó là tam giác cân.
B. Một tam giác có hai góc bằng nhau là điều kiện đủ để tam giác đó là tam giác cân.
C. Một tam giác có hai góc bằng nhau khi và chỉ khi tam giác đó là tam giác đều.
D. Nếu một tam giác là tam giác cân thì tam giác đó có hai góc bằng nhau.
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
II. PHẦN TỰ LUẬN
Câu 1.
a) Cho hai tập hợp \(A = \{ x \in \mathbb{Z}|(2x + 1)({x^2} - 9) = 0\} \) và \(B = \{ x \in \mathbb{N}|x < 4\} \). Xác định các tập hợp \(A \cap B,A \cup B,A{\rm{\backslash }}B\)
b) Cho hai tập hợp \(M = (0;3)\) và \(N = [m;m + 1)\). Tìm \(m \in \mathbb{Z}\) để \(M \cap N = N\)
Câu 2. Trong một đợt quảng cáo và bán khuyến mãi sản phẩm mới, công ty X cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, mỗi chiếc chở được tối đa 20 người và 0,6 tấn hàng, giá thuê là 4 triệu; xe loại B có 9 chiếc, mỗi chiếc chở được tối đa 10 người và 1,5 tấn hàng, giá thuê là 3 triệu. Hỏi công ty cần thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất?
Câu 3. Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi như hình dưới. Biết rằng AB = 70m, phương nhìn AC tạo với phương nằm ngang góc \({30^o}\), phương nhìn BC tạo với phương nằm ngang góc \({15^o}30'\). Tính chiều cao của ngọn núi (làm tròn đến hàng đơn vị).
Câu 4. Cho \(\sin (a + b) = 2\cos (a - b)\). Chứng minh biểu thức \(M = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}}\) không phụ thuộc vào a,b.
I. PHẦN TRẮC NGHIỆM
1. B | 2. C | 3. D | 4. A | 5. C |
6. B | 7. A | 8. D | 9. B | 10. B |
11. B | 12. C | 13. B | 14. B | 15. A |
Câu 1.
Cách giải:
Ta có: \(P(2) = 5,P(4) = 17,P(3) = 10,P(7) = 50\)
Chọn B
Câu 2.
Cách giải:
Thay \(x = 1,y = - 1\) vào từng bất phương trình, ta được:
\(1 + ( - 1) - 3 = 3 < 0\) => Lọai A
\( - 1 - ( - 1) = 0\) => Loại B
\(1 + 3.( - 1) + 1 = - 1 < 0\) => Chọn C
\( - 1 - 3.( - 1) - 1 = 1 > 0\) => Loại D
Chọn C
Câu 3.
Cách giải:
Viết lại mệnh đề đã cho: P: “\(\exists x \in \mathbb{R},{x^2} \le 0\)”
Suy ra \(\overline P :\) “\(\forall x \in \mathbb{R},{x^2} > 0\)”
Chọn D
Câu 4.
Cách giải:
Ta có: \(b = AC = 3\sqrt 3 ,c = AB = 3,a = BC = 6\)
\(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{6^2} + {3^2} - {{\left( {3\sqrt 3 } \right)}^2}}}{{2.6.3}} = \frac{1}{2}\)
\( \Rightarrow B = {60^ \circ }\)
Chọn A
Câu 5.
Cách giải:
Ta có: \(\cos {30^o} + \sin {60^o} = \frac{{\sqrt 3 }}{2} + \frac{{\sqrt 3 }}{2} = \sqrt 3 \)
Chọn C
Câu 6.
Cách giải:
Ta có: \(X \cup Y = \{ 1;3;5;7;8;9\} \)
Chọn B
Câu 7.
Cách giải:
Ta có: \({C_\mathbb{R}}A = [ - 3;11) \Rightarrow A = ( - \infty ; - 3) \cup [11; + \infty )\)
\({C_\mathbb{R}}B = ( - 8;1] \Rightarrow B = ( - \infty ; - 8] \cup (1; + \infty )\)
\(\begin{array}{l} \Rightarrow A \cap B = ( - \infty ; - 8] \cup [11; + \infty )\\ \Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = ( - 8;11)\end{array}\)
Chọn A
Câu 8.
Cách giải:
Phủ định của mệnh đề đó là: “Mọi học sinh trong lớp 10A đều thích học môn Toán”.
Chọn D
Câu 9.
Cách giải:
Ta có
\(\begin{array}{l}A = \tan {5^o}.\tan {10^o}.\tan {15^o}...\tan {80^o}.\tan {85^o}\\ = \left( {\tan {5^o}.\tan {{85}^o}} \right).\left( {\tan {{10}^o}.\tan {{80}^o}} \right)...\left( {\tan {{40}^o}.\tan {{50}^o}} \right).\tan {45^o}\\ = \left( {\tan {5^o}.\cot {5^o}} \right).\left( {\tan {{10}^o}.\cot {{10}^o}} \right)...\left( {\tan {{40}^o}.\cot {{40}^o}} \right).\tan {45^o}\\ = \tan {45^o} = 1\end{array}\)
Chọn B
Câu 10.
Cách giải:
Theo định lí sin, ta có \(\frac{a}{{\sin A}} = 2R\)
Chọn B
Câu 11.
Cách giải:
+ Xác định đường thẳng là bở của miền nghiệm:
Đường thẳng d đi qua \(A(\frac{3}{2};0)\) và \(B(0; - 3)\) \( \Rightarrow d:2x - y = 3\)
+ Điểm O(0;0) thuộc miền nghiệm và \(2.0 - 0 = 0 < 3\)
Do đó BPT cần tìm là \(2x - y < 3\)
Chọn B
Câu 12.
Cách giải:
\(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} = \{ 0;2;4;6;8;...\} \)
\(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} = \{ 0;6;12;18;24;...\} \)
\(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} = \{ 1;2\} \)
\(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} = \{ 1;2;3;6\} \)
Ta có: \(N \subset M\) và \(P \subset Q\)
Do đó: \(M \cap N = N\) và \(P \cap Q = P\)
Chọn C
Câu 13.
Cách giải:
Thay \(x = 2,y = 3\) vào từng bất phương trình, ta được:
\(2.2 - 3.3 - 1 = - 6 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(2x - 3y - 1 < 0\)
\(2 - 3 = - 1 < 0 \Rightarrow A(2;3)\) không là nghiệm của BPT \(x - y > 0\)
\(4.2 - 3.3 = - 1 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(4x - 3y < 0\)
\(2 + 3.3 - 7 = 4 \ge 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(x + 3y - 7 \ge 0\)
Chọn B
Câu 14.
Phương pháp
Định lí “Nếu P thì Q” còn được phát biểu là:
“P là điều kiện đủ để có Q”
“Q là điều kiện cần để có P”
Cách giải:
Cách phát biểu khác là: “Một tam giác có hai góc bằng nhau là điều kiện đủ để tam giác đó là tam giác cân”
Chọn B
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
Cách giải:
\(B \subset A \Leftrightarrow (m; + \infty ) \subset (2; + \infty ) \Leftrightarrow m \ge 2\)
Chọn A
II. PHẦN TỰ LUẬN
Câu 1:
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Ta có: \((2x + 1)({x^2} - 9) = 0 \Leftrightarrow (2x + 1)(x - 3)(x + 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - 3 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = 3\\x = - 3\end{array} \right.\)
Mà \( - \frac{1}{2} \notin \mathbb{Z}\)\( \Rightarrow A = \{ - 3;3\} \)
\(B = \{ x \in \mathbb{N}|x < 4\} = \{ 0;1;2;3\} \)
Do đó \(A \cap B = \{ 3\} ,A \cup B = \{ - 3;0;1;2;3\} ,A{\rm{\backslash }}B = \{ - 3\} \)
b) \(M = (0;3)\) và. Để \(M \cap N = N \Leftrightarrow N \subset M\)
\(\begin{array}{l} \Leftrightarrow [m;m + 1) \subset (0;3)\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m + 1 \le 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m \le 2\end{array} \right. \Leftrightarrow 0 < m \le 2\end{array}\)
Mà \(m \in \mathbb{Z}\) nên \(m = 1\) hoặc \(m = 2\).
Vậy \(m = 1\) hoặc \(m = 2\) thì \(M \cap N = N.\)
Câu 2:
Cách giải:
Gọi x là số xe loại A, y là số xe loại B mà công ty cần thuê (đơn vị: chiếc). \((x,y \in \mathbb{N})\)
Theo đề bài ta có: \(0 \le x \le 10\) và \(0 \le y \le 9\)
Tổng chi phí thuê xe là \(F(x;y) = 4x + 3y\) (triệu đồng)
Số người cần chở là 140 mà mỗi xe A chở tối đa 20 người, mỗi xe B chở tối đa 10 người nên ta có \(20x + 10y \ge 140\) hay \(2x + y \ge 14\)
Số hàng cần chở là 9 tấn mà mỗi xe A chở được 0,6 tấn, mỗi xe B chở được 1,5 tấn nên ta có \(0,6x + 1,5y \ge 9\) hay \(2x + 5y \ge 30\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\2x + y \ge 14\\2x + 5y \ge 30\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
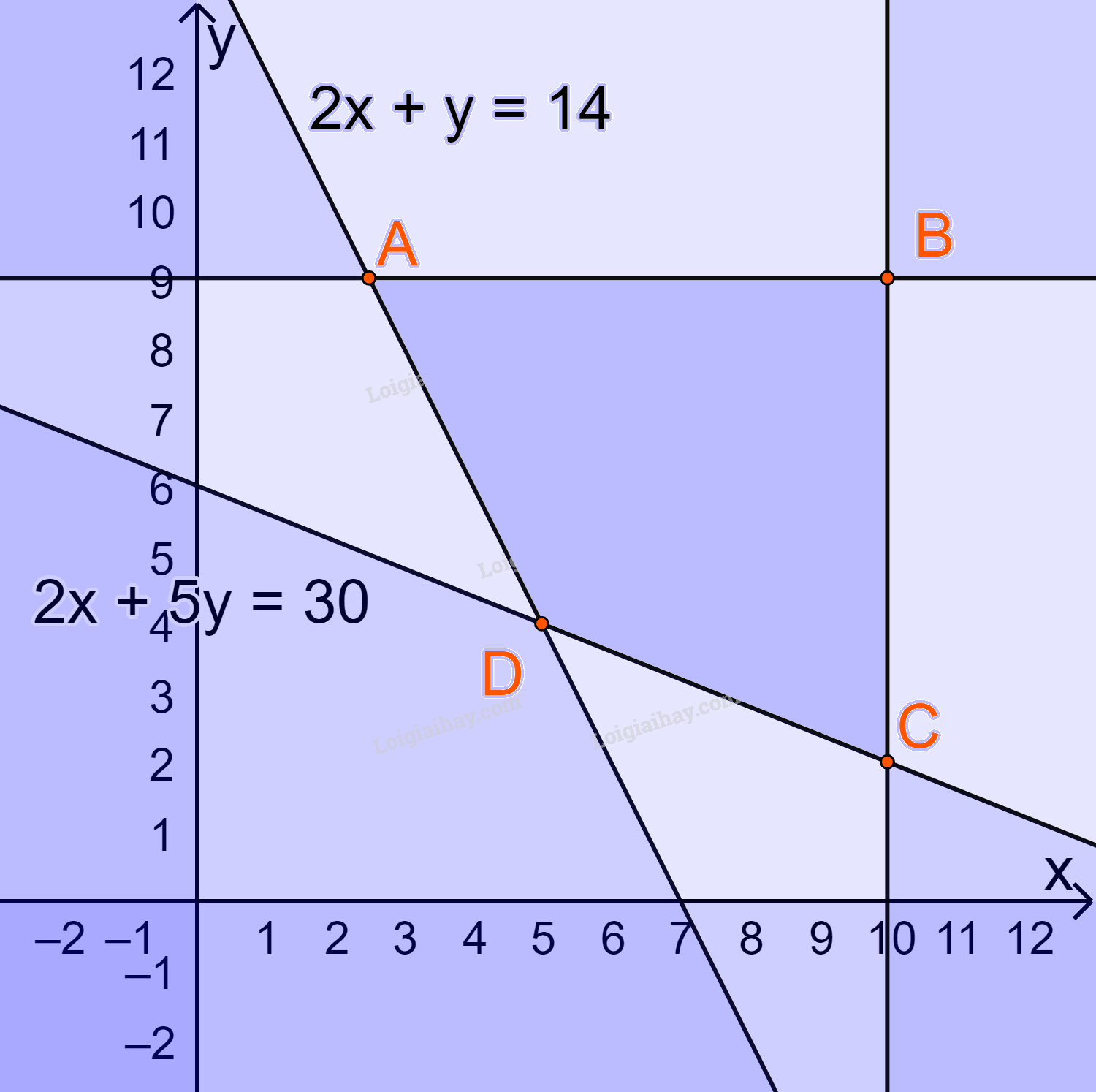
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(\frac{5}{2};9),B(10;9),C(10;2),D(5;4)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 4x + 3y\) ta được:
\(\begin{array}{l}F(\frac{5}{2};9) = 4.\frac{5}{2} + 3.9 = 37\\F(10;9) = 4.10 + 3.9 = 67\\F(10;2) = 4.10 + 3.2 = 46\\F(5;4) = 4.5 + 3.4 = 32\end{array}\)
Do đó F đạt giá trị nhỏ nhất bằng 32 tại \(x = 5;y = 4\)
Vậy công ty đó cần thuê 5 xe loại A và 4 xe loại B.
Câu 3:
Phương pháp:
Áp dụng định lí sin: \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
Cách giải:
Từ hình vẽ, ta suy ra tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} = {90^ \circ } - {30^ \circ } = {60^ \circ }\\\widehat {ABC} = {90^ \circ } + {15^ \circ }30' = {105^ \circ }30'\\AB = 70\end{array}\)
Vì \(A + B + C = {180^ \circ }\) nên \(C = {180^ \circ } - (A + B) = {180^ \circ } - \left( {{{60}^ \circ } + {{105}^ \circ }30'} \right) = {14^ \circ }30'\)
Áp dụn định lí sin trong tam giác ABC ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^ \circ }30'.\frac{{70}}{{\sin {{14}^ \circ }30'}} \approx 269,4\) (m)
Gọi CH là chiều cao ngọn núi
Tam giác ACH vuông tại H, \(\widehat {CAH} = {30^ \circ }\)
\( \Rightarrow CH = AC.\sin A = 269,4.\sin {30^ \circ } = 134,7\)(m)
Vậy ngọn núi cao khoảng 135m.
Câu 4:
Cách giải:
Đặt \(2u = \sin (a + b) = 2\cos (a - b)\)
Dễ thấy \(u \ne \pm 1\) do \(\left| {2u} \right| = \left| {\sin (a + b)} \right| \le 1\).
Ta có:
\(\begin{array}{l}M = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}} = \frac{{2 - \sin 2b + 2 - \sin 2a}}{{\left( {2 - \sin 2a} \right)\left( {2 - \sin 2b} \right)}}\\ = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2\sin 2a - 2\sin 2b + \sin 2a.\sin 2b}}\\ = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2(\sin 2a + \sin 2b) + \sin 2a.\sin 2b}}\end{array}\)
Mà:
\(\sin 2a + \sin 2b = 2\sin \frac{{2a + 2b}}{2}\cos \frac{{2a - 2b}}{2}\)\( = 2\sin \left( {a + b} \right)\cos \left( {a - b} \right) = 2.2u.u = 4{u^2}\);
\(\begin{array}{l}\sin 2a.\sin 2b = - \frac{1}{2}\left[ {\cos \left( {2a + 2b} \right) - \cos \left( {2a - 2b} \right)} \right]\\ = - \frac{1}{2}\left[ {1 - 2{{\sin }^2}(a + b) - 2{{\cos }^2}(a - b) + 1} \right]\\ = {\cos ^2}(a + b) + {\sin ^2}(a - b) - 1\\ = {u^2} + {(2u)^2} - 1 = 5{u^2} - 1\end{array}\)
\( \Rightarrow M = \frac{{4 - 4{u^2}}}{{4 - 2.4{u^2} + 5{u^2} - 1}} = \frac{{4 - 4{u^2}}}{{3 - 3{u^2}}} = \frac{4}{3}\)
Vậy \(M = \frac{4}{3}\) không phụ thuộc vào a,b.
Đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 5 là một công cụ hữu ích cho học sinh trong quá trình ôn tập và chuẩn bị cho kỳ thi quan trọng. Đề thi này không chỉ giúp học sinh đánh giá năng lực hiện tại mà còn làm quen với các dạng bài tập thường gặp trong đề thi chính thức.
Đề thi thường bao gồm hai phần chính: trắc nghiệm và tự luận. Phần trắc nghiệm thường chiếm khoảng 40-50% tổng số điểm, tập trung vào các kiến thức cơ bản và khả năng vận dụng nhanh của học sinh. Phần tự luận chiếm khoảng 50-60% tổng số điểm, đòi hỏi học sinh phải trình bày bài giải một cách logic và chính xác.
Để giúp học sinh hiểu rõ hơn về cấu trúc đề thi và cách giải các bài tập, chúng ta sẽ cùng nhau phân tích một số bài tập tiêu biểu trong đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 5.
Cho hai tập hợp A = {1, 2, 3} và B = {2, 4, 5}. Tìm A ∪ B và A ∩ B.
Giải:
Cho hàm số y = 2x + 1. Tìm giá trị của y khi x = 3.
Giải:
Thay x = 3 vào hàm số y = 2x + 1, ta được y = 2 * 3 + 1 = 7.
Giải bất phương trình 3x - 2 > 1.
Giải:
Vậy tập nghiệm của bất phương trình là x > 1.
Ngoài đề thi giữa kì 1 Toán 10 Kết nối tri thức - Đề số 5, giaitoan.edu.vn còn cung cấp nhiều tài liệu tham khảo và hỗ trợ học tập khác, như:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi giữa kì 1 Toán 10 Kết nối tri thức!