Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 10 Kết nối tri thức - Đề số 1, được biên soạn theo chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp các em học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ các kiến thức trọng tâm của chương trình học kì 2. Cùng với đề thi, chúng tôi cung cấp đáp án chi tiết để các em có thể tự đánh giá kết quả và rút kinh nghiệm.
Phần trắc nghiệm (7 điểm) Câu 1: Tập xác định của hàm số \( y = \frac{x+1}{x-1}\) là:
Phần trắc nghiệm (7 điểm)
Câu 1: Tập xác định của hàm số \(y = \frac{{x + 1}}{{x - 1}}\) là:
A. \(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\).
B. \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
C. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
D. \(\left( {1; + \infty } \right)\).
Câu 2: Trong các hàm số sau, hàm số nào nghịch biến trên \(\mathbb{R}\)?
A. \(y = x\).
B. \(y = - 2x\).
C. \(y = 2x\).
D. \(y = \frac{1}{2}x\)
Câu 3: Cho hàm số \(f\left( x \right) = \sqrt {2{x^2} + 1} \). Giá trị \(f\left( { - 2} \right)\) bằng
A. \( - 3\).
B. \(3\).
C. \(4\).
D. Không xác định.
Câu 4: Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là
A. \(\left( { - \infty ; - 2} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Câu 5: Trục đối xứng của đồ thị hàm số\(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
A. \(x = - \frac{b}{{2a}}.\)
B. \(x = - \frac{c}{{2a}}.\)
C. \(x = - \frac{\Delta }{{4a}}.\)
D. \(x = \frac{b}{{2a}}\).
Câu 6: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng?
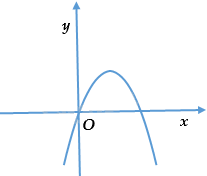
A. \(a > 0.\)
B. \(a < 0.\)
C. \(a = 1.\)
D. \(a = 2.\)
Câu 7: Cho \(f\left( x \right) = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) và \(\Delta = {b^2} - 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).
A. \(\Delta < 0\).
B. \(\Delta = 0\).
C. \(\Delta > 0\).
D. \(\Delta \ge 0\).
Câu 8: Tập nghiệm \(S\) của bất phương trình \({x^2} - x - 6 \le 0\).
A. \(S = \left( { - \infty ; - 3} \right) \cup \left( {2: + \infty } \right)\).
B. \(\left[ { - 2;3} \right]\).
C. \(\left[ { - 3;2} \right]\).
D. \(\left( { - \infty ; - 3} \right] \cup \left[ {2; + \infty } \right)\).
Câu 9: Tìm tập nghiệm \(S\) của bất phương trình \({x^2} - 4x + 4 > 0\).
A. \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
B. \(S = \mathbb{R}\).
C. \(S = \left( {2; + \infty } \right)\).
D. \(S = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Câu 10: Phương trình \(\sqrt {x - 1} = x - 3\) có tập nghiệm là
A. \(S = \left\{ 5 \right\}\).
B. \(S = \left\{ {2;5} \right\}\).
C. \(S = \left\{ 2 \right\}\).
D. \(S = \emptyset \).
Câu 11: Số nghiệm của phương trình \(\sqrt {{x^2} - 4x + 3} = \sqrt {1 - x} \)là
A. Vô số.
B. 2.
C. 1.
D. 0.
Câu 12: Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,ax + by + c = 0,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {a; - b} \right)\).
B. \(\overrightarrow n = \left( {b;a} \right)\).
C. \(\overrightarrow n = \left( {b; - a} \right)\).
D. \(\overrightarrow n = \left( {a;b} \right)\).
Câu 13: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\).
Câu 14: Trong mặt phẳng \(Oxy\), đường thẳng \(d:\,x - 2y - 1 = 0\) song song với đường thẳng có phương trình nào sau đây?
A. \(x + 2y + 1 = 0\).
B. \(2x - y = 0\).
C. \( - x + 2y + 1 = 0\).
D. \( - 2x + 4y - 1 = 0\).
Câu 15: Tính góc giữa hai đường thẳng \(\Delta :x - \sqrt 3 y + 2 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\).
A. \({90^ \circ }\).
B. \({120^ \circ }\).
C. \({60^ \circ }\).
D. \({30^ \circ }\).
Câu 16: Khoảng cách từ điểm \(M\left( {5\,;\, - 1} \right)\) đến đường thẳng \(3x + 2y + 13 = 0\) là:
A. \(2\sqrt {13} \).
B. \(\frac{{28}}{{\sqrt {13} }}\).
C. \(26\).
D. \(\frac{{\sqrt {13} }}{2}\).
Câu 17: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - 6x - 10y + 30 = 0\).
B. \({x^2} + {y^2} - 3x - 2y + 30 = 0\).
C. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).
D. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).
Câu 18: Phương trình nào sau đây là phương trình của đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính bằng \(3\)?
A. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
B. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
C. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
Câu 19: Đường elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\) cắt trục tung tại hai điểm \({B_1}\), \({B_2}\). Độ dài \({B_1}{B_2}\) bằng
A. \(2\sqrt 7 \).
B. \(\sqrt 7 \).
C. \(3\).
D. \(6\).
Câu 20: Tọa độ các tiêu điểm của hypebol \(\left( H \right):\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\) là
A. \({F_1} = \left( { - 5;0} \right);{F_2} = \left( {5;0} \right)\).
B. \({F_1} = \left( {0; - 5} \right);{F_2} = \left( {0;5} \right)\).
C. \({F_1} = \left( {0; - \sqrt 7 } \right);{F_2} = \left( {0;\sqrt 7 } \right)\).
D. \({F_1} = \left( { - \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Câu 21: Tập xác định của hàm số \(y = \sqrt {4 - x} + \sqrt {x - 2} \) là
A. \(D = \left( {2;4} \right)\)
B. \(D = \left[ {2;4} \right]\)
C. \(D = \left\{ {2;4} \right\}\)
D. \(D = \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)\)
Câu 22: Cho hàm số có đồ thị như hình bên dưới.
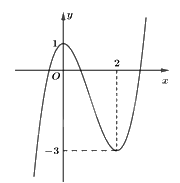
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { - \infty ;3} \right)\).
Câu 23: Đồ thị hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}2x + 3{\rm{ }}\,\,\,khi{\rm{ }}x \le 2\\{x^2} - 3{\rm{ }}\,\,\,khi{\rm{ }}x > 2\end{array} \right.\) đi qua điểm có tọa độ nào sau đây ?
A. \(\left( {0; - 3} \right)\)
B. \(\left( {3;6} \right)\)
C. \(\left( {2;5} \right)\)
D. \(\left( {2;1} \right)\)
Câu 24: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau
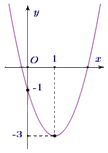
Phương trình của parabol này là
A. \(y = - {x^2} + x - 1\).
B. \(y = 2{x^2} + 4x - 1\).
C. \(y = {x^2} - 2x - 1\).
D. \(y = 2{x^2} - 4x - 1\).
Câu 25: Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} - 4x\) với đường thẳng \(d\,:\,y = - x - 2\) là
A. \(M\left( {0;\, - 2} \right)\), \(N\left( {2;\, - 4} \right)\).
B. \(M\left( { - 1;\, - 1} \right)\), \(N\left( { - 2;\,0} \right)\).
C. \(M\left( {\, - 3;\,1} \right)\), \(N\left( {3;\, - 5} \right)\).
D. \(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Câu 26: Số nghiệm nguyên của bất phương trình \(2{x^2} - 3x - 15 \le 0\) là
A. \(6\).
B. \(5\).
C. \(8\).
D. \(7\).
Câu 27: Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} - \left( {m + 2} \right)x + 8m + 1 \le 0\) vô nghiệm.
A. \(m \in \left[ {0;28} \right]\).
B. \(m \in \left( { - \infty ;0} \right) \cup \left( {28; + \infty } \right)\).
C. \(m \in \left( { - \infty ;0} \right] \cup \left[ {28; + \infty } \right)\).
D. \(m \in \left( {0;28} \right)\).
Câu 28: Số nghiệm của phương trình \(\sqrt {{x^2} - 3x + 1} = 4x - 1\) là
A. \(0\).
B. \(3\).
C. \(2\).
D. \(1\).
Câu 29: Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng \(d\) là
A. \(2x + y - 1 = 0\).
B. \( - 2x + y - 1 = 0\).
C. \(x + 2y + 1 = 0\).
D. \(2x + 3y - 1 = 0\).
Câu 30: Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;1} \right)\) và vuông góc với đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + 5t\end{array} \right.\) có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = - 2 - 3t\\y = 1 + 5t\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x = - 2 + 5t\\y = 1 + 3t\end{array} \right..\)
C. \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 2 + 5t\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x = 1 + 5t\\y = 2 + 3t\end{array} \right..\)
Câu 31: Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( { - 1;2} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(2\sqrt 5 \).
A. \(m = 2.\)
B. \(\left[ \begin{array}{l}m = - 2\\m = \frac{1}{2}\end{array} \right.\).
C. \(m = - \frac{1}{2}\).
D. Không tồn tại \(m\).
Câu 32: Trong mặt phẳng \(Oxy\), đường tròn đi qua ba điểm \(A\left( {1;2} \right)\), \(B\left( {5;2} \right)\), \(C\left( {1; - 3} \right)\) có phương trình là.
A. \({x^2} + {y^2} + 25x + 19y - 49 = 0\).
B. \(2{x^2} + {y^2} - 6x + y - 3 = 0\).
C. \({x^2} + {y^2} - 6x + y - 1 = 0\).
D. \({x^2} + {y^2} - 6x + xy - 1 = 0\).
Câu 33: Trong hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;\,2} \right),\,B\left( {3,\,4} \right)\) và tiếp xúc với đường thẳng \(\Delta :\,3x + y - 3 = 0\), biết tâm của \(\left( C \right)\) có tọa độ là những số nguyên. Phương trình đường tròn \(\left( C \right)\) là
A. \({x^2} + {y^2} - 3x - 7y + 12 = 0.\)
B. \({x^2} + {y^2} - 6x - 4y + 5 = 0.\)
C. \({x^2} + {y^2} - 8x - 2y + 7 = 0.\)
D. \({x^2} + {y^2} - 2x - 8y + 20 = 0.\)
Câu 34: Cho đường hypebol có phương trình \(\left( H \right):100{x^2} - 25{y^2} = 100\). Tiêu cự của hypebol đó là
A. \(2\sqrt {10} \).
B. \(2\sqrt {104} \).
C. \(\sqrt {10} \).
D. \(\sqrt {104} \).
Câu 35: Cho parabol \(\left( P \right):{y^2} = 8x\) có tiêu điểm là
A. \(F\left( {0;4} \right)\).
B. \(F\left( {0;2} \right)\).
C. \(F\left( {2;0} \right)\).
D. \(F\left( {4;0} \right)\).
Phần tự luận (3 điểm)
Bài 1. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B.
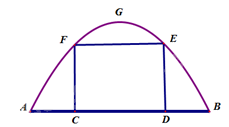
Bài 2. Cho tam giác \(ABC\) có \(A\left( {1;3} \right)\) và hai đường trung tuyến \(BM:x + 7y - 10 = 0\)và p\(CN:x - 2y + 2 = 0\). Viết phương trình đường thẳng chứa cạnh \(BC\) của tam giác \(ABC\).
Bài 3. Tìm tất cả các giá trị thực của tham số \(m\)để hàm số \(y = \frac{{mx}}{{\sqrt {x - m + 2} - 1}}\)xác định trên \(\left( {0;1} \right)\).
Bài 4. Cho tam giác \(ABC\) biết \(H\left( {3;2} \right)\), \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\) lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng \(BC\) có phương trình \(x + 2y - 2 = 0\). Tìm phương trình đường tròn ngoại tiếp tam giác \(ABC\)?
-------- Hết --------
Phần trắc nghiệm
Câu 1. C | Câu 2. B | Câu 3. B | Câu 4. D | Câu 5. A | Câu 6. B | Câu 7. A |
Câu 8. B | Câu 9. A | Câu 10. A | Câu 11. C | Câu 12. D | Câu 13. D | Câu 14. D |
Câu 15. C | Câu 16. A | Câu 17. A | Câu 18. D | Câu 19. A | Câu 20. D | Câu 21. B |
Câu 22. C | Câu 23. B | Câu 24. D | Câu 25. D | Câu 26. A | Câu 27. D | Câu 28. D |
Câu 29. A | Câu 30. B | Câu 31. B | Câu 32. C | Câu 33. C | Câu 34. B | Câu 35. C |
Câu 1: Tập xác định của hàm số \(y = \frac{{x + 1}}{{x - 1}}\) là:
A. \(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\).
B. \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
C. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
D. \(\left( {1; + \infty } \right)\).
Lời giải
Điều kiện xác định: \(x - 1 \ne 0 \Leftrightarrow x \ne 1\)
Vậy tập xác định của hàm số \(y = \frac{{x + 1}}{{x - 1}}\) là \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
Đáp án C.
Câu 2: Trong các hàm số sau, hàm số nào nghịch biến trên \(\mathbb{R}\)?
A. \(y = x\).
B. \(y = - 2x\).
C. \(y = 2x\).
D. \(y = \frac{1}{2}x\)
Lời giải
Hàm số \(y = ax + b\) với \(a \ne 0\) nghịch biến trên \(\mathbb{R}\) khi và chỉ khi \(a < 0\).
Đáp án B.
Câu 3: Cho hàm số \(f\left( x \right) = \sqrt {2{x^2} + 1} \). Giá trị \(f\left( { - 2} \right)\) bằng
A. \( - 3\).
B. \(3\).
C. \(4\).
D. Không xác định.
Lời giải
Ta có \(f\left( { - 2} \right) = \sqrt {2.{{\left( { - 2} \right)}^2} + 1} = 3\).
Đáp án B.
Câu 4: Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là
A. \(\left( { - \infty ; - 2} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Lời giải
Hàm số \(y = {x^2} - 4x + 3\)có \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\).
Vì vậy hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
Đáp án D.
Câu 5: Trục đối xứng của đồ thị hàm số \(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
A. \(x = - \frac{b}{{2a}}.\)
B. \(x = - \frac{c}{{2a}}.\)
C. \(x = - \frac{\Delta }{{4a}}.\)
D. \(x = \frac{b}{{2a}}\).
Lời giải
Đáp án A.
Câu 6: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng?
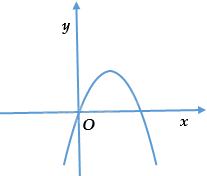
A. \(a > 0.\)
B. \(a < 0.\)
C. \(a = 1.\)
D. \(a = 2.\)
Lời giải
Bề lõm hướng xuống \(a < 0.\)
Đáp án B.
Câu 7: Cho \(f\left( x \right) = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) và \(\Delta = {b^2} - 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).
A. \(\Delta < 0\).
B. \(\Delta = 0\).
C. \(\Delta > 0\).
D. \(\Delta \ge 0\).
Lời giải
Theo định lý về dấu của tam thức bậc hai thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\) khi \(\Delta < 0\).
Đáp án A.
Câu 8: Tập nghiệm \(S\) của bất phương trình \({x^2} - x - 6 \le 0\).
A. \(S = \left( { - \infty ; - 3} \right) \cup \left( {2: + \infty } \right)\).
B. \(\left[ { - 2;3} \right]\).
C. \(\left[ { - 3;2} \right]\).
D. \(\left( { - \infty ; - 3} \right] \cup \left[ {2; + \infty } \right)\).
Lời giải
Ta có: \({x^2} - x - 6 \le 0 \Leftrightarrow - 2 \le x \le 3\).
Tập nghiệm bất phương trình là: \(S = \left[ { - 2;3} \right]\).
Đáp án B.
Câu 9: Tìm tập nghiệm \(S\) của bất phương trình \({x^2} - 4x + 4 > 0\).
A. \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
B. \(S = \mathbb{R}\).
C. \(S = \left( {2; + \infty } \right)\).
D. \(S = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Lời giải
* Bảng xét dấu:
\(x\) | \( - \infty \) | \(2\) | \( + \infty \) |
\({x^2} - 4x + 4\) | \( + \) | \(0\) | \( + \) |
* Tập nghiệm của bất phương trình là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
Đáp án A.
Câu 10: Phương trình \(\sqrt {x - 1} = x - 3\) có tập nghiệm là
A. \(S = \left\{ 5 \right\}\).
B. \(S = \left\{ {2;5} \right\}\).
C. \(S = \left\{ 2 \right\}\).
D. \(S = \emptyset \).
Lời giải
Ta có: \(\sqrt {x - 1} = x - 3 \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\x - 1 = {\left( {x - 3} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} - 7x + 10 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 2\\x = 5\end{array} \right.\end{array} \right. \Leftrightarrow x = 5\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ 5 \right\}\).
Đáp án A.
Câu 11: Số nghiệm của phương trình \(\sqrt {{x^2} - 4x + 3} = \sqrt {1 - x} \)là
A. Vô số.
B. 2.
C. 1.
D. 0.
Lời giải
Ta có \(\sqrt {{x^2} - 4x + 3} = \sqrt {1 - x} \)
\( \Leftrightarrow \) \(\left\{ \begin{array}{l}1 - x \ge 0\\{x^2} - 4x + 3 = 1 - x\end{array} \right.\)\( \Leftrightarrow \)\(\left\{ \begin{array}{l}x \le 1\\{x^2} - 3x + 2 = 0\end{array} \right.\)\( \Leftrightarrow \) \(\left\{ \begin{array}{l}x \le 1\\\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \)\(x = 1\).
Vậy phương trình đã cho có 1 nghiệm.
Đáp án C.
Câu 12: Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,ax + by + c = 0,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {a; - b} \right)\).
B. \(\overrightarrow n = \left( {b;a} \right)\).
C. \(\overrightarrow n = \left( {b; - a} \right)\).
D. \(\overrightarrow n = \left( {a;b} \right)\).
Lời giải
Ta có một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)là \(\overrightarrow n = \left( {a;b} \right)\).
Do đó chọn đáp án
D. \(\overrightarrow {{n_1}} = \left( { - a;b} \right).\)
Đáp án D.
Câu 13: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\).
Lời giải
Vectơ chỉ phương \(\overrightarrow {AB} = \left( {0;6} \right)\).
Phương trình đường thẳng \(AB\) đi qua \(A\) và có vecto chỉ phương \(\overrightarrow {AB} = \left( {0;6} \right)\) là \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\)
Đáp án D.
Câu 14: Trong mặt phẳng \(Oxy\), đường thẳng \(d:\,x - 2y - 1 = 0\) song song với đường thẳng có phương trình nào sau đây?
A. \(x + 2y + 1 = 0\).
B. \(2x - y = 0\).
C. \( - x + 2y + 1 = 0\).
D. \( - 2x + 4y - 1 = 0\).
Lời giải
Ta kiểm tra lần lượt các đường thẳng
.+) Với \(d{}_1:x + 2y + 1 = 0\) có \(\frac{1}{1} \ne \frac{2}{{ - 2}} \Rightarrow d\) cắt \(d{}_1\).
.+) Với \(d{}_2:2x - y = 0\) có \(\frac{2}{1} \ne \frac{{ - 1}}{{ - 2}} \Rightarrow d\)cắt \(d{}_2\).
.+) Với \(d{}_3: - x + 2y + 1 = 0\) có \(\frac{{ - 1}}{1} = \frac{2}{{ - 2}} \ne \frac{1}{{ - 1}} \Rightarrow d\)trùng \(d{}_3\).
.+) Với \(d{}_4: - 2x + 4y - 1 = 0\) có \(\frac{1}{{ - 2}} = \frac{{ - 2}}{4} \ne \frac{{ - 1}}{{ - 1}} \Rightarrow d\) song song \(d{}_4\).
Đáp án D.
Câu 15: Tính góc giữa hai đường thẳng \(\Delta :x - \sqrt 3 y + 2 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\).
A. \({90^ \circ }\).
B. \({120^ \circ }\).
C. \({60^ \circ }\).
D. \({30^ \circ }\).
Lời giải
Đường thẳng \(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {1; - \sqrt 3 } \right)\), đường thẳng \(\Delta '\) có vectơ pháp tuyến \(\overrightarrow {n'} = \left( {1;\sqrt 3 } \right)\).
Gọi \(\alpha \) là góc giữa hai đường thẳng \(\Delta ,\Delta '.\)\(\cos \alpha = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {1 - 3} \right|}}{{\sqrt {1 + 3} .\sqrt {1 + 3} }} = \frac{1}{2} \Rightarrow \alpha = {60^ \circ }\).
Đáp án C.
Câu 16: Khoảng cách từ điểm \(M\left( {5\,;\, - 1} \right)\) đến đường thẳng \(3x + 2y + 13 = 0\) là:
A. \(2\sqrt {13} \).
B. \(\frac{{28}}{{\sqrt {13} }}\).
C. \(26\).
D. \(\frac{{\sqrt {13} }}{2}\).
Lời giải
Khoảng cách \(d = \frac{{\left| {3.5 + 2.\left( { - 1} \right) + 13} \right|}}{{\sqrt {{3^2} + {2^2}} }} = \frac{{26}}{{\sqrt {13} }} = 2\sqrt {13} \).
Đáp án A.
Câu 17: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - 6x - 10y + 30 = 0\).
B. \({x^2} + {y^2} - 3x - 2y + 30 = 0\).
C. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).
D. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).
Lời giải
Phương trình đường tròn đã cho có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình đường tròn\( \Leftrightarrow {a^2} + {b^2} - c > 0.\)
Xét đáp án A, ta có \(a = 3,\,b = 5,\,c = 30\) \( \Rightarrow {a^2} + {b^2} - c = 4 > 0\).
Đáp án A.
Câu 18: Phương trình nào sau đây là phương trình của đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính bằng \(3\)?
A. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
B. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
C. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
Lời giải
Phương trình đường tròn tâm \(I\left( { - 1;2} \right)\) và bán kính \(R = 3\) là: \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
Đáp án D.
Câu 19: Đường elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\) cắt trục tung tại hai điểm \({B_1}\), \({B_2}\). Độ dài \({B_1}{B_2}\) bằng
A. \(2\sqrt 7 \).
B. \(\sqrt 7 \).
C. \(3\).
D. \(6\).
Lời giải
Ta có \(x = 0 \Rightarrow y = \pm \sqrt 7 \).
Elip cắt trục tung tại hai điểm \({B_1}\left( {0; - \sqrt 7 } \right)\), \({B_2}\left( {0;\sqrt 7 } \right)\). Suy ra \({B_1}{B_2} = 2\sqrt 7 \).
Đáp án A.
Câu 20: Tọa độ các tiêu điểm của hypebol \(\left( H \right):\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\) là
A. \({F_1} = \left( { - 5;0} \right);{F_2} = \left( {5;0} \right)\).
B. \({F_1} = \left( {0; - 5} \right);{F_2} = \left( {0;5} \right)\).
C. \({F_1} = \left( {0; - \sqrt 7 } \right);{F_2} = \left( {0;\sqrt 7 } \right)\).
D. \({F_1} = \left( { - \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Lời giải
Gọi \({F_1} = \left( { - c;0} \right);{F_2} = \left( {c;0} \right)\) là hai tiêu điểm của \(\left( H \right)\).
Từ phương trình \(\left( H \right):\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\), ta có: \({a^2} = 4\) và \({b^2} = 3\) suy ra \({c^2} = {a^2} + {b^2} = 7 \Rightarrow c = \sqrt 7 ,\left( {c > 0} \right)\).
Vậy tọa độ các tiêu điểm của \(\left( H \right)\)là \({F_1} = \left( { - \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Đáp án D.
Câu 21: Tập xác định của hàm số \(y = \sqrt {4 - x} + \sqrt {x - 2} \) là
A. \(D = \left( {2;4} \right)\)
B. \(D = \left[ {2;4} \right]\)
C. \(D = \left\{ {2;4} \right\}\)
D. \(D = \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)\)
Lời giải
Điều kiện: \(\left\{ \begin{array}{l}4 - x \ge 0\\x - 2 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \le 4\\x \ge 2\end{array} \right.\) suy ra TXĐ: \(D = \left[ {2;4} \right]\).
Đáp án B.
Câu 22: Cho hàm số có đồ thị như hình bên dưới.
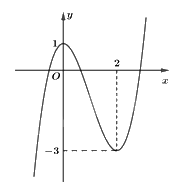
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { - \infty ;3} \right)\).
Lời giải
Trên khoảng \(\left( {0;2} \right)\), đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Đáp án C.
Câu 23: Đồ thị hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}2x + 3{\rm{ }}\,\,\,khi{\rm{ }}x \le 2\\{x^2} - 3{\rm{ }}\,\,\,khi{\rm{ }}x > 2\end{array} \right.\) đi qua điểm có tọa độ nào sau đây ?
A. \(\left( {0; - 3} \right)\)
B. \(\left( {3;6} \right)\)
C. \(\left( {2;5} \right)\)
D. \(\left( {2;1} \right)\)
Lời giải
Thay tọa độ điểm \(\left( {0; - 3} \right)\)vào hàm số ta được : \(f\left( 0 \right) = 3 \ne - 3\) nên loại đáp án A
Thay tọa độ điểm \(\left( {3;6} \right)\)vào hàm số ta được : \(f\left( 3 \right) = 9 - 3 = 6\), thỏa mãn nên chọn đáp án B
Đáp án B.
Câu 24: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau
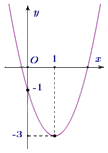
Phương trình của parabol này là
A. \(y = - {x^2} + x - 1\).
B. \(y = 2{x^2} + 4x - 1\).
C. \(y = {x^2} - 2x - 1\).
D. \(y = 2{x^2} - 4x - 1\).
Lời giải
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, - 1} \right)\) nên \(c = - 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, - 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 1\\a{.1^2} + b.1 - 1 = - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 4\end{array} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} - 4x - 1\).
Đáp án D.
Câu 25: Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} - 4x\) với đường thẳng \(d\,:\,y = - x - 2\) là
A. \(M\left( {0;\, - 2} \right)\), \(N\left( {2;\, - 4} \right)\).
B. \(M\left( { - 1;\, - 1} \right)\), \(N\left( { - 2;\,0} \right)\).
C. \(M\left( {\, - 3;\,1} \right)\), \(N\left( {3;\, - 5} \right)\).
D. \(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Lời giải
Hoành độ giao điểm của \(\left( P \right)\) và \(d\) là nghiệm của phương trình:
\({x^2} - 4x = - x - 2\, \Leftrightarrow \,{x^2} - 3x + 2 = 0\, \Leftrightarrow \,\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\).
Vậy tọa độ giao điểm của \(\left( P \right)\) và \(d\) là \(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Đáp án D.
Câu 26: Số nghiệm nguyên của bất phương trình \(2{x^2} - 3x - 15 \le 0\) là
A. \(6\).
B. \(5\).
C. \(8\).
D. \(7\).
Lời giải
Xét \(f\left( x \right) = 2{x^2} - 3x - 15\).
\(f\left( x \right) = 0\)\( \Leftrightarrow x = \frac{{3 \pm \sqrt {129} }}{4}\).
Ta có bảng xét dấu:
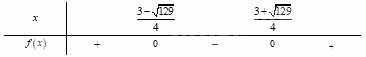
Tập nghiệm của bất phương trình là \(S = \left[ {\frac{{3 - \sqrt {129} }}{4};\,\frac{{3 + \sqrt {129} }}{4}} \right]\).
Do đó bất phương trình có \(6\) nghiệm nguyên là \( - 2\), \( - 1\), \(0\), \(1\), \(2\), \(3\).
Đáp án A.
Câu 27: Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} - \left( {m + 2} \right)x + 8m + 1 \le 0\) vô nghiệm.
A. \(m \in \left[ {0;28} \right]\).
B. \(m \in \left( { - \infty ;0} \right) \cup \left( {28; + \infty } \right)\).
C. \(m \in \left( { - \infty ;0} \right] \cup \left[ {28; + \infty } \right)\).
D. \(m \in \left( {0;28} \right)\).
Lời giải
Bất phương trình vô nghiệm khi và chỉ khi \({\left( {m + 2} \right)^2} - 4\left( {8m + 1} \right) < 0\)\( \Leftrightarrow {m^2} - 28m < 0\) \(0 < m < 28\)
Đáp án D.
Câu 28: Số nghiệm của phương trình \(\sqrt {{x^2} - 3x + 1} = 4x - 1\) là
A. \(0\).
B. \(3\).
C. \(2\).
D. \(1\).
Lời giải
Phương trình \(\sqrt {{x^2} - 3x + 1} = 4x - 1\)\( \Leftrightarrow \left\{ \begin{array}{l}4x - 1 \ge 0\\{x^2} - 3x + 1 = {\left( {4x - 1} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{4}\\15{x^2} - 5x = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{4}\\\left[ \begin{array}{l}x = 0\left( l \right)\\x = \frac{1}{3}\left( n \right)\end{array} \right.\end{array} \right.\)\( \Leftrightarrow x = \frac{1}{3}\).
Đáp án B.
Câu 29: Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng \(d\) là
A. \(2x + y - 1 = 0\).
B. \( - 2x + y - 1 = 0\).
C. \(x + 2y + 1 = 0\).
D. \(2x + 3y - 1 = 0\).
Lời giải
Đường thẳng \(\left( d \right):\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}t = x - 5\\y = - 9 - 2t\end{array} \right.\)\( \Rightarrow y = - 9 - 2\left( {x - 5} \right)\)\( \Leftrightarrow 2x + y - 1 = 0\).
Đáp án A.
Câu 30: Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;1} \right)\) và vuông góc với đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + 5t\end{array} \right.\) có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = - 2 - 3t\\y = 1 + 5t\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x = - 2 + 5t\\y = 1 + 3t\end{array} \right..\)
C. \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 2 + 5t\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x = 1 + 5t\\y = 2 + 3t\end{array} \right..\)
Lời giải
\(\left\{ \begin{array}{l}M\left( { - 2;1} \right) \in d\\{{\vec u}_\Delta } = \left( { - 3;5} \right)\\d \bot \Delta \end{array} \right. \to \left\{ \begin{array}{l}M\left( { - 2;1} \right) \in d\\{{\vec n}_d} = \left( { - 3;5} \right) \to {{\vec u}_d} = \left( {5;3} \right)\end{array} \right. \to d:\left\{ \begin{array}{l}x = - 2 + 5t\\y = 1 + 3t\end{array} \right.\left( {t \in \mathbb{R}} \right).\)
Đáp án B.
Câu 31: Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( { - 1;2} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(2\sqrt 5 \).
A. \(m = 2.\)
B. \(\left[ \begin{array}{l}m = - 2\\m = \frac{1}{2}\end{array} \right.\).
C. \(m = - \frac{1}{2}\).
D. Không tồn tại \(m\).
Lời giải
\(d\left( {A;\Delta } \right) = \frac{{\left| { - m + 2 - m + 4} \right|}}{{\sqrt {{m^2} + 1} }} = 2\sqrt 5 \Leftrightarrow \left| {m - 3} \right| = \sqrt 5 .\sqrt {{m^2} + 1} \Leftrightarrow 4{m^2} + 6m - 4 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}m = - 2\\m = \frac{1}{2}\end{array} \right..\)
Đáp án B.
Câu 32: Trong mặt phẳng \(Oxy\), đường tròn đi qua ba điểm \(A\left( {1;2} \right)\), \(B\left( {5;2} \right)\), \(C\left( {1; - 3} \right)\) có phương trình là.
A. \({x^2} + {y^2} + 25x + 19y - 49 = 0\).
B. \(2{x^2} + {y^2} - 6x + y - 3 = 0\).
C. \({x^2} + {y^2} - 6x + y - 1 = 0\).
D. \({x^2} + {y^2} - 6x + xy - 1 = 0\).
Lời giải
Gọi \(\left( C \right)\) là phương trình đường tròn đi qua ba điểm \(A,B,C\) với tâm \(I\left( {a;b} \right)\)
\( \Rightarrow \left( C \right)\)có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\). Vì đường tròn \(\left( C \right)\) đi qua qua ba điểm \(A,B,C\) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}1 + 4 - 2a - 4b + c = 0\\25 + 4 - 10a - 4b + c = 0\\1 + 9 - 2a + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2a - 4b + c = - 5\\ - 10a - 4b + c = - 29\\ - 2a + 6b + c = - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - \frac{1}{2}\\c = - 1\end{array} \right.\).
Vậy phương trình đường tròn cần tìm là \({x^2} + {y^2} - 6x + y - 1 = 0\).
Đáp án C.
Câu 33: Trong hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;\,2} \right),\,B\left( {3,\,4} \right)\) và tiếp xúc với đường thẳng \(\Delta :\,3x + y - 3 = 0\), biết tâm của \(\left( C \right)\) có tọa độ là những số nguyên. Phương trình đường tròn \(\left( C \right)\) là
A. \({x^2} + {y^2} - 3x - 7y + 12 = 0.\)
B. \({x^2} + {y^2} - 6x - 4y + 5 = 0.\)
C. \({x^2} + {y^2} - 8x - 2y + 7 = 0.\)
D. \({x^2} + {y^2} - 2x - 8y + 20 = 0.\)
Lời giải
Ta có : \(\overrightarrow {AB} = (2;2)\) ; đoạn \(AB\) có trung điểm \(M\left( {2;\,3} \right)\)
\( \Rightarrow \)Phương trình đường trung trực của đoạn \(AB\) là \(d:\,x + y - 5 = 0\).
Gọi \(I\) là tâm của \(\left( C \right)\) \( \Rightarrow I \in d\)\( \Rightarrow I\left( {a;\,5 - a} \right)\,,\,a \in \mathbb{Z}.\)
Ta có: \(R = IA = d\left( {I;\,\Delta } \right) = \sqrt {{{\left( {a - 1} \right)}^2} + {{\left( {a - 3} \right)}^2}} = \frac{{\left| {2a + 2} \right|}}{{\sqrt {10} }} \Leftrightarrow a = 4 \Rightarrow I\left( {4;\,1} \right),\,R = \sqrt {10} .\)
Vậy phương trình đường tròn là: \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 10 \Leftrightarrow {x^2} + {y^2} - 8x - 2y + 7 = 0.\)
Đáp án C.
Câu 34: Cho đường hypebol có phương trình \(\left( H \right):100{x^2} - 25{y^2} = 100\). Tiêu cự của hypebol đó là
A. \(2\sqrt {10} \).
B. \(2\sqrt {104} \).
C. \(\sqrt {10} \).
D. \(\sqrt {104} \).
Lời giải
\(\left( H \right):100{x^2} - 25{y^2} = 100 \Leftrightarrow \frac{{{x^2}}}{{100}} - \frac{{{y^2}}}{4} = 1\).
\(a = 10,b = 2 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {104} \).
Tiêu cự của hypebol là \(2\sqrt {104} \).
Đáp án B.
Câu 35: Cho parabol \(\left( P \right):{y^2} = 8x\) có tiêu điểm là
A. \(F\left( {0;4} \right)\).
B. \(F\left( {0;2} \right)\).
C. \(F\left( {2;0} \right)\).
D. \(F\left( {4;0} \right)\).
Lời giải
Ta có \(2p = 8 \Rightarrow p = 4\).
Parabol có tiêu điểm \(F\left( {2;0} \right)\).
Đáp án C.
Phần tự luận (3 điểm)
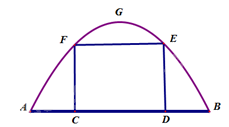
Bài 1. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B.
Lời giải
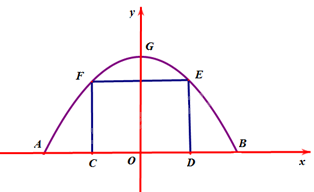
Gắn hệ trục tọa độ Oxy như hình vẽ, chiếc cổng là 1 phần của parabol \(\left( P \right):y = a{x^2} + bx + c\) với \(a < 0\).
Do parabol \((P)\) đối xứng qua trục tung nên có trục đối xứng \(x = 0 \Rightarrow - \frac{b}{{2a}} = 0 \Leftrightarrow b = 0\) .
Chiều cao của cổng parabol là 4m nên \(G\left( {0;4} \right) \Rightarrow c = 4\)
\( \Rightarrow \left( P \right):y = a{x^2} + 4\).
Lại có, kích thước cửa ở giữa là 3m x 4m nên \(E\left( {2;3} \right) \Rightarrow 3 = 4a + 4 \Rightarrow a = - \frac{1}{4}\) .
Vậy \(\left( P \right):y = - \frac{1}{4}{x^2} + 4\).
Ta có \( - \frac{1}{4}{x^2} + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\) nên \(A\left( { - 4;0} \right);B\left( {4;0} \right)\) hay \(AB = 8\).
Bài 2. Cho tam giác \(ABC\) có \(A\left( {1;3} \right)\) và hai đường trung tuyến \(BM:x + 7y - 10 = 0\) và \(CN:x - 2y + 2 = 0\). Viết phương trình đường thẳng chứa cạnh \(BC\) của tam giác \(ABC\).
Lời giải
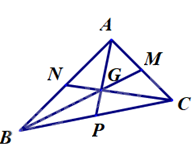
Vì \(B \in BM\) nên tọa độ điểm \(B\) có dạng \(B\left( { - 7b + 10;\,b} \right)\).
Gọi \(G\) là trọng tâm của tam giác \(ABC\).
Khi đó tọa độ điểm \(G\) là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}x + 7y - 10 = 0\\x - 2y + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{2}{3}\\y = \frac{4}{3}\end{array} \right. \Rightarrow G\left( {\frac{2}{3};\,\frac{4}{3}} \right)\).
Gọi \(P\left( {x;\,y} \right)\) là trung điểm của \(BC\).
Khi đó \(AP\) là đường trung tuyến của tam giác \(ABC\).
Suy ra \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AP} \Leftrightarrow \left\{ \begin{array}{l}\frac{2}{3} - 1 = \frac{2}{3}\left( {x - 1} \right)\\\frac{4}{3} - 3 = \frac{2}{3}\left( {y - 3} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{1}{2}\end{array} \right. \Rightarrow P\left( {\frac{1}{2};\,\frac{1}{2}} \right)\).
Vì \(P\) là trung điểm của \(BC\) nên \(\left\{ \begin{array}{l}{x_C} = 2{x_P} - {x_B}\\{y_C} = 2{y_P} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 7b - 9\\{y_C} = 1 - b\end{array} \right.\) \( \Rightarrow C\left( {7b - 9;\,1 - b} \right)\).
Vì \(C \in CN\) nên \(7b - 9 - 2.\left( {1 - b} \right) + 2 = 0 \Leftrightarrow b = 1\).
Khi đó \(B\left( {3;\,1} \right)\), \(C\left( { - 2;\,0} \right)\).
Vậy phương trình đường thẳng \(BC\) đi qua hai điểm \(B\) và \(C\) là \(x - 5y + 2 = 0\).
Bài 3. Tìm tất cả các giá trị thực của tham số \(m\)để hàm số \(y = \frac{{mx}}{{\sqrt {x - m + 2} - 1}}\)xác định trên \(\left( {0;1} \right)\).
Lời giải
Hàm số xác định trên \(\left( {0;1} \right) \Leftrightarrow \left\{ \begin{array}{l}x - m + 2 \ge 0\\\sqrt {x - m + 2} - 1 \ne 0\end{array} \right.\forall x \in \left( {0;1} \right)\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge m - 2\\\sqrt {x - m + 2} \ne 1\end{array} \right.\forall x \in \left( {0;1} \right) \Leftrightarrow \left\{ \begin{array}{l}x \ge m - 2\\x \ne m - 1\end{array} \right.\forall x \in \left( {0;1} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}m - 2 \le 0\\\left[ \begin{array}{l}m - 1 \ge 1\\m - 1 \le 0\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 2\\\left[ \begin{array}{l}m \ge 2\\m \le 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \le 1\\m = 2\end{array} \right.\)
Vậy \(m \in \left( { - \infty ;1} \right] \cup \left\{ 2 \right\}\).
Bài 4. Cho tam giác \(ABC\) biết \(H\left( {3;2} \right)\), \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\) lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng \(BC\) có phương trình \(x + 2y - 2 = 0\). Tìm phương trình đường tròn ngoại tiếp tam giác \(ABC\)?
Lời giải
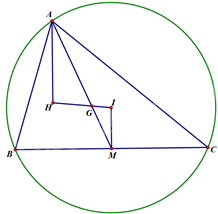
*) Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
\( \Rightarrow \overrightarrow {HI} = \frac{3}{2}\overrightarrow {HG} \)\( \Rightarrow \left\{ \begin{array}{l}{x_I} - 3 = \frac{3}{2}\left( {\frac{5}{3} - 3} \right)\\{y_I} - 2 = \frac{3}{2}\left( {\frac{8}{3} - 2} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_I} = 1\\{y_I} = 3\end{array} \right.\)
*) Gọi \(M\) là trung điểm của \(BC\) \( \Rightarrow IM \bot BC\) \( \Rightarrow IM:2x - y + 1 = 0\).
\(M = IM \cap BC\) \( \Rightarrow \left\{ \begin{array}{l}2x - y = - 1\\x + 2y = 2\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}x = 0\\y = 1\end{array} \right.\)\( \Rightarrow M\left( {0;1} \right)\).
Lại có: \(\overrightarrow {MA} = 3\overrightarrow {MG} \) \( \Rightarrow \left\{ \begin{array}{l}{x_A} = 3.\frac{5}{3}\\{y_A} - 1 = 3.\left( {\frac{8}{3} - 1} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_A} = 5\\{y_A} = 6\end{array} \right.\).
Suy ra: bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = IA = 5\).
Vậy phương trình đường tròn ngoại tiếp tam giác \(ABC\) là \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 25\).
Tải về
Phần trắc nghiệm (7 điểm)
Câu 1: Tập xác định của hàm số \(y = \frac{{x + 1}}{{x - 1}}\) là:
A. \(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\).
B. \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
C. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
D. \(\left( {1; + \infty } \right)\).
Câu 2: Trong các hàm số sau, hàm số nào nghịch biến trên \(\mathbb{R}\)?
A. \(y = x\).
B. \(y = - 2x\).
C. \(y = 2x\).
D. \(y = \frac{1}{2}x\)
Câu 3: Cho hàm số \(f\left( x \right) = \sqrt {2{x^2} + 1} \). Giá trị \(f\left( { - 2} \right)\) bằng
A. \( - 3\).
B. \(3\).
C. \(4\).
D. Không xác định.
Câu 4: Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là
A. \(\left( { - \infty ; - 2} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Câu 5: Trục đối xứng của đồ thị hàm số\(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
A. \(x = - \frac{b}{{2a}}.\)
B. \(x = - \frac{c}{{2a}}.\)
C. \(x = - \frac{\Delta }{{4a}}.\)
D. \(x = \frac{b}{{2a}}\).
Câu 6: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng?
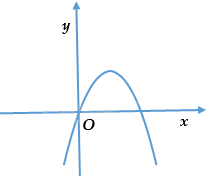
A. \(a > 0.\)
B. \(a < 0.\)
C. \(a = 1.\)
D. \(a = 2.\)
Câu 7: Cho \(f\left( x \right) = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) và \(\Delta = {b^2} - 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).
A. \(\Delta < 0\).
B. \(\Delta = 0\).
C. \(\Delta > 0\).
D. \(\Delta \ge 0\).
Câu 8: Tập nghiệm \(S\) của bất phương trình \({x^2} - x - 6 \le 0\).
A. \(S = \left( { - \infty ; - 3} \right) \cup \left( {2: + \infty } \right)\).
B. \(\left[ { - 2;3} \right]\).
C. \(\left[ { - 3;2} \right]\).
D. \(\left( { - \infty ; - 3} \right] \cup \left[ {2; + \infty } \right)\).
Câu 9: Tìm tập nghiệm \(S\) của bất phương trình \({x^2} - 4x + 4 > 0\).
A. \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
B. \(S = \mathbb{R}\).
C. \(S = \left( {2; + \infty } \right)\).
D. \(S = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Câu 10: Phương trình \(\sqrt {x - 1} = x - 3\) có tập nghiệm là
A. \(S = \left\{ 5 \right\}\).
B. \(S = \left\{ {2;5} \right\}\).
C. \(S = \left\{ 2 \right\}\).
D. \(S = \emptyset \).
Câu 11: Số nghiệm của phương trình \(\sqrt {{x^2} - 4x + 3} = \sqrt {1 - x} \)là
A. Vô số.
B. 2.
C. 1.
D. 0.
Câu 12: Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,ax + by + c = 0,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {a; - b} \right)\).
B. \(\overrightarrow n = \left( {b;a} \right)\).
C. \(\overrightarrow n = \left( {b; - a} \right)\).
D. \(\overrightarrow n = \left( {a;b} \right)\).
Câu 13: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\).
Câu 14: Trong mặt phẳng \(Oxy\), đường thẳng \(d:\,x - 2y - 1 = 0\) song song với đường thẳng có phương trình nào sau đây?
A. \(x + 2y + 1 = 0\).
B. \(2x - y = 0\).
C. \( - x + 2y + 1 = 0\).
D. \( - 2x + 4y - 1 = 0\).
Câu 15: Tính góc giữa hai đường thẳng \(\Delta :x - \sqrt 3 y + 2 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\).
A. \({90^ \circ }\).
B. \({120^ \circ }\).
C. \({60^ \circ }\).
D. \({30^ \circ }\).
Câu 16: Khoảng cách từ điểm \(M\left( {5\,;\, - 1} \right)\) đến đường thẳng \(3x + 2y + 13 = 0\) là:
A. \(2\sqrt {13} \).
B. \(\frac{{28}}{{\sqrt {13} }}\).
C. \(26\).
D. \(\frac{{\sqrt {13} }}{2}\).
Câu 17: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - 6x - 10y + 30 = 0\).
B. \({x^2} + {y^2} - 3x - 2y + 30 = 0\).
C. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).
D. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).
Câu 18: Phương trình nào sau đây là phương trình của đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính bằng \(3\)?
A. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
B. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
C. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
Câu 19: Đường elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\) cắt trục tung tại hai điểm \({B_1}\), \({B_2}\). Độ dài \({B_1}{B_2}\) bằng
A. \(2\sqrt 7 \).
B. \(\sqrt 7 \).
C. \(3\).
D. \(6\).
Câu 20: Tọa độ các tiêu điểm của hypebol \(\left( H \right):\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\) là
A. \({F_1} = \left( { - 5;0} \right);{F_2} = \left( {5;0} \right)\).
B. \({F_1} = \left( {0; - 5} \right);{F_2} = \left( {0;5} \right)\).
C. \({F_1} = \left( {0; - \sqrt 7 } \right);{F_2} = \left( {0;\sqrt 7 } \right)\).
D. \({F_1} = \left( { - \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Câu 21: Tập xác định của hàm số \(y = \sqrt {4 - x} + \sqrt {x - 2} \) là
A. \(D = \left( {2;4} \right)\)
B. \(D = \left[ {2;4} \right]\)
C. \(D = \left\{ {2;4} \right\}\)
D. \(D = \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)\)
Câu 22: Cho hàm số có đồ thị như hình bên dưới.
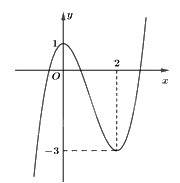
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { - \infty ;3} \right)\).
Câu 23: Đồ thị hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}2x + 3{\rm{ }}\,\,\,khi{\rm{ }}x \le 2\\{x^2} - 3{\rm{ }}\,\,\,khi{\rm{ }}x > 2\end{array} \right.\) đi qua điểm có tọa độ nào sau đây ?
A. \(\left( {0; - 3} \right)\)
B. \(\left( {3;6} \right)\)
C. \(\left( {2;5} \right)\)
D. \(\left( {2;1} \right)\)
Câu 24: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau
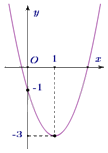
Phương trình của parabol này là
A. \(y = - {x^2} + x - 1\).
B. \(y = 2{x^2} + 4x - 1\).
C. \(y = {x^2} - 2x - 1\).
D. \(y = 2{x^2} - 4x - 1\).
Câu 25: Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} - 4x\) với đường thẳng \(d\,:\,y = - x - 2\) là
A. \(M\left( {0;\, - 2} \right)\), \(N\left( {2;\, - 4} \right)\).
B. \(M\left( { - 1;\, - 1} \right)\), \(N\left( { - 2;\,0} \right)\).
C. \(M\left( {\, - 3;\,1} \right)\), \(N\left( {3;\, - 5} \right)\).
D. \(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Câu 26: Số nghiệm nguyên của bất phương trình \(2{x^2} - 3x - 15 \le 0\) là
A. \(6\).
B. \(5\).
C. \(8\).
D. \(7\).
Câu 27: Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} - \left( {m + 2} \right)x + 8m + 1 \le 0\) vô nghiệm.
A. \(m \in \left[ {0;28} \right]\).
B. \(m \in \left( { - \infty ;0} \right) \cup \left( {28; + \infty } \right)\).
C. \(m \in \left( { - \infty ;0} \right] \cup \left[ {28; + \infty } \right)\).
D. \(m \in \left( {0;28} \right)\).
Câu 28: Số nghiệm của phương trình \(\sqrt {{x^2} - 3x + 1} = 4x - 1\) là
A. \(0\).
B. \(3\).
C. \(2\).
D. \(1\).
Câu 29: Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng \(d\) là
A. \(2x + y - 1 = 0\).
B. \( - 2x + y - 1 = 0\).
C. \(x + 2y + 1 = 0\).
D. \(2x + 3y - 1 = 0\).
Câu 30: Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;1} \right)\) và vuông góc với đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + 5t\end{array} \right.\) có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = - 2 - 3t\\y = 1 + 5t\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x = - 2 + 5t\\y = 1 + 3t\end{array} \right..\)
C. \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 2 + 5t\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x = 1 + 5t\\y = 2 + 3t\end{array} \right..\)
Câu 31: Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( { - 1;2} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(2\sqrt 5 \).
A. \(m = 2.\)
B. \(\left[ \begin{array}{l}m = - 2\\m = \frac{1}{2}\end{array} \right.\).
C. \(m = - \frac{1}{2}\).
D. Không tồn tại \(m\).
Câu 32: Trong mặt phẳng \(Oxy\), đường tròn đi qua ba điểm \(A\left( {1;2} \right)\), \(B\left( {5;2} \right)\), \(C\left( {1; - 3} \right)\) có phương trình là.
A. \({x^2} + {y^2} + 25x + 19y - 49 = 0\).
B. \(2{x^2} + {y^2} - 6x + y - 3 = 0\).
C. \({x^2} + {y^2} - 6x + y - 1 = 0\).
D. \({x^2} + {y^2} - 6x + xy - 1 = 0\).
Câu 33: Trong hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;\,2} \right),\,B\left( {3,\,4} \right)\) và tiếp xúc với đường thẳng \(\Delta :\,3x + y - 3 = 0\), biết tâm của \(\left( C \right)\) có tọa độ là những số nguyên. Phương trình đường tròn \(\left( C \right)\) là
A. \({x^2} + {y^2} - 3x - 7y + 12 = 0.\)
B. \({x^2} + {y^2} - 6x - 4y + 5 = 0.\)
C. \({x^2} + {y^2} - 8x - 2y + 7 = 0.\)
D. \({x^2} + {y^2} - 2x - 8y + 20 = 0.\)
Câu 34: Cho đường hypebol có phương trình \(\left( H \right):100{x^2} - 25{y^2} = 100\). Tiêu cự của hypebol đó là
A. \(2\sqrt {10} \).
B. \(2\sqrt {104} \).
C. \(\sqrt {10} \).
D. \(\sqrt {104} \).
Câu 35: Cho parabol \(\left( P \right):{y^2} = 8x\) có tiêu điểm là
A. \(F\left( {0;4} \right)\).
B. \(F\left( {0;2} \right)\).
C. \(F\left( {2;0} \right)\).
D. \(F\left( {4;0} \right)\).
Phần tự luận (3 điểm)
Bài 1. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B.
Bài 2. Cho tam giác \(ABC\) có \(A\left( {1;3} \right)\) và hai đường trung tuyến \(BM:x + 7y - 10 = 0\)và p\(CN:x - 2y + 2 = 0\). Viết phương trình đường thẳng chứa cạnh \(BC\) của tam giác \(ABC\).
Bài 3. Tìm tất cả các giá trị thực của tham số \(m\)để hàm số \(y = \frac{{mx}}{{\sqrt {x - m + 2} - 1}}\)xác định trên \(\left( {0;1} \right)\).
Bài 4. Cho tam giác \(ABC\) biết \(H\left( {3;2} \right)\), \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\) lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng \(BC\) có phương trình \(x + 2y - 2 = 0\). Tìm phương trình đường tròn ngoại tiếp tam giác \(ABC\)?
-------- Hết --------
Phần trắc nghiệm
Câu 1. C | Câu 2. B | Câu 3. B | Câu 4. D | Câu 5. A | Câu 6. B | Câu 7. A |
Câu 8. B | Câu 9. A | Câu 10. A | Câu 11. C | Câu 12. D | Câu 13. D | Câu 14. D |
Câu 15. C | Câu 16. A | Câu 17. A | Câu 18. D | Câu 19. A | Câu 20. D | Câu 21. B |
Câu 22. C | Câu 23. B | Câu 24. D | Câu 25. D | Câu 26. A | Câu 27. D | Câu 28. D |
Câu 29. A | Câu 30. B | Câu 31. B | Câu 32. C | Câu 33. C | Câu 34. B | Câu 35. C |
Câu 1: Tập xác định của hàm số \(y = \frac{{x + 1}}{{x - 1}}\) là:
A. \(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\).
B. \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
C. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
D. \(\left( {1; + \infty } \right)\).
Lời giải
Điều kiện xác định: \(x - 1 \ne 0 \Leftrightarrow x \ne 1\)
Vậy tập xác định của hàm số \(y = \frac{{x + 1}}{{x - 1}}\) là \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
Đáp án C.
Câu 2: Trong các hàm số sau, hàm số nào nghịch biến trên \(\mathbb{R}\)?
A. \(y = x\).
B. \(y = - 2x\).
C. \(y = 2x\).
D. \(y = \frac{1}{2}x\)
Lời giải
Hàm số \(y = ax + b\) với \(a \ne 0\) nghịch biến trên \(\mathbb{R}\) khi và chỉ khi \(a < 0\).
Đáp án B.
Câu 3: Cho hàm số \(f\left( x \right) = \sqrt {2{x^2} + 1} \). Giá trị \(f\left( { - 2} \right)\) bằng
A. \( - 3\).
B. \(3\).
C. \(4\).
D. Không xác định.
Lời giải
Ta có \(f\left( { - 2} \right) = \sqrt {2.{{\left( { - 2} \right)}^2} + 1} = 3\).
Đáp án B.
Câu 4: Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\)là
A. \(\left( { - \infty ; - 2} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( { - 2; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Lời giải
Hàm số \(y = {x^2} - 4x + 3\)có \(a = 1 > 0\) nên đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\).
Vì vậy hàm số đồng biến trên \(\left( {2; + \infty } \right)\).
Đáp án D.
Câu 5: Trục đối xứng của đồ thị hàm số \(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
A. \(x = - \frac{b}{{2a}}.\)
B. \(x = - \frac{c}{{2a}}.\)
C. \(x = - \frac{\Delta }{{4a}}.\)
D. \(x = \frac{b}{{2a}}\).
Lời giải
Đáp án A.
Câu 6: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng?
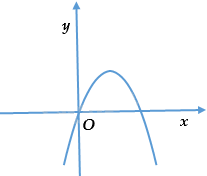
A. \(a > 0.\)
B. \(a < 0.\)
C. \(a = 1.\)
D. \(a = 2.\)
Lời giải
Bề lõm hướng xuống \(a < 0.\)
Đáp án B.
Câu 7: Cho \(f\left( x \right) = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) và \(\Delta = {b^2} - 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).
A. \(\Delta < 0\).
B. \(\Delta = 0\).
C. \(\Delta > 0\).
D. \(\Delta \ge 0\).
Lời giải
Theo định lý về dấu của tam thức bậc hai thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\) khi \(\Delta < 0\).
Đáp án A.
Câu 8: Tập nghiệm \(S\) của bất phương trình \({x^2} - x - 6 \le 0\).
A. \(S = \left( { - \infty ; - 3} \right) \cup \left( {2: + \infty } \right)\).
B. \(\left[ { - 2;3} \right]\).
C. \(\left[ { - 3;2} \right]\).
D. \(\left( { - \infty ; - 3} \right] \cup \left[ {2; + \infty } \right)\).
Lời giải
Ta có: \({x^2} - x - 6 \le 0 \Leftrightarrow - 2 \le x \le 3\).
Tập nghiệm bất phương trình là: \(S = \left[ { - 2;3} \right]\).
Đáp án B.
Câu 9: Tìm tập nghiệm \(S\) của bất phương trình \({x^2} - 4x + 4 > 0\).
A. \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
B. \(S = \mathbb{R}\).
C. \(S = \left( {2; + \infty } \right)\).
D. \(S = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Lời giải
* Bảng xét dấu:
\(x\) | \( - \infty \) | \(2\) | \( + \infty \) |
\({x^2} - 4x + 4\) | \( + \) | \(0\) | \( + \) |
* Tập nghiệm của bất phương trình là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\).
Đáp án A.
Câu 10: Phương trình \(\sqrt {x - 1} = x - 3\) có tập nghiệm là
A. \(S = \left\{ 5 \right\}\).
B. \(S = \left\{ {2;5} \right\}\).
C. \(S = \left\{ 2 \right\}\).
D. \(S = \emptyset \).
Lời giải
Ta có: \(\sqrt {x - 1} = x - 3 \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\x - 1 = {\left( {x - 3} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} - 7x + 10 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 2\\x = 5\end{array} \right.\end{array} \right. \Leftrightarrow x = 5\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ 5 \right\}\).
Đáp án A.
Câu 11: Số nghiệm của phương trình \(\sqrt {{x^2} - 4x + 3} = \sqrt {1 - x} \)là
A. Vô số.
B. 2.
C. 1.
D. 0.
Lời giải
Ta có \(\sqrt {{x^2} - 4x + 3} = \sqrt {1 - x} \)
\( \Leftrightarrow \) \(\left\{ \begin{array}{l}1 - x \ge 0\\{x^2} - 4x + 3 = 1 - x\end{array} \right.\)\( \Leftrightarrow \)\(\left\{ \begin{array}{l}x \le 1\\{x^2} - 3x + 2 = 0\end{array} \right.\)\( \Leftrightarrow \) \(\left\{ \begin{array}{l}x \le 1\\\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \)\(x = 1\).
Vậy phương trình đã cho có 1 nghiệm.
Đáp án C.
Câu 12: Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,ax + by + c = 0,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {a; - b} \right)\).
B. \(\overrightarrow n = \left( {b;a} \right)\).
C. \(\overrightarrow n = \left( {b; - a} \right)\).
D. \(\overrightarrow n = \left( {a;b} \right)\).
Lời giải
Ta có một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)là \(\overrightarrow n = \left( {a;b} \right)\).
Do đó chọn đáp án
D. \(\overrightarrow {{n_1}} = \left( { - a;b} \right).\)
Đáp án D.
Câu 13: Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\).
Lời giải
Vectơ chỉ phương \(\overrightarrow {AB} = \left( {0;6} \right)\).
Phương trình đường thẳng \(AB\) đi qua \(A\) và có vecto chỉ phương \(\overrightarrow {AB} = \left( {0;6} \right)\) là \(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\)
Đáp án D.
Câu 14: Trong mặt phẳng \(Oxy\), đường thẳng \(d:\,x - 2y - 1 = 0\) song song với đường thẳng có phương trình nào sau đây?
A. \(x + 2y + 1 = 0\).
B. \(2x - y = 0\).
C. \( - x + 2y + 1 = 0\).
D. \( - 2x + 4y - 1 = 0\).
Lời giải
Ta kiểm tra lần lượt các đường thẳng
.+) Với \(d{}_1:x + 2y + 1 = 0\) có \(\frac{1}{1} \ne \frac{2}{{ - 2}} \Rightarrow d\) cắt \(d{}_1\).
.+) Với \(d{}_2:2x - y = 0\) có \(\frac{2}{1} \ne \frac{{ - 1}}{{ - 2}} \Rightarrow d\)cắt \(d{}_2\).
.+) Với \(d{}_3: - x + 2y + 1 = 0\) có \(\frac{{ - 1}}{1} = \frac{2}{{ - 2}} \ne \frac{1}{{ - 1}} \Rightarrow d\)trùng \(d{}_3\).
.+) Với \(d{}_4: - 2x + 4y - 1 = 0\) có \(\frac{1}{{ - 2}} = \frac{{ - 2}}{4} \ne \frac{{ - 1}}{{ - 1}} \Rightarrow d\) song song \(d{}_4\).
Đáp án D.
Câu 15: Tính góc giữa hai đường thẳng \(\Delta :x - \sqrt 3 y + 2 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\).
A. \({90^ \circ }\).
B. \({120^ \circ }\).
C. \({60^ \circ }\).
D. \({30^ \circ }\).
Lời giải
Đường thẳng \(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {1; - \sqrt 3 } \right)\), đường thẳng \(\Delta '\) có vectơ pháp tuyến \(\overrightarrow {n'} = \left( {1;\sqrt 3 } \right)\).
Gọi \(\alpha \) là góc giữa hai đường thẳng \(\Delta ,\Delta '.\)\(\cos \alpha = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {1 - 3} \right|}}{{\sqrt {1 + 3} .\sqrt {1 + 3} }} = \frac{1}{2} \Rightarrow \alpha = {60^ \circ }\).
Đáp án C.
Câu 16: Khoảng cách từ điểm \(M\left( {5\,;\, - 1} \right)\) đến đường thẳng \(3x + 2y + 13 = 0\) là:
A. \(2\sqrt {13} \).
B. \(\frac{{28}}{{\sqrt {13} }}\).
C. \(26\).
D. \(\frac{{\sqrt {13} }}{2}\).
Lời giải
Khoảng cách \(d = \frac{{\left| {3.5 + 2.\left( { - 1} \right) + 13} \right|}}{{\sqrt {{3^2} + {2^2}} }} = \frac{{26}}{{\sqrt {13} }} = 2\sqrt {13} \).
Đáp án A.
Câu 17: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - 6x - 10y + 30 = 0\).
B. \({x^2} + {y^2} - 3x - 2y + 30 = 0\).
C. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).
D. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).
Lời giải
Phương trình đường tròn đã cho có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình đường tròn\( \Leftrightarrow {a^2} + {b^2} - c > 0.\)
Xét đáp án A, ta có \(a = 3,\,b = 5,\,c = 30\) \( \Rightarrow {a^2} + {b^2} - c = 4 > 0\).
Đáp án A.
Câu 18: Phương trình nào sau đây là phương trình của đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính bằng \(3\)?
A. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
B. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\).
C. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
D. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
Lời giải
Phương trình đường tròn tâm \(I\left( { - 1;2} \right)\) và bán kính \(R = 3\) là: \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
Đáp án D.
Câu 19: Đường elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\) cắt trục tung tại hai điểm \({B_1}\), \({B_2}\). Độ dài \({B_1}{B_2}\) bằng
A. \(2\sqrt 7 \).
B. \(\sqrt 7 \).
C. \(3\).
D. \(6\).
Lời giải
Ta có \(x = 0 \Rightarrow y = \pm \sqrt 7 \).
Elip cắt trục tung tại hai điểm \({B_1}\left( {0; - \sqrt 7 } \right)\), \({B_2}\left( {0;\sqrt 7 } \right)\). Suy ra \({B_1}{B_2} = 2\sqrt 7 \).
Đáp án A.
Câu 20: Tọa độ các tiêu điểm của hypebol \(\left( H \right):\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\) là
A. \({F_1} = \left( { - 5;0} \right);{F_2} = \left( {5;0} \right)\).
B. \({F_1} = \left( {0; - 5} \right);{F_2} = \left( {0;5} \right)\).
C. \({F_1} = \left( {0; - \sqrt 7 } \right);{F_2} = \left( {0;\sqrt 7 } \right)\).
D. \({F_1} = \left( { - \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Lời giải
Gọi \({F_1} = \left( { - c;0} \right);{F_2} = \left( {c;0} \right)\) là hai tiêu điểm của \(\left( H \right)\).
Từ phương trình \(\left( H \right):\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\), ta có: \({a^2} = 4\) và \({b^2} = 3\) suy ra \({c^2} = {a^2} + {b^2} = 7 \Rightarrow c = \sqrt 7 ,\left( {c > 0} \right)\).
Vậy tọa độ các tiêu điểm của \(\left( H \right)\)là \({F_1} = \left( { - \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\).
Đáp án D.
Câu 21: Tập xác định của hàm số \(y = \sqrt {4 - x} + \sqrt {x - 2} \) là
A. \(D = \left( {2;4} \right)\)
B. \(D = \left[ {2;4} \right]\)
C. \(D = \left\{ {2;4} \right\}\)
D. \(D = \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)\)
Lời giải
Điều kiện: \(\left\{ \begin{array}{l}4 - x \ge 0\\x - 2 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \le 4\\x \ge 2\end{array} \right.\) suy ra TXĐ: \(D = \left[ {2;4} \right]\).
Đáp án B.
Câu 22: Cho hàm số có đồ thị như hình bên dưới.
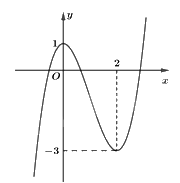
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\).
B. Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { - \infty ;3} \right)\).
Lời giải
Trên khoảng \(\left( {0;2} \right)\), đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Đáp án C.
Câu 23: Đồ thị hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}2x + 3{\rm{ }}\,\,\,khi{\rm{ }}x \le 2\\{x^2} - 3{\rm{ }}\,\,\,khi{\rm{ }}x > 2\end{array} \right.\) đi qua điểm có tọa độ nào sau đây ?
A. \(\left( {0; - 3} \right)\)
B. \(\left( {3;6} \right)\)
C. \(\left( {2;5} \right)\)
D. \(\left( {2;1} \right)\)
Lời giải
Thay tọa độ điểm \(\left( {0; - 3} \right)\)vào hàm số ta được : \(f\left( 0 \right) = 3 \ne - 3\) nên loại đáp án A
Thay tọa độ điểm \(\left( {3;6} \right)\)vào hàm số ta được : \(f\left( 3 \right) = 9 - 3 = 6\), thỏa mãn nên chọn đáp án B
Đáp án B.
Câu 24: Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau
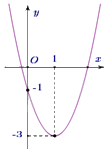
Phương trình của parabol này là
A. \(y = - {x^2} + x - 1\).
B. \(y = 2{x^2} + 4x - 1\).
C. \(y = {x^2} - 2x - 1\).
D. \(y = 2{x^2} - 4x - 1\).
Lời giải
Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, - 1} \right)\) nên \(c = - 1\).
Tọa độ đỉnh \(I\left( {1\,\,;\, - 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 1\\a{.1^2} + b.1 - 1 = - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 4\end{array} \right.\).
Vậy parabol cần tìm là: \(y = 2{x^2} - 4x - 1\).
Đáp án D.
Câu 25: Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} - 4x\) với đường thẳng \(d\,:\,y = - x - 2\) là
A. \(M\left( {0;\, - 2} \right)\), \(N\left( {2;\, - 4} \right)\).
B. \(M\left( { - 1;\, - 1} \right)\), \(N\left( { - 2;\,0} \right)\).
C. \(M\left( {\, - 3;\,1} \right)\), \(N\left( {3;\, - 5} \right)\).
D. \(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Lời giải
Hoành độ giao điểm của \(\left( P \right)\) và \(d\) là nghiệm của phương trình:
\({x^2} - 4x = - x - 2\, \Leftrightarrow \,{x^2} - 3x + 2 = 0\, \Leftrightarrow \,\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\).
Vậy tọa độ giao điểm của \(\left( P \right)\) và \(d\) là \(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Đáp án D.
Câu 26: Số nghiệm nguyên của bất phương trình \(2{x^2} - 3x - 15 \le 0\) là
A. \(6\).
B. \(5\).
C. \(8\).
D. \(7\).
Lời giải
Xét \(f\left( x \right) = 2{x^2} - 3x - 15\).
\(f\left( x \right) = 0\)\( \Leftrightarrow x = \frac{{3 \pm \sqrt {129} }}{4}\).
Ta có bảng xét dấu:
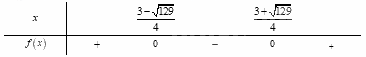
Tập nghiệm của bất phương trình là \(S = \left[ {\frac{{3 - \sqrt {129} }}{4};\,\frac{{3 + \sqrt {129} }}{4}} \right]\).
Do đó bất phương trình có \(6\) nghiệm nguyên là \( - 2\), \( - 1\), \(0\), \(1\), \(2\), \(3\).
Đáp án A.
Câu 27: Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} - \left( {m + 2} \right)x + 8m + 1 \le 0\) vô nghiệm.
A. \(m \in \left[ {0;28} \right]\).
B. \(m \in \left( { - \infty ;0} \right) \cup \left( {28; + \infty } \right)\).
C. \(m \in \left( { - \infty ;0} \right] \cup \left[ {28; + \infty } \right)\).
D. \(m \in \left( {0;28} \right)\).
Lời giải
Bất phương trình vô nghiệm khi và chỉ khi \({\left( {m + 2} \right)^2} - 4\left( {8m + 1} \right) < 0\)\( \Leftrightarrow {m^2} - 28m < 0\) \(0 < m < 28\)
Đáp án D.
Câu 28: Số nghiệm của phương trình \(\sqrt {{x^2} - 3x + 1} = 4x - 1\) là
A. \(0\).
B. \(3\).
C. \(2\).
D. \(1\).
Lời giải
Phương trình \(\sqrt {{x^2} - 3x + 1} = 4x - 1\)\( \Leftrightarrow \left\{ \begin{array}{l}4x - 1 \ge 0\\{x^2} - 3x + 1 = {\left( {4x - 1} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{4}\\15{x^2} - 5x = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{4}\\\left[ \begin{array}{l}x = 0\left( l \right)\\x = \frac{1}{3}\left( n \right)\end{array} \right.\end{array} \right.\)\( \Leftrightarrow x = \frac{1}{3}\).
Đáp án B.
Câu 29: Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng \(d\) là
A. \(2x + y - 1 = 0\).
B. \( - 2x + y - 1 = 0\).
C. \(x + 2y + 1 = 0\).
D. \(2x + 3y - 1 = 0\).
Lời giải
Đường thẳng \(\left( d \right):\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}t = x - 5\\y = - 9 - 2t\end{array} \right.\)\( \Rightarrow y = - 9 - 2\left( {x - 5} \right)\)\( \Leftrightarrow 2x + y - 1 = 0\).
Đáp án A.
Câu 30: Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;1} \right)\) và vuông góc với đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + 5t\end{array} \right.\) có phương trình tham số là:
A. \(\left\{ \begin{array}{l}x = - 2 - 3t\\y = 1 + 5t\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x = - 2 + 5t\\y = 1 + 3t\end{array} \right..\)
C. \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 2 + 5t\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x = 1 + 5t\\y = 2 + 3t\end{array} \right..\)
Lời giải
\(\left\{ \begin{array}{l}M\left( { - 2;1} \right) \in d\\{{\vec u}_\Delta } = \left( { - 3;5} \right)\\d \bot \Delta \end{array} \right. \to \left\{ \begin{array}{l}M\left( { - 2;1} \right) \in d\\{{\vec n}_d} = \left( { - 3;5} \right) \to {{\vec u}_d} = \left( {5;3} \right)\end{array} \right. \to d:\left\{ \begin{array}{l}x = - 2 + 5t\\y = 1 + 3t\end{array} \right.\left( {t \in \mathbb{R}} \right).\)
Đáp án B.
Câu 31: Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( { - 1;2} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(2\sqrt 5 \).
A. \(m = 2.\)
B. \(\left[ \begin{array}{l}m = - 2\\m = \frac{1}{2}\end{array} \right.\).
C. \(m = - \frac{1}{2}\).
D. Không tồn tại \(m\).
Lời giải
\(d\left( {A;\Delta } \right) = \frac{{\left| { - m + 2 - m + 4} \right|}}{{\sqrt {{m^2} + 1} }} = 2\sqrt 5 \Leftrightarrow \left| {m - 3} \right| = \sqrt 5 .\sqrt {{m^2} + 1} \Leftrightarrow 4{m^2} + 6m - 4 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}m = - 2\\m = \frac{1}{2}\end{array} \right..\)
Đáp án B.
Câu 32: Trong mặt phẳng \(Oxy\), đường tròn đi qua ba điểm \(A\left( {1;2} \right)\), \(B\left( {5;2} \right)\), \(C\left( {1; - 3} \right)\) có phương trình là.
A. \({x^2} + {y^2} + 25x + 19y - 49 = 0\).
B. \(2{x^2} + {y^2} - 6x + y - 3 = 0\).
C. \({x^2} + {y^2} - 6x + y - 1 = 0\).
D. \({x^2} + {y^2} - 6x + xy - 1 = 0\).
Lời giải
Gọi \(\left( C \right)\) là phương trình đường tròn đi qua ba điểm \(A,B,C\) với tâm \(I\left( {a;b} \right)\)
\( \Rightarrow \left( C \right)\)có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\). Vì đường tròn \(\left( C \right)\) đi qua qua ba điểm \(A,B,C\) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}1 + 4 - 2a - 4b + c = 0\\25 + 4 - 10a - 4b + c = 0\\1 + 9 - 2a + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2a - 4b + c = - 5\\ - 10a - 4b + c = - 29\\ - 2a + 6b + c = - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - \frac{1}{2}\\c = - 1\end{array} \right.\).
Vậy phương trình đường tròn cần tìm là \({x^2} + {y^2} - 6x + y - 1 = 0\).
Đáp án C.
Câu 33: Trong hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;\,2} \right),\,B\left( {3,\,4} \right)\) và tiếp xúc với đường thẳng \(\Delta :\,3x + y - 3 = 0\), biết tâm của \(\left( C \right)\) có tọa độ là những số nguyên. Phương trình đường tròn \(\left( C \right)\) là
A. \({x^2} + {y^2} - 3x - 7y + 12 = 0.\)
B. \({x^2} + {y^2} - 6x - 4y + 5 = 0.\)
C. \({x^2} + {y^2} - 8x - 2y + 7 = 0.\)
D. \({x^2} + {y^2} - 2x - 8y + 20 = 0.\)
Lời giải
Ta có : \(\overrightarrow {AB} = (2;2)\) ; đoạn \(AB\) có trung điểm \(M\left( {2;\,3} \right)\)
\( \Rightarrow \)Phương trình đường trung trực của đoạn \(AB\) là \(d:\,x + y - 5 = 0\).
Gọi \(I\) là tâm của \(\left( C \right)\) \( \Rightarrow I \in d\)\( \Rightarrow I\left( {a;\,5 - a} \right)\,,\,a \in \mathbb{Z}.\)
Ta có: \(R = IA = d\left( {I;\,\Delta } \right) = \sqrt {{{\left( {a - 1} \right)}^2} + {{\left( {a - 3} \right)}^2}} = \frac{{\left| {2a + 2} \right|}}{{\sqrt {10} }} \Leftrightarrow a = 4 \Rightarrow I\left( {4;\,1} \right),\,R = \sqrt {10} .\)
Vậy phương trình đường tròn là: \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 10 \Leftrightarrow {x^2} + {y^2} - 8x - 2y + 7 = 0.\)
Đáp án C.
Câu 34: Cho đường hypebol có phương trình \(\left( H \right):100{x^2} - 25{y^2} = 100\). Tiêu cự của hypebol đó là
A. \(2\sqrt {10} \).
B. \(2\sqrt {104} \).
C. \(\sqrt {10} \).
D. \(\sqrt {104} \).
Lời giải
\(\left( H \right):100{x^2} - 25{y^2} = 100 \Leftrightarrow \frac{{{x^2}}}{{100}} - \frac{{{y^2}}}{4} = 1\).
\(a = 10,b = 2 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {104} \).
Tiêu cự của hypebol là \(2\sqrt {104} \).
Đáp án B.
Câu 35: Cho parabol \(\left( P \right):{y^2} = 8x\) có tiêu điểm là
A. \(F\left( {0;4} \right)\).
B. \(F\left( {0;2} \right)\).
C. \(F\left( {2;0} \right)\).
D. \(F\left( {4;0} \right)\).
Lời giải
Ta có \(2p = 8 \Rightarrow p = 4\).
Parabol có tiêu điểm \(F\left( {2;0} \right)\).
Đáp án C.
Phần tự luận (3 điểm)
Bài 1. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B.
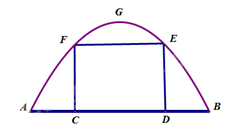
Lời giải
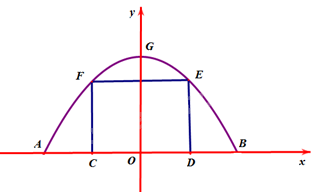
Gắn hệ trục tọa độ Oxy như hình vẽ, chiếc cổng là 1 phần của parabol \(\left( P \right):y = a{x^2} + bx + c\) với \(a < 0\).
Do parabol \((P)\) đối xứng qua trục tung nên có trục đối xứng \(x = 0 \Rightarrow - \frac{b}{{2a}} = 0 \Leftrightarrow b = 0\) .
Chiều cao của cổng parabol là 4m nên \(G\left( {0;4} \right) \Rightarrow c = 4\)
\( \Rightarrow \left( P \right):y = a{x^2} + 4\).
Lại có, kích thước cửa ở giữa là 3m x 4m nên \(E\left( {2;3} \right) \Rightarrow 3 = 4a + 4 \Rightarrow a = - \frac{1}{4}\) .
Vậy \(\left( P \right):y = - \frac{1}{4}{x^2} + 4\).
Ta có \( - \frac{1}{4}{x^2} + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\) nên \(A\left( { - 4;0} \right);B\left( {4;0} \right)\) hay \(AB = 8\).
Bài 2. Cho tam giác \(ABC\) có \(A\left( {1;3} \right)\) và hai đường trung tuyến \(BM:x + 7y - 10 = 0\) và \(CN:x - 2y + 2 = 0\). Viết phương trình đường thẳng chứa cạnh \(BC\) của tam giác \(ABC\).
Lời giải
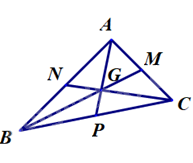
Vì \(B \in BM\) nên tọa độ điểm \(B\) có dạng \(B\left( { - 7b + 10;\,b} \right)\).
Gọi \(G\) là trọng tâm của tam giác \(ABC\).
Khi đó tọa độ điểm \(G\) là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}x + 7y - 10 = 0\\x - 2y + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{2}{3}\\y = \frac{4}{3}\end{array} \right. \Rightarrow G\left( {\frac{2}{3};\,\frac{4}{3}} \right)\).
Gọi \(P\left( {x;\,y} \right)\) là trung điểm của \(BC\).
Khi đó \(AP\) là đường trung tuyến của tam giác \(ABC\).
Suy ra \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AP} \Leftrightarrow \left\{ \begin{array}{l}\frac{2}{3} - 1 = \frac{2}{3}\left( {x - 1} \right)\\\frac{4}{3} - 3 = \frac{2}{3}\left( {y - 3} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{1}{2}\end{array} \right. \Rightarrow P\left( {\frac{1}{2};\,\frac{1}{2}} \right)\).
Vì \(P\) là trung điểm của \(BC\) nên \(\left\{ \begin{array}{l}{x_C} = 2{x_P} - {x_B}\\{y_C} = 2{y_P} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 7b - 9\\{y_C} = 1 - b\end{array} \right.\) \( \Rightarrow C\left( {7b - 9;\,1 - b} \right)\).
Vì \(C \in CN\) nên \(7b - 9 - 2.\left( {1 - b} \right) + 2 = 0 \Leftrightarrow b = 1\).
Khi đó \(B\left( {3;\,1} \right)\), \(C\left( { - 2;\,0} \right)\).
Vậy phương trình đường thẳng \(BC\) đi qua hai điểm \(B\) và \(C\) là \(x - 5y + 2 = 0\).
Bài 3. Tìm tất cả các giá trị thực của tham số \(m\)để hàm số \(y = \frac{{mx}}{{\sqrt {x - m + 2} - 1}}\)xác định trên \(\left( {0;1} \right)\).
Lời giải
Hàm số xác định trên \(\left( {0;1} \right) \Leftrightarrow \left\{ \begin{array}{l}x - m + 2 \ge 0\\\sqrt {x - m + 2} - 1 \ne 0\end{array} \right.\forall x \in \left( {0;1} \right)\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge m - 2\\\sqrt {x - m + 2} \ne 1\end{array} \right.\forall x \in \left( {0;1} \right) \Leftrightarrow \left\{ \begin{array}{l}x \ge m - 2\\x \ne m - 1\end{array} \right.\forall x \in \left( {0;1} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}m - 2 \le 0\\\left[ \begin{array}{l}m - 1 \ge 1\\m - 1 \le 0\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 2\\\left[ \begin{array}{l}m \ge 2\\m \le 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \le 1\\m = 2\end{array} \right.\)
Vậy \(m \in \left( { - \infty ;1} \right] \cup \left\{ 2 \right\}\).
Bài 4. Cho tam giác \(ABC\) biết \(H\left( {3;2} \right)\), \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\) lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng \(BC\) có phương trình \(x + 2y - 2 = 0\). Tìm phương trình đường tròn ngoại tiếp tam giác \(ABC\)?
Lời giải
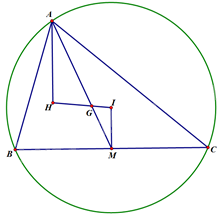
*) Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
\( \Rightarrow \overrightarrow {HI} = \frac{3}{2}\overrightarrow {HG} \)\( \Rightarrow \left\{ \begin{array}{l}{x_I} - 3 = \frac{3}{2}\left( {\frac{5}{3} - 3} \right)\\{y_I} - 2 = \frac{3}{2}\left( {\frac{8}{3} - 2} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_I} = 1\\{y_I} = 3\end{array} \right.\)
*) Gọi \(M\) là trung điểm của \(BC\) \( \Rightarrow IM \bot BC\) \( \Rightarrow IM:2x - y + 1 = 0\).
\(M = IM \cap BC\) \( \Rightarrow \left\{ \begin{array}{l}2x - y = - 1\\x + 2y = 2\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}x = 0\\y = 1\end{array} \right.\)\( \Rightarrow M\left( {0;1} \right)\).
Lại có: \(\overrightarrow {MA} = 3\overrightarrow {MG} \) \( \Rightarrow \left\{ \begin{array}{l}{x_A} = 3.\frac{5}{3}\\{y_A} - 1 = 3.\left( {\frac{8}{3} - 1} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_A} = 5\\{y_A} = 6\end{array} \right.\).
Suy ra: bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = IA = 5\).
Vậy phương trình đường tròn ngoại tiếp tam giác \(ABC\) là \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 25\).
Đề thi giữa kì 2 Toán 10 Kết nối tri thức - Đề số 1 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một nửa học kì. Đề thi này không chỉ kiểm tra kiến thức đã học mà còn rèn luyện kỹ năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết một số câu hỏi điển hình.
Thông thường, đề thi giữa kì 2 Toán 10 Kết nối tri thức - Đề số 1 có cấu trúc bao gồm hai phần chính:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 10 Kết nối tri thức - Đề số 1:
Ví dụ 1: Giải phương trình bậc hai 2x2 - 5x + 3 = 0
Lời giải:
Phương trình có dạng ax2 + bx + c = 0 với a = 2, b = -5, c = 3.
Tính delta (Δ) = b2 - 4ac = (-5)2 - 4 * 2 * 3 = 25 - 24 = 1
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + 1) / (2 * 2) = 3/2
x2 = (-b - √Δ) / 2a = (5 - 1) / (2 * 2) = 1
Vậy phương trình có hai nghiệm x1 = 3/2 và x2 = 1.
Ví dụ 2: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Lời giải:
Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25
Suy ra BC = √25 = 5cm.
Giaitoan.edu.vn hy vọng rằng với những thông tin và hướng dẫn trên, các em học sinh sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi giữa kì 2 Toán 10 Kết nối tri thức - Đề số 1.