Chào mừng các em học sinh lớp 11 đến với đề thi giữa kì 1 môn Toán chương trình Kết nối tri thức - Đề số 6. Đề thi này được thiết kế để giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự đánh giá năng lực của bản thân.
Giaitoan.edu.vn cung cấp đề thi có đáp án chi tiết, giúp các em hiểu rõ phương pháp giải và tránh những sai lầm không đáng có.
Góc có số đo \({75^o}\) bằng bao nhiêu radian?
\(\frac{{5\pi }}{{12}}\)
\(\frac{{7\pi }}{{12}}\)
\(\frac{\pi }{2}\)
\(\frac{\pi }{6}\)
Cho \(\sin \alpha = \frac{2}{3}\) với \(\frac{\pi }{2} < \alpha < \pi \). Giá trị của \(\cos \alpha \) là?
\(\cos \alpha = \frac{2}{3}\)
\(\cos \alpha = - \frac{{\sqrt 5 }}{3}\)
\(\cos \alpha = \frac{{\sqrt 5 }}{3}\)
\(\cos \alpha = \frac{3}{2}\)
Giá trị lượng giác \(\sin \left( {\frac{{5\pi }}{{12}}} \right)\) bằng?
0,9
\(\frac{{\sqrt 2 (1 + \sqrt 3 )}}{2}\)
\(\frac{{\sqrt 3 (1 + \sqrt 2 )}}{4}\)
\(\frac{{\sqrt 2 (1 + \sqrt 3 )}}{4}\)
Hàm số nào sau đây là hàm số chẵn?
\(y = - \cos x\)
\(y = - 2\sin x\)
\(y = 2\sin ( - x)\)
\(y = \sin x - \cos x\)
Nghiệm của phương trình \(\sin x = 0\) là?
\(x = k2\pi ,k \in \mathbb{Z}\)
\(x = k\pi ,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\)
Số hạng thứ 4 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = \frac{1}{{{u_{n - 1}} + 2}}}\end{array}} \right.\) là?
\(\frac{7}{{17}}\)
\(\frac{7}{{15}}\)
\(\frac{8}{7}\)
\(\frac{3}{8}\)
Dãy số nào sau đây là cấp số cộng?
1; 3; 6; 9
1; 3; 5; 7; 9
1; 2; 4; 6; 8
1; -3; -5; -7; -9
Cho cấp số nhân 32; 16; 8; 4; 2. Công bội của cấp số nhân là?
\(q = 2\)
\(q = \frac{1}{2}\)
\(q = \frac{1}{4}\)
\(q = \frac{1}{3}\)
Cho bảng số liệu khảo sát về tuổi thọ (đơn vị: nghìn giờ) của một loại bóng đèn:

Có bao nhiêu bóng đèn được khảo sát và bao nhiêu bóng đèn có tuổi thọ từ 9 nghìn giờ trở lên?
34
8
50
42
Cho mẫu số liệu về chiều cao của các học sinh lớp 11B (đơn vị: cm)

Khoảng biến thiến của mẫu số liệu trên là
17
18
19
20
Nghiệm của phương trình \(\cos \left( {\frac{x}{2}} \right) = - \frac{1}{2}\) là
\(x = \frac{{4\pi }}{3} + k2\pi \) hoặc \(x = - \frac{{4\pi }}{3} + k2\pi \), \(k \in \mathbb{Z}\)
\(x = \frac{{2\pi }}{3} + k2\pi \) hoặc \(x = - \frac{{2\pi }}{3} + k2\pi \), \(k \in \mathbb{Z}\)
\(x = \frac{{4\pi }}{3} + k\pi \) hoặc \(x = - \frac{{4\pi }}{3} + k\pi \), \(k \in \mathbb{Z}\)
\(x = \frac{\pi }{3} + k\pi \) hoặc \(x = - \frac{\pi }{3} + k\pi \), \(k \in \mathbb{Z}\)
Cho cấp số cộng \(({u_n})\) có \({u_1} = - 2\) và công sai \(d = 5\). Số 198 là số hạng thứ bao nhiêu của cấp số cộng?
25
39
40
41
Cho hàm số \(y = \sin x\). Khi đó
a) \(\sin x < 0\) khi \( - \frac{\pi }{2} < x < 0\)
b) Hàm số \(y = \sin x\) lẻ với mọi \(x \in \mathbb{R}\)
c) Phương trình \(\sin x = 1\) có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\)
d) Hàm số \(y = \sin x\) có chặn dưới là 0
Cho \(\sin \alpha = \frac{1}{3}\) và \(0 < \alpha < \frac{\pi }{2}\). Khi đó
a) \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}\)
b) \(\cos \alpha = \frac{{2\sqrt 2 }}{3}\)
c) \(\tan \alpha = \frac{{\sqrt 2 }}{4}\)
d) \(\cot \alpha = - 2\sqrt 2 \)
Cho dãy số \(({u_n})\) được xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 3}\\{{u_{n + 1}} = 2{u_n}}\end{array}} \right.\) với \(n \ge 1\). Khi đó
a) Dãy số \(({u_n})\) là dãy số giảm
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_2} = 6\)
d) Công thức tổng quát của \(({u_n})\) là \({u_n} = {2^{n - 1}}.3\)
Cho mẫu số liệu về thống kê nhiệt độ tại một địa điểm trong 30 ngày, ta có bảng số liệu sau:

a) Mẫu số liệu đã cho là mẫu số liệu ghép nhóm
b) Khoảng biến thiên của mẫu số liệu trên là 16
c) Số ngày có nhiệt độ thấp hơn 25 là 19
d) Nhiệt độ trung bình tại địa điểm đó trong 30 ngày (làm tròn đến chữ số hàng đơn vị) là 26 độ C
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác \(\alpha = (Ox,OM)\) theo hàm số \({v_x} = 0,25\sin \alpha \) (m/s). Vận tốc lớn nhất của cabin là (Viết dưới dạng số thập phân)?
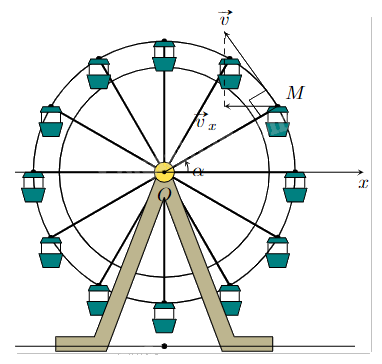
Đáp án:
Cho vận tốc v (cm/s) của một con lắc đơn theo thời gian t (giây) được xác định bởi công thức \(v = - 4\sin \left( {1,5t + \frac{\pi }{4}} \right)\) với \(0 \le t \le 2\). Xác định thời điểm vận tốc con lắc bằng 2 cm/s (Làm tròn kết quả đến hàng phần mười)?
Đáp án:
Khán đài D của một sân vận động có 20 hàng ghế xếp theo hình quạt. hàng thứ nhất có 13 ghế, hàng thứ hai có 16 ghế, hàng thứ ba có 19 ghế,…, cứ thế tiếp tục cho đến hàng cuối cùng. Số ghế ở hàng cuối cùng là?
Đáp án:
Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gỉa sử tỉ lệ tăng dân số là không đổi. Tính số dân (đơn vị: triệu người) của tỉnh đó sau 10 năm kể từ năm 2020 (Làm tròn đến hàng phần trăm)?
Đáp án:
Cho mẫu số liệu về thời gian (phút) đi từ nhà đến trường của một số học sinh như sau:

Tìm mốt của mẫu số liệu trên (Làm tròn đến hàng phần trăm).
Đáp án:
Cho mẫu số liệu về thời gian (phút) đi từ nhà đến trường của một số học sinh như sau:

Tính trung vị của mẫu số liệu trên.
Đáp án:
Góc có số đo \({75^o}\) bằng bao nhiêu radian?
\(\frac{{5\pi }}{{12}}\)
\(\frac{{7\pi }}{{12}}\)
\(\frac{\pi }{2}\)
\(\frac{\pi }{6}\)
Đáp án : A
Áp dụng quan hệ giữa radian và độ: \(1rad = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \frac{\pi }{{180}}rad\).
Ta có: \({75^o} = 75.\frac{\pi }{{180}} = \frac{{5\pi }}{{12}}\).
Cho \(\sin \alpha = \frac{2}{3}\) với \(\frac{\pi }{2} < \alpha < \pi \). Giá trị của \(\cos \alpha \) là?
\(\cos \alpha = \frac{2}{3}\)
\(\cos \alpha = - \frac{{\sqrt 5 }}{3}\)
\(\cos \alpha = \frac{{\sqrt 5 }}{3}\)
\(\cos \alpha = \frac{3}{2}\)
Đáp án : B
Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và sử dụng đường tròn lượng giác để xét dấu.
Ta có: \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{3}{2}} \right)^2} = \frac{5}{9}\), suy ra \(\cos \alpha = \pm \frac{{\sqrt 5 }}{3}\).
Vì \(\frac{\pi }{2} < \alpha < \pi \) nên điểm cuối của cung \(\alpha \) thuộc cung phần tư thứ II, do đó \(\cos \alpha < 0\).
Vậy \(\cos \alpha = - \frac{{\sqrt 5 }}{3}\).
Giá trị lượng giác \(\sin \left( {\frac{{5\pi }}{{12}}} \right)\) bằng?
0,9
\(\frac{{\sqrt 2 (1 + \sqrt 3 )}}{2}\)
\(\frac{{\sqrt 3 (1 + \sqrt 2 )}}{4}\)
\(\frac{{\sqrt 2 (1 + \sqrt 3 )}}{4}\)
Đáp án : D
Sử dụng công thức cộng lượng giác \(\sin (a + b) = \sin a.\cos b + \sin b.\cos a\).
\(\sin \frac{{5\pi }}{{12}} = \sin \left( {\frac{\pi }{4} + \frac{\pi }{6}} \right) = \sin \frac{\pi }{4}.\cos \frac{\pi }{6} + \sin \frac{\pi }{6}.\cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4} = \frac{{\sqrt 2 (1 + \sqrt 3 )}}{4}\).
Hàm số nào sau đây là hàm số chẵn?
\(y = - \cos x\)
\(y = - 2\sin x\)
\(y = 2\sin ( - x)\)
\(y = \sin x - \cos x\)
Đáp án : A
Cho hàm số y = f(x) liên tục và xác định trên khoảng (đoạn) K. Với mỗi \(x \in K\) thì \( - x \in K\).
- Nếu f(x) = f(-x) thì hàm số y = f(x) là hàm số chẵn trên tập xác định.
- Nếu f(-x) = -f(x) thì hàm số y = f(x) là hàm số lẻ trên tập xác định.
Xét phương án A, hàm số \(y = - \cos x\) có tập xác định D = R, suy ra có \(x \in R\) thì \( - x \in R\).
Mặt khác, f(-x) = - cos(-x) = - cosx = f(x).
Vậy hàm số đã cho là hàm số chẵn.
Nghiệm của phương trình \(\sin x = 0\) là?
\(x = k2\pi ,k \in \mathbb{Z}\)
\(x = k\pi ,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\)
Đáp án : B
Nghiệm của phương trình lượng giác cơ bản.
\(\sin x = 0 \Rightarrow x = k\pi ,k \in \mathbb{Z}\).
Số hạng thứ 4 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = \frac{1}{{{u_{n - 1}} + 2}}}\end{array}} \right.\) là?
\(\frac{7}{{17}}\)
\(\frac{7}{{15}}\)
\(\frac{8}{7}\)
\(\frac{3}{8}\)
Đáp án : A
Tìm lần lượt \({u_2},{u_3},{u_4}\) bằng cách thay n vào công thức tổng quát.
Ta có:
\({u_2} = \frac{1}{{{u_1} + 2}} = \frac{1}{{1 + 2}} = \frac{1}{3}\)
\({u_3} = \frac{1}{{{u_2} + 2}} = \frac{1}{{\frac{1}{3} + 2}} = \frac{3}{7}\)
\({u_4} = \frac{1}{{{u_3} + 2}} = \frac{1}{{\frac{3}{7} + 2}} = \frac{7}{{17}}\)
Dãy số nào sau đây là cấp số cộng?
1; 3; 6; 9
1; 3; 5; 7; 9
1; 2; 4; 6; 8
1; -3; -5; -7; -9
Đáp án : B
Dãy số lập thành một cấp số cộng khi và chỉ khi hai phần tử liên tiếp sai khác nhau một hằng số.
Xét hiệu các phần tử liên tiếp trong các dãy số, chỉ có dãy ở đáp án B phần tử sau hơn phần tử liền trước 2 đơn vị (9 – 7 = 7 – 5 = 5 – 3 = 3 – 1 = 2).
Cho cấp số nhân 32; 16; 8; 4; 2. Công bội của cấp số nhân là?
\(q = 2\)
\(q = \frac{1}{2}\)
\(q = \frac{1}{4}\)
\(q = \frac{1}{3}\)
Đáp án : B
\(q = \frac{{{u_{n + 1}}}}{{{u_n}}}\).
Ta có: \(\frac{{16}}{{32}} = \frac{8}{{16}} = \frac{4}{8} = \frac{2}{4} = \frac{1}{2}\). Vậy \(q = \frac{1}{2}\).
Cho bảng số liệu khảo sát về tuổi thọ (đơn vị: nghìn giờ) của một loại bóng đèn:

Có bao nhiêu bóng đèn được khảo sát và bao nhiêu bóng đèn có tuổi thọ từ 9 nghìn giờ trở lên?
34
8
50
42
Đáp án : C
Quan sát bảng số liệu, tính số bóng đèn trong hai nhóm [9;11) và [11;13).
Số bóng đèn có tuổi thọ từ 9 nghìn giờ trở lên là 42 + 8 = 50.
Cho mẫu số liệu về chiều cao của các học sinh lớp 11B (đơn vị: cm)

Khoảng biến thiến của mẫu số liệu trên là
17
18
19
20
Đáp án : A
Khoảng biến thiên bằng hiệu giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu.
Giá trị nhỏ nhất của mẫu là 156, giá trị lớn nhất là 173 nên khoảng biến thiên là 173 – 156 = 17.
Nghiệm của phương trình \(\cos \left( {\frac{x}{2}} \right) = - \frac{1}{2}\) là
\(x = \frac{{4\pi }}{3} + k2\pi \) hoặc \(x = - \frac{{4\pi }}{3} + k2\pi \), \(k \in \mathbb{Z}\)
\(x = \frac{{2\pi }}{3} + k2\pi \) hoặc \(x = - \frac{{2\pi }}{3} + k2\pi \), \(k \in \mathbb{Z}\)
\(x = \frac{{4\pi }}{3} + k\pi \) hoặc \(x = - \frac{{4\pi }}{3} + k\pi \), \(k \in \mathbb{Z}\)
\(x = \frac{\pi }{3} + k\pi \) hoặc \(x = - \frac{\pi }{3} + k\pi \), \(k \in \mathbb{Z}\)
Đáp án : A
Giải phương trình lượng giác \(\cos x = a\):
- Nếu \(\left| a \right| > 1\) thì phương trình vô nghiệm.
- Nếu \(\left| a \right| \le 1\) thì chọn cung \(\alpha \) sao cho \(\cos \alpha = a\). Khi đó phương trình trở thành:
\(\cos x = \cos \alpha \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = - \alpha + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\).
Do \(\cos \frac{{2\pi }}{3} = - \frac{1}{2}\) nên \(\cos \frac{x}{2} = \cos \frac{{2\pi }}{3} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\frac{x}{2} = \frac{{2\pi }}{3} + k2\pi }\\{\frac{x}{2} = - \frac{{2\pi }}{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{4\pi }}{3} + k2\pi }\\{x = - \frac{{4\pi }}{3} + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\).
Cho cấp số cộng \(({u_n})\) có \({u_1} = - 2\) và công sai \(d = 5\). Số 198 là số hạng thứ bao nhiêu của cấp số cộng?
25
39
40
41
Đáp án : D
Cấp số cộng \(({u_n})\) có số hạng đầu \({u_1}\) và công sai \(d\) thì số hạng thứ n là \({u_n} = {u_1} + (n - 1)d\).
Gọi 198 là số hạng thứ n của dãy. Ta có: \(198 = {u_1} + (n - 1)d = - 2 + (n - 1).5 \Leftrightarrow 5n = 205 \Leftrightarrow n = 41\).
Cho hàm số \(y = \sin x\). Khi đó
a) \(\sin x < 0\) khi \( - \frac{\pi }{2} < x < 0\)
b) Hàm số \(y = \sin x\) lẻ với mọi \(x \in \mathbb{R}\)
c) Phương trình \(\sin x = 1\) có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\)
d) Hàm số \(y = \sin x\) có chặn dưới là 0
a) \(\sin x < 0\) khi \( - \frac{\pi }{2} < x < 0\)
b) Hàm số \(y = \sin x\) lẻ với mọi \(x \in \mathbb{R}\)
c) Phương trình \(\sin x = 1\) có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\)
d) Hàm số \(y = \sin x\) có chặn dưới là 0
a) Dựa vào góc phần tư của đường tròn lượng giác.
b) Cho hàm số y = f(x) liên tục và xác định trên khoảng (đoạn) K. Với mỗi \(x \in K\) thì \( - x \in K\).
- Nếu f(x) = f(-x) thì hàm số y = f(x) là hàm số chẵn trên tập xác định.
- Nếu f(-x) = -f(x) thì hàm số y = f(x) là hàm số lẻ trên tập xác định.
c) Giải phương trình lượng giác \(\sin x = a\):
- Nếu \(\left| a \right| > 1\) thì phương trình vô nghiệm.
- Nếu \(\left| a \right| \le 1\) thì chọn cung \(\alpha \) sao cho \(\sin \alpha = a\). Khi đó phương trình trở thành:
\(\sin x = \sin \alpha \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\).
d) Xét tập giá trị của hàm số \(y = \sin x\).
a)Đúng. \( - \frac{\pi }{2} < x < 0\) suy ra điểm cuối cung x thuộc góc phần tư thứ IV. Khi đó \(\sin x < 0\).
b) Đúng. Tập xác định: D = R. Mặt khác, \(f( - x) = \sin ( - x) = - \sin x = - f(x)\). Vậy \(y = \sin x\) là hàm số lẻ.
c) Sai. Do \(\sin \frac{\pi }{2} = 1\) nên \(\sin x = \sin \frac{\pi }{2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k2\pi }\\{x = \pi - \frac{\pi }{2} + k2\pi }\end{array}} \right. \Leftrightarrow x = \frac{\pi }{2} + k2\pi \) với \(k \in \mathbb{Z}\).
d) Sai. Hàm số \(y = \sin x\) có chặn dưới là -1.
Cho \(\sin \alpha = \frac{1}{3}\) và \(0 < \alpha < \frac{\pi }{2}\). Khi đó
a) \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}\)
b) \(\cos \alpha = \frac{{2\sqrt 2 }}{3}\)
c) \(\tan \alpha = \frac{{\sqrt 2 }}{4}\)
d) \(\cot \alpha = - 2\sqrt 2 \)
a) \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}\)
b) \(\cos \alpha = \frac{{2\sqrt 2 }}{3}\)
c) \(\tan \alpha = \frac{{\sqrt 2 }}{4}\)
d) \(\cot \alpha = - 2\sqrt 2 \)
a) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu.
b) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu.
c) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{1}{{\cot \alpha }}\)
d) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\tan \alpha }}\)
a)Sai. \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{1}{3}} \right)^2} = \frac{8}{9} \Rightarrow \cos \alpha = \pm \frac{{2\sqrt 2 }}{3}\).
Vì \(0 < \alpha < \frac{\pi }{2}\) nên điểm cuối của cung \(\alpha \) thuộc góc phần tư thứ I nên \(\cos \alpha > 0\). Vậy \(\cos \alpha = \frac{{2\sqrt 2 }}{3}\).
b) Đúng. Từ câu a) ta tính được \(\cos \alpha = \frac{{2\sqrt 2 }}{3}\).
c) Đúng. \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\frac{1}{3}}}{{\frac{{2\sqrt 2 }}{3}}} = \frac{1}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{4}\).
d) Sai. \(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{\frac{{\sqrt 2 }}{4}}} = 2\sqrt 2 \).
Cho dãy số \(({u_n})\) được xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 3}\\{{u_{n + 1}} = 2{u_n}}\end{array}} \right.\) với \(n \ge 1\). Khi đó
a) Dãy số \(({u_n})\) là dãy số giảm
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_2} = 6\)
d) Công thức tổng quát của \(({u_n})\) là \({u_n} = {2^{n - 1}}.3\)
a) Dãy số \(({u_n})\) là dãy số giảm
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_2} = 6\)
d) Công thức tổng quát của \(({u_n})\) là \({u_n} = {2^{n - 1}}.3\)
a) Dãy số \(({u_n})\) là dãy số giảm nếu \({u_n} > {u_{n + 1}}\). Dãy số \(({u_n})\) là dãy số tăng nếu \({u_n} < {u_{n + 1}}\).
b) Dãy số \(({u_n})\) là dãy số bị chặn nếu \(({u_n})\) vừa bị chặn trên vừa bị chặn dưới, tức tồn tại hai số m, M sao cho \(m \le {u_n} \le M\) \(\forall n \in \mathbb{N}*\).
c) Tính \({u_2}\) bằng công thức \({u_{n + 1}} = 2{u_n}\).
d) Tìm số hạng đầu \({u_1}\) và công sai d. Công thức tổng quát: \({u_n} = {u_1}.{q^{n - 1}}\).
a) Sai. Ta có: \({u_1} = 3 > 0\). Với n = 1, ta được \({u_2} = 2{u_1} = 2.3 = 6 > 0\).
Giả sử n = k, ta cần chứng minh \({u_k} > 0\) thì \({u_{k + 1}} > 0\).
Thật vậy, \({u_{k + 1}} = 2{u_k} > 0\) vì \({u_k} > 0\).
Vậy \({u_n} > 0\) \(\forall n \ge 1\).
Ta có: \({u_{n + 1}} - {u_n} = 2{u_n} - {u_n} = {u_n} > 0\). Suy ra \({u_n} < {u_{n + 1}}\). Vậy dãy số trên là dãy số tăng.
b) Sai. Ta có: \(({u_n})\) là dãy số tăng nên \(({u_n})\) bị chặn dưới tại \({u_1} = 3\).
Mặt khác, \(({u_n})\) là cấp số nhân có công bội \(q = \frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{2{u_n}}}{{{u_n}}} = 2\) và số hạng đầu \({u_1} = 3\) nên công thức tổng quát là \({u_n} = {3.2^{n - 1}}\). Ta có \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = \mathop {\lim }\limits_{n \to + \infty } {3.2^{n - 1}} = + \infty \) nên dãy không bị chặn trên.
Vậy dãy số không bị chặn.
c) Đúng. \({u_2} = 2{u_1} = 2.3 = 6\).
d) Đúng. Theo câu b), công thức tổng quát là \({u_n} = {3.2^{n - 1}}\).
Cho mẫu số liệu về thống kê nhiệt độ tại một địa điểm trong 30 ngày, ta có bảng số liệu sau:

a) Mẫu số liệu đã cho là mẫu số liệu ghép nhóm
b) Khoảng biến thiên của mẫu số liệu trên là 16
c) Số ngày có nhiệt độ thấp hơn 25 là 19
d) Nhiệt độ trung bình tại địa điểm đó trong 30 ngày (làm tròn đến chữ số hàng đơn vị) là 26 độ C
a) Mẫu số liệu đã cho là mẫu số liệu ghép nhóm
b) Khoảng biến thiên của mẫu số liệu trên là 16
c) Số ngày có nhiệt độ thấp hơn 25 là 19
d) Nhiệt độ trung bình tại địa điểm đó trong 30 ngày (làm tròn đến chữ số hàng đơn vị) là 26 độ C
Sử dụng công thức tính khoảng biến thiên, số trung bình của mẫu số liệu ghép nhóm.
a) Đúng. Mẫu số liệu đã cho là mẫu số liệu ghép nhóm.
b) Đúng. Khoảng biến thiên của mẫu số liệu trên là 34 – 18 = 16.
c) Sai. Số ngày có nhiệt độ thấp hơn 25 là 3 + 6 = 9.
d) Đúng. Số trung bình là \(\overline x = \frac{{\frac{{18 + 22}}{2}.2 + \frac{{22 + 25}}{2}.6 + \frac{{25 + 28}}{2}.10 + \frac{{28 + 31}}{2}.5 + \frac{{31 + 34}}{2}.6}}{{30}} \approx 26\).
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác \(\alpha = (Ox,OM)\) theo hàm số \({v_x} = 0,25\sin \alpha \) (m/s). Vận tốc lớn nhất của cabin là (Viết dưới dạng số thập phân)?
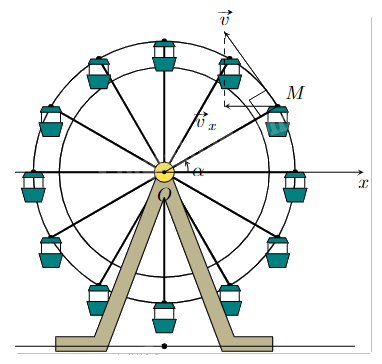
Đáp án:
Đáp án:
Tìm giá trị lớn nhất của hàm số \({v_x} = 0,25\sin \alpha \).
Vì \(\sin \alpha \le 1\) nên \(0,25\sin \alpha \le 0,25\). Vậy giá trị nhỏ nhất của \({v_x} = 0,25\sin \alpha \) là 0,25 (m/s).
Cho vận tốc v (cm/s) của một con lắc đơn theo thời gian t (giây) được xác định bởi công thức \(v = - 4\sin \left( {1,5t + \frac{\pi }{4}} \right)\) với \(0 \le t \le 2\). Xác định thời điểm vận tốc con lắc bằng 2 cm/s (Làm tròn kết quả đến hàng phần mười)?
Đáp án:
Đáp án:
Thay \(v = 2\) vào công thức \(v = - 4\sin \left( {1,5t + \frac{\pi }{4}} \right)\) và tìm t.
\(2 = - 4\sin \left( {1,5t + \frac{\pi }{4}} \right) \Leftrightarrow - \frac{1}{2} = \sin \left( {1,5t + \frac{\pi }{4}} \right) \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1,5t + \frac{\pi }{4} = - \frac{\pi }{6} + k2\pi }\\{1,5t + \frac{\pi }{4} = \frac{{7\pi }}{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - \frac{{5\pi }}{{18}} + k\frac{{4\pi }}{3}}\\{t = \frac{{25\pi }}{{18}} + k\frac{{4\pi }}{3}}\end{array}} \right.\) với \(k \in \mathbb{Z}\).
Vì \(0 \le t \le 2\) nên chỉ có 1 giá trị của t thỏa mãn là \(t = \frac{\pi }{{18}} \approx 0,17\).
Khán đài D của một sân vận động có 20 hàng ghế xếp theo hình quạt. hàng thứ nhất có 13 ghế, hàng thứ hai có 16 ghế, hàng thứ ba có 19 ghế,…, cứ thế tiếp tục cho đến hàng cuối cùng. Số ghế ở hàng cuối cùng là?
Đáp án:
Đáp án:
Số ghế mỗi hàng ở khán đài lập thành một cấp số cộng với 20 hàng tương đương 20 số hạng. Tìm số hạng đầu, công sai từ đó tìm số hạng thứ 20.
Số ghế mỗi hàng ở khán đài lập thành một cấp số cộng với 20 hàng tương đương 20 số hạng.
Ta có: \({u_1} = 13,{u_2} = 16,{u_3} = 19\) nên công sai bằng \(d = {u_2} - {u_1} = {u_3} - {u_2} = 3\).
Số ghế hàng cuối cùng là: \({u_{20}} = 13 + (20 - 1).3 = 70\).
Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gỉa sử tỉ lệ tăng dân số là không đổi. Tính số dân (đơn vị: triệu người) của tỉnh đó sau 10 năm kể từ năm 2020 (Làm tròn đến hàng phần trăm)?
Đáp án:
Đáp án:
Số dân mỗi năm lập thành môt cấp số nhân. Tìm công thức tổng quát của cấp số nhân đó và tìm số hạng thứ 10.
Số dân mỗi năm lập thành môt cấp số nhân \({u_n}\) với số hạng đầu \({u_1} = 2\) triệu người và công sai \(q = 1 + 1\% = 1,01\).
Khi đó, số hạng tổng quát \({u_n} = 2.1,{01^{n - 1}}\).
(*) Số dân tỉnh đó sau 1 năm là \({u_2}\), sau 2 năm là \({u_3}\),...
Số dân tỉnh đó sau 10 năm là \({u_{11}} = 2.1,{01^{11 - 1}} \approx 2,21\) (triệu người).
Lưu ý: Đọc kĩ (*) để tránh nhầm lẫn tính \({u_{10}}\).
Cho mẫu số liệu về thời gian (phút) đi từ nhà đến trường của một số học sinh như sau:

Tìm mốt của mẫu số liệu trên (Làm tròn đến hàng phần trăm).
Đáp án:
Đáp án:
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: [aj; aj+1).
Bước 2: Mốt được xác định là
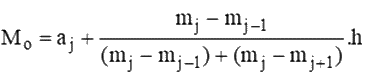
trong đó mj là tần số của nhóm j (quy ước mo = mk+1 = 0) và h là độ dài của nhóm.
\({M_o} = 20 + \frac{{12 - 7}}{{(12 - 7) + (12 - 5)}}.5 = \frac{{265}}{{12}} \approx 22,08\).
Cho mẫu số liệu về thời gian (phút) đi từ nhà đến trường của một số học sinh như sau:

Tính trung vị của mẫu số liệu trên.
Đáp án:
Đáp án:
Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: [ap; ap+1).
Bước 2: Trung vị
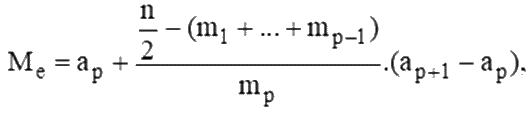
trong đó n là cỡ mẫu, mp là tần số nhóm p. Với p = 1, ta quy ước m1 + ….+ mp-1 = 0.
Cỡ mẫu là n = 7 + 12 + 5 + 7 + 3 + 5 + 1 = 40.
Gọi \({x_1},{x_2},...,{x_{40}}\) là thời gian đi từ nhà đến trường của 40 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần.
Khi đó, trung vị là \(\frac{{{x_{20}} + {x_{21}}}}{2}\). Do hai giá trị \({x_{20}},{x_{21}}\) thuộc nhóm [25; 30) nên nhóm này chứa trung vị.
Trung vị là \({M_e} = 25 + \frac{{\frac{{40}}{2} - (7 + 12)}}{5}.5 = 26\).
Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 6 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức và kỹ năng của học sinh sau một nửa học kỳ đầu tiên. Đề thi bao gồm các dạng bài tập thuộc chương trình đại số và hình học, tập trung vào các chủ đề chính như hàm số bậc hai, phương trình và bất phương trình, lượng giác, và vector trong mặt phẳng.
Thông thường, đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 6 có cấu trúc gồm các phần sau:
Phần này thường kiểm tra các kiến thức về:
Các dạng bài tập thường gặp:
Kiến thức trọng tâm:
Các chủ đề thường được đề cập:
Để giải tốt đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 6, học sinh cần:
Việc luyện tập với đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 6 mang lại nhiều lợi ích cho học sinh:
Ngoài việc luyện tập với đề thi, học sinh nên tham khảo thêm các tài liệu ôn tập hữu ích như:
Hãy dành thời gian ôn tập và luyện tập một cách nghiêm túc để đạt kết quả tốt nhất trong kỳ thi giữa kì 1 Toán 11 Kết nối tri thức. Chúc các em thành công!