Giaitoan.edu.vn xin giới thiệu Đề thi học kì 2 Toán 11 - Đề số 1, một công cụ ôn tập hiệu quả giúp các em học sinh nắm vững kiến thức và tự tin bước vào kỳ thi. Đề thi được biên soạn theo chuẩn chương trình học, bao gồm các dạng bài tập thường gặp và có đáp án chi tiết.
Với đề thi này, các em có thể tự đánh giá năng lực, rèn luyện kỹ năng giải đề và làm quen với cấu trúc đề thi chính thức. Đây là cơ hội tuyệt vời để các em củng cố kiến thức và đạt kết quả tốt nhất trong kỳ thi sắp tới.
Tính giá trị của biểu thức \(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}}\).
Chọn đáp án đúng:
Một chất điểm chuyển động có phương trình \(s\left( t \right) = {t^2} + 2t\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng.
Cho hàm số \(y = 2\sin x - 3\cos x + 3\)có đạo hàm\(y' = a\cos x + b\sin x + c\).Khi đó \(S = 2a + b - c\) có kết quả bằng:
Hàm số \(y = \sqrt {2 + 2{x^2}} \)có đạo hàm \(y' = \frac{{a + bx}}{{\sqrt {2 + 2{x^2}} }}\). Khi đó \(S = a - 2b\) có kết quả bằng
Có hai túi đựng các viên bi có cùng kích thước và khối lượng. Túi I có 3 viên bi màu xanh và 7 viên bi màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bi. Xác suất để hai viên bi được lấy có cùng màu xanh bằng:
Cho hàm số \(y = - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\)Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên tập số thực. Tìm hệ thức đúng
Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, \(SA = SC\). Gọi I, K lần lượt là trung điểm của AB và BC. Góc giữa hai đường thẳng SO và IK bằng:
Cho hình chóp S.ABC. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. Qua S kẻ đường thẳng vuông góc với mặt phẳng (ABC) và cắt mặt phẳng đó tại H. Khi đó, góc giữa SH và MP bằng bao nhiêu độ?:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = x. Tìm x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 60°
Cho hình chóp tam giác đều có cạnh đáy bằng với chiều cao. Tính góc tạo bởi cạnh bên và mặt đáy?
Một cuộc thi bắn súng, có 3 người tham gia thi. Trong đó xác suất bắn trúng của người thứ nhất là 0,9; người thứ 2 là 0,7 và người thứ 3 là 0,8.
a) Xác suất để cả ba người đều bắn trúng là 0,504
b) Xác suất để đúng 2 người bắn trúng là 0,398
c) Xác suất để không người nào bắn trúng là 0,006
d) Xác suất để ít nhất một người bắn trúng là 0,856
Cho hàm số \(y = f(x) = \frac{1}{3}{x^3} - \frac{1}{2}{x^2} + 1\) có đồ thị (C):
a) Phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc bằng 2 là: \(y = 2x + 3\) hoặc \(y = 2x - 3\)
b) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \(({d_1})\) : \(y = - \frac{1}{6}x + 1\) là \(y = 6x - \frac{{25}}{2}\) hoặc \(y = 6x + \frac{{25}}{3}\)
c) Phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng \(({d_2})\):\(y = 2020\)là y = 1 hoặc \(y = \frac{5}{6}\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng \(({d_3}):4x + y - 5 = 0\)là \(y = - 4x - 2\)
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt đáy (ABCD).
a) \(CD \bot (SHM)\)
b) \(AC \bot (SHM)\)
c) Khoảng cách từ B đến mặt phẳng (SCD) là \(\frac{{\sqrt {21} }}{7}\)
d) Khoảng cách từ O đến mặt phẳng (SCD) là \(\frac{{\sqrt {21} }}{{14}}\)
Cho hàm số \(y = \sqrt {2x - {x^2}} .\)
a) Đạo hàm của hàm số là \(y' = (\sqrt {2x - {x^2}} )' = \frac{{1 - x}}{{\sqrt {2x - {x^2}} }}\)
b) Biểu thức \(y'(1) = 0\)
c) Biểu thức \(y''1) = 0\)
d) \({y^3}y'' + 1 = 0,\forall x \in (0;2).\)
Cho hàm số: \(y = \frac{1}{4}\sqrt {\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right)} \)
Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định có tập xác định là \(\mathbb{R}\).
Giải bất phương trình \({\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}\left( {x + \sqrt {{x^2} - 1} } \right) = {\log _6}\left| {x - \sqrt {{x^2} - 1} } \right|\).
Một chất điểm chuyển động có quãng đường được cho bởi phương trình\(s\left( t \right) = \frac{1}{4}{t^4} - {t^3} + \frac{5}{2}{t^2} + 10t\), trong đó \(t > 0\) với \(t\) tính bằng giây (s) và \(s\) tính bằng mét (m). Tính vận tốc chuyển động của chất điểm tại thời điểm chất điểm có gia tốc chuyển động nhỏ nhất.
Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để chọn được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó chỉ có đúng một tấm thẻ chia hết cho 10.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B.\) Biết \(AD = 2a,\,AB = BC = SA = a.\) Cạnh bên \(SA\) vuông góc với mặt đáy, gọi \(M\) là trung điểm của \(AD.\) Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {SCD} \right)\) theo \(a.\)
Cho hàm số \(y = f\left( x \right) = \frac{{x + 1}}{{x + 2}}\) có đồ thị \(\left( C \right)\). Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục hoành
Tính giá trị của biểu thức \(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}}\).
Đáp án : B
Sử dụng công thức mũ và lũy thừa để tính.
\(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{4^{5 + \sqrt 3 }}{{.3}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{2^{10 + 2\sqrt 3 }}{{.3}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{2^5}}}{{{3^2}}} = \frac{{32}}{9}\).
Đáp án B.
Chọn đáp án đúng:
Đáp án : B
\(\sqrt[n]{{{a^n}}} = \left| a \right|\) khi n chẵn (với các biểu thức đều có nghĩa).
\(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} = \left| {x - 1} \right|\)
Đáp án C.
Một chất điểm chuyển động có phương trình \(s\left( t \right) = {t^2} + 2t\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng.
Đáp án : C
Phương trình vận tốc của chất điểm: \(v\left( t \right) = s'\left( t \right)\)
\(v\left( t \right) = s'\left( t \right) = ({t^2} + 2t)' = 2t + 2\)
Tại thời điểm \(t = 3s\), vận tốc tức thời của chất điểm là: \(v = 2.3 + 2 = 8\)
Vậy tại thời điểm \(t = 3s\)vận tốc tức thời của chất điểm là \(8m/s.\)
Đáp án C.
Cho hàm số \(y = 2\sin x - 3\cos x + 3\)có đạo hàm\(y' = a\cos x + b\sin x + c\).Khi đó \(S = 2a + b - c\) có kết quả bằng:
Đáp án : B
Sử dụng công thức tính đạo hàm
\(\begin{array}{l}y' = (2\sin x - 3\cos x + 3)' = 2\cos x + 3\sin x\\ \Rightarrow a = 2,b = 3,c = 0\end{array}\)
Vậy \(S = 2a + b - c = 2.2 + 3 - 0 = 7\)
Vậy PT có tất cả 1 nghiệm
Đáp án B.
Hàm số \(y = \sqrt {2 + 2{x^2}} \)có đạo hàm \(y' = \frac{{a + bx}}{{\sqrt {2 + 2{x^2}} }}\). Khi đó \(S = a - 2b\) có kết quả bằng
Đáp án : A
Sử dụng công thức tính đạo hàm của hàm hợp
\(\begin{array}{l}y' = (\sqrt {2 + 2{x^2}} )' = \frac{{(2 + 2{x^2})'}}{{2\sqrt {2 + 2{x^2}} }} = \frac{{4x}}{{2\sqrt {2 + 2{x^2}} }} = \frac{{2x}}{{\sqrt {2 + 2{x^2}} }}\\ \Rightarrow a = 0,b = 2\\ \Rightarrow S = - 4\end{array}\)
Đáp án A.
Có hai túi đựng các viên bi có cùng kích thước và khối lượng. Túi I có 3 viên bi màu xanh và 7 viên bi màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bi. Xác suất để hai viên bi được lấy có cùng màu xanh bằng:
Đáp án : B
Bước 1: Xác định biến cố của các xác suất, có thể gọi tên các biến cố A; B; C; D để biểu diễn.
Bước 2: Tìm mối quan hệ giữa các biến cố vừa đặt tên, biểu diễn biến cố trung gian và quan trọng nhất là biến cố đề bài đang yêu cầu tính xác suất thông qua các biến cố ở bước 1.
Bước 3: Sử dụng các mối quan hệ vừa xác định ở bước 2 để chọn công thức cộng hay công thức nhân phù hợp.
Xác suất lấy được viên bi màu xanh từ túi I là \(\frac{3}{{10}}\)
Xác suất lấy được viên bi màu xanh từ túi II là \(\frac{{10}}{{16}} = \frac{5}{8}\)
Xác suất lấy được hai viên bi cùng màu xanh là \(\frac{3}{{10}}.\frac{5}{8} = \frac{3}{{16}}\)
Đáp án B.
Cho hàm số \(y = - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\)Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là
Đáp án : C
Tìm tọa độ giao điểm của \(\left( C \right)\) với trục tung
Phương trình tiếp tuyến với đồ thị (C): \(y = f(x)\)tại điểm \(M({x_0};f({x_0}))\)là:
\(y = f'({x_0})(x - {x_0}) + f({x_0})\)
Trong đó:
\(M({x_0};f({x_0}))\)gọi là tiếp điểm.
\(k = f'({x_0})\)là hệ số góc.
(C) cắt trục tung tại điểm \(M(0; - 2)\)
\(y' = ( - {x^3} + 3x - 2)' = - 3{x^2} + 3\)
Phương trình tiếp tuyến với đồ thị (C) tại điểm \(M(0; - 2)\)là:
\(y = f'(0)(x - 0) + f(0) = 3x - 2\)
Đáp án C.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên tập số thực. Tìm hệ thức đúng
Đáp án : A
Sử dụng định nghĩa về đạo hàm tại một điểm.
Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a; b). Nếu tồn tại giới hạn (hữu hạn) thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại x0 và kí hiệu là f’(x0) (hoặc y’(x0)), tức là: \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f({x_0})}}{{x - {x_0}}}\)
\(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\)
Đáp án A.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, \(SA = SC\). Gọi I, K lần lượt là trung điểm của AB và BC. Góc giữa hai đường thẳng SO và IK bằng:
Đáp án : B
+ Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
+ Hai đường thẳng a, b được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\).
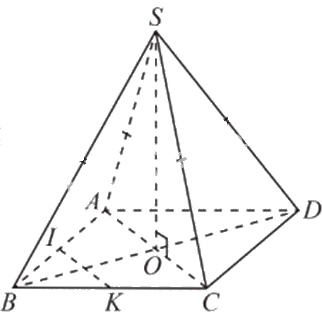
Vì tứ giác ABCD là hình thoi nên O là trung điểm của AC.
Vì \(SA = SC\) nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao. Do đó, \(SO \bot AC\)
Vì I, K lần lượt là trung điểm của AB và BC nên IK là đường trung bình của tam giác BAC. Do đó, IK//AC.
Vì \(SO \bot AC\), IK//AC nên \(IK \bot SO\). Do đó, góc giữa hai đường thẳng SO và IK bằng \({90^0}\).
Đáp án B.
Cho hình chóp S.ABC. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. Qua S kẻ đường thẳng vuông góc với mặt phẳng (ABC) và cắt mặt phẳng đó tại H. Khi đó, góc giữa SH và MP bằng bao nhiêu độ?:
Đáp án : B
+ Nếu đường thẳng d vuông góc với mặt phẳng (P) thì đường thẳng d cũng vuông góc với các mặt phẳng song song với (P).
+ Đường thẳng d gọi là vuông góc với mặt phẳng (P) nếu nó vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P).
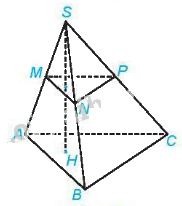
Vì M, N lần lượt là trung điểm của SA, SB nên MN là đường trung bình của tam giác SAB. Do đó, MN//AB.
Vì P, N lần lượt là trung điểm của SC, SB nên PN là đường trung bình của tam giác SBC. Do đó, PN//CB.
Vì MN//AB, PN//CB nên (MNP)// (ABC).
Mặt khác, \(SH \bot \left( {ABC} \right)\) nên \(SH \bot \left( {MNP} \right)\). Mà \(MP \subset \left( {MNP} \right) \Rightarrow SH \bot MP\)
Do đó, góc giữa hai đường thẳng MP và SH bằng \({90^0}\).
Đáp án B.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = x. Tìm x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 60°
Đáp án : D
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
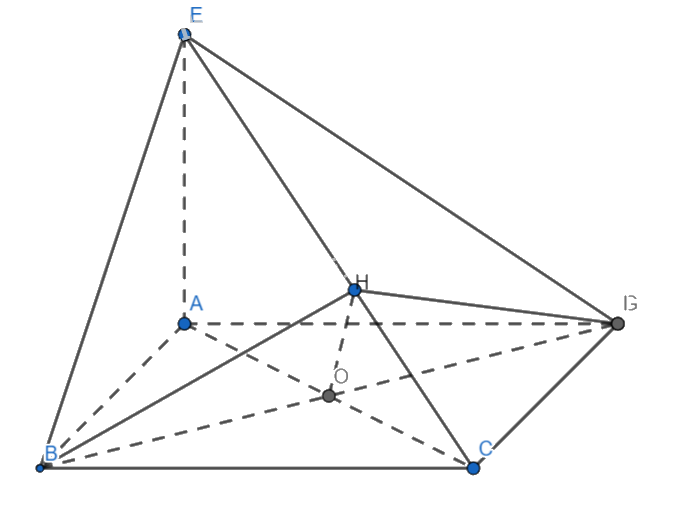
Kẻ \(BH \bot SC \Rightarrow DH \bot SC\)(hai đường cao tương ứng của hai tam giác bằng nhau)
\( \Rightarrow \left( {(SBC),(SCD)} \right) = \left( {BH,DH} \right) = {60^0}\)
Có hai trường hợp xảy ra:
TH1:
\(\begin{array}{l}\widehat {BHD} = {60^0} \Rightarrow \widehat {BHO} = {30^0}\\OB = \frac{a}{{\sqrt 2 }},\tan {30^0} = \frac{{OB}}{{OH}} \Rightarrow OH = \frac{{\frac{a}{{\sqrt 2 }}}}{{\frac{1}{{\sqrt 3 }}}} = a\sqrt {\frac{3}{2}} \end{array}\)
Xét hai tam giác đồng dạng SAC và OHC ta có:
\(\begin{array}{l}\frac{{OH}}{{OC}} = \frac{{SA}}{{SC}} \Leftrightarrow \frac{{a\sqrt {\frac{3}{2}} }}{{\frac{a}{{\sqrt 2 }}}} = \frac{x}{{\sqrt {{x^2} + 2{a^2}} }} \Leftrightarrow \sqrt 3 = \frac{x}{{\sqrt {{x^2} + 2{a^2}} }} \Leftrightarrow 3({x^2} + 2{a^2}) = {x^2}\\ \Leftrightarrow 2{x^2} + 6{a^2} = 0\end{array}\)
\( \Leftrightarrow x = a\sqrt 3 \)(không có đáp án nào thỏa mãn)
TH2:
\(\begin{array}{l}\widehat {BHD} = {120^0} \Rightarrow \widehat {BHO} = {60^0}\\OB = \frac{a}{{\sqrt 2 }},\tan {60^0} = \frac{{OB}}{{OH}} \Rightarrow OH = \frac{{\frac{a}{{\sqrt 2 }}}}{{\sqrt 3 }} = \frac{a}{{\sqrt 6 }}\end{array}\)
Xét hai tam giác đồng dạng SAC và OHC ta có:
\(\begin{array}{l}\frac{{OH}}{{OC}} = \frac{{SA}}{{SC}} \Leftrightarrow \frac{{\frac{a}{{\sqrt 6 }}}}{{\frac{a}{{\sqrt 2 }}}} = \frac{x}{{\sqrt {{x^2} + 2{a^2}} }} \Leftrightarrow \frac{1}{{\sqrt 3 }} = \frac{x}{{\sqrt {{x^2} + 2{a^2}} }} \Leftrightarrow {x^2} + 2{a^2} = 3{x^2}\\ \Leftrightarrow x = a\end{array}\)
Đáp án D.
Cho hình chóp tam giác đều có cạnh đáy bằng với chiều cao. Tính góc tạo bởi cạnh bên và mặt đáy?
Đáp án : B
Sử dụng phương pháp tính góc tạo bởi cạnh bên và mặt đáy của chóp
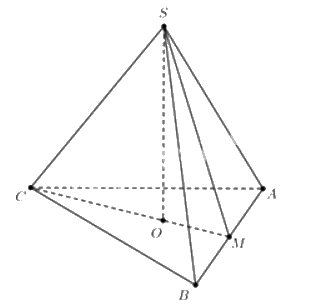
Xét hình chóp tam giác đều S.ABC, O là tâm của tam giác ABC, M là trung điểm AB.
Giả sử, AB = a, khi đó SO = a.
Ta có: \(CM = \frac{{a\sqrt 3 }}{2},CO = \frac{2}{3}CM = \frac{a}{{\sqrt 3 }}\).
\(\begin{array}{l}(SC,(ABC)) = \widehat {SCO}\\\tan \widehat {SCO} = \frac{{SO}}{{CO}} = \sqrt 3 \Leftrightarrow \widehat {SCO} = {60^0}\end{array}\).
Vậy \((SC,(ABC)) = {60^0}\).
Một cuộc thi bắn súng, có 3 người tham gia thi. Trong đó xác suất bắn trúng của người thứ nhất là 0,9; người thứ 2 là 0,7 và người thứ 3 là 0,8.
a) Xác suất để cả ba người đều bắn trúng là 0,504
b) Xác suất để đúng 2 người bắn trúng là 0,398
c) Xác suất để không người nào bắn trúng là 0,006
d) Xác suất để ít nhất một người bắn trúng là 0,856
a) Xác suất để cả ba người đều bắn trúng là 0,504
b) Xác suất để đúng 2 người bắn trúng là 0,398
c) Xác suất để không người nào bắn trúng là 0,006
d) Xác suất để ít nhất một người bắn trúng là 0,856
Bước 1: Xác định biến cố của các xác suất, có thể gọi tên các biến cố A; B; C; D để biểu diễn.
Bước 2: Tìm mối quan hệ giữa các biến cố vừa đặt tên, biểu diễn biến cố trung gian và quan trọng nhất là biến cố đề bài đang yêu cầu tính xác suất thông qua các biến cố ở bước 1.
Bước 3: Sử dụng các mối quan hệ vừa xác định ở bước 2 để chọn công thức cộng hay công thức nhân phù hợp.
Gọi A là biến cố: “Người thứ nhất bắn trúng”; P(A) = 0,9
B là biến cố: “Người thứ hai bắn trúng”; P(B) = 0,7
C là biến cố: “Người thứ ba bắn trúng”; P(C) = 0,8
A, B, C là ba biến cố độc lập
Khi đó:
\(\overline A \)là biến cố: “Người thứ nhất bắn không trúng”; \(P(\overline A ) = 1 - 0,9 = 0,1\)
\(\overline B \)là biến cố: “Người thứ hai bắn không trúng”; \(P(\overline B ) = 1 - 0,7 = 0,3\)
\(\overline C \) là biến cố: “Người thứ ba bắn không trúng”; \(P(\overline C ) = 1 - 0,8 = 0,2\)
Xác suất để cả ba người bắn trúng là:
\(P(A \cap B \cap C) = 0,9.0,7.0,8 = 0,504\)
Ta có: \(D = (A \cap B \cap \overline C ) \cup (A \cap \overline B \cap C) \cup (\overline A \cap B \cap C)\)
Xác suất để có đúng hai người bắn trúng là:
P(D) = 0,9.0,7.0,2 + 0,9.0,3.0,8 + 0,1.0,7.0,8 = 0,398.
c)\(E = (\overline A \cap \overline B \cap \overline C )\)là biến cố: “Không người nào người bắn trúng”
Xác suất để không người nào người bắn trúng là:
\(P(E) = P(\overline A \cap \overline B \cap \overline C ) = P(\overline A ).P(\overline B ).P(\overline C ) = 0,1.0,3.0,2 = 0,006\)
d)\(\overline E \) là biến cố: “Ít nhất một người bắn trúng”
Xác suất để có ít nhất một người bắn trúng là: \(P(\overline E ) = 1 - P(E) = 1 - 0,006 = 0,994\)
Cho hàm số \(y = f(x) = \frac{1}{3}{x^3} - \frac{1}{2}{x^2} + 1\) có đồ thị (C):
a) Phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc bằng 2 là: \(y = 2x + 3\) hoặc \(y = 2x - 3\)
b) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \(({d_1})\) : \(y = - \frac{1}{6}x + 1\) là \(y = 6x - \frac{{25}}{2}\) hoặc \(y = 6x + \frac{{25}}{3}\)
c) Phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng \(({d_2})\):\(y = 2020\)là y = 1 hoặc \(y = \frac{5}{6}\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng \(({d_3}):4x + y - 5 = 0\)là \(y = - 4x - 2\)
a) Phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc bằng 2 là: \(y = 2x + 3\) hoặc \(y = 2x - 3\)
b) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \(({d_1})\) : \(y = - \frac{1}{6}x + 1\) là \(y = 6x - \frac{{25}}{2}\) hoặc \(y = 6x + \frac{{25}}{3}\)
c) Phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng \(({d_2})\):\(y = 2020\)là y = 1 hoặc \(y = \frac{5}{6}\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng \(({d_3}):4x + y - 5 = 0\)là \(y = - 4x - 2\)
Bước 1: Gọi M(x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k
Bước 2: Giải phương trình f'(x0) = k với ẩn là x0.
Bước 3:Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0).
Ta có\(y' = f'(x) = {x^2} - x\)
\( \Rightarrow f'({x_0}) = 2 \Leftrightarrow x_0^2 - {x_0} = 2 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = - 1\end{array} \right.\)
* Với \({x_0} = 2\) ta có \({y_0} = f(0) = \frac{1}{3}{.2^3} - \frac{1}{2}{.2^2} + 1 = \frac{5}{3} \Rightarrow {M_1}(2;\frac{5}{3})\)
Phương trình tiếp tuyến của (C) tại điểm \({M_1}(2;\frac{5}{3})\) là \(y = 2(x - 2) + \frac{5}{3}\,\,hay\,\,y = 2x - \frac{7}{3}\)
* Với \({x_0} = - 1\)ta có \({y_0} = f( - 1) = \frac{1}{6} \Rightarrow {M_2}( - 1;\frac{1}{6})\)
Phương trình tiếp tuyến của (C) tại điểm \({M_2}( - 1;\frac{1}{6})\) là \(y = 2(x + 1) + \frac{1}{6}\,\,hay\,\,y = 2x + \frac{{13}}{6}\)
Do tiếp tuyến vuông góc với \((d):y = - \frac{1}{6}x + 1\) nên \( - \frac{1}{6}k = - 1 \Leftrightarrow k = 6\)
Gọi \(M({x_0},{y_0}) \in (C)\)mà tiếp tuyến của (C) tại M có hệ số góc k = 6.
\(f'({x_0}) = 6 \Rightarrow x_0^2 - {x_0} = 6 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 3\\{x_0} = - 2\end{array} \right.\)
* Với \({x_0} = 3\) ta có \({y_0} = f(3) = \frac{{11}}{2} \Rightarrow {M_1}(3;\frac{{11}}{2}) \in (C)\)
Phương trình tiếp tuyến của (C) tại \({M_1}(3;\frac{{11}}{2}\)) là \(y = 6(x - 3) + \frac{{11}}{2}\,\,hay\,\,y = 6x - \frac{{25}}{2}\)
* Với \({x_0} = - 2\) ta có \({y_0} = f( - 2) = - \frac{{11}}{3} \Rightarrow {M_2}( - 2; - \frac{{11}}{3}) \in (C)\)
Phương trình tiếp tuyến của (C) tại \({M_2}( - 2; - \frac{{11}}{3})\) là \(y = 6(x + 2) - \frac{{11}}{3}\,\,hay\,\,y = 6x + \frac{{25}}{3}\)
Do tiếp tuyến song song với (d') : y = 2020 với hệ số góc là 0
⇒ k = 0
Gọi \(M({x_0},{y_0}) \in (C)\)mà tiếp tuyến của (C) tại M có hệ số góc k = 0
\( \Rightarrow f'({x_0}) = 0 \Rightarrow x_0^2 - {x_0} = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 0\\{x_0} = 1\end{array} \right.\)
* Với \({x_0} = 0\)ta có \({y_0} = f(0) = 1 \Rightarrow {M_1}(0;1) \in (C)\)
Phương trình tiếp tuyến của (C) tại \({M_1}(0;1)\)là y = 1.
* Với \({x_0} = 1\)ta có\({y_0} = f(1) = \frac{5}{6} \Rightarrow {M_2}(1;\frac{5}{6}) \in (C)\)
Phương trình tiếp tuyến của (C) tại \({M_2}(1;\frac{5}{6})\) là \(y = \frac{5}{6}\)
d)\(({d_3}):4x + y - 5 = 0\) hay \(({d_3}):y = - 4x + 5\)
Gọi k là hệ số góc của tiếp tuyến của đồ thị (C).
Do tiếp tuyến song song với \(({d_3}):y = - 4x + 5\)với hệ số góc là – 4
Nên k = -4
\( \Rightarrow f'({x_0}) = - 4 \Rightarrow x_0^2 - {x_0} = - 4 \Rightarrow \)PT vô nghiệm
Suy ra không tổn tại tiếp tuyến thỏa mãn yêu cầu đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt đáy (ABCD).
a) \(CD \bot (SHM)\)
b) \(AC \bot (SHM)\)
c) Khoảng cách từ B đến mặt phẳng (SCD) là \(\frac{{\sqrt {21} }}{7}\)
d) Khoảng cách từ O đến mặt phẳng (SCD) là \(\frac{{\sqrt {21} }}{{14}}\)
a) \(CD \bot (SHM)\)
b) \(AC \bot (SHM)\)
c) Khoảng cách từ B đến mặt phẳng (SCD) là \(\frac{{\sqrt {21} }}{7}\)
d) Khoảng cách từ O đến mặt phẳng (SCD) là \(\frac{{\sqrt {21} }}{{14}}\)
Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng
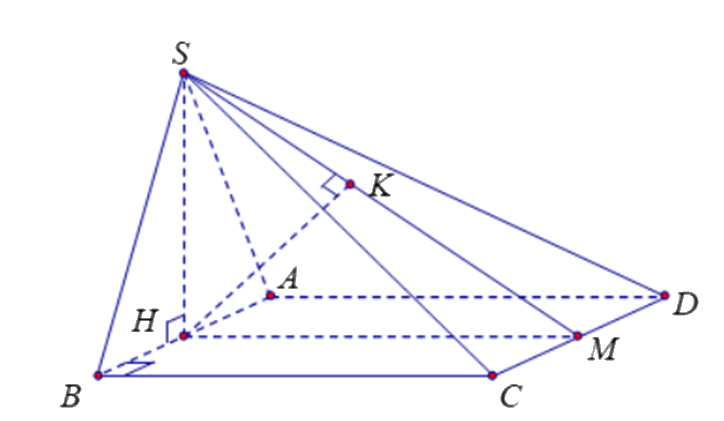
a) \(\left\{ \begin{array}{l}CD \bot HM\\CD \bot SH\\SM,SH \subset (SHM)\\SM \cap SH\end{array} \right. \Rightarrow CD \bot (SHM)\)
b) AC không vuông góc với (SHM)
c) Gọi H, M lần lượt là trung điểm của AB và CD .
Suy ra HM =1, SH = \(\frac{{\sqrt 3 }}{2}\)và SM =\(\frac{{\sqrt 7 }}{2}\)
Vì tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD) nên SH⊥(ABCD)
Vì AB//CD nên AB// (SCD).
Do đó d (B; (SCD)) = d(H; (SCD)) = HK với HK⊥SM trong (SHM).
Ta có:
\(\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{M^2}}} \Rightarrow HK = \frac{{\sqrt {21} }}{7}\)
d) \(\begin{array}{l}d(H,(SCD)) = 2.d(O,(SCD))\\ \Rightarrow d(O,(SCD)) = \frac{{\sqrt {21} }}{{14}}\end{array}\)
Cho hàm số \(y = \sqrt {2x - {x^2}} .\)
a) Đạo hàm của hàm số là \(y' = (\sqrt {2x - {x^2}} )' = \frac{{1 - x}}{{\sqrt {2x - {x^2}} }}\)
b) Biểu thức \(y'(1) = 0\)
c) Biểu thức \(y''1) = 0\)
d) \({y^3}y'' + 1 = 0,\forall x \in (0;2).\)
a) Đạo hàm của hàm số là \(y' = (\sqrt {2x - {x^2}} )' = \frac{{1 - x}}{{\sqrt {2x - {x^2}} }}\)
b) Biểu thức \(y'(1) = 0\)
c) Biểu thức \(y''1) = 0\)
d) \({y^3}y'' + 1 = 0,\forall x \in (0;2).\)
Sử dụng công thức tính đạo hàm của hàm hợp
a) \(y' = (\sqrt {2x - {x^2}} )' = \frac{{(2x - {x^2})'}}{{2\sqrt {2x - {x^2}} }} = \frac{{2 - 2x}}{{2\sqrt {2x - {x^2}} }} = \frac{{1 - x}}{{\sqrt {2x - {x^2}} }}\)
b) \(y'(1) = \frac{{1 - 1}}{{\sqrt {2.1 - {1^2}} }} = 0\)
c) \(\begin{array}{l}y'' = (\frac{{1 - x}}{{\sqrt {2x - {x^2}} }})' = \frac{{(1 - x)'.(\sqrt {2x - {x^2}} ) - (1 - x).\left( {\sqrt {2x - {x^2}} } \right)'}}{{{{(\sqrt {2x - {x^2}} )}^2}}} = \frac{{ - \sqrt {2x - {x^2}} - (1 - x).\frac{{1 - x}}{{\sqrt {2x - {x^2}} }}}}{{2x - {x^2}}}\\ = \frac{{ - (2x - {x^2}) - {{(1 - x)}^2}}}{{(2x - {x^2})\sqrt {2x - {x^2}} }} = \frac{{ - 1}}{{(2x - {x^2})\sqrt {2x - {x^2}} }} = \frac{{ - 1}}{{{{\left( {\sqrt {2x - {x^2}} } \right)}^3}}}\\ \Rightarrow y''(1) = \frac{{ - 1}}{{{{\left( {\sqrt {2x - {x^2}} } \right)}^3}}} = - 1\end{array}\)
d)\({y^3}y'' + 1 = {\left( {\sqrt {2x - {x^2}} } \right)^3}.\frac{{ - 1}}{{{{\left( {\sqrt {2x - {x^2}} } \right)}^3}}} + 1 = - 1 + 1 = 0\)
Cho hàm số: \(y = \frac{1}{4}\sqrt {\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right)} \)
Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định có tập xác định là \(\mathbb{R}\).
Hàm số \(y = \log u\left( x \right)\) xác định khi \(u\left( x \right) > 0\).
Hàm số \(y = \sqrt {u\left( x \right)} \) xác định khi \(u\left( x \right) \ge 0\).
Hàm số \(y = \frac{1}{4}\sqrt {\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right)} \)
Điều kiện: \(\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right) \ge 0\) với mọi \(x \in \mathbb{R}\)
\( \Leftrightarrow \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5 \ge 1\) với mọi \(x \in \mathbb{R}\)
\( \Leftrightarrow \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4 \ge 0\) với mọi \(x \in \mathbb{R}\)
Đặt \(f\left( x \right) = \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4\)
Trường hợp 1: Với \(m = - 1\) ta có: \(f\left( x \right) = 4 \ge 0\). Do đó, f(x) xác định với mọi giá trị thực của x. Do đó, \(m = - 1\) thỏa mãn.
Trường hợp 2: \(m \ne - 1\).
Hàm số \(f\left( x \right) = \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4 \ge 0\) với mọi \(x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ \begin{array}{l}m + 1 > 0\\\Delta ' = {\left[ { - \left( {m + 1} \right)} \right]^2} - 4\left( {m + 1} \right) \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - 1\\\left( {m + 1} \right)\left( {m - 3} \right) \le 0\end{array} \right. \Leftrightarrow - 1 < m \le 3\)
Vậy với \(m \in \left[ { - 1;3} \right]\) thì hàm số \(y = \frac{1}{4}\sqrt {\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right)} \) có tập xác định là \(\mathbb{R}\).
Đáp án
\(m \in \left[ { - 1;3} \right]\)
Giải bất phương trình \({\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}\left( {x + \sqrt {{x^2} - 1} } \right) = {\log _6}\left| {x - \sqrt {{x^2} - 1} } \right|\).
Nếu \(a > 0,a \ne 1\) thì \({\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.\) (có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\))
Điều kiện: \(\left\{ \begin{array}{l} - 1 \le x \le 1\\x - \sqrt {{x^2} - 1} > 0\end{array} \right.\left( * \right)\)
\({\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}\left( {x + \sqrt {{x^2} - 1} } \right) = {\log _6}\left| {x - \sqrt {{x^2} - 1} } \right|\)
\( \Leftrightarrow {\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}\frac{1}{{x - \sqrt {{x^2} - 1} }} = {\log _6}\left( {x - \sqrt {{x^2} - 1} } \right)\)
\( \Leftrightarrow - {\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}6.{\log _6}\left( {x - \sqrt {{x^2} - 1} } \right) = {\log _6}\left( {x - \sqrt {{x^2} - 1} } \right)\)
\( \Leftrightarrow {\log _6}\left( {x - \sqrt {{x^2} - 1} } \right)\left[ {{{\log }_3}6.{{\log }_2}\left( {x - \sqrt {{x^2} - 1} } \right) + 1} \right] = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{\log _6}\left( {x - \sqrt {{x^2} - 1} } \right) = 0\;\left( 1 \right)\\{\log _3}6.{\log _2}\left( {x - \sqrt {{x^2} - 1} } \right) + 1 = 0\;\left( 2 \right)\end{array} \right.\)
\(\left( 1 \right) \Leftrightarrow x - \sqrt {{x^2} - 1} = 1 \Leftrightarrow \sqrt {{x^2} - 1} = x - 1 \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 1 = {\left( {x - 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x = 1\end{array} \right. \Leftrightarrow x = 1\left( {tm\left( * \right)} \right)\)
\(\left( 2 \right) \Leftrightarrow {\log _3}6.{\log _2}\left( {x - \sqrt {{x^2} - 1} } \right) = - 1 \Leftrightarrow {\log _2}\left( {x + \sqrt {{x^2} - 1} } \right) = {\log _6}3\)
\( \Leftrightarrow x + \sqrt {{x^2} - 1} = {2^{{{\log }_6}3}} \Leftrightarrow \left\{ \begin{array}{l}x \le {2^{{{\log }_6}3}}\\{x^2} - 1 = {\left( {{2^{{{\log }_6}3}} - x} \right)^2}\end{array} \right. \Leftrightarrow x = \frac{1}{2}\left( {{2^{{{\log }_6}3}} + {2^{ - {{\log }_6}3}}} \right)\) (thỏa mãn điều kiện)
Đáp án
\(x = \frac{1}{2}\left( {{2^{{{\log }_6}3}} + {2^{ - {{\log }_6}3}}} \right)\)
Một chất điểm chuyển động có quãng đường được cho bởi phương trình\(s\left( t \right) = \frac{1}{4}{t^4} - {t^3} + \frac{5}{2}{t^2} + 10t\), trong đó \(t > 0\) với \(t\) tính bằng giây (s) và \(s\) tính bằng mét (m). Tính vận tốc chuyển động của chất điểm tại thời điểm chất điểm có gia tốc chuyển động nhỏ nhất.
Phương trình vận tốc và gia tốc của chất điểm: \(\left\{ \begin{array}{l}v\left( t \right) = s'\left( t \right)\\a\left( t \right) = v'\left( t \right)\end{array} \right.\)
Gọi \(v\left( t \right)\), \(a\left( t \right)\) lần lượt là vận tốc và gia tốc của chất điểm.
Theo ý nghĩa hình học của đạo hàm, ta suy ra \(\left\{ \begin{array}{l}v\left( t \right) = s'\left( t \right) = {t^3} - 3{t^2} + 5t + 10\\a\left( t \right) = v'\left( t \right) = 3{t^2} - 6t + 5\end{array} \right.\).
Mà \(a\left( t \right) = 3{t^2} - 6t + 5 = 3{\left( {t - 1} \right)^2} + 2 \ge 2\) với mọi \(t\), dấu “\( = \)” xảy ra khi chỉ khi \(t = 1\).
Suy ra gia tốc chuyển động của chất điểm nhỏ nhất bằng \(2\) khi \(t = 1\).
Vận tốc chuyển động của chất điểm tại thời điểm gia tốc nhỏ nhất là
\(v\left( 1 \right) = {\left( 1 \right)^3} - 3 \cdot {1^2} + 5 \cdot 1 + 10 = 13\) \(\left( {m/\,s} \right)\).
Đáp án
13 \(\left( {m/\,s} \right)\)
Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để chọn được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó chỉ có đúng một tấm thẻ chia hết cho 10.
Sử dụng Quy tắc nhân
Số phần tử không gian mẫu là : \({n_\Omega } = C_{30}^{10} = 30045015\)
Gọi A là biến cố lấy được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn trong đó chỉ có đúng một tấm thẻ chia hết cho 10.
\({n_A} = C_{15}^5.C_3^1.C_{12}^4 = 4459455\)
Vậy xác suất biến cố A là \(P(A) = \frac{{99}}{{667}}\)
Đáp án
\(\frac{{99}}{{667}}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B.\) Biết \(AD = 2a,\,AB = BC = SA = a.\) Cạnh bên \(SA\) vuông góc với mặt đáy, gọi \(M\) là trung điểm của \(AD.\) Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {SCD} \right)\) theo \(a.\)
+ Sử dụng phương pháp: Nếu đường thẳng // mặt phẳng thì khoảng cách giữa các điểm thuộc đường thẳng đó đến mặt phẳng sẽ bằng nhau.
+ Sử dụng phương pháp tính khoảng cách từ chân đường cao đến mặt bên của chóp.
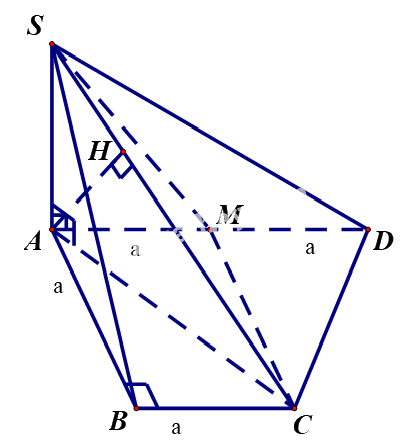
Ta có:
\(\frac{{d\left( {M,\left( {SCD} \right)} \right)}}{{d\left( {A,\left( {SCD} \right)} \right)}} = \frac{{DM}}{{DA}} = \frac{1}{2} \Rightarrow d\left( {M,\left( {SCD} \right)} \right) = \frac{1}{2}d\left( {A,\left( {SCD} \right)} \right).\)
Vì \(M\)là trung điểm của \(AD\) nên có: \(AM = MD = \frac{1}{2}AD = a.\)
Tứ giác \(ABCM\) có: \(BC//AM\,\,\left( {gt} \right)\) và \(BC = AM = a\) nên nó là hình bình hành.
Suy ra: \(CM = AB = a.\)
Tam giác \(ACD\) có \(CM\) là đường trung tuyến và \(CM = AM = MD = \frac{1}{2}AD\) nên tam giác \(ACD\)là tam giác vuông tại \(C.\)
Suy ra: \(CD \bot AC.\)
Ta có:
\(\left\{ \begin{array}{l}CD \bot AC\,\,\left( {cmt} \right)\\CD \bot SA\,\,\,\left( {do\,\,SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right).\)
Ta có:
\(\left\{ \begin{array}{l}CD \bot \left( {SAC} \right)\\CD \subset \left( {SCD} \right)\end{array} \right. \Rightarrow \left( {SCD} \right) \bot \left( {SAC} \right).\)
Trong mặt phẳng \(\left( {SAC} \right),\) kẻ \(AH \bot SC\,\,\left( {H \in SC} \right).\)
Ta có:
\(\left\{ \begin{array}{l}\left( {SCD} \right) \bot \left( {SAC} \right)\\\left( {SCD} \right) \cap \left( {SAC} \right) = SC\\AH \bot SC\\AH \subset \left( {SAC} \right)\end{array} \right. \Rightarrow AH \bot \left( {SCD} \right).\)
Suy ra: \(d\left( {A,\left( {SCD} \right)} \right) = AH.\)
Tam giác \(ABC\) vuông cân tại \(B\) có \(AB = BC = a\) nên \(AC = a\sqrt 2 .\)
Tam giác \(SAC\) vuông tại \(A\,\,\left( {do\,SA \bot \left( {ABCD} \right)} \right)\) có :
\(AH = \frac{{AS.AC}}{{\sqrt {A{S^2} + A{C^2}} }} = \frac{{a.\,a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{3}.\)
Suy ra: \(d\left( {A,\left( {SCD} \right)} \right) = AH = \frac{{a\sqrt 6 }}{3}.\)
Suy ra: \(d\left( {M,\left( {SCD} \right)} \right) = \frac{1}{2}.\frac{{a\sqrt 6 }}{3} = \frac{{a\sqrt 6 }}{6}.\)
Vậy \(d\left( {M,\left( {SCD} \right)} \right) = \frac{{a\sqrt 6 }}{6}.\)
Đáp án
\(\frac{{a\sqrt 6 }}{6}\)
Cho hàm số \(y = f\left( x \right) = \frac{{x + 1}}{{x + 2}}\) có đồ thị \(\left( C \right)\). Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục hoành
Tìm tọa độ giao điểm của \(\left( C \right)\) với trục hoành
Phương trình tiếp tuyến với đồ thị (C): \(y = f(x)\)tại điểm \(M({x_0};f({x_0}))\)là:
\(y = f'({x_0})(x - {x_0}) + f({x_0})\)
Trong đó:
\(M({x_0};f({x_0}))\)gọi là tiếp điểm.
\(k = f'({x_0})\)là hệ số góc.
Giao điểm của (C) với trục hoành là \({M_0}\left( { - 1\,\,;\,\,0} \right)\)
Ta có: \(y' = \frac{1}{{{{\left( {x + 2} \right)}^2}}}\) \( \Rightarrow k = y'( - 1) = 1\)
Vậy phương trình tiếp tuyến tại \({M_0}\left( { - 1\,\,;\,\,0} \right)\) là : \(y = 1(x + 1) + 0 = x + 1\)
Đáp án
\(y = x + 1\)
Đề thi học kì 2 Toán 11 - Đề số 1 là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức của học sinh sau một học kỳ học tập. Đề thi thường bao gồm các chủ đề chính như hàm số, đạo hàm, tích phân, hình học không gian và các ứng dụng của toán học trong thực tế.
Cấu trúc đề thi có thể thay đổi tùy theo từng trường và từng địa phương, nhưng nhìn chung, đề thi thường bao gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi học kì 2 Toán 11 - Đề số 1:
Để giải tốt đề thi học kì 2 Toán 11 - Đề số 1, học sinh cần:
Bài 1: Cho hàm số y = x3 - 3x2 + 2. Tìm tập xác định và tập giá trị của hàm số.
Giải:
Để chuẩn bị tốt nhất cho kỳ thi học kì 2 Toán 11, học sinh có thể tham khảo các tài liệu sau:
Hãy dành thời gian ôn tập kiến thức một cách nghiêm túc và có kế hoạch. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 11!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số | Cao |
| Đạo hàm | Cao |
| Tích phân | Trung bình |
| Hình học không gian | Trung bình |