Giaitoan.edu.vn xin giới thiệu Đề thi học kì 2 Toán 11 - Đề số 2, một công cụ hỗ trợ học sinh ôn luyện và đánh giá năng lực một cách hiệu quả. Đề thi được biên soạn theo chuẩn chương trình học, bao gồm các dạng bài tập thường gặp trong đề thi chính thức.
Với đáp án chi tiết và lời giải dễ hiểu, học sinh có thể tự học, tự kiểm tra kiến thức và khắc phục những điểm còn yếu. Đây là tài liệu không thể thiếu cho các em học sinh đang chuẩn bị cho kỳ thi học kì 2 môn Toán lớp 11.
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\) có nghiệm là
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\) Phương trình của (d) là
Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}}\) bằng
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\) là
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm \({x_0} = 1\)thì m bằng:
Tìm đạo hàm của hàm số sau\(y = {x^4} - 3{x^2} + 2x - 1\)
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
\(AC \bot (SBD)\)
\(AB \bot (SAD)\)
\(AC \bot (SBD)\)
\(SO \bot (ABCD)\)
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}}\); g'(2) bằng
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x - 2}}{{x - 1}}\)
a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
Cho hàm số \(y = \sin x\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Tính giới hạn: \(\mathop {lim}\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}}\).
Cho hàm số: \(y = {\left( {{x^4} - 1} \right)^4}\). Tính \(y'(1)\)
Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 1}}\,\,\,\;khi\,\,x \ne 1\\1 - mx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\)liên tục tại điểm\({x_0} = 1\)
Cho hình chóp S.ABCD đáy là hình vuông cạnh a , cạnh bên SA \( \bot \)(ABCD) và
SA = a\(\sqrt 2 \). Tính tan của góc giữa hai mp (SBC) và (ABCD).
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\). Tìm tọa độ điểm M thuộc đồ thị sao cho khoảng cách từ điểm \(I( - 1;2)\)tới tiếp tuyến của đồ thị tại M là lớn nhất.
Với mức tiêu thụ thức ăn cho cá hàng ngày của hộ gia đình A không đổi như dự định thì lượng thức ăn dự trữ sẽ hết sau 50 ngày. Nhưng trên thực tế, mức tiêu thụ thức ăn tăng thêm 3% từ ngày đầu tiên và cứ tiếp tục như vậy, ngày sau tăng thêm 3% so với ngày kề trước đó. Hỏi thực tế, lượng thức ăn dự trữ đó sẽ hết sau bao nhiêu ngày? (làm tròn đến hàng đơn vị).
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\) có nghiệm là
Đáp án : C
Sử dụng công thức đạo hàm.
\(\begin{array}{l}f'(x) = (\frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6)' = {x^2} - 3x - 4\\f'(x) = 0\,\,hay\,\,{x^2} - 3x - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 4\end{array} \right.\end{array}\)
Đáp án C.
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\) Phương trình của (d) là
Đáp án : C
Phương trình tiếp tuyến với đồ thị (C): \(y = f(x)\)tại điểm \(M({x_0};f({x_0}))\)là:
\(y = f'({x_0})(x - {x_0}) + f({x_0})\)
Trong đó:
\(M({x_0};f({x_0}))\)gọi là tiếp điểm.
\(k = f'({x_0})\)là hệ số góc.
\(y' = f'(x) = ( - {x^3} + x)' = - 3{x^2} + 1\)
Phương trình tiếp tuyến của đồ thị \(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\)
\(y = f'( - 2)(x + 2) + 6\,\,hay\,\,y = - 11(x + 2) + 6 = - 11x - 16\)
Đáp án C.
Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}}\) bằng
Đáp án : A
Nhận biết dạng vô định \(\frac{0}{0}\): Tính \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x)}}{{g(x)}}\)trong đó \(f(x{}_0) = g({x_0}) = 0\)
Khử dạng vô định \(\frac{0}{0}\): Phân tích tử thức và mẫu thức sao cho xuất hiện nhân tử chung \((x - {x_0})\)
\(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}} = \mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{(\sqrt {x + 1} + 2)(9 - {x^2})}} = \mathop {\lim }\limits_{x \to 3} \frac{{ - 1}}{{(\sqrt {x + 1} + 2)(3 + x)}} = \frac{{ - 1}}{{24}}\)
Đáp án A.
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
Đáp án : A
Áp dụng công thức tính đạo hàm
\({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^2}}}\)
\(\left( {u + v} \right)' = u' + v'\)
\({\left( {k.u} \right)^\prime } = k.u'\)
\(\left( {u.v} \right)' = u'.v + u.v'\)
Đáp án A.
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\) là
Đáp án : B
Sử dụng công thức tính đạo hàm của hàm phân thức: \(y' = \left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
\(y' = \left( {\frac{{2x - 1}}{{1 - x}}} \right)' = \left( {\frac{{2x - 1}}{{ - x + 1}}} \right)' = \frac{{2.1 - ( - 1).( - 1)}}{{{{( - x + 1)}^2}}} = \frac{1}{{{{( - x + 1)}^2}}}\)
Đáp án B.
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm \({x_0} = 1\)thì m bằng:
Đáp án : C
Bước 1: Tính f(x0) = f2(x0).
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\)
Bước 3: Nếu f2(x0) = L thì hàm số f(x) liên tục tại x0.
Nếu f2(x0) ≠ L thì hàm số f(x) không liên tục tại x0.
(Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m)
Hàm số đã cho xác định trên R
Ta có:
\(\begin{array}{l}f(1) = m\\\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x + 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x + 1) = 2\end{array}\)
Ta thấy \(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\)
Nên m = 2
Vậy khi m = 2 thì hàm số liên tục tại \({x_0} = 1\)
Đáp án C.
Tìm đạo hàm của hàm số sau\(y = {x^4} - 3{x^2} + 2x - 1\)
Đáp án : D
Sử dụng công thức tính đạo hàm của hàm hợp
\(y' = \left( {{x^4} - 3{x^2} + 2x - 1} \right)' = 4{x^3} - 6x + 2\)
Đáp án D.
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
Đáp án : A
Nhận dạng: \(\mathop {\lim }\limits_{x \to \pm \infty } \frac{{f(x)}}{{g(x)}} = \)\(\frac{\infty }{\infty }\) với \(\mathop {\lim }\limits_{x \to \pm \infty } f(x) = \pm \infty ,\mathop {\lim }\limits_{x \to \pm \infty } g(x) = \pm \infty \)
TH1: Nếu f(x) , g(x) là các đa thức thì chia cả tử và mẫu cho lũy thừa cao nhất của x.
TH2: Nếu f(x) , g(x) chứa căn thì có thể chia cả tử và mẫu cho lũy thừa cao nhất của x hoặc nhân lượng liên hợp
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2}(a + \frac{4}{x} + \frac{3}{{{x^2}}})}}{{{x^2}(\frac{3}{x} - 2a)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{a + \frac{4}{x} + \frac{3}{{{x^2}}}}}{{\frac{3}{x} - 2a}} = \frac{a}{{ - 2a}} = - \frac{1}{2}\)
Đáp án A.
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
Đáp án : B
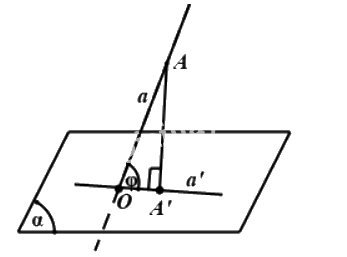
Bước 1: Tìm giao điểm O của đường thẳng a và \(\left( \alpha \right)\)
Bước 2: Xác định hình chiếu A’ của một điểm \(A \in \left( \alpha \right)\)xuống \(\left( \alpha \right)\)
Bước 3: Suy ra: \((a;\left( \alpha \right)) = (a;a') = \widehat {AOA'}\)
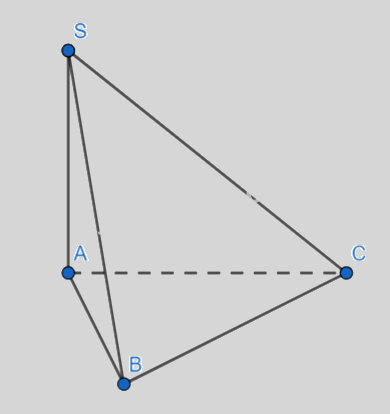
Do \(SA \bot (ABC)\) nên A là hình chiếu của S lên (ABC)
Ta có: \((SB,(ABC)) = (SB,AB) = \widehat {SBA}\)
Xét \(\Delta SAB:c{\rm{os}}\widehat {SBA} = \frac{{AB}}{{SB}} = \frac{a}{{2a}} = \frac{1}{2}\)
Suy ra: \(\widehat {SBA} = {60^0}\)
Đáp án B.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
Đáp án : B
Sử dụng định lý đường thẳng vuông góc với mặt phẳng và hai mặt phẳng vuông góc với nhau
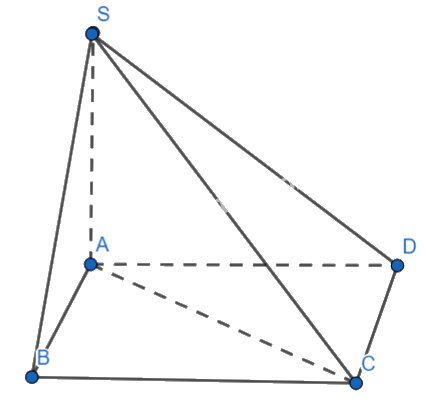
Ta có:
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,(do\,\,SA \bot (ABC{\rm{D}}))\\AD,SA \subset (SAD)\\AD \cap SA\end{array} \right. \Rightarrow CD \bot (SAD)\)
Mặt khác:
\(CD \subset (SCD) \Rightarrow (SCD) \bot (SAD)\)
Đáp án B.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
\(AC \bot (SBD)\)
\(AB \bot (SAD)\)
\(AC \bot (SBD)\)
\(SO \bot (ABCD)\)
Đáp án : C
Sử dụng định lý đường thẳng vuông góc với mặt phẳng
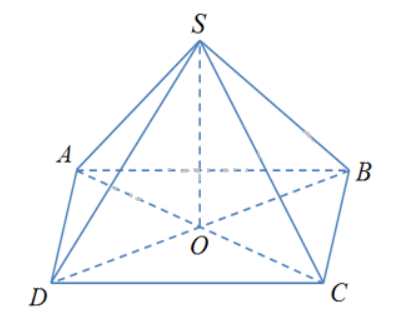
Ta có:
\(\left\{ \begin{array}{l}AC \bot BD\\AC \bot SO\\BD,SO \subset (SBD)\\BD \cap SO\end{array} \right. \Rightarrow AC \bot (SBD)\)
Đáp án C.
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}}\); g'(2) bằng
Đáp án : B
Sử dụng phương tính đạo hàm của hàm hợp.
\(g'\left( x \right) = \frac{{\left[ {\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}} \right]'(x - 1) - \left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}.(x - 1)'}}{{{{\left( {x - 1} \right)}^2}}} \)
\(= \frac{{\left[ {2{{\left( {2 - 3x} \right)}^2} + (2x + 1).2\left( {2 - 3x} \right).( - 3)} \right] + \left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{{{\left( {x - 1} \right)}^2}}}\)
\( = \frac{{3x(3x - 2)(4x - 5)}}{{{{\left( {x - 1} \right)}^2}}}\)
\( \Rightarrow g'\left( 2 \right) = \frac{{3x(3x - 2)(4x - 5)}}{{{{\left( {x - 1} \right)}^2}}} = 72\).
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Sử dụng các quy tắc đếm để xác định số phần tử của không gian mẫu và biến cố
Không gian mẫu: \((\Omega ) = C_{20}^3 = 1140\)
a) Gọi A là biến cố: “3 viên bi lấy ra đều màu đỏ”; \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_8^3}}{{C_{20}^3}} = \frac{{56}}{{1140}} = \frac{{14}}{{285}}\)
b) B là biến cố: “3 viên bi lấy ra có không quá hai màu”
TH1: Số cách lấy ra 3 viên bi lấy ra chỉ có một màu: \(C_8^3 + C_7^3 + C_5^3 = 101\)
TH2: Số cách lấy ra 3 viên bi lấy ra chỉ có đúng hai màu: \(\left[ {C_{15}^3 - \left( {C_8^3 + C_7^3} \right)} \right] + \left[ {C_{13}^3 - \left( {C_8^3 + C_5^3} \right)} \right] + \left[ {C_{12}^3 - \left( {C_5^3 + C_7^3} \right)} \right] = 759\)
Nên: \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{101 + 759}}{{1140}} = \frac{{43}}{{57}}\)
c) C là biến cố: “3 viên bi lấy ra đều có màu vàng”; \(P(C) = \frac{{n(C)}}{{n(\Omega )}} = \frac{{C_5^3}}{{C_{20}^3}} = \frac{{10}}{{1140}} = \frac{1}{{114}}\)
d) D là biến cố: “3 viên bi lấy ra có đủ cả ba màu”: \(P(D) = \frac{{n(D)}}{{n(\Omega )}} = \frac{{C_8^1.C_7^1.C_5^1}}{{C_{20}^3}} = \frac{{280}}{{1140}} = \frac{{14}}{{57}}\)
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x - 2}}{{x - 1}}\)
a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
Bước 1: Gọi M(x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k
Bước 2: Giải phương trình f'(x0) = k với ẩn là x0.
Bước 3:Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0)
\(y' = f'(x) = \left( {\frac{{x - 2}}{{x - 1}}} \right)' = \frac{1}{{{{\left( {x - 1} \right)}^2}}}\)
a) Gọi \(M({x_0};{y_0})\) là tiếp điểm. M có tung độ bằng 4 nên \(M(\frac{2}{3};4)\)
Gọi k là hệ số góc của tiếp tuyển tại M nên \(k = f'\left( {\frac{2}{3}} \right) = 9\)
Phương trình tiếp tuyến của (C) tại điểm \(M(\frac{2}{3};4)\) là \(y = 9(x - \frac{2}{3}) + 4\,\,hay\,\,y = 9x - 2\)
b) Gọi \(M({x_0};{y_0})\) là tiếp điểm. M là giao của đồ thị với trục hoành nên \(M(2;0)\)
Gọi k là hệ số góc của tiếp tuyến tại M nên \(k = f'\left( 2 \right) = 1\)
Phương trình tiếp tuyến của (C) (C) tại điểm \(M(2;0)\) là \(\,y = x - 2\)
c) Gọi \(M({x_0};{y_0})\) là tiếp điểm.
M là giao điểm của đồ thị với trục tung nên \(M(0;2)\)
Gọi k là hệ số góc của tiếp tuyến tại M. Khi đó \(k = f'\left( 0 \right) = 1\)
Phương trình tiếp tuyến tại M là: \(\,y = (x - 0) + 2\,\,hay\,\,y = x + 2\)
d) Gọi k là hệ số góc của tiếp tuyến của đồ thị (C)
Do tiếp tuyến vuông góc với \((d):y = - x + 1\) nên \( - 1.k = - 1 \Leftrightarrow k = 1\)
Gọi \(M({x_0},{y_0}) \in (C)\)mà tiếp tuyến của (C) tại M có hệ số góc k = 1
\(f'({x_0}) = 1 \Rightarrow \frac{1}{{{{(x - 1)}^2}}} = 1 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = 0\end{array} \right.\)
* Với \({x_0} = 2\) ta có \({y_0} = f(2) = 0 \Rightarrow {M_1}(2;0) \in (C)\)
Phương trình tiếp tuyến của (C) tại \({M_1}(2;0)\)) là \(y = x - 2\)
* Với \({x_0} = 0\) ta có \({y_0} = f(0) = 2 \Rightarrow {M_2}(0;2) \in (C)\)
Phương trình tiếp tuyến của (C) tại \({M_2}(0;2)\) là \(\,y = x + 2\)
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng và khoảng cách từ đường thẳng đến mặt phẳng
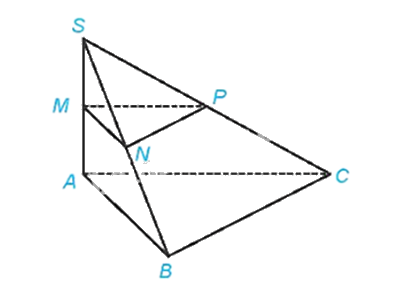
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB. Suy ra \(MN//AB\),do đó \(MN//(ABC)\)
Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC. Suy ra \(PN//BC\),do đó \(PN//(ABC)\)
Khi đó, \(d((MNP),(ABC)) = d(M,(ABC))\)
Vì \(SA \bot (ABC)\) nên \(MA \bot (ABC)\). Do đó \(d(M,(ABC)) = MA\)
Vì M là trung điểm SA nên \(AM = \frac{{SA}}{2} = \frac{h}{2}\)
Do đó \(d((MNP),(ABC)) = \frac{h}{2}\)
b) Vì \(PN//(ABC)\) nên \(d(NP,(ABC)) = d(N,(ABC))\)
Vì \(MN//(ABC)\) nên \(d(N,(ABC)) = d(M,(ABC)) = MA = \frac{h}{2}\)
Vậy \(d(N,(ABC)) = \frac{h}{2}\)
c) Vì tam giác ABC là tam giác vuông tại B nên \(BC \bot AB\)
Vì \(SA \bot (ABC)\) nên \(SA \bot BC\)mà \(BC \bot AB\) nên \(BC \bot (SAB)\), suy ra \((SBC) \bot (SAB)\)
Kẻ \(AH \bot SB\) tại H
Vì \(\left\{ \begin{array}{l}(SBC) \bot (SAB)\\(SBC) \cap (SAB) = SB\\AH \subset (SAB)\\AH \bot SB\end{array} \right. \Rightarrow AH \bot (SBC)\)
Khi đó \(d(A,(SBC)) = AH\)\(\)
Vì \(SA \bot (SBC)\) nên \(SA \bot AB\)
Xét tam giác SAB vuông tại A, AH là đường cao, có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{a^2}{h^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Vậy \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d)\(MN//(ABC)\) mà \(MN \subset (MNP) \Rightarrow (MNP)//(ABC)\)
Cho hàm số \(y = \sin x\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Sử dụng công thức tính đạo hàm của hàm số lượng giác
a) \(y' = (\sin x)' = cosx\)
b) \(y'(\frac{\pi }{2}) = \cos \frac{\pi }{2} = 0\)
c) \(\begin{array}{l}y'' = \left( {cosx} \right)' = - \sin x\\y''\left( {\frac{\pi }{2}} \right) = - 1\end{array}\)
d) \(\begin{array}{l}{y^{(n)}} = \sin (x + n\frac{\pi }{2})\\{y^{(2024)}} = \sin (x + 1012\pi )\end{array}\)
Tính giới hạn: \(\mathop {lim}\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}}\).
Sử dụng phương pháp nhân liên hợp và phân tích thành nhân tử.
\(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {\sqrt {4x + 1} - 3} \right)\left( {\sqrt {4x + 1} + 3} \right)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{(4x + 1) - 9}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}}\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{4x - 8}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{4(x - 2)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{4}{{\sqrt {4x + 1} + 3}} = \frac{4}{{\sqrt {4.2 + 1} + 3}} = \frac{2}{3}\).
Cho hàm số: \(y = {\left( {{x^4} - 1} \right)^4}\). Tính \(y'(1)\)
Sử dụng công thức tính đạo hàm của hàm hợp
\(\begin{array}{l}y' = \left[ {{{\left( {{x^4} - 1} \right)}^4}} \right]' = 4.{\left( {{x^4} - 1} \right)^3}.4{x^3} = 16{x^3}{\left( {{x^4} - 1} \right)^3}\\y'(1) = 0\end{array}\)
Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 1}}\,\,\,\;khi\,\,x \ne 1\\1 - mx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\)liên tục tại điểm\({x_0} = 1\)
Bước 1:Tính \(f({x_0}) = {f_2}({x_0})\)
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\)
Bước 3: Nếu \({f_2}({x_0}) = L\) thì hàm số f(x) liên tục tại \({x_0}\)
Nếu \({f_2}({x_0}) \ne L\)thì hàm số f(x) không liên tục tại \({x_0}\).
(Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m)
Hàm số đã cho xác định trên R
Ta có: \(f(1) = 1 - m\)
\(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x - 2)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x - 2) = - 1\)
Để hàm số liên tục tại x = 1 khi \(f(1) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} \Leftrightarrow 1 - m = - 1 \Leftrightarrow m = 2\)
Cho hình chóp S.ABCD đáy là hình vuông cạnh a , cạnh bên SA \( \bot \)(ABCD) và
SA = a\(\sqrt 2 \). Tính tan của góc giữa hai mp (SBC) và (ABCD).
Sử dụng phương pháp tính góc giữa hai mặt phẳng
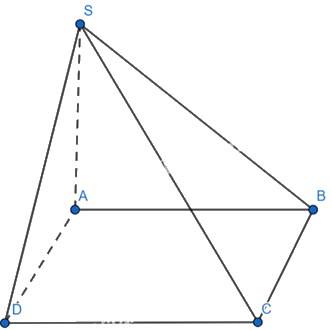
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\,\\BC \bot SA\,\,(Do\,\,SA \bot (ABCD))\\AB,SA \subset (SAB)\\AB \cap SA\end{array} \right. \Rightarrow BC \bot (SAB)\\ \Rightarrow BC \bot SB\end{array}\)\(SA \bot (ABCD) \Rightarrow SA \bot AB\)
Ta có: \(\left\{ \begin{array}{l}(SBC) \cap (ABCD) = BC\\SB \subset (SBC),SB \bot BC\\AB \subset (ABCD),AB \bot BC\end{array} \right. \Rightarrow \left( {(SBC),(ABCD)} \right) = (SB,AB)\)
Do \(SA \bot (ABCD) \Rightarrow SA \bot AB\). Xét tam giác SAB vuông tại A có:
\(\tan (SB,AB) = \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 2 }}{a} = \sqrt 2 \)
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\). Tìm tọa độ điểm M thuộc đồ thị sao cho khoảng cách từ điểm \(I( - 1;2)\)tới tiếp tuyến của đồ thị tại M là lớn nhất.
Lập biểu thức tính khoảng cách từ điểm \(I( - 1;2)\) tới tiếp tuyển của đồ thị
Sử dụng BĐT Cauchy để tìm giá trị lớn nhất của biểu thức
Giả sử \(M({x_0};2 - \frac{3}{{{x_0} + 1}}) \in (C)\). PTTT của (C) tại M là:
\(y = \frac{3}{{{{({x_0} + 1)}^2}}}(x - {x_0}) + 2 - \frac{3}{{{x_0} + 1}}\,\,\,(\Delta )\)
Hay \(\begin{array}{l}(\Delta ):\,\,\,\frac{3}{{{{({x_0} + 1)}^2}}}x - y + \left[ {\frac{{3{x_0}}}{{{{({x_0} + 1)}^2}}} + 2 - \frac{3}{{{x_0} + 1}}} \right] = 0\,\,\,\\(\Delta ):\,\frac{3}{{{{({x_0} + 1)}^2}}}x - y + 2 - \frac{3}{{{{({x_0} + 1)}^2}}} = 0\\d(I,\Delta ) = \frac{{|\frac{3}{{{{({x_0} + 1)}^2}}}{x_0} - (2 - \frac{3}{{{x_0} + 1}}) + 2 - \frac{3}{{{{({x_0} + 1)}^2}}}|}}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^4}}} + 1} }} = \frac{{6|{x_0} + 1|}}{{\sqrt {9 + {{({x_0} + 1)}^4}} }} = \frac{6}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^2}}} + {{({x_0} + 1)}^2}} }}\end{array}\)
Áp dụng BĐT Cauchy: \(\frac{9}{{{{({x_0} + 1)}^2}}} + {({x_0} + 1)^2} \ge 2\sqrt 9 = 6 \Rightarrow d \le \sqrt 6 \)
Dấu “=” xảy ra khi \(\frac{9}{{{{({x_0} + 1)}^2}}} = {({x_0} + 1)^2} \Leftrightarrow {x_0} = - 1 \pm \sqrt 3 \)
Vậy có hai điểm cần tìm là \(M( - 1 + \sqrt 3 ;2 - \sqrt 3 )\) hoặc \(M( - 1 - \sqrt 3 ;2 + \sqrt 3 )\)
Với mức tiêu thụ thức ăn cho cá hàng ngày của hộ gia đình A không đổi như dự định thì lượng thức ăn dự trữ sẽ hết sau 50 ngày. Nhưng trên thực tế, mức tiêu thụ thức ăn tăng thêm 3% từ ngày đầu tiên và cứ tiếp tục như vậy, ngày sau tăng thêm 3% so với ngày kề trước đó. Hỏi thực tế, lượng thức ăn dự trữ đó sẽ hết sau bao nhiêu ngày? (làm tròn đến hàng đơn vị).
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(M{(1 + r\% )^{k - 1}},k \in N*\)
Trong đó:
M: là lượng thứ ăn trang trại ăn hết trong mỗi ngày
r (%): là % mức tiêu thụ thức ăn tăng thêm mỗi ngày
Theo dự định, mỗi ngày, trang trại ăn hết: \(1:50 = \frac{1}{{50}}\)(lượng thức ăn)
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(\frac{1}{{50}}{(1 + 3\% )^{k - 1}},k \in N*\)
Xác định số tự nhiên n nhỏ nhât để:
\(\begin{array}{l}\frac{1}{{50}} + \frac{1}{{50}}(1 + 3\% ) + \frac{1}{{50}}{(1 + 3\% )^2} + ... + \frac{1}{{50}}{(1 + 3\% )^{n - 1}} \ge 1\\ \Leftrightarrow \frac{1}{{50}}(1 + 1,03 + 1,{03^2} + ... + 1,{03^{n - 1}}) \ge 1\\ \Leftrightarrow \frac{1}{{50}}.\frac{{1,{{03}^{n - 1}} - 1}}{{1,03 - 1}} \ge 1 \Leftrightarrow 1,{03^{n - 1}} - 1 \ge 1,5 \Leftrightarrow 1,{03^{n - 1}} \ge 2,5 \Leftrightarrow n - 1 \ge {\log _{1,03}}2,5 \Leftrightarrow n \ge 31,99 \Rightarrow {n_{Min}} = 32\end{array}\)
Kỳ thi học kì 2 Toán 11 là một bước quan trọng trong quá trình học tập của học sinh. Để đạt kết quả tốt nhất, việc ôn tập và làm quen với các dạng đề thi là vô cùng cần thiết. Đề thi học kì 2 Toán 11 - Đề số 2 tại giaitoan.edu.vn được thiết kế để đáp ứng nhu cầu này, cung cấp một nguồn tài liệu ôn tập chất lượng và hiệu quả.
Đề thi học kì 2 Toán 11 thường bao gồm các chủ đề chính sau:
Câu 1: Giải phương trình lượng giác cos(2x) = 1/2. (Độ khó: Dễ)
Hướng dẫn giải: Sử dụng công thức cos(2x) = 2cos2(x) - 1, ta có phương trình 2cos2(x) - 1 = 1/2. Giải phương trình này, ta tìm được các nghiệm x = π/3 + kπ và x = -π/3 + kπ, với k là số nguyên.
Câu 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2. (Độ khó: Trung bình)
Hướng dẫn giải: Tính đạo hàm y' = 3x2 - 6x. Giải phương trình y' = 0, ta tìm được các điểm cực trị x = 0 và x = 2. Tính giá trị của hàm số tại các điểm này, ta xác định được điểm cực đại và cực tiểu.
Câu 3: Tính tích phân ∫0π/2 sin(x) dx. (Độ khó: Trung bình)
Hướng dẫn giải: Nguyên hàm của sin(x) là -cos(x). Do đó, ∫0π/2 sin(x) dx = [-cos(x)]0π/2 = -cos(π/2) + cos(0) = 1.
Luyện tập thường xuyên là yếu tố then chốt để đạt kết quả tốt trong kỳ thi học kì 2 Toán 11. Việc giải nhiều đề thi khác nhau sẽ giúp học sinh làm quen với các dạng bài tập, rèn luyện kỹ năng giải quyết vấn đề và nâng cao tốc độ làm bài. Đề thi học kì 2 Toán 11 - Đề số 2 tại giaitoan.edu.vn là một nguồn tài liệu luyện tập hữu ích, giúp học sinh tự tin bước vào kỳ thi.
Kiến thức Toán 11 không chỉ quan trọng trong học tập mà còn có ứng dụng rộng rãi trong thực tế. Ví dụ, kiến thức về hàm số lượng giác được sử dụng trong các lĩnh vực như vật lý, kỹ thuật, và khoa học máy tính. Kiến thức về đạo hàm và tích phân được sử dụng trong các bài toán tối ưu hóa, tính diện tích, thể tích, và tốc độ thay đổi. Do đó, việc nắm vững kiến thức Toán 11 là rất quan trọng cho sự phát triển của học sinh.
Giaitoan.edu.vn cam kết cung cấp các tài liệu học tập chất lượng, đáp ứng nhu cầu của học sinh. Chúng tôi luôn cập nhật các đề thi mới nhất, đáp án chi tiết và lời giải dễ hiểu. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác.
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số lượng giác | Cao |
| Phương trình lượng giác | Cao |
| Đạo hàm | Cao |
| Tích phân | Trung bình |
| Số phức | Trung bình |
| Hình học không gian | Trung bình |