Chào mừng các em học sinh lớp 4 đến với đề thi học kì 2 môn Toán chương trình Chân trời sáng tạo - Đề số 5.
Đề thi này được thiết kế để giúp các em ôn luyện và củng cố kiến thức đã học trong học kì, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Phân số nào không bằng phân số \(\frac{9}{{15}}\)?
Sắp xếp các phân số \(\frac{{15}}{{18}};\frac{3}{2};\frac{5}{2};\frac{5}{7}\) theo thứ tự từ lớn đến bé là:
Có bao nhiêu hình thoi trong hình dưới đây:
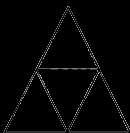
Một hộp bóng có \(\frac{1}{2}\) số bóng màu đỏ, \(\frac{1}{3}\)số bóng màu xanh, còn lại là bóng màu vàng. Tìm phân số chỉ số bóng màu vàng.
Số thứ nhất hơn số thứ hai là 129. Biết rằng nếu lấy số thứ nhất cộng với số thứ hai rồi cộng với tổng của chúng thì được 2010. Tìm số thứ nhất.
940
567
438
1 070
\(\frac{7}{{10}}\)của hình chữ nhật đã được tô màu có nghĩa là:
Tính
a) \(\frac{7}{{12}} + \frac{3}{4} \times \frac{2}{9}\)
b) \(\frac{1}{4} + \frac{5}{{24}}:\frac{2}{3}\)
Tìm giá trị của ? biết rằng:
a) ? + 686 = 2 897
b) 49 524 - ? = 42 123
c) ? x 34 = 7 990
d) 67 x ? = 18 760
Điền số thích hợp vào chỗ chấm.
a) 160 009 mm2 = ……. dm2 …. mm2
b) \(\frac{1}{{25}}\)tấn = …….. yến
c) 12 m 3 cm = ….… mm
d) \(\frac{5}{{12}}\) giờ = ……. phút
Cửa hàng nhập về 56 kg thóc. Buổi sáng bán \(\frac{1}{2}\)tổng số thóc. Buổi chiều bán được \(\frac{3}{4}\) số thóc còn lại. Hỏi cửa hàng đã bán tất cả bao nhiêu ki-lô-gam thóc?
Một trại chăn nuôi 200 con vịt, ngan và ngỗng. Số vịt bằng tổng số ngan và ngỗng, số ngan nhiều hơn số ngỗng là 40 con. Hỏi trại đó có bao nhiêu con ngan, vịt, ngỗng?
Tính bằng cách thuận tiện.
a) \(\frac{1}{2} \times \frac{{12}}{{13}} + \frac{1}{3} \times \frac{{12}}{{13}} + \frac{1}{4} \times \frac{{12}}{{13}}\)
b) \((1 - \frac{1}{2})\)×\((1 - \frac{1}{3})\)×\((1 - \frac{1}{4})\)×\((1 - \frac{1}{5})\)
Phân số nào không bằng phân số \(\frac{9}{{15}}\)?
Đáp án : C
Dựa vào tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
\(\frac{{21}}{{35}} = \frac{{21:7}}{{35:7}} = \frac{3}{5} = \frac{{3 \times 3}}{{5 \times 3}} = \frac{9}{{15}}\)
\(\frac{{18}}{{30}} = \frac{{18:2}}{{30:2}} = \frac{9}{{15}}\)
\(\frac{3}{5} = \frac{{3 \times 3}}{{5 \times 3}} = \frac{9}{{15}}\)
Đáp án C.
Sắp xếp các phân số \(\frac{{15}}{{18}};\frac{3}{2};\frac{5}{2};\frac{5}{7}\) theo thứ tự từ lớn đến bé là:
Đáp án : D
- So sánh các phân số
- Sắp xếp theo thứ tự từ bé đến lớn
- Các phân số lớn hơn 1:\(\frac{3}{2};\frac{5}{2}\)
Ta có: \(\frac{5}{2} > \frac{3}{2}\) Vì đây là 2 phân số có mẫu số giống nhau (đều là 2); có tử số (5>3)
- Các phân số nhỏ hơn 1:\(\frac{{15}}{{18}};\frac{5}{7}\)
Ta có:
\(\frac{{15}}{{18}} = \frac{5}{6}\) Ta so sánh \(\frac{5}{6}\)>\(\frac{5}{7}\) (Vì hai phân số có tử số giống nhau, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn)
Nên \(\frac{{15}}{{18}}\)>\(\frac{5}{7}\)
Vậy sắp xếp các phân số theo thứ tự từ bé đến lớn là: \(\frac{5}{2};\frac{3}{2};\frac{{15}}{{18}};\frac{5}{7}\)
Đáp án D.
Có bao nhiêu hình thoi trong hình dưới đây:
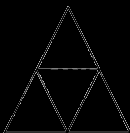
Đáp án : D
Hình thoi có hai cặp cạnh đối diện song song và độ dài bốn cạnh bằng nhau.
Vậy hình bên có 3 hình thoi.
Đáp án D.
Một hộp bóng có \(\frac{1}{2}\) số bóng màu đỏ, \(\frac{1}{3}\)số bóng màu xanh, còn lại là bóng màu vàng. Tìm phân số chỉ số bóng màu vàng.
Đáp án : B
- Phân số chỉ số bóng màu đỏ và màu xanh = Phân số chỉ số bóng màu đỏ + Phân số chỉ số bóng màu xanh.
- Phân số chỉ số bóng màu vàng = Phân số chỉ tổng số bóng có trong hộp - Phân số chỉ số bóng màu đỏ và màu xanh
Phân số chỉ số bóng màu đỏ và màu xanh là:
\(\frac{1}{2}\)+\(\frac{1}{3}\)=\(\frac{5}{6}\)
Số bỏng màu đỏ và màu xanh chiếm \(\frac{5}{6}\) phần hộp bóng có nghĩa là: hộp bóng được chia ra làm 6 phần bằng nhau. Số bóng đỏ và xanh chiếm 5 phần. Còn lại là số bóng màu vàng. Ta có thể tính phân số chỉ số bóng màu vàng như sau:
\(\frac{6}{6}\)-\(\frac{5}{6}\)=\(\frac{1}{6}\) (phần) hoặc lấy 1-\(\frac{5}{6}\)=\(\frac{1}{6}\)
Đáp án B.
Số thứ nhất hơn số thứ hai là 129. Biết rằng nếu lấy số thứ nhất cộng với số thứ hai rồi cộng với tổng của chúng thì được 2010. Tìm số thứ nhất.
940
567
438
1 070
Đáp án : B
Tổng hai số = số thứ nhất + số thứ hai
Số thứ nhất + số thứ hai + tổng = tổng + tổng = 2 x tổng = 2010
Tổng của hai số là:
2010 : 2 = 1005
Số thứ nhất là:
(1005 + 129) : 2 = 567
Đáp án: B
\(\frac{7}{{10}}\)của hình chữ nhật đã được tô màu có nghĩa là:
Đáp án : B
Dựa vào kiến thức đã học về phân số
\(\frac{7}{{10}}\)của hình chữ nhật đã được tô màu có nghĩa là: Chia hình chữ nhật thành 10 phần bằng nhau, tô màu 7 phần
Đáp án B.
Tính
a) \(\frac{7}{{12}} + \frac{3}{4} \times \frac{2}{9}\)
b) \(\frac{1}{4} + \frac{5}{{24}}:\frac{2}{3}\)
- Muốn cộng hoặc trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số đó, rồi cộng hoặc trừ hai phân số sau khi quy đồng.
- Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai.
a) \(\frac{7}{{12}} + \frac{3}{4} \times \frac{2}{9} = \frac{7}{{12}} + \frac{1}{6} = \frac{9}{{12}} = \frac{3}{4}\)
b) \(\frac{1}{4} + \frac{5}{{24}}:\frac{2}{3} = \frac{1}{4} + \frac{5}{{16}} = \frac{9}{{16}}\)
Tìm giá trị của ? biết rằng:
a) ? + 686 = 2 897
b) 49 524 - ? = 42 123
c) ? x 34 = 7 990
d) 67 x ? = 18 760
Dựa vào cách tìm thành phần chưa biết của phép tính
a) ? + 686 = 2 897
? = 2 897 - 686
? = 2 211
b) 49 524 - ? = 42 123
? = 49 524 - 42 123
? = 7 401
c) ? x 34 = 7 990
? = 7 990 : 34
? = 235
d) ? : 280 = 67
? = 280 x 67
? = 18 760
Điền số thích hợp vào chỗ chấm.
a) 160 009 mm2 = ……. dm2 …. mm2
b) \(\frac{1}{{25}}\)tấn = …….. yến
c) 12 m 3 cm = ….… mm
d) \(\frac{5}{{12}}\) giờ = ……. phút
Áp dụng cách đổi: 1 tấn = 100 yến
1 giờ = 60 phút
1 m = 1 000 mm; 1 cm = 10 mm
1 dm2 = 10 000 mm2
a) 160 009 mm2 = 16 dm2 9 mm2
b) \(\frac{1}{{25}}\)tấn = 4 yến
c) 12 m 3 cm = 12 030 mm
d) \(\frac{5}{{12}}\) giờ = 25 phút
Cửa hàng nhập về 56 kg thóc. Buổi sáng bán \(\frac{1}{2}\)tổng số thóc. Buổi chiều bán được \(\frac{3}{4}\) số thóc còn lại. Hỏi cửa hàng đã bán tất cả bao nhiêu ki-lô-gam thóc?
- Số ki-lô-gam thóc cửa hàng bán được vào buổi sáng = Số ki-lô-gam thóc cửa hàng nhập về x \(\frac{1}{2}\)
- Số ki-lô-gam thóc cửa hàng còn lại = Số ki-lô-gam thóc cửa hàng nhập về - Số ki-lô-gam thóc cửa hàng bán được vào buổi sáng
- Số ki-lô-gam thóc cửa hàng bán được vào buổi chiều = Số ki-lô-gam thóc cửa hàng còn lại x \(\frac{3}{4}\)
- Cửa hàng đã bán tất cả số ki-lô-gam thóc = Số ki-lô-gam thóc cửa hàng bán được vào buổi sáng + Số ki-lô-gam thóc cửa hàng bán được vào buổi chiều
Buổi sáng cửa hàng bán được số ki-lô-gam thóc là:
56 x \(\frac{1}{2}\) = 28 (kg)
Cửa hàng còn lại số ki-lô-gam thóc là:
56 – 28 = 28 (kg)
Buổi chiều cửa hàng bán được số ki-lô-gam thóc là:
28 x \(\frac{3}{4}\)= 21 (kg)
Cửa hàng đã bán tất cả số ki-lô-gam thóc là:
28 + 21 = 49 (kg)
Đáp số: 49 kg thóc
Một trại chăn nuôi 200 con vịt, ngan và ngỗng. Số vịt bằng tổng số ngan và ngỗng, số ngan nhiều hơn số ngỗng là 40 con. Hỏi trại đó có bao nhiêu con ngan, vịt, ngỗng?
Số vịt = Tổng số ngan và ngỗng = Tổng 3 loại : 2
Bài toán tìm hai số khi biết tổng và hiệu:
Số ngỗng = (Tổng – Hiệu) : 2
Số ngan = Tổng – Số ngỗng
Vì số vịt bằng tổng số ngan và ngỗng nên số vịt là:
200 : 2 = 100 (con)
Số ngỗng là:
(100 - 40) : 2 = 30 (con)
Số ngan là:
100 – 30 = 70 (con)
Đáp số: Vịt: 100 con
Ngỗng: 30 con
Ngan: 70 con
Tính bằng cách thuận tiện.
a) \(\frac{1}{2} \times \frac{{12}}{{13}} + \frac{1}{3} \times \frac{{12}}{{13}} + \frac{1}{4} \times \frac{{12}}{{13}}\)
b) \((1 - \frac{1}{2})\)×\((1 - \frac{1}{3})\)×\((1 - \frac{1}{4})\)×\((1 - \frac{1}{5})\)
- Áp dụng công thức: a x b + a x c = a x (b + c)
- Tính bằng cách thuận tiện với phép nhân phân số
a) \(\frac{1}{2} \times \frac{{12}}{{13}} + \frac{1}{3} \times \frac{{12}}{{13}} + \frac{1}{4} \times \frac{{12}}{{13}}\)
\(\begin{array}{l} = \frac{{12}}{{13}} \times (\frac{1}{2} + \frac{1}{3} + \frac{1}{4})\\ = \frac{{12}}{{13}} \times \frac{{13}}{{12}}\\ = 1\end{array}\)
b) \((1 - \frac{1}{2})\)×\((1 - \frac{1}{3})\)×\((1 - \frac{1}{4})\)×\((1 - \frac{1}{5})\)
\(\begin{array}{l} = \frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times \frac{4}{5}\\ = \frac{1}{5}\end{array}\)
Kỳ thi học kì 2 Toán 4 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một học kỳ rèn luyện. Đề thi học kì 2 Toán 4 Chân trời sáng tạo - Đề số 5 là một công cụ hữu ích giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự đánh giá trình độ của bản thân.
Đề thi thường bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã được học trong chương trình Toán 4 Chân trời sáng tạo. Cụ thể:
Các chủ đề thường xuất hiện trong đề thi:
Để đạt kết quả tốt trong kỳ thi, học sinh cần nắm vững kiến thức cơ bản, rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập thường gặp. Dưới đây là một số hướng dẫn giải chi tiết cho các dạng bài tập thường xuất hiện trong đề thi:
Đây là dạng bài tập đòi hỏi học sinh phải đọc kỹ đề bài, xác định đúng các yếu tố đã cho và yêu cầu của bài toán, sau đó lựa chọn phép tính phù hợp để giải.
Học sinh cần nắm vững công thức tính chu vi và diện tích của các hình vuông, hình chữ nhật, hình tam giác.
| Hình | Công thức tính chu vi | Công thức tính diện tích |
|---|---|---|
| Hình vuông | P = 4 x a (a là độ dài cạnh) | S = a x a |
| Hình chữ nhật | P = 2 x (a + b) (a, b là chiều dài, chiều rộng) | S = a x b |
| Hình tam giác | P = a + b + c (a, b, c là độ dài các cạnh) | S = (a x h) / 2 (a là độ dài đáy, h là chiều cao) |
Học sinh cần nắm vững các quy tắc thực hiện các phép tính cộng, trừ, nhân, chia số tự nhiên, đặc biệt là thứ tự thực hiện các phép tính.
Để đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 4, học sinh nên:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi học kì 2 Toán 4 Chân trời sáng tạo - Đề số 5!