Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 5, được biên soạn theo chuẩn chương trình học mới nhất. Đề thi này là tài liệu ôn tập và luyện thi vô cùng hữu ích cho các em học sinh.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, giúp các em làm quen với cấu trúc đề thi thực tế và rèn luyện kỹ năng giải toán.
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai? A. \(P(2)\) B. \(P(4)\). C. \(P(3)\). D. \(P(7)\)
I. PHẦN TRẮC NGHIỆM
1. B | 2. C | 3. D | 4. C | 5. B |
6. B | 7. A | 8. D | 9. A | 10. C |
11. B | 12. C | 13. B | 14. D | 15. A |
Câu 1.
Cách giải:
Ta có: \(P(2) = 5,P(4) = 17,P(3) = 10,P(7) = 50\)
Chọn B
Câu 2.
Cách giải:
Thay \(x = 1,y = - 1\) vào từng bất phương trình, ta được:
\(1 + ( - 1) - 3 = 3 < 0\) => Lọai A
\( - 1 - ( - 1) = 0\) => Loại B
\(1 + 3.( - 1) + 1 = - 1 < 0\) => Chọn C
\( - 1 - 3.( - 1) - 1 = 1 > 0\) => Loại D
Chọn C
Câu 3.
Cách giải:
Viết lại mệnh đề đã cho: P: “\(\exists x \in \mathbb{R},{x^2} \le 0\)”
Suy ra \(\overline P :\) “\(\forall x \in \mathbb{R},{x^2} > 0\)”
Chọn D
Câu 4.
Cách giải:
Hàm số \(y = \frac{{x + 2}}{{{x^2} - 4x + 3}} + \sqrt {{x^2} - 9} \) xác định khi \(\left\{ \begin{array}{l}{x^2} - 4x + 3 \ne 0\\{x^2} - 9 \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}(x - 1)(x - 3) \ne 0\\{x^2} \ge 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left\{ \begin{array}{l}x \ne 1\\x \ne 3\end{array} \right.\\\left[ \begin{array}{l}x \ge 3\\x \le - 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 3\\x \le - 3\end{array} \right.\)
Vậy tập xác định \(D = ( - \infty ; - 3] \cup (3; + \infty ) = \mathbb{R}{\rm{\backslash }}( - 3;3]\)
Chọn C
Câu 5.
Cách giải:
Từ đồ thị hàm số ta thấy:
Hàm số đồng biến trên (0;12) và nghịch biến trên các khoảng \(( - \infty ;0)\) và \((12; + \infty )\)
Vì \( - 5 < - 1\) nên \(f( - 5) > f( - 1)\) => Loại A.
Vì \(7 < 11\) nên \(f(7) < f(11)\) => Chọn B.
Vì \(1 < 6\) nên \(f(1) < f(6)\) => Loại C.
Vì \(2022 > 20\) nên \(f(2022) < f(20)\) => Loại D.
Chọn B
Câu 6.
Cách giải:
Ta có: \(X \cup Y = \{ 1;3;5;7;8;9\} \)
Chọn B
Câu 7.
Cách giải:
Ta có: \({C_\mathbb{R}}A = [ - 3;11) \Rightarrow A = ( - \infty ; - 3) \cup [11; + \infty )\)
\({C_\mathbb{R}}B = ( - 8;1] \Rightarrow B = ( - \infty ; - 8] \cup (1; + \infty )\)
\(\begin{array}{l} \Rightarrow A \cap B = ( - \infty ; - 8] \cup [11; + \infty )\\ \Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = ( - 8;11)\end{array}\)
Chọn A
Câu 8.
Cách giải:
Phủ định của mệnh đề đó là: “Mọi học sinh trong lớp 10A đều thích học môn Toán”.
Chọn D
Câu 9.
Cách giải:
Hàm số \(f(x) = - {x^2} + 2x - 5\) có \(a = - 1 < 0,b = 2, - \frac{b}{{2a}} = 1\) và \(f(1) = - 4\)
Ta có bảng biến thiên:
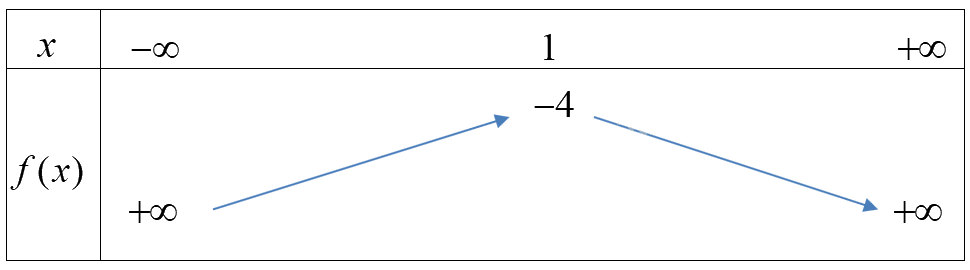
Hàm số đồng biến trên \(( - \infty ;1)\)và nghịch biến trên\((1; + \infty )\).
Chọn A
Câu 10.
Cách giải:
Tại \(x = 3 \ge 2\) thì \(f(3) = \sqrt {3 - 2} + 5 = 6\)
Tại \(x = 1 < 2\) thì \(f(1) = {3.1^2} - 1 + 1 = 3\)
\( \Rightarrow 2.f(3) - 4.f(1) = 2.6 - 4.3 = 0\)
Chọn C
Câu 11.
Cách giải:
+ Xác định đường thẳng là bở của miền nghiệm:
Đường thẳng d đi qua \(A(\frac{3}{2};0)\) và \(B(0; - 3)\) \( \Rightarrow d:2x - y = 3\)
+ Điểm O(0;0) thuộc miền nghiệm và \(2.0 - 0 = 0 < 3\)
Do đó BPT cần tìm là \(2x - y < 3\)
Chọn B
Câu 12.
Cách giải:
\(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} = \{ 0;2;4;6;8;...\} \)
\(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} = \{ 0;6;12;18;24;...\} \)
\(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} = \{ 1;2\} \)
\(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} = \{ 1;2;3;6\} \)
Ta có: \(N \subset M\) và \(P \subset Q\)
Do đó: \(M \cap N = N\) và \(P \cap Q = P\)
Chọn C
Câu 13.
Cách giải:
Thay \(x = 2,y = 3\) vào từng bất phương trình, ta được:
\(2.2 - 3.3 - 1 = - 6 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(2x - 3y - 1 < 0\)
\(2 - 3 = - 1 < 0 \Rightarrow A(2;3)\) không là nghiệm của BPT \(x - y > 0\)
\(4.2 - 3.3 = - 1 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(4x - 3y < 0\)
\(2 + 3.3 - 7 = 4 \ge 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(x + 3y - 7 \ge 0\)
Chọn B
Câu 14.
Cách giải:
Hàm số \(y = {x^2} - 2x + 108\) có \(a = 1 > 0,b = - 2,c = 108\)
\( \Rightarrow - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1;f(1) = 107\)
\( \Rightarrow \)Đồ thị hàm số có đỉnh \(I(1;107)\) và trục đối xứng \(x = 1\)
Hàm số đồng biến trên \((1; + \infty )\)và nghịch biến trên\(( - \infty ;1) \supset ( - 5;0)\).
Chọn D
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
Cách giải:
\(B \subset A \Leftrightarrow (m; + \infty ) \subset (2; + \infty ) \Leftrightarrow m \ge 2\)
Chọn A
II. PHẦN TỰ LUẬN
Câu 1:
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Ta có: \((2x + 1)({x^2} - 9) = 0 \Leftrightarrow (2x + 1)(x - 3)(x + 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - 3 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = 3\\x = - 3\end{array} \right.\)
Mà \( - \frac{1}{2} \notin \mathbb{Z}\)\( \Rightarrow A = \{ - 3;3\} \)
\(B = \{ x \in \mathbb{N}|x < 4\} = \{ 0;1;2;3\} \)
Do đó \(A \cap B = \{ 3\} ,A \cup B = \{ - 3;0;1;2;3\} ,A{\rm{\backslash }}B = \{ - 3\} \)
b) \(M = (0;3)\) và. Để \(M \cap N = N \Leftrightarrow N \subset M\)
\(\begin{array}{l} \Leftrightarrow [m;m + 1) \subset (0;3)\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m + 1 \le 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m \le 2\end{array} \right. \Leftrightarrow 0 < m \le 2\end{array}\)
Mà \(m \in \mathbb{Z}\) nên \(m = 1\) hoặc \(m = 2\).
Vậy \(m = 1\) hoặc \(m = 2\) thì \(M \cap N = N.\)
Câu 2:
Cách giải:
Gọi x là số xe loại A, y là số xe loại B mà công ty cần thuê (đơn vị: chiếc). \((x,y \in \mathbb{N})\)
Theo đề bài ta có: \(0 \le x \le 10\) và \(0 \le y \le 9\)
Tổng chi phí thuê xe là \(F(x;y) = 4x + 3y\) (triệu đồng)
Số người cần chở là 140 mà mỗi xe A chở tối đa 20 người, mỗi xe B chở tối đa 10 người nên ta có \(20x + 10y \ge 140\) hay \(2x + y \ge 14\)
Số hàng cần chở là 9 tấn mà mỗi xe A chở được 0,6 tấn, mỗi xe B chở được 1,5 tấn nên ta có \(0,6x + 1,5y \ge 9\) hay \(2x + 5y \ge 30\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\2x + y \ge 14\\2x + 5y \ge 30\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
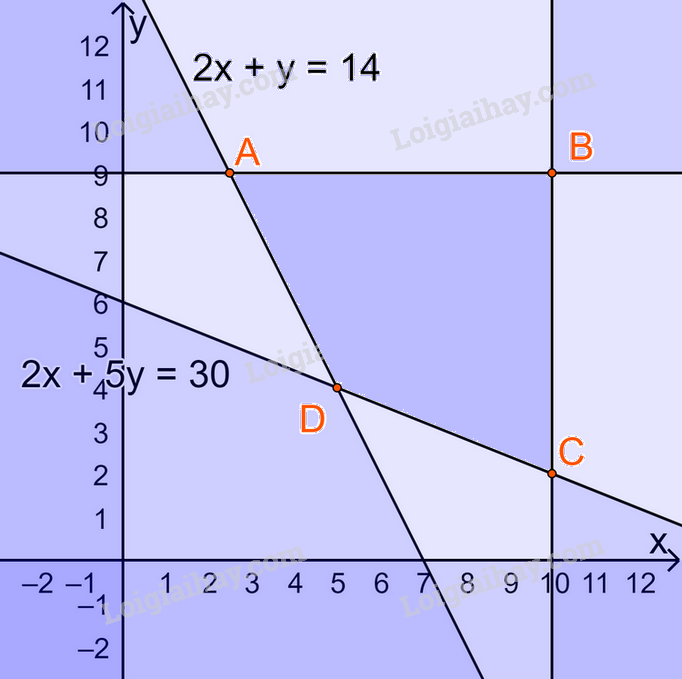
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(\frac{5}{2};9),B(10;9),C(10;2),D(5;4)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 4x + 3y\) ta được:
\(\begin{array}{l}F(\frac{5}{2};9) = 4.\frac{5}{2} + 3.9 = 37\\F(10;9) = 4.10 + 3.9 = 67\\F(10;2) = 4.10 + 3.2 = 46\\F(5;4) = 4.5 + 3.4 = 32\end{array}\)
Do đó F đạt giá trị nhỏ nhất bằng 32 tại \(x = 5;y = 4\)
Vậy công ty đó cần thuê 5 xe loại A và 4 xe loại B.
Câu 3
Cách giải:
a) Parabol \((P):y = a{x^2} + bx + c\) đi qua A(2;-2) nên \( - 2 = a{.2^2} + b.2 + c \Leftrightarrow 4a + 2b + c = - 2\)
Lại có: (P) có đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = \frac{5}{2}\\a.{\left( {\frac{5}{2}} \right)^2} + b.\left( {\frac{5}{2}} \right) + c = \frac{{ - 9}}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5a + b = 0\\25a + 10b + 4c = - 9\end{array} \right.\)
Thay \(b = - 5a\) ta được \(\left\{ \begin{array}{l}4a + 2.( - 5a) + c = - 2\\25a + 10.( - 5b) + 4c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6a + c = - 2\\ - 25a + 4c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = 4\end{array} \right.\)
Suy ra \(b = - 5a = - 5\)
Vậy parabol đó là \((P):y = {x^2} - 5x + 4\)
b) Parabol \((P):y = {x^2} - 5x + 4\) có \(a = 1 > 0,b = - 5\)
Bảng biến thiên
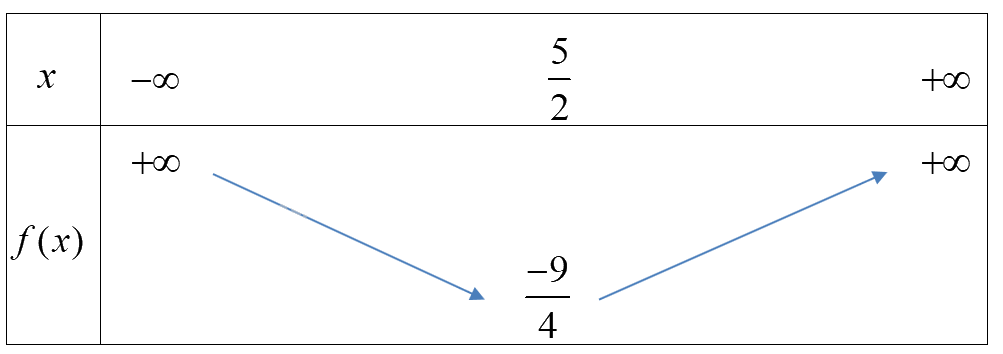
Hàm số đồng biến trên \((\frac{5}{2}; + \infty )\)và nghịch biến trên\(( - \infty ;\frac{5}{2})\).
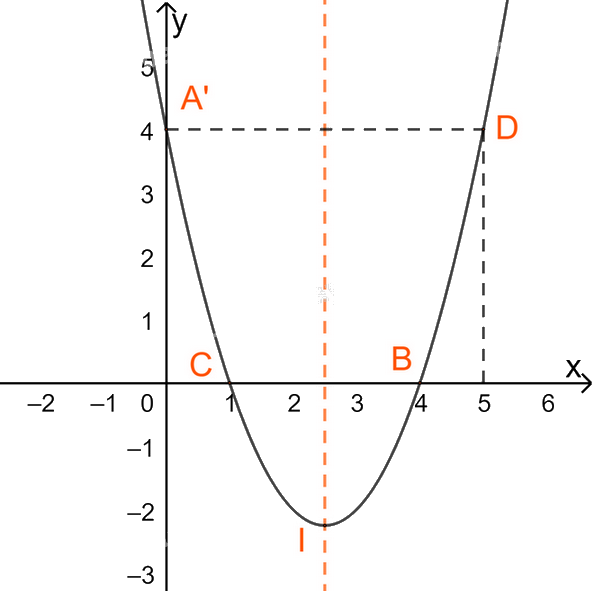
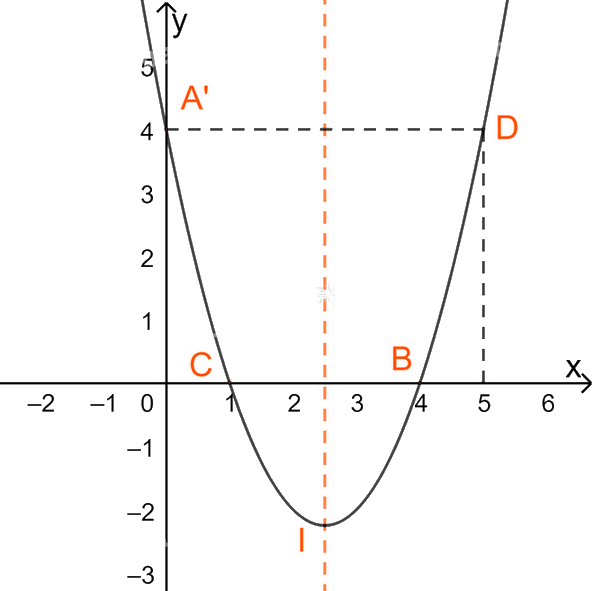
+ Vẽ đồ thị
Đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
(P) giao Oy tại điểm \(A'\left( {0;4} \right)\)
(P) giao Ox tại \(B(4;0)\) và \(C(1;0)\)
Điểm \(D(5;4)\) đối xứng với \(A'\left( {0;4} \right)\) qua trục đối xứng.
Câu 4.
Cách giải:
Hàm số \(y = 3{x^2} - 6x + 7\) có \(a = 3 > 0,b = - 6 \Rightarrow - \frac{b}{{2a}} = 1;\;y(1) = 4\).
Ta có bảng biến thiên
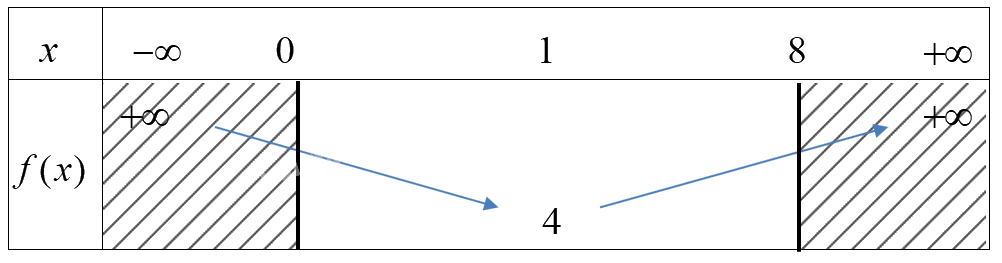
Mà \(f(0) = 7,f(8) = 151,f(1) = 4\)
\( \Rightarrow \) Trên [0;8]
Hàm số đạt GTLN bằng 151 tại \(x = 8\), đạt GTNN bằng 4 tại \(x = 1\).
I. PHẦN TRẮC NGHIỆM
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai?
A. \(P(2)\) B. \(P(4)\). C. \(P(3)\). D. \(P(7)\)
Câu 2. Cặp số \((1; - 1)\) là nghiệm của bất phương trình nào sau đây?
A. \(x + y - 3 > 0\) B. \( - x - y < 0\). C. \(x + 3y + 1 < 0\). D. \( - x - 3y - 1 < 0\)
Câu 3. Mệnh đề phủ định của mệnh đề “Có một số thực sao cho bình phương của nó không là số nguyên dương”
A. \(\exists x \in \mathbb{R},{x^2} > 0\) B. \(\exists x \in \mathbb{R},{x^2} \le 0\). C. \(\forall x \in \mathbb{R},{x^2} \le 0\). D. \(\forall x \in \mathbb{R},{x^2} > 0\)
Câu 4. Tập xác định của hàm số \(y = \frac{{x + 2}}{{{x^2} - 4x + 3}} + \sqrt {{x^2} - 9} \)
A. \((3; + \infty )\). B. \(\mathbb{R}{\rm{\backslash }}\{ 1;3\} \) C. \(\mathbb{R}{\rm{\backslash }}( - 3;3]\). D. \(\mathbb{R}{\rm{\backslash }}[ - 3;3]\).
Câu 5. Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
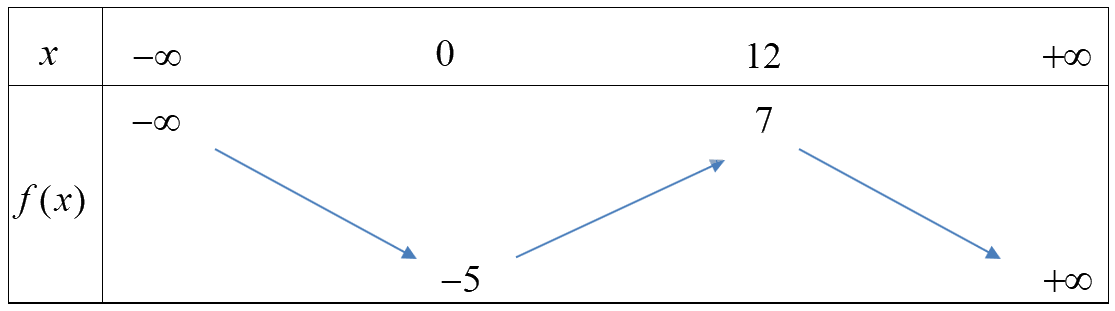
Khẳng định nào sau đây đúng?
A. \(f( - 5) < f( - 1)\) B. \(f(7) < f(11)\) C. \(f(1) > f(6)\) D. \(f(2022) > f(20)\)
Câu 6. Cho hai tập hợp \(X = \{ 1;3;5;8\} ,Y = \{ 3;5;7;9\} \). Tập hợp \(X \cup Y\) bằng tập hợp nào sau đây?
A. \(\{ 3;5\} \) B. \(\{ 1;3;5;7;8;9\} \). C. \(\{ 1;7;9\} \). D. \(\{ 1;3;5\} \)
Câu 7. Biết rằng \({C_\mathbb{R}}A = [ - 3;11)\) và \({C_\mathbb{R}}B = ( - 8;1]\). Khi đó, \({C_\mathbb{R}}\left( {A \cap B} \right)\) bằng?
A. \(( - 8;11)\) B. \([3;1]\). C. \(( - \infty ; - 8] \cup [11; + \infty )\). D. \(( - \infty ; - 3) \cup (1; + \infty )\)
Câu 8. Cho mệnh đề: “Có học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:
A. Mọi học sinh trong lớp 10A đều thích học môn Văn.
B. Mọi học sinh trong lớp 10A đều không thích học môn Toán.
C. Có học sinh trong lớp 10A thích học môn Toán.
D. Mọi học sinh trong lớp 10A đều thích học môn Toán.
Câu 9. Cho hàm số \(f(x) = - {x^2} + 2x - 5\). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên \(( - \infty ;1)\), nghịch biến trên\((1; + \infty )\).
B. Hàm số đồng biến trên \((1; + \infty )\), nghịch biến trên\(( - \infty ;1)\).
C. Hàm số nghịch biến trên\(\mathbb{R}\).
D. Hàm số đồng biến trên\(\mathbb{R}\).
Câu 10. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\sqrt {x - 2} + 5\quad (x \ge 2)\\3{x^2} - x + 1\quad (x < 2)\end{array} \right.\). Giá trị của \(2.f(3) - 4.f(1)\) là:
A. \(38\) B. \(12\) C. \(0\). D. \( - 4\).
Câu 11. Trong mặt phẳng Oxy, phần nửa mặt phẳng không tô màu (không kể bờ) trong hình dưới đây biểu diễn tập nghiệm của bất phương trình nào?
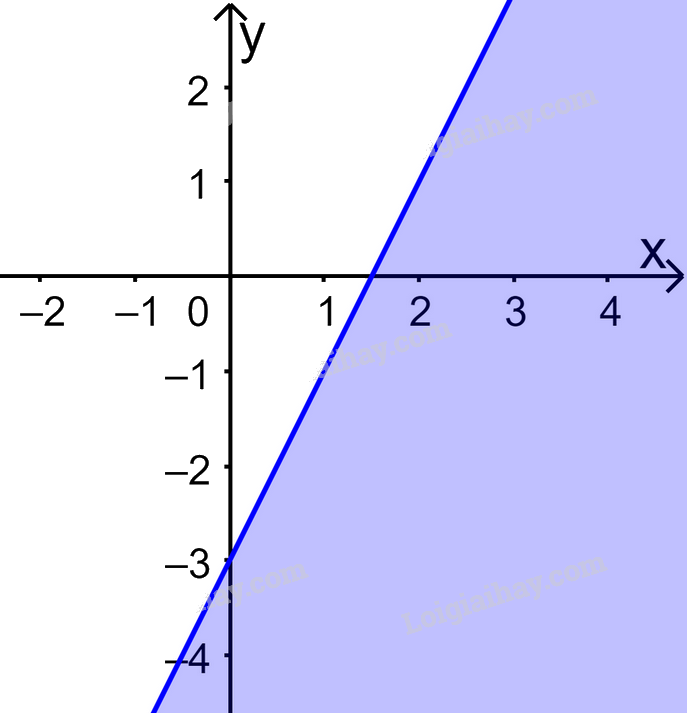
A.\(2x - y > 3\). B. \(2x - y < 3\). C. \(x - 2y > 3\). D. \(x - 2y < 3\).
Câu 12. Cho \(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} \), \(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} \), \(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} \), \(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} \). Khẳng định nào dưới đây đúng?
A.\(M \subset N\). B. \(Q \subset P\). C.\(M \cap N = N\). D. \(P \cap Q = Q\).
Câu 13. Cặp số \((2;3)\) không là nghiệm của bất phương trình nào sau đây?
A.\(2x - 3y - 1 < 0\). B. \(x - y > 0\). C.\(4x - 3y < 0\). D. \(x + 3y - 7 \ge 0\).
Câu 14. Cho hàm số \(y = {x^2} - 2x + 108\), mệnh đề nào sai?
A. Đồ thị hàm số nhận \(I(1;107)\) làm đỉnh
B. Hàm số đồng biến trên \((1; + \infty )\).
C. Hàm số nghịch biến trên\(( - 5;0)\).
D. Đồ thị hàm số có trục đối xứng \(x = - 1\).
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
II. PHẦN TỰ LUẬN
Câu 1.
a) Cho hai tập hợp \(A = \{ x \in \mathbb{Z}|(2x + 1)({x^2} - 9) = 0\} \) và \(B = \{ x \in \mathbb{N}|x < 4\} \). Xác định các tập hợp \(A \cap B,A \cup B,A{\rm{\backslash }}B\)
b) Cho hai tập hợp \(M = (0;3)\) và \(N = [m;m + 1)\). Tìm \(m \in \mathbb{Z}\) để \(M \cap N = N\)
Câu 2. Trong một đợt quảng cáo và bán khuyến mãi sản phẩm mới, công ty X cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, mỗi chiếc chở được tối đa 20 người và 0,6 tấn hàng, giá thuê là 4 triệu; xe loại B có 9 chiếc, mỗi chiếc chở được tối đa 10 người và 1,5 tấn hàng, giá thuê là 3 triệu. Hỏi công ty cần thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất?
Câu 3.
a) Xác định parabol (P) biết \((P):y = a{x^2} + bx + c\) đi qua A(2;-2) và có đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
b) Xét sự biến thiên và vẽ đồ thị hàm số trên.
Câu 4. Tìm giá trị lớn nhất, nhỏ nhất (nếu có) của hàm số: \(y = 3{x^2} - 6x + 7\) trên đoạn [0;8].
Tải về
I. PHẦN TRẮC NGHIỆM
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai?
A. \(P(2)\) B. \(P(4)\). C. \(P(3)\). D. \(P(7)\)
Câu 2. Cặp số \((1; - 1)\) là nghiệm của bất phương trình nào sau đây?
A. \(x + y - 3 > 0\) B. \( - x - y < 0\). C. \(x + 3y + 1 < 0\). D. \( - x - 3y - 1 < 0\)
Câu 3. Mệnh đề phủ định của mệnh đề “Có một số thực sao cho bình phương của nó không là số nguyên dương”
A. \(\exists x \in \mathbb{R},{x^2} > 0\) B. \(\exists x \in \mathbb{R},{x^2} \le 0\). C. \(\forall x \in \mathbb{R},{x^2} \le 0\). D. \(\forall x \in \mathbb{R},{x^2} > 0\)
Câu 4. Tập xác định của hàm số \(y = \frac{{x + 2}}{{{x^2} - 4x + 3}} + \sqrt {{x^2} - 9} \)
A. \((3; + \infty )\). B. \(\mathbb{R}{\rm{\backslash }}\{ 1;3\} \) C. \(\mathbb{R}{\rm{\backslash }}( - 3;3]\). D. \(\mathbb{R}{\rm{\backslash }}[ - 3;3]\).
Câu 5. Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
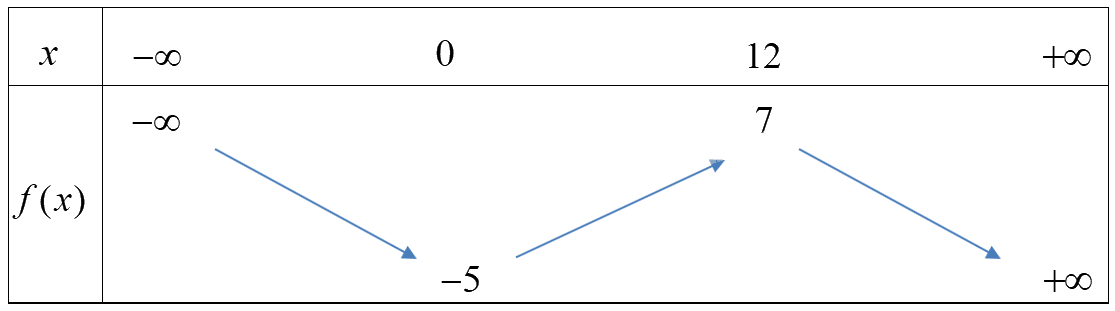
Khẳng định nào sau đây đúng?
A. \(f( - 5) < f( - 1)\) B. \(f(7) < f(11)\) C. \(f(1) > f(6)\) D. \(f(2022) > f(20)\)
Câu 6. Cho hai tập hợp \(X = \{ 1;3;5;8\} ,Y = \{ 3;5;7;9\} \). Tập hợp \(X \cup Y\) bằng tập hợp nào sau đây?
A. \(\{ 3;5\} \) B. \(\{ 1;3;5;7;8;9\} \). C. \(\{ 1;7;9\} \). D. \(\{ 1;3;5\} \)
Câu 7. Biết rằng \({C_\mathbb{R}}A = [ - 3;11)\) và \({C_\mathbb{R}}B = ( - 8;1]\). Khi đó, \({C_\mathbb{R}}\left( {A \cap B} \right)\) bằng?
A. \(( - 8;11)\) B. \([3;1]\). C. \(( - \infty ; - 8] \cup [11; + \infty )\). D. \(( - \infty ; - 3) \cup (1; + \infty )\)
Câu 8. Cho mệnh đề: “Có học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:
A. Mọi học sinh trong lớp 10A đều thích học môn Văn.
B. Mọi học sinh trong lớp 10A đều không thích học môn Toán.
C. Có học sinh trong lớp 10A thích học môn Toán.
D. Mọi học sinh trong lớp 10A đều thích học môn Toán.
Câu 9. Cho hàm số \(f(x) = - {x^2} + 2x - 5\). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên \(( - \infty ;1)\), nghịch biến trên\((1; + \infty )\).
B. Hàm số đồng biến trên \((1; + \infty )\), nghịch biến trên\(( - \infty ;1)\).
C. Hàm số nghịch biến trên\(\mathbb{R}\).
D. Hàm số đồng biến trên\(\mathbb{R}\).
Câu 10. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\sqrt {x - 2} + 5\quad (x \ge 2)\\3{x^2} - x + 1\quad (x < 2)\end{array} \right.\). Giá trị của \(2.f(3) - 4.f(1)\) là:
A. \(38\) B. \(12\) C. \(0\). D. \( - 4\).
Câu 11. Trong mặt phẳng Oxy, phần nửa mặt phẳng không tô màu (không kể bờ) trong hình dưới đây biểu diễn tập nghiệm của bất phương trình nào?
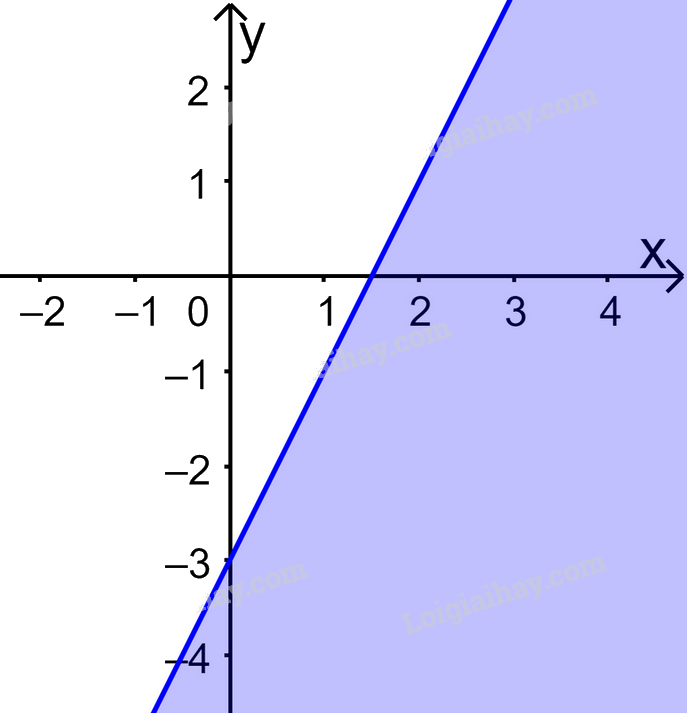
A.\(2x - y > 3\). B. \(2x - y < 3\). C. \(x - 2y > 3\). D. \(x - 2y < 3\).
Câu 12. Cho \(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} \), \(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} \), \(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} \), \(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} \). Khẳng định nào dưới đây đúng?
A.\(M \subset N\). B. \(Q \subset P\). C.\(M \cap N = N\). D. \(P \cap Q = Q\).
Câu 13. Cặp số \((2;3)\) không là nghiệm của bất phương trình nào sau đây?
A.\(2x - 3y - 1 < 0\). B. \(x - y > 0\). C.\(4x - 3y < 0\). D. \(x + 3y - 7 \ge 0\).
Câu 14. Cho hàm số \(y = {x^2} - 2x + 108\), mệnh đề nào sai?
A. Đồ thị hàm số nhận \(I(1;107)\) làm đỉnh
B. Hàm số đồng biến trên \((1; + \infty )\).
C. Hàm số nghịch biến trên\(( - 5;0)\).
D. Đồ thị hàm số có trục đối xứng \(x = - 1\).
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
II. PHẦN TỰ LUẬN
Câu 1.
a) Cho hai tập hợp \(A = \{ x \in \mathbb{Z}|(2x + 1)({x^2} - 9) = 0\} \) và \(B = \{ x \in \mathbb{N}|x < 4\} \). Xác định các tập hợp \(A \cap B,A \cup B,A{\rm{\backslash }}B\)
b) Cho hai tập hợp \(M = (0;3)\) và \(N = [m;m + 1)\). Tìm \(m \in \mathbb{Z}\) để \(M \cap N = N\)
Câu 2. Trong một đợt quảng cáo và bán khuyến mãi sản phẩm mới, công ty X cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, mỗi chiếc chở được tối đa 20 người và 0,6 tấn hàng, giá thuê là 4 triệu; xe loại B có 9 chiếc, mỗi chiếc chở được tối đa 10 người và 1,5 tấn hàng, giá thuê là 3 triệu. Hỏi công ty cần thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất?
Câu 3.
a) Xác định parabol (P) biết \((P):y = a{x^2} + bx + c\) đi qua A(2;-2) và có đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
b) Xét sự biến thiên và vẽ đồ thị hàm số trên.
Câu 4. Tìm giá trị lớn nhất, nhỏ nhất (nếu có) của hàm số: \(y = 3{x^2} - 6x + 7\) trên đoạn [0;8].
I. PHẦN TRẮC NGHIỆM
1. B | 2. C | 3. D | 4. C | 5. B |
6. B | 7. A | 8. D | 9. A | 10. C |
11. B | 12. C | 13. B | 14. D | 15. A |
Câu 1.
Cách giải:
Ta có: \(P(2) = 5,P(4) = 17,P(3) = 10,P(7) = 50\)
Chọn B
Câu 2.
Cách giải:
Thay \(x = 1,y = - 1\) vào từng bất phương trình, ta được:
\(1 + ( - 1) - 3 = 3 < 0\) => Lọai A
\( - 1 - ( - 1) = 0\) => Loại B
\(1 + 3.( - 1) + 1 = - 1 < 0\) => Chọn C
\( - 1 - 3.( - 1) - 1 = 1 > 0\) => Loại D
Chọn C
Câu 3.
Cách giải:
Viết lại mệnh đề đã cho: P: “\(\exists x \in \mathbb{R},{x^2} \le 0\)”
Suy ra \(\overline P :\) “\(\forall x \in \mathbb{R},{x^2} > 0\)”
Chọn D
Câu 4.
Cách giải:
Hàm số \(y = \frac{{x + 2}}{{{x^2} - 4x + 3}} + \sqrt {{x^2} - 9} \) xác định khi \(\left\{ \begin{array}{l}{x^2} - 4x + 3 \ne 0\\{x^2} - 9 \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}(x - 1)(x - 3) \ne 0\\{x^2} \ge 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left\{ \begin{array}{l}x \ne 1\\x \ne 3\end{array} \right.\\\left[ \begin{array}{l}x \ge 3\\x \le - 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 3\\x \le - 3\end{array} \right.\)
Vậy tập xác định \(D = ( - \infty ; - 3] \cup (3; + \infty ) = \mathbb{R}{\rm{\backslash }}( - 3;3]\)
Chọn C
Câu 5.
Cách giải:
Từ đồ thị hàm số ta thấy:
Hàm số đồng biến trên (0;12) và nghịch biến trên các khoảng \(( - \infty ;0)\) và \((12; + \infty )\)
Vì \( - 5 < - 1\) nên \(f( - 5) > f( - 1)\) => Loại A.
Vì \(7 < 11\) nên \(f(7) < f(11)\) => Chọn B.
Vì \(1 < 6\) nên \(f(1) < f(6)\) => Loại C.
Vì \(2022 > 20\) nên \(f(2022) < f(20)\) => Loại D.
Chọn B
Câu 6.
Cách giải:
Ta có: \(X \cup Y = \{ 1;3;5;7;8;9\} \)
Chọn B
Câu 7.
Cách giải:
Ta có: \({C_\mathbb{R}}A = [ - 3;11) \Rightarrow A = ( - \infty ; - 3) \cup [11; + \infty )\)
\({C_\mathbb{R}}B = ( - 8;1] \Rightarrow B = ( - \infty ; - 8] \cup (1; + \infty )\)
\(\begin{array}{l} \Rightarrow A \cap B = ( - \infty ; - 8] \cup [11; + \infty )\\ \Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = ( - 8;11)\end{array}\)
Chọn A
Câu 8.
Cách giải:
Phủ định của mệnh đề đó là: “Mọi học sinh trong lớp 10A đều thích học môn Toán”.
Chọn D
Câu 9.
Cách giải:
Hàm số \(f(x) = - {x^2} + 2x - 5\) có \(a = - 1 < 0,b = 2, - \frac{b}{{2a}} = 1\) và \(f(1) = - 4\)
Ta có bảng biến thiên:
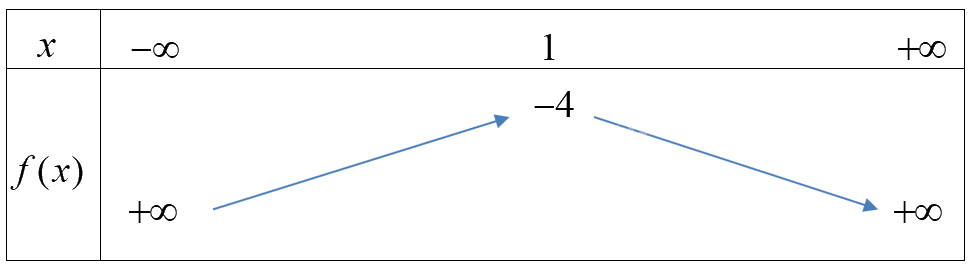
Hàm số đồng biến trên \(( - \infty ;1)\)và nghịch biến trên\((1; + \infty )\).
Chọn A
Câu 10.
Cách giải:
Tại \(x = 3 \ge 2\) thì \(f(3) = \sqrt {3 - 2} + 5 = 6\)
Tại \(x = 1 < 2\) thì \(f(1) = {3.1^2} - 1 + 1 = 3\)
\( \Rightarrow 2.f(3) - 4.f(1) = 2.6 - 4.3 = 0\)
Chọn C
Câu 11.
Cách giải:
+ Xác định đường thẳng là bở của miền nghiệm:
Đường thẳng d đi qua \(A(\frac{3}{2};0)\) và \(B(0; - 3)\) \( \Rightarrow d:2x - y = 3\)
+ Điểm O(0;0) thuộc miền nghiệm và \(2.0 - 0 = 0 < 3\)
Do đó BPT cần tìm là \(2x - y < 3\)
Chọn B
Câu 12.
Cách giải:
\(M = \{ x \in \mathbb{N}|x\) là bội của \(2\} = \{ 0;2;4;6;8;...\} \)
\(N = \{ x \in \mathbb{N}|x\) là bội của \(6\} = \{ 0;6;12;18;24;...\} \)
\(P = \{ x \in \mathbb{N}|x\) là ước của \(2\} = \{ 1;2\} \)
\(Q = \{ x \in \mathbb{N}|x\) là ước của \(6\} = \{ 1;2;3;6\} \)
Ta có: \(N \subset M\) và \(P \subset Q\)
Do đó: \(M \cap N = N\) và \(P \cap Q = P\)
Chọn C
Câu 13.
Cách giải:
Thay \(x = 2,y = 3\) vào từng bất phương trình, ta được:
\(2.2 - 3.3 - 1 = - 6 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(2x - 3y - 1 < 0\)
\(2 - 3 = - 1 < 0 \Rightarrow A(2;3)\) không là nghiệm của BPT \(x - y > 0\)
\(4.2 - 3.3 = - 1 < 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(4x - 3y < 0\)
\(2 + 3.3 - 7 = 4 \ge 0 \Rightarrow A(2;3)\) là nghiệm của BPT \(x + 3y - 7 \ge 0\)
Chọn B
Câu 14.
Cách giải:
Hàm số \(y = {x^2} - 2x + 108\) có \(a = 1 > 0,b = - 2,c = 108\)
\( \Rightarrow - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1;f(1) = 107\)
\( \Rightarrow \)Đồ thị hàm số có đỉnh \(I(1;107)\) và trục đối xứng \(x = 1\)
Hàm số đồng biến trên \((1; + \infty )\)và nghịch biến trên\(( - \infty ;1) \supset ( - 5;0)\).
Chọn D
Câu 15. Cho \(A = (2; + \infty )\) và \(B = (m; + \infty )\). Điều kiện cần và đủ của m để \(B \subset A\) là
A.\(m \ge 2\). B. \(m \le 2\). C.\(m = 2\). D. \(m > 2\).
Cách giải:
\(B \subset A \Leftrightarrow (m; + \infty ) \subset (2; + \infty ) \Leftrightarrow m \ge 2\)
Chọn A
II. PHẦN TỰ LUẬN
Câu 1:
Phương pháp:
a) \(A \cap B = \{ x \in A|x \in B\} \)
b) \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
c) \(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
Cách giải:
a) Ta có: \((2x + 1)({x^2} - 9) = 0 \Leftrightarrow (2x + 1)(x - 3)(x + 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 0\\x - 3 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{1}{2}\\x = 3\\x = - 3\end{array} \right.\)
Mà \( - \frac{1}{2} \notin \mathbb{Z}\)\( \Rightarrow A = \{ - 3;3\} \)
\(B = \{ x \in \mathbb{N}|x < 4\} = \{ 0;1;2;3\} \)
Do đó \(A \cap B = \{ 3\} ,A \cup B = \{ - 3;0;1;2;3\} ,A{\rm{\backslash }}B = \{ - 3\} \)
b) \(M = (0;3)\) và. Để \(M \cap N = N \Leftrightarrow N \subset M\)
\(\begin{array}{l} \Leftrightarrow [m;m + 1) \subset (0;3)\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m + 1 \le 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m \le 2\end{array} \right. \Leftrightarrow 0 < m \le 2\end{array}\)
Mà \(m \in \mathbb{Z}\) nên \(m = 1\) hoặc \(m = 2\).
Vậy \(m = 1\) hoặc \(m = 2\) thì \(M \cap N = N.\)
Câu 2:
Cách giải:
Gọi x là số xe loại A, y là số xe loại B mà công ty cần thuê (đơn vị: chiếc). \((x,y \in \mathbb{N})\)
Theo đề bài ta có: \(0 \le x \le 10\) và \(0 \le y \le 9\)
Tổng chi phí thuê xe là \(F(x;y) = 4x + 3y\) (triệu đồng)
Số người cần chở là 140 mà mỗi xe A chở tối đa 20 người, mỗi xe B chở tối đa 10 người nên ta có \(20x + 10y \ge 140\) hay \(2x + y \ge 14\)
Số hàng cần chở là 9 tấn mà mỗi xe A chở được 0,6 tấn, mỗi xe B chở được 1,5 tấn nên ta có \(0,6x + 1,5y \ge 9\) hay \(2x + 5y \ge 30\)
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\2x + y \ge 14\\2x + 5y \ge 30\end{array} \right.\)
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:
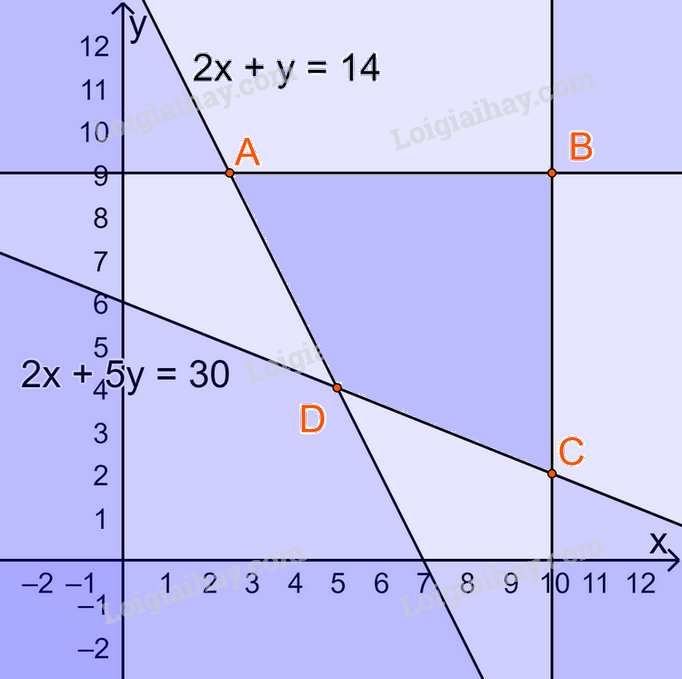
Miền nghiệm là miền tứ giác ABCD (kể cả các cạnh) , trong đó \(A(\frac{5}{2};9),B(10;9),C(10;2),D(5;4)\)
Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = 4x + 3y\) ta được:
\(\begin{array}{l}F(\frac{5}{2};9) = 4.\frac{5}{2} + 3.9 = 37\\F(10;9) = 4.10 + 3.9 = 67\\F(10;2) = 4.10 + 3.2 = 46\\F(5;4) = 4.5 + 3.4 = 32\end{array}\)
Do đó F đạt giá trị nhỏ nhất bằng 32 tại \(x = 5;y = 4\)
Vậy công ty đó cần thuê 5 xe loại A và 4 xe loại B.
Câu 3
Cách giải:
a) Parabol \((P):y = a{x^2} + bx + c\) đi qua A(2;-2) nên \( - 2 = a{.2^2} + b.2 + c \Leftrightarrow 4a + 2b + c = - 2\)
Lại có: (P) có đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
\( \Rightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = \frac{5}{2}\\a.{\left( {\frac{5}{2}} \right)^2} + b.\left( {\frac{5}{2}} \right) + c = \frac{{ - 9}}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5a + b = 0\\25a + 10b + 4c = - 9\end{array} \right.\)
Thay \(b = - 5a\) ta được \(\left\{ \begin{array}{l}4a + 2.( - 5a) + c = - 2\\25a + 10.( - 5b) + 4c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6a + c = - 2\\ - 25a + 4c = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = 4\end{array} \right.\)
Suy ra \(b = - 5a = - 5\)
Vậy parabol đó là \((P):y = {x^2} - 5x + 4\)
b) Parabol \((P):y = {x^2} - 5x + 4\) có \(a = 1 > 0,b = - 5\)
Bảng biến thiên
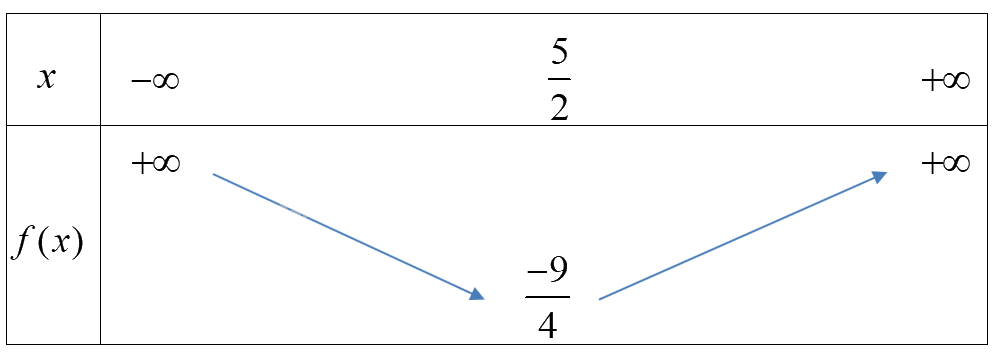
Hàm số đồng biến trên \((\frac{5}{2}; + \infty )\)và nghịch biến trên\(( - \infty ;\frac{5}{2})\).
+ Vẽ đồ thị
Đỉnh \(I(\frac{5}{2};\frac{{ - 9}}{4})\)
(P) giao Oy tại điểm \(A'\left( {0;4} \right)\)
(P) giao Ox tại \(B(4;0)\) và \(C(1;0)\)
Điểm \(D(5;4)\) đối xứng với \(A'\left( {0;4} \right)\) qua trục đối xứng.
Câu 4.
Cách giải:
Hàm số \(y = 3{x^2} - 6x + 7\) có \(a = 3 > 0,b = - 6 \Rightarrow - \frac{b}{{2a}} = 1;\;y(1) = 4\).
Ta có bảng biến thiên
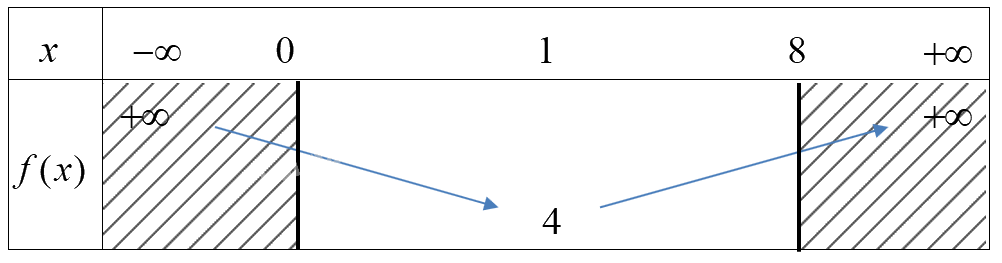
Mà \(f(0) = 7,f(8) = 151,f(1) = 4\)
\( \Rightarrow \) Trên [0;8]
Hàm số đạt GTLN bằng 151 tại \(x = 8\), đạt GTNN bằng 4 tại \(x = 1\).
Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 5 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kì đầu tiên. Đề thi này thường bao gồm các chủ đề chính như tập số thực, bất phương trình, hệ bất phương trình, hàm số bậc nhất và bậc hai, và các ứng dụng của chúng.
Cấu trúc đề thi có thể thay đổi tùy theo từng trường và giáo viên, nhưng nhìn chung, đề thi thường được chia thành hai phần chính:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 5:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 5, học sinh cần:
Ngoài việc luyện tập các đề thi, học sinh có thể tham khảo thêm các tài liệu ôn tập hữu ích sau:
Hãy dành thời gian ôn tập và luyện tập một cách nghiêm túc để đạt kết quả tốt nhất trong kỳ thi giữa kì 1 Toán 10 Chân trời sáng tạo - Đề số 5. Chúc các em học sinh thành công!