Chào mừng các em học sinh đến với đề kiểm tra học kì 2 môn Toán 10, đề số 4, chương trình Chân trời sáng tạo. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi với đầy đủ các dạng bài tập, từ cơ bản đến nâng cao, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải quyết vấn đề.
I. PHẦN TRẮC NGHIỆM ( 35 câu - 7,0 điểm ).
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1. Tập xác định của hàm số \(y = \frac{x}{{x - 2}}\) là
A. \(\mathbb{R}\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\mathbb{R}\backslash \left\{ 2 \right\}\).
D. \(\left( {2; + \infty } \right)\).
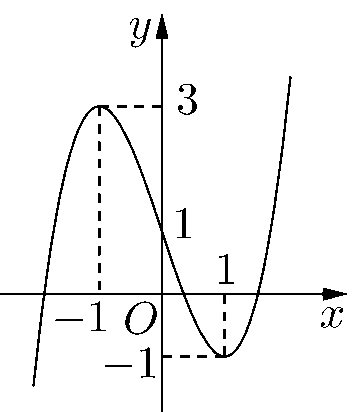
Câu 2. Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên
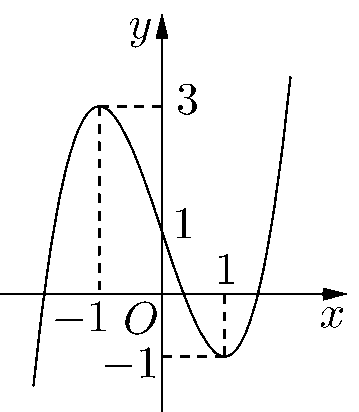
Điểm nào sau đây thuộc đồ thị hàm số ?
A. \(M\left( {1; - 1} \right)\).
B. \(N\left( { - 1;1} \right)\).
C. \(P\left( {1;0} \right)\).
D. \(Q\left( {3; - 1} \right)\).
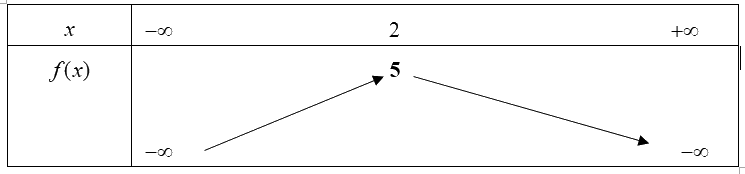
Câu 3. Cho hàm số bậc hai \(f(x)\)có bảng biến
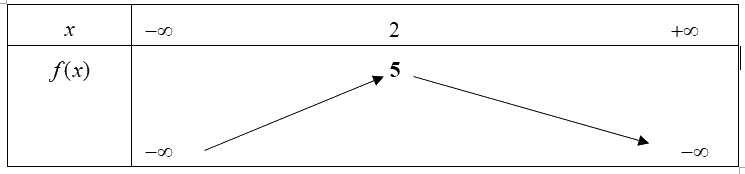
Hàm số \(f(x)\)đồng biến trên khoảng
A. \(\left( { - \infty ;5} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( {5; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Câu 4. Tọa độ đỉnh của Parabol \(y = {x^2} - 6x + 5\) là
A. \(I\left( {3; - 4} \right)\).
B. \(I\left( { - 3; - 4} \right)\).
C. \(I\left( { - 4;3} \right)\).
D. \(I\left( { - 6;5} \right)\).
Câu 5. Biểu thức nào sau đây là tam thức bậc hai
A. \(f\left( x \right) = 2{x^2} - 5x + 3\).
B. \(f\left( x \right) = 2x - 3\).
C. \(f\left( x \right) = 3{x^3} + 2{x^2} - x - 1\).
D. \(f\left( x \right) = {x^4} - {x^2} + 1\).
Câu 6. Cho tam thức bậc hai \(f(x) = 3 - 4x + {x^2}\) . Tìm tất cả giá trị của \(x\) để \(f\left( x \right) < 0\)
A. \(x \in \left( {1;3} \right).\)
B. \(x \in \left( { - \infty ;1} \right).\)
C. \(x \in \left( {3; + \infty } \right).\)
D. \(x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right).\)
Câu 7. Tập nghiệm của phương trình \(\sqrt {3{x^2} - 4x - 1} = \sqrt {2{x^2} - 4x + 3} \) là
A. \(\left\{ 2 \right\}\).
B. \(\left\{ { - 2} \right\}\).
C. \(\left\{ { - 2;2} \right\}\).
D. \(\emptyset \).
Câu 8. Tổng các nghiệm của phương trình \(\sqrt {2{x^2} + x + 3} = 1 - x\)
A. \( - 3\).
B. \(3\).
C. \( - 2\).
D. \(2\).
Câu 9. Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,2x - 3y + 1 = 0\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {2; - 3} \right)\).
B. \(\overrightarrow n = \left( {2;3} \right)\).
C. \(\overrightarrow n = \left( { - 3;2} \right)\).
D. \(\overrightarrow n = \left( {3;2} \right)\).
Câu 10. Đường thẳng \(\left( d \right):\,\,2x + 3y - 1 = 0\) đi qua điểm nào sau đây
A. \(A\left( {2; - 1} \right)\).
B. \(B\left( {2;5} \right)\).
C. \(C\left( {2;3} \right)\).
D. \(D\left( { - 1;2} \right)\).
Câu 11. Trong mặt phẳng \(Oxy\), phương trình đường thẳng \(\Delta \) đi qua điểm \(M(2;1)\)và có véc tơ pháp tuyến \(\overrightarrow n = \left( {3;\, - 4} \right)\) là
A. \(3x - 4y - 2 = 0\).
B. \(3x - 4y + 2 = 0\).
C. \( - 4x + 3y + 5 = 0\).
D. \(4x + 3y - 2 = 0\).
Câu 12. Tính góc giữa hai đường thẳng \(\Delta :\sqrt 3 x + y + 1 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\).
A. \({90^ \circ }\).
B. \({120^ \circ }\).
C. \({60^ \circ }\).
D. \({30^ \circ }\).
Câu 13. Khoảng cách từ điểm \(M\left( {3\,;\, - 2} \right)\) đến đường thẳng \(\Delta :\,\,4x - 3y + 2 = 0\) là:
A. \(5\).
B. \(4\).
C. \(\frac{8}{5}\).
D. \(\frac{{18}}{5}\).
Câu 14. Cho hai đường thẳng \(\Delta :4x - 2y + 3 = 0\) và \(\Delta ': - 2x + y + 3 = 0\). Khẳng định nào sau đây là đúng?
A. \(\Delta \) và \(\Delta '\)cắt nhau.
B. \(\Delta \) và \(\Delta '\)song song với nhau.
C. \(\Delta \) và \(\Delta '\)trùng nhau.
D. \(\Delta \) và \(\Delta '\)vuông góc với nhau.
Câu 15. Tọa độ tâm của đường tròn có phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) là
A. \(I\left( {2; - 3} \right)\).
B. \(I\left( {2;3} \right)\).
C. \(I\left( { - 2;3} \right)\).
D. \(I\left( { - 2; - 3} \right)\).
Câu 16. Bán kính của đường tròn có phương trình \({x^2} + {y^2} - 6x + 10y + 30 = 0\) là
A. \(2\).
B. \(4\).
C. \(16\).
D. \(6\).
Câu 17. Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - 2x + 4y - 4 = 0\).
B. \({x^2} + {y^2} + 6x - 2y + 15 = 0\).
C. \(2{x^2} + {y^2} - 8x + 10y - 1 = 0\).
D. \({x^2} + {y^2} + 5xy - 8y - 1 = 0.\).
Câu 18. Phương trình của đường tròn tâm \(I\left( { - 3;4} \right)\), bán kính bằng \(5\) là
A. \({\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = 25\).
B. \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\).
C. \({\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = 5\).
D. \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 5\).
Câu 19. Đường elip \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)có tiêu cự bằng
A. \(10\).
B. \(8\).
C. \(3\).
D. \(6\).
Câu 20. Tọa độ tiêu điểm của Parabol \(\left( P \right):\,{y^2} = 10x\) là
A. \(F\left( {5;0} \right)\).
B. \(F\left( {\frac{5}{2};0} \right)\).
C. \(F\left( { - 5;0} \right)\).
D. \(F\left( { - \frac{5}{2};0} \right)\).
Câu 21. Từ Đà Nẵng đi Hà Nội mỗi ngày có 7 chuyến tàu hỏa và 3 chuyến máy bay. Bạn Anh ở Đà nẵng muốn đi Hà Nội chơi vào ngày chủ nhật bằng tàu hỏa hoặc máy bay. Bạn Anh có bao nhiêu cách chọn chuyến đi ?
A. \(7\)
B. \(3\)
C. \(10\)
D. \(21\)
Câu 22. Có \(10\) cái bút khác nhau và \(8\) quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn \(1\) cái bút và \(1\) quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A. \(80\).
B. \(60\).
C. \(90\).
D. \(70\).
Câu 23. Một người vào một nhà hàng ăn, người đó chọn thực đơn 1 gồm một món chính và một món tráng miệng. Nhà hàng đưa ra danh sách: Món chính có 5 loại thịt và 3 loại cá; món tráng miệng có 4 loại quả và 3 loại bánh. Có bao nhiêu cách chọn một thực đơn?
A. \(15\)
B. \(27\)
C. \(56\)
D. \(180\)
Câu 24. Cho các số \(1\),\(5\), \(6\),\(7\). Có bao nhiêu số tự nhiên có \(4\) chữ số với các số khác nhau lập từ các số đã cho.
A. \(64\). B. \(24\). C. \(256\). D. \(12\).
Câu 25. Lớp \(10A\) có 42 học sinh. Đại hội Chi đoàn \(10A\)bầu ra một ban chấp hành gồm 1 Bí thư, 1 phó Bí thư và 1 Ủy viên ( Giả sử bạn nào cũng có năng lực như nhau). Chi đoàn \(10A\) có bao nhiêu cách bầu một ban chấp hành?
A. \(A_{42}^3\). B. \({P_{42}}\). C. \(C_{42}^3\). D. \({42^3}\).
Câu 26. Có bao nhiêu cách chọn hai học sinh đi dự trại hè từ một nhóm \(38\) học sinh?
A. \({2^{38}}\) B. \(C_{38}^2\) C. \({38^2}\) D. \(A_{38}^2\)
Câu 27. Ngân hàng đề thi gồm \(15\) câu hỏi trắc nghiệm khác nhau và \(8\) câu hỏi tự luận khác nhau. Hỏi có thể lập được bao nhiêu đề thi sao cho mỗi đề thi gồm 10 câu hỏi trắc nghiệm khác nhau và \(4\) câu hỏi tự luận khác nhau.
A. \(C_{15}^{10}.C_8^4\).
B. \(C_{15}^{10} + C_8^4\).
C. \(A_{15}^{10}.A_8^4\).
D. \(A_{15}^{10} + A_8^4\).
Câu 28. Một lớp có \(40\) học sinh gồm \(25\) nam và \(15\) nữ. Giáo viên chủ nhiệm muốn chọn \(4\) em trực cờ đỏ. Hỏi có bao nhiêu cách chọn nếu ít nhất phải có một nam?
A. \(C_{40}^4 - C_{15}^4\) (cách).
B. \(C_{25}^4\) (cách).
C. \(C_{25}^1C_{15}^3\) (cách).
D. \(C_{40}^4 + C_{15}^4\) (cách).
Câu 29. Có bao nhiêu số hạng trong khai triển nhị thức \({\left( {2021x + 2022} \right)^{2023}}\)
A. \(2021\). B. \(2022\). C. \(2023\). D. \(2024\).
Câu 30. Cho \(A\), \(B\) là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
A. \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)
B. \(P\left( {A \cup B} \right) = P\left( A \right).P\left( B \right)\)
C. \(P\left( {A \cup B} \right) = P\left( A \right) - P\left( B \right)\)
D. \(P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\)
Câu 31. Gieo một đồng tiền hai lần. Xác định biến cố: A: “ Lần đầu xuất hiện mặt ngửa”?
A. \(A = \left\{ {NS,NN} \right\}\)
B. \(A = \left\{ {NS,SN} \right\}\)
C.\(A = \left\{ {NN} \right\}\)
D. \(A = \left\{ {NS} \right\}\)
Câu 32. Gieo một con súc sắc hai lần. Số phần tử của không gian mẫu là?
A. \(6\). B. \(12\). C. \(18\). D. \(36\).
Câu 33. Gieo một con súc sắc cân đối và đồng chất một lần. Xác suất để mặt chấm là số nguyên tố xuất hiện là:
A. \(\frac{1}{5}\) B. \(\frac{3}{{10}}\). C. \(\frac{2}{5}\) D. \(\frac{1}{2}\).
Câu 34. Trên giá sách có \(4\) quyển sách Toán, \(3\) quyển sách Vật lý, \(3\) quyển sách Hoá học. Lấy ngẫu nhiên \(3\) quyển sách trên kệ sách ấy. Tính xác suất để \(3\) quyển được lấy ra đều là sách Toán.
A. \(\frac{1}{40}\). B. \(\frac{1}{{12}}\). C. \(\frac{{1}}{{30}}\). D. \(\frac{1}{{5}}\).
Câu 35. Một tổ học có 5 nam và 6 nữ. Giáo viên chủ nhiệm cần chọn ngẫu nhiên 3 người. Xác suất để chọn được ít nhất một nam là.
A. \(\frac{{29}}{{33}}\). B. \(\frac{{31}}{{33}}\). C. \(\frac{2}{{33}}\). D. \(\frac{4}{{33}}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36. Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Câu 37. Viết phương trình chính tắc đường elip \(\left( E \right)\) thãn mãn \(\left\{ {M \in \left( E \right)|\,M{F_1} + M{F_2} = 20} \right\}\), \({F_1}{F_2} = 12\)với \({F_1},\,{F_2}\,\)là các tiêu điểm của \(\left( E \right)\).
Câu 38. Xếp \(6\) học sinh nam và \(4\) học sinh nữ vào một dãy có \(10\) ghế xếp hàng ngang. Tính xác suất sao cho không có hai học sinh nữ nào ngồi cạnh nhau.
Câu 39. Trong mặt phẳng với hệ trục tọa độ \(Oxy,\) cho hình chữ nhật\(ABCD\) có \(AB = 2BC.\) Gọi \(M\) là trung điểm của đoạn \(AB\) và \(G\) là trọng tâm tam giác \(ACD.\) Viết phương trình đường thẳng \(AD,\) biết rằng \(M\left( {1;\;2} \right)\) và \(G\left( {\frac{5}{3};\;0} \right).\)
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Tập xác định của hàm số \(y = \frac{x}{{x - 2}}\) là
A. \(R\).
B. \(\left( { - \infty ;2} \right)\).
C. \(R\backslash \left\{ 2 \right\}\).
D. \(\left( {2; + \infty } \right)\).
Phương pháp
- Phân thức xác định khi mẫu thức khác 0
Lời giải
Chọn C
Điều kiện xác định: \(x - 2 \ne 0 \Leftrightarrow x \ne 2\)
Vậy tập xác định của hàm số \(y = \frac{x}{{x - 2}}\) là \(D = \mathbb{R}\backslash \left\{ 2 \right\}\)
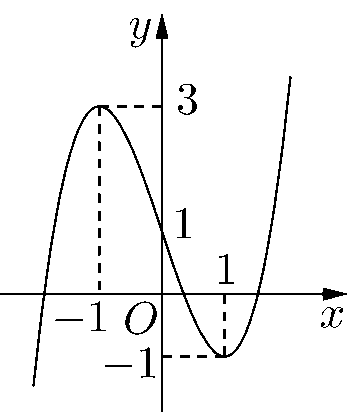
Câu 2: Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên
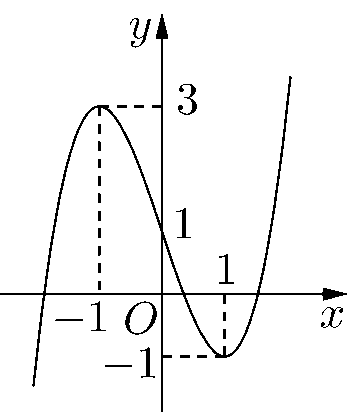
Điểm nào sau đây thuộc đồ thị hàm số ?
A. \(M\left( {1; - 1} \right)\).
B. \(N\left( { - 1;1} \right)\).
C. \(P\left( {1;0} \right)\).
D. \(Q\left( {3; - 1} \right)\).
Phương pháp
- Nhìn hình vẽ
Lời giải
Chọn A
Nhìn vào đồ thị ta thấy khi \(x = 1\) thì \(y = - 1\) nên điểm \(M\left( {1; - 1} \right)\) thuộc đồ thị của hàm số
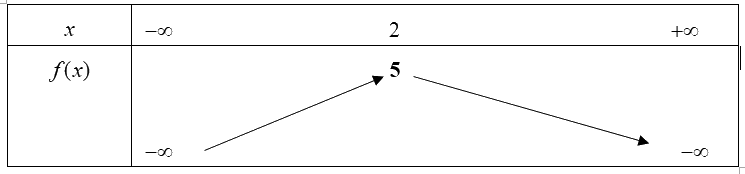
Câu 3: Cho hàm số bậc hai \(f(x)\)có bảng biến
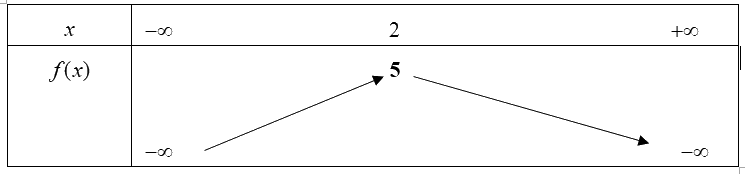
Hàm số \(f(x)\)đồng biến trên khoảng
A. \(\left( { - \infty ;5} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( {5; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Phương pháp
- Nhìn vào bảng biến thiên
Lời giải
Chọn B
Dựa vào bảng biến thiên ta thấy mũi tên đi lên khi \(x \in \left( { - \infty ;2} \right)\) nên hàm số đồng biến trên khoảng \(\left( { - \infty ;2} \right)\).
Câu 4: Tọa độ đỉnh của Parabol \(y = {x^2} - 6x + 5\) là
A. \(I\left( {3; - 4} \right)\).
B. \(I\left( { - 3; - 4} \right)\).
C. \(I\left( { - 4;3} \right)\).
D. \(I\left( { - 6;5} \right)\).
Phương pháp
Tọa độ đỉnh của Parabol là \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
Lời giải
Chọn A
Tọa độ đỉnh của Parabol là \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) nên \(I\left( {3; - 4} \right)\)
Câu 5: Biểu thức nào sau đây là tam thức bậc hai
A. \(f\left( x \right) = 2{x^2} - 5x + 3\).
B. \(f\left( x \right) = 2x - 3\).
C. \(f\left( x \right) = 3{x^3} + 2{x^2} - x - 1\).
D. \(f\left( x \right) = {x^4} - {x^2} + 1\).
Phương pháp
Tam thức bậc hai có dạng \(f(x) = a{x^2} + bx + c,\,a \ne 0\)
Lời giải
Chọn A
Tam thức bậc hai có dạng \(f(x) = a{x^2} + bx + c,\,a \ne 0\) nên chọn A.
Câu 6: Cho tam thức bậc hai \(f(x) = 3 - 4x + {x^2}\) . Tìm tất cả giá trị của \(x\) để \(f\left( x \right) < 0\)
A. \(x \in \left( {1;3} \right).\)
B. \(x \in \left( { - \infty ;1} \right).\)
C. \(x \in \left( {3; + \infty } \right).\)
D. \(x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right).\)
Phương pháp
Sử dụng dấu của tam thức bậc hai
Lời giải
Chọn A
Ta có \(f(x) = 0 \Rightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\), và a >0
Do đó \(f(x) < 0 \Rightarrow x \in \left( {1;3} \right)\).
Câu 7: Tập nghiệm của phương trình \(\sqrt {3{x^2} - 4x - 1} = \sqrt {2{x^2} - 4x + 3} \) là
A. \(\left\{ 2 \right\}\).
B. \(\left\{ { - 2} \right\}\).
C. \(\left\{ { - 2;2} \right\}\).
D. \(\emptyset \).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Chọn C
\(\begin{array}{l}\sqrt {3{x^2} - 4x - 1} = \sqrt {2{x^2} - 4x + 3} \Rightarrow 3{x^2} - 4x - 1 = 2{x^2} - 4x + 3\\ \Rightarrow {x^2} = 4 \Rightarrow x = \pm 2\end{array}\)
Thử lại thì \(x = \pm 2\) thõa mãn phương trình. Vậy phương trình có tập nghiệm \(\left\{ { - 2;2} \right\}\).
Câu 8: Tổng các nghiệm của phương trình \(\sqrt {2{x^2} + x + 3} = 1 - x\)
A. \( - 3\). B. \(3\). C. \( - 2\). D. \(2\).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Chọn A
Ta có
\(\begin{array}{l}\sqrt {2{x^2} + x + 3} = 1 - x \Rightarrow 2{x^2} + x + 3 = {\left( {1 - x} \right)^2}\\ \Rightarrow {x^2} + 3x + 2 = 0 \Rightarrow \left[ \begin{array}{l}x = - 1\\x = - 2\end{array} \right.\end{array}\)
Thử lại thõa mãn .
Vậy tổng hai nghiệm của phương trình là \( - 3.\)
Câu 9: Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,2x - 3y + 1 = 0\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {2; - 3} \right)\).
B. \(\overrightarrow n = \left( {2;3} \right)\).
C. \(\overrightarrow n = \left( { - 3;2} \right)\).
D. \(\overrightarrow n = \left( {3;2} \right)\).
Phương pháp
Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)
Lời giải
Chọn A
Véc tơ pháp tuyến của đường thẳng \(d:ax + by + c = 0\)là \(\overrightarrow n = \left( {a;b} \right)\). Vậy véc tơ pháp tuyến của đường thẳng \(\left( d \right):\,\,2x - 3y + 1 = 0\)là \(\overrightarrow n = \left( {2; - 3} \right)\).
Câu 10: Đường thẳng \(\left( d \right):\,\,2x + 3y - 1 = 0\) đi qua điểm nào sau đây
A. \(A\left( {2; - 1} \right)\).
B. \(B\left( {2;5} \right)\).
C. \(C\left( {2;3} \right)\).
D. \(D\left( { - 1;2} \right)\).
Phương pháp
Thay tọa độ các điểm ở đáp án vào phương trình đường thẳng (d)
Lời giải
Chọn A
Điểm \(M\left( {{x_0};{y_0}} \right) \in (d):ax + by + c = 0 \Leftrightarrow a{x_0} + b{y_0} + c = 0\).
Ta có \(2.2 + 3.\left( { - 1} \right) - 1 = 0\) nên \(A\left( {2; - 1} \right) \in \left( d \right).\)
Câu 11: Trong mặt phẳng \(Oxy\), phương trình đường thẳng \(\Delta \) đi qua điểm \(M(2;1)\)và có véc tơ pháp tuyến \(\overrightarrow n = \left( {3;\, - 4} \right)\) là
A. \(3x - 4y - 2 = 0\). B. \(3x - 4y + 2 = 0\). C. \( - 4x + 3y + 5 = 0\). D. \(4x + 3y - 2 = 0\).
Phương pháp
Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\)có véc tơ pháp tuyến \(\overrightarrow n = \left( {a;b} \right)\)là
\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Lời giải
Chọn A
Phương trình đường thẳng \(\Delta \) đi qua điểm \(M(2;1)\)và có véc tơ pháp tuyến \(\overrightarrow n = \left( {3;\, - 4} \right)\) là \(3\left( {x - 2} \right) - 4\left( {y - 1} \right) = 0 \Rightarrow 3x - 4y - 2 = 0\).
Câu 12: Tính góc giữa hai đường thẳng \(\Delta :\sqrt 3 x + y + 1 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\).
A. \({90^ \circ }\). B. \({120^ \circ }\). C. \({60^ \circ }\). D. \({30^ \circ }\).
Phương pháp
Áp dụng công thức tính góc giữa hai đường thẳng có: \(\cos \left( {{d_1},{d_2}} \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\).
Lời giải
Chọn D
Đường thẳng \(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {\sqrt 3 ;1} \right)\), đường thẳng \(\Delta '\) có vectơ pháp tuyến \(\overrightarrow {n'} = \left( {1;\sqrt 3 } \right)\).
Gọi \(\alpha \) là góc giữa hai đường thẳng \(\Delta ,\Delta '.\)\(\cos \alpha = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {\sqrt 3 + \sqrt 3 } \right|}}{{\sqrt {1 + 3} .\sqrt {1 + 3} }} = \frac{{\sqrt 3 }}{2} \Rightarrow \alpha = {30^ \circ }\).
Câu 13: Khoảng cách từ điểm \(M\left( {3\,;\, - 2} \right)\) đến đường thẳng \(\Delta :\,\,4x - 3y + 2 = 0\) là:
A. \(5\). B. \(4\). C. \(\frac{8}{5}\). D. \(\frac{{18}}{5}\).
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn B
Khoảng cách \(d = \frac{{\left| {4.3 - 3.\left( { - 2} \right) + 2} \right|}}{{\sqrt {{4^2} + {{( - 3)}^2}} }} = \frac{{20}}{5} = 4\).
Câu 14: Cho hai đường thẳng \(\Delta :4x - 2y + 3 = 0\) và \(\Delta ': - 2x + y + 3 = 0\). Khẳng định nào sau đây là đúng?
A. \(\Delta \) và \(\Delta '\)cắt nhau.
B. \(\Delta \) và \(\Delta '\)song song với nhau.
C. \(\Delta \) và \(\Delta '\)trùng nhau.
D. \(\Delta \) và \(\Delta '\)vuông góc với nhau.
Phương pháp
Sử dụng công thức vị trí tương đối của hai đường thẳng.
Lời giải
Chọn B
Ta có \(\frac{4}{{ - 2}} = \frac{{ - 2}}{1} \ne \frac{3}{3}\) nên \(\Delta \) và \(\Delta '\)song song với nhau.
Câu 15: Tọa độ tâm của đường tròn có phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) là
A. \(I\left( {2; - 3} \right)\).
B. \(I\left( {2;3} \right)\).
C. \(I\left( { - 2;3} \right)\).
D. \(I\left( { - 2; - 3} \right)\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn A
Đường tròn \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) có tâm \(I\left( {2; - 3} \right)\).
Câu 16: Bán kính của đường tròn có phương trình \({x^2} + {y^2} - 6x + 10y + 30 = 0\) là
A. \(2\). B. \(4\). C. \(16\). D. \(6\).
Phương pháp
Phương trình tổng quát của đường tròn có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(I\left( {a;\,\,b} \right)\) là tâm và bán kính được tính bằng công thức \(R = \sqrt {{a^2} + {b^2} - c} \)
Lời giải
Chọn A
Bán kính của đường tròn là \(r = \sqrt {{3^2} + {{( - 5)}^2} - 30} = 2\)
Câu 17: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - 2x + 4y - 4 = 0\). B. \({x^2} + {y^2} + 6x - 2y + 15 = 0\).
C. \(2{x^2} + {y^2} - 8x + 10y - 1 = 0\). D. \({x^2} + {y^2} + 5xy - 8y - 1 = 0.\)
Phương pháp
Phương trình tổng quát của đường tròn có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(I\left( {a;\,\,b} \right)\) là tâm và bán kính được tính bằng công thức \(R = \sqrt {{a^2} + {b^2} - c} \)
Lời giải
Chọn A
Vì \({1^2} + {\left( { - 2} \right)^2} - \left( { - 4} \right) = 9 > 0\)nên \({x^2} + {y^2} - 2x + 4y - 4 = 0\)là pt đường tròn
Vì \({\left( { - 3} \right)^2} + {1^2} - 15 = - 5 < 0\)nên \({x^2} + {y^2} + 6x - 2y + 15 = 0\) không phải pt đường tròn.
Hệ số của \({x^2},\,{y^2}\)khác nhau nên \(2{x^2} + {y^2} - 8x + 10y - 1 = 0\) không phải pt đường tròn.
Trong pt có chứa tích \(xy\) nên \({x^2} + {y^2} + 5xy - 8y - 1 = 0.\) không phải pt đường tròn.
Câu 18: Phương trình của đường tròn tâm \(I\left( { - 3;4} \right)\), bán kính bằng \(5\) là
A. \({\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = 25\).
B. \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\).
C. \({\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = 5\).
D. \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 5\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn B
Phương trình của đường tròn tâm \(I\left( { - 3;4} \right)\), bán kính bằng \(5\) là \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\).
Câu 19: Đường elip \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)có tiêu cự bằng
A. \(10\).B. \(8\). C. \(3\). D. \(6\).
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tiêu cự là 2c với \({c^2} = {a^2} - {b^2}\)
Lời giải
Chọn B
Ta có \({a^2} = 25,\,{b^2} = 9 \Rightarrow {c^2} = {a^2} - {b^2} = 16 \Rightarrow c = 4\).
Vậy tiêu cự của elip là \(2c = 8.\)
Câu 20: Tọa độ tiêu điểm của Parabol \(\left( P \right):\,{y^2} = 10x\) là
A. \(F\left( {5;0} \right)\).
B. \(F\left( {\frac{5}{2};0} \right)\).
C. \(F\left( { - 5;0} \right)\).
D. \(F\left( { - \frac{5}{2};0} \right)\).
Phương pháp
Tọa độ tiêu điểm của Parabol \(\left( P \right):\,{y^2} = 2px\) là \(F\left( {\frac{p}{2};0} \right)\)
Lời giải
Chọn B
Ta có \(2p = 10 \Rightarrow p = 5\). Vậy tọa độ tiêu điểm là \(F\left( {\frac{5}{2};0} \right)\).
Câu 21: Từ Đà Nẵng đi Hà Nội mỗi ngày có 7 chuyến tàu hỏa và 3 chuyến máy bay. Bạn Anh ở Đà nẵng muốn đi Hà Nội chơi vào ngày chủ nhật bằng tàu hỏa hoặc máy bay. Bạn Anh có bao nhiêu cách chọn chuyến đi ?
A. \(7\). B. \(3\). C. \(10\). D. \(21\).
Phương pháp
Áp dụng quy tắc cộng
Lời giải
Chọn C
Theo quy tắc cộng, Bạn Anh có số cách chọn chuyến đi là \(7 + 3 = 10\).
Câu 22: Có \(10\) cái bút khác nhau và \(8\) quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn \(1\) cái bút và \(1\) quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A. \(80\). B. \(60\). C. \(90\). D. \(70\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn A
Theo quy tắc nhân, Bạn học sinh có số cách chọn là \(10.8 = 80\)cách
Câu 23: Một người vào một nhà hàng ăn, người đó chọn thực đơn 1 gồm một món chính và một món tráng miệng. Nhà hàng đưa ra danh sách: Món chính có 5 loại thịt và 3 loại cá; món tráng miệng có 4 loại quả và 3 loại bánh. Có bao nhiêu cách chọn một thực đơn?
A. \(15\). B. \(27\). C. \(56\). D. \(180\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn C
Số cách chọn món chính: \(5 + 3 = 8.\)
Số cách chọn món tráng miệng: \(4 + 3 = 7.\)
Số cách chọn một thực đơn là \(8.7 = 56\).
Câu 24: Cho các số \(1\),\(5\), \(6\),\(7\). Có bao nhiêu số tự nhiên có \(4\) chữ số với các số khác nhau lập từ các số đã cho.
A. \(64\). B. \(24\). C. \(256\). D. \(12\).
Phương pháp
Áp dụng công thức hoán vị
Lời giải
Chọn B
Mỗi số tự nhiên gồm 4 chữ số khác nhau được lập từ \(1\),\(5\), \(6\),\(7\)là một hoán vị 4 phần tử. Do đó số các số tự nhiên gồm 4 chữ số khác nhau được lập là \(4! = 24\).
Câu 25: Lớp \(10A\) có 42 học sinh. Đại hội Chi đoàn \(10A\)bầu ra một ban chấp hành gồm 1 Bí thư, 1 phó Bí thư và 1 Ủy viên ( Giả sử bạn nào cũng có năng lực như nhau). Chi đoàn \(10A\) có bao nhiêu cách bầu một ban chấp hành?
A. \(A_{42}^3\). B. \({P_{42}}\). C. \(C_{42}^3\). D. \({42^3}\).
Phương pháp
Áp dụng công thức chỉnh hợp
Lời giải
Chọn A
Mỗi cách bầu một BCH gồm 3 bạn là một chỉnh hợp chập 3 của 42 phần tử. Vậy số cách bầu là \(A_{42}^3\).
Câu 26: Có bao nhiêu cách chọn hai học sinh đi dự trại hè từ một nhóm \(38\) học sinh?
A. \({2^{38}}\). B. \(C_{38}^2\). C. \({38^2}\). D. \(A_{38}^2\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn B
Mỗi cách chọn 2 học sinh từ 38 học sinh là một tổ hợp chập 2 của 38 phần tử. Vậy số cách chọn là \(C_{38}^2\).
Câu 27: Ngân hàng đề thi gồm \(15\) câu hỏi trắc nghiệm khác nhau và \(8\) câu hỏi tự luận khác nhau. Hỏi có thể lập được bao nhiêu đề thi sao cho mỗi đề thi gồm 10 câu hỏi trắc nghiệm khác nhau và \(4\) câu hỏi tự luận khác nhau.
A. \(C_{15}^{10}.C_8^4\).
B. \(C_{15}^{10} + C_8^4\).
C. \(A_{15}^{10}.A_8^4\).
D. \(A_{15}^{10} + A_8^4\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn A
Số cách chọn 10 câu hỏi trắc nghiệm là \(C_{15}^{10}\)
Số cách chọn câu hỏi tự luận là \(C_8^4\)
Vậy số cách lập đề thi là \(C_{15}^{10}.C_8^4\).
Câu 28: Một lớp có \(40\) học sinh gồm \(25\) nam và \(15\) nữ. Giáo viên chủ nhiệm muốn chọn \(4\) em trực cờ đỏ. Hỏi có bao nhiêu cách chọn nếu ít nhất phải có một nam?
A. \(C_{40}^4 - C_{15}^4\) (cách).
B. \(C_{25}^4\) (cách).
C. \(C_{25}^1C_{15}^3\) (cách).
D. \(C_{40}^4 + C_{15}^4\) (cách).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn A
Số cách chọn 4 bạn trong 40 bạn là \(C_{40}^4\)
Số cách chọn bốn bạn nữ trong 15 bạn nữ là \(C_{15}^4\)
Vậy số cách chọn 4 bạn có ít nhất 1 nam là: \(C_{40}^4 - C_{15}^4\).
Câu 29: Có bao nhiêu số hạng trong khai triển nhị thức \({\left( {2021x + 2022} \right)^{2023}}\)
A. \(2021\). B. \(2022\). C. \(2023\). D. \(2024\).
Phương pháp
Áp dụng khai triển công thức nhị thức Newton
Lời giải
Chọn D
Tổng số số hạng của khai triển \({\left( {2021x + 2022} \right)^{2023}}\) là \(2023 + 1 = 2024.\)
Câu 30: Cho \(A\), \(B\) là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
A. \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
B. \(P\left( {A \cup B} \right) = P\left( A \right).P\left( B \right)\).
C. \(P\left( {A \cup B} \right) = P\left( A \right) - P\left( B \right)\).
D. \(P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\).
Phương pháp
Do \(A,\,B\) xung khắc nên \(A \cap B = \emptyset \). Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Lời giải
Chọn A
Do \(A,\,B\) xung khắc nên \(A \cap B = \emptyset \). Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Câu 31: Gieo một đồng tiền hai lần. Xác định biến cố: \(A\): “ Lần đầu xuất hiện mặt ngửa”?
A. \(A = \left\{ {NS,NN} \right\}\).
B. \(A = \left\{ {NS,SN} \right\}\).
C.\(A = \left\{ {NN} \right\}\).
D. \(A = \left\{ {NS} \right\}\).
Phương pháp
Sử dụng quy tắc đếm.
Lời giải
Chọn A
Ta có không gian mẫu: \(\Omega = \left\{ {SS,SN,NN,NS} \right\}\)
\(A\): “ Lần đầu xuất hiện mặt ngửa” nên \(A = \left\{ {NS,NN} \right\}\).
Câu 32: Gieo một con xúc xắc hai lần. Số phần tử của không gian mẫu là?
A. \(6\). B. \(12\). C. \(18\). D. \(36\).
Phương pháp
Sử dụng quy tắc đếm.
Lời giải
Chọn D
Ta có \(n\left( \Omega \right) = 6.6 = 36\).
Câu 33: Gieo một con xúc xắc cân đối và đồng chất một lần. Xác suất để mặt chấm là số nguyên tố xuất hiện là:
A. \(\frac{1}{5}\) B. \(\frac{3}{{10}}\). C. \(\frac{2}{5}\) D. \(\frac{1}{2}\).
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Chọn D
Ta có \(\Omega = \left\{ {1;2;3;4;5;6} \right\},\,\,n\left( \Omega \right) = 6\)
Gọi biến cố \(A\): “Mặt chấm là số nguyên tố” suy ra \(A = \left\{ {2;3;5} \right\}\), \(n(A) = 3\)
Xác suất của biến cố \(A\) là \(P\left( A \right) = \frac{{n(A)}}{{n\left( \Omega \right)}} = \frac{3}{6} = \frac{1}{2}\).
Câu 34: Trên giá sách có \(4\) quyển sách Toán, \(3\) quyển sách Vật lý, \(3\) quyển sách Hoá học. Lấy ngẫu nhiên \(3\) quyển sách trên kệ sách ấy. Tính xác suất để \(3\) quyển được lấy ra đều là sách Toán.
A. \(\frac{1}{{40}}\). B. \(\frac{1}{{12}}\). C. \(\frac{1}{{30}}\). D. \(\frac{1}{5}\).
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Chọn C
Số cách lấy \(3\) quyển sách là \(n\left( \Omega \right) = C_{10}^3 = 120\)
Số cách lấy \(3\) quyển sách toán là \(n\left( A \right) = C_4^3 = 4\).
Vậy xác suất để \(3\) quyển được lấy ra đều là sách Toán là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{{120}} = \frac{1}{{30}}\)
Câu 35: Một tổ học có 5 nam và 6 nữ. Giáo viên chủ nhiệm cần chọn ngẫu nhiên 3 người. Xác suất để chọn được ít nhất một nam là.
A. \(\frac{{29}}{{33}}\). B. \(\frac{{31}}{{33}}\). C. \(\frac{2}{{33}}\). D. \(\frac{4}{{33}}\).
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Chọn A
Số cách chọn \(3\)bạn trong 11 bạn là \(n\left( \Omega \right) = C_{11}^3 = 165\)
Số cách chọn \(3\)bạn có ít nhất một nam là \(n\left( A \right) = C_{11}^3 - C_6^3 = 145\)
Xác suất chọn 3 bạn có ít nhất một nam là:
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{145}}{{165}} = \frac{{29}}{{33}}\) .
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36. Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Phương pháp
Bình phương hai vế của phương trình đã cho để đưa về giải phương trình bậc hai
Lời giải
Bình phương hai vế của phương trình ta được:
\(2{x^2} - 5x - 9 = {x^2} - 2x + 1\).
Sau khi thu gọn ta được \({x^2} - 3x - 10 = 0\).
Từ đó tìm được \(x = - 2\) hoặc \(x = 5\).
Thay lần lượt hai giá trị này của \(x\) vào phương trình đã cho, ta thấy chỉ có \(x = 5\) thỏa mãn.
Vậy nghiệm của phương trình đã cho là \(x = 5\).
Câu 37. Viết phương trình chính tắc đường elip \(\left( E \right)\) thỏa mãn \(\left\{ {M \in \left( E \right)|\,M{F_1} + M{F_2} = 20} \right\}\), \({F_1}{F_2} = 12\)với \({F_1},\,{F_2}\,\)là các tiêu điểm của \(\left( E \right)\).
Phương pháp
Phương trình chính tắc của \(\left( E \right)\) là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\).
Lời giải
Ta có:
\(\begin{array}{l}M \in (E) \Rightarrow M{F_1} + M{F_2} = 2a \Rightarrow 2a = 20 \Rightarrow a = 10\\{F_1}{F_2} = 2c \Rightarrow 2c = 12 \Rightarrow c = 6\end{array}\)
Vậy phương trình chính tắc của \(\left( E \right)\) là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\).
Câu 38. Xếp \(6\) học sinh nam và \(4\) học sinh nữ vào một dãy có \(10\) ghế xếp hàng ngang. Tính xác suất sao cho không có hai học sinh nữ nào ngồi cạnh nhau.
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Ta có \(n\left( \Omega \right) = 10! = 3628800.\)
Gọi biến cố A: “ Không có hai học sinh nữ nào ngồi cạnh nhau”
Số cách xếp \(6\) học sinh nam thành hàng ngang là \(6! = 720\) cách.
Ứng với mỗi cách sắp xếp này, ta có \(7\) khoảng trống (\(2\) khoảng trống ở hai đầu và \(5\) khoảng trống ở giữa). Xếp \(4\) học sinh nữ vào các khoảng trống đó, có \(A_7^4 = 840\) cách.
Suy ra \(n\left( A \right) = 720.840 = 604800\). Do đó \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{604800}}{{3628800}} = \frac{1}{6}.\)
Câu 39. Trong mặt phẳng với hệ trục tọa độ \(Oxy,\) cho hình chữ nhật\(ABCD\) có \(AB = 2BC.\) Gọi \(M\) là trung điểm của đoạn \(AB\) và \(G\) là trọng tâm tam giác \(ACD.\) Viết phương trình đường thẳng \(AD,\) biết rằng \(M\left( {1;\;2} \right)\) và \(G\left( {\frac{5}{3};\;0} \right).\)
Phương pháp
Đường thẳng cần viết phương trình đi qua \(A({x_0};{y_0})\)và vecto pháp tuyến là \(\overrightarrow n = (a,b)\) nên có phương trình tổng quát \(a(x - {x_0}) + b(y - {y_0}) = 0\)
Lời giải
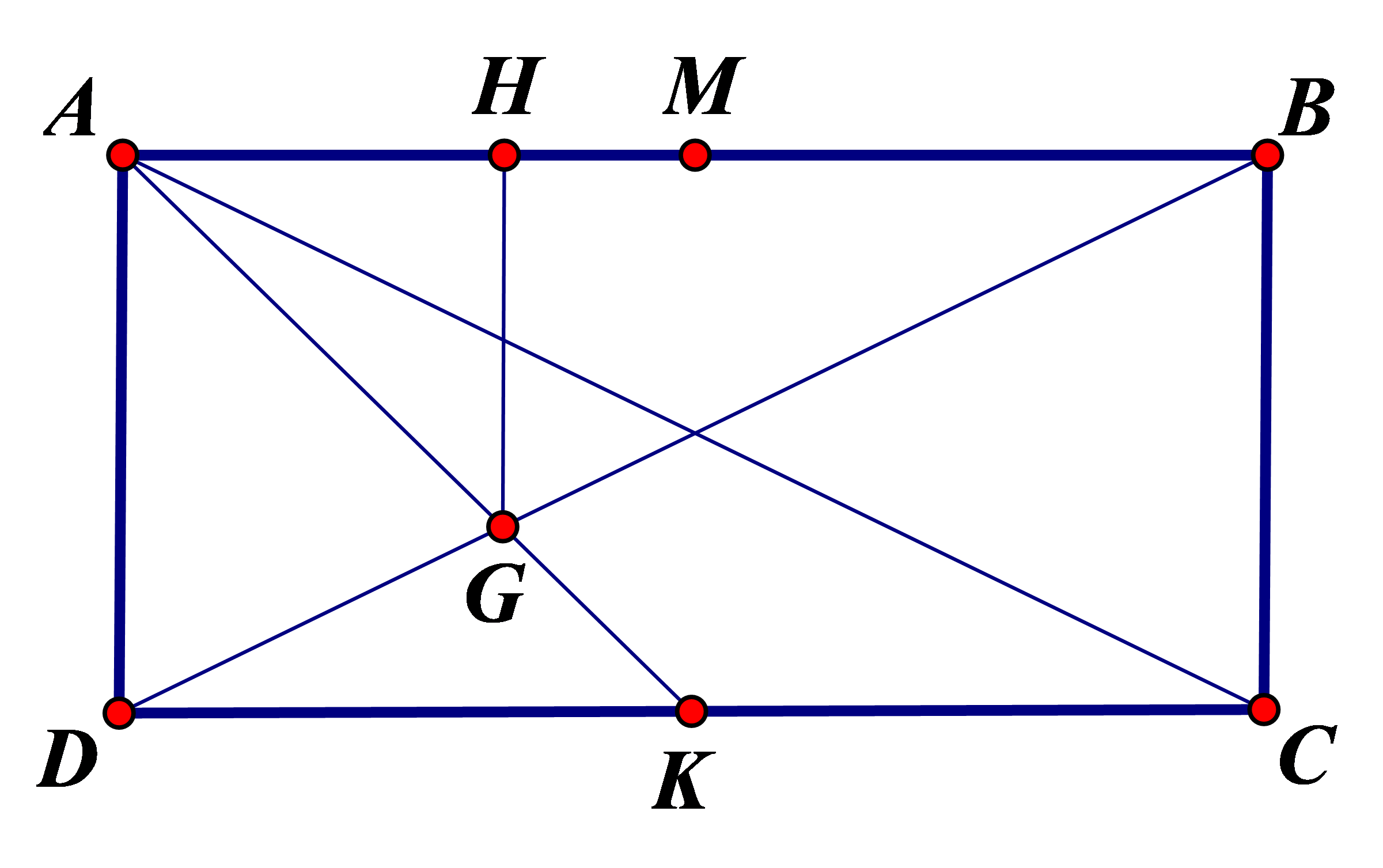
Gọi \(H\) là hình chiếu vuông góc của \(G\) lên \(AB\) và \(K\) là trung điểm đoạn \(CD.\)
Đặt \(BC = 3a > 0,\) suy ra \(AB = 6a,\;GH = 2a,\;HM = a.\)
\(M{G^2} = 4{a^2} + {a^2} \Leftrightarrow \frac{{40}}{9} = 5{a^2} \Leftrightarrow {a^2} = \frac{8}{9} \Leftrightarrow a = \frac{{2\sqrt 2 }}{3}.\)
Suy ra \(AM = 3a = 2\sqrt 2 ,\)\(AG = \frac{2}{3}AK = \frac{2}{3}\left( {3a\sqrt 2 } \right) = \frac{8}{3}.\)
Gọi \(A(x,y)\). Khi đó : \(\left\{ {\begin{array}{*{20}{c}}{AM = 2\sqrt 2 }\\{AG = \frac{8}{3}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\left( {1 - x} \right)}^2} + {{\left( {2 - y} \right)}^2} = 8}\\{{{\left( {\frac{5}{3} - x} \right)}^2} + {y^2} = \frac{{64}}{9}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x^2} + {y^2} - 2x - 4y = 3}\\{x = 3y - 1}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 3y - 1}\\{\left[ {\begin{array}{*{20}{c}}{y = 0}\\{y = \frac{8}{5}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1,y = 0}\\{x = \frac{{19}}{5},y = \frac{8}{5}}\end{array}} \right.\)
+) Nếu \(A\left( { - 1,0} \right)\). Đường thẳng \(AD\) đi qua \(A\) và vuông góc với đường thẳng \(AM\) nên phương trình đường thẳng \(AD\) là \(x + y + 1 = 0.\)
+) Nếu \(A\left( {\frac{{19}}{5},\frac{8}{5}} \right)\). Đường thẳng \(AD\) đi qua \(A\) và vuông góc với đường thẳng \(AM\) nên phương trình đường thẳng \(AD\) là \(7x - y - 25 = 0.\)
---------- HẾT ----------
Tải về
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1. Tập xác định của hàm số \(y = \frac{x}{{x - 2}}\) là
A. \(\mathbb{R}\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\mathbb{R}\backslash \left\{ 2 \right\}\).
D. \(\left( {2; + \infty } \right)\).
Câu 2. Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên
Điểm nào sau đây thuộc đồ thị hàm số ?
A. \(M\left( {1; - 1} \right)\).
B. \(N\left( { - 1;1} \right)\).
C. \(P\left( {1;0} \right)\).
D. \(Q\left( {3; - 1} \right)\).
Câu 3. Cho hàm số bậc hai \(f(x)\)có bảng biến
Hàm số \(f(x)\)đồng biến trên khoảng
A. \(\left( { - \infty ;5} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( {5; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Câu 4. Tọa độ đỉnh của Parabol \(y = {x^2} - 6x + 5\) là
A. \(I\left( {3; - 4} \right)\).
B. \(I\left( { - 3; - 4} \right)\).
C. \(I\left( { - 4;3} \right)\).
D. \(I\left( { - 6;5} \right)\).
Câu 5. Biểu thức nào sau đây là tam thức bậc hai
A. \(f\left( x \right) = 2{x^2} - 5x + 3\).
B. \(f\left( x \right) = 2x - 3\).
C. \(f\left( x \right) = 3{x^3} + 2{x^2} - x - 1\).
D. \(f\left( x \right) = {x^4} - {x^2} + 1\).
Câu 6. Cho tam thức bậc hai \(f(x) = 3 - 4x + {x^2}\) . Tìm tất cả giá trị của \(x\) để \(f\left( x \right) < 0\)
A. \(x \in \left( {1;3} \right).\)
B. \(x \in \left( { - \infty ;1} \right).\)
C. \(x \in \left( {3; + \infty } \right).\)
D. \(x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right).\)
Câu 7. Tập nghiệm của phương trình \(\sqrt {3{x^2} - 4x - 1} = \sqrt {2{x^2} - 4x + 3} \) là
A. \(\left\{ 2 \right\}\).
B. \(\left\{ { - 2} \right\}\).
C. \(\left\{ { - 2;2} \right\}\).
D. \(\emptyset \).
Câu 8. Tổng các nghiệm của phương trình \(\sqrt {2{x^2} + x + 3} = 1 - x\)
A. \( - 3\).
B. \(3\).
C. \( - 2\).
D. \(2\).
Câu 9. Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,2x - 3y + 1 = 0\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {2; - 3} \right)\).
B. \(\overrightarrow n = \left( {2;3} \right)\).
C. \(\overrightarrow n = \left( { - 3;2} \right)\).
D. \(\overrightarrow n = \left( {3;2} \right)\).
Câu 10. Đường thẳng \(\left( d \right):\,\,2x + 3y - 1 = 0\) đi qua điểm nào sau đây
A. \(A\left( {2; - 1} \right)\).
B. \(B\left( {2;5} \right)\).
C. \(C\left( {2;3} \right)\).
D. \(D\left( { - 1;2} \right)\).
Câu 11. Trong mặt phẳng \(Oxy\), phương trình đường thẳng \(\Delta \) đi qua điểm \(M(2;1)\)và có véc tơ pháp tuyến \(\overrightarrow n = \left( {3;\, - 4} \right)\) là
A. \(3x - 4y - 2 = 0\).
B. \(3x - 4y + 2 = 0\).
C. \( - 4x + 3y + 5 = 0\).
D. \(4x + 3y - 2 = 0\).
Câu 12. Tính góc giữa hai đường thẳng \(\Delta :\sqrt 3 x + y + 1 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\).
A. \({90^ \circ }\).
B. \({120^ \circ }\).
C. \({60^ \circ }\).
D. \({30^ \circ }\).
Câu 13. Khoảng cách từ điểm \(M\left( {3\,;\, - 2} \right)\) đến đường thẳng \(\Delta :\,\,4x - 3y + 2 = 0\) là:
A. \(5\).
B. \(4\).
C. \(\frac{8}{5}\).
D. \(\frac{{18}}{5}\).
Câu 14. Cho hai đường thẳng \(\Delta :4x - 2y + 3 = 0\) và \(\Delta ': - 2x + y + 3 = 0\). Khẳng định nào sau đây là đúng?
A. \(\Delta \) và \(\Delta '\)cắt nhau.
B. \(\Delta \) và \(\Delta '\)song song với nhau.
C. \(\Delta \) và \(\Delta '\)trùng nhau.
D. \(\Delta \) và \(\Delta '\)vuông góc với nhau.
Câu 15. Tọa độ tâm của đường tròn có phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) là
A. \(I\left( {2; - 3} \right)\).
B. \(I\left( {2;3} \right)\).
C. \(I\left( { - 2;3} \right)\).
D. \(I\left( { - 2; - 3} \right)\).
Câu 16. Bán kính của đường tròn có phương trình \({x^2} + {y^2} - 6x + 10y + 30 = 0\) là
A. \(2\).
B. \(4\).
C. \(16\).
D. \(6\).
Câu 17. Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - 2x + 4y - 4 = 0\).
B. \({x^2} + {y^2} + 6x - 2y + 15 = 0\).
C. \(2{x^2} + {y^2} - 8x + 10y - 1 = 0\).
D. \({x^2} + {y^2} + 5xy - 8y - 1 = 0.\).
Câu 18. Phương trình của đường tròn tâm \(I\left( { - 3;4} \right)\), bán kính bằng \(5\) là
A. \({\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = 25\).
B. \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\).
C. \({\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = 5\).
D. \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 5\).
Câu 19. Đường elip \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)có tiêu cự bằng
A. \(10\).
B. \(8\).
C. \(3\).
D. \(6\).
Câu 20. Tọa độ tiêu điểm của Parabol \(\left( P \right):\,{y^2} = 10x\) là
A. \(F\left( {5;0} \right)\).
B. \(F\left( {\frac{5}{2};0} \right)\).
C. \(F\left( { - 5;0} \right)\).
D. \(F\left( { - \frac{5}{2};0} \right)\).
Câu 21. Từ Đà Nẵng đi Hà Nội mỗi ngày có 7 chuyến tàu hỏa và 3 chuyến máy bay. Bạn Anh ở Đà nẵng muốn đi Hà Nội chơi vào ngày chủ nhật bằng tàu hỏa hoặc máy bay. Bạn Anh có bao nhiêu cách chọn chuyến đi ?
A. \(7\)
B. \(3\)
C. \(10\)
D. \(21\)
Câu 22. Có \(10\) cái bút khác nhau và \(8\) quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn \(1\) cái bút và \(1\) quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A. \(80\).
B. \(60\).
C. \(90\).
D. \(70\).
Câu 23. Một người vào một nhà hàng ăn, người đó chọn thực đơn 1 gồm một món chính và một món tráng miệng. Nhà hàng đưa ra danh sách: Món chính có 5 loại thịt và 3 loại cá; món tráng miệng có 4 loại quả và 3 loại bánh. Có bao nhiêu cách chọn một thực đơn?
A. \(15\)
B. \(27\)
C. \(56\)
D. \(180\)
Câu 24. Cho các số \(1\),\(5\), \(6\),\(7\). Có bao nhiêu số tự nhiên có \(4\) chữ số với các số khác nhau lập từ các số đã cho.
A. \(64\). B. \(24\). C. \(256\). D. \(12\).
Câu 25. Lớp \(10A\) có 42 học sinh. Đại hội Chi đoàn \(10A\)bầu ra một ban chấp hành gồm 1 Bí thư, 1 phó Bí thư và 1 Ủy viên ( Giả sử bạn nào cũng có năng lực như nhau). Chi đoàn \(10A\) có bao nhiêu cách bầu một ban chấp hành?
A. \(A_{42}^3\). B. \({P_{42}}\). C. \(C_{42}^3\). D. \({42^3}\).
Câu 26. Có bao nhiêu cách chọn hai học sinh đi dự trại hè từ một nhóm \(38\) học sinh?
A. \({2^{38}}\) B. \(C_{38}^2\) C. \({38^2}\) D. \(A_{38}^2\)
Câu 27. Ngân hàng đề thi gồm \(15\) câu hỏi trắc nghiệm khác nhau và \(8\) câu hỏi tự luận khác nhau. Hỏi có thể lập được bao nhiêu đề thi sao cho mỗi đề thi gồm 10 câu hỏi trắc nghiệm khác nhau và \(4\) câu hỏi tự luận khác nhau.
A. \(C_{15}^{10}.C_8^4\).
B. \(C_{15}^{10} + C_8^4\).
C. \(A_{15}^{10}.A_8^4\).
D. \(A_{15}^{10} + A_8^4\).
Câu 28. Một lớp có \(40\) học sinh gồm \(25\) nam và \(15\) nữ. Giáo viên chủ nhiệm muốn chọn \(4\) em trực cờ đỏ. Hỏi có bao nhiêu cách chọn nếu ít nhất phải có một nam?
A. \(C_{40}^4 - C_{15}^4\) (cách).
B. \(C_{25}^4\) (cách).
C. \(C_{25}^1C_{15}^3\) (cách).
D. \(C_{40}^4 + C_{15}^4\) (cách).
Câu 29. Có bao nhiêu số hạng trong khai triển nhị thức \({\left( {2021x + 2022} \right)^{2023}}\)
A. \(2021\). B. \(2022\). C. \(2023\). D. \(2024\).
Câu 30. Cho \(A\), \(B\) là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
A. \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)
B. \(P\left( {A \cup B} \right) = P\left( A \right).P\left( B \right)\)
C. \(P\left( {A \cup B} \right) = P\left( A \right) - P\left( B \right)\)
D. \(P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\)
Câu 31. Gieo một đồng tiền hai lần. Xác định biến cố: A: “ Lần đầu xuất hiện mặt ngửa”?
A. \(A = \left\{ {NS,NN} \right\}\)
B. \(A = \left\{ {NS,SN} \right\}\)
C.\(A = \left\{ {NN} \right\}\)
D. \(A = \left\{ {NS} \right\}\)
Câu 32. Gieo một con súc sắc hai lần. Số phần tử của không gian mẫu là?
A. \(6\). B. \(12\). C. \(18\). D. \(36\).
Câu 33. Gieo một con súc sắc cân đối và đồng chất một lần. Xác suất để mặt chấm là số nguyên tố xuất hiện là:
A. \(\frac{1}{5}\) B. \(\frac{3}{{10}}\). C. \(\frac{2}{5}\) D. \(\frac{1}{2}\).
Câu 34. Trên giá sách có \(4\) quyển sách Toán, \(3\) quyển sách Vật lý, \(3\) quyển sách Hoá học. Lấy ngẫu nhiên \(3\) quyển sách trên kệ sách ấy. Tính xác suất để \(3\) quyển được lấy ra đều là sách Toán.
A. \(\frac{1}{40}\). B. \(\frac{1}{{12}}\). C. \(\frac{{1}}{{30}}\). D. \(\frac{1}{{5}}\).
Câu 35. Một tổ học có 5 nam và 6 nữ. Giáo viên chủ nhiệm cần chọn ngẫu nhiên 3 người. Xác suất để chọn được ít nhất một nam là.
A. \(\frac{{29}}{{33}}\). B. \(\frac{{31}}{{33}}\). C. \(\frac{2}{{33}}\). D. \(\frac{4}{{33}}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36. Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Câu 37. Viết phương trình chính tắc đường elip \(\left( E \right)\) thãn mãn \(\left\{ {M \in \left( E \right)|\,M{F_1} + M{F_2} = 20} \right\}\), \({F_1}{F_2} = 12\)với \({F_1},\,{F_2}\,\)là các tiêu điểm của \(\left( E \right)\).
Câu 38. Xếp \(6\) học sinh nam và \(4\) học sinh nữ vào một dãy có \(10\) ghế xếp hàng ngang. Tính xác suất sao cho không có hai học sinh nữ nào ngồi cạnh nhau.
Câu 39. Trong mặt phẳng với hệ trục tọa độ \(Oxy,\) cho hình chữ nhật\(ABCD\) có \(AB = 2BC.\) Gọi \(M\) là trung điểm của đoạn \(AB\) và \(G\) là trọng tâm tam giác \(ACD.\) Viết phương trình đường thẳng \(AD,\) biết rằng \(M\left( {1;\;2} \right)\) và \(G\left( {\frac{5}{3};\;0} \right).\)
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Tập xác định của hàm số \(y = \frac{x}{{x - 2}}\) là
A. \(R\).
B. \(\left( { - \infty ;2} \right)\).
C. \(R\backslash \left\{ 2 \right\}\).
D. \(\left( {2; + \infty } \right)\).
Phương pháp
- Phân thức xác định khi mẫu thức khác 0
Lời giải
Chọn C
Điều kiện xác định: \(x - 2 \ne 0 \Leftrightarrow x \ne 2\)
Vậy tập xác định của hàm số \(y = \frac{x}{{x - 2}}\) là \(D = \mathbb{R}\backslash \left\{ 2 \right\}\)
Câu 2: Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên
Điểm nào sau đây thuộc đồ thị hàm số ?
A. \(M\left( {1; - 1} \right)\).
B. \(N\left( { - 1;1} \right)\).
C. \(P\left( {1;0} \right)\).
D. \(Q\left( {3; - 1} \right)\).
Phương pháp
- Nhìn hình vẽ
Lời giải
Chọn A
Nhìn vào đồ thị ta thấy khi \(x = 1\) thì \(y = - 1\) nên điểm \(M\left( {1; - 1} \right)\) thuộc đồ thị của hàm số
Câu 3: Cho hàm số bậc hai \(f(x)\)có bảng biến
Hàm số \(f(x)\)đồng biến trên khoảng
A. \(\left( { - \infty ;5} \right)\).
B. \(\left( { - \infty ;2} \right)\).
C. \(\left( {5; + \infty } \right)\).
D. \(\left( {2; + \infty } \right)\).
Phương pháp
- Nhìn vào bảng biến thiên
Lời giải
Chọn B
Dựa vào bảng biến thiên ta thấy mũi tên đi lên khi \(x \in \left( { - \infty ;2} \right)\) nên hàm số đồng biến trên khoảng \(\left( { - \infty ;2} \right)\).
Câu 4: Tọa độ đỉnh của Parabol \(y = {x^2} - 6x + 5\) là
A. \(I\left( {3; - 4} \right)\).
B. \(I\left( { - 3; - 4} \right)\).
C. \(I\left( { - 4;3} \right)\).
D. \(I\left( { - 6;5} \right)\).
Phương pháp
Tọa độ đỉnh của Parabol là \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
Lời giải
Chọn A
Tọa độ đỉnh của Parabol là \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) nên \(I\left( {3; - 4} \right)\)
Câu 5: Biểu thức nào sau đây là tam thức bậc hai
A. \(f\left( x \right) = 2{x^2} - 5x + 3\).
B. \(f\left( x \right) = 2x - 3\).
C. \(f\left( x \right) = 3{x^3} + 2{x^2} - x - 1\).
D. \(f\left( x \right) = {x^4} - {x^2} + 1\).
Phương pháp
Tam thức bậc hai có dạng \(f(x) = a{x^2} + bx + c,\,a \ne 0\)
Lời giải
Chọn A
Tam thức bậc hai có dạng \(f(x) = a{x^2} + bx + c,\,a \ne 0\) nên chọn A.
Câu 6: Cho tam thức bậc hai \(f(x) = 3 - 4x + {x^2}\) . Tìm tất cả giá trị của \(x\) để \(f\left( x \right) < 0\)
A. \(x \in \left( {1;3} \right).\)
B. \(x \in \left( { - \infty ;1} \right).\)
C. \(x \in \left( {3; + \infty } \right).\)
D. \(x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right).\)
Phương pháp
Sử dụng dấu của tam thức bậc hai
Lời giải
Chọn A
Ta có \(f(x) = 0 \Rightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\), và a >0
Do đó \(f(x) < 0 \Rightarrow x \in \left( {1;3} \right)\).
Câu 7: Tập nghiệm của phương trình \(\sqrt {3{x^2} - 4x - 1} = \sqrt {2{x^2} - 4x + 3} \) là
A. \(\left\{ 2 \right\}\).
B. \(\left\{ { - 2} \right\}\).
C. \(\left\{ { - 2;2} \right\}\).
D. \(\emptyset \).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Chọn C
\(\begin{array}{l}\sqrt {3{x^2} - 4x - 1} = \sqrt {2{x^2} - 4x + 3} \Rightarrow 3{x^2} - 4x - 1 = 2{x^2} - 4x + 3\\ \Rightarrow {x^2} = 4 \Rightarrow x = \pm 2\end{array}\)
Thử lại thì \(x = \pm 2\) thõa mãn phương trình. Vậy phương trình có tập nghiệm \(\left\{ { - 2;2} \right\}\).
Câu 8: Tổng các nghiệm của phương trình \(\sqrt {2{x^2} + x + 3} = 1 - x\)
A. \( - 3\). B. \(3\). C. \( - 2\). D. \(2\).
Phương pháp
Bình phương hai vế của phương trình
Lời giải
Chọn A
Ta có
\(\begin{array}{l}\sqrt {2{x^2} + x + 3} = 1 - x \Rightarrow 2{x^2} + x + 3 = {\left( {1 - x} \right)^2}\\ \Rightarrow {x^2} + 3x + 2 = 0 \Rightarrow \left[ \begin{array}{l}x = - 1\\x = - 2\end{array} \right.\end{array}\)
Thử lại thõa mãn .
Vậy tổng hai nghiệm của phương trình là \( - 3.\)
Câu 9: Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,2x - 3y + 1 = 0\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
A. \(\overrightarrow n = \left( {2; - 3} \right)\).
B. \(\overrightarrow n = \left( {2;3} \right)\).
C. \(\overrightarrow n = \left( { - 3;2} \right)\).
D. \(\overrightarrow n = \left( {3;2} \right)\).
Phương pháp
Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)
Lời giải
Chọn A
Véc tơ pháp tuyến của đường thẳng \(d:ax + by + c = 0\)là \(\overrightarrow n = \left( {a;b} \right)\). Vậy véc tơ pháp tuyến của đường thẳng \(\left( d \right):\,\,2x - 3y + 1 = 0\)là \(\overrightarrow n = \left( {2; - 3} \right)\).
Câu 10: Đường thẳng \(\left( d \right):\,\,2x + 3y - 1 = 0\) đi qua điểm nào sau đây
A. \(A\left( {2; - 1} \right)\).
B. \(B\left( {2;5} \right)\).
C. \(C\left( {2;3} \right)\).
D. \(D\left( { - 1;2} \right)\).
Phương pháp
Thay tọa độ các điểm ở đáp án vào phương trình đường thẳng (d)
Lời giải
Chọn A
Điểm \(M\left( {{x_0};{y_0}} \right) \in (d):ax + by + c = 0 \Leftrightarrow a{x_0} + b{y_0} + c = 0\).
Ta có \(2.2 + 3.\left( { - 1} \right) - 1 = 0\) nên \(A\left( {2; - 1} \right) \in \left( d \right).\)
Câu 11: Trong mặt phẳng \(Oxy\), phương trình đường thẳng \(\Delta \) đi qua điểm \(M(2;1)\)và có véc tơ pháp tuyến \(\overrightarrow n = \left( {3;\, - 4} \right)\) là
A. \(3x - 4y - 2 = 0\). B. \(3x - 4y + 2 = 0\). C. \( - 4x + 3y + 5 = 0\). D. \(4x + 3y - 2 = 0\).
Phương pháp
Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\)có véc tơ pháp tuyến \(\overrightarrow n = \left( {a;b} \right)\)là
\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Lời giải
Chọn A
Phương trình đường thẳng \(\Delta \) đi qua điểm \(M(2;1)\)và có véc tơ pháp tuyến \(\overrightarrow n = \left( {3;\, - 4} \right)\) là \(3\left( {x - 2} \right) - 4\left( {y - 1} \right) = 0 \Rightarrow 3x - 4y - 2 = 0\).
Câu 12: Tính góc giữa hai đường thẳng \(\Delta :\sqrt 3 x + y + 1 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\).
A. \({90^ \circ }\). B. \({120^ \circ }\). C. \({60^ \circ }\). D. \({30^ \circ }\).
Phương pháp
Áp dụng công thức tính góc giữa hai đường thẳng có: \(\cos \left( {{d_1},{d_2}} \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\).
Lời giải
Chọn D
Đường thẳng \(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {\sqrt 3 ;1} \right)\), đường thẳng \(\Delta '\) có vectơ pháp tuyến \(\overrightarrow {n'} = \left( {1;\sqrt 3 } \right)\).
Gọi \(\alpha \) là góc giữa hai đường thẳng \(\Delta ,\Delta '.\)\(\cos \alpha = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {\sqrt 3 + \sqrt 3 } \right|}}{{\sqrt {1 + 3} .\sqrt {1 + 3} }} = \frac{{\sqrt 3 }}{2} \Rightarrow \alpha = {30^ \circ }\).
Câu 13: Khoảng cách từ điểm \(M\left( {3\,;\, - 2} \right)\) đến đường thẳng \(\Delta :\,\,4x - 3y + 2 = 0\) là:
A. \(5\). B. \(4\). C. \(\frac{8}{5}\). D. \(\frac{{18}}{5}\).
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Chọn B
Khoảng cách \(d = \frac{{\left| {4.3 - 3.\left( { - 2} \right) + 2} \right|}}{{\sqrt {{4^2} + {{( - 3)}^2}} }} = \frac{{20}}{5} = 4\).
Câu 14: Cho hai đường thẳng \(\Delta :4x - 2y + 3 = 0\) và \(\Delta ': - 2x + y + 3 = 0\). Khẳng định nào sau đây là đúng?
A. \(\Delta \) và \(\Delta '\)cắt nhau.
B. \(\Delta \) và \(\Delta '\)song song với nhau.
C. \(\Delta \) và \(\Delta '\)trùng nhau.
D. \(\Delta \) và \(\Delta '\)vuông góc với nhau.
Phương pháp
Sử dụng công thức vị trí tương đối của hai đường thẳng.
Lời giải
Chọn B
Ta có \(\frac{4}{{ - 2}} = \frac{{ - 2}}{1} \ne \frac{3}{3}\) nên \(\Delta \) và \(\Delta '\)song song với nhau.
Câu 15: Tọa độ tâm của đường tròn có phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) là
A. \(I\left( {2; - 3} \right)\).
B. \(I\left( {2;3} \right)\).
C. \(I\left( { - 2;3} \right)\).
D. \(I\left( { - 2; - 3} \right)\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn A
Đường tròn \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) có tâm \(I\left( {2; - 3} \right)\).
Câu 16: Bán kính của đường tròn có phương trình \({x^2} + {y^2} - 6x + 10y + 30 = 0\) là
A. \(2\). B. \(4\). C. \(16\). D. \(6\).
Phương pháp
Phương trình tổng quát của đường tròn có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(I\left( {a;\,\,b} \right)\) là tâm và bán kính được tính bằng công thức \(R = \sqrt {{a^2} + {b^2} - c} \)
Lời giải
Chọn A
Bán kính của đường tròn là \(r = \sqrt {{3^2} + {{( - 5)}^2} - 30} = 2\)
Câu 17: Phương trình nào sau đây là phương trình đường tròn?
A. \({x^2} + {y^2} - 2x + 4y - 4 = 0\). B. \({x^2} + {y^2} + 6x - 2y + 15 = 0\).
C. \(2{x^2} + {y^2} - 8x + 10y - 1 = 0\). D. \({x^2} + {y^2} + 5xy - 8y - 1 = 0.\)
Phương pháp
Phương trình tổng quát của đường tròn có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(I\left( {a;\,\,b} \right)\) là tâm và bán kính được tính bằng công thức \(R = \sqrt {{a^2} + {b^2} - c} \)
Lời giải
Chọn A
Vì \({1^2} + {\left( { - 2} \right)^2} - \left( { - 4} \right) = 9 > 0\)nên \({x^2} + {y^2} - 2x + 4y - 4 = 0\)là pt đường tròn
Vì \({\left( { - 3} \right)^2} + {1^2} - 15 = - 5 < 0\)nên \({x^2} + {y^2} + 6x - 2y + 15 = 0\) không phải pt đường tròn.
Hệ số của \({x^2},\,{y^2}\)khác nhau nên \(2{x^2} + {y^2} - 8x + 10y - 1 = 0\) không phải pt đường tròn.
Trong pt có chứa tích \(xy\) nên \({x^2} + {y^2} + 5xy - 8y - 1 = 0.\) không phải pt đường tròn.
Câu 18: Phương trình của đường tròn tâm \(I\left( { - 3;4} \right)\), bán kính bằng \(5\) là
A. \({\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = 25\).
B. \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\).
C. \({\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = 5\).
D. \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 5\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Chọn B
Phương trình của đường tròn tâm \(I\left( { - 3;4} \right)\), bán kính bằng \(5\) là \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\).
Câu 19: Đường elip \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)có tiêu cự bằng
A. \(10\).B. \(8\). C. \(3\). D. \(6\).
Phương pháp
Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tiêu cự là 2c với \({c^2} = {a^2} - {b^2}\)
Lời giải
Chọn B
Ta có \({a^2} = 25,\,{b^2} = 9 \Rightarrow {c^2} = {a^2} - {b^2} = 16 \Rightarrow c = 4\).
Vậy tiêu cự của elip là \(2c = 8.\)
Câu 20: Tọa độ tiêu điểm của Parabol \(\left( P \right):\,{y^2} = 10x\) là
A. \(F\left( {5;0} \right)\).
B. \(F\left( {\frac{5}{2};0} \right)\).
C. \(F\left( { - 5;0} \right)\).
D. \(F\left( { - \frac{5}{2};0} \right)\).
Phương pháp
Tọa độ tiêu điểm của Parabol \(\left( P \right):\,{y^2} = 2px\) là \(F\left( {\frac{p}{2};0} \right)\)
Lời giải
Chọn B
Ta có \(2p = 10 \Rightarrow p = 5\). Vậy tọa độ tiêu điểm là \(F\left( {\frac{5}{2};0} \right)\).
Câu 21: Từ Đà Nẵng đi Hà Nội mỗi ngày có 7 chuyến tàu hỏa và 3 chuyến máy bay. Bạn Anh ở Đà nẵng muốn đi Hà Nội chơi vào ngày chủ nhật bằng tàu hỏa hoặc máy bay. Bạn Anh có bao nhiêu cách chọn chuyến đi ?
A. \(7\). B. \(3\). C. \(10\). D. \(21\).
Phương pháp
Áp dụng quy tắc cộng
Lời giải
Chọn C
Theo quy tắc cộng, Bạn Anh có số cách chọn chuyến đi là \(7 + 3 = 10\).
Câu 22: Có \(10\) cái bút khác nhau và \(8\) quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn \(1\) cái bút và \(1\) quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A. \(80\). B. \(60\). C. \(90\). D. \(70\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn A
Theo quy tắc nhân, Bạn học sinh có số cách chọn là \(10.8 = 80\)cách
Câu 23: Một người vào một nhà hàng ăn, người đó chọn thực đơn 1 gồm một món chính và một món tráng miệng. Nhà hàng đưa ra danh sách: Món chính có 5 loại thịt và 3 loại cá; món tráng miệng có 4 loại quả và 3 loại bánh. Có bao nhiêu cách chọn một thực đơn?
A. \(15\). B. \(27\). C. \(56\). D. \(180\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn C
Số cách chọn món chính: \(5 + 3 = 8.\)
Số cách chọn món tráng miệng: \(4 + 3 = 7.\)
Số cách chọn một thực đơn là \(8.7 = 56\).
Câu 24: Cho các số \(1\),\(5\), \(6\),\(7\). Có bao nhiêu số tự nhiên có \(4\) chữ số với các số khác nhau lập từ các số đã cho.
A. \(64\). B. \(24\). C. \(256\). D. \(12\).
Phương pháp
Áp dụng công thức hoán vị
Lời giải
Chọn B
Mỗi số tự nhiên gồm 4 chữ số khác nhau được lập từ \(1\),\(5\), \(6\),\(7\)là một hoán vị 4 phần tử. Do đó số các số tự nhiên gồm 4 chữ số khác nhau được lập là \(4! = 24\).
Câu 25: Lớp \(10A\) có 42 học sinh. Đại hội Chi đoàn \(10A\)bầu ra một ban chấp hành gồm 1 Bí thư, 1 phó Bí thư và 1 Ủy viên ( Giả sử bạn nào cũng có năng lực như nhau). Chi đoàn \(10A\) có bao nhiêu cách bầu một ban chấp hành?
A. \(A_{42}^3\). B. \({P_{42}}\). C. \(C_{42}^3\). D. \({42^3}\).
Phương pháp
Áp dụng công thức chỉnh hợp
Lời giải
Chọn A
Mỗi cách bầu một BCH gồm 3 bạn là một chỉnh hợp chập 3 của 42 phần tử. Vậy số cách bầu là \(A_{42}^3\).
Câu 26: Có bao nhiêu cách chọn hai học sinh đi dự trại hè từ một nhóm \(38\) học sinh?
A. \({2^{38}}\). B. \(C_{38}^2\). C. \({38^2}\). D. \(A_{38}^2\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn B
Mỗi cách chọn 2 học sinh từ 38 học sinh là một tổ hợp chập 2 của 38 phần tử. Vậy số cách chọn là \(C_{38}^2\).
Câu 27: Ngân hàng đề thi gồm \(15\) câu hỏi trắc nghiệm khác nhau và \(8\) câu hỏi tự luận khác nhau. Hỏi có thể lập được bao nhiêu đề thi sao cho mỗi đề thi gồm 10 câu hỏi trắc nghiệm khác nhau và \(4\) câu hỏi tự luận khác nhau.
A. \(C_{15}^{10}.C_8^4\).
B. \(C_{15}^{10} + C_8^4\).
C. \(A_{15}^{10}.A_8^4\).
D. \(A_{15}^{10} + A_8^4\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn A
Số cách chọn 10 câu hỏi trắc nghiệm là \(C_{15}^{10}\)
Số cách chọn câu hỏi tự luận là \(C_8^4\)
Vậy số cách lập đề thi là \(C_{15}^{10}.C_8^4\).
Câu 28: Một lớp có \(40\) học sinh gồm \(25\) nam và \(15\) nữ. Giáo viên chủ nhiệm muốn chọn \(4\) em trực cờ đỏ. Hỏi có bao nhiêu cách chọn nếu ít nhất phải có một nam?
A. \(C_{40}^4 - C_{15}^4\) (cách).
B. \(C_{25}^4\) (cách).
C. \(C_{25}^1C_{15}^3\) (cách).
D. \(C_{40}^4 + C_{15}^4\) (cách).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Chọn A
Số cách chọn 4 bạn trong 40 bạn là \(C_{40}^4\)
Số cách chọn bốn bạn nữ trong 15 bạn nữ là \(C_{15}^4\)
Vậy số cách chọn 4 bạn có ít nhất 1 nam là: \(C_{40}^4 - C_{15}^4\).
Câu 29: Có bao nhiêu số hạng trong khai triển nhị thức \({\left( {2021x + 2022} \right)^{2023}}\)
A. \(2021\). B. \(2022\). C. \(2023\). D. \(2024\).
Phương pháp
Áp dụng khai triển công thức nhị thức Newton
Lời giải
Chọn D
Tổng số số hạng của khai triển \({\left( {2021x + 2022} \right)^{2023}}\) là \(2023 + 1 = 2024.\)
Câu 30: Cho \(A\), \(B\) là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
A. \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
B. \(P\left( {A \cup B} \right) = P\left( A \right).P\left( B \right)\).
C. \(P\left( {A \cup B} \right) = P\left( A \right) - P\left( B \right)\).
D. \(P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\).
Phương pháp
Do \(A,\,B\) xung khắc nên \(A \cap B = \emptyset \). Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Lời giải
Chọn A
Do \(A,\,B\) xung khắc nên \(A \cap B = \emptyset \). Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Câu 31: Gieo một đồng tiền hai lần. Xác định biến cố: \(A\): “ Lần đầu xuất hiện mặt ngửa”?
A. \(A = \left\{ {NS,NN} \right\}\).
B. \(A = \left\{ {NS,SN} \right\}\).
C.\(A = \left\{ {NN} \right\}\).
D. \(A = \left\{ {NS} \right\}\).
Phương pháp
Sử dụng quy tắc đếm.
Lời giải
Chọn A
Ta có không gian mẫu: \(\Omega = \left\{ {SS,SN,NN,NS} \right\}\)
\(A\): “ Lần đầu xuất hiện mặt ngửa” nên \(A = \left\{ {NS,NN} \right\}\).
Câu 32: Gieo một con xúc xắc hai lần. Số phần tử của không gian mẫu là?
A. \(6\). B. \(12\). C. \(18\). D. \(36\).
Phương pháp
Sử dụng quy tắc đếm.
Lời giải
Chọn D
Ta có \(n\left( \Omega \right) = 6.6 = 36\).
Câu 33: Gieo một con xúc xắc cân đối và đồng chất một lần. Xác suất để mặt chấm là số nguyên tố xuất hiện là:
A. \(\frac{1}{5}\) B. \(\frac{3}{{10}}\). C. \(\frac{2}{5}\) D. \(\frac{1}{2}\).
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Chọn D
Ta có \(\Omega = \left\{ {1;2;3;4;5;6} \right\},\,\,n\left( \Omega \right) = 6\)
Gọi biến cố \(A\): “Mặt chấm là số nguyên tố” suy ra \(A = \left\{ {2;3;5} \right\}\), \(n(A) = 3\)
Xác suất của biến cố \(A\) là \(P\left( A \right) = \frac{{n(A)}}{{n\left( \Omega \right)}} = \frac{3}{6} = \frac{1}{2}\).
Câu 34: Trên giá sách có \(4\) quyển sách Toán, \(3\) quyển sách Vật lý, \(3\) quyển sách Hoá học. Lấy ngẫu nhiên \(3\) quyển sách trên kệ sách ấy. Tính xác suất để \(3\) quyển được lấy ra đều là sách Toán.
A. \(\frac{1}{{40}}\). B. \(\frac{1}{{12}}\). C. \(\frac{1}{{30}}\). D. \(\frac{1}{5}\).
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Chọn C
Số cách lấy \(3\) quyển sách là \(n\left( \Omega \right) = C_{10}^3 = 120\)
Số cách lấy \(3\) quyển sách toán là \(n\left( A \right) = C_4^3 = 4\).
Vậy xác suất để \(3\) quyển được lấy ra đều là sách Toán là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{4}{{120}} = \frac{1}{{30}}\)
Câu 35: Một tổ học có 5 nam và 6 nữ. Giáo viên chủ nhiệm cần chọn ngẫu nhiên 3 người. Xác suất để chọn được ít nhất một nam là.
A. \(\frac{{29}}{{33}}\). B. \(\frac{{31}}{{33}}\). C. \(\frac{2}{{33}}\). D. \(\frac{4}{{33}}\).
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Chọn A
Số cách chọn \(3\)bạn trong 11 bạn là \(n\left( \Omega \right) = C_{11}^3 = 165\)
Số cách chọn \(3\)bạn có ít nhất một nam là \(n\left( A \right) = C_{11}^3 - C_6^3 = 145\)
Xác suất chọn 3 bạn có ít nhất một nam là:
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{145}}{{165}} = \frac{{29}}{{33}}\) .
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36. Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).
Phương pháp
Bình phương hai vế của phương trình đã cho để đưa về giải phương trình bậc hai
Lời giải
Bình phương hai vế của phương trình ta được:
\(2{x^2} - 5x - 9 = {x^2} - 2x + 1\).
Sau khi thu gọn ta được \({x^2} - 3x - 10 = 0\).
Từ đó tìm được \(x = - 2\) hoặc \(x = 5\).
Thay lần lượt hai giá trị này của \(x\) vào phương trình đã cho, ta thấy chỉ có \(x = 5\) thỏa mãn.
Vậy nghiệm của phương trình đã cho là \(x = 5\).
Câu 37. Viết phương trình chính tắc đường elip \(\left( E \right)\) thỏa mãn \(\left\{ {M \in \left( E \right)|\,M{F_1} + M{F_2} = 20} \right\}\), \({F_1}{F_2} = 12\)với \({F_1},\,{F_2}\,\)là các tiêu điểm của \(\left( E \right)\).
Phương pháp
Phương trình chính tắc của \(\left( E \right)\) là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\).
Lời giải
Ta có:
\(\begin{array}{l}M \in (E) \Rightarrow M{F_1} + M{F_2} = 2a \Rightarrow 2a = 20 \Rightarrow a = 10\\{F_1}{F_2} = 2c \Rightarrow 2c = 12 \Rightarrow c = 6\end{array}\)
Vậy phương trình chính tắc của \(\left( E \right)\) là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\).
Câu 38. Xếp \(6\) học sinh nam và \(4\) học sinh nữ vào một dãy có \(10\) ghế xếp hàng ngang. Tính xác suất sao cho không có hai học sinh nữ nào ngồi cạnh nhau.
Phương pháp
Sử dụng công thức tính xác suất
Lời giải
Ta có \(n\left( \Omega \right) = 10! = 3628800.\)
Gọi biến cố A: “ Không có hai học sinh nữ nào ngồi cạnh nhau”
Số cách xếp \(6\) học sinh nam thành hàng ngang là \(6! = 720\) cách.
Ứng với mỗi cách sắp xếp này, ta có \(7\) khoảng trống (\(2\) khoảng trống ở hai đầu và \(5\) khoảng trống ở giữa). Xếp \(4\) học sinh nữ vào các khoảng trống đó, có \(A_7^4 = 840\) cách.
Suy ra \(n\left( A \right) = 720.840 = 604800\). Do đó \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{604800}}{{3628800}} = \frac{1}{6}.\)
Câu 39. Trong mặt phẳng với hệ trục tọa độ \(Oxy,\) cho hình chữ nhật\(ABCD\) có \(AB = 2BC.\) Gọi \(M\) là trung điểm của đoạn \(AB\) và \(G\) là trọng tâm tam giác \(ACD.\) Viết phương trình đường thẳng \(AD,\) biết rằng \(M\left( {1;\;2} \right)\) và \(G\left( {\frac{5}{3};\;0} \right).\)
Phương pháp
Đường thẳng cần viết phương trình đi qua \(A({x_0};{y_0})\)và vecto pháp tuyến là \(\overrightarrow n = (a,b)\) nên có phương trình tổng quát \(a(x - {x_0}) + b(y - {y_0}) = 0\)
Lời giải
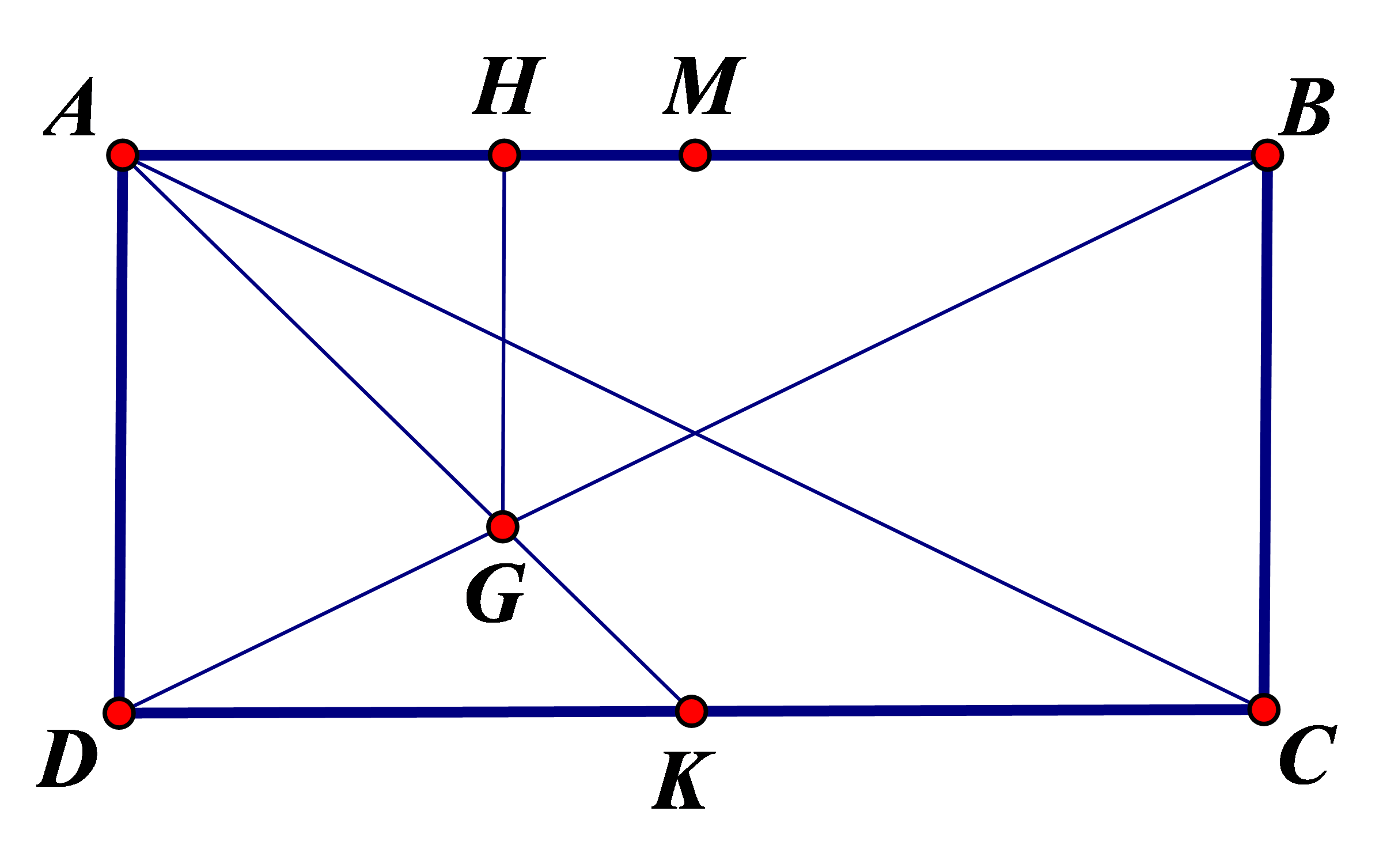
Gọi \(H\) là hình chiếu vuông góc của \(G\) lên \(AB\) và \(K\) là trung điểm đoạn \(CD.\)
Đặt \(BC = 3a > 0,\) suy ra \(AB = 6a,\;GH = 2a,\;HM = a.\)
\(M{G^2} = 4{a^2} + {a^2} \Leftrightarrow \frac{{40}}{9} = 5{a^2} \Leftrightarrow {a^2} = \frac{8}{9} \Leftrightarrow a = \frac{{2\sqrt 2 }}{3}.\)
Suy ra \(AM = 3a = 2\sqrt 2 ,\)\(AG = \frac{2}{3}AK = \frac{2}{3}\left( {3a\sqrt 2 } \right) = \frac{8}{3}.\)
Gọi \(A(x,y)\). Khi đó : \(\left\{ {\begin{array}{*{20}{c}}{AM = 2\sqrt 2 }\\{AG = \frac{8}{3}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\left( {1 - x} \right)}^2} + {{\left( {2 - y} \right)}^2} = 8}\\{{{\left( {\frac{5}{3} - x} \right)}^2} + {y^2} = \frac{{64}}{9}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x^2} + {y^2} - 2x - 4y = 3}\\{x = 3y - 1}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 3y - 1}\\{\left[ {\begin{array}{*{20}{c}}{y = 0}\\{y = \frac{8}{5}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1,y = 0}\\{x = \frac{{19}}{5},y = \frac{8}{5}}\end{array}} \right.\)
+) Nếu \(A\left( { - 1,0} \right)\). Đường thẳng \(AD\) đi qua \(A\) và vuông góc với đường thẳng \(AM\) nên phương trình đường thẳng \(AD\) là \(x + y + 1 = 0.\)
+) Nếu \(A\left( {\frac{{19}}{5},\frac{8}{5}} \right)\). Đường thẳng \(AD\) đi qua \(A\) và vuông góc với đường thẳng \(AM\) nên phương trình đường thẳng \(AD\) là \(7x - y - 25 = 0.\)
---------- HẾT ----------
Đề kiểm tra học kì 2 Toán 10 - Đề số 4 chương trình Chân trời sáng tạo là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong suốt học kì. Đề thi bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải có khả năng vận dụng linh hoạt các kiến thức và kỹ năng đã được trang bị.
Đề thi thường bao gồm các phần sau:
Nội dung đề thi thường bao gồm các chủ đề sau:
Để giải tốt đề thi, học sinh cần:
Bài 1: Giải bất đẳng thức sau: 2x + 3 > 5
Giải:
2x + 3 > 5
2x > 2
x > 1
Vậy, tập nghiệm của bất đẳng thức là x > 1.
Luyện đề là một bước quan trọng trong quá trình ôn thi học kì. Việc luyện đề giúp học sinh:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, đề thi và đáp án chi tiết. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn sẽ giúp các em học sinh học toán hiệu quả và đạt kết quả cao.
Hãy dành thời gian ôn tập kỹ lưỡng kiến thức và luyện tập thường xuyên với các đề thi khác nhau. Chúc các em học sinh đạt kết quả tốt trong kỳ thi học kì 2!