Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 10 Chân trời sáng tạo - Đề số 1, được biên soạn theo chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ đầy đủ các kiến thức trọng tâm của chương trình học kì 2 Toán 10 Chân trời sáng tạo.
Phần trắc nghiệm (7 điểm) Câu 1: Biểu thức nào sau đây là tam thức bậc hai?
Phần trắc nghiệm (7 điểm)
Câu 1: Biểu thức nào sau đây là tam thức bậc hai?
A. \(0{x^2} + 5x - 3\).
B. \(\frac{1}{{{x^2}}} + \frac{1}{x} + 1\).
C. \(7x - {x^2} + 5\).
D. \({\left( {{x^2} - 2x + 3} \right)^2}\).
Câu 2: Chọn từ thích hợp để điền vào chỗ (.).
Nếu tam thức bậc hai \(f(x) = a{x^2} + bx + c(a \ne 0)\) có hai nghiệm phân biệt \({x_1},{x_2}\) \(\left( {{x_1} < {x_2}} \right)\) thì \(f(x) \ldots \ldots ..(1) \ldots ...\) với hệ số \(a\) với mọi \(x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\) và \(f(x)\).(2). với hệ số \(a\) với mọi \(x \in \left( {{x_1};{x_2}} \right)\).
A. (1) trái dấu - (2) cùng dấu.
B. (1) trái dấu - (2) trái dấu.
C. (1) cùng dấu - (2) trái dấu.
D. (1) cùng dấu - (2) cùng dấu.
Câu 3: Tập nghiệm của bất phương trình \({x^2} - 2x + 3 > 0\) là:
A. \(\emptyset \).
B. \(\mathbb{R}\).
C. \(( - \infty ; - 1) \cup (3; + \infty )\).
D. \(( - 1;3)\).
Câu 4: Tam thức bậc hai \( - {x^2} + 7x - 12\) nhận giá trị dương khi nào?
A. \(x \in (3;4)\).
B. \(x \in [3;4]\).
C. \(x \in ( - \infty ;3) \cup (4; + \infty )\).
D. \(x \in ( - \infty ;3] \cup [4; + \infty )\).
Câu 5: Cô Mai có \(60\;m\) lưới muốn rào một mảnh vườn hình chữ nhật để trồng rau. Biết rằng một cạnh là tường (nên không cần rào), cô Mai chỉ cần rào ba cạnh còn lại của hình chữ nhật để làm vườn. Để diện tích mảnh vườn không ít hơn \(400\;{m^2}\) thì chiều rộng của vườn cần có giá trị nhỏ nhất là bao nhiêu?
A. \(20\;m\).
B. \(15\;m\).
C. \(10\;m\).
D. \(9\;m\).
Câu 6: Nghiệm của bất phương trình \({x^2} - 9x + 20 > 0\) là:
A. \(x \in [4;5]\).
B. \(x \in (4;5)\).
C. \(x \in ( - \infty ;4] \cup [5; + \infty )\).
D. \(x \in ( - \infty ;4) \cup (5; + \infty )\).
Câu 7: Tập ngiệm của bất phương trình: \( - {x^2} + 6x + 7 \ge 0\) là:
A. \(( - \infty ; - 1] \cup [7; + \infty )\).
B. \([ - 1;7]\).
C. \(( - \infty ; - 7] \cup [1; + \infty )\).
D. \([ - 7;1]\).
Câu 8: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{(x + 3)(4 - x) > 0}\\{x - m + 1 < 0}\end{array}} \right.\) vô nghiệm khi và chỉ khi:
A. \(m \le - 2\).
B. \(m > - 2\).
C. \(m < - 1\).
D. \(m = 0\).
Câu 9: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 1 \le 0}\\{x - m > 0}\end{array}} \right.\) có nghiệm khi:
A. \(m > 1\).
B. \(m = 1\).
C. \(m < 1\).
D. \(m \ne 1\).
Câu 10: Cho tam thức bậc hai \(f(x) = {x^2} - bx + 3\). Với giá trị nào của \(b\) thì \(f(x)\) có hai nghiệm phân biệt?
A. \(b \in [ - 2\sqrt 3 ;2\sqrt 3 ]\).
B. \(b \in ( - 2\sqrt 3 ;2\sqrt 3 )\).
C. \(b \in ( - \infty ; - 2\sqrt 3 ] \cup [2\sqrt 3 ; + \infty )\).
D. \(b \in ( - \infty ; - 2\sqrt 3 ) \cup (2\sqrt 3 ; + \infty )\).
Câu 11: Tập hợp tất cả các giá trị của \(m\) để phương trình bậc hai \({x^2} + 2(m + 1)x + 3m = 0\) có nghiệm là
A. \(\{ 0\} \)
B. \(\mathbb{R}\backslash \{ 0\} \).
C. \(\mathbb{R}\).
D. \(\emptyset \).
Câu 12: Phương trình \(m{x^2} - mx + 2 = 0\) có nghiệm khi và chỉ khi:
A. \(m \le 0\) hoặc \(m \ge 8\).
C. \(0 < m \le 8\).
B. \(m < 0\) hoặc \(m \ge 8\).
D. \(0 \le m \le 8\).
Câu 13: Giá trị \(x = 2\) là nghiệm của phương trình nào sau đây?
A. \(\sqrt {{x^2} - x - 4} = \sqrt {x - 4} \).
B. \(x - 1 = \sqrt {x - 3} \).
C. \(x + 2 = 2\sqrt {3x - 2} \).
D. \(x + 2 = \sqrt {x - 1} \).
Câu 14: Số nghiệm của phương trình \(\sqrt {{x^2} - 2x - 3} = \sqrt {2{x^2} + x - 3} \) là:
A. 1.
B. 2.
C. 0.
D. 3.
Câu 15: Tập nghiệm của phương trình \(\sqrt {{x^2} - 3x + 1} = x - 1\) là:
A. \(S = \{ 1\} \).
B. \(S = \{ 2\} \).
C. \(S = \{ 0\} \).
D. \(S = \emptyset \).
Câu 16: Cho phương trình \(\sqrt {{x^2} - mx + {m^2}} = x - m\) (với \(m\) là tham số). Giá trị của \(m\) đê phương trình nhận \(x = 2\) làm nghiệm là:
A. \(m = 2\).
B. \(m = 3\).
C. \(m = 0\).
D. \(m = 1\).
Câu 17: Phương trình \(\left( {{x^2} - 6x} \right)\sqrt {17 - {x^2}} = {x^2} - 6x\) có bao nhiêu nghiệm thực phân biệt?
A. 2.
B. 1.
C. 4.
D. 3.
Câu 18: Tổng các nghiệm của phương trình \(\sqrt {3x + 7} - \sqrt {x + 1} = 2\) là
A. 2.
B. \( - 1\).
C. \( - 2\).
D. 4.
Câu 19: Trong mặt phẳng toạ độ \(Oxy\), toạ độ của vectơ \(2\vec i - 7\vec j\) là:
A. \((2;7)\).
B. \(( - 2;7)\).
C. \((2; - 7)\).
D. \(( - 7;2)\).
Câu 20: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(3; - 2)\). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. \((3; - 2)\).
B. \(( - 3;2)\).
C. \(( - 2;3)\).
D. \((2; - 3)\).
Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(A( - 3;2),B(5; - 1)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \((2;1)\).
B. \((8; - 3)\).
C. \(( - 8;3)\).
D. \(( - 2; - 1)\).
Câu 22: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 0.
B. 1.
C. 2.
D. Vô số.
Câu 23: Một vectơ pháp tuyến của đường thẳng \(\Delta :y = 2x + 1\) là:
A. \(\overrightarrow {{n_\Delta }} (2; - 1)\).
B. \(\overrightarrow {{n_\Delta }} (1; - 1)\).
C. \(\overrightarrow {{n_\Delta }} ( - 2; - 1)\).
D. \(\overrightarrow {{n_\Delta }} (1;1)\).
Câu 24: Đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow {{u_\Delta }} (12; - 13)\). Vectơ nào sau đây là vectơ pháp tuyến của \(\Delta \)?
A. \(\overrightarrow {{n_\Delta }} ( - 13;12)\).
B. \(\overrightarrow {{n_\Delta }} (12;13)\).
C. \(\overrightarrow {{n_\Delta }} (13;12)\).
D. \(\overrightarrow {{n_\Delta }} ( - 12; - 13)\).
Câu 25: Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:
A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).
B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).
C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).
D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Câu 26: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và có vectơ pháp tuyến \(\vec n(11; - 12)\) là:
A. \(5x + 4y + 7 = 0\).
B. \(5x + 4y - 7 = 0\).
C. \(11x - 12y - 7 = 0\).
D. \(11x - 12y + 7 = 0\).
Câu 27: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và vuông góc với đường thẳng \(x - 2y + 5 = 0\) là:
A. \(x - 2y + 3 = 0\).
B. \(2x + y - 14 = 0\).
C. \(x + 2y - 13 = 0\).
D. \(2x + y = 0\).
Câu 28: Cho đường thẳng \(\Delta \) có phương trình tổng quát là \(x - 2y - 5 = 0\). Phương trình nào sau đây là phương trình tham số của \(\Delta \)?
A. \(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = 4 - t}\end{array}} \right.\).
B. \(\left\{ {\begin{array}{*{20}{l}}{x = t}\\{y = 5 + 2t}\end{array}} \right.\).
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 4t}\\{y = 1 - 2t}\end{array}} \right.\).
D. \(\left\{ {\begin{array}{*{20}{l}}{x = 5 + 2t}\\{y = t}\end{array}} \right.\).
Câu 29: Trong mặt phẳng toạ độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\), \({\Delta _2}:3x - y + 7 = 0\). Nhận định nào sau đây là đúng?
A. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
B. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
C. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trùng nhau.
D. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
Câu 30: Người ta quy ước góc giữa hai đường thẳng song song hoặc trùng nhau là:
A. \({180^0}\).
B. \({120^0}\).
C. \({90^0}\).
D. \({0^0}\).
Câu 31: Cho \(\alpha \) là góc tạo bởi hai đường thẳng \({\Delta _1}:2x - 3y + 5 = 0\) và \({\Delta _2}:3x + y - 14 = 0\). Giá trị của cosa là:
A. \(\frac{{ - 3}}{{130}}\).
B. \(\frac{3}{{\sqrt {130} }}\).
C. \(\frac{{\sqrt 3 }}{{130}}\).
D. \(\frac{{ - 3}}{{\sqrt {130} }}\).
Câu 32: Góc giữa hai đường thẳng \({\Delta _1}:2x + 4y - 1 = 0\) và \({\Delta _2}:x - 3y + 1 = 0\) là:
A. \({0^0}\).
B. \({45^0}\).
C. \({60^0}\).
D. \({90^0}\).
Câu 33: Cho đường tròn \((C):{(x - 1)^2} + {(y - 2)^2} = 25\). Đường tròn \((C)\) có:
A. Tâm \(I(1;2)\) và bán kính \(R = 25\).
B. Tâm \(I( - 1; - 2)\) và bán kính \(R = 25\).
C. Tâm \(I(1;2)\) và bán kính \(R = 5\).
D. Tâm \(I( - 1; - 2)\) và bán kính \(R = 5\).
Câu 34: Cho đường tròn \((C):{x^2} + {y^2} + 6x - 4y + 2 = 0\). Đường tròn \((C)\) có:
A. Tâm \(I( - 3;2)\) và bán kính \(R = 11\).
B. Tâm \(I( - 3;2)\) và bán kính \(R = \sqrt {11} \).
C. Tâm \(I(3; - 2)\) và bán kính \(R = 11\).
D. Tâm \(I(3; - 2)\) và bán kính \(R = \sqrt {11} \).
Câu 35: Phương trình nào sau đây là phương trình của một đường tròn?
A. \({x^2} - {y^2} + 6x - 4y + 2 = 0\).
B. \({x^2} + {y^2} + 2x - 4y + 8 = 0\).
C. \({x^2} + {y^2} + 6x - 10y + 45 = 0\).
D. \({x^2} + {y^2} + 4x - 8y + 13 = 0\)
Phần tự luận (3 điểm)
Bài 1. Giải phương trình sau: \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \)
Bài 2. Tìm \(m\) để các bất phương trình sau nghiệm đúng với mọi \(x\):
a) \(3{x^2} - 2(m - 1)x + {m^2} + 4 > 0\)
b) \(m{x^2} + (m - 1)x + m - 1 < 0\)
Bài 3. Cho các vectơ \(\vec a = (2;0),\vec b = \left( { - 1;\frac{1}{2}} \right),\vec c = (4; - 6)\).
a) Tìm tọa độ của vectơ \(\vec d = 2\vec a - 3\vec b + 5\vec c\).
b) Biểu diễn vectơ \(\vec c\) theo cặp vectơ không cùng phương \(\vec a,\vec b\).
Bài 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x - y + 4 = 0\).
a) Viết phương trình đường cao \(AH\) của tam giác.
b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.
-------- Hết --------
Phần trắc nghiệm
Câu 1. C | Câu 2. C | Câu 3. B | Câu 4. A | Câu 5. C | Câu 6. D | Câu 7. B |
Câu 8. A | Câu 9. C | Câu 10. D | Câu 11. C | Câu 12. B | Câu 13. C | Câu 14. A |
Câu 15. D | Câu 16. C | Câu 17. D | Câu 18. A | Câu 19. C | Câu 20. A | Câu 21. B |
Câu 22. D | Câu 23. A | Câu 24. C | Câu 25. D | Câu 26. C | Câu 27. B | Câu 28. D |
Câu 29. D | Câu 30. D | Câu 31. B | Câu 32. B | Câu 33. C | Câu 34. B | Câu 35. D |
Câu 1: Biểu thức nào sau đây là tam thức bậc hai?
A. \(0{x^2} + 5x - 3\).
B. \(\frac{1}{{{x^2}}} + \frac{1}{x} + 1\).
C. \(7x - {x^2} + 5\).
D. \({\left( {{x^2} - 2x + 3} \right)^2}\).
Lời giải
Đáp án C.
Câu 2: Chọn từ thích hợp để điền vào chỗ (.).
Nếu tam thức bậc hai \(f(x) = a{x^2} + bx + c(a \ne 0)\) có hai nghiệm phân biệt \({x_1},{x_2}\) \(\left( {{x_1} < {x_2}} \right)\) thì \(f(x) \ldots \ldots ..(1) \ldots ...\) với hệ số \(a\) với mọi \(x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\) và \(f(x)\).(2). với hệ số \(a\) với mọi \(x \in \left( {{x_1};{x_2}} \right)\).
A. (1) trái dấu - (2) cùng dấu.
B. (1) trái dấu - (2) trái dấu.
C. (1) cùng dấu - (2) trái dấu.
D. (1) cùng dấu - (2) cùng dấu.
Lời giải
Đáp án C.
Câu 3: Tập nghiệm của bất phương trình \({x^2} - 2x + 3 > 0\) là:
A. \(\emptyset \).
B. \(\mathbb{R}\).
C. \(( - \infty ; - 1) \cup (3; + \infty )\).
D. \(( - 1;3)\).
Lời giải
Ta có: \({x^2} - 2x + 3 > 0 \Leftrightarrow {(x - 1)^2} + 2 > 0,\forall x \in \mathbb{R}\).
Đáp án B.
Câu 4: Tam thức bậc hai \( - {x^2} + 7x - 12\) nhận giá trị dương khi nào?
A. \(x \in (3;4)\).
B. \(x \in [3;4]\).
C. \(x \in ( - \infty ;3) \cup (4; + \infty )\).
D. \(x \in ( - \infty ;3] \cup [4; + \infty )\).
Lời giải
Đáp án A.
Câu 5: Cô Mai có \(60\;m\) lưới muốn rào một mảnh vườn hình chữ nhật để trồng rau. Biết rằng một cạnh là tường (nên không cần rào), cô Mai chỉ cần rào ba cạnh còn lại của hình chữ nhật để làm vườn. Để diện tích mảnh vườn không ít hơn \(400\;{m^2}\) thì chiều rộng của vườn cần có giá trị nhỏ nhất là bao nhiêu?
A. \(20\;m\).
B. \(15\;m\).
C. \(10\;m\).
D. \(9\;m\).
Lời giải
Gọi \(x,y(0 < x,y < 60)\) lần lượt là độ dài hai cạnh của hình chữ nhật.
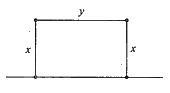
Ta có \(2x + y = 60 \Rightarrow y = 60 - 2x\).
Diện tích hình chữ nhật là \(S = xy = x(60 - 2x)\).
Ta xét bất phương trình \(x(60 - 2x) \ge 400 \Leftrightarrow 10 \le x \le 20\).
Vậy giá trị tối thiểu của chiều rộng là \(10\;m\).
Đáp án C.
Câu 6: Nghiệm của bất phương trình \({x^2} - 9x + 20 > 0\) là:
A. \(x \in [4;5]\).
B. \(x \in (4;5)\).
C. \(x \in ( - \infty ;4] \cup [5; + \infty )\).
D. \(x \in ( - \infty ;4) \cup (5; + \infty )\).
Lời giải
Đáp án D.
Câu 7: Tập ngiệm của bất phương trình: \( - {x^2} + 6x + 7 \ge 0\) là:
A. \(( - \infty ; - 1] \cup [7; + \infty )\).
B. \([ - 1;7]\).
C. \(( - \infty ; - 7] \cup [1; + \infty )\).
D. \([ - 7;1]\).
Lời giải
Xét \( - {x^2} + 6x + 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x = - 1\\x = 7\end{array}\end{array}} \right.{\rm{. }}\)
Bảng xét dấu:

Ta có \(: - {x^2} + 6x + 7 \ge 0 \Leftrightarrow x \in [ - 1;7]\).
Đáp án B.
Câu 8: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{(x + 3)(4 - x) > 0}\\{x - m + 1 < 0}\end{array}} \right.\) vô nghiệm khi và chỉ khi:
A. \(m \le - 2\).
B. \(m > - 2\).
C. \(m < - 1\).
D. \(m = 0\).
Lời giải
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{(x + 3)(4 - x) > 0}\\{x - m + 1 < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 3 < x < 4}\\{x < m - 1}\end{array}} \right.\left( * \right)\).
Hệ \(\left( * \right)\) vô nghiệm \( \Leftrightarrow m - 1 \le - 3 \Leftrightarrow m \le - 2\).
Đáp án A.
Câu 9: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 1 \le 0}\\{x - m > 0}\end{array}} \right.\) có nghiệm khi:
A. \(m > 1\).
B. \(m = 1\).
C. \(m < 1\).
D. \(m \ne 1\).
Lời giải
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 1 \le 0}\\{x - m > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 1 \le x \le 1}\\{x > m}\end{array}\quad (*)} \right.} \right.\)
Do đó hệ \(\left( * \right)\) có nghiệm khi và chỉ khi \(m < 1\).
Đáp án C.
Câu 10: Cho tam thức bậc hai \(f(x) = {x^2} - bx + 3\). Với giá trị nào của \(b\) thì \(f(x)\) có hai nghiệm phân biệt?
A. \(b \in [ - 2\sqrt 3 ;2\sqrt 3 ]\).
B. \(b \in ( - 2\sqrt 3 ;2\sqrt 3 )\).
C. \(b \in ( - \infty ; - 2\sqrt 3 ] \cup [2\sqrt 3 ; + \infty )\).
D. \(b \in ( - \infty ; - 2\sqrt 3 ) \cup (2\sqrt 3 ; + \infty )\).
Lời giải
\(f(x)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta = {b^2} - 12 > 0\). Xét \(\Delta = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}}{b = - 2\sqrt 3 }\\{b = 2\sqrt 3 }\end{array}} \right.\).
Bảng xét dấu:
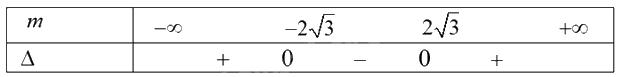
Ta có: \(\Delta = {b^2} - 12 > 0 \Leftrightarrow b \in ( - \infty ; - 2\sqrt 3 ) \cup (2\sqrt 3 ; + \infty )\).
Đáp án D.
Câu 11: Tập hợp tất cả các giá trị của \(m\) để phương trình bậc hai \({x^2} + 2(m + 1)x + 3m = 0\) có nghiệm là
A. \(\{ 0\} \)
B. \(\mathbb{R}\backslash \{ 0\} \).
C. \(\mathbb{R}\).
D. \(\emptyset \).
Lời giải
Phương trình \({x^2} + 2(m + 1)x + 3m = 0\) có nghiệm khi và chỉ khi \({\Delta ^\prime } \ge 0\) \( \Leftrightarrow {(m + 1)^2} - 3m \ge 0 \Leftrightarrow {m^2} - m + 1 \ge 0\).
Xét \(f(m) = {m^2} - m + 1\) có \({\Delta _f} = 1 - 4 = - 3 < 0\) nên \(f(m)\) luôn dương (do cùng dấu \(\left. {{a_f} = 1} \right)\).
Vậy \({m^2} - m + 1 \ge 0 \Leftrightarrow m \in \mathbb{R}\).
Đáp án C.
Câu 12: Phương trình \(m{x^2} - mx + 2 = 0\) có nghiệm khi và chỉ khi:
A. \(m \le 0\) hoặc \(m \ge 8\).
C. \(0 < m \le 8\).
B. \(m < 0\) hoặc \(m \ge 8\).
D. \(0 \le m \le 8\).
Lời giải
Trường hợp 1: \(m = 0\). Thay vào phương trình: \(2 = 0\) (vô nghiệm). Vì vậy \(m = 0\)
không thỏa mãn.
Trường hợp 2: \(m \ne 0\).
Phương trình có nghiệm khi \(\Delta \ge 0 \Leftrightarrow {( - m)^2} - 8m \ge 0 \Leftrightarrow {m^2} - 8m \ge 0\).
Xét \(f(m) = {m^2} - 8m;f(m) = 0 \Leftrightarrow m = 0 \vee m = 8\).
Bảng xét dấu:

Ta có: \(f(m) = {m^2} - 8m \ge 0 \Leftrightarrow m \in ( - \infty ;0) \cup (8; + \infty )\).
So với điều kiện, ta có \(m < 0\) hoặc \(m \ge 8\) thỏa mãn đề bài.
Đáp án B.
Câu 13: Giá trị \(x = 2\) là nghiệm của phương trình nào sau đây?
A. \(\sqrt {{x^2} - x - 4} = \sqrt {x - 4} \).
B. \(x - 1 = \sqrt {x - 3} \).
C. \(x + 2 = 2\sqrt {3x - 2} \).
D. \(x + 2 = \sqrt {x - 1} \).
Lời giải
Đáp án C.
Câu 14: Số nghiệm của phương trình \(\sqrt {{x^2} - 2x - 3} = \sqrt {2{x^2} + x - 3} \) là:
A. 1.
B. 2.
C. 0.
D. 3.
Lời giải
Đáp án A.
Câu 15: Tập nghiệm của phương trình \(\sqrt {{x^2} - 3x + 1} = x - 1\) là:
A. \(S = \{ 1\} \).
B. \(S = \{ 2\} \).
C. \(S = \{ 0\} \).
D. \(S = \emptyset \).
Lời giải
Đáp án D.
Câu 16: Cho phương trình \(\sqrt {{x^2} - mx + {m^2}} = x - m\) (với \(m\) là tham số). Giá trị của \(m\) đê phương trình nhận \(x = 2\) làm nghiệm là:
A. \(m = 2\).
B. \(m = 3\).
C. \(m = 0\).
D. \(m = 1\).
Lời giải
Đáp án C.
Câu 17: Phương trình \(\left( {{x^2} - 6x} \right)\sqrt {17 - {x^2}} = {x^2} - 6x\) có bao nhiêu nghiệm thực phân biệt?
A. 2.
B. 1.
C. 4.
D. 3.
Lời giải
Điều kiện: \(17 - {x^2} \ge 0 \Leftrightarrow - \sqrt {17} \le x \le \sqrt {17} \).
Ta có: \(\left( {{x^2} - 6x} \right)\sqrt {17 - {x^2}} = {x^2} - 6x \Leftrightarrow \left( {{x^2} - 6x} \right)\left( {\sqrt {17 - {x^2}} - 1} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}{x^2} - 6x = 0\\\sqrt {17 - {x^2}} = 1\end{array}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x(x - 6) = 0\\16 - {x^2} = 0\end{array}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x = 0 & (T)\\x = 6 & (L)\\x = \pm 4 & (T)\end{array}\end{array}} \right.} \right.} \right.\)
Vậy phương trình có 3 thực phân biệt.
Đáp án D.
Câu 18: Tổng các nghiệm của phương trình \(\sqrt {3x + 7} - \sqrt {x + 1} = 2\) là
A. 2.
B. \( - 1\).
C. \( - 2\).
D. 4.
Lời giải
\(\sqrt {3x + 7} - \sqrt {x + 1} = 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge - 1}\\{\sqrt {3x + 7} = 2 + \sqrt {x + 1} }\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge - 1\\3x + 7 = 4 + x + 1 + 4\sqrt {x + 1} \end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge - 1\\x + 1 = 2\sqrt {x + 1} \end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge - 1\\{x^2} - 2x - 3 = 0\end{array}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x = - 1\\x = 3\end{array}\end{array}.} \right.} \right.} \right.} \right.\)
Vậy tổng các nghiệm của phương trình là 2.
Đáp án A.
Câu 19: Trong mặt phẳng toạ độ \(Oxy\), toạ độ của vectơ \(2\vec i - 7\vec j\) là:
A. \((2;7)\).
B. \(( - 2;7)\).
C. \((2; - 7)\).
D. \(( - 7;2)\).
Lời giải
Đáp án C.
Câu 20: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(3; - 2)\). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. \((3; - 2)\).
B. \(( - 3;2)\).
C. \(( - 2;3)\).
D. \((2; - 3)\).
Lời giải
Đáp án A.
Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(A( - 3;2),B(5; - 1)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \((2;1)\).
B. \((8; - 3)\).
C. \(( - 8;3)\).
D. \(( - 2; - 1)\).
Lời giải
Đáp án B.
Câu 22: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải
Đáp án D.
Câu 23: Một vectơ pháp tuyến của đường thẳng \(\Delta :y = 2x + 1\) là:
A. \(\overrightarrow {{n_\Delta }} (2; - 1)\).
B. \(\overrightarrow {{n_\Delta }} (1; - 1)\).
C. \(\overrightarrow {{n_\Delta }} ( - 2; - 1)\).
D. \(\overrightarrow {{n_\Delta }} (1;1)\).
Lời giải
Đáp án A.
Câu 24: Đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow {{u_\Delta }} (12; - 13)\). Vectơ nào sau đây là vectơ pháp tuyến của \(\Delta \)?
A. \(\overrightarrow {{n_\Delta }} ( - 13;12)\).
B. \(\overrightarrow {{n_\Delta }} (12;13)\).
C. \(\overrightarrow {{n_\Delta }} (13;12)\).
D. \(\overrightarrow {{n_\Delta }} ( - 12; - 13)\).
Lời giải
Đáp án C.
Câu 25: Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:
A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).
B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).
C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).
D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Lời giải
Đáp án D.
Câu 26: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và có vectơ pháp tuyến \(\vec n(11; - 12)\) là:
A. \(5x + 4y + 7 = 0\).
B. \(5x + 4y - 7 = 0\).
C. \(11x - 12y - 7 = 0\).
D. \(11x - 12y + 7 = 0\).
Lời giải
Đáp án C.
Câu 27: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và vuông góc với đường thẳng \(x - 2y + 5 = 0\) là:
A. \(x - 2y + 3 = 0\).
B. \(2x + y - 14 = 0\).
C. \(x + 2y - 13 = 0\).
D. \(2x + y = 0\).
Lời giải
Đáp án B.
Câu 28: Cho đường thẳng \(\Delta \) có phương trình tổng quát là \(x - 2y - 5 = 0\). Phương trình nào sau đây là phương trình tham số của \(\Delta \)?
A. \(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = 4 - t}\end{array}} \right.\).
B. \(\left\{ {\begin{array}{*{20}{l}}{x = t}\\{y = 5 + 2t}\end{array}} \right.\).
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 4t}\\{y = 1 - 2t}\end{array}} \right.\).
D. \(\left\{ {\begin{array}{*{20}{l}}{x = 5 + 2t}\\{y = t}\end{array}} \right.\).
Lời giải
Đáp án D.
Câu 29: Trong mặt phẳng toạ độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\), \({\Delta _2}:3x - y + 7 = 0\). Nhận định nào sau đây là đúng?
A. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
B. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
C. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trùng nhau.
D. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
Lời giải
Đáp án D.
Câu 30: Người ta quy ước góc giữa hai đường thẳng song song hoặc trùng nhau là:
A. \({180^0}\).
B. \({120^0}\).
C. \({90^0}\).
D. \({0^0}\).
Lời giải
Đáp án D.
Câu 31: Cho \(\alpha \) là góc tạo bởi hai đường thẳng \({\Delta _1}:2x - 3y + 5 = 0\) và \({\Delta _2}:3x + y - 14 = 0\). Giá trị của cosa là:
A. \(\frac{{ - 3}}{{130}}\).
B. \(\frac{3}{{\sqrt {130} }}\).
C. \(\frac{{\sqrt 3 }}{{130}}\).
D. \(\frac{{ - 3}}{{\sqrt {130} }}\).
Lời giải
Đáp án B.
Câu 32: Góc giữa hai đường thẳng \({\Delta _1}:2x + 4y - 1 = 0\) và \({\Delta _2}:x - 3y + 1 = 0\) là:
A. \({0^0}\).
B. \({45^0}\).
C. \({60^0}\).
D. \({90^0}\).
Lời giải
Đáp án B.
Câu 33: Cho đường tròn \((C):{(x - 1)^2} + {(y - 2)^2} = 25\). Đường tròn \((C)\) có:
A. Tâm \(I(1;2)\) và bán kính \(R = 25\).
B. Tâm \(I( - 1; - 2)\) và bán kính \(R = 25\).
C. Tâm \(I(1;2)\) và bán kính \(R = 5\).
D. Tâm \(I( - 1; - 2)\) và bán kính \(R = 5\).
Lời giải
Đáp án C.
Câu 34: Cho đường tròn \((C):{x^2} + {y^2} + 6x - 4y + 2 = 0\). Đường tròn \((C)\) có:
A. Tâm \(I( - 3;2)\) và bán kính \(R = 11\).
B. Tâm \(I( - 3;2)\) và bán kính \(R = \sqrt {11} \).
C. Tâm \(I(3; - 2)\) và bán kính \(R = 11\).
D. Tâm \(I(3; - 2)\) và bán kính \(R = \sqrt {11} \).
Lời giải
Đáp án B.
Câu 35: Phương trình nào sau đây là phương trình của một đường tròn?
A. \({x^2} - {y^2} + 6x - 4y + 2 = 0\).
B. \({x^2} + {y^2} + 2x - 4y + 8 = 0\).
C. \({x^2} + {y^2} + 6x - 10y + 45 = 0\).
D. \({x^2} + {y^2} + 4x - 8y + 13 = 0\)
Lời giải
Đáp án D.
Phần tự luận (3 điểm)
Bài 1. Giải phương trình sau: \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \)
Lời giải
Cách 1:
Bình phương hai vế phương trình, ta được:
\({x^2} + 2x + 4 = 2 - x \Leftrightarrow {x^2} + 3x + 2 = 0 \Leftrightarrow x = - 1 \vee x = - 2.{\rm{ }}\)
Thay giá trị \(x = - 1\) vào phương trình: \(\sqrt 3 = \sqrt 3 \) (thỏa mãn).
Thay giá trị \(x = - 2\) vào phương trình: \(\sqrt 4 = \sqrt 4 \) (thỏa mãn).
Vậy tập nghiệm phương trình là \(S = \{ - 1; - 2\} \).
Cách 2:
Ta có: \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2 - x \ge 0}\\{{x^2} + 2x + 4 = 2 - x}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \le 2\\{x^2} + 3x + 2 = 0\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \le 2\\x = - 1 \vee x = - 2\end{array}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x = - 1\\x = - 2\end{array}\end{array}} \right.} \right.} \right.\)
Vậy tập nghiệm phương trình là \(S = \{ - 1; - 2\} \).
Bài 2. Tìm \(m\) để các bất phương trình sau nghiệm đúng với mọi \(x\):
a) \(3{x^2} - 2(m - 1)x + {m^2} + 4 > 0\)
b) \(m{x^2} + (m - 1)x + m - 1 < 0\)
Lời giải
a) Đặt \(f(x) = 3{x^2} - 2(m - 1)x + {m^2} + 4\) với \(a = 3,{b^\prime } = - (m - 1),c = {m^2} + 4\).
Theo giả thiết:
\(f(x) = 3{x^2} - 2(m - 1)x + {m^2} + 4> 0,\forall x \in \mathbb{R}\left( * \right)\).
Đặt \(f(m) = - 2{m^2} - 2m - 11\) có \({\Delta _f} = {( - 2)^2} - ( - 2)( - 11) = - 18 < 0\).
Vì vậy \(f(m)\) luôn cùng dấu với \( - 2\) tức là \(f(m) < 0,\forall m \in \mathbb{R}\). Do đó (*) luôn đúng.
Vậy, với mọi \(m\) thuộc \(\mathbb{R}\) thì \(f(x) > 0,\forall x \in \mathbb{R}\).
b) Đặt \(f(x) = m{x^2} + (m - 1)x + m - 1\) với \(a = m,{b^\prime } = m - 1,c = m - 1\).
Theo giả thiết: \(f(x) = m{x^2} + (m - 1)x + m - 1 < 0,\forall x \in \mathbb{R}\left( * \right)\).
Trường hợp 1: \(a = m = 0\).
Thay vào \((*): - x - 1 < 0,\forall x \in \mathbb{R} \Leftrightarrow x > - 1,\forall x \in \mathbb{R}\) (sai).
Suy ra \(m = 0\) không thỏa mãn.
Trường hợp 2: \(a = m \ne 0\).
Ta có: \((*) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta < 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 0}\\{{{(m - 1)}^2} - 4m(m - 1) < 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 0}\\{ - 3{m^2} + 2m + 1 < 0}\end{array}} \right.} \right.} \right.\)
Xét \(g(m) = - 3{m^2} + 2m + 1;g(m) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 1}\\{m = - \frac{1}{3}}\end{array}} \right.\).
Bảng xét dấu \(g(m)\):
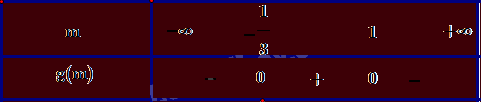
Ta có: \(g(m) < 0 \Leftrightarrow m \in \left( { - \infty ; - \frac{1}{3}} \right) \cup (1; + \infty )\). Vậy \((1) \Leftrightarrow m \in \left( { - \infty ; - \frac{1}{3}} \right)\). Kết hợp hai trường hợp đã xét, ta thu được \(m \in \left( { - \infty ; - \frac{1}{3}} \right)\) thỏa mãn đề bài
Bài 3. Cho các vectơ \(\vec a = (2;0),\vec b = \left( { - 1;\frac{1}{2}} \right),\vec c = (4; - 6)\).
a) Tìm tọa độ của vectơ \(\vec d = 2\vec a - 3\vec b + 5\vec c\).
b) Biểu diễn vectơ \(\vec c\) theo cặp vectơ không cùng phương \(\vec a,\vec b\).
Lời giải
a) Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{2\vec a = (4;0)}\\{ - 3\vec b = \left( {3; - \frac{3}{2}} \right) \Rightarrow \vec d = 2\vec a - 3\vec b + 5\vec c = \left( {27; - \frac{{63}}{2}} \right)}\\{5\vec c = (20; - 30)}\end{array}} \right.\)
b) Gọi: \(\vec c = x\vec a + y\vec b(x,y \in \mathbb{R})\). Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{4 = x \cdot 2 + y( - 1)}\\{ - 6 = x \cdot 0 + y \cdot \frac{1}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 4}\\{y = - 12}\end{array}} \right.} \right.\) Vậy \(\vec c = - 4\vec a - 12\vec b\).
Bài 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x - y + 4 = 0\).
a) Viết phương trình đường cao \(AH\) của tam giác.
b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.
Lời giải
a) Đường cao \(AH\) vuông góc với \(BC\) nên nhận \(\vec u = (1; - 1)\) làm vectơ chỉ phương, suy ra \(AH\) có một vectơ pháp tuyến là \(\vec n = (1;1)\).
Phương trình tổng quát \(AH:1(x + 1) + 1(y + 2) = 0\) hay \(x + y + 3 = 0\).
b) Chọn điểm \(K(0;4)\) thuộc \(BC\), gọi \(E\) là trung điểm đoạn \(AK\) nên \(E\left( { - \frac{1}{2};1} \right)\). Gọi \(d\) là đường trung bình ứng với cạnh đáy \(BC\) của tam giác \(ABC\), suy ra \(d\) qua \(E\) và có một vectơ pháp tuyến .
Phương trình tổng quát \(d:1\left( {x + \frac{1}{2}} \right) - 1(y - 1) = 0\) hay \(2x - 2y + 3 = 0\).
Tải về
Phần trắc nghiệm (7 điểm)
Câu 1: Biểu thức nào sau đây là tam thức bậc hai?
A. \(0{x^2} + 5x - 3\).
B. \(\frac{1}{{{x^2}}} + \frac{1}{x} + 1\).
C. \(7x - {x^2} + 5\).
D. \({\left( {{x^2} - 2x + 3} \right)^2}\).
Câu 2: Chọn từ thích hợp để điền vào chỗ (.).
Nếu tam thức bậc hai \(f(x) = a{x^2} + bx + c(a \ne 0)\) có hai nghiệm phân biệt \({x_1},{x_2}\) \(\left( {{x_1} < {x_2}} \right)\) thì \(f(x) \ldots \ldots ..(1) \ldots ...\) với hệ số \(a\) với mọi \(x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\) và \(f(x)\).(2). với hệ số \(a\) với mọi \(x \in \left( {{x_1};{x_2}} \right)\).
A. (1) trái dấu - (2) cùng dấu.
B. (1) trái dấu - (2) trái dấu.
C. (1) cùng dấu - (2) trái dấu.
D. (1) cùng dấu - (2) cùng dấu.
Câu 3: Tập nghiệm của bất phương trình \({x^2} - 2x + 3 > 0\) là:
A. \(\emptyset \).
B. \(\mathbb{R}\).
C. \(( - \infty ; - 1) \cup (3; + \infty )\).
D. \(( - 1;3)\).
Câu 4: Tam thức bậc hai \( - {x^2} + 7x - 12\) nhận giá trị dương khi nào?
A. \(x \in (3;4)\).
B. \(x \in [3;4]\).
C. \(x \in ( - \infty ;3) \cup (4; + \infty )\).
D. \(x \in ( - \infty ;3] \cup [4; + \infty )\).
Câu 5: Cô Mai có \(60\;m\) lưới muốn rào một mảnh vườn hình chữ nhật để trồng rau. Biết rằng một cạnh là tường (nên không cần rào), cô Mai chỉ cần rào ba cạnh còn lại của hình chữ nhật để làm vườn. Để diện tích mảnh vườn không ít hơn \(400\;{m^2}\) thì chiều rộng của vườn cần có giá trị nhỏ nhất là bao nhiêu?
A. \(20\;m\).
B. \(15\;m\).
C. \(10\;m\).
D. \(9\;m\).
Câu 6: Nghiệm của bất phương trình \({x^2} - 9x + 20 > 0\) là:
A. \(x \in [4;5]\).
B. \(x \in (4;5)\).
C. \(x \in ( - \infty ;4] \cup [5; + \infty )\).
D. \(x \in ( - \infty ;4) \cup (5; + \infty )\).
Câu 7: Tập ngiệm của bất phương trình: \( - {x^2} + 6x + 7 \ge 0\) là:
A. \(( - \infty ; - 1] \cup [7; + \infty )\).
B. \([ - 1;7]\).
C. \(( - \infty ; - 7] \cup [1; + \infty )\).
D. \([ - 7;1]\).
Câu 8: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{(x + 3)(4 - x) > 0}\\{x - m + 1 < 0}\end{array}} \right.\) vô nghiệm khi và chỉ khi:
A. \(m \le - 2\).
B. \(m > - 2\).
C. \(m < - 1\).
D. \(m = 0\).
Câu 9: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 1 \le 0}\\{x - m > 0}\end{array}} \right.\) có nghiệm khi:
A. \(m > 1\).
B. \(m = 1\).
C. \(m < 1\).
D. \(m \ne 1\).
Câu 10: Cho tam thức bậc hai \(f(x) = {x^2} - bx + 3\). Với giá trị nào của \(b\) thì \(f(x)\) có hai nghiệm phân biệt?
A. \(b \in [ - 2\sqrt 3 ;2\sqrt 3 ]\).
B. \(b \in ( - 2\sqrt 3 ;2\sqrt 3 )\).
C. \(b \in ( - \infty ; - 2\sqrt 3 ] \cup [2\sqrt 3 ; + \infty )\).
D. \(b \in ( - \infty ; - 2\sqrt 3 ) \cup (2\sqrt 3 ; + \infty )\).
Câu 11: Tập hợp tất cả các giá trị của \(m\) để phương trình bậc hai \({x^2} + 2(m + 1)x + 3m = 0\) có nghiệm là
A. \(\{ 0\} \)
B. \(\mathbb{R}\backslash \{ 0\} \).
C. \(\mathbb{R}\).
D. \(\emptyset \).
Câu 12: Phương trình \(m{x^2} - mx + 2 = 0\) có nghiệm khi và chỉ khi:
A. \(m \le 0\) hoặc \(m \ge 8\).
C. \(0 < m \le 8\).
B. \(m < 0\) hoặc \(m \ge 8\).
D. \(0 \le m \le 8\).
Câu 13: Giá trị \(x = 2\) là nghiệm của phương trình nào sau đây?
A. \(\sqrt {{x^2} - x - 4} = \sqrt {x - 4} \).
B. \(x - 1 = \sqrt {x - 3} \).
C. \(x + 2 = 2\sqrt {3x - 2} \).
D. \(x + 2 = \sqrt {x - 1} \).
Câu 14: Số nghiệm của phương trình \(\sqrt {{x^2} - 2x - 3} = \sqrt {2{x^2} + x - 3} \) là:
A. 1.
B. 2.
C. 0.
D. 3.
Câu 15: Tập nghiệm của phương trình \(\sqrt {{x^2} - 3x + 1} = x - 1\) là:
A. \(S = \{ 1\} \).
B. \(S = \{ 2\} \).
C. \(S = \{ 0\} \).
D. \(S = \emptyset \).
Câu 16: Cho phương trình \(\sqrt {{x^2} - mx + {m^2}} = x - m\) (với \(m\) là tham số). Giá trị của \(m\) đê phương trình nhận \(x = 2\) làm nghiệm là:
A. \(m = 2\).
B. \(m = 3\).
C. \(m = 0\).
D. \(m = 1\).
Câu 17: Phương trình \(\left( {{x^2} - 6x} \right)\sqrt {17 - {x^2}} = {x^2} - 6x\) có bao nhiêu nghiệm thực phân biệt?
A. 2.
B. 1.
C. 4.
D. 3.
Câu 18: Tổng các nghiệm của phương trình \(\sqrt {3x + 7} - \sqrt {x + 1} = 2\) là
A. 2.
B. \( - 1\).
C. \( - 2\).
D. 4.
Câu 19: Trong mặt phẳng toạ độ \(Oxy\), toạ độ của vectơ \(2\vec i - 7\vec j\) là:
A. \((2;7)\).
B. \(( - 2;7)\).
C. \((2; - 7)\).
D. \(( - 7;2)\).
Câu 20: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(3; - 2)\). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. \((3; - 2)\).
B. \(( - 3;2)\).
C. \(( - 2;3)\).
D. \((2; - 3)\).
Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(A( - 3;2),B(5; - 1)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \((2;1)\).
B. \((8; - 3)\).
C. \(( - 8;3)\).
D. \(( - 2; - 1)\).
Câu 22: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 0.
B. 1.
C. 2.
D. Vô số.
Câu 23: Một vectơ pháp tuyến của đường thẳng \(\Delta :y = 2x + 1\) là:
A. \(\overrightarrow {{n_\Delta }} (2; - 1)\).
B. \(\overrightarrow {{n_\Delta }} (1; - 1)\).
C. \(\overrightarrow {{n_\Delta }} ( - 2; - 1)\).
D. \(\overrightarrow {{n_\Delta }} (1;1)\).
Câu 24: Đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow {{u_\Delta }} (12; - 13)\). Vectơ nào sau đây là vectơ pháp tuyến của \(\Delta \)?
A. \(\overrightarrow {{n_\Delta }} ( - 13;12)\).
B. \(\overrightarrow {{n_\Delta }} (12;13)\).
C. \(\overrightarrow {{n_\Delta }} (13;12)\).
D. \(\overrightarrow {{n_\Delta }} ( - 12; - 13)\).
Câu 25: Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:
A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).
B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).
C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).
D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Câu 26: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và có vectơ pháp tuyến \(\vec n(11; - 12)\) là:
A. \(5x + 4y + 7 = 0\).
B. \(5x + 4y - 7 = 0\).
C. \(11x - 12y - 7 = 0\).
D. \(11x - 12y + 7 = 0\).
Câu 27: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và vuông góc với đường thẳng \(x - 2y + 5 = 0\) là:
A. \(x - 2y + 3 = 0\).
B. \(2x + y - 14 = 0\).
C. \(x + 2y - 13 = 0\).
D. \(2x + y = 0\).
Câu 28: Cho đường thẳng \(\Delta \) có phương trình tổng quát là \(x - 2y - 5 = 0\). Phương trình nào sau đây là phương trình tham số của \(\Delta \)?
A. \(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = 4 - t}\end{array}} \right.\).
B. \(\left\{ {\begin{array}{*{20}{l}}{x = t}\\{y = 5 + 2t}\end{array}} \right.\).
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 4t}\\{y = 1 - 2t}\end{array}} \right.\).
D. \(\left\{ {\begin{array}{*{20}{l}}{x = 5 + 2t}\\{y = t}\end{array}} \right.\).
Câu 29: Trong mặt phẳng toạ độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\), \({\Delta _2}:3x - y + 7 = 0\). Nhận định nào sau đây là đúng?
A. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
B. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
C. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trùng nhau.
D. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
Câu 30: Người ta quy ước góc giữa hai đường thẳng song song hoặc trùng nhau là:
A. \({180^0}\).
B. \({120^0}\).
C. \({90^0}\).
D. \({0^0}\).
Câu 31: Cho \(\alpha \) là góc tạo bởi hai đường thẳng \({\Delta _1}:2x - 3y + 5 = 0\) và \({\Delta _2}:3x + y - 14 = 0\). Giá trị của cosa là:
A. \(\frac{{ - 3}}{{130}}\).
B. \(\frac{3}{{\sqrt {130} }}\).
C. \(\frac{{\sqrt 3 }}{{130}}\).
D. \(\frac{{ - 3}}{{\sqrt {130} }}\).
Câu 32: Góc giữa hai đường thẳng \({\Delta _1}:2x + 4y - 1 = 0\) và \({\Delta _2}:x - 3y + 1 = 0\) là:
A. \({0^0}\).
B. \({45^0}\).
C. \({60^0}\).
D. \({90^0}\).
Câu 33: Cho đường tròn \((C):{(x - 1)^2} + {(y - 2)^2} = 25\). Đường tròn \((C)\) có:
A. Tâm \(I(1;2)\) và bán kính \(R = 25\).
B. Tâm \(I( - 1; - 2)\) và bán kính \(R = 25\).
C. Tâm \(I(1;2)\) và bán kính \(R = 5\).
D. Tâm \(I( - 1; - 2)\) và bán kính \(R = 5\).
Câu 34: Cho đường tròn \((C):{x^2} + {y^2} + 6x - 4y + 2 = 0\). Đường tròn \((C)\) có:
A. Tâm \(I( - 3;2)\) và bán kính \(R = 11\).
B. Tâm \(I( - 3;2)\) và bán kính \(R = \sqrt {11} \).
C. Tâm \(I(3; - 2)\) và bán kính \(R = 11\).
D. Tâm \(I(3; - 2)\) và bán kính \(R = \sqrt {11} \).
Câu 35: Phương trình nào sau đây là phương trình của một đường tròn?
A. \({x^2} - {y^2} + 6x - 4y + 2 = 0\).
B. \({x^2} + {y^2} + 2x - 4y + 8 = 0\).
C. \({x^2} + {y^2} + 6x - 10y + 45 = 0\).
D. \({x^2} + {y^2} + 4x - 8y + 13 = 0\)
Phần tự luận (3 điểm)
Bài 1. Giải phương trình sau: \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \)
Bài 2. Tìm \(m\) để các bất phương trình sau nghiệm đúng với mọi \(x\):
a) \(3{x^2} - 2(m - 1)x + {m^2} + 4 > 0\)
b) \(m{x^2} + (m - 1)x + m - 1 < 0\)
Bài 3. Cho các vectơ \(\vec a = (2;0),\vec b = \left( { - 1;\frac{1}{2}} \right),\vec c = (4; - 6)\).
a) Tìm tọa độ của vectơ \(\vec d = 2\vec a - 3\vec b + 5\vec c\).
b) Biểu diễn vectơ \(\vec c\) theo cặp vectơ không cùng phương \(\vec a,\vec b\).
Bài 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x - y + 4 = 0\).
a) Viết phương trình đường cao \(AH\) của tam giác.
b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.
-------- Hết --------
Phần trắc nghiệm
Câu 1. C | Câu 2. C | Câu 3. B | Câu 4. A | Câu 5. C | Câu 6. D | Câu 7. B |
Câu 8. A | Câu 9. C | Câu 10. D | Câu 11. C | Câu 12. B | Câu 13. C | Câu 14. A |
Câu 15. D | Câu 16. C | Câu 17. D | Câu 18. A | Câu 19. C | Câu 20. A | Câu 21. B |
Câu 22. D | Câu 23. A | Câu 24. C | Câu 25. D | Câu 26. C | Câu 27. B | Câu 28. D |
Câu 29. D | Câu 30. D | Câu 31. B | Câu 32. B | Câu 33. C | Câu 34. B | Câu 35. D |
Câu 1: Biểu thức nào sau đây là tam thức bậc hai?
A. \(0{x^2} + 5x - 3\).
B. \(\frac{1}{{{x^2}}} + \frac{1}{x} + 1\).
C. \(7x - {x^2} + 5\).
D. \({\left( {{x^2} - 2x + 3} \right)^2}\).
Lời giải
Đáp án C.
Câu 2: Chọn từ thích hợp để điền vào chỗ (.).
Nếu tam thức bậc hai \(f(x) = a{x^2} + bx + c(a \ne 0)\) có hai nghiệm phân biệt \({x_1},{x_2}\) \(\left( {{x_1} < {x_2}} \right)\) thì \(f(x) \ldots \ldots ..(1) \ldots ...\) với hệ số \(a\) với mọi \(x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\) và \(f(x)\).(2). với hệ số \(a\) với mọi \(x \in \left( {{x_1};{x_2}} \right)\).
A. (1) trái dấu - (2) cùng dấu.
B. (1) trái dấu - (2) trái dấu.
C. (1) cùng dấu - (2) trái dấu.
D. (1) cùng dấu - (2) cùng dấu.
Lời giải
Đáp án C.
Câu 3: Tập nghiệm của bất phương trình \({x^2} - 2x + 3 > 0\) là:
A. \(\emptyset \).
B. \(\mathbb{R}\).
C. \(( - \infty ; - 1) \cup (3; + \infty )\).
D. \(( - 1;3)\).
Lời giải
Ta có: \({x^2} - 2x + 3 > 0 \Leftrightarrow {(x - 1)^2} + 2 > 0,\forall x \in \mathbb{R}\).
Đáp án B.
Câu 4: Tam thức bậc hai \( - {x^2} + 7x - 12\) nhận giá trị dương khi nào?
A. \(x \in (3;4)\).
B. \(x \in [3;4]\).
C. \(x \in ( - \infty ;3) \cup (4; + \infty )\).
D. \(x \in ( - \infty ;3] \cup [4; + \infty )\).
Lời giải
Đáp án A.
Câu 5: Cô Mai có \(60\;m\) lưới muốn rào một mảnh vườn hình chữ nhật để trồng rau. Biết rằng một cạnh là tường (nên không cần rào), cô Mai chỉ cần rào ba cạnh còn lại của hình chữ nhật để làm vườn. Để diện tích mảnh vườn không ít hơn \(400\;{m^2}\) thì chiều rộng của vườn cần có giá trị nhỏ nhất là bao nhiêu?
A. \(20\;m\).
B. \(15\;m\).
C. \(10\;m\).
D. \(9\;m\).
Lời giải
Gọi \(x,y(0 < x,y < 60)\) lần lượt là độ dài hai cạnh của hình chữ nhật.
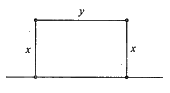
Ta có \(2x + y = 60 \Rightarrow y = 60 - 2x\).
Diện tích hình chữ nhật là \(S = xy = x(60 - 2x)\).
Ta xét bất phương trình \(x(60 - 2x) \ge 400 \Leftrightarrow 10 \le x \le 20\).
Vậy giá trị tối thiểu của chiều rộng là \(10\;m\).
Đáp án C.
Câu 6: Nghiệm của bất phương trình \({x^2} - 9x + 20 > 0\) là:
A. \(x \in [4;5]\).
B. \(x \in (4;5)\).
C. \(x \in ( - \infty ;4] \cup [5; + \infty )\).
D. \(x \in ( - \infty ;4) \cup (5; + \infty )\).
Lời giải
Đáp án D.
Câu 7: Tập ngiệm của bất phương trình: \( - {x^2} + 6x + 7 \ge 0\) là:
A. \(( - \infty ; - 1] \cup [7; + \infty )\).
B. \([ - 1;7]\).
C. \(( - \infty ; - 7] \cup [1; + \infty )\).
D. \([ - 7;1]\).
Lời giải
Xét \( - {x^2} + 6x + 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x = - 1\\x = 7\end{array}\end{array}} \right.{\rm{. }}\)
Bảng xét dấu:

Ta có \(: - {x^2} + 6x + 7 \ge 0 \Leftrightarrow x \in [ - 1;7]\).
Đáp án B.
Câu 8: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{(x + 3)(4 - x) > 0}\\{x - m + 1 < 0}\end{array}} \right.\) vô nghiệm khi và chỉ khi:
A. \(m \le - 2\).
B. \(m > - 2\).
C. \(m < - 1\).
D. \(m = 0\).
Lời giải
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{(x + 3)(4 - x) > 0}\\{x - m + 1 < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 3 < x < 4}\\{x < m - 1}\end{array}} \right.\left( * \right)\).
Hệ \(\left( * \right)\) vô nghiệm \( \Leftrightarrow m - 1 \le - 3 \Leftrightarrow m \le - 2\).
Đáp án A.
Câu 9: Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 1 \le 0}\\{x - m > 0}\end{array}} \right.\) có nghiệm khi:
A. \(m > 1\).
B. \(m = 1\).
C. \(m < 1\).
D. \(m \ne 1\).
Lời giải
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 1 \le 0}\\{x - m > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 1 \le x \le 1}\\{x > m}\end{array}\quad (*)} \right.} \right.\)
Do đó hệ \(\left( * \right)\) có nghiệm khi và chỉ khi \(m < 1\).
Đáp án C.
Câu 10: Cho tam thức bậc hai \(f(x) = {x^2} - bx + 3\). Với giá trị nào của \(b\) thì \(f(x)\) có hai nghiệm phân biệt?
A. \(b \in [ - 2\sqrt 3 ;2\sqrt 3 ]\).
B. \(b \in ( - 2\sqrt 3 ;2\sqrt 3 )\).
C. \(b \in ( - \infty ; - 2\sqrt 3 ] \cup [2\sqrt 3 ; + \infty )\).
D. \(b \in ( - \infty ; - 2\sqrt 3 ) \cup (2\sqrt 3 ; + \infty )\).
Lời giải
\(f(x)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta = {b^2} - 12 > 0\). Xét \(\Delta = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}}{b = - 2\sqrt 3 }\\{b = 2\sqrt 3 }\end{array}} \right.\).
Bảng xét dấu:
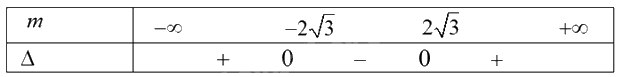
Ta có: \(\Delta = {b^2} - 12 > 0 \Leftrightarrow b \in ( - \infty ; - 2\sqrt 3 ) \cup (2\sqrt 3 ; + \infty )\).
Đáp án D.
Câu 11: Tập hợp tất cả các giá trị của \(m\) để phương trình bậc hai \({x^2} + 2(m + 1)x + 3m = 0\) có nghiệm là
A. \(\{ 0\} \)
B. \(\mathbb{R}\backslash \{ 0\} \).
C. \(\mathbb{R}\).
D. \(\emptyset \).
Lời giải
Phương trình \({x^2} + 2(m + 1)x + 3m = 0\) có nghiệm khi và chỉ khi \({\Delta ^\prime } \ge 0\) \( \Leftrightarrow {(m + 1)^2} - 3m \ge 0 \Leftrightarrow {m^2} - m + 1 \ge 0\).
Xét \(f(m) = {m^2} - m + 1\) có \({\Delta _f} = 1 - 4 = - 3 < 0\) nên \(f(m)\) luôn dương (do cùng dấu \(\left. {{a_f} = 1} \right)\).
Vậy \({m^2} - m + 1 \ge 0 \Leftrightarrow m \in \mathbb{R}\).
Đáp án C.
Câu 12: Phương trình \(m{x^2} - mx + 2 = 0\) có nghiệm khi và chỉ khi:
A. \(m \le 0\) hoặc \(m \ge 8\).
C. \(0 < m \le 8\).
B. \(m < 0\) hoặc \(m \ge 8\).
D. \(0 \le m \le 8\).
Lời giải
Trường hợp 1: \(m = 0\). Thay vào phương trình: \(2 = 0\) (vô nghiệm). Vì vậy \(m = 0\)
không thỏa mãn.
Trường hợp 2: \(m \ne 0\).
Phương trình có nghiệm khi \(\Delta \ge 0 \Leftrightarrow {( - m)^2} - 8m \ge 0 \Leftrightarrow {m^2} - 8m \ge 0\).
Xét \(f(m) = {m^2} - 8m;f(m) = 0 \Leftrightarrow m = 0 \vee m = 8\).
Bảng xét dấu:

Ta có: \(f(m) = {m^2} - 8m \ge 0 \Leftrightarrow m \in ( - \infty ;0) \cup (8; + \infty )\).
So với điều kiện, ta có \(m < 0\) hoặc \(m \ge 8\) thỏa mãn đề bài.
Đáp án B.
Câu 13: Giá trị \(x = 2\) là nghiệm của phương trình nào sau đây?
A. \(\sqrt {{x^2} - x - 4} = \sqrt {x - 4} \).
B. \(x - 1 = \sqrt {x - 3} \).
C. \(x + 2 = 2\sqrt {3x - 2} \).
D. \(x + 2 = \sqrt {x - 1} \).
Lời giải
Đáp án C.
Câu 14: Số nghiệm của phương trình \(\sqrt {{x^2} - 2x - 3} = \sqrt {2{x^2} + x - 3} \) là:
A. 1.
B. 2.
C. 0.
D. 3.
Lời giải
Đáp án A.
Câu 15: Tập nghiệm của phương trình \(\sqrt {{x^2} - 3x + 1} = x - 1\) là:
A. \(S = \{ 1\} \).
B. \(S = \{ 2\} \).
C. \(S = \{ 0\} \).
D. \(S = \emptyset \).
Lời giải
Đáp án D.
Câu 16: Cho phương trình \(\sqrt {{x^2} - mx + {m^2}} = x - m\) (với \(m\) là tham số). Giá trị của \(m\) đê phương trình nhận \(x = 2\) làm nghiệm là:
A. \(m = 2\).
B. \(m = 3\).
C. \(m = 0\).
D. \(m = 1\).
Lời giải
Đáp án C.
Câu 17: Phương trình \(\left( {{x^2} - 6x} \right)\sqrt {17 - {x^2}} = {x^2} - 6x\) có bao nhiêu nghiệm thực phân biệt?
A. 2.
B. 1.
C. 4.
D. 3.
Lời giải
Điều kiện: \(17 - {x^2} \ge 0 \Leftrightarrow - \sqrt {17} \le x \le \sqrt {17} \).
Ta có: \(\left( {{x^2} - 6x} \right)\sqrt {17 - {x^2}} = {x^2} - 6x \Leftrightarrow \left( {{x^2} - 6x} \right)\left( {\sqrt {17 - {x^2}} - 1} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}{x^2} - 6x = 0\\\sqrt {17 - {x^2}} = 1\end{array}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x(x - 6) = 0\\16 - {x^2} = 0\end{array}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x = 0 & (T)\\x = 6 & (L)\\x = \pm 4 & (T)\end{array}\end{array}} \right.} \right.} \right.\)
Vậy phương trình có 3 thực phân biệt.
Đáp án D.
Câu 18: Tổng các nghiệm của phương trình \(\sqrt {3x + 7} - \sqrt {x + 1} = 2\) là
A. 2.
B. \( - 1\).
C. \( - 2\).
D. 4.
Lời giải
\(\sqrt {3x + 7} - \sqrt {x + 1} = 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge - 1}\\{\sqrt {3x + 7} = 2 + \sqrt {x + 1} }\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge - 1\\3x + 7 = 4 + x + 1 + 4\sqrt {x + 1} \end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge - 1\\x + 1 = 2\sqrt {x + 1} \end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \ge - 1\\{x^2} - 2x - 3 = 0\end{array}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x = - 1\\x = 3\end{array}\end{array}.} \right.} \right.} \right.} \right.\)
Vậy tổng các nghiệm của phương trình là 2.
Đáp án A.
Câu 19: Trong mặt phẳng toạ độ \(Oxy\), toạ độ của vectơ \(2\vec i - 7\vec j\) là:
A. \((2;7)\).
B. \(( - 2;7)\).
C. \((2; - 7)\).
D. \(( - 7;2)\).
Lời giải
Đáp án C.
Câu 20: Trong mặt phẳng toạ độ \(Oxy\), cho \(A(3; - 2)\). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. \((3; - 2)\).
B. \(( - 3;2)\).
C. \(( - 2;3)\).
D. \((2; - 3)\).
Lời giải
Đáp án A.
Câu 21: Trong mặt phẳng toạ độ \(Oxy\), cho \(A( - 3;2),B(5; - 1)\). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. \((2;1)\).
B. \((8; - 3)\).
C. \(( - 8;3)\).
D. \(( - 2; - 1)\).
Lời giải
Đáp án B.
Câu 22: Một đường thẳng có bao nhiêu vectơ pháp tuyến?
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải
Đáp án D.
Câu 23: Một vectơ pháp tuyến của đường thẳng \(\Delta :y = 2x + 1\) là:
A. \(\overrightarrow {{n_\Delta }} (2; - 1)\).
B. \(\overrightarrow {{n_\Delta }} (1; - 1)\).
C. \(\overrightarrow {{n_\Delta }} ( - 2; - 1)\).
D. \(\overrightarrow {{n_\Delta }} (1;1)\).
Lời giải
Đáp án A.
Câu 24: Đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow {{u_\Delta }} (12; - 13)\). Vectơ nào sau đây là vectơ pháp tuyến của \(\Delta \)?
A. \(\overrightarrow {{n_\Delta }} ( - 13;12)\).
B. \(\overrightarrow {{n_\Delta }} (12;13)\).
C. \(\overrightarrow {{n_\Delta }} (13;12)\).
D. \(\overrightarrow {{n_\Delta }} ( - 12; - 13)\).
Lời giải
Đáp án C.
Câu 25: Phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến \(\vec n(a;b)\) là:
A. \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\).
B. \(b\left( {x - {x_0}} \right) - a\left( {y - {y_0}} \right) = 0\).
C. \(a\left( {x + {x_0}} \right) + b\left( {y + {y_0}} \right) = 0\).
D. \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
Lời giải
Đáp án D.
Câu 26: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và có vectơ pháp tuyến \(\vec n(11; - 12)\) là:
A. \(5x + 4y + 7 = 0\).
B. \(5x + 4y - 7 = 0\).
C. \(11x - 12y - 7 = 0\).
D. \(11x - 12y + 7 = 0\).
Lời giải
Đáp án C.
Câu 27: Phương trình của đường thẳng \(\Delta \) đi qua điểm \(M(5;4)\) và vuông góc với đường thẳng \(x - 2y + 5 = 0\) là:
A. \(x - 2y + 3 = 0\).
B. \(2x + y - 14 = 0\).
C. \(x + 2y - 13 = 0\).
D. \(2x + y = 0\).
Lời giải
Đáp án B.
Câu 28: Cho đường thẳng \(\Delta \) có phương trình tổng quát là \(x - 2y - 5 = 0\). Phương trình nào sau đây là phương trình tham số của \(\Delta \)?
A. \(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = 4 - t}\end{array}} \right.\).
B. \(\left\{ {\begin{array}{*{20}{l}}{x = t}\\{y = 5 + 2t}\end{array}} \right.\).
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + 4t}\\{y = 1 - 2t}\end{array}} \right.\).
D. \(\left\{ {\begin{array}{*{20}{l}}{x = 5 + 2t}\\{y = t}\end{array}} \right.\).
Lời giải
Đáp án D.
Câu 29: Trong mặt phẳng toạ độ \(Oxy\), cho hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\), \({\Delta _2}:3x - y + 7 = 0\). Nhận định nào sau đây là đúng?
A. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
B. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
C. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trùng nhau.
D. Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
Lời giải
Đáp án D.
Câu 30: Người ta quy ước góc giữa hai đường thẳng song song hoặc trùng nhau là:
A. \({180^0}\).
B. \({120^0}\).
C. \({90^0}\).
D. \({0^0}\).
Lời giải
Đáp án D.
Câu 31: Cho \(\alpha \) là góc tạo bởi hai đường thẳng \({\Delta _1}:2x - 3y + 5 = 0\) và \({\Delta _2}:3x + y - 14 = 0\). Giá trị của cosa là:
A. \(\frac{{ - 3}}{{130}}\).
B. \(\frac{3}{{\sqrt {130} }}\).
C. \(\frac{{\sqrt 3 }}{{130}}\).
D. \(\frac{{ - 3}}{{\sqrt {130} }}\).
Lời giải
Đáp án B.
Câu 32: Góc giữa hai đường thẳng \({\Delta _1}:2x + 4y - 1 = 0\) và \({\Delta _2}:x - 3y + 1 = 0\) là:
A. \({0^0}\).
B. \({45^0}\).
C. \({60^0}\).
D. \({90^0}\).
Lời giải
Đáp án B.
Câu 33: Cho đường tròn \((C):{(x - 1)^2} + {(y - 2)^2} = 25\). Đường tròn \((C)\) có:
A. Tâm \(I(1;2)\) và bán kính \(R = 25\).
B. Tâm \(I( - 1; - 2)\) và bán kính \(R = 25\).
C. Tâm \(I(1;2)\) và bán kính \(R = 5\).
D. Tâm \(I( - 1; - 2)\) và bán kính \(R = 5\).
Lời giải
Đáp án C.
Câu 34: Cho đường tròn \((C):{x^2} + {y^2} + 6x - 4y + 2 = 0\). Đường tròn \((C)\) có:
A. Tâm \(I( - 3;2)\) và bán kính \(R = 11\).
B. Tâm \(I( - 3;2)\) và bán kính \(R = \sqrt {11} \).
C. Tâm \(I(3; - 2)\) và bán kính \(R = 11\).
D. Tâm \(I(3; - 2)\) và bán kính \(R = \sqrt {11} \).
Lời giải
Đáp án B.
Câu 35: Phương trình nào sau đây là phương trình của một đường tròn?
A. \({x^2} - {y^2} + 6x - 4y + 2 = 0\).
B. \({x^2} + {y^2} + 2x - 4y + 8 = 0\).
C. \({x^2} + {y^2} + 6x - 10y + 45 = 0\).
D. \({x^2} + {y^2} + 4x - 8y + 13 = 0\)
Lời giải
Đáp án D.
Phần tự luận (3 điểm)
Bài 1. Giải phương trình sau: \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \)
Lời giải
Cách 1:
Bình phương hai vế phương trình, ta được:
\({x^2} + 2x + 4 = 2 - x \Leftrightarrow {x^2} + 3x + 2 = 0 \Leftrightarrow x = - 1 \vee x = - 2.{\rm{ }}\)
Thay giá trị \(x = - 1\) vào phương trình: \(\sqrt 3 = \sqrt 3 \) (thỏa mãn).
Thay giá trị \(x = - 2\) vào phương trình: \(\sqrt 4 = \sqrt 4 \) (thỏa mãn).
Vậy tập nghiệm phương trình là \(S = \{ - 1; - 2\} \).
Cách 2:
Ta có: \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2 - x \ge 0}\\{{x^2} + 2x + 4 = 2 - x}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \le 2\\{x^2} + 3x + 2 = 0\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x \le 2\\x = - 1 \vee x = - 2\end{array}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}\begin{array}{l}x = - 1\\x = - 2\end{array}\end{array}} \right.} \right.} \right.\)
Vậy tập nghiệm phương trình là \(S = \{ - 1; - 2\} \).
Bài 2. Tìm \(m\) để các bất phương trình sau nghiệm đúng với mọi \(x\):
a) \(3{x^2} - 2(m - 1)x + {m^2} + 4 > 0\)
b) \(m{x^2} + (m - 1)x + m - 1 < 0\)
Lời giải
a) Đặt \(f(x) = 3{x^2} - 2(m - 1)x + {m^2} + 4\) với \(a = 3,{b^\prime } = - (m - 1),c = {m^2} + 4\).
Theo giả thiết:
\(f(x) = 3{x^2} - 2(m - 1)x + {m^2} + 4> 0,\forall x \in \mathbb{R}\left( * \right)\).
Đặt \(f(m) = - 2{m^2} - 2m - 11\) có \({\Delta _f} = {( - 2)^2} - ( - 2)( - 11) = - 18 < 0\).
Vì vậy \(f(m)\) luôn cùng dấu với \( - 2\) tức là \(f(m) < 0,\forall m \in \mathbb{R}\). Do đó (*) luôn đúng.
Vậy, với mọi \(m\) thuộc \(\mathbb{R}\) thì \(f(x) > 0,\forall x \in \mathbb{R}\).
b) Đặt \(f(x) = m{x^2} + (m - 1)x + m - 1\) với \(a = m,{b^\prime } = m - 1,c = m - 1\).
Theo giả thiết: \(f(x) = m{x^2} + (m - 1)x + m - 1 < 0,\forall x \in \mathbb{R}\left( * \right)\).
Trường hợp 1: \(a = m = 0\).
Thay vào \((*): - x - 1 < 0,\forall x \in \mathbb{R} \Leftrightarrow x > - 1,\forall x \in \mathbb{R}\) (sai).
Suy ra \(m = 0\) không thỏa mãn.
Trường hợp 2: \(a = m \ne 0\).
Ta có: \((*) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta < 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 0}\\{{{(m - 1)}^2} - 4m(m - 1) < 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 0}\\{ - 3{m^2} + 2m + 1 < 0}\end{array}} \right.} \right.} \right.\)
Xét \(g(m) = - 3{m^2} + 2m + 1;g(m) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 1}\\{m = - \frac{1}{3}}\end{array}} \right.\).
Bảng xét dấu \(g(m)\):
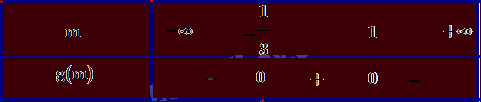
Ta có: \(g(m) < 0 \Leftrightarrow m \in \left( { - \infty ; - \frac{1}{3}} \right) \cup (1; + \infty )\). Vậy \((1) \Leftrightarrow m \in \left( { - \infty ; - \frac{1}{3}} \right)\). Kết hợp hai trường hợp đã xét, ta thu được \(m \in \left( { - \infty ; - \frac{1}{3}} \right)\) thỏa mãn đề bài
Bài 3. Cho các vectơ \(\vec a = (2;0),\vec b = \left( { - 1;\frac{1}{2}} \right),\vec c = (4; - 6)\).
a) Tìm tọa độ của vectơ \(\vec d = 2\vec a - 3\vec b + 5\vec c\).
b) Biểu diễn vectơ \(\vec c\) theo cặp vectơ không cùng phương \(\vec a,\vec b\).
Lời giải
a) Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{2\vec a = (4;0)}\\{ - 3\vec b = \left( {3; - \frac{3}{2}} \right) \Rightarrow \vec d = 2\vec a - 3\vec b + 5\vec c = \left( {27; - \frac{{63}}{2}} \right)}\\{5\vec c = (20; - 30)}\end{array}} \right.\)
b) Gọi: \(\vec c = x\vec a + y\vec b(x,y \in \mathbb{R})\). Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{4 = x \cdot 2 + y( - 1)}\\{ - 6 = x \cdot 0 + y \cdot \frac{1}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 4}\\{y = - 12}\end{array}} \right.} \right.\) Vậy \(\vec c = - 4\vec a - 12\vec b\).
Bài 4. Cho tam giác \(ABC\) với \(A( - 1; - 2)\) và phương trình đường thẳng chứa cạnh \(BC\) là \(x - y + 4 = 0\).
a) Viết phương trình đường cao \(AH\) của tam giác.
b) Viết phương trình đường trung bình ứng với cạnh đáy \(BC\) của tam giác.
Lời giải
a) Đường cao \(AH\) vuông góc với \(BC\) nên nhận \(\vec u = (1; - 1)\) làm vectơ chỉ phương, suy ra \(AH\) có một vectơ pháp tuyến là \(\vec n = (1;1)\).
Phương trình tổng quát \(AH:1(x + 1) + 1(y + 2) = 0\) hay \(x + y + 3 = 0\).
b) Chọn điểm \(K(0;4)\) thuộc \(BC\), gọi \(E\) là trung điểm đoạn \(AK\) nên \(E\left( { - \frac{1}{2};1} \right)\). Gọi \(d\) là đường trung bình ứng với cạnh đáy \(BC\) của tam giác \(ABC\), suy ra \(d\) qua \(E\) và có một vectơ pháp tuyến .
Phương trình tổng quát \(d:1\left( {x + \frac{1}{2}} \right) - 1(y - 1) = 0\) hay \(2x - 2y + 3 = 0\).
Đề thi giữa kì 2 Toán 10 Chân trời sáng tạo - Đề số 1 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một nửa học kì. Đề thi này không chỉ kiểm tra kiến thức đã học mà còn rèn luyện kỹ năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết một số câu hỏi điển hình.
Thông thường, đề thi giữa kì 2 Toán 10 Chân trời sáng tạo - Đề số 1 có cấu trúc bao gồm hai phần chính:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 10 Chân trời sáng tạo - Đề số 1:
Ví dụ 1: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol.
Giải:
Tọa độ đỉnh của parabol y = ax2 + bx + c là I(-b/2a, -Δ/4a), với Δ = b2 - 4ac.
Trong trường hợp này, a = 1, b = -4, c = 3. Vậy Δ = (-4)2 - 4(1)(3) = 16 - 12 = 4.
Tọa độ đỉnh của parabol là I(-(-4)/2(1), -4/4(1)) = I(2, -1).
Ví dụ 2: Tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4).
Giải:
Phương trình đường thẳng đi qua hai điểm A(x1; y1) và B(x2; y2) có dạng:
(y - y1) / (x - x1) = (y2 - y1) / (x2 - x1)
Thay A(1; 2) và B(3; 4) vào phương trình, ta được:
(y - 2) / (x - 1) = (4 - 2) / (3 - 1) = 2 / 2 = 1
Vậy phương trình đường thẳng là y - 2 = x - 1, hay y = x + 1.
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi giữa kì 2 Toán 10 Chân trời sáng tạo - Đề số 1!