Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 11 Cánh diều - Đề số 1, được biên soạn theo chuẩn chương trình học mới nhất của Bộ Giáo dục và Đào tạo. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi thực tế và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 1 môn Toán 11 Cánh diều. Đi kèm với đề thi là đáp án chi tiết, giúp học sinh tự đánh giá kết quả và tìm ra những điểm cần cải thiện.
Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là:
Chọn đáp án đúng
Nghiệm của phương trình \(\sin x = \sin \frac{\pi }{3}\) là:
Tập xác định của D của hàm số \(y = \cot x\) là:
Hàm số \(y = \tan x\)tuần hoàn với chu kì là:
Trong các dãy số sau, dãy số nào là dãy số tăng?
Trong các dãy số sau, dãy số nào là cấp số cộng?
Dãy số nào dưới đây được viết dưới dạng công thức của số hạng tổng quát?
Biết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\). Chọn đáp án đúng
Hàm số nào sau đây liên tục trên \(\mathbb{R}\)?
Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } \frac{4}{n}\) bằng:
Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left( {x - 3} \right)\) là:
Cho lăng trụ tam giác ABC.A’B’C’. Khẳng định nào sau đây là đúng?
Cho đường thẳng d và mặt phẳng \(\left( \alpha \right)\) không có điểm chung. Kết luận nào sau đây là đúng?
Cho hai đường thẳng a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
Nếu d là giao tuyến của hai mặt phẳng phân biệt (P) và (Q) thì:
Cho tứ diện ABCD. Chọn đáp án đúng.
Giá trị lớn nhất của hàm số \(y = 2\cos x + 1\) bằng:
Tìm tất cả các giá trị của m để phương trình \({\cos ^2}x - {\sin ^2}x - m = 0\) có nghiệm?
Cho góc \(\alpha \) thỏa mãn \(\sin \alpha = \frac{1}{2}\) và \(\frac{\pi }{2} < \alpha < \pi \). Tính \(\cos \alpha \).
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + 2{u_{n - 2}}\end{array} \right.\left( {n \ge 3,n \in \mathbb{N}} \right)\). Giá trị của \({u_3} + {u_4}\) là:
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2,q = 3\). Tính tổng của mười số hạng đầu tiên của cấp số nhân đó.
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2;d = 3\). Khi đó, \({u_4} + {u_6}\) bằng:
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 16}}{{x - 2}}\) là:
Biết rằng \(\mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{{x^2} - 3}}{{x - \sqrt 3 }} = a\sqrt b \) (với a, b là các số nguyên). Chọn đáp án đúng:
Với giá trị nào của m thì hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 1\;khi\;x \ne -1\\m\;\;\;\;\;\;\,khi\;x = -1\end{array} \right.\) liên tục tại \({x_0} = - 1\)?
Cho tam giác ABC và một điểm S không thuộc mặt phẳng ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó, giao tuyến của hai mặt phẳng (SBN) và (SCM) là:
Cho 4 điểm phân biệt A, B, C, D trong đó không có ba điểm nào thẳng hàng. Xác định được tất cả bao nhiêu từ 3 trong 4 điểm đã cho?
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là:
Cho hình hộp ABCD. A’B’C’D’ có AC cắt BD tại O và A’C’ cắt B’D’ tại O’. Khi đó, mặt phẳng (AB’D’) song song với mặt phẳng nào dưới đây?
Tính giới hạn sau: \(I = \mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {3 + x} - 4x}}{{2x - 2}}\)
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. M là điểm nằm trên cạnh BC sao cho \(MB = 2MC\). Chứng minh rằng MG // (ACD).
Cho hai số thực a và b thỏa mãn điều kiện \(\sin \left( {a + b} \right) - 2\cos \left( {a - b} \right) = 0\). Tính giá trị của biểu thức \(A = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}}\).
Chứng minh rằng dãy số \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \ldots + \frac{1}{{n(n + 1)}}\) tăng và bị chặn trên.
Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là:
Đáp án : B
Sử dụng công thức: \({\alpha ^0} = \alpha .\frac{\pi }{{180}}rad\).
Ta có: \({20^0} = 20.\frac{\pi }{{180}} = \frac{\pi }{9}\)
Chọn đáp án đúng
Đáp án : C
Sử dụng công thức: \(\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b\).
Ta có:\(\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b\)
Nghiệm của phương trình \(\sin x = \sin \frac{\pi }{3}\) là:
Đáp án : A
Phương trình \(\sin x = \sin \alpha \)có nghiệm: \(x = \alpha + k2\pi ,k \in \mathbb{Z}\) và \(x = \pi - \alpha + k2\pi ,k \in \mathbb{Z}\)
\(\sin x = \sin \frac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \pi - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Tập xác định của D của hàm số \(y = \cot x\) là:
Đáp án : D
Sử dụng kiến thức về tập xác định của hàm số lượng giác: Hàm số \(y = \cot x\) có tập xác định là \(D = \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\)
Hàm số \(y = \cot x\) có tập xác định là \(D = \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\)
Hàm số \(y = \tan x\)tuần hoàn với chu kì là:
Đáp án : B
Sử dụng kiến thức về đồ thị và tính chất của hàm số \(y = \tan x\): Hàm số \(y = \tan x\) tuần hoàn với chu kì \(\pi \)
Hàm số \(y = \tan x\) tuần hoàn với chu kì \(\pi \)
Trong các dãy số sau, dãy số nào là dãy số tăng?
Đáp án : A
Sử dụng kiến thức về dãy số tăng: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số tăng nếu ta có: \({u_{n + 1}} > {u_n}\) với mọi \(n \in \mathbb{N}*\)
Trong các dãy số trên, chỉ có dãy số 1; 2; 3; 4; … có \(1 < 2 < 3 < 4...\) nên dãy số 1; 2; 3; 4; … là dãy số tăng.
Trong các dãy số sau, dãy số nào là cấp số cộng?
Đáp án : B
Sử dụng kiến thức về cấp số cộng: Cấp số cộng là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Trong các dãy số trên, chỉ có dãy số 1; 3; 5; 7; 9; … có kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d \(\left( {d = 2} \right)\)
Dãy số nào dưới đây được viết dưới dạng công thức của số hạng tổng quát?
Đáp án : D
Sử dụng kiến thức về cách cho một dãy số.
Dãy số được viết dưới dạng công thức của số hạng tổng quát là: \({u_n} = \frac{1}{n}\left( {n \in \mathbb{N}*} \right)\)
Biết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\). Chọn đáp án đúng
Đáp án : A
Sử dụng quy tắc về giới hạn vô cực của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = + \infty \).
Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = + \infty \).
Hàm số nào sau đây liên tục trên \(\mathbb{R}\)?
Đáp án : D
Sử dụng kiến thức về hàm số liên tục trên một khoảng: Hàm số \(y = f\left( x \right)\) được gọi là liên tục trên khoảng (a; b) nếu nó liên tục tại mọi điểm trên khoảng này.
Hàm số \(y = \frac{{x - 1}}{{{x^2} + 1}}\) liên tục trên \(\mathbb{R}\)
Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } \frac{4}{n}\) bằng:
Đáp án : B
Sử dụng công thức: \(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0\)
Ta có: \(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0\) nên \(\mathop {\lim }\limits_{n \to + \infty } \frac{4}{n} = 0\)
Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left( {x - 3} \right)\) là:
Đáp án : C
Sử dụng quy tắc tính giới hạn của hàm số tại một điểm: Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) - g\left( x \right)} \right] = L - M\)
\(\mathop {\lim }\limits_{x \to 1} \left( {x - 3} \right) = 1 - 3 = - 2\)
Cho lăng trụ tam giác ABC.A’B’C’. Khẳng định nào sau đây là đúng?
Đáp án : D
Sử dụng kiến thức về hình lăng trụ tam giác: Hình lăng trụ có hai đáy song song với nhau.
Hình lăng trụ tam giác ABC.A’B’C’ có (ABC) // (A’B’C’).
Cho đường thẳng d và mặt phẳng \(\left( \alpha \right)\) không có điểm chung. Kết luận nào sau đây là đúng?
Đáp án : A
Sử dụng kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng: Nếu d và \(\left( \alpha \right)\) không có điểm chung thì \(d//\left( \alpha \right)\)
Nếu d và \(\left( \alpha \right)\) không có điểm chung thì \(d//\left( \alpha \right)\)
Cho hai đường thẳng a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
Đáp án : C
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng: Có bốn vị trí tương đối của hai đường thẳng a và b trong không gian: cắt nhau, trùng nhau, song song và chéo nhau.
Hai đường thẳng a và b có thể: cắt nhau, trùng nhau, song song, chéo nhau.
Nếu d là giao tuyến của hai mặt phẳng phân biệt (P) và (Q) thì:
Đáp án : C
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó.
Vì d là giao tuyến của hai mặt phẳng phân biệt (P) và (Q) thì \(d \subset \left( P \right)\) và \(d \subset \left( Q \right)\)
Cho tứ diện ABCD. Chọn đáp án đúng.
Đáp án : D
Sử dụng kiến thức về hai đường thẳng chéo nhau: Nếu hai đường thẳng a và b không cùng nằm trong bất kì một mặt phẳng nào thì ta nó a và b chéo nhau.
Vì hai đường thẳng AB và CD không cùng nằm trong một mặt phẳng nào nên AB và CD là hai đường thẳng chéo nhau.
Giá trị lớn nhất của hàm số \(y = 2\cos x + 1\) bằng:
Đáp án : C
Sử dụng kiến thức về hàm số lượng giác: \( - 1 \le \cos x \le 1\) với mọi số thực x.
Vì \(\cos x \le 1\;\forall x \in \mathbb{R} \Rightarrow 2\cos x \le 2\;\forall x \in \mathbb{R} \Rightarrow 2\cos x + 1 \le 3\;\forall x \in \mathbb{R}\)
Do đó, giá trị lớn nhất của hàm số \(y = 2\cos x + 1\) là 3
Tìm tất cả các giá trị của m để phương trình \({\cos ^2}x - {\sin ^2}x - m = 0\) có nghiệm?
Đáp án : B
Sử dụng kiến thức về điều kiện có nghiệm của phương trình \(\cos x = m\): Phương trình \(\cos x = m\) có nghiệm khi và chỉ khi \(\left| m \right| \le 1\)
Ta có: \({\cos ^2}x - {\sin ^2}x - m = 0 \Leftrightarrow \cos 2x = m\left( 1 \right)\)
Để phương trình (1) có nghiệm thì \(\left| m \right| \le 1 \Leftrightarrow - 1 \le m \le 1\)
Cho góc \(\alpha \) thỏa mãn \(\sin \alpha = \frac{1}{2}\) và \(\frac{\pi }{2} < \alpha < \pi \). Tính \(\cos \alpha \).
Đáp án : A
Sử dụng công thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = \pm \sqrt {1 - {{\sin }^2}\alpha } = \pm \frac{{\sqrt 3 }}{2}\).
Mà \(\frac{\pi }{2} < \alpha < \pi \) nên điểm cuối của \(\alpha\) thuộc góc phần tư thứ II, suy ra \(\cos \alpha < 0\). Do đó, \(\cos \alpha = \frac{{ - \sqrt 3 }}{2}\).
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + 2{u_{n - 2}}\end{array} \right.\left( {n \ge 3,n \in \mathbb{N}} \right)\). Giá trị của \({u_3} + {u_4}\) là:
Đáp án : C
Tính các giá trị \({u_3}\) và \({u_4}\) rồi tính tổng.
Ta có: \({u_3} = {u_2} + 2{u_1} = 1 + 2.1 = 3;{u_4} = {u_3} + 2{u_2} = 3 + 2.1 = 5\). Do đó, \({u_3} + {u_4} = 3 + 5 = 8\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2,q = 3\). Tính tổng của mười số hạng đầu tiên của cấp số nhân đó.
Đáp án : A
Sử dụng kiến thức về tổng của n số hạng đầu của một cấp số nhân: Cho cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q \ne 1\). Khi đó, tổng của n số hạng đầu tiên trong cấp số nhân là: \({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\)
Tổng của 10 số hạng đầu tiên của cấp số nhân là: \(S = \frac{{2.\left( {1 - {3^{10}}} \right)}}{{1 - 3}} = 59048\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2;d = 3\). Khi đó, \({u_4} + {u_6}\) bằng:
Đáp án : D
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số cộng: Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).
Ta có: \({u_4} = {u_1} + 3d = 2 + 3.3 = 11;{u_6} = {u_1} + 5d = 2 + 5.3 = 17\)
Do đó, \({u_4} + {u_6} = 11 + 17 = 28\)
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 16}}{{x - 2}}\) là:
Đáp án : C
Sử dụng kiến thức tính giới hạn của thương \(\frac{{f\left( x \right)}}{{g\left( x \right)}}\): Nếu \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L < 0\), \(\mathop {\lim }\limits_{x \to x_0^ + } g\left( x \right) = 0\) và \(g\left( x \right) > 0\) thì \(\mathop {\lim }\limits_{x \to x_0^ + } \frac{{f\left( x \right)}}{{g\left( x \right)}} = - \infty \)
Ta có: \(\mathop {\lim }\limits_{x \to {2^ + }} \left( {x - 16} \right) = 2 - 16 = - 14 < 0,\mathop {\lim }\limits_{x \to {2^ + }} \left( {x - 2} \right) = 0\)
Với \(x \to {2^ + }\) thì \(x > 2\) nên \(x - 2 > 0\). Do đó, \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 16}}{{x - 2}} = - \infty \)
Biết rằng \(\mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{{x^2} - 3}}{{x - \sqrt 3 }} = a\sqrt b \) (với a, b là các số nguyên). Chọn đáp án đúng:
Đáp án : A
Sử dụng kiến thức về giới hạn hàm số để làm: Nhận thấy \(x = \sqrt 3 \) là nghiệm của cả tử thức và mẫu thức nên ta cần rút phân thức trước khi tính giới hạn.
Ta có: \(\mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{{x^2} - 3}}{{x - \sqrt 3 }} = \mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{\left( {x - \sqrt 3 } \right)\left( {x + \sqrt 3 } \right)}}{{x - \sqrt 3 }} = \mathop {\lim }\limits_{x \to \sqrt 3 } \left( {x + \sqrt 3 } \right) = \sqrt 3 + \sqrt 3 = 2\sqrt 3 \).
Do đó, \(a = 2,b = 3\). Suy ra: \({a^2} + {b^2} = {2^2} + {3^2} = 13\).
Với giá trị nào của m thì hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 1\;khi\;x \ne -1\\m\;\;\;\;\;\;\,khi\;x = -1\end{array} \right.\) liên tục tại \({x_0} = - 1\)?
Đáp án : D
Sử dụng kiến thức về hàm số liên tục: Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) chứa điểm \({x_0}\). Hàm số \(f\left( x \right)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Tập xác định của hàm số f(x) là \(D = \mathbb{R}\).
Ta có: \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \left( {2x + 1} \right) = - 1\).
Hàm số đã cho liên tục tại \({x_0} = - 1\) khi \(f\left( { - 1} \right) = \mathop {\lim }\limits_{x \to - 1} f\left( x \right) \Leftrightarrow m = - 1\).
Cho tam giác ABC và một điểm S không thuộc mặt phẳng ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó, giao tuyến của hai mặt phẳng (SBN) và (SCM) là:
Đáp án : A
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó.
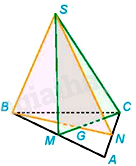
Xét mặt phẳng (ABC), gọi G là giao điểm của BN và CM.
Vì \(G \in BN \Rightarrow G \in \left( {SBN} \right);G \in CM \Rightarrow G \in \left( {SCM} \right)\) nên G là điểm chung của hai mặt phẳng (SBN) và (SCM)
Ta có: \(S \in SB \Rightarrow S \in \left( {SBN} \right),S \in SC \Rightarrow S \in \left( {SCM} \right)\) nên S là điểm chung của hai mặt phẳng (SBN) và (SCM)
Do đó, SG là giao tuyến của hai mặt phẳng (SBN) và (SCM).
Cho 4 điểm phân biệt A, B, C, D trong đó không có ba điểm nào thẳng hàng. Xác định được tất cả bao nhiêu từ 3 trong 4 điểm đã cho?
Đáp án : D
Sử dụng kiến thức về cách xác định một mặt phẳng: Một mặt phẳng hoàn toàn được xác định qua ba điểm không thẳng hàng.
Ta xác định được các mặt phẳng (ABC), (ABD), (ACD), (BCD). Do đó, xác định được 4 mặt phẳng.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là:
Đáp án : B
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
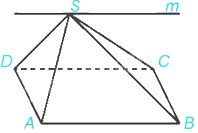
Ta có: Vì ABCD là hình bình hành nên AB // CD. Mà \(AB \subset \left( {SAB} \right),CD \subset \left( {SCD} \right)\)
Do đó, giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng m qua S song song với AB.
Cho hình hộp ABCD. A’B’C’D’ có AC cắt BD tại O và A’C’ cắt B’D’ tại O’. Khi đó, mặt phẳng (AB’D’) song song với mặt phẳng nào dưới đây?
Đáp án : C
Sử dụng kiến thức về hai mặt phẳng song song: Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng (Q) thì (P) và (Q) song song với nhau.
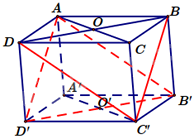
Vì BD // B’D’ nên B’D’ // (BDC’). Vì AD’ // BC’ nên AD’ // (BDC’)
Lại có hai đường thẳng AD’ và B’D’ cắt nhau và nằm trong mặt phẳng (AB’D’). Do đó, (AB’D’) // (BDC’)
Tính giới hạn sau: \(I = \mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {3 + x} - 4x}}{{2x - 2}}\)
Sử dụng kiến thức về giới hạn của hàm số: Rút gọn biểu thức \(\frac{{2\sqrt {3 + x} - 4x}}{{2x - 2}}\) rồi áp dụng quy tắc về giới hạn để tính.
\(I = \mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {3 + x} - 4x}}{{2x - 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {2\sqrt {3 + x} - 4x} \right)\left( {2\sqrt {3 + x} + 4x} \right)}}{{2\left( {x - 1} \right)\left( {2\sqrt {3 + x} + 4x} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{4\left( {x + 3} \right) - 16{x^2}}}{{2\left( {x - 1} \right)\left( {2\sqrt {3 + x} + 4x} \right)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{ - 16{x^2} + 4x + 12}}{{2\left( {x - 1} \right)\left( {2\sqrt {3 + x} + 4x} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - 4\left( {x - 1} \right)\left( {4x + 3} \right)}}{{4\left( {x - 1} \right)\left( {\sqrt {3 + x} + 2x} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - \left( {4x + 3} \right)}}{{\sqrt {3 + x} + 2x}} = \frac{{ - 7}}{4}\)
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. M là điểm nằm trên cạnh BC sao cho \(MB = 2MC\). Chứng minh rằng MG // (ACD).
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
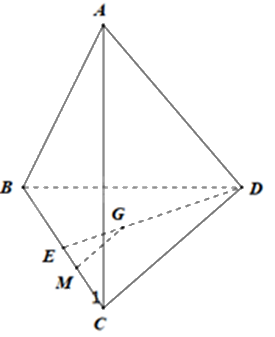
Gọi E là trung điểm của BC. Vì G là trọng tâm của tam giác BCD nên \(\frac{{GD}}{{ED}} = \frac{2}{3}\)
Mà \(MB = 2MC \Rightarrow 3MC = BC\). Lại có: \(EC = BE = \frac{1}{2}BC \Rightarrow \frac{{MC}}{{EC}} = \frac{2}{3}\)
Tam giác EDC có: \(\frac{{GD}}{{ED}} = \frac{{MC}}{{EC}}\left( { = \frac{2}{3}} \right)\) nên MG // CD (định lý Thalès đảo)
Mà \(CD \subset \left( {ACD} \right)\) nên MG // (ACD)
Cho hai số thực a và b thỏa mãn điều kiện \(\sin \left( {a + b} \right) - 2\cos \left( {a - b} \right) = 0\). Tính giá trị của biểu thức \(A = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}}\).
Sử dụng công thức: \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2};\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\)
\(A = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}} = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{\left( {2 - \sin 2a} \right)\left( {2 - \sin 2b} \right)}} = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2\left( {\sin 2a + \sin 2b} \right) + \sin 2a.\sin 2b}}\)
Vì \(\sin \left( {a + b} \right) - 2\cos \left( {a - b} \right) = 0 \Rightarrow \sin \left( {a + b} \right) = 2\cos \left( {a - b} \right)\)
Ta có: \(4 - \left( {\sin 2a + \sin 2b} \right) = 4 - 2\sin \left( {a + b} \right)\cos \left( {a - b} \right) = 4 - 4{\cos ^2}\left( {a - b} \right) = 4{\sin ^2}\left( {a - b} \right)\)
Lại có: \(4 - 2\left( {\sin 2a + \sin 2b} \right) + \sin 2a.\sin 2b\)
\( = 4 - 4\sin \left( {a + b} \right)\cos \left( {a - b} \right) + \frac{1}{2}\left[ {\cos \left( {2a - 2b} \right) - \cos \left( {2a + 2b} \right)} \right]\)
\( = 4 - 8{\cos ^2}\left( {a - b} \right) + \frac{1}{2}\left[ {2{{\cos }^2}\left( {a - b} \right) - 1 - 1 + 2{{\sin }^2}\left( {a + b} \right)} \right]\)
\( = 3 - 7{\cos ^2}\left( {a - b} \right) + {\sin ^2}\left( {a + b} \right) = 3 - 3{\cos ^2}\left( {a - b} \right) = 3{\sin ^2}\left( {a - b} \right)\)
Vậy \(A = \frac{{4{{\sin }^2}\left( {a - b} \right)}}{{3{{\sin }^2}\left( {a - b} \right)}} = \frac{4}{3}\)
Chứng minh rằng dãy số \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \ldots + \frac{1}{{n(n + 1)}}\) tăng và bị chặn trên.
Sử dụng kiến thức về dãy số tăng: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số tăng nếu \({u_{n + 1}} > {u_n}\) với mọi \(n \in \mathbb{N}*\)
Sử dụng kiến thức về dãy số bị chặn trên: Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn trên nếu tồn tại một số M sao cho \({u_n} \le M\) với mọi \(n \in \mathbb{N}*\).
Ta có: \({u_n} = \frac{{2 - 1}}{{1.2}} + \frac{{3 - 2}}{{2.3}} + \frac{{4 - 3}}{{3.4}} + \ldots + \frac{{(n + 1) - n}}{{n(n + 1)}} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \ldots + \frac{1}{n} - \frac{1}{{n + 1}} = 1 - \frac{1}{{n + 1}}\)
Xét hiệu: \({u_{n + 1}} - {u_n} = 1 - \frac{1}{{n + 2}} - \left( {1 - \frac{1}{{n + 1}}} \right) = \frac{1}{{n + 1}} - \frac{1}{{n + 2}} > 0 \Rightarrow \left( {{u_n}} \right)\) tăng
Nhận thấy \({u_n} = 1 - \frac{1}{{n + 1}} < 1 \Rightarrow \left( {{u_n}} \right)\) bị chặn trên.
Đề thi học kì 1 Toán 11 Cánh diều - Đề số 1 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một học kì. Đề thi này không chỉ kiểm tra kiến thức lý thuyết mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Việc nắm vững cấu trúc đề thi và các dạng bài tập thường gặp là yếu tố then chốt để đạt kết quả cao.
Thông thường, đề thi học kì 1 Toán 11 Cánh diều - Đề số 1 sẽ bao gồm các phần sau:
Đề thi học kì 1 Toán 11 Cánh diều - Đề số 1 thường tập trung vào các chủ đề sau:
Để giải phương trình lượng giác, cần biến đổi phương trình về dạng cơ bản và sử dụng các công thức lượng giác để tìm nghiệm. Ví dụ:
sin(x) = 0 => x = kπ, k ∈ Z
Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm của hàm số. Ví dụ:
(x2)' = 2x
Sử dụng đạo hàm để tìm cực trị, khoảng đồng biến, nghịch biến của hàm số. Ví dụ:
Tìm đạo hàm f'(x), giải phương trình f'(x) = 0 để tìm điểm cực trị.
Để chuẩn bị tốt nhất cho kỳ thi, học sinh nên luyện tập với nhiều đề thi mẫu khác nhau. Việc giải đề thi không chỉ giúp học sinh làm quen với cấu trúc đề thi mà còn giúp học sinh rèn luyện kỹ năng giải toán và quản lý thời gian hiệu quả.
Trước khi làm bài thi, hãy đọc kỹ đề bài, xác định rõ yêu cầu của từng câu hỏi và lập kế hoạch giải bài hợp lý. Trong quá trình làm bài, hãy kiểm tra lại kết quả và đảm bảo rằng các câu trả lời của bạn là chính xác và đầy đủ.
Đề thi học kì 1 Toán 11 Cánh diều - Đề số 1 là một công cụ hữu ích giúp học sinh ôn tập và chuẩn bị cho kỳ thi. Bằng cách nắm vững kiến thức, luyện tập thường xuyên và áp dụng các kỹ năng giải toán hiệu quả, học sinh có thể đạt kết quả cao trong kỳ thi này.