Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 11 Cánh diều - Đề số 2, một công cụ hỗ trợ học sinh ôn luyện và đánh giá năng lực một cách hiệu quả. Đề thi được biên soạn theo chương trình học mới, bám sát kiến thức trọng tâm và có đáp án chi tiết đi kèm.
Với đề thi này, các em học sinh có thể tự kiểm tra kiến thức đã học, rèn luyện kỹ năng giải đề và làm quen với cấu trúc đề thi thực tế. Đây là bước chuẩn bị quan trọng để đạt kết quả tốt nhất trong kỳ thi học kì 1 sắp tới.
Chọn đáp án đúng
Một cung của đường tròn bán kính R và có số đo \(\alpha \) rad thì có độ dài là:
Nghiệm của phương trình \(\cos x = 1\) là:
Hàm số \(y = \tan x\) đồng biến trên:
Chọn đáp án đúng:
Trong các dãy số sau, dãy số nào là dãy số giảm?
Trong các dãy số sau, dãy số nào là cấp số nhân?
Dãy số nào dưới đây được viết dưới dạng hệ thức truy hồi?
Biết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a < 0\). Chọn đáp án đúng
Cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với công bội q, số hạng đầu \({u_1}\) thì có tổng là:
Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } {\left( {\frac{2}{3}} \right)^n}\) bằng:
Giá trị của \(\mathop {\lim }\limits_{x \to \frac{1}{3}} \left( {3x + 2} \right)\) là:
3
2
- 2
\( + \infty \)
Chọn đáp án đúng.
Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD được gọi là hình gì?
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có bao nhiêu đường thẳng song song với đường thẳng đã cho?
Cho hình hộp ABCD. A’B’C’D’. Hình hộp này có bao nhiêu đường chéo?
Chọn đáp án đúng.
Chọn đáp án đúng:
Giá trị của biểu thức \(\cos \left( {\frac{\pi }{2} - \alpha } \right) - \sin \left( {\pi - \alpha } \right)\) bằng:
Cho tam giác ABC. Chọn đáp án đúng:
Nghiệm của phương trình \(\sin x\cos x = \frac{{\sqrt 3 }}{4}\) là:
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \(u\left( n \right) = \frac{1}{{{n^2} + 2n + 4}}\). Giá trị của \({u_6} - {u_3}\) là:
Cho cấp số cộng 3; 7; 11; 15; … Số hạng thứ 15 của cấp số cộng trên là:
Cho cấp số nhân 2; 6; 18; … Số 39 366 là số hạng thứ bao nhiêu của cấp số nhân trên?
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to {4^ - }} \frac{{2x - 16}}{{x - 4}}\) là:
Chọn đáp án đúng:
Tính tổng sau: \(S = 1 - \frac{1}{3} + \frac{1}{9} - \frac{1}{{27}} + ... + {\left( {\frac{{ - 1}}{3}} \right)^{n - 1}} + ...\)
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của SA và SC. Chọn khẳng định đúng.
Cho tứ diện ABCD. Gọi I là trung điểm của AB, J là điểm thuộc cạnh AD sao cho \(JA = 3JD\). Giao điểm của đường thẳng IJ và mặt phẳng (BDC) là:
Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi O là giao điểm của hai đường chéo, M là trung điểm của SD. Gọi I là điểm thuộc cạnh AB sao cho \(BI = \frac{1}{2}AI\). Giao tuyến của hai mặt phẳng (SAB) và (IOM) là:
Tính giới hạn sau: \(I = \mathop {\lim }\limits_{n \to + \infty } \frac{{2 + {2^2} + {2^2} + ... + {2^n}}}{{3 + {3^2} + {3^3} + ... + {3^n}}}\)
Cho tứ diện ABCD, gọi I và J theo thứ tự là trung điểm của AD và AC, G là trọng tâm của tam giác BCD. Tìm thiết diện của mặt phẳng (IJG) với tứ diện ABCD. Thiết diện là hình gì?
Biết rằng \(\cos 2A + \frac{1}{{64{{\cos }^4}A}} - \left( {2\cos 2B + 4\sin B} \right) + \frac{{13}}{4} \le 0\) với A, B, C là ba góc của tam giác ABC. Chứng minh rằng \(\widehat B + \widehat C = {120^0}\)
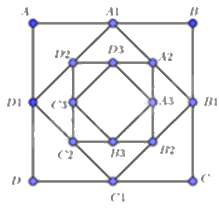
Cho hình vuông ABCD có cạnh bằng 4cm. Người ta dựng hình vuông \({A_1}{B_1}{C_1}{D_1}\) có cạnh bằng \(\frac{1}{2}\) đường chéo của hình vuông ABCD; dựng hình vuông \({A_2}{B_2}{C_2}{D_2}\) có cạnh bằng \(\frac{1}{2}\) đường chéo của hình vuông \({A_1}{B_1}{C_1}{D_1}\) và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Tổng diện tích tất cả các hình vuông ABCD, \({A_1}{B_1}{C_1}{D_1}\), \({A_2}{B_2}{C_2}{D_2}\), … bằng bao nhiêu?
Chọn đáp án đúng
Đáp án : A
Sử dụng công thức: \(\cos \left( { - \alpha } \right) = \cos \alpha \).
Ta có: \(\cos \left( { - \alpha } \right) = \cos \alpha \)
Một cung của đường tròn bán kính R và có số đo \(\alpha \) rad thì có độ dài là:
Đáp án : C
Sử dụng kiến thức về tính độ dài cung tròn: Một cung của đường tròn bán kính R và có số đo \(\alpha \) rad thì có độ dài là \(l = R\alpha \).
Sử dụng kiến thức về tính độ dài cung tròn: Một cung của đường tròn bán kính R và có số đo \(\alpha \) rad thì có độ dài là \(l = R\alpha \).
Nghiệm của phương trình \(\cos x = 1\) là:
Đáp án : D
Phương trình \(\cos x = 1\) có nghiệm là \(x = k2\pi \left( {k \in \mathbb{Z}} \right)\)
Phương trình \(\cos x = 1\) có nghiệm là \(x = k2\pi \left( {k \in \mathbb{Z}} \right)\)
Hàm số \(y = \tan x\) đồng biến trên:
Đáp án : B
Sử dụng kiến thức về đồng biến của hàm số lương giác: Hàm số \(y = \tan x\) đồng biến trên mỗi khoảng \(\left( {\frac{{ - \pi }}{2} + k\pi ;\frac{\pi }{2} + k\pi } \right),k \in \mathbb{Z}\).
Hàm số \(y = \tan x\) đồng biến trên mỗi khoảng \(\left( {\frac{{ - \pi }}{2} + k\pi ;\frac{\pi }{2} + k\pi } \right),k \in \mathbb{Z}\)
Chọn đáp án đúng:
Đáp án : A
Sử dụng công thức: \(\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\)
\(\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\)
Trong các dãy số sau, dãy số nào là dãy số giảm?
Đáp án : B
Sử dụng kiến thức về dãy số giảm: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có: \({u_{n + 1}} < {u_n}\) với mọi \(n \in \mathbb{N}*\)
Trong các dãy số trên, chỉ có dãy số 4; 3; 2; 0; … có \(4 < 3 < 2 < 0...\) nên dãy số 4; 3; 2; 0; … là dãy số giảm
Trong các dãy số sau, dãy số nào là cấp số nhân?
Đáp án : C
Sử dụng kiến thức về cấp số nhân: Cấp số nhân là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó nhân với một số không đổi q.
Trong các dãy số trên, chỉ có dãy số 1; 2; 4; 8; 16; …. có kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó nhân với một số không đổi q \(\left( {q = 2} \right)\).
Dãy số nào dưới đây được viết dưới dạng hệ thức truy hồi?
Đáp án : C
Sử dụng kiến thức về cách cho một dãy số.
Dãy số được viết dưới dạng hệ thức truy hồi là: \({u_1} = 1;\;{u_n} = 2{u_{n - 1}} + 1\) với \(n \ge 2\)
Biết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a < 0\). Chọn đáp án đúng
Đáp án : B
Sử dụng quy tắc về giới hạn vô cực của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a < 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = - \infty \).
Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a < 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = - \infty \).
Cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với công bội q, số hạng đầu \({u_1}\) thì có tổng là:
Đáp án : D
Sử dụng kiến thức về tổng cấp số nhân lùi vô hạn: Cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với công bội q, số hạng đầu \({u_1}\) thì có tổng là \(S = \frac{{{u_1}}}{{1 - q}}\)
Cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với công bội q, số hạng đầu \({u_1}\) thì có tổng là \(S = \frac{{{u_1}}}{{1 - q}}\)
Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } {\left( {\frac{2}{3}} \right)^n}\) bằng:
Đáp án : B
Sử dụng công thức: \(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\) với \(\left| q \right| < 1\)
Ta có: \(\frac{2}{3} < 0\) nên \(\mathop {\lim }\limits_{n \to + \infty } {\left( {\frac{2}{3}} \right)^n} = 0\)
Giá trị của \(\mathop {\lim }\limits_{x \to \frac{1}{3}} \left( {3x + 2} \right)\) là:
3
2
- 2
\( + \infty \)
Đáp án : A
Sử dụng quy tắc tính giới hạn của hàm số tại một điểm: Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\).
\(\mathop {\lim }\limits_{x \to \frac{1}{3}} \left( {3x + 2} \right) = 3.\frac{1}{3} + 2 = 3\).
Chọn đáp án đúng.
Đáp án : C
Sử dụng kiến thức về cách xác định một mặt phẳng: Một mặt phẳng hoàn toàn được xác định qua ba điểm không thẳng hàng.
Sử dụng kiến thức về cách xác định một mặt phẳng: Một mặt phẳng hoàn toàn được xác định qua ba điểm không thẳng hàng.
Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD được gọi là hình gì?
Đáp án : A
Sử dụng kiến thức về hình tứ diện: Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD được gọi là hình tứ diện.
Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD được gọi là hình tứ diện.
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có bao nhiêu đường thẳng song song với đường thẳng đã cho?
Đáp án : A
Sử dụng kiến thức về tính chất của hai đường thẳng song song: Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.
Cho hình hộp ABCD. A’B’C’D’. Hình hộp này có bao nhiêu đường chéo?
Đáp án : C
Sử dụng kiến thức về hình hộp: Hình hộp ABCD. A’B’C’D’ có bốn đường chéo là AC’, BD’, CA’ và DB’
Hình hộp ABCD. A’B’C’D’ có bốn đường chéo là AC’, BD’, CA’ và DB’
Chọn đáp án đúng.
Đáp án : A
Sử dụng kiến thức về tính chất của phép chiếu song song: Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến đường thẳng thành đường thẳng.
Chọn đáp án đúng:
Đáp án : B
Sử dụng kiến thức về tính chất hai đường thẳng song song: Trong không gian, hai đường thẳng phân biệt cùng song song với một đường thẳng thì chúng song song với nhau.
Trong không gian, hai đường thẳng phân biệt cùng song song với một đường thẳng thì chúng song song với nhau.
Giá trị của biểu thức \(\cos \left( {\frac{\pi }{2} - \alpha } \right) - \sin \left( {\pi - \alpha } \right)\) bằng:
Đáp án : D
Sử dụng kiến thức về giá trị lượng giác của các góc lượng giác có liên quan đặc biệt: \(\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \); \(\sin \left( {\pi - \alpha } \right) = \sin \alpha \).
\(\cos \left( {\frac{\pi }{2} - \alpha } \right) - \sin \alpha = \sin \alpha - \sin \alpha = 0\)
Cho tam giác ABC. Chọn đáp án đúng:
Đáp án : C
Sử dụng công thức \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b,\sin \left( {\pi - \alpha } \right) = \sin \alpha \)
Ta có: \(\sin B\cos C + \sin C\cos B = \sin \left( {B + C} \right) = \sin \left[ {\pi - \left( {B + C} \right)} \right] = \sin A\)
Nghiệm của phương trình \(\sin x\cos x = \frac{{\sqrt 3 }}{4}\) là:
Đáp án : D
Sử dụng kiến thức về cách giải phương trình \(\sin x = m\): Xét phương trình \(\sin x = m\)
+ Nếu \(\left| m \right| > 1\) thì phương trình vô nghiệm.
+ Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm: \(x = \alpha + k2\pi ,k \in \mathbb{Z}\) và \(x = \pi - \alpha + k2\pi ,k \in \mathbb{Z}\), với \(\alpha \) là góc thuộc \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
\(\sin x\cos x = \frac{{\sqrt 3 }}{4} \Leftrightarrow 2\sin x\cos x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin 2x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin 2x = \sin \frac{\pi }{3}\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = \pi - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = \frac{\pi }{3} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \(u\left( n \right) = \frac{1}{{{n^2} + 2n + 4}}\). Giá trị của \({u_6} - {u_3}\) là:
Đáp án : B
Tính các giá trị \({u_6}\) và \({u_3}\) rồi tính hiệu.
Ta có: \({u_6} = \frac{1}{{{6^2} + 6.2 + 4}} = \frac{1}{{52}};{u_3} = \frac{1}{{{3^2} + 3.2 + 4}} = \frac{1}{{19}}\). Do đó, \({u_6} - {u_3} = \frac{1}{{52}} - \frac{1}{{19}} = \frac{{ - 33}}{{988}}\)
Cho cấp số cộng 3; 7; 11; 15; … Số hạng thứ 15 của cấp số cộng trên là:
Đáp án : C
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số cộng: Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).
Cấp số cộng trên có số hạng đầu \({u_1} = 3\), công sai \(d = 4\). Do đó, số hạng thứ 15 của cấp số cộng trên là:
\({u_{15}} = {u_1} + 14d = 3 + 14.4 = 59\)
Cho cấp số nhân 2; 6; 18; … Số 39 366 là số hạng thứ bao nhiêu của cấp số nhân trên?
Đáp án : A
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số nhân: Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội q thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1}.{q^{n - 1}}\).
Cấp số nhân trên có số hạng đầu \({u_1} = 2\), công bội \(q = 3\).
Ta có: \(39\;366 = {2.3^{n - 1}} \Leftrightarrow {3^{n - 1}} = 19\;683 \Leftrightarrow {3^{n - 1}} = {3^9} \Leftrightarrow n - 1 = 9 \Leftrightarrow n = 10\)
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to {4^ - }} \frac{{2x - 16}}{{x - 4}}\) là:
Đáp án : D
Sử dụng kiến thức tính giới hạn của thương \(\frac{{f\left( x \right)}}{{g\left( x \right)}}\): Nếu \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = L < 0\), \(\mathop {\lim }\limits_{x \to x_0^ + } g\left( x \right) = 0\) và \(g\left( x \right) < 0\) thì \(\mathop {\lim }\limits_{x \to x_0^ - } \frac{{f\left( x \right)}}{{g\left( x \right)}} = + \infty \).
Ta có: \(\mathop {\lim }\limits_{x \to {4^ - }} \left( {2x - 16} \right) = 2.4 - 16 = - 8 < 0,\mathop {\lim }\limits_{x \to {4^ - }} \left( {x - 4} \right) = 0\)
Với \(x \to {4^ - }\) thì \(x < 4\) nên \(x - 4 < 0\). Do đó, \(\mathop {\lim }\limits_{x \to {4^ - }} \frac{{2x - 16}}{{x - 4}} = + \infty \)
Chọn đáp án đúng:
Đáp án : B
Sử dụng quy tắc về giới hạn vô cực của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = + \infty \).
Ta có: \({n^2} - 4n = {n^2}\left( {1 - \frac{4}{n}} \right)\)
Vì \(\mathop {\lim }\limits_{n \to + \infty } {n^2} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } \left( {1 - \frac{4}{n}} \right) = 1 > 0\) nên \(\mathop {\lim }\limits_{n \to + \infty } \left( {{n^2} - 4n} \right) = + \infty \)
Tính tổng sau: \(S = 1 - \frac{1}{3} + \frac{1}{9} - \frac{1}{{27}} + ... + {\left( {\frac{{ - 1}}{3}} \right)^{n - 1}} + ...\)
Đáp án : C
Sử dụng kiến thức về tổng cấp số nhân lùi vô hạn: Cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với công bội q, số hạng đầu \({u_1}\) thì có tổng là \(S = \frac{{{u_1}}}{{1 - q}}\).
Tổng trên là cấp số nhân lùi vô hạn có \({u_1} = 1,\) công bội \(q = \frac{{ - 1}}{3}\)
Do đó, \(S = \frac{1}{{1 - \left( {\frac{{ - 1}}{3}} \right)}} = \frac{3}{4}\)
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của SA và SC. Chọn khẳng định đúng.
Đáp án : A
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
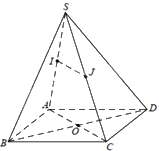
Vì I, J lần lượt là trung điểm của SA và SC nên IJ là đường trung bình của tam giác SAC. Do đó, IJ // AC.
Mà \(AC \subset \left( {ABCD} \right)\) nên IJ // (ABCD).
Cho tứ diện ABCD. Gọi I là trung điểm của AB, J là điểm thuộc cạnh AD sao cho \(JA = 3JD\). Giao điểm của đường thẳng IJ và mặt phẳng (BDC) là:
Đáp án : D
Sử dụng kiến thức về cách tìm giao điểm của đường thẳng và mặt phẳng: Để tìm giao điểm của đường thẳng a và mặt phẳng \(\left( \alpha \right)\) ta làm như sau:
+ Tìm trong mặt phẳng \(\left( \alpha \right)\) đường thẳng b sao cho b cắt a tại A.
+ Khi đó, A là giao điểm của đường thẳng a và mặt phẳng \(\left( \alpha \right)\).
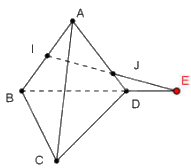
Trong mặt phẳng (ABD), gọi E là giao điểm của IJ và BD.
Ta có: \(\left\{ \begin{array}{l}E \in IJ\\E \in BD \subset \left( {CBD} \right)\end{array} \right.\) nên E là giao điểm của đường thẳng IJ và mặt phẳng (BDC).
Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi O là giao điểm của hai đường chéo, M là trung điểm của SD. Gọi I là điểm thuộc cạnh AB sao cho \(BI = \frac{1}{2}AI\). Giao tuyến của hai mặt phẳng (SAB) và (IOM) là:
Đáp án : B
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
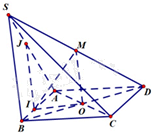
Vì M, O lần lượt là trung điểm của SD, BD nên MO là đường trung bình của tam giác SBD. Do đó, OM // SB.
Mà I là điểm chung của hai mặt phẳng (SAB) và (IOM); \(OM \subset \left( {IOM} \right),SB \subset \left( {SAB} \right)\)
Nên giao tuyến của hai mặt phẳng (SAB) và (IOM) là đường thẳng qua I và song song với OM, cắt SA tại J.
Tính giới hạn sau: \(I = \mathop {\lim }\limits_{n \to + \infty } \frac{{2 + {2^2} + {2^2} + ... + {2^n}}}{{3 + {3^2} + {3^3} + ... + {3^n}}}\)
Sử dụng kiến thức về giới hạn của của dãy số để tính: \(\lim {q^n} = 0\left( {\left| q \right| < 1} \right)\)
Mẫu thức là tổng của n số hạng đầu tiên của một cấp số nhân có số hạng đầu \({u_1} = 3\) và công bội \(q = 3\)
Do đó, \(3 + {3^2} + {3^3} + .. + {3^n} = \frac{{3\left( {{3^n} - 1} \right)}}{{3 - 1}} = \frac{3}{2}\left( {{3^n} - 1} \right)\)
Tử thức là tổng của n số hạng đầu tiên của một cấp số nhân có số hạng đầu \({u_1} = 2\) và công bội \(q = 2\)
Do đó, \(2 + {2^2} + {2^2} + ... + {2^n} = \frac{{2\left( {{2^n} - 1} \right)}}{{2 - 1}} = 2\left( {{2^n} - 1} \right)\)
Khi đó, \(I = \mathop {\lim }\limits_{n \to + \infty } \left( {\frac{4}{3}.\frac{{{2^n} - 1}}{{{3^n} - 1}}} \right) = \frac{4}{3}\mathop {\lim }\limits_{n \to + \infty } \frac{{{2^n} - 1}}{{{3^n} - 1}} = \frac{4}{3}\mathop {\lim }\limits_{n \to + \infty } \frac{{{{\left( {\frac{2}{3}} \right)}^n} - \frac{1}{{{3^n}}}}}{{1 - \frac{1}{{{3^n}}}}} = 0\)
Cho tứ diện ABCD, gọi I và J theo thứ tự là trung điểm của AD và AC, G là trọng tâm của tam giác BCD. Tìm thiết diện của mặt phẳng (IJG) với tứ diện ABCD. Thiết diện là hình gì?
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
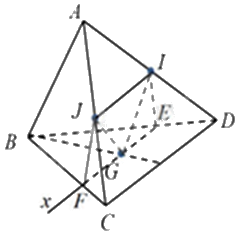
Vì I và J theo thứ tự là trung điểm của AD và AC nên IJ là đường trung bình của tam giác ACD.
Do đó, IJ // CD. Mà \(IJ \subset \left( {GIJ} \right),CD \subset \left( {BCD} \right),\) G là điểm chung của hai mặt phẳng (GIJ) và (BCD).
Do đó, giao tuyến của hai mặt phẳng (GIJ) và (BCD) là Gx // CD // IJ.
Trong (BCD), gọi E, F lần lượt là giao điểm của Gx với BD và BC.
Tứ giác IJFE có: IJ // FE nên tứ giác IJFE là hình thang.
Ta có: \(\left\{ \begin{array}{l}IJ = \left( {GIJ} \right) \cap \left( {ACD} \right)\\EI = \left( {GIJ} \right) \cap \left( {ABD} \right)\\EF = \left( {GIJ} \right) \cap \left( {BCD} \right)\\FJ = \left( {GIJ} \right) \cap \left( {ABC} \right)\end{array} \right.\)
Do đó, thiết diện của mặt phẳng (GIJ) với tứ diện ABCD là hình thang IJFE.
Biết rằng \(\cos 2A + \frac{1}{{64{{\cos }^4}A}} - \left( {2\cos 2B + 4\sin B} \right) + \frac{{13}}{4} \le 0\) với A, B, C là ba góc của tam giác ABC. Chứng minh rằng \(\widehat B + \widehat C = {120^0}\)
Sử dụng công thức: \(\cos 2x = 1 - 2{\sin ^2}x = 2{\cos ^2}x - 1\)
\(\cos 2A + \frac{1}{{64{{\cos }^4}A}} - \left( {2\cos 2B + 4\sin B} \right) + \frac{{13}}{4} \le 0\)
\( \Leftrightarrow 2{\cos ^2}A - 1 + \frac{1}{{64{{\cos }^4}A}} - \left( {2 - 4{{\sin }^2}B + 4\sin B} \right) + \frac{{13}}{4} \le 0\)
\( \Leftrightarrow {\cos ^2}A + {\cos ^2}A + \frac{1}{{64{{\cos }^4}A}} + 4{\sin ^2}B - 4\sin B + 1 \le \frac{3}{4}\left( * \right)\)
Áp dụng BĐT Cauchy ta có: \({\cos ^2}A + {\cos ^2}A + \frac{1}{{64{{\cos }^4}A}} \ge \frac{3}{4}\left( 1 \right)\)
Mặt khác: \(4{\sin ^2}B - 4\sin B + 1 = {\left( {2\sin B - 1} \right)^2} \ge 0\left( 2 \right)\)
Từ (1) và (2) suy ra bất đẳng thức (*) thỏa mãn khi và chỉ khi:
\(\left\{ \begin{array}{l}{\cos ^2}A = \frac{1}{{64{{\cos }^4}A}}\\\sin B = \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos A = \frac{1}{2}\\\sin B = \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\widehat A = {60^0}\\\widehat B = {30^0}\\\widehat C = {90^0}\end{array} \right.\)
Do đó, \(\widehat B + \widehat C = {120^0}\)
Cho hình vuông ABCD có cạnh bằng 4cm. Người ta dựng hình vuông \({A_1}{B_1}{C_1}{D_1}\) có cạnh bằng \(\frac{1}{2}\) đường chéo của hình vuông ABCD; dựng hình vuông \({A_2}{B_2}{C_2}{D_2}\) có cạnh bằng \(\frac{1}{2}\) đường chéo của hình vuông \({A_1}{B_1}{C_1}{D_1}\) và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Tổng diện tích tất cả các hình vuông ABCD, \({A_1}{B_1}{C_1}{D_1}\), \({A_2}{B_2}{C_2}{D_2}\), … bằng bao nhiêu?
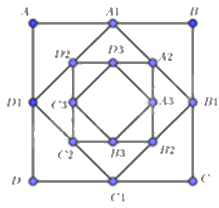
Sử dụng kiến thức về tổng cấp số nhân lùi vô hạn: Cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với công bội q, số hạng đầu \({u_1}\) thì có tổng là \(S = \frac{{{u_1}}}{{1 - q}}\)
Ta có: \({S_1} = {S_{ABCD}} = {4^2};{S_2} = {S_{{A_1}{B_1}{C_1}{D_1}}} = {\left( {\frac{{4\sqrt 2 }}{2}} \right)^2} = \frac{{{4^2}}}{2};{S_3} = {S_{{A_2}{B_2}{C_2}{D_2}}} = {\left( {\frac{{4\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2}} \right)^2} = \frac{{{4^2}}}{{{2^2}}}\);…
\({S_n} = {S_{{A_n}{B_n}{C_n}{D_n}}} = {4^2}.\frac{1}{{{2^{n - 1}}}}\);…
Như vậy, các số \({S_1};{S_2};...;{S_n};...\) lập thành một cấp số nhân lùi vô hạn có \({S_1} = {4^2},q = \frac{1}{2}\)
Do đó: \(S = {S_1} + {S_2} + ... + {S_n} + ... = \frac{{{S_1}}}{{1 - q}} = \frac{{{4^2}}}{{1 - \frac{1}{2}}} = {2.4^2} = 32\left( {c{m^2}} \right)\)
Đề thi học kì 1 Toán 11 Cánh diều - Đề số 2 là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau một học kỳ học tập. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như hàm số, lượng giác, và các kiến thức đại số cơ bản.
Đề thi thường được chia thành các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để giải đề thi hiệu quả, học sinh cần:
Câu 1: (Trắc nghiệm) Hàm số y = x2 - 4x + 3 có tập xác định là?
A. R
B. [0; +∞)
C. (-∞; 0]
D. (0; +∞)
Giải: Hàm số y = x2 - 4x + 3 là hàm số bậc hai, tập xác định của hàm số bậc hai là R. Vậy đáp án đúng là A.
Luyện đề thường xuyên là một phương pháp học tập hiệu quả giúp học sinh:
Giaitoan.edu.vn cung cấp một kho đề thi học kì 1 Toán 11 Cánh diều - Đề số 2 và các đề thi khác với đáp án chi tiết, giúp học sinh ôn luyện và chuẩn bị tốt nhất cho kỳ thi. Ngoài ra, chúng tôi còn cung cấp các bài giảng, tài liệu học tập, và các công cụ hỗ trợ học tập khác để giúp học sinh học toán hiệu quả hơn.
Để đạt kết quả tốt nhất trong kỳ thi học kì 1, học sinh cần:
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi học kì 1!