Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 11 Cánh diều - Đề số 6, một công cụ hỗ trợ học sinh ôn luyện và đánh giá năng lực một cách hiệu quả. Đề thi được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi thực tế và rèn luyện kỹ năng giải quyết bài toán.
Đề thi này bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề quan trọng trong chương trình học kì 1 Toán 11 Cánh diều.
Hàm số nào sau đây có tập xác định \(\mathbb{R}\)?
\(y = \tan x\)
\(y = \cot x\)
\(y = \frac{1}{{{{\sin }^2}x + 1}}\)
\(y = \frac{1}{{\cot x}}\)
Tổng các nghiệm của phương trình \(\tan (2x - {15^o}) = 1\) trên khoảng \(( - {90^o};{90^o})\) bằng
\({30^o}\)
\( - {60^o}\)
\({0^o}\)
\( - {30^o}\)
Cho dãy số \(\left( {{u_n}} \right) = {2024^n}\). Tính \({u_{n + 1}}\)?
\({u_{n + 1}} = {2024^n} + 2024\)
\({u_{n + 1}} = {2024^n} + 1\)
\({u_{n + 1}} = {2024^{n + 1}}\)
\({u_{n + 1}} = 2024(n + 1)\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công sai d = -5. Khi đó –32 là số hạng thứ mấy của cấp số cộng đã cho?
7
10
9
8
Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu \({u_1} = 1\), công bội q = 2. Tổng ba số hạng đầu của cấp số nhân là
3
7
9
5
Phát biểu nào sau đây là sai?
\(\lim {u_n} = c\) (\({u_n} = c\) là hằng số)
\(\lim {q^n} = 0\) \(\left( {\left| q \right| > 1} \right)\)
\(\lim \frac{1}{n} = 0\)
\(\lim \frac{1}{{{n^k}}} = 0\) \((k > 1)\)
Hàm số \(y = \frac{1}{{2x - 4}}\) gián đoạn tại điểm nào dưới đây?
x = 1
x = 0
x = 2
x = -1
Trong các mệnh đề sau đây, mệnh đề nào sai?
Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa
Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất
Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất
Hai mặt phẳng cùng đi qua 3 điểm A, B, C không thẳng hàng thì hai mặt phẳng đó trùng nhau
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi M, N lần lượt là trung điểm của SA và SC. Khẳng định nào sau đây đúng?
MN//(ABCD)
AB//(SCD)
BC//(SAD)
MN//(SBD)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Mặt phẳng nào dưới đây chứa đường thẳng OE?
(SBC)
(ABCD)
(SAC)
(CDE)
Nếu \(\mathop {\lim }\limits_{x \to 2} f(x) = 5\) thì \(\mathop {\lim }\limits_{x \to 2} \left[ {2023 - 4f(x)} \right]\) bằng
2013
2003
1993
2015
Tập giá trị của hàm số \(y = \sin x\) là
[-1;1]
[0;2]
\(\mathbb{R}\)
[-2;2]
Cho phương trình \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\).
a) Phương trình đã cho được viết lại như sau: \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
b) Ta có \(\cos (2x + \pi ) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\) \((k \in \mathbb{Z})\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \(\left\{ \begin{array}{l}{u_1} = - 1\\{u_{n + 1}} = {u_n} + 3\end{array} \right.\) với \(n \ge 1\).
a) Bốn số hạng đầu tiên của dãy số lần lượt là -1; 2; 5; 8.
b) Số hạng thứ 5 của dãy là 13.
c) Công thức số hạng tổng quát của dãy số là \({u_n} = 2n - 3\).
d) 101 là số hạng thứ 35 của dãy số đã cho.
Biết \(\lim \frac{{2{n^2} - n + 4}}{{a{n^2} + n + 3}} = 2\) và \(\lim \frac{{{3^n} + {4^{n + 1}}}}{{{4^n} + 3}} = b\).
a) Giá trị của a = 2.
b) Giá trị của b = 4.
c) a; 2; b lập thành một cấp số cộng.
d) a; b; 16 lập thành một cấp số nhân.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy P sao cho BP = 2PD.
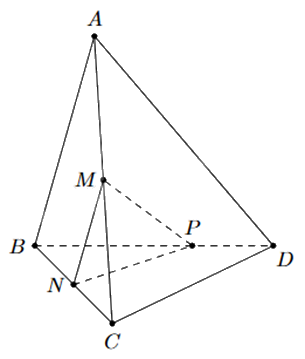
a) Gọi \(I = CD \cap (MNP)\). Ba điểm I, N, P thẳng hàng.
b) MN//(ABD).
c) Giao tuyến của hai mặt phẳng (MNP) và (ABD) là đường thẳng PQ song song với AB, với Q thuộc AD.
d) Tứ giác MNPQ là hình bình hành.
Hằng ngày mức nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mức nước trong kênh được tính tại thời điểm t (giờ) trong một ngày (t > 0) bởi công thức \(h = 4\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) + 16\). Mực nước của kênh cao nhất khi t bằng bao nhiêu?
Đáp án:
Một rạp hát có 18 hàng ghế xếp theo hình quạt. Hàng thứ nhất có 16 ghế, hàng thứ hai có 20 ghế, hàng thứ ba có 24 ghế,... cứ thế cho đến hàng cuối cùng. Hỏi tổng số ghế có trong rạp là bao nhiêu?
Đáp án:
Tính giới hạn \(\lim \left[ {\frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{(2n - 1)(2n + 1)}}} \right]\). Viết kết quả dưới dạng số thập phân.
Đáp án:
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{\sqrt[3]{{x + 7}} - \sqrt {3x + 1} }}{{x - 1}}\\ax\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne 1\\x = 1\end{array}\). Tìm giá trị của a để hàm số liên tục tại \({x_0} = 1\) (làm tròn kết quả đến hàng phần mười).
Đáp án:
Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Gọi I là giao điểm của đường thẳng AM với mặt phẳng (SBD). Tính tỉ số \(\frac{{IA}}{{IM}}\)?
Đáp án:
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, AC = 6, BD = 8; tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho AI = x (0 < x < 3), (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD). Diện tích của hình tạo bởi các đoạn giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD bằng \(\frac{{a{x^2}\sqrt 3 }}{b}\). Tính giá trị của biểu thức P = a + b.
Đáp án:
Hàm số nào sau đây có tập xác định \(\mathbb{R}\)?
\(y = \tan x\)
\(y = \cot x\)
\(y = \frac{1}{{{{\sin }^2}x + 1}}\)
\(y = \frac{1}{{\cot x}}\)
Đáp án : C
Tìm tập xác định của từng hàm số.
Hàm số \(y = \tan x\) xác định \(\forall x \ne \frac{\pi }{2} + k\pi \) \(\left( {k \in \mathbb{Z}} \right)\).
Hàm số \(y = \cot x\) xác định \(\forall x \ne k\pi \) \(\left( {k \in \mathbb{Z}} \right)\).
Hàm số \(y = \frac{1}{{\cot x}}\) xác định \(\forall x \ne \frac{{k\pi }}{2}\) \(\left( {k \in \mathbb{Z}} \right)\).
Hàm số \(y = \frac{1}{{{{\sin }^2}x + 1}}\) xác định với mọi giá trị của x.
Tổng các nghiệm của phương trình \(\tan (2x - {15^o}) = 1\) trên khoảng \(( - {90^o};{90^o})\) bằng
\({30^o}\)
\( - {60^o}\)
\({0^o}\)
\( - {30^o}\)
Đáp án : D
\(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \) \((k \in \mathbb{Z})\).
\(\tan (2x - {15^o}) = 1 \Leftrightarrow 2x - {15^o} = {45^o} + k{180^o} \Leftrightarrow x = {30^o} + k{90^o}\) \((k \in \mathbb{Z})\).
Xét \( - {90^o} < x < {90^o} \Leftrightarrow - {90^o} < {30^o} + k{90^o} < {90^o} \Leftrightarrow - \frac{4}{3} < k < \frac{2}{3}\).
Suy ra k = -1 hoặc k = 0.
Với k = -1, ta được \(x = - {60^o}\).
Với k = 0, ta được \(x = {30^o}\).
Vậy tổng các nghiệm là \( - {60^o} + {30^o} = - {30^o}\).
Cho dãy số \(\left( {{u_n}} \right) = {2024^n}\). Tính \({u_{n + 1}}\)?
\({u_{n + 1}} = {2024^n} + 2024\)
\({u_{n + 1}} = {2024^n} + 1\)
\({u_{n + 1}} = {2024^{n + 1}}\)
\({u_{n + 1}} = 2024(n + 1)\)
Đáp án : C
Thay n + 1 vào n.
Ta có \({u_{n + 1}} = {2024^{n + 1}}\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công sai d = -5. Khi đó –32 là số hạng thứ mấy của cấp số cộng đã cho?
7
10
9
8
Đáp án : D
Công thức số hạng tổng quát: \({u_n} = {u_1} + (n - 1)d\).
-32 là số hạng thứ n của cấp số cộng. Ta có \(32 = 3 + (n - 1)( - 5) \Leftrightarrow n = 8\).
Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu \({u_1} = 1\), công bội q = 2. Tổng ba số hạng đầu của cấp số nhân là
3
7
9
5
Đáp án : B
Công thức tổng n số hạng đầu của cấp số nhân: \({S_n} = {u_1}\frac{{1 - {q^n}}}{{1 - q}}\).
Áp dụng công thức tổng số hạng của cấp số nhân ta có: \({S_3} = 1.\frac{{1 - {2^3}}}{{1 - 2}} = 7\).
Phát biểu nào sau đây là sai?
\(\lim {u_n} = c\) (\({u_n} = c\) là hằng số)
\(\lim {q^n} = 0\) \(\left( {\left| q \right| > 1} \right)\)
\(\lim \frac{1}{n} = 0\)
\(\lim \frac{1}{{{n^k}}} = 0\) \((k > 1)\)
Đáp án : B
Theo định nghĩa giới hạn hữu hạn của dãy số.
Ta có \(\lim {q^n} = 0\) \(\left( {\left| q \right| < 1} \right)\) nên B sai.
Hàm số \(y = \frac{1}{{2x - 4}}\) gián đoạn tại điểm nào dưới đây?
x = 1
x = 0
x = 2
x = -1
Đáp án : C
Tìm điểm mà tại đó hàm số không xác định
Hàm số có tập xác định là \(D = \mathbb{R}\backslash \{ 2\} \), suy ra hàm số gián đoạn tại x = 2.
Trong các mệnh đề sau đây, mệnh đề nào sai?
Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa
Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất
Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất
Hai mặt phẳng cùng đi qua 3 điểm A, B, C không thẳng hàng thì hai mặt phẳng đó trùng nhau
Đáp án : B
Sử dụng kiến thức về vị trí tương đối giữa hai mặt phẳng.
B sai vì hai mặt phẳng có một điểm chung thì chúng có thể trùng nhau. Khi đó chúng có vô số điểm chung và chung nhau vô số đường thẳng.
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi M, N lần lượt là trung điểm của SA và SC. Khẳng định nào sau đây đúng?
MN//(ABCD)
AB//(SCD)
BC//(SAD)
MN//(SBD)
Đáp án : A
Đường thẳng song song với mặt phẳng nếu nó song song với một đường thuộc mặt phẳng đó.

Vì MN là đường trung bình của tam giác SAC nên MN//AC.
Mà AC thuộc mặt phẳng (ABCD) suy ra MN//(ABCD).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Mặt phẳng nào dưới đây chứa đường thẳng OE?
(SBC)
(ABCD)
(SAC)
(CDE)
Đáp án : C
Mặt phẳng cần tìm chứa cả hai điểm O và E.
Ta có \(\left\{ \begin{array}{l}O \in AC\\E \in SA\end{array} \right.\) nên \(OE \subset (SAC)\).
Nếu \(\mathop {\lim }\limits_{x \to 2} f(x) = 5\) thì \(\mathop {\lim }\limits_{x \to 2} \left[ {2023 - 4f(x)} \right]\) bằng
2013
2003
1993
2015
Đáp án : B
Sử dụng tính chất của giới hạn.
\(\mathop {\lim }\limits_{x \to 2} \left[ {2023 - 4f(x)} \right] = \mathop {\lim }\limits_{x \to 2} 2023 - 4\mathop {\lim }\limits_{x \to 2} f(x) = 2023 - 4.5 = 2003\).
Tập giá trị của hàm số \(y = \sin x\) là
[-1;1]
[0;2]
\(\mathbb{R}\)
[-2;2]
Đáp án : A
Tập giá trị là tập hợp tất cả các giá trị mà y có thể nhận.
Ta có \( - 1 \le \sin x \le 1\) nên tập giá trị của \(y = \sin x\) là [-1;1].
Cho phương trình \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\).
a) Phương trình đã cho được viết lại như sau: \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
b) Ta có \(\cos (2x + \pi ) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\) \((k \in \mathbb{Z})\).
a) Phương trình đã cho được viết lại như sau: \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
b) Ta có \(\cos (2x + \pi ) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\) \((k \in \mathbb{Z})\).
a) Sử dụng công thức \({\sin ^2}x + {\cos ^2}x = 1\).
b) Sử dụng công thức \(\cos (x + \pi ) = - \cos x\).
c) Sử dụng công thức hạ bậc \({\sin ^2}x = \frac{{1 - \cos 2x}}{2}\), \({\cos ^2}x = \frac{{\cos 2x + 1}}{2}\).
d) Sử dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
a) Đúng. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1 - {\cos ^2}\left( {2x + \frac{\pi }{4}} \right)\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = {\sin ^2}\left( {2x + \frac{\pi }{4}} \right)\).
b) Đúng. \(\cos (2x + \pi ) = - \cos 2x\).
c) Đúng. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = {\sin ^2}\left( {2x + \frac{\pi }{4}} \right)\)
\( \Leftrightarrow \frac{{\cos \left( {2x + \pi } \right) + 1}}{2} = \frac{{1 - \cos \left( {4x + \frac{\pi }{2}} \right)}}{2}\)
\( \Leftrightarrow \cos \left( {2x + \pi } \right) = - \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow - \cos 2x = - \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow \cos 2x = \cos \left( {4x + \frac{\pi }{2}} \right)\).
d) Sai. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1 \Leftrightarrow \cos 2x = \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = 4x + \frac{\pi }{2} + k2\pi \\2x = - 4x - \frac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 4x + \frac{\pi }{2} + k2\pi \\2x = - 4x - \frac{\pi }{2} + k2\pi \end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l} - 2x = \frac{\pi }{2} + k2\pi \\6x = - \frac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{4} + k\pi \\x = - \frac{\pi }{{12}} + k\frac{\pi }{3}\end{array} \right.\) \((k \in \mathbb{Z})\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \(\left\{ \begin{array}{l}{u_1} = - 1\\{u_{n + 1}} = {u_n} + 3\end{array} \right.\) với \(n \ge 1\).
a) Bốn số hạng đầu tiên của dãy số lần lượt là -1; 2; 5; 8.
b) Số hạng thứ 5 của dãy là 13.
c) Công thức số hạng tổng quát của dãy số là \({u_n} = 2n - 3\).
d) 101 là số hạng thứ 35 của dãy số đã cho.
a) Bốn số hạng đầu tiên của dãy số lần lượt là -1; 2; 5; 8.
b) Số hạng thứ 5 của dãy là 13.
c) Công thức số hạng tổng quát của dãy số là \({u_n} = 2n - 3\).
d) 101 là số hạng thứ 35 của dãy số đã cho.
Sử dụng các công thức số hạng tổng quát của cấp số cộng.
a) Đúng. Ta có:
\({u_1} = - 1\);
\({u_2} = {u_1} + 3 = - 1 + 3 = 2\);
\({u_3} = {u_2} + 3 = 2 + 3 = 5\);
\({u_4} = {u_2} + 3 = 5 + 3 = 8\).
b) Sai. Ta có \({u_5} = {u_4} + 3 = 8 + 3 = 11\).
c) Sai. Ta có \({u_{n + 1}} = {u_n} + 3 \Leftrightarrow {u_{n + 1}} - {u_n} = 3\) nên \(\left( {{u_n}} \right)\) là một cấp số cộng với \({u_1} = - 1\) và d = 3.
Số hạng tổng quát của \(\left( {{u_n}} \right)\) là \({u_n} = {u_1} + (n - 1)d \Leftrightarrow {u_n} = - 1 + (n - 1).3 = 3n - 4\).
d) Đúng. Áp dụng công thức số hạng tổng quát vừa tìm được, ta có số hạng thứ 35 của dãy là:
\({u_{35}} = 3.35 - 4 = 101\).
Biết \(\lim \frac{{2{n^2} - n + 4}}{{a{n^2} + n + 3}} = 2\) và \(\lim \frac{{{3^n} + {4^{n + 1}}}}{{{4^n} + 3}} = b\).
a) Giá trị của a = 2.
b) Giá trị của b = 4.
c) a; 2; b lập thành một cấp số cộng.
d) a; b; 16 lập thành một cấp số nhân.
a) Giá trị của a = 2.
b) Giá trị của b = 4.
c) a; 2; b lập thành một cấp số cộng.
d) a; b; 16 lập thành một cấp số nhân.
Sử dụng các quy tắc tìm giới hạn của dãy số.
a) Sai. Ta có: \(\lim \frac{{2{n^2} - n + 4}}{{a{n^2} + n + 3}} = \lim \frac{{{n^2}\left( {2 - \frac{1}{n} + \frac{4}{{{n^2}}}} \right)}}{{{n^2}\left( {a + \frac{1}{n} + \frac{3}{{{n^2}}}} \right)}} = \lim \frac{{2 - \frac{1}{n} + \frac{4}{{{n^2}}}}}{{a + \frac{1}{n} + \frac{3}{{{n^2}}}}} = \frac{2}{a} = 2\).
Suy ra a = 1.
b) Đúng. Ta có: \(\lim \frac{{{3^n} + {4^{n + 1}}}}{{{4^n} + 3}} = \lim \frac{{{3^n} + {4^n}.4}}{{{4^n} + 3}} = \lim \frac{{{{\left( {\frac{3}{4}} \right)}^n} + 4}}{{1 + 3.{{\left( {\frac{1}{4}} \right)}^n}}} = \frac{{0 + 4}}{{1 + 0}} = 4 = b\).
c) Sai. 1; 2; 4 không lập thành một cấp số cộng.
d) Đúng. 1; 4; 16 lập thành một cấp số nhân với số hạng đầu là 1, công bội bằng 4.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy P sao cho BP = 2PD.
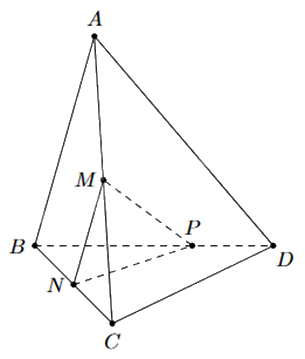
a) Gọi \(I = CD \cap (MNP)\). Ba điểm I, N, P thẳng hàng.
b) MN//(ABD).
c) Giao tuyến của hai mặt phẳng (MNP) và (ABD) là đường thẳng PQ song song với AB, với Q thuộc AD.
d) Tứ giác MNPQ là hình bình hành.
a) Gọi \(I = CD \cap (MNP)\). Ba điểm I, N, P thẳng hàng.
b) MN//(ABD).
c) Giao tuyến của hai mặt phẳng (MNP) và (ABD) là đường thẳng PQ song song với AB, với Q thuộc AD.
d) Tứ giác MNPQ là hình bình hành.
Sử dụng các điều kiện, tính chất của đường thẳng và mặt phẳng song song.
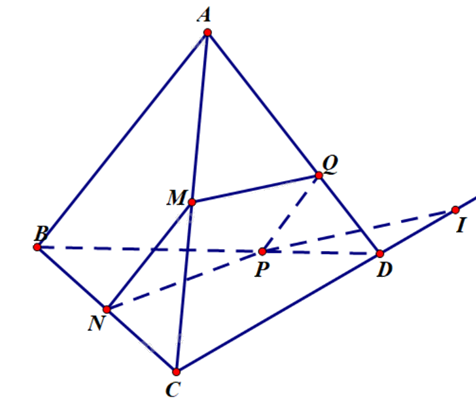
a) Sai. Xét trong mặt phẳng (BCD):
Vì NP không song song với CD nên giả sử NP giao CD tại O.
Khi đó \(\left\{ \begin{array}{l}O \in CD\\O \in NP \subset (MNP)\end{array} \right.\) nên \(O = CD \cap (MNP)\).
Vậy \(O \equiv I\). Vì \(O \in NP\) suy ra I, N, P thẳng hàng.
b) Đúng. Vì MN là đường trung bình của tam giác ABC nên MN//AB.
c) Đúng. Ta có \(\left\{ \begin{array}{l}MN//AB\\MN \subset (MNP)\\AB \subset (ABD)\\(MNP) \cap (ABD) = \{ P\} \end{array} \right.\) suy ra giao tuyến của (MNP) và (ABD) là đường thẳng qua P và song song với AB, MN.
Theo giả thiết, PQ//AB nên PQ chính là giao tuyến cần tìm.
d) Sai. Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}AB\) (1).
Theo giả thiết, BP = 2PD nên suy ra \(\frac{{DP}}{{DB}} = \frac{1}{3}\).
Xét tam giác ABD có PQ//AB:
\(\frac{{DQ}}{{DA}} = \frac{{DP}}{{DB}} = \frac{{PQ}}{{AB}} = \frac{1}{3}\) (hệ quả định lý Thales).
Suy ra \(PQ = \frac{1}{3}AB\) (2).
Từ (1) và (2) suy ra \(MN \ne PQ\).
Vậy MNPQ không phải hình bình hành.
Hằng ngày mức nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mức nước trong kênh được tính tại thời điểm t (giờ) trong một ngày (t > 0) bởi công thức \(h = 4\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) + 16\). Mực nước của kênh cao nhất khi t bằng bao nhiêu?
Đáp án:
Đáp án:
\(h = 4\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) + 16\) lớn nhất khi \(\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) = 1\).
Sử dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
\(\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) = 1 \Leftrightarrow \frac{{\pi t}}{8} + \frac{{5\pi }}{8} = \frac{\pi }{2} + k2\pi \Leftrightarrow \frac{{\pi t}}{8} = - \frac{\pi }{8} + k2\pi \)
\( \Leftrightarrow \frac{t}{8} = - \frac{1}{8} + 2k \Leftrightarrow t = - 1 + 16k\) \((k \in \mathbb{Z})\).
Ta có \(0 < t \le 24 \Leftrightarrow 0 < - 1 + 16k \le 24 \Leftrightarrow 1 < 16k \le 24 \Leftrightarrow \frac{1}{{16}} < k \le \frac{3}{2}\).
Vậy k = 1. Khi đó t = -1 + 16.1 = 15.
Vậy mực nước của kênh cao nhất khi t = 15 (giờ).
Một rạp hát có 18 hàng ghế xếp theo hình quạt. Hàng thứ nhất có 16 ghế, hàng thứ hai có 20 ghế, hàng thứ ba có 24 ghế,... cứ thế cho đến hàng cuối cùng. Hỏi tổng số ghế có trong rạp là bao nhiêu?
Đáp án:
Đáp án:
Sử dụng công thức tổng n số hạng đầu của cấp số cộng: \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2}\).
Số ghế mỗi hàng lập thành một cấp số cộng với \({u_1} = 16\) và d = 4.
Tổng số ghế trong rạp là \({S_{18}} = \frac{{18\left[ {2.16 + (18 - 1).4} \right]}}{2} = 900\).
Tính giới hạn \(\lim \left[ {\frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{(2n - 1)(2n + 1)}}} \right]\). Viết kết quả dưới dạng số thập phân.
Đáp án:
Đáp án:
Sử dụng quy tắc tính giới hạn tại vô cực.
\(\lim \left[ {\frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{(2n - 1)(2n + 1)}}} \right]\)
\( = \lim \frac{1}{2}\left( {1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + ... + \frac{1}{{2n - 1}} + \frac{1}{{2n + 1}}} \right)\)
\( = \lim \frac{1}{2}\left( {1 - \frac{1}{{2n + 1}}} \right) = \frac{1}{2}\left( {1 - 0} \right) = \frac{1}{2} = 0,5\).
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{\sqrt[3]{{x + 7}} - \sqrt {3x + 1} }}{{x - 1}}\\ax\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne 1\\x = 1\end{array}\). Tìm giá trị của a để hàm số liên tục tại \({x_0} = 1\) (làm tròn kết quả đến hàng phần mười).
Đáp án:
Đáp án:
Hàm số liên tục tại \({x_0}\) khi \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).
Ta có: \(\frac{{\sqrt[3]{{x + 7}} - \sqrt {3x + 1} }}{{x - 1}} = \frac{{\sqrt[3]{{x + 7}} - 2 + 2 - \sqrt {3x + 1} }}{{x - 1}} = \frac{{\sqrt[3]{{x + 7}} - 2}}{{x - 1}} + \frac{{2 - \sqrt {3x + 1} }}{{x - 1}}\)
\( = \frac{{x + 7 - 8}}{{\left( {x - 1} \right)\left( {\sqrt {x + 7} + \sqrt[2]{{x + 7}}.2 + 4} \right)}} + \frac{{4 - \left( {3x + 1} \right)}}{{\left( {x - 1} \right)\left( {2 + \sqrt {3x + 1} } \right)}}\)
\( = \frac{1}{{\sqrt {x + 7} + \sqrt[2]{{x + 7}}.2 + 4}} + \frac{{3 - 3x}}{{\left( {x - 1} \right)\left( {2 + \sqrt {3x + 1} } \right)}}\)
\( = \frac{1}{{\sqrt {x + 7} + \sqrt[2]{{x + 7}}.2 + 4}} - \frac{3}{{2 + \sqrt {3x + 1} }}\).
Ta có: \(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[3]{{x + 7}} - \sqrt {3x + 1} }}{{x - 1}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {x + 7} + \sqrt[2]{{x + 7}}.2 + 4}} - \frac{3}{{2 + \sqrt {3x + 1} }}\)
\( = \frac{1}{{\sqrt {1 + 7} + \sqrt[2]{{1 + 7}}.2 + 4}} - \frac{3}{{2 + \sqrt {3.1 + 1} }} \approx - 0,7\).
Mà \(f(1) = a.1 = a\).
Để hàm số liên tục tại \({x_0} = 1\) thì \(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\), suy ra \(a \approx - 0,7\).
Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Gọi I là giao điểm của đường thẳng AM với mặt phẳng (SBD). Tính tỉ số \(\frac{{IA}}{{IM}}\)?
Đáp án:
Đáp án:
Sử dụng các khái niệm, tính chất của điểm, đường thẳng, mặt phẳng trong không gian.
Sử dụng tính chất trọng tâm tam giác.
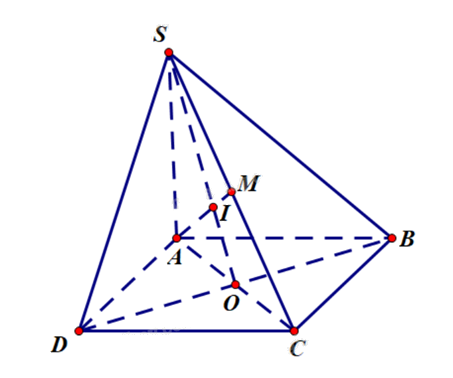
Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC, BD (vì ABCD là hình bình hành).
Dễ dàng chứng minh \(SO \subset (SBD)\), \(SO \subset (SAC)\) và \(AM \subset (SAC)\).
Xét trong mặt phẳng (SAC), giả sử AM giao SO tại I’.
Ta có \(\left\{ \begin{array}{l}I' \in AM\\I' \in SO \subset (SBD)\end{array} \right.\) suy ra I’ là giao điểm của AM và mặt phẳng (SBD).
Suy ra I’ trùng I.
Xét tam giác SAC có AM, SO là các đường trung tuyến cắt nhau tại I.
Suy ra I là trọng tâm của tam giác SAC. Vậy \(\frac{{IA}}{{IM}} = 2\).
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, AC = 6, BD = 8; tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho AI = x (0 < x < 3), (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD). Diện tích của hình tạo bởi các đoạn giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD bằng \(\frac{{a{x^2}\sqrt 3 }}{b}\). Tính giá trị của biểu thức P = a + b.
Đáp án:
Đáp án:
Sử dụng tính chất giao tuyến, hệ quả định lí Thales, công thức tính diện tích tam giác đều khi biết độ dài cạnh.
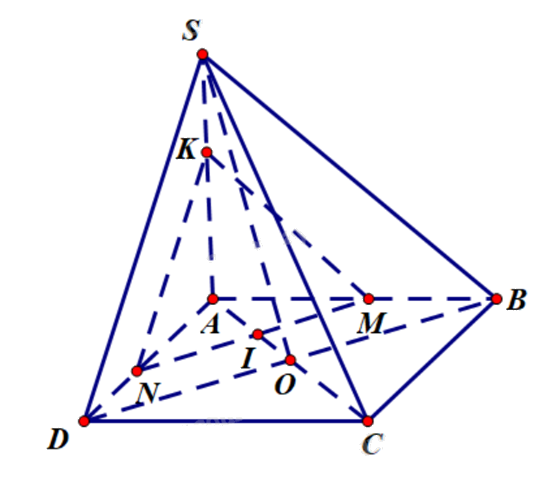
Vì (P)//(SBD) suy ra BD//(P) và SB//(P).
Ta có \(\left\{ \begin{array}{l}I \in (P) \cap (ABCD)\\BD \subset (ABCD)\\BD//(P)\end{array} \right.\) suy ra giao tuyến của (P) và (ABCD) là đường thẳng qua I song song với BD. Giao tuyến này cắt AB tại M, cắt AD tại N.
Tương tự \(\left\{ \begin{array}{l}M \in (P) \cap (SAB)\\SB \subset (SAB)\\SB//(P)\end{array} \right.\) suy ra giao tuyến của (P) và (SAB) là đường thẳng qua M song song với SB.
Giao tuyến này cắt SA tại K.
Thiết diện cần tìm là tam giác MNK.
Hai tam giác KMN và SBD có các cặp cạnh tương ứng song song nên chúng đồng dạng. Mà tam giác SBD đều nên tam giác KMN đều.
Xét tam giác AOD có IN//DO: \(\frac{{AI}}{{AO}} = \frac{{IN}}{{DO}}\) (hệ quả định lí Thales).
Xét tam giác AOB có IM//BO: \(\frac{{AI}}{{AO}} = \frac{{IM}}{{BO}}\) (hệ quả định lí Thales).
Suy ra \(\frac{{IN}}{{DO}} = \frac{{IM}}{{BO}}\). Do đó \(\frac{{AI}}{{AO}} = \frac{{IN + IM}}{{DO + BO}}\) hay \(\frac{{AI}}{{AO}} = \frac{{MN}}{{BD}} \Leftrightarrow \frac{x}{{\frac{{AC}}{2}}} = \frac{{MN}}{{BD}}\)
\( \Leftrightarrow \frac{x}{3} = \frac{{MN}}{8} \Leftrightarrow MN = \frac{{8x}}{3}\).
Diện tích tam giác đều KMN là \(S = \frac{{M{N^2}\sqrt 3 }}{4} = \frac{{{{\left( {\frac{{8x}}{3}} \right)}^2}\sqrt 3 }}{4} = \frac{{16{x^2}\sqrt 3 }}{9}\).
Suy ra a = 16, b = 9.
Vậy P = a + b = 16 + 9 = 25.
Đề thi học kì 1 Toán 11 Cánh diều - Đề số 6 là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức và kỹ năng đã học trong học kì. Đề thi bao gồm các chủ đề chính như hàm số bậc hai, hàm số lượng giác, và các kiến thức về vectơ trong mặt phẳng tọa độ. Việc làm quen với cấu trúc đề thi và luyện tập giải các bài toán tương tự là rất cần thiết để đạt kết quả tốt nhất.
Đề thi thường được chia thành hai phần chính: phần trắc nghiệm và phần tự luận. Phần trắc nghiệm thường chiếm khoảng 40-50% tổng số điểm, tập trung vào việc kiểm tra kiến thức cơ bản và khả năng áp dụng công thức. Phần tự luận chiếm khoảng 50-60% tổng số điểm, yêu cầu học sinh trình bày lời giải chi tiết và chứng minh các kết quả.
Để giải quyết các bài toán trong đề thi, học sinh cần nắm vững các kiến thức cơ bản về hàm số, phương trình, và vectơ. Đối với phần trắc nghiệm, học sinh cần đọc kỹ đề bài và lựa chọn đáp án chính xác. Đối với phần tự luận, học sinh cần trình bày lời giải một cách rõ ràng, logic, và đầy đủ các bước. Việc sử dụng các công thức và định lý một cách chính xác cũng rất quan trọng.
Để đạt kết quả tốt nhất trong kỳ thi, học sinh nên dành thời gian luyện tập giải các đề thi thử và ôn tập lại các kiến thức đã học. Việc làm thêm các bài tập trong sách giáo khoa và sách bài tập cũng rất hữu ích. Ngoài ra, học sinh có thể tham gia các khóa học online hoặc tìm kiếm sự giúp đỡ từ các thầy cô giáo.
Trước khi làm bài thi, học sinh nên đọc kỹ hướng dẫn làm bài và phân bổ thời gian hợp lý cho từng phần. Trong quá trình làm bài, học sinh nên giữ bình tĩnh và tự tin. Sau khi làm xong bài, học sinh nên kiểm tra lại toàn bộ bài làm để đảm bảo không có sai sót.
| Chủ đề | Kiến thức trọng tâm |
|---|---|
| Hàm số bậc hai | Định nghĩa, tập xác định, tập giá trị, đỉnh, trục đối xứng, tính đơn điệu, cực trị. |
| Hàm số lượng giác | Định nghĩa, tập xác định, tập giá trị, chu kỳ, tính đơn điệu, đồ thị. |
| Vectơ | Định nghĩa, các phép toán trên vectơ, tích vô hướng, ứng dụng của vectơ trong hình học. |
Hy vọng rằng đề thi học kì 1 Toán 11 Cánh diều - Đề số 6 và hướng dẫn giải chi tiết này sẽ giúp các em học sinh ôn luyện và đạt kết quả tốt nhất trong kỳ thi sắp tới.