Chào mừng các em học sinh đến với Đề thi học kì 2 Toán 11 Cánh diều - Đề số 10 tại giaitoan.edu.vn. Đề thi này được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo.
Đây là cơ hội tuyệt vời để các em tự đánh giá năng lực, rèn luyện kỹ năng giải đề và chuẩn bị tốt nhất cho kỳ thi sắp tới.
Nghiệm của phương trình \({3^x} = 4\) là
\({\log _3}4\)
\({\log _4}3\)
\(\sqrt[3]{5}\)
\(\frac{5}{3}\)
Tập xác định của hàm số \(y = {\log _5}{x^2}\) là
\(\left( { - \infty ;0} \right)\)
\(\left( {0; + \infty } \right)\)
\(\left( { - \infty ; + \infty } \right)\)
\(\left( { - \infty ;0} \right) \cup \left( {0; + \infty } \right)\)
Thống kê số tiền (đơn vị: nghìn đồng) mà 60 khách mua ở một siêu thị mini trong một ngày thu được kết quả như sau:

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
69,83
63,16
77,39
70,87
Khẳng định nào sau đây sai?
\(\left( {\sin x} \right)' = \cos x\)
\(\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}}\)
\(\left( {\cot x} \right)' = \frac{1}{{{{\sin }^2}x}}\)
\(\left( {\cos x} \right)' = - \sin x\)
Cho hàm số \(y = {\left( {\ln x} \right)^3}\). Đạo hàm của hàm số đã cho là
\(y' = \frac{3}{x}\)
\(y' = \frac{{3{{\left( {\ln x} \right)}^2}}}{x}\)
\(y' = \frac{{\ln x}}{x}\)
\(y' = 3\ln x\)
Đạo hàm của hàm số \({x^2} + {3^x}\) trên \(\mathbb{R}\) là
\(y' = 2x + {3^x}\)
\(y' = 2x + {3^x}\ln 3\)
\(y' = 2x + x{3^{x - 1}}\)
\(y' = x + {3^x}\ln 3\)
Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = {x^2} - 3x + 2\) tại điểm x = -1 là
-1
-5
2
6
Cho A, B là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
\(P(A \cup B) = P(A) + P(B)\)
\(P(A \cup B) = P(A).P(B)\)
\(P(A \cup B) = P(A) - P(B)\)
\(P(A \cap B) = P(A) + P(B)\)
Cho hai biến cố A và B độc lập. Tìm mệnh đề sai trong các mệnh đề sau:
Hai biến cố \(A\) và \(\overline B \) độc lập
Hai biến cố \(A\) và \(B\) độc lập
Hai biến cố \(\overline A \) và \(\overline B \) độc lập
Hai biến cố \(A\) và \(\overline A \) độc lập
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, \(SA \bot (ABCD)\). Khẳng định nào sau đây sai?
\(AC \bot (SBD)\)
\(BD \bot (SAC)\)
\(CD \bot (SAD)\)
\(BC \bot (SAB)\)
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(SA \bot (ABCD)\). Khẳng định nào sau đây sai?
\(d\left( {S,(ABCD)} \right) = SA\)
\(d\left( {D,(SAB)} \right) = DA\)
\(d\left( {A,(SBC)} \right) = AB\)
\(d\left( {D,(SAB)} \right) = d\left( {C,(SAB)} \right)\)
Cho khối chóp có đáy là hình vuông cạnh 3a và chiều cao bằng 5a. Thể tích khối chóp đã cho bằng
\(25{a^3}\)
\(45{a^3}\)
\(5{a^3}\)
\(15{a^3}\)
Cho hàm số \(y = f(x) = 2{x^3} + 2\).
a) Đạo hàm của hàm số y = f(x) tại điểm \({x_0} = 1\) là \(f'(1) = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{f(x) - f(1)}}{{x - 1}}\).
b) Hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0} = 1\) là f’(1) = 6.
c) Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0} = 1\) là y = 6x – 2.
d) Đồ thị hàm số y = f(x) có hai tiếp tuyến vuông góc với nhau.
Một hộp đựng 30 tấm thẻ có đánh số từ 1 đến 30, hai tấm thẻ khác nhau đánh hai số khác nhau. Lấy ngẫu nhiên một tấm thẻ từ hộp. Gọi A là biến cố “Thẻ lấy được chia hết cho 4”, B là biến cố “Thẻ lấy được chia hết cho 3”.
a) A và B xung khắc.
b) Xác suất để lấy được thẻ đánh số chia hết cho 4 bằng \(\frac{{11}}{{30}}\).
c) Xác suất để lấy được thẻ đánh số chia hết cho 3 và chia hết cho 4 bằng \(\frac{1}{{15}}\).
d) Xác suất để lấy được thẻ đánh số chia hết cho 3 hoặc 4 bằng \(\frac{1}{2}\).
Một vật chuyển động có quãng đường được xác định bởi phương trình \(s(t) = 2{t^2} + 5t + 2\), trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời của vật tại thời điểm t = 4.
Mai, Lan và 5 bạn cùng lớp xếp thành một hàng ngang theo thứ tự ngẫu nhiên. Tính xác suất của biến cố "Có ít nhất một trong hai bạn Mai và Lan đứng ở đầu hàng" (kết quả làm tròn đến hàng phần trăm)?
Giả sử số lượng một bầy ruồi tại thời điểm t được tính theo công thức là \(N(t) = {N_0}.{e^{kt}}\), trong đó \({N_0}\) là số lượng bầy ruồi tại thời điểm t = 0 và k là hằng số tương trưởng của bầy ruồi. Biết số lượng bầy ruồi tăng lên gấp đôi sau 9 ngày và biết \({N_0} = 100\) con. Hỏi sau bao nhiêu ngày bầy ruồi có 800 con?
Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21 m và cạnh đáy dài 34 m. Góc nhị diện tạo bởi hai mặt bên có chung một cạnh của kim tứ tháp có số đo bằng bao nhiêu độ (làm tròn đến hàng đơn vị)?

Cho hàm số \(y = \frac{9}{x}\) có đồ thị là (C). Biết tiếp tuyến của đồ thị (C) tại điểm M(3;3) tạo với hai trục tọa độ một tam giác. Tính diện tích tam giác đó.
Có bao nhiêu nghiệm nguyên thuộc [-2024; 2024] của bất phương trình \({\log _2}\left( {{2^x} + 1} \right) > 2 + x\)?
Cho hình chóp S.ABCD có đáy là tam giác vuông tại B có AB = a, \(BC = a\sqrt 3 \). Biết SA = 2a và \(SA \bot (ABC)\).
a) Tính khoảng cách từ A đến mặt phẳng (SBC).
b) Gọi M là trung điểm của AC. Tính khoảng cách từ A đến mặt phẳng (SBM).
Nghiệm của phương trình \({3^x} = 4\) là
\({\log _3}4\)
\({\log _4}3\)
\(\sqrt[3]{5}\)
\(\frac{5}{3}\)
Đáp án : A
Với a > 0: \({a^x} = b \Leftrightarrow x = {\log _a}b\).
\({3^x} = 4 \Leftrightarrow {\log _3}4\).
Tập xác định của hàm số \(y = {\log _5}{x^2}\) là
\(\left( { - \infty ;0} \right)\)
\(\left( {0; + \infty } \right)\)
\(\left( { - \infty ; + \infty } \right)\)
\(\left( { - \infty ;0} \right) \cup \left( {0; + \infty } \right)\)
Đáp án : D
Tìm ĐKXĐ của hàm số.
ĐKXĐ: \({x^2} > 0 \Leftrightarrow x \ne 0\). Vậy tập xác định của \(y = {\log _5}{x^2}\) là \(\left( { - \infty ;0} \right) \cup \left( {0; + \infty } \right)\).
Thống kê số tiền (đơn vị: nghìn đồng) mà 60 khách mua ở một siêu thị mini trong một ngày thu được kết quả như sau:

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
69,83
63,16
77,39
70,87
Đáp án : B
Áp dụng công thức tính tứ phân vị của mẫu số liệu ghép nhóm.
Cỡ mẫu: n = 3 + 6 + 19 + 23 + 9 = 60.
Tứ phân vị thứ nhất \({Q_1} = \frac{{{x_{15}} + {x_{16}}}}{2} \in [60;70)\).
\({Q_1} = 60 + \frac{{\frac{{60}}{4} - 3 - 6}}{{19}}(70 - 60) = \frac{{1200}}{{19}} \approx 63,16\).
Khẳng định nào sau đây sai?
\(\left( {\sin x} \right)' = \cos x\)
\(\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}}\)
\(\left( {\cot x} \right)' = \frac{1}{{{{\sin }^2}x}}\)
\(\left( {\cos x} \right)' = - \sin x\)
Đáp án : C
Áp dụng công thức tính đạo hàm của hàm số lượng giác.
Ta có \(\left( {\cot x} \right)' = - \frac{1}{{{{\sin }^2}x}}\) nên C sai.
Cho hàm số \(y = {\left( {\ln x} \right)^3}\). Đạo hàm của hàm số đã cho là
\(y' = \frac{3}{x}\)
\(y' = \frac{{3{{\left( {\ln x} \right)}^2}}}{x}\)
\(y' = \frac{{\ln x}}{x}\)
\(y' = 3\ln x\)
Đáp án : B
Áp dụng công thức công thức đạo hàm hợp \(\left( {{u^\alpha }} \right)' = u'.\alpha .{u^{\alpha - 1}}\).
\(y' = \left[ {{{\left( {\ln x} \right)}^3}} \right]' = 3.\left( {\ln x} \right)'{\left( {\ln x} \right)^2} = \frac{{3{{\left( {\ln x} \right)}^2}}}{x}\).
Đạo hàm của hàm số \({x^2} + {3^x}\) trên \(\mathbb{R}\) là
\(y' = 2x + {3^x}\)
\(y' = 2x + {3^x}\ln 3\)
\(y' = 2x + x{3^{x - 1}}\)
\(y' = x + {3^x}\ln 3\)
Đáp án : C
Áp dụng công thức đạo hàm \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\) và \(\left( {{a^x}} \right)' = {a^x}\ln a\).
\(y' = \left( {{x^2} + {3^x}} \right)' = 2x + {3^x}\ln 3\).
Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = {x^2} - 3x + 2\) tại điểm x = -1 là
-1
-5
2
6
Đáp án : B
Tính f’(-1).
\(f'(x) = \left( {{x^2} - 3x + 2} \right)' = 2x - 3\).
Hệ số góc của tiếp tuyến là f’(-1) = 2.(-1) – 3 = -5.
Cho A, B là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
\(P(A \cup B) = P(A) + P(B)\)
\(P(A \cup B) = P(A).P(B)\)
\(P(A \cup B) = P(A) - P(B)\)
\(P(A \cap B) = P(A) + P(B)\)
Đáp án : A
Áp dụng công thức cộng xác suất cho hai biến cố xung khắc.
Hai biến cố A, B xung khắc thì \(P(A \cup B) = P(A) + P(B)\).
Cho hai biến cố A và B độc lập. Tìm mệnh đề sai trong các mệnh đề sau:
Hai biến cố \(A\) và \(\overline B \) độc lập
Hai biến cố \(A\) và \(B\) độc lập
Hai biến cố \(\overline A \) và \(\overline B \) độc lập
Hai biến cố \(A\) và \(\overline A \) độc lập
Đáp án : D
Áp dụng lí thuyết về hai biến cố độc lập: Hai biến cố được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia.
Vì \(P(\overline A ) = 1 - P(A)\) nên xác suất của \(\overline A \) và \(A\) phụ thuộc vào nhau. Do đó hai biến cố trên không độc lập.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, \(SA \bot (ABCD)\). Khẳng định nào sau đây sai?
\(AC \bot (SBD)\)
\(BD \bot (SAC)\)
\(CD \bot (SAD)\)
\(BC \bot (SAB)\)
Đáp án : A
Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng.
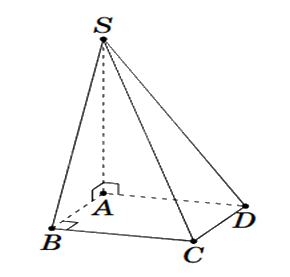
Ta có:
\(\left\{ \begin{array}{l}BD \bot SA\\BD \bot AC\end{array} \right. \Rightarrow BD \bot (SAC) \Rightarrow \) Đáp án B đúng.
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot (SAD) \Rightarrow \) Đáp án C đúng.
\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow \) Đáp án D đúng.
Vì AC chỉ vuông góc với BD trong (SBD) nên AC không vuông góc với (SBD).
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(SA \bot (ABCD)\). Khẳng định nào sau đây sai?
\(d\left( {S,(ABCD)} \right) = SA\)
\(d\left( {D,(SAB)} \right) = DA\)
\(d\left( {A,(SBC)} \right) = AB\)
\(d\left( {D,(SAB)} \right) = d\left( {C,(SAB)} \right)\)
Đáp án : C
Khoảng cách từ một điểm tới một mặt phẳng là khoảng cách từ điểm đó đến hình chiếu của nó trên mặt phẳng.
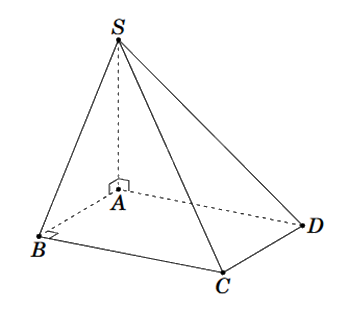
Vì B không phải hình chiếu vuông góc của A lên (SBC) nên \(d\left( {A,(SBC)} \right) \ne AB\).
Cho khối chóp có đáy là hình vuông cạnh 3a và chiều cao bằng 5a. Thể tích khối chóp đã cho bằng
\(25{a^3}\)
\(45{a^3}\)
\(5{a^3}\)
\(15{a^3}\)
Đáp án : D
Áp dụng công thức tính thể tích khối chóp \(V = \frac{1}{3}Bh\).
\(V = \frac{1}{3}Bh = \frac{1}{3}{\left( {3a} \right)^2}.5a = 15{a^3}\).
Cho hàm số \(y = f(x) = 2{x^3} + 2\).
a) Đạo hàm của hàm số y = f(x) tại điểm \({x_0} = 1\) là \(f'(1) = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{f(x) - f(1)}}{{x - 1}}\).
b) Hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0} = 1\) là f’(1) = 6.
c) Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0} = 1\) là y = 6x – 2.
d) Đồ thị hàm số y = f(x) có hai tiếp tuyến vuông góc với nhau.
a) Đạo hàm của hàm số y = f(x) tại điểm \({x_0} = 1\) là \(f'(1) = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{f(x) - f(1)}}{{x - 1}}\).
b) Hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0} = 1\) là f’(1) = 6.
c) Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0} = 1\) là y = 6x – 2.
d) Đồ thị hàm số y = f(x) có hai tiếp tuyến vuông góc với nhau.
a) Đạo hàm của hàm số y = f(x) tại điểm \({x_0}\) là \(f'(1) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\).
b) Hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0}\) là \(f'({x_0})\).
c) Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0}\) là \(y = f'({x_0})(x - {x_0}) + {y_0}\).
d) Kiểm tra tích của hai hệ số góc có thể bằng -1 không.
a) Sai. Đạo hàm của hàm số y = f(x) tại điểm \({x_0} = 1\) là \(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}}\).
b) Đúng. \(f'(x) = 6{x^2} \Rightarrow f'(1) = {6.1^2} = 6\).
Vậy hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0} = 1\) là f’(1) = 6.
c) Đúng. Ta có \(f(1) = {2.1^3} + 2 = 4\).
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \({x_0} = 1\) là:
\(y = 6(x - 1) + 4 \Leftrightarrow y = 6x - 2\).
d) Sai. Với \({x_0}\) bất kì, ta có \(f'({x_0}) = 6{x_0}^2\).
Gọi A và B là hai tiếp điểm của hai tiếp tuyến của đồ thị hàm số y = f(x). Khi đó:
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm A là \(f'({x_A}) = 6{x_A}^2\).
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm B là \(f'({x_B}) = 6{x_B}^2\).
Để tiếp tuyến tại A và B vuông góc với nhau thì \(f'({x_A}).f'({x_B}) = - 1 \Leftrightarrow 6{x_A}^2.6{x_B}^2 = - 1\) (vô lí).
Vậy không tồn tại hai tiếp tuyến của đồ thị hàm số y = f(x) vuông góc với nhau.
Một hộp đựng 30 tấm thẻ có đánh số từ 1 đến 30, hai tấm thẻ khác nhau đánh hai số khác nhau. Lấy ngẫu nhiên một tấm thẻ từ hộp. Gọi A là biến cố “Thẻ lấy được chia hết cho 4”, B là biến cố “Thẻ lấy được chia hết cho 3”.
a) A và B xung khắc.
b) Xác suất để lấy được thẻ đánh số chia hết cho 4 bằng \(\frac{{11}}{{30}}\).
c) Xác suất để lấy được thẻ đánh số chia hết cho 3 và chia hết cho 4 bằng \(\frac{1}{{15}}\).
d) Xác suất để lấy được thẻ đánh số chia hết cho 3 hoặc 4 bằng \(\frac{1}{2}\).
a) A và B xung khắc.
b) Xác suất để lấy được thẻ đánh số chia hết cho 4 bằng \(\frac{{11}}{{30}}\).
c) Xác suất để lấy được thẻ đánh số chia hết cho 3 và chia hết cho 4 bằng \(\frac{1}{{15}}\).
d) Xác suất để lấy được thẻ đánh số chia hết cho 3 hoặc 4 bằng \(\frac{1}{2}\).
Áp dụng quy tắc nhân xác suất và tính xác suất của biến cố đối.
a)Sai. Ta có \(A \cap B\) là biến cố: “Lấy được thẻ đánh số chia hết cho 3 và chia hết cho 4”.
Suy ra \(A \cap B = \{ 12;24\} \ne \emptyset \) nên A và B không xung khắc.
b) Sai. A = {4; 8; 12; 16; 20; 24; 28}.
Vậy xác để lấy được thẻ đánh số chia hết cho 4 là \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{7}{{30}}\).
c) Đúng. \(n(A \cap B) = 2\) nên xác suất để lấy được thẻ đánh số chia hết cho 3 và chia hết cho 4 là \(P(A \cap B) = \frac{{n(A \cap B)}}{{n(\Omega )}} = \frac{2}{{30}}\).
d) Đúng. B = {3; 6; 9; 12; 15; 18; 21; 24; 27; 30}.
Xác để lấy được thẻ đánh số chia hết cho 3 là \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{10}}{{30}} = \frac{1}{{10}}\).
\(P(A \cap B) = P(A) + P(B) - P(A \cap B) = \frac{7}{{30}} + \frac{1}{3} - \frac{2}{{30}} = \frac{1}{2}\).
Một vật chuyển động có quãng đường được xác định bởi phương trình \(s(t) = 2{t^2} + 5t + 2\), trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời của vật tại thời điểm t = 4.
Tính v(4) = s’(4).
Vận tốc của vật tại thời điểm t là v(t) = s’(t) = 4t + 5.
Vận tốc tức thời của vật tại thời điểm t = 4 là v(4) = 4.4 + 5 = 21 (m/s).
Mai, Lan và 5 bạn cùng lớp xếp thành một hàng ngang theo thứ tự ngẫu nhiên. Tính xác suất của biến cố "Có ít nhất một trong hai bạn Mai và Lan đứng ở đầu hàng" (kết quả làm tròn đến hàng phần trăm)?
Áp dụng phương pháp tổ hợp và công thức cộng xác suất.
Số cách xếp 7 người thành một hàng ngang là 7!.
Gọi các biến cố:
A: “Mai đứng ở đầu hàng”; B: “Lan đứng ở đầu hàng”.
* Xác suất Mai đứng đầu hàng:
+ Có 2 cách xếp Mai đứng ở đầu hàng (ngoài cùng bên trái hoặc phải).
+ Có 6! cách xếp các bạn còn lại.
Vậy xác suất Mai đứng đầu hàng là \(P(A) = \frac{{2.6!}}{{7!}} = \frac{2}{7}\).
* Xác suất Lan đứng đầu hàng: Tương tự Mai: \(P(B) = \frac{{2.6!}}{{7!}} = \frac{2}{7}\).
* Xác suất cả Mai và Lan đứng đầu hàng:
+ Có 2 cách xếp Mai và Lan cùng đứng đầu hàng (hai bạn đổi chỗ cho nhau).
+ Có 5! cách xếp các bạn còn lại.
Vậy xác suất cả Mai và Lan đứng đầu hàng là \(P(A \cap B) = \frac{{2.5!}}{{7!}} = \frac{1}{{21}}\).
Xác suất của biến cố “Có ít nhất một trong hai bạn Mai và Lan đứng ở đầu hàng” là:
\(P(A \cup B) = P(A) + P(B) - P(A \cap B) = \frac{2}{7} + \frac{2}{7} - \frac{1}{{21}} = \frac{{11}}{{21}} \approx 0,52\).
Giả sử số lượng một bầy ruồi tại thời điểm t được tính theo công thức là \(N(t) = {N_0}.{e^{kt}}\), trong đó \({N_0}\) là số lượng bầy ruồi tại thời điểm t = 0 và k là hằng số tương trưởng của bầy ruồi. Biết số lượng bầy ruồi tăng lên gấp đôi sau 9 ngày và biết \({N_0} = 100\) con. Hỏi sau bao nhiêu ngày bầy ruồi có 800 con?
Thay các dữ kiện từ để bài để tìm k, từ đó giải phương trình mũ tìm t.
Vì số lượng bầy ruồi tăng lên gấp đôi sau 9 ngày nên ta có:
\(2{N_0} = {N_0}.{e^{9k}} \Leftrightarrow k = \frac{{\ln 2}}{9}\).
Để được 800 con ruồi, cần:
\(800 = 100.{e^{t\frac{{\ln 2}}{9}}} \Leftrightarrow {e^{t\frac{{\ln 2}}{9}}} = 8 \Leftrightarrow t\frac{{\ln 2}}{9} = \ln 8 \Leftrightarrow t = 9\frac{{\ln 8}}{{\ln 2}} = 27\) (ngày).
Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21 m và cạnh đáy dài 34 m. Góc nhị diện tạo bởi hai mặt bên có chung một cạnh của kim tứ tháp có số đo bằng bao nhiêu độ (làm tròn đến hàng đơn vị)?

Mô hình hóa kim tự tháp bằng chóp tứ giác đều S.ABCD như hình. O là tâm đáy ABCD.
Gọi H là hình chiếu vuông góc của O lên SD.
Tính \([A,SD,C] = \widehat {AHC}\).
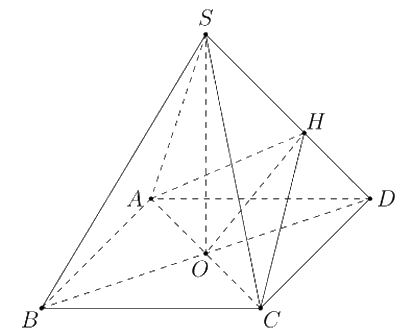
Mô hình hóa kim tự tháp bằng chóp tứ giác đều S.ABCD như hình. O là tâm đáy ABCD.
Khi đó, SO = 21 và AB = 34 (m).
Vì S.ABCD là chóp đều nên \(SO \bot (ABCD) \Rightarrow SO \bot AC\).
Ta có \(\left\{ \begin{array}{l}AC \bot SO\\AC \bot BD\end{array} \right. \Rightarrow AC \bot (SBD) \Rightarrow AC \bot SD\) (1)
Gọi H là hình chiếu vuông góc của O lên SD, do đó \(OH \bot SD\) (2)
Từ (1) và (2) suy ra \(SD \bot (AHC)\), do đó \(HC \bot SD\) và \(HA \bot SD\).
Như vậy \([A,SD,C] = \widehat {AHC}\).
Ta có \(OD = \frac{{BD}}{2} = \frac{{CD\sqrt 2 }}{2} = \frac{{34\sqrt 2 }}{2} = 17\sqrt 2 \).
Xét \(\Delta SOD\) vuông tại O, đường cao OH:
\(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{D^2}}} \Rightarrow OH = \frac{{SO.OD}}{{\sqrt {S{O^2} + O{D^2}} }} = \frac{{21.17\sqrt 2 }}{{\sqrt {{{21}^2} + {{\left( {17\sqrt 2 } \right)}^2}} }} = \frac{{357\sqrt 2 }}{{\sqrt {1019} }}\).
\(AH = CH = \sqrt {O{H^2} + O{C^2}} = \sqrt {\frac{{843880}}{{1019}}} \).
Xét \(\Delta AHC\): \(\cos \widehat {AHC} = \frac{{A{H^2} + C{H^2} - A{C^2}}}{{2AH.CH}} = - \frac{{289}}{{730}} \Rightarrow \widehat {AHC} \approx {113^o}\).
Góc nhị diện tạo bởi hai mặt bên có chung một cạnh của kim tứ tháp có số đo xấp xỉ \({113^o}\).
Cho hàm số \(y = \frac{9}{x}\) có đồ thị là (C). Biết tiếp tuyến của đồ thị (C) tại điểm M(3;3) tạo với hai trục tọa độ một tam giác. Tính diện tích tam giác đó.
Viết phương trình tiếp tuyến của (C) tại M.
Tìm giao điểm A, B của tiếp tuyến với hai trục tọa độ.
Diện tích tam giác là \(S = \frac{1}{2}OA.OB\).
Ta có \(y' = \frac{{9'.x - 9.x'}}{{{x^2}}} = - \frac{9}{{{x^2}}}\), hệ số góc của tiếp tuyến tại điểm M là \(y'(3) = - \frac{9}{{{3^2}}} = - 1\).
Phương trình tiếp tuyến d với (C) tại M là:
\(y = - 1(x - 3) + 3 \Leftrightarrow y = - x + 6\).
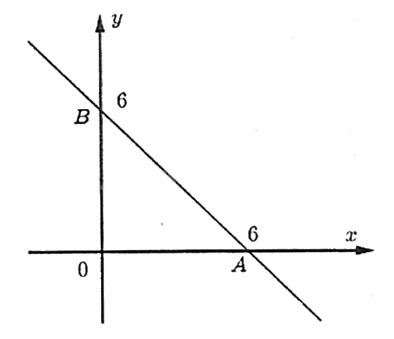
d cắt trục tung hoành và trục tung lần lượt tại hai điểm A(6;0) và B(0;6) nên diện tích tam giác OAB là:
\(S = \frac{1}{2}OA.OB = \frac{1}{2}6.6 = 18\) (đvdt).
Có bao nhiêu nghiệm nguyên thuộc [-2024; 2024] của bất phương trình \({\log _2}\left( {{2^x} + 1} \right) > 2 + x\)?
Tìm ĐKXĐ và giải bất phương trình.
ĐKXĐ: \({2^x} + 1 > 0\) (luôn đúng).
Khi đó \({\log _2}\left( {{2^x} + 1} \right) > 2 + x \Leftrightarrow {\log _2}\left( {{2^x} + 1} \right) > {\log _2}{2^{2 + x}} \Leftrightarrow {2^x} + 1 > {2^{2 + x}}\)
\( \Leftrightarrow {2^x} + 1 > {4.2^x} \Leftrightarrow 1 > {3.2^x} \Leftrightarrow {2^x} < \frac{1}{3} \Leftrightarrow x < {\log _2}\frac{1}{3}\).
Vậy tập nghiệm của bất phương trình là \(S = \left( { - \infty ;{{\log }_2}\frac{1}{3}} \right)\).
Nghiệm nguyên thuộc [-2024; 2024] của bất phương trình là {-2024; -2023; ...; -3; -2}.
Vậy có tất cả 2023 nghiệm nguyên thỏa mãn.
Cho hình chóp S.ABCD có đáy là tam giác vuông tại B có AB = a, \(BC = a\sqrt 3 \). Biết SA = 2a và \(SA \bot (ABC)\).
a) Tính khoảng cách từ A đến mặt phẳng (SBC).
b) Gọi M là trung điểm của AC. Tính khoảng cách từ A đến mặt phẳng (SBM).
a) Kẻ \(AH \bot SB\), H thuộc SB. Chứng minh \(d\left( {A,(SBC)} \right) = AH\).
b) Kẻ \(AE \bot BM\), \(AF \bot SE\). Chứng minh
\(d\left( {A,(SBM)} \right) = AF\).
Áp dụng hệ thức lượng trong tam giác vuông để tính độ dài các cạnh trên.
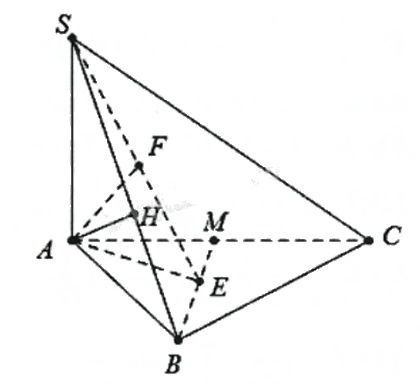
a) Kẻ \(AH \bot SB\), H thuộc SB.
Vì \(SA \bot (ABC)\) nên \(SA \bot BC\).
Ta có \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AH\).
Mặt khác \(\left\{ \begin{array}{l}AH \bot BC\\AH \bot SB\end{array} \right. \Rightarrow AH \bot (SBC)\).
Khi đó \(d\left( {A,(SBC)} \right) = AH = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{2a.a}}{{\sqrt {{{(2a)}^2} + {a^2}} }} = \frac{{2\sqrt 5 }}{5}a\).
b) Kẻ \(AE \bot BM\), \(AF \bot SE\).
Vì \(SA \bot (ABC)\) nên \(SA \bot BM\).
Ta có \(\left\{ \begin{array}{l}BM \bot AE\\BM \bot SA\end{array} \right. \Rightarrow BM \bot (SAE) \Rightarrow BM \bot AF\).
Mặt khác \(\left\{ \begin{array}{l}AF \bot BM\\AF \bot SE\end{array} \right. \Rightarrow AF \bot (SBM) \Rightarrow d\left( {A,(SBM)} \right) = AF\).
Xét \(\Delta ABC\) vuông tại B: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}} = 2a\).
Vì BM là đường trung tuyến ứng với cạnh huyển AC nên \(AM = BM = \frac{{AC}}{2} = \frac{{2a}}{2} = a\).
Khi đó \(\Delta ABM\) là tam giác đều cạnh a, suy ra \(AE = \frac{{a\sqrt 3 }}{2}\).
Khi đó \(d\left( {A,(SBM)} \right) = AF = \frac{{AE.SA}}{{\sqrt {A{E^2} + S{A^2}} }} = \frac{{\frac{{a\sqrt 3 }}{2}.2a}}{{\sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {2a} \right)}^2}} }} = \frac{{2\sqrt {57} }}{{19}}a\).
Kỳ thi học kì 2 Toán 11 đóng vai trò quan trọng trong việc đánh giá kết quả học tập của học sinh trong suốt một học kỳ. Đề thi Đề thi học kì 2 Toán 11 Cánh diều - Đề số 10 được thiết kế để kiểm tra kiến thức và kỹ năng của học sinh về các chủ đề chính trong chương trình Toán 11, bao gồm:
Đề thi thường bao gồm các dạng câu hỏi sau:
Để đạt kết quả tốt trong kỳ thi, học sinh cần:
Dạng 1: Giải phương trình lượng giác
Ví dụ: Giải phương trình sin(2x) = cos(x)
Lời giải:
sin(2x) = cos(x) ⇔ 2sin(x)cos(x) = cos(x) ⇔ cos(x)(2sin(x) - 1) = 0
⇔ cos(x) = 0 hoặc 2sin(x) - 1 = 0
Giải từng phương trình, ta được nghiệm x = π/2 + kπ hoặc x = π/6 + k2π, x = 5π/6 + k2π (k ∈ Z)
Dạng 2: Tính đạo hàm
Ví dụ: Tính đạo hàm của hàm số y = x3 - 2x2 + 5x - 1
Lời giải:
y' = 3x2 - 4x + 5
Hãy dành thời gian ôn tập kỹ lưỡng và làm quen với các dạng bài tập khác nhau. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em đạt kết quả tốt nhất trong kỳ thi học kì 2!