Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 8, một công cụ ôn tập hiệu quả dành cho học sinh lớp 6. Đề thi được biên soạn theo chương trình Cánh diều, bao gồm các dạng bài tập thường gặp trong đề thi thực tế.
Với đề thi này, học sinh có thể tự đánh giá năng lực, rèn luyện kỹ năng giải toán và làm quen với cấu trúc đề thi. Đồng thời, đề thi còn đi kèm với đáp án chi tiết, giúp học sinh hiểu rõ phương pháp giải và khắc phục những sai lầm.
Trong các cách viết sau, cách viết nào không phải là phân số?
Phân số nghịch đảo của phân số \(\frac{{ - 7}}{3}\) là
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) khi
Tìm khẳng định đúng trong các khẳng định sau.
Kết quả của phép tính \(\frac{{ - 12}}{{15}} + \frac{7}{5}\) bằng
An liệt kê năm sinh một số thành viên trong gia đình để làm bài tập môn Toán 6, được dãy dữ liệu như sau: 1971; 2021; 1999; 2050.
Giá trị không hợp lý trong dãy dữ liệu về năm sinh của các thành viên trong gia đình An là:
Khi tung đồng xu 1 lần. Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là:
Lấy ngẫu nhiên 1 thẻ từ 1 hộp 30 thẻ được đánh số từ 1 đến 30. Tính xác suất để thẻ được lấy ghi số 6.
Quan sát hình và cho biết đâu là khẳng định đúng?
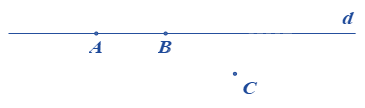
Chọn khẳng định đúng trong các khẳng định dưới đây?
Quan sát hình vẽ bên, khẳng định nào sau đây là đúng?

Cho đoạn \(AB = 6\)cm. \(M\) là điểm thuộc đoạn \(AB\) sao cho \(MB = 5\)cm
Khi đó độ dài đoạn \(MA\) bằng
Thực hiện các phép tính sau (tính hợp lý nếu có thể).
a) \(\frac{{ - 4}}{7} + \frac{{ - 3}}{7}\)
b)\(\frac{3}{5} + \frac{{ - 4}}{9}\)
c) \(\frac{3}{5} + \frac{2}{5}.\frac{{15}}{8}\)
d) \(\frac{7}{2}.\frac{8}{{13}} + \frac{8}{{13}}.\frac{{ - 5}}{2} + \frac{8}{{13}}\)
Tìm \(x\), biết:
a) \(x + \frac{{11}}{{12}} = \frac{{23}}{{24}}\)
b) \(\frac{{11}}{8} - \frac{3}{8} \cdot x = \frac{1}{8}\)
c) \({\left( {{\rm{x}} - \frac{1}{2}} \right)^{\rm{2}}}{\rm{ = }}\frac{{\rm{1}}}{4}\)
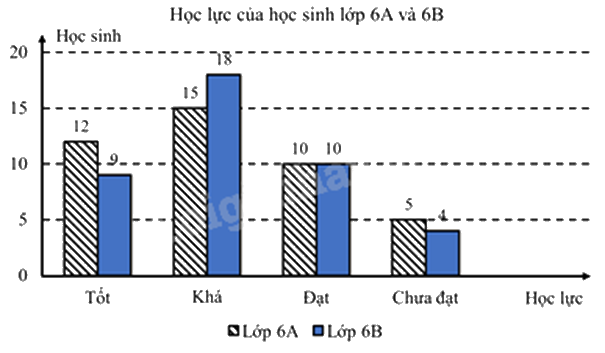
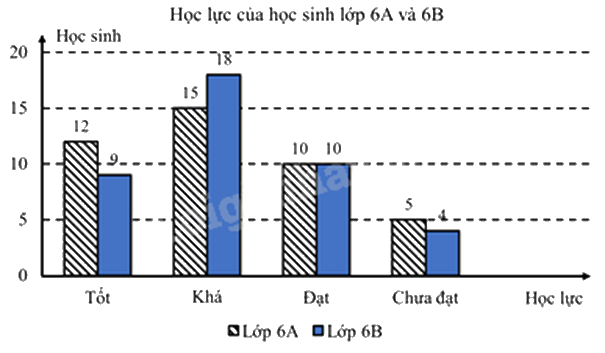
1. Cho biểu đồ cột kép thống kê về học lực của học sinh lớp 6A và 6B của một trường THCS. Dựa vào biểu đồ em hãy:
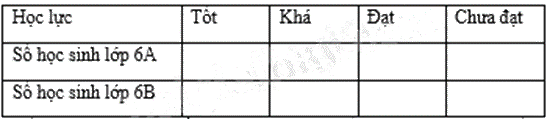
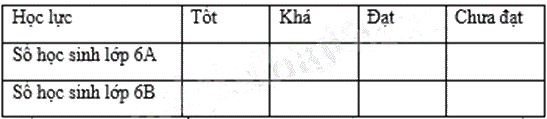
a) Vẽ bảng số liệu vào giấy và điền các dữ liệu còn thiếu vào bảng số liệu sau:
b) Hãy cho biết lớp 6B có bao nhiêu học sinh? So sánh số học sinh có học lực tốt của hai lớp?
2. Nếu tung đồng xu 22 lần liên tiếp, có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
Cho điểm \(A\) thuộc tia \(Ox\) sao cho \(OA = 5\,cm\). Trên tia \(Ox\) lấy điểm \(B\) sao cho \(OB = {\rm{ }}3\,cm\)
a) Trong ba điểm \(A,\,\,O,\,\,B\) điểm nào nằm giữa hai điểm còn lại. Tính độ dài đoạn thẳng \(AB\)
b) Lấy điểm \(C\) trên tia \(Ox\) sao cho A nằm giữa hai điểm \(O\) và \(C\)và \(AC = 1\,cm\). Điểm \(B\) có là trung điểm của \(OC\) không? Vì sao?
Tìm các giá trị của \(n\) để phân số \(M = \frac{{n - 5}}{{n - 2}}\) (n\( \in \mathbb{Z}\); n\( \ne \)2) tối giản.
Trong các cách viết sau, cách viết nào không phải là phân số?
Đáp án : C
Dựa vào khái niệm về phân số.
\(\frac{1}{7};\frac{{ - 5}}{3};\frac{0}{{ - 3}}\) là phân số vì có tử số, mẫu số là số nguyên và mẫu số khác 0.
\(\frac{7}{{1,5}}\) không phải phân số vì \(1,5 \notin \mathbb{Z}\).
Đáp án C.
Phân số nghịch đảo của phân số \(\frac{{ - 7}}{3}\) là
Đáp án : A
Nghịch đảo của phân số \(\frac{a}{b}\) là \(\frac{b}{a}\) \(\left( {\frac{a}{b}.\frac{b}{a} = 1} \right)\).
Phân số nghịch đảo của phân số \(\frac{{ - 7}}{3}\) là\(\frac{{ - 3}}{7}\).
Đáp án A.
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) khi
Đáp án : B
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) nếu \(ad = bc\).
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) khi \(a.d = b.c\).
Đáp án B.
Tìm khẳng định đúng trong các khẳng định sau.
Đáp án : B
Dựa vào cách so sánh hai phân số.
\( - 5 > - 14\) nên \(\frac{{ - 5}}{{11}} > \frac{{ - 14}}{{11}}\) nên A sai.
\(\frac{{ - 5}}{3} < 0\) nên B đúng.
\(13 < 15\) nên \(\frac{2}{{13}} > \frac{2}{{15}}\) nên C sai.
\( - 5 < 8\) nên \(\frac{{ - 5}}{{21}} < \frac{8}{{21}}\) nên D sai.
Đáp án B.
Kết quả của phép tính \(\frac{{ - 12}}{{15}} + \frac{7}{5}\) bằng
Đáp án : B
Dựa vào quy tắc cộng hai phân số khác mẫu số.
\(\frac{{ - 12}}{{15}} + \frac{7}{5} = \frac{{ - 12}}{{15}} + \frac{{21}}{{15}} = \frac{9}{{15}} = \frac{3}{5}\).
Đáp án B.
An liệt kê năm sinh một số thành viên trong gia đình để làm bài tập môn Toán 6, được dãy dữ liệu như sau: 1971; 2021; 1999; 2050.
Giá trị không hợp lý trong dãy dữ liệu về năm sinh của các thành viên trong gia đình An là:
Đáp án : A
Dựa vào các năm sinh được liệt kê để xác định năm chưa hợp lí.
Năm 2050 chưa xảy ra nên An liệt kê năm sinh của một thành viên là năm 2050 không hợp lý.
Đáp án A.
Khi tung đồng xu 1 lần. Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là:
Đáp án : B
Khi tung đồng xu một lần có hai kết quả có thể xảy ra với mặt xuất hiện của đồng xu, đó là: mặt S; mặt N.
Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là: \(\left\{ {S;N} \right\}\).
Đáp án B.
Lấy ngẫu nhiên 1 thẻ từ 1 hộp 30 thẻ được đánh số từ 1 đến 30. Tính xác suất để thẻ được lấy ghi số 6.
Đáp án : A
Dựa vào công thức tính xác suất.
Xác suất để thẻ được lấy ghi số 6 là \(\frac{1}{{30}}\).
Đáp án A.
Quan sát hình và cho biết đâu là khẳng định đúng?
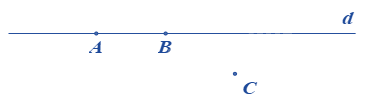
Đáp án : A
Quan sát hình vẽ để trả lời
Quan sát hình vẽ ta thấy A, B thuộc đường thẳng d và C không thuộc đường thẳng d nên A đúng.
Do đó A, B, C không thẳng hàng và AB không đi qua điểm C.
Đáp án A.
Chọn khẳng định đúng trong các khẳng định dưới đây?
Đáp án : C
Dựa vào kiến thức về ba điểm thẳng hàng.
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng nên C đúng.
Đáp án C.
Quan sát hình vẽ bên, khẳng định nào sau đây là đúng?

Đáp án : C
Dựa vào kiến thức về điểm.
J nằm giữa K và L nhưng không nằm chính giữa nên A sai.
Ngoài điểm L còn có điểm J nằm giữa hai điểm K và N nên B sai.
Quan sát hình vẽ ta thấy hai điểm L và N nằm cùng phía so với điểm K nên C đúng.
Khẳng định D sai.
Đáp án C.
Cho đoạn \(AB = 6\)cm. \(M\) là điểm thuộc đoạn \(AB\) sao cho \(MB = 5\)cm
Khi đó độ dài đoạn \(MA\) bằng
Đáp án : A
Dựa vào kiến thức về điểm thuộc đoạn thẳng.
Vì M thuộc đoạn AB nên AB = AM + MB
Suy ra AM = AB – MB = 6 – 5 = 1(cm)
Đáp án A.
Thực hiện các phép tính sau (tính hợp lý nếu có thể).
a) \(\frac{{ - 4}}{7} + \frac{{ - 3}}{7}\)
b)\(\frac{3}{5} + \frac{{ - 4}}{9}\)
c) \(\frac{3}{5} + \frac{2}{5}.\frac{{15}}{8}\)
d) \(\frac{7}{2}.\frac{8}{{13}} + \frac{8}{{13}}.\frac{{ - 5}}{2} + \frac{8}{{13}}\)
Dựa vào quy tắc tính với phân số.
a) \(\frac{{ - 4}}{7} + \frac{{ - 3}}{7} = \frac{{ - 7}}{7} = - 1\)
b)\(\frac{3}{5} + \frac{{ - 4}}{9}\) \( = \frac{{27}}{{45}} + \frac{{ - 20}}{{45}} = \frac{7}{{45}}\)
c) \(\frac{3}{5} + \frac{2}{5}.\frac{{15}}{8}\)\( = \frac{3}{5} + \frac{3}{4} = \frac{{12}}{{20}} + \frac{{15}}{{20}} = \frac{{27}}{{20}}\)
d) \(\frac{7}{2}.\frac{8}{{13}} + \frac{8}{{13}}.\frac{{ - 5}}{2} + \frac{8}{{13}}\)\( = \frac{8}{{13}}.\left( {\frac{7}{2} + \frac{{ - 5}}{2} + 1} \right) = \frac{8}{{13}}.2 = \frac{{16}}{{13}}\)
Tìm \(x\), biết:
a) \(x + \frac{{11}}{{12}} = \frac{{23}}{{24}}\)
b) \(\frac{{11}}{8} - \frac{3}{8} \cdot x = \frac{1}{8}\)
c) \({\left( {{\rm{x}} - \frac{1}{2}} \right)^{\rm{2}}}{\rm{ = }}\frac{{\rm{1}}}{4}\)
Dựa vào quy tắc tính với phân số.
a) \(x + \frac{{11}}{{12}} = \frac{{23}}{{24}}\)
\(\begin{array}{l}x = \frac{{23}}{{24}} - \frac{{11}}{{12}}\\x = \frac{{23}}{{24}} - \frac{{22}}{{24}}\\x = \frac{1}{{24}}\end{array}\)
Vậy \(x = \frac{1}{{24}}\)
b) \(\frac{{11}}{8} - \frac{3}{8} \cdot x = \frac{1}{8}\)
\(\begin{array}{l}\frac{{11}}{8} - \frac{3}{8} \cdot x = \frac{1}{8}\\\frac{3}{8}x = \frac{{11}}{8} - \frac{1}{8}\\\frac{3}{8}x = \frac{5}{4}\\x = \frac{5}{4}:\frac{3}{8}\\x = \frac{{10}}{3}\end{array}\)
Vậy \(x = \frac{{10}}{3}\)
c) \({\left( {{\rm{x}} - \frac{1}{2}} \right)^{\rm{2}}}{\rm{ = }}\frac{{\rm{1}}}{4}\)
\(\begin{array}{l}\left[ \begin{array}{l}{\rm{x}} - \frac{1}{2}{\rm{ = }}\frac{{\rm{1}}}{2}\\{\rm{x}} - \frac{1}{2}{\rm{ = }}\frac{{ - 1}}{2}\end{array} \right.\\\left[ \begin{array}{l}x = \frac{{\rm{1}}}{2} + \frac{1}{2}\\x = \frac{{ - 1}}{2} + \frac{1}{2}\end{array} \right.\\\left[ \begin{array}{l}x = 1\\x = 0\end{array} \right.\end{array}\)
Vậy \(x = 1;x = 0\).
1. Cho biểu đồ cột kép thống kê về học lực của học sinh lớp 6A và 6B của một trường THCS. Dựa vào biểu đồ em hãy:
a) Vẽ bảng số liệu vào giấy và điền các dữ liệu còn thiếu vào bảng số liệu sau:
b) Hãy cho biết lớp 6B có bao nhiêu học sinh? So sánh số học sinh có học lực tốt của hai lớp?
2. Nếu tung đồng xu 22 lần liên tiếp, có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
1. Quan sát biểu đồ để trả lời câu hỏi.
2. Xác suất thực nghiệm xuất hiện mặt N khi tung đồng xu nhiều lần bằng tỉ số giữa số lần mặt N xuất hiện với tổng số lần tung đồng xu.
1.
a) Ta có biểu đồ:
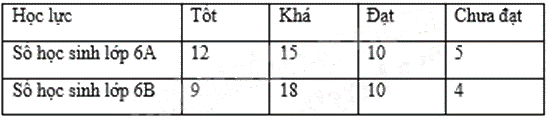
b) Số học sinh lớp 6B là \(9 + 18 + 10 + 4 = 41\)
Số học sinh đạt loại Tốt của lớp 6A nhiều hơn số học sinh đạt loại Tốt của lớp 6B là 12 – 9 = 3 học sinh.
2. Nếu tung đồng xu 22 lần liên tiếp, có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng \(\frac{{13}}{{22}}\).
Cho điểm \(A\) thuộc tia \(Ox\) sao cho \(OA = 5\,cm\). Trên tia \(Ox\) lấy điểm \(B\) sao cho \(OB = {\rm{ }}3\,cm\)
a) Trong ba điểm \(A,\,\,O,\,\,B\) điểm nào nằm giữa hai điểm còn lại. Tính độ dài đoạn thẳng \(AB\)
b) Lấy điểm \(C\) trên tia \(Ox\) sao cho A nằm giữa hai điểm \(O\) và \(C\)và \(AC = 1\,cm\). Điểm \(B\) có là trung điểm của \(OC\) không? Vì sao?
Vẽ hình theo yêu cầu.
a) Quan sát hình vẽ để xác định điểm nào nằm giữa. Từ đó tính độ dài đoạn thẳng AB theo OA và OB.
b) So sánh OB và BC để xác định.

a) Điểm \(B\) nằm giữa hai điểm \(A\) và \(O\)
Suy ra \(OB + AB = OA\).
Thay \(OA = 5\,cm\); \(OB = 3\,cm\), ta có: \(3 + AB = 5\) suy ra \(AB = 5 - 3\) suy ra \(AB = 2\left( {cm} \right)\)
b) Vì điểm \(A\) nằm giữa hai điểm \(B\) và \(C\) nên \(AB + CA = BC\).
Thay \(CA = {\rm{ }}1\,cm\); \(AB = 2\,cm\), ta có: \(2 + {\rm{ }}1{\rm{ }} = {\rm{ }}BC\) suy ra\({\rm{ }}BC = 3\left( {cm} \right)\)
Vì điểm \(B\) nằm giữa hai điểm \(C\) và \(O\) và \(BC = OB = 3\left( {cm} \right)\)
Vậy \(B\)là trung điểm của \(OC\).
Tìm các giá trị của \(n\) để phân số \(M = \frac{{n - 5}}{{n - 2}}\) (n\( \in \mathbb{Z}\); n\( \ne \)2) tối giản.
Để \(M\) là phân số tối giản thì ƯCLN của \(n - 5\) và \(n - 2\) là 1.
Gọi d là ƯCLN của \(n - 5\) và \(n - 2\).
Khi đó \(\left( {n - 5} \right) \vdots d\)và \(\left( {n - 2} \right) \vdots d\).
Suy ra\(\left[ {n - 5 - \left( {n - 2} \right)} \right] \vdots d\) suy ra \( - 3 \vdots d\).
Mà d = 1 hoặc d = -1 nên M là phân số tối giản thì \(n - 5\) và \(n - 2\) không chia hết cho 3.
Do đó \(n \ne 3k + 5\)và \(n \ne 3k + 2\)
Hay \(n \ne 3k + 2\)\(\left( {k \in \mathbb{Z}} \right)\).
Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 8 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau nửa học kỳ 2. Đề thi bao gồm các chủ đề chính như số nguyên, phân số, tỉ số, phần trăm, hình học cơ bản và biểu đồ.
Thông thường, đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 8 có cấu trúc sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 8:
Các bài tập về số nguyên thường yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia số nguyên, so sánh số nguyên, tìm giá trị tuyệt đối của số nguyên và giải các bài toán liên quan đến số nguyên âm, số nguyên dương.
Các bài tập về phân số thường yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia phân số, so sánh phân số, rút gọn phân số và giải các bài toán liên quan đến phân số tối giản.
Các bài tập về tỉ số và phần trăm thường yêu cầu học sinh tính tỉ số của hai đại lượng, tính phần trăm của một đại lượng, giải các bài toán liên quan đến tỉ lệ và phần trăm.
Các bài tập về hình học cơ bản thường yêu cầu học sinh tính diện tích, chu vi của các hình phẳng như hình vuông, hình chữ nhật, hình tam giác, hình tròn. Ngoài ra, các bài tập còn yêu cầu học sinh nhận biết các loại góc, đường thẳng, đoạn thẳng và các tính chất của chúng.
Các bài tập về biểu đồ thường yêu cầu học sinh đọc và phân tích các loại biểu đồ như biểu đồ cột, biểu đồ đường, biểu đồ tròn. Sau đó, học sinh cần trả lời các câu hỏi liên quan đến thông tin được thể hiện trên biểu đồ.
Để ôn thi giữa kì 2 Toán 6 Cánh diều - Đề số 8 hiệu quả, học sinh cần:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu ôn tập Toán 6, bao gồm đề thi, bài giảng, bài tập và đáp án chi tiết. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn sẽ giúp học sinh ôn thi giữa kì 2 Toán 6 Cánh diều - Đề số 8 một cách hiệu quả nhất.
Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 8 là một cơ hội để học sinh đánh giá năng lực và rèn luyện kỹ năng giải toán. Bằng cách nắm vững kiến thức cơ bản, luyện tập thường xuyên và sử dụng các tài liệu ôn tập hiệu quả, học sinh có thể tự tin đạt kết quả tốt trong kỳ thi.