Chào mừng các em học sinh lớp 6 đến với đề thi học kì 2 môn Toán, đề số 13, chương trình Cánh diều. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi với cấu trúc bám sát chương trình học, độ khó phù hợp, giúp các em làm quen với dạng đề thi thực tế và tự tin hơn trong kỳ thi sắp tới.
Cách viết nào sau đây không phải phân số?
Số đối của phân số \(\frac{{ - 15}}{{16}}\) là
Số nguyên \(x\) thỏa mãn điều kiện \(\frac{x}{3} = \frac{6}{{ - 9}}\) là
Tỉ số phần trăm của 16 và 20 là
Nam mua một quyển sách có giá bìa là 50000 đồng. Khi trả tiền được cửa hàng giảm giá \(10\% \). Hỏi Nam mua quyển sách đó hết bao nhiêu tiền?
Làm tròn số 131,2956 đến hàng phần trăm được kết quả là
Biết \(\frac{3}{5}\) của một số bằng (-30), số đó là
Đổi hỗn số \( - 3\frac{2}{5}\) ra phân số, kết quả là:
Dựa vào hình vẽ, hãy chọn khẳng định đúng trong các khẳng định sau?
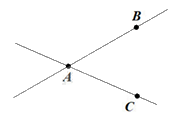
Hai tia đối nhau trong hình vẽ dưới đây là

Trên đường thẳng a lấy 10 điểm phân biệt. Số đoạn thẳng trong hình vẽ là:
Lúc 10 giờ, góc tạo bởi kim giờ và kim phút là:
1) Thực hiện phép tính:
a) \(\frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - 0,5} \right)\)
b) \(1\frac{3}{{25}} - \frac{{17}}{{19}} - \frac{3}{{25}} + \frac{{2022}}{{2023}} - \frac{2}{{19}}\)
2) Tìm \(x\) biết:
a) \(\frac{2}{3}x - \frac{1}{2} = \frac{1}{{10}}\)
b) \(5,16 - 2x = (5,7 + 2,3) \cdot ( - 0,3)\)
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại.
a) Tính số học sinh mỗi loại của lớp?
b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp?
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại.
a) Tính số học sinh mỗi loại của lớp?
b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp?
Cho hai tia \({\rm{Ox}},{\rm{Oy}}\) đối nhau. Trên tia \({\rm{Ox}}\) lấy điểm \({\rm{A}}\) sao cho \({\rm{OA}} = 4\;{\rm{cm}}\). Trên tia \({\rm{Oy}}\) lấy điểm \({\rm{B}}\) sao cho \({\rm{OB}} = 2\;{\rm{cm}}\). Gọi \({\rm{C}}\) là trung điểm của đoạn thẳng \({\rm{OA}}\).
a) Tính độ dài đoạn thẳng \({\rm{AB}}\).
b) Điểm \({\rm{O}}\) có là trung điểm của đoạn thẳng \({\rm{BC}}\) không? Vì sao?
c) Vẽ tia \({\rm{Oz}}\) khác các tia \({\rm{Ox}},{\rm{Oy}}\). Viết tên các góc có trong hình vẽ.
So sánh S với 2, biết \(S = \frac{1}{2} + \frac{2}{{{2^2}}} + \frac{3}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2023}}}}\).
Cách viết nào sau đây không phải phân số?
Đáp án : C
Phân số có dạng \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).
\(\frac{{2,5}}{3}\) không phải là phân số vì \(2,5 \notin \mathbb{Z}\).
Đáp án C.
Số đối của phân số \(\frac{{ - 15}}{{16}}\) là
Đáp án : B
Hai phân số được gọi là đối nhau nếu tổng của chúng bằng 0.
Vì \(\frac{{ - 15}}{{16}} + \frac{{15}}{{16}} = 0\) nên \(\frac{{15}}{{16}}\) là số đối của phân số \(\frac{{ - 15}}{{16}}\).
Đáp án B.
Số nguyên \(x\) thỏa mãn điều kiện \(\frac{x}{3} = \frac{6}{{ - 9}}\) là
Đáp án : B
Hai phân số \(\frac{a}{b} = \frac{c}{d}\left( {b,d \ne 0} \right)\) nếu \(a.d = c.b\)
\(\begin{array}{l}\frac{x}{3} = \frac{6}{{ - 9}}\\x.\left( { - 9} \right) = 6.3\\ - 9x = 18\\x = - 2\end{array}\)
Đáp án B.
Tỉ số phần trăm của 16 và 20 là
Đáp án : D
Tỉ số phần trăm của a và b là \(\frac{a}{b}.100\% \).
Tỉ số phần trăm của 16 và 20 là \(\frac{{16}}{{20}}.100\% = 0,8.100\% = 80\% \).
Đáp án D.
Nam mua một quyển sách có giá bìa là 50000 đồng. Khi trả tiền được cửa hàng giảm giá \(10\% \). Hỏi Nam mua quyển sách đó hết bao nhiêu tiền?
Đáp án : D
m% của a là \(m\% .a\).
Vì cửa hàng giảm giá 10% nên số tiền Nam trả ứng với:
100% - 10% = 90%.
Vậy Nam mua quyển sách đó hết:
\(90\% .50000 = 45000\) (đồng)
Đáp án D.
Làm tròn số 131,2956 đến hàng phần trăm được kết quả là
Đáp án : A
Dựa vào kiến thức làm tròn số.
Số 131,2956 làm tròn đến hàng phần trăm ta được 131,30.
Đáp án A.
Biết \(\frac{3}{5}\) của một số bằng (-30), số đó là
Đáp án : C
Biết \(\frac{m}{n}\) của a là b, ta tính được \(a = b:\frac{m}{n}\)
Số cần tìm là: \( - 30:\frac{3}{5} = - 50\).
Đáp án C.
Đổi hỗn số \( - 3\frac{2}{5}\) ra phân số, kết quả là:
Đáp án : A
Sử dụng quy tắc đổi hỗn số thành phân số.
Ta có: \( - 3\frac{2}{5} = - \frac{{3.5 + 2}}{5} = - \frac{{17}}{5}\).
Đáp án A.
Dựa vào hình vẽ, hãy chọn khẳng định đúng trong các khẳng định sau?
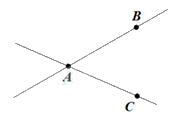
Đáp án : B
Quan sát hình vẽ để trả lời.
Hình vẽ trên là hai đường thẳng AB và AC cắt nhau tại A, chỉ có 1 điểm chung nên ta chọn đáp án B.
Đáp án B.
Hai tia đối nhau trong hình vẽ dưới đây là

Đáp án : B
Quan sát hình vẽ để trả lời câu hỏi.
Hai tia đối nhau phải là hai tia có chung gốc nên đáp án A, C, D sai.
Chỉ có Bx và By đúng.
Đáp án B.
Trên đường thẳng a lấy 10 điểm phân biệt. Số đoạn thẳng trong hình vẽ là:
Đáp án : C
Đếm số đoạn thẳng
Số đoạn thẳng là 45.
Đáp án C.
Lúc 10 giờ, góc tạo bởi kim giờ và kim phút là:
Đáp án : A
Vẽ hình mô tả để xác định

Lúc 10 giờ, góc tạo bởi kim giờ và kim phút là: góc nhọn.
Đáp án A.
1) Thực hiện phép tính:
a) \(\frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - 0,5} \right)\)
b) \(1\frac{3}{{25}} - \frac{{17}}{{19}} - \frac{3}{{25}} + \frac{{2022}}{{2023}} - \frac{2}{{19}}\)
2) Tìm \(x\) biết:
a) \(\frac{2}{3}x - \frac{1}{2} = \frac{1}{{10}}\)
b) \(5,16 - 2x = (5,7 + 2,3) \cdot ( - 0,3)\)
Áp dụng quy tắc cộng, trừ, nhân, chia.
1)
a) \(\frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - 0,5} \right)\)\( = \frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - \frac{1}{2}} \right)\)\( = \frac{1}{4} + \frac{3}{4} \cdot \frac{1}{6}\)\( = \frac{1}{4} + \frac{1}{8}\)\( = \frac{3}{8}\)
b) \(1\frac{3}{{25}} - \frac{{17}}{{19}} - \frac{3}{{25}} + \frac{{2022}}{{2023}} - \frac{2}{{19}}\)\( = \left( {1\frac{3}{{25}} - \frac{3}{{25}}} \right) + \left( {\frac{{ - 17}}{{19}} + \frac{{ - 2}}{{19}}} \right) + \frac{{2022}}{{2023}}\) \( = 1 + ( - 1) + \frac{{2022}}{{2023}}\) \( = \frac{{2022}}{{2023}}.\)
2)
a) \(\frac{2}{3}x - \frac{1}{2} = \frac{1}{{10}}\)
\(\frac{2}{3}x = \frac{1}{{10}} + \frac{1}{2}\)
\(\frac{2}{3}x = \frac{3}{5}\)
\(x = \frac{3}{5}:\frac{2}{3}\)
\(x = \frac{3}{5}.\frac{3}{2}\)
\(x = \frac{9}{{10}}\)
Vậy \(x = \frac{9}{{10}}\).
b) \(5,16 - 2x = (5,7 + 2,3) \cdot ( - 0,3)\)
\(5,16 - 2x = - 2,4\)
\(2x = 5,16 - ( - 2,4)\)
\(2x = 7,56\)
\(x = 7,56:2\)
\(x = 3,78\)
Vậy \(x = 3,78\)
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại.
a) Tính số học sinh mỗi loại của lớp?
b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp?
a) Tính \(\frac{m}{n}\) của a bằng \(\frac{m}{n}.a\).
b) Số phần trăm của a với b là \(\frac{{a.100}}{b}\% \)
a) Số học sinh xếp loại tốt là: \(40 \cdot \frac{2}{5} = 16\) ( học sinh)
Số học sinh xếp loại khá là: \((40 - 16) \cdot \frac{5}{8} = 15\) (học sinh)
Số học sinh xếp loại đạt là: \(40 - 16 - 15 = 9\) (học sinh)
b) Số học sinh xếp loại đạt chiếm số phần trảm của lớp là: \(\frac{{9.100}}{{40}}\% = 22,5\% \)
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại.
a) Tính số học sinh mỗi loại của lớp?
b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp?
a) Tính \(\frac{m}{n}\) của a bằng \(\frac{m}{n}.a\).
b) Số phần trăm của a với b là \(\frac{{a.100}}{b}\% \)
a) Số học sinh xếp loại tốt là: \(40 \cdot \frac{2}{5} = 16\) ( học sinh)
Số học sinh xếp loại khá là: \((40 - 16) \cdot \frac{5}{8} = 15\) (học sinh)
Số học sinh xếp loại đạt là: \(40 - 16 - 15 = 9\) (học sinh)
b) Số học sinh xếp loại đạt chiếm số phần trảm của lớp là: \(\frac{{9.100}}{{40}}\% = 22,5\% \)
Cho hai tia \({\rm{Ox}},{\rm{Oy}}\) đối nhau. Trên tia \({\rm{Ox}}\) lấy điểm \({\rm{A}}\) sao cho \({\rm{OA}} = 4\;{\rm{cm}}\). Trên tia \({\rm{Oy}}\) lấy điểm \({\rm{B}}\) sao cho \({\rm{OB}} = 2\;{\rm{cm}}\). Gọi \({\rm{C}}\) là trung điểm của đoạn thẳng \({\rm{OA}}\).
a) Tính độ dài đoạn thẳng \({\rm{AB}}\).
b) Điểm \({\rm{O}}\) có là trung điểm của đoạn thẳng \({\rm{BC}}\) không? Vì sao?
c) Vẽ tia \({\rm{Oz}}\) khác các tia \({\rm{Ox}},{\rm{Oy}}\). Viết tên các góc có trong hình vẽ.
Vẽ hình theo hướng dẫn.
a) Xác định độ dài đoạn thẳng AB qua OA và OB.
b) Chứng minh OB = OC và O nằm giữa B và C nên O là trung điểm của BC.
c) Vẽ tia Oz và kể tên các góc trong hình.
Vẽ hình

a) Theo hình vẽ: \(AB = OA + OB = 4 + 2 = 6\;{\rm{cm}}\)
Vậy \(AB = 6\;{\rm{cm}}\)
b) Vì C là trung điểm của đoạn thẳng \({\rm{OA}}\) nên \(OC = \frac{{OA}}{2} = \frac{4}{2} = 2\;{\rm{cm}}\)
Suy ra \({\rm{OB}} = {\rm{OC}}\)
Lại có \({\rm{O}}\) nằm giữa \({\rm{B}}\) và \({\rm{C}}\)
Do đó O là trung điểm của đoạn thẳng \({\rm{BC}}\)
Vậy \({\rm{O}}\) là trung điểm của đoạn thẳng \({\rm{BC}}\).
c)
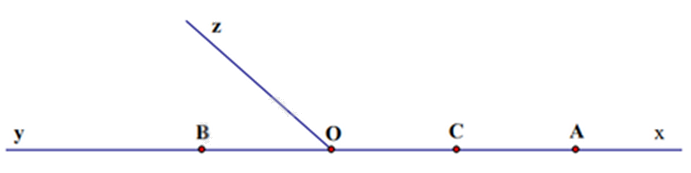
Các góc có trong hình vẽ là:
\(\widehat {{\rm{xOz}}};\widehat {{\rm{yOz}}};\widehat {{\rm{xOy}}},\widehat {xAy},\widehat {xCy},\widehat {xBy}\)
So sánh S với 2, biết \(S = \frac{1}{2} + \frac{2}{{{2^2}}} + \frac{3}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2023}}}}\).
Nhân hai vế của S với 2 để rút gọn S.
\(S = \frac{1}{2} + \frac{2}{{{2^2}}} + \frac{3}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2023}}}}\)
\(2S = 1 + \frac{2}{2} + \frac{3}{{{2^2}}} + \frac{4}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2022}}}}\)
\(2S - S = \left(1 + \frac{2}{2} + \frac{3}{{{2^2}}} + \frac{4}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2022}}}}\right) - \left(\frac{1}{2} + \frac{2}{{{2^2}}} + \frac{3}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2023}}}}\right)\)
\(2S - S = 1 + \left(\frac{2}{2} - \frac{1}{2}\right) + \left(\frac{3}{{{2^2}}} - \frac{2}{{{2^2}}}\right) + \left(\frac{4}{{{2^3}}} - \frac{3}{{{2^3}}}\right) + \ldots + \left(\frac{{2023}}{{{2^{2022}}}} - \frac{{2022}}{{{2^{2022}}}}\right) - \frac{{2023}}{{{2^{2023}}}}\)
\(2S - S = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{2022}}}} - \frac{{2023}}{{{2^{2023}}}}\)
\(S = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{2022}}}} - \frac{{2023}}{{{2^{2023}}}}\)
\(2S = 2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{2021}}}} - \frac{{2023}}{{{2^{2022}}}}\)
\(2S - S = \left(2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{2021}}}} - \frac{{2023}}{{{2^{2022}}}}\right) - \left(1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{2022}}}} - \frac{{2023}}{{{2^{2023}}}}\right)\)
\(2S - S = 2 + \left(1 - 1\right) + \left(\frac{1}{2} - \frac{1}{2}\right) + \left(\frac{1}{{{2^2}}} - \frac{1}{{{2^2}}}\right) + \ldots + \left(- \frac{{2023}}{{{2^{2022}}}} -\frac{1}{{{2^{2022}}}}\right) - \frac{{2023}}{{{2^{2023}}}}\)
\(2S - S = 2 - \frac{{2024}}{{{2^{2022}}}} + \frac{{2023}}{{{2^{2023}}}}\)
\(S = 2 - \frac{{4048 - 2023}}{{{2^{2023}}}}\)
Vậy \(S < 2\).
Đề thi học kì 2 Toán 6 - Đề số 13, chương trình Cánh diều, là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức và kỹ năng của học sinh sau một học kì học tập. Đề thi này bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, đòi hỏi học sinh phải có sự hiểu biết sâu sắc về các khái niệm và phương pháp giải toán đã học.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để giúp học sinh ôn tập và làm bài thi hiệu quả, giaitoan.edu.vn cung cấp hướng dẫn giải chi tiết cho từng câu hỏi trong đề thi. Các hướng dẫn này được trình bày một cách rõ ràng, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin hơn khi làm bài.
Câu hỏi: Tính giá trị của biểu thức: (1/2 + 1/3) x 6
Giải:
Luyện tập thường xuyên là yếu tố quan trọng để đạt kết quả tốt trong kỳ thi. Học sinh nên giải nhiều đề thi khác nhau để làm quen với các dạng bài tập và rèn luyện kỹ năng giải toán. Ngoài ra, học sinh cũng nên tham khảo các tài liệu ôn tập và tìm kiếm sự giúp đỡ của giáo viên hoặc bạn bè khi gặp khó khăn.
Giaitoan.edu.vn là một website cung cấp các tài liệu học tập Toán 6 uy tín và chất lượng. Chúng tôi cung cấp đầy đủ các dạng bài tập, đề thi, hướng dẫn giải chi tiết và các tài liệu ôn tập khác để giúp học sinh học tập và ôn thi hiệu quả. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu hữu ích khác.
| Chủ đề | Mức độ quan trọng |
|---|---|
| Số tự nhiên | Cao |
| Phân số | Trung bình |
| Số thập phân | Trung bình |
| Tỉ số và tỉ lệ | Thấp |
| Hình học cơ bản | Trung bình |
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi học kì 2!