Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 6 - Đề số 5 - Cánh diều, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 6, tập trung vào các kiến thức trọng tâm và có đáp án chi tiết đi kèm.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và áp dụng kiến thức vào thực tế.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. C | 2. B | 3. D | 4. A |
Câu 1
Phương pháp:
Điểm \(E\) nằm giữa hai điểm \(I\) và \(K\) thì \(IE + IK = EK\).
Cách giải:
Vì điểm \(E\) nằm giữa hai điểm \(I\) và \(K\) nên ta có: \(IE + IK = EK\)
\( \Rightarrow IK = EK + IE\)\( = 10cm + 4cm = 14 cm\)
Vậy độ dài \(IK\) là \(14cm\).
Chọn C.
Câu 2
Phương pháp:
\(I\) là trung điểm của đoạn thẳng \(MN\) thì \(IM = IN = \dfrac{{MN}}{2}\).
Cách giải:
Vì \(I\) là trung điểm của đoạn thẳng \(MN\) nên \(IM = IN = \dfrac{{MN}}{2}\)
\( \Rightarrow MN = 2.IN = 2.8cm = 16cm\).
Vậy \(MN = 16cm\).
Chọn B.
Câu 3
Phương pháp:
Sử dụng lý thuyết biểu đồ cột kép.
Cách giải:
Quốc gia có cân nặng của Nam lớn nhất nhất là Malaysia.
Quốc gia có cân nặng của Nữ nhỏ nhất nhất là Việt Nam.
Chọn D.
Câu 4
Phương pháp:
Muốn viết hỗn số về dạng phân số ta lấy phần nguyên nhân với mẫu số của phần phân số rồi cộng với tử số của phần phân số làm tử số, mẫu số là mẫu số của phần phân số.
Tổng quát: \(a\dfrac{b}{c} = a + \dfrac{b}{c}\) Cách giải:
Ta có: \( - 3\dfrac{2}{5} = - \dfrac{{5.3 + 2}}{5} = - \dfrac{{17}}{5}\)
Chọn A
Phần II: Tự luận
Bài 1
Phương pháp
a) Thực hiện cộng hai phân số khác mẫu, ta quy đồng mẫu số hai phân số đó, rồi cộng tử với tử và giữ nguyên mẫu.
b) Nhận thấy số chia là một phân số có mẫu số là 10, ta chuyển \( - 1,8\) về dạng phân số có mẫu số là 10. Sau đó thự hiện chia hai phân số. Muốn chia hai phân số ta lấy số bị chia nhân với phân số nghịch đảo của số chia.
c) Sử dụng tính chất phân phối của phép nhân đối với phép cộng :
\(a.b + a.c + a.d = a.\left( {b + c + d} \right)\)
Cách giải:
\(a)\,\dfrac{7}{{15}} + \dfrac{6}{5} = \dfrac{7}{{15}} + \dfrac{{18}}{{15}} = \dfrac{{25}}{{15}} = \dfrac{5}{3}\)
\(b)\, - 1,8:\left( {1 - \dfrac{7}{{10}}} \right) = \dfrac{{ - 18}}{{10}}:\dfrac{3}{{10}} = \dfrac{{ - 18}}{{10}}.\dfrac{{10}}{3} = - 6\)
\(\begin{array}{l}c)\,\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\\\,\,\,\,\, = \dfrac{{ - 5}}{7}.\left( {\dfrac{2}{{13}} + \dfrac{3}{{13}} + \dfrac{8}{{13}}} \right)\\\,\,\,\, = \dfrac{{ - 5}}{7}.\,1\\\,\,\, = \dfrac{{ - 5}}{7}\end{array}\)
Bài 2:
Phương pháp: a) Đổi hỗn số về phân số, rồi thực hiện quy tắc chuyển vế, chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu, rồi thực hiện phép cộng hai phân số khác mẫu, muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số của hai phân số đó rồi thực hiện cộng tử với tử, mẫu số giữ nguyên.
b) Chuyển hỗn số về phân số, rồi thực hiện chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu. Sau đó, thực hiện cộng hai phân số có cùng mẫu số (ta cộng tử với tử, giữ nguyên mẫu).
Để tìm x ta lấy kết quả cộng hai phân số chia cho \(\dfrac{1}{2}\).
Cách giải:
\(\begin{array}{l}a)\,x - 1\dfrac{2}{5} = \dfrac{3}{4}\\\,\,\,\,\,x\, - \,\dfrac{7}{5} = \dfrac{3}{4}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{4} + \dfrac{7}{5}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{{43}}{{20}}\end{array}\)
Vậy \(x = \dfrac{{43}}{{20}}\)
\(\begin{array}{l}b)\,\dfrac{1}{2}x - \dfrac{4}{7} = 1\dfrac{3}{7}\\\,\,\,\,\,\dfrac{1}{2}x - \dfrac{4}{7} = \dfrac{{10}}{7}\\\,\,\,\,\,\dfrac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \dfrac{{10}}{7} + \dfrac{4}{7}\\\,\,\,\,\,\dfrac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \dfrac{{14}}{7}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{{14}}{7}:\dfrac{1}{2}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = 4\end{array}\)
Vậy \(x = 4\)
\(\begin{array}{l}c)\,\,\dfrac{2}{3}x - \dfrac{3}{2}\left( {x - \dfrac{1}{2}} \right)\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\dfrac{2}{3}x - \left( {\dfrac{3}{2}x - \dfrac{3}{2} \cdot \dfrac{1}{2}} \right) = \dfrac{5}{{12}}\\\,\,\,\,\,\,\dfrac{2}{3}x - \dfrac{3}{2}x + \dfrac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x + \dfrac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}} - \dfrac{3}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{3}:\dfrac{{ - 5}}{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\dfrac{2}{5}\end{array}\)
Vậy \(x = \dfrac{2}{5}\)
Bài 3
Phương pháp:
Đọc dữ liệu ở biểu đồ tranh, thực hiện phép tính nhân, cộng và trừ.
Cách giải:
a) Tháng 2 có 4 hình nên khối lượng táo bán được của thánh 2 là nhiều nhất.
Khối lượng táo bán được trong tháng 2 là: \(4.10 = 40\) (tấn)
b) Tổng số có \(9,5\) hình nên khối lượng táo trong 4 tháng đã bán được của hệ thống siêu thị là:
\(9,5.10 = 95\)(tấn)
c) Khối lượng táo bán được trong tháng 1 là: \(1.10 = 10\) (tấn)
Khối lượng táo bán được trong tháng tháng 3 là: \(2,5.10 = 20 + 5 = 25\) (tấn)
Khối lượng táo chệnh lệch của tháng 1 và tháng 3 là: \(10 - 25 = - 15\) (tấn)
Vậy tháng 1 bán được ít táo hơn tháng 3 là \(15\) tấn.
Bài 4
Phương pháp:
a) Áp dụng định nghĩa hai tia đối nhau: Hai tia đối nhau có chung gốc và chúng tạo thành một đường thẳng.
b) Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\) thì \(OA + OB = AB\).
c) Điểm \(O\) là trung điểm của đoạn thẳng \(AB\) nếu: Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\); \(OA = OB\)
Cách giải:
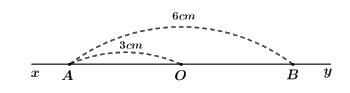
a) Kế tên các cặp tia đối nhau gốc \(A\) đến hình vẽ?
Các cặp tia đối nhau gốc \(A\) là: \(Ax\) và \(AO\); \(Ax\) và \(AB\); \(Ax\) và \(Ay\)
b) Tính độ dài đoạn thẳng \(OB\).
Ta có:
+ Điểm \(O\) thuộc đường thẳng \(xy\) nên \(Ox\) và \(Oy\) thuộc hai tia đối nhau.
+ \(A \in Ox\)
+ \(B \in Oy\)
Suy ra, điểm \(O\) nằm giữa hai điểm \(A\) và \(B\).
Khi đó, ta có: \(OA + OB = AB\)
\( \Rightarrow OB = AB - OA\)\( = 6\,cm - 3\,cm = 3\,cm\)
Vậy \(OB = 3cm\).
c) Điểm \(O\) có là trung điểm của đoạn thẳng \(AB\) không? Vì sao?
Ta có:
+ Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\).
+ \(OA = OB = 3cm\)
Suy ra, điểm \(O\) là trung điểm của đoạn thẳng \(AB\).
Bài 5
Phương pháp:
Áp dụng bất đẳng thức: \(\dfrac{1}{{{n^2}}} < \dfrac{1}{{\left( {n - 1} \right).n}}\) với \(n \in {\mathbb{N}^*},\,\,n > 1\) và đẳng thức: \(\dfrac{1}{{n\left( {n - 1} \right)}} = \dfrac{1}{{n - 1}} - \dfrac{1}{n}.\)
Cách giải:
Ta có :
\(\begin{array}{l}A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2014}^2}}}\\A = \dfrac{1}{4} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{2014.2014}}\\A < \dfrac{1}{4} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{2013.2014}}\\A < \dfrac{1}{4} + \left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{2013}} - \dfrac{1}{{2014}}} \right)\\A < \dfrac{1}{4} + \dfrac{1}{2} - \dfrac{1}{{2014}}\\A < \dfrac{3}{4} - \dfrac{1}{{2014}}\\ \Rightarrow A < \dfrac{3}{4}\end{array}\)
Vậy \(A < \dfrac{3}{4}\).
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho điểm \(E\) nằm giữa hai điểm \(I\) và \(K\), biết \(IE = 4cm,\,\,EK = 10cm\). Độ dài \(IK\) là:
A.\(4\,cm\)
B.\(7\,cm\)
C. \(14\,cm\)
D. \(6\,cm\)
Câu 2: Cho \(I\) là trung điểm của đoạn thẳng \(MN\). Biết\(NI = 8cm\), khi đó độ dài \(MN\) là
A.\(4\,cm\)
B. \(16\,cm\)
C. \(21\,cm\)
D. \(24\,cm\)
Câu 3: Cho bảng thống kê về cân nặng trung bình (đơn vị: ki-lô-gam) của nam, nữ tại một số quốc gia Đông Nam Á như sau:
Quốc gia | Việt Nam | Thái Lan | Malaysia | Indonesia |
Nam | \(61,2\) | \(69,8\) | \(71,5\) | \(61,4\) |
Nữ | \(54\) | \(63,3\) | \(64,4\) | \(56,2\) |
Biểu đồ chưa hoàn thiện dưới đây biểu diễn bằng bảng thông kê trên.
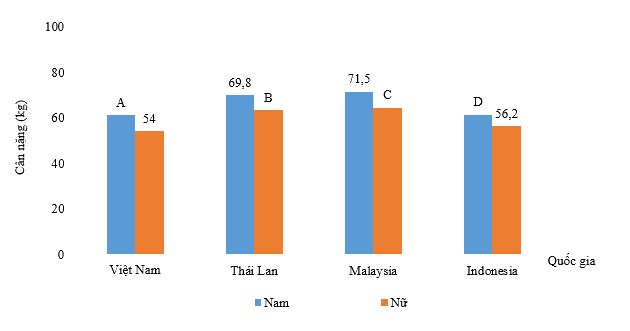
Quốc gia có cân nặng của nam lớn nhất, nữ nhỏ nhất lần lượt là
A. Malaysia, Thái Lan
B. Việt Nam, Malaysia
C. Thái Lan, Malaysia
D. Malaysia, Việt Nam
Câu 4:Hỗn số \( - 3\dfrac{2}{5}\) viết dưới dạng phân số là:
A. \(\dfrac{{ - 17}}{5};\)
B.\(\dfrac{{17}}{5}\)
C.\( - \dfrac{6}{5};\)
D.\( - \dfrac{{13}}{5}.\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể) :
\(a)\,\dfrac{7}{{15}} + \dfrac{6}{5}\)
\(b)\, - 1,8:\left( {1 - \dfrac{7}{{10}}} \right)\)
\(c)\,\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\(a)\,x - 1\dfrac{2}{5} = \dfrac{3}{4}\)
\(b)\,\dfrac{1}{2}x - \dfrac{4}{7} = 1\dfrac{3}{7}\)
\(c)\,\,\dfrac{2}{3}x - \dfrac{3}{2}\left( {x - \dfrac{1}{2}} \right) = \dfrac{5}{{12}}\)
Bài 3 (1,5 điểm) Biểu đồ tranh dưới đây thống kê khối lượng táo bán được trong bốn tháng đầu năm 2020 của một hệ thống siêu thị.
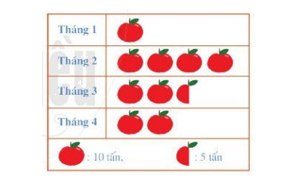
Quan sát biểu đồ tranh và trả lời các câu hỏi sau:
a) Tháng nào hệ thống siêu thị bán được nhiều táo nhất? Tính khối lượng táo được bán được trong tháng đó?
b) Tính tổng khối lượng táo trong 4 tháng đã bán được của hệ thống siêu thị?
c) Hãy cho biết khối lượng táo bán được của tháng 1 ít hơn hay nhiều hơn khối lượng táo bán được của tháng 3 là bao nhiêu tấn?
Bài 4: (2,5 điểm) Cho đường thẳng \(xy\). Lấy điểm \(O\) thuộc đường thẳng \(xy\). Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA = 3cm\). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(AB = 6cm\).
a) Kế tên các cặp tia đối nhau gốc \(A\) đến hình vẽ?
b) Tính độ dài đoạn thẳng \(OB\).
c) Điểm \(O\) có là trung điểm của đoạn thẳng \(AB\) không? Vì sao?
Bài 5:(0,5 điểm)Cho \(A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2014}^2}}}\). Chứng tỏ: \(A < \dfrac{3}{4}\).
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho điểm \(E\) nằm giữa hai điểm \(I\) và \(K\), biết \(IE = 4cm,\,\,EK = 10cm\). Độ dài \(IK\) là:
A.\(4\,cm\)
B.\(7\,cm\)
C. \(14\,cm\)
D. \(6\,cm\)
Câu 2: Cho \(I\) là trung điểm của đoạn thẳng \(MN\). Biết\(NI = 8cm\), khi đó độ dài \(MN\) là
A.\(4\,cm\)
B. \(16\,cm\)
C. \(21\,cm\)
D. \(24\,cm\)
Câu 3: Cho bảng thống kê về cân nặng trung bình (đơn vị: ki-lô-gam) của nam, nữ tại một số quốc gia Đông Nam Á như sau:
Quốc gia | Việt Nam | Thái Lan | Malaysia | Indonesia |
Nam | \(61,2\) | \(69,8\) | \(71,5\) | \(61,4\) |
Nữ | \(54\) | \(63,3\) | \(64,4\) | \(56,2\) |
Biểu đồ chưa hoàn thiện dưới đây biểu diễn bằng bảng thông kê trên.
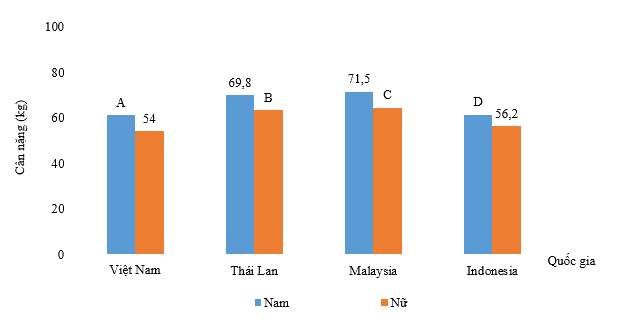
Quốc gia có cân nặng của nam lớn nhất, nữ nhỏ nhất lần lượt là
A. Malaysia, Thái Lan
B. Việt Nam, Malaysia
C. Thái Lan, Malaysia
D. Malaysia, Việt Nam
Câu 4:Hỗn số \( - 3\dfrac{2}{5}\) viết dưới dạng phân số là:
A. \(\dfrac{{ - 17}}{5};\)
B.\(\dfrac{{17}}{5}\)
C.\( - \dfrac{6}{5};\)
D.\( - \dfrac{{13}}{5}.\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể) :
\(a)\,\dfrac{7}{{15}} + \dfrac{6}{5}\)
\(b)\, - 1,8:\left( {1 - \dfrac{7}{{10}}} \right)\)
\(c)\,\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\)
Bài 2 (1,5 điểm) Tìm \(x\):
\(a)\,x - 1\dfrac{2}{5} = \dfrac{3}{4}\)
\(b)\,\dfrac{1}{2}x - \dfrac{4}{7} = 1\dfrac{3}{7}\)
\(c)\,\,\dfrac{2}{3}x - \dfrac{3}{2}\left( {x - \dfrac{1}{2}} \right) = \dfrac{5}{{12}}\)
Bài 3 (1,5 điểm) Biểu đồ tranh dưới đây thống kê khối lượng táo bán được trong bốn tháng đầu năm 2020 của một hệ thống siêu thị.
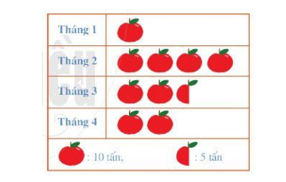
Quan sát biểu đồ tranh và trả lời các câu hỏi sau:
a) Tháng nào hệ thống siêu thị bán được nhiều táo nhất? Tính khối lượng táo được bán được trong tháng đó?
b) Tính tổng khối lượng táo trong 4 tháng đã bán được của hệ thống siêu thị?
c) Hãy cho biết khối lượng táo bán được của tháng 1 ít hơn hay nhiều hơn khối lượng táo bán được của tháng 3 là bao nhiêu tấn?
Bài 4: (2,5 điểm) Cho đường thẳng \(xy\). Lấy điểm \(O\) thuộc đường thẳng \(xy\). Trên tia \(Ox\) lấy điểm \(A\) sao cho \(OA = 3cm\). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(AB = 6cm\).
a) Kế tên các cặp tia đối nhau gốc \(A\) đến hình vẽ?
b) Tính độ dài đoạn thẳng \(OB\).
c) Điểm \(O\) có là trung điểm của đoạn thẳng \(AB\) không? Vì sao?
Bài 5:(0,5 điểm)Cho \(A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2014}^2}}}\). Chứng tỏ: \(A < \dfrac{3}{4}\).
Phần I: Trắc nghiệm
1. C | 2. B | 3. D | 4. A |
Câu 1
Phương pháp:
Điểm \(E\) nằm giữa hai điểm \(I\) và \(K\) thì \(IE + IK = EK\).
Cách giải:
Vì điểm \(E\) nằm giữa hai điểm \(I\) và \(K\) nên ta có: \(IE + IK = EK\)
\( \Rightarrow IK = EK + IE\)\( = 10cm + 4cm = 14 cm\)
Vậy độ dài \(IK\) là \(14cm\).
Chọn C.
Câu 2
Phương pháp:
\(I\) là trung điểm của đoạn thẳng \(MN\) thì \(IM = IN = \dfrac{{MN}}{2}\).
Cách giải:
Vì \(I\) là trung điểm của đoạn thẳng \(MN\) nên \(IM = IN = \dfrac{{MN}}{2}\)
\( \Rightarrow MN = 2.IN = 2.8cm = 16cm\).
Vậy \(MN = 16cm\).
Chọn B.
Câu 3
Phương pháp:
Sử dụng lý thuyết biểu đồ cột kép.
Cách giải:
Quốc gia có cân nặng của Nam lớn nhất nhất là Malaysia.
Quốc gia có cân nặng của Nữ nhỏ nhất nhất là Việt Nam.
Chọn D.
Câu 4
Phương pháp:
Muốn viết hỗn số về dạng phân số ta lấy phần nguyên nhân với mẫu số của phần phân số rồi cộng với tử số của phần phân số làm tử số, mẫu số là mẫu số của phần phân số.
Tổng quát: \(a\dfrac{b}{c} = a + \dfrac{b}{c}\) Cách giải:
Ta có: \( - 3\dfrac{2}{5} = - \dfrac{{5.3 + 2}}{5} = - \dfrac{{17}}{5}\)
Chọn A
Phần II: Tự luận
Bài 1
Phương pháp
a) Thực hiện cộng hai phân số khác mẫu, ta quy đồng mẫu số hai phân số đó, rồi cộng tử với tử và giữ nguyên mẫu.
b) Nhận thấy số chia là một phân số có mẫu số là 10, ta chuyển \( - 1,8\) về dạng phân số có mẫu số là 10. Sau đó thự hiện chia hai phân số. Muốn chia hai phân số ta lấy số bị chia nhân với phân số nghịch đảo của số chia.
c) Sử dụng tính chất phân phối của phép nhân đối với phép cộng :
\(a.b + a.c + a.d = a.\left( {b + c + d} \right)\)
Cách giải:
\(a)\,\dfrac{7}{{15}} + \dfrac{6}{5} = \dfrac{7}{{15}} + \dfrac{{18}}{{15}} = \dfrac{{25}}{{15}} = \dfrac{5}{3}\)
\(b)\, - 1,8:\left( {1 - \dfrac{7}{{10}}} \right) = \dfrac{{ - 18}}{{10}}:\dfrac{3}{{10}} = \dfrac{{ - 18}}{{10}}.\dfrac{{10}}{3} = - 6\)
\(\begin{array}{l}c)\,\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\\\,\,\,\,\, = \dfrac{{ - 5}}{7}.\left( {\dfrac{2}{{13}} + \dfrac{3}{{13}} + \dfrac{8}{{13}}} \right)\\\,\,\,\, = \dfrac{{ - 5}}{7}.\,1\\\,\,\, = \dfrac{{ - 5}}{7}\end{array}\)
Bài 2:
Phương pháp: a) Đổi hỗn số về phân số, rồi thực hiện quy tắc chuyển vế, chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu, rồi thực hiện phép cộng hai phân số khác mẫu, muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số của hai phân số đó rồi thực hiện cộng tử với tử, mẫu số giữ nguyên.
b) Chuyển hỗn số về phân số, rồi thực hiện chuyển số hạng không chứa x sang bên phải, nhớ rằng chuyển vế thì phải đổi dấu. Sau đó, thực hiện cộng hai phân số có cùng mẫu số (ta cộng tử với tử, giữ nguyên mẫu).
Để tìm x ta lấy kết quả cộng hai phân số chia cho \(\dfrac{1}{2}\).
Cách giải:
\(\begin{array}{l}a)\,x - 1\dfrac{2}{5} = \dfrac{3}{4}\\\,\,\,\,\,x\, - \,\dfrac{7}{5} = \dfrac{3}{4}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{4} + \dfrac{7}{5}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{{43}}{{20}}\end{array}\)
Vậy \(x = \dfrac{{43}}{{20}}\)
\(\begin{array}{l}b)\,\dfrac{1}{2}x - \dfrac{4}{7} = 1\dfrac{3}{7}\\\,\,\,\,\,\dfrac{1}{2}x - \dfrac{4}{7} = \dfrac{{10}}{7}\\\,\,\,\,\,\dfrac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \dfrac{{10}}{7} + \dfrac{4}{7}\\\,\,\,\,\,\dfrac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \dfrac{{14}}{7}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{{14}}{7}:\dfrac{1}{2}\\\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = 4\end{array}\)
Vậy \(x = 4\)
\(\begin{array}{l}c)\,\,\dfrac{2}{3}x - \dfrac{3}{2}\left( {x - \dfrac{1}{2}} \right)\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\dfrac{2}{3}x - \left( {\dfrac{3}{2}x - \dfrac{3}{2} \cdot \dfrac{1}{2}} \right) = \dfrac{5}{{12}}\\\,\,\,\,\,\,\dfrac{2}{3}x - \dfrac{3}{2}x + \dfrac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x + \dfrac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{12}} - \dfrac{3}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ - 5}}{6}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{3}:\dfrac{{ - 5}}{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\dfrac{2}{5}\end{array}\)
Vậy \(x = \dfrac{2}{5}\)
Bài 3
Phương pháp:
Đọc dữ liệu ở biểu đồ tranh, thực hiện phép tính nhân, cộng và trừ.
Cách giải:
a) Tháng 2 có 4 hình nên khối lượng táo bán được của thánh 2 là nhiều nhất.
Khối lượng táo bán được trong tháng 2 là: \(4.10 = 40\) (tấn)
b) Tổng số có \(9,5\) hình nên khối lượng táo trong 4 tháng đã bán được của hệ thống siêu thị là:
\(9,5.10 = 95\)(tấn)
c) Khối lượng táo bán được trong tháng 1 là: \(1.10 = 10\) (tấn)
Khối lượng táo bán được trong tháng tháng 3 là: \(2,5.10 = 20 + 5 = 25\) (tấn)
Khối lượng táo chệnh lệch của tháng 1 và tháng 3 là: \(10 - 25 = - 15\) (tấn)
Vậy tháng 1 bán được ít táo hơn tháng 3 là \(15\) tấn.
Bài 4
Phương pháp:
a) Áp dụng định nghĩa hai tia đối nhau: Hai tia đối nhau có chung gốc và chúng tạo thành một đường thẳng.
b) Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\) thì \(OA + OB = AB\).
c) Điểm \(O\) là trung điểm của đoạn thẳng \(AB\) nếu: Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\); \(OA = OB\)
Cách giải:
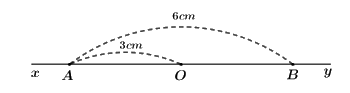
a) Kế tên các cặp tia đối nhau gốc \(A\) đến hình vẽ?
Các cặp tia đối nhau gốc \(A\) là: \(Ax\) và \(AO\); \(Ax\) và \(AB\); \(Ax\) và \(Ay\)
b) Tính độ dài đoạn thẳng \(OB\).
Ta có:
+ Điểm \(O\) thuộc đường thẳng \(xy\) nên \(Ox\) và \(Oy\) thuộc hai tia đối nhau.
+ \(A \in Ox\)
+ \(B \in Oy\)
Suy ra, điểm \(O\) nằm giữa hai điểm \(A\) và \(B\).
Khi đó, ta có: \(OA + OB = AB\)
\( \Rightarrow OB = AB - OA\)\( = 6\,cm - 3\,cm = 3\,cm\)
Vậy \(OB = 3cm\).
c) Điểm \(O\) có là trung điểm của đoạn thẳng \(AB\) không? Vì sao?
Ta có:
+ Điểm \(O\) nằm giữa hai điểm \(A\) và \(B\).
+ \(OA = OB = 3cm\)
Suy ra, điểm \(O\) là trung điểm của đoạn thẳng \(AB\).
Bài 5
Phương pháp:
Áp dụng bất đẳng thức: \(\dfrac{1}{{{n^2}}} < \dfrac{1}{{\left( {n - 1} \right).n}}\) với \(n \in {\mathbb{N}^*},\,\,n > 1\) và đẳng thức: \(\dfrac{1}{{n\left( {n - 1} \right)}} = \dfrac{1}{{n - 1}} - \dfrac{1}{n}.\)
Cách giải:
Ta có :
\(\begin{array}{l}A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{2014}^2}}}\\A = \dfrac{1}{4} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{2014.2014}}\\A < \dfrac{1}{4} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{2013.2014}}\\A < \dfrac{1}{4} + \left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{2013}} - \dfrac{1}{{2014}}} \right)\\A < \dfrac{1}{4} + \dfrac{1}{2} - \dfrac{1}{{2014}}\\A < \dfrac{3}{4} - \dfrac{1}{{2014}}\\ \Rightarrow A < \dfrac{3}{4}\end{array}\)
Vậy \(A < \dfrac{3}{4}\).
Đề thi giữa kì 2 Toán 6 - Đề số 5 - Cánh diều là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kỳ. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính như số tự nhiên, phân số, số thập phân, hình học cơ bản và biểu thức đại số đơn giản.
Thông thường, đề thi giữa kì 2 Toán 6 - Cánh diều sẽ có cấu trúc như sau:
Dưới đây là một số chủ đề chính thường xuất hiện trong đề thi giữa kì 2 Toán 6 - Cánh diều:
Để giải các bài toán về số tự nhiên, học sinh cần nắm vững các phép toán cộng, trừ, nhân, chia và các tính chất chia hết, ước và bội. Ví dụ:
Bài toán: Tìm tất cả các ước của 12.
Giải: Các ước của 12 là: 1, 2, 3, 4, 6, 12.
Để giải các bài toán về phân số, học sinh cần nắm vững khái niệm phân số, cách so sánh phân số và các phép toán cộng, trừ, nhân, chia phân số. Ví dụ:
Bài toán: Tính: 1/2 + 1/3
Giải: 1/2 + 1/3 = 3/6 + 2/6 = 5/6
Để giải các bài toán về hình học, học sinh cần nắm vững các khái niệm về điểm, đường thẳng, đoạn thẳng, góc, tam giác, hình vuông, hình chữ nhật và các công thức tính diện tích, chu vi. Ví dụ:
Bài toán: Tính chu vi của hình chữ nhật có chiều dài 5cm và chiều rộng 3cm.
Giải: Chu vi của hình chữ nhật là: (5 + 3) x 2 = 16cm
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu học tập, bài tập và đề thi Toán 6, giúp học sinh ôn luyện và nâng cao kiến thức một cách hiệu quả. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu hữu ích khác!