Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 6 - Đề số 3 - Cánh diều, một công cụ hỗ trợ học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 6, sách Cánh diều, bao gồm các dạng bài tập đa dạng và có đáp án chi tiết.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và áp dụng kiến thức vào thực tế.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1. D | 2. A | 3. D | 4. C |
Câu 1
Phương pháp:
Dựa vào tính chất điểm nằm giữa hai điểm: Khi M nằm giữa A và B thì \(AM + MB = AB\)
Cách giải:
Vì K nằm giữa A và B nên ta có: \(AK + KB = AB\)
Hay \(4 + KB = 6\)
Suy ra: \(KB = 6 - 4 = 2\left( {cm} \right)\)
Chọn D.
Câu 2
Phương pháp:
Liệt kê tất cả các đoạn thẳng.
Cách giải:
Có 6 đoạn thẳng là: OA, OB, OC, AB, AC, BC.
Chọn A.
Câu 3
Phương pháp:
Giữ nguyên mẫu số.
Tử số mới = Phần nguyên × Mẫu số + Tử số.
Cách giải:
\(3\dfrac{2}{5} = \dfrac{{3.5 + 2}}{5} = \dfrac{{17}}{5}\)
Chọn D.
Câu 4
Phương pháp:
Quy đồng mẫu số để tìm y, quy đồng tử số để tìm x.
Cách giải:
Ta có: \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{3}{{12}}\)
Vậy: \(x = 12;y = 3\)
Chọn C.
Phần II: Tự luận
Bài 1
Phương pháp
Tính giá trị biểu thức theo các quy tắc:
+) Biểu thức có dấu ngoặc thì ưu tiên tính trong ngoặc trước, ngoài ngoặc sau.
+) Biểu thức có chứa các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, phép tính cộng, trừ sau.
Cách giải:
\(\begin{array}{l}a)\,\,\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\,\, = \dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} + \dfrac{{ - 3}}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\dfrac{{ - 10}}{{13}} + \dfrac{{ - 3}}{{13}}} \right) + \left( {\dfrac{5}{{17}} + \dfrac{{12}}{{17}}} \right) - \dfrac{{11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 13}}{{13}} + \dfrac{{17}}{{17}} - \dfrac{{11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = ( - 1) + 1 - \dfrac{{11}}{{20}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0 - \dfrac{{11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \dfrac{{11}}{{20}}\end{array}\)
\(\begin{array}{l}b)\,\,\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}} = \,\,\dfrac{3}{4} + \dfrac{{ - 5}}{6} + \dfrac{{11}}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\dfrac{9}{{12}}\, + \dfrac{{ - 10}}{{12}} + \dfrac{{11}}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{9 + ( - 10) + 11}}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{10}}{{12}} = \dfrac{5}{6}\end{array}\)
\(\begin{array}{l}c)\,\,\left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}\,\, = \,\left( {13 + \dfrac{4}{9} + 2 + \dfrac{1}{9}} \right) - \left( {3 + \dfrac{4}{9}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 13 + \dfrac{4}{9} + 2 + \dfrac{1}{9} - 3 - \dfrac{4}{9}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = (13 + 2 - 3) + \left( {\dfrac{4}{9} - \dfrac{4}{9}} \right) + \dfrac{1}{9}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 12 + 0 + \dfrac{1}{9}\,\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 12\dfrac{1}{9}\,\,\,\end{array}\)
Bài 2:
Phương pháp: Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Cách giải:
\(\begin{array}{l}a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\\\,\,\,\,\,\,x - \dfrac{1}{3} = \dfrac{{ - 5}}{{12}}\,\,\,\\\,\,\,\,\,\,x = \dfrac{{ - 5}}{{12}}\, + \dfrac{1}{3}\,\\\,\,\,\,\,\,x = \dfrac{{ - 1}}{{12}}\,\end{array}\)
Vậy \(x = \dfrac{{ - 1}}{{12}}\)
\(\begin{array}{l}\,b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\,\\\,\,\,\,\,\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = \dfrac{1}{5}\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{1}{5} - \dfrac{3}{4}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{{ - 11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\,\dfrac{{ - 11}}{{20}}:\dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\dfrac{{ - 11}}{5}\end{array}\)
Vậy \(x = \dfrac{{ - 11}}{5}\)
\(\begin{array}{l}c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\\\,\dfrac{1}{{12}}.{x^2} = \dfrac{4}{3}\\{x^2} = \dfrac{4}{3}:\dfrac{1}{{12}}\\{x^2} = 16\\ \Rightarrow \,\left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\end{array}\)
Vậy \(x \in \left\{ {4; - 4} \right\}\)
Bài 3
Phương pháp:
Sử dụng lý thuyết biểu đồ cột.
Cách giải:
a) Biểu đồ biểu thị tổng lượng mưa của thành phố Hà Nội trong các năm từ 2015 đến 2019.
b) Đơn vị đo của tổng lượng mưa là milimét.
c) Bảng thống kê:
Năm | 2015 | 2016 | 2017 | 2018 | 2019 |
Tổng lượng mưa (mm) | 1520 | 1631 | 1858 | 1685 | 1311 |
Bài 4
Phương pháp
Vẽ hình, sau đó dựa vào tính chất của điểm nằm giữa hai điểm và trung điểm của đoạn thẳng.
Cách giải:
a)

Ta có tia OM và tia ON đối nhau (Vì N thuộc tia đối của tia OM)
Suy ra: Điểm O nằm giữa hai điểm M và N
Suy ra: \(OM + ON = MN\)
Thay \(OM = 5cm;{\rm{ }}ON = 7cm\), ta có
\(MN = 5 + 7 = 12\left( {cm} \right)\). Vậy \(MN = 12cm.\)
b) Gọi K là trung điểm của đoạn thẳng MN. Tính độ dài đoạn thẳng MK.
Ta có K là trung điểm của đoạn thẳng MN
Suy ra: \(MK = NK = \dfrac{{MN}}{2} = \dfrac{{12}}{2} = 6\left( {cm} \right)\)
Bài 5
Phương pháp
Viết các thừa số thành phân số, rút gọn các thừa số giống nhau ở tử và mẫu.
Cách giải:
\(A = 1\dfrac{1}{2}.1\dfrac{1}{3}.1\dfrac{1}{4}. \ldots .1\dfrac{1}{{2023}}\)
\( = \dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}. \ldots .\dfrac{{2024}}{{2023}}\)
\(\begin{array}{l} = \dfrac{{2024}}{2}\\ = 1012.\end{array}\)
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho đoạn thẳng AB = 6 cm. Điểm K nằm giữa AB, biết KA = 4 cm thì đoạn thẳng KB bằng:
A. 10 cm
B. 6 cm
C. 4 cm
D. 2 cm
Câu 2:Cho ba điểm A, B, C thẳng hàng theo thứ tự đó. Lấy điểm O không thuộc đường thẳng AB. Nối điểm O với các điểm A, B, C. Trên hình vẽ có bao nhiêu đoạn thẳng?
A. 6
B. 8
C. 9
D. 10
Câu 3: Viết hỗn số \(3\dfrac{2}{5}\) dưới dạng phân số ta được:
A. \(\dfrac{{11}}{5}\)
B. \(\dfrac{6}{5}\)
C. \(\dfrac{{13}}{5}\)
D. \(\dfrac{{17}}{5}\)
Câu 4:Cho \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{1}{4}\) thì giá trị của \(x\) và \(y\) là:
A. \(x = 4;y = 9\)
B. \(x = - 4;y = - 9\)
C. \(x = 12;y = 3\)
D. \(x = - 12;y = - 3\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (Tính hợp lý nếu có thể)
\(a)\,\,\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\,\,\)
\(b)\,\,\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}}\)
\(c)\,\,\left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}\,\)
Bài 2:(1,5 điểm)Tìm x biết:
\(a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\,\)
\(b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\)
\(c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\)
Bài 3 (1,5 điểm) Biểu đồ dưới đây cho biết tổng lượng mưa tại thành phố Hà Nội trong một số năm:
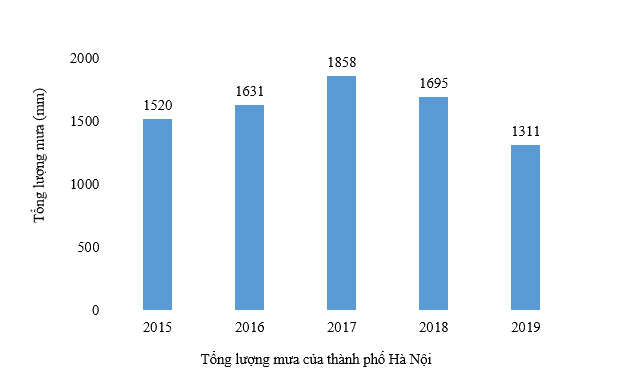
a) Biểu đồ biểu thị thông tin gì và ở những năm nào?
b) Đơn vị đo tổng lượng mưa của thành phố Hà Nội trong biểu đồ là gì?
c) Lập bảng thống kê biểu thị dữ liệu trong biểu đồ.
Bài 4: (2,5 điểm) Cho điểm M trên tia OM sao cho OM = 5cm. Gọi N là điểm trên tia đối của tia OM và cách O một khoảng bằng 7cm.
a) Vẽ hình và tính độ dài đoạn thẳng MN.
b) Gọi K là trung điểm của đoạn thảng MN. Tính độ dài đoạn thẳng MK.
Bài 5:(0,5 điểm)Tính giá trị của biểu thức: \(A = 1\dfrac{1}{2}.1\dfrac{1}{3}.1\dfrac{1}{4}. \ldots .1\dfrac{1}{{2023}}\)
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Cho đoạn thẳng AB = 6 cm. Điểm K nằm giữa AB, biết KA = 4 cm thì đoạn thẳng KB bằng:
A. 10 cm
B. 6 cm
C. 4 cm
D. 2 cm
Câu 2:Cho ba điểm A, B, C thẳng hàng theo thứ tự đó. Lấy điểm O không thuộc đường thẳng AB. Nối điểm O với các điểm A, B, C. Trên hình vẽ có bao nhiêu đoạn thẳng?
A. 6
B. 8
C. 9
D. 10
Câu 3: Viết hỗn số \(3\dfrac{2}{5}\) dưới dạng phân số ta được:
A. \(\dfrac{{11}}{5}\)
B. \(\dfrac{6}{5}\)
C. \(\dfrac{{13}}{5}\)
D. \(\dfrac{{17}}{5}\)
Câu 4:Cho \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{1}{4}\) thì giá trị của \(x\) và \(y\) là:
A. \(x = 4;y = 9\)
B. \(x = - 4;y = - 9\)
C. \(x = 12;y = 3\)
D. \(x = - 12;y = - 3\)
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (Tính hợp lý nếu có thể)
\(a)\,\,\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\,\,\)
\(b)\,\,\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}}\)
\(c)\,\,\left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}\,\)
Bài 2:(1,5 điểm)Tìm x biết:
\(a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\,\)
\(b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\)
\(c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\)
Bài 3 (1,5 điểm) Biểu đồ dưới đây cho biết tổng lượng mưa tại thành phố Hà Nội trong một số năm:
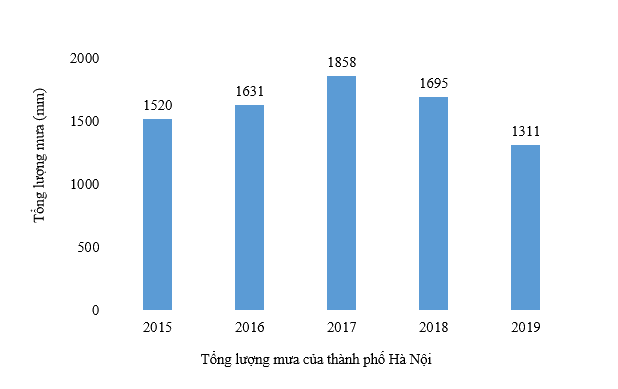
a) Biểu đồ biểu thị thông tin gì và ở những năm nào?
b) Đơn vị đo tổng lượng mưa của thành phố Hà Nội trong biểu đồ là gì?
c) Lập bảng thống kê biểu thị dữ liệu trong biểu đồ.
Bài 4: (2,5 điểm) Cho điểm M trên tia OM sao cho OM = 5cm. Gọi N là điểm trên tia đối của tia OM và cách O một khoảng bằng 7cm.
a) Vẽ hình và tính độ dài đoạn thẳng MN.
b) Gọi K là trung điểm của đoạn thảng MN. Tính độ dài đoạn thẳng MK.
Bài 5:(0,5 điểm)Tính giá trị của biểu thức: \(A = 1\dfrac{1}{2}.1\dfrac{1}{3}.1\dfrac{1}{4}. \ldots .1\dfrac{1}{{2023}}\)
Phần I: Trắc nghiệm
1. D | 2. A | 3. D | 4. C |
Câu 1
Phương pháp:
Dựa vào tính chất điểm nằm giữa hai điểm: Khi M nằm giữa A và B thì \(AM + MB = AB\)
Cách giải:
Vì K nằm giữa A và B nên ta có: \(AK + KB = AB\)
Hay \(4 + KB = 6\)
Suy ra: \(KB = 6 - 4 = 2\left( {cm} \right)\)
Chọn D.
Câu 2
Phương pháp:
Liệt kê tất cả các đoạn thẳng.
Cách giải:
Có 6 đoạn thẳng là: OA, OB, OC, AB, AC, BC.
Chọn A.
Câu 3
Phương pháp:
Giữ nguyên mẫu số.
Tử số mới = Phần nguyên × Mẫu số + Tử số.
Cách giải:
\(3\dfrac{2}{5} = \dfrac{{3.5 + 2}}{5} = \dfrac{{17}}{5}\)
Chọn D.
Câu 4
Phương pháp:
Quy đồng mẫu số để tìm y, quy đồng tử số để tìm x.
Cách giải:
Ta có: \(\dfrac{3}{x} = \dfrac{y}{{12}} = \dfrac{3}{{12}}\)
Vậy: \(x = 12;y = 3\)
Chọn C.
Phần II: Tự luận
Bài 1
Phương pháp
Tính giá trị biểu thức theo các quy tắc:
+) Biểu thức có dấu ngoặc thì ưu tiên tính trong ngoặc trước, ngoài ngoặc sau.
+) Biểu thức có chứa các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, phép tính cộng, trừ sau.
Cách giải:
\(\begin{array}{l}a)\,\,\dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\,\, = \dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} + \dfrac{{ - 3}}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\dfrac{{ - 10}}{{13}} + \dfrac{{ - 3}}{{13}}} \right) + \left( {\dfrac{5}{{17}} + \dfrac{{12}}{{17}}} \right) - \dfrac{{11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - 13}}{{13}} + \dfrac{{17}}{{17}} - \dfrac{{11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = ( - 1) + 1 - \dfrac{{11}}{{20}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0 - \dfrac{{11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \dfrac{{11}}{{20}}\end{array}\)
\(\begin{array}{l}b)\,\,\dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}} = \,\,\dfrac{3}{4} + \dfrac{{ - 5}}{6} + \dfrac{{11}}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\dfrac{9}{{12}}\, + \dfrac{{ - 10}}{{12}} + \dfrac{{11}}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{9 + ( - 10) + 11}}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{10}}{{12}} = \dfrac{5}{6}\end{array}\)
\(\begin{array}{l}c)\,\,\left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}\,\, = \,\left( {13 + \dfrac{4}{9} + 2 + \dfrac{1}{9}} \right) - \left( {3 + \dfrac{4}{9}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 13 + \dfrac{4}{9} + 2 + \dfrac{1}{9} - 3 - \dfrac{4}{9}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = (13 + 2 - 3) + \left( {\dfrac{4}{9} - \dfrac{4}{9}} \right) + \dfrac{1}{9}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 12 + 0 + \dfrac{1}{9}\,\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 12\dfrac{1}{9}\,\,\,\end{array}\)
Bài 2:
Phương pháp: Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Cách giải:
\(\begin{array}{l}a)\,\,x - \dfrac{1}{3} = \dfrac{5}{{14}} \cdot \dfrac{{ - 7}}{6}\,\\\,\,\,\,\,\,x - \dfrac{1}{3} = \dfrac{{ - 5}}{{12}}\,\,\,\\\,\,\,\,\,\,x = \dfrac{{ - 5}}{{12}}\, + \dfrac{1}{3}\,\\\,\,\,\,\,\,x = \dfrac{{ - 1}}{{12}}\,\end{array}\)
Vậy \(x = \dfrac{{ - 1}}{{12}}\)
\(\begin{array}{l}\,b)\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = 0,2\,\\\,\,\,\,\,\,\,\dfrac{3}{4} + \dfrac{1}{4} \cdot x = \dfrac{1}{5}\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{1}{5} - \dfrac{3}{4}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{4} \cdot x = \dfrac{{ - 11}}{{20}}\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\,\dfrac{{ - 11}}{{20}}:\dfrac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \,\dfrac{{ - 11}}{5}\end{array}\)
Vậy \(x = \dfrac{{ - 11}}{5}\)
\(\begin{array}{l}c)\,\,\dfrac{1}{{12}}.{x^2} = 1\dfrac{1}{3}\\\,\dfrac{1}{{12}}.{x^2} = \dfrac{4}{3}\\{x^2} = \dfrac{4}{3}:\dfrac{1}{{12}}\\{x^2} = 16\\ \Rightarrow \,\left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\end{array}\)
Vậy \(x \in \left\{ {4; - 4} \right\}\)
Bài 3
Phương pháp:
Sử dụng lý thuyết biểu đồ cột.
Cách giải:
a) Biểu đồ biểu thị tổng lượng mưa của thành phố Hà Nội trong các năm từ 2015 đến 2019.
b) Đơn vị đo của tổng lượng mưa là milimét.
c) Bảng thống kê:
Năm | 2015 | 2016 | 2017 | 2018 | 2019 |
Tổng lượng mưa (mm) | 1520 | 1631 | 1858 | 1685 | 1311 |
Bài 4
Phương pháp
Vẽ hình, sau đó dựa vào tính chất của điểm nằm giữa hai điểm và trung điểm của đoạn thẳng.
Cách giải:
a)

Ta có tia OM và tia ON đối nhau (Vì N thuộc tia đối của tia OM)
Suy ra: Điểm O nằm giữa hai điểm M và N
Suy ra: \(OM + ON = MN\)
Thay \(OM = 5cm;{\rm{ }}ON = 7cm\), ta có
\(MN = 5 + 7 = 12\left( {cm} \right)\). Vậy \(MN = 12cm.\)
b) Gọi K là trung điểm của đoạn thẳng MN. Tính độ dài đoạn thẳng MK.
Ta có K là trung điểm của đoạn thẳng MN
Suy ra: \(MK = NK = \dfrac{{MN}}{2} = \dfrac{{12}}{2} = 6\left( {cm} \right)\)
Bài 5
Phương pháp
Viết các thừa số thành phân số, rút gọn các thừa số giống nhau ở tử và mẫu.
Cách giải:
\(A = 1\dfrac{1}{2}.1\dfrac{1}{3}.1\dfrac{1}{4}. \ldots .1\dfrac{1}{{2023}}\)
\( = \dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}. \ldots .\dfrac{{2024}}{{2023}}\)
\(\begin{array}{l} = \dfrac{{2024}}{2}\\ = 1012.\end{array}\)
Đề thi giữa kì 2 Toán 6 - Đề số 3 - Cánh diều là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kỳ. Đề thi bao gồm các chủ đề chính như số tự nhiên, phép tính với số tự nhiên, hình học cơ bản và các bài toán thực tế liên quan.
Đề thi thường được chia thành các phần sau:
Các chủ đề thường xuất hiện trong đề thi:
Bài 1: Tính giá trị của biểu thức: 123 + 456 - 789
Lời giải:
123 + 456 - 789 = 579 - 789 = -210
Bài 2: Vẽ đoạn thẳng AB dài 5cm. Trên đoạn thẳng AB, lấy điểm M sao cho AM = 2cm. Tính độ dài đoạn thẳng MB.
Lời giải:
MB = AB - AM = 5cm - 2cm = 3cm
Bài 3: Một cửa hàng có 250kg gạo. Buổi sáng cửa hàng bán được 1/5 số gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Lời giải:
Số gạo bán được buổi sáng là: 250 x 1/5 = 50kg
Số gạo còn lại là: 250 - 50 = 200kg
Việc luyện tập thường xuyên với các đề thi giữa kì 2 Toán 6 - Cánh diều sẽ giúp học sinh:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu học tập Toán 6, bao gồm:
Hãy truy cập Giaitoan.edu.vn để học tập và ôn luyện Toán 6 hiệu quả!
| Dạng bài tập | Ví dụ |
|---|---|
| Tính giá trị biểu thức | 12 x 5 + 30 : 2 |
| Giải bài toán có lời văn | Một người có 100000 đồng, mua 2kg gạo giá 20000 đồng/kg. Hỏi người đó còn lại bao nhiêu tiền? |
| Vận dụng kiến thức hình học | Vẽ tam giác ABC biết AB = 3cm, BC = 4cm, AC = 5cm. |
Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi giữa kì 2 Toán 6 - Cánh diều!