Chào mừng các em học sinh lớp 6 đến với đề thi học kì 2 môn Toán, đề số 12, chương trình Cánh diều. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi với cấu trúc tương tự đề thi chính thức, giúp các em làm quen với dạng bài và rèn luyện kỹ năng giải quyết vấn đề. Đề thi đi kèm với đáp án chi tiết, giúp các em tự kiểm tra và rút kinh nghiệm.
Số đối của phân số \(\frac{{ - 5}}{4}\) là
Trong các cách viết sau, cách viết nào cho ta phân số là
Tìm số nguyên x, biết: \(\frac{{ - 7}}{5} = \frac{x}{5}\)
Cho hỗn số \(5\frac{1}{3}\). Cho biết đâu là câu trả lời đúng:
Viết phân số \(\frac{{ - 2023}}{{10}}\) dưới dạng số thập phân ta được
Viết số thập phân 0,15 dưới dạng phân số tối giản ta được
Điểm A thuộc đường thẳng d thì được kí hiệu là
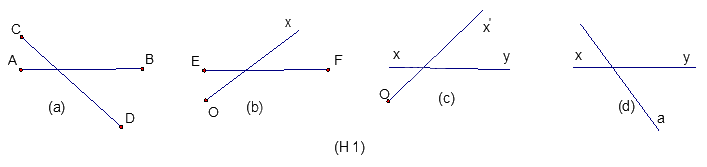
Trong các hình vẽ sau, hình nào là hai đường thẳng cắt nhau?
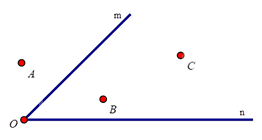
Các điểm nằm trong góc mOn trong hình bên là
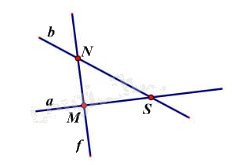
Điểm nào thuộc đường thẳng a?
Cho hai đường thẳng a, b. Khi đó a, b có thể:
Cho các góc sau \(\widehat A = {30^0};\widehat B = {60^0};\widehat C = {110^0};\widehat D = {90^0}\). Chọn câu sai.
So sánh các số sau:
a) \(\frac{{ - 2}}{7}\) và \(\frac{{ - 3}}{7}\)
b) 5,14 và 5,139
Thực hiện phép tính: \(\frac{1}{2} - \frac{5}{4}.\frac{{ - 7}}{{10}}\).
a) Hãy vẽ các đoạn thẳng sau: AB = 5 cm; CD = 3,5
b) So sánh độ dài hai đoạn thẳng AB và CD.
c) Nhìn hình vẽ, đọc số đo các góc xOt; tOt’; xOy.
Một lớp có 40 học sinh xếp loại học lực gồm ba loại: Giỏi, Khá, Trung bình và không có loại Yếu. Số học sinh Giỏi chiếm \(\frac{1}{5}\) số học sinh cả lớp. Số học sinh Trung bình bằng \(\frac{3}{{16}}\)số học sinh còn lại.
a) Tính số học sinh Giỏi.
b) Tính số học sinh Trung bình.
c) Tính tỉ số phần trăm số học sinh Khá so với cả lớp.
Tìm x biết \({x^3} - {x^2} + x - 1 = 0\)
Số đối của phân số \(\frac{{ - 5}}{4}\) là
Đáp án : C
Hai phân số được gọi là đối nhau nếu tổng của chúng bằng 0.
Số đối của phân số \(\frac{{ - 5}}{4}\) là \(\frac{5}{4}\).
Đáp án C.
Trong các cách viết sau, cách viết nào cho ta phân số là
Đáp án : D
Phân số có dạng \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).
\(\frac{{ - 2}}{5}\) cho ta phân số.
Đáp án D.
Tìm số nguyên x, biết: \(\frac{{ - 7}}{5} = \frac{x}{5}\)
Đáp án : A
Hai phân số \(\frac{a}{b} = \frac{c}{d}\left( {b,d \ne 0} \right)\) nếu \(a.d = c.b\)
\(\begin{array}{l}\frac{{ - 7}}{5} = \frac{x}{5}\\ - 7.5 = x.5\\5x = - 35\\x = - 7\end{array}\)
Đáp án A.
Cho hỗn số \(5\frac{1}{3}\). Cho biết đâu là câu trả lời đúng:
Đáp án : B
Dựa vào kiến thức về hỗn số.
Hỗn số \(5\frac{1}{3}\) có 5 là phần số nguyên và \(\frac{1}{3}\) là phần phân số nên ta chọn đáp án B.
Đáp án B.
Viết phân số \(\frac{{ - 2023}}{{10}}\) dưới dạng số thập phân ta được
Đáp án : D
Dựa vào kiến thức về số thập phân.
Ta có: \(\frac{{ - 2023}}{{10}} = - 202,3\).
Đáp án D.
Viết số thập phân 0,15 dưới dạng phân số tối giản ta được
Đáp án : D
Dựa vào kiến thức về số thập phân.
Ta có: \(0,15 = \frac{{15}}{{100}} = \frac{{3.5}}{{20.5}} = \frac{3}{{20}}\).
Đáp án D.
Điểm A thuộc đường thẳng d thì được kí hiệu là
Đáp án : A
Dựa vào kiến thức về điểm và đường thẳng.
Điểm A thuộc đường thẳng d thì được kí hiệu là \(A \in d\).
Đáp án A.
Trong các hình vẽ sau, hình nào là hai đường thẳng cắt nhau?
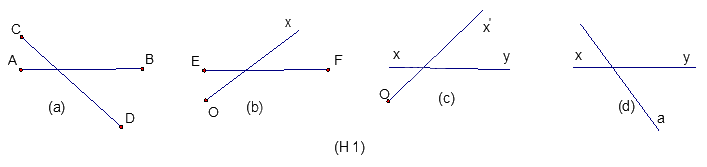
Đáp án : D
Quan sát xem hình vẽ nào biểu diễn hai đường thẳng cắt nhau.
Hình a là hình biểu diễn đoạn thẳng AB cắt đoạn thẳng CD.
Hình b là hình biểu diễn đoạn thẳng EF cắt tia Ox.
Hình c là hình biểu diễn đường thẳng xy cắt tia Ox’.
Hình d là hình biểu diễn đường thẳng xy cắt đường thẳng a nên chọn đáp án D.
Đáp án D.
Các điểm nằm trong góc mOn trong hình bên là
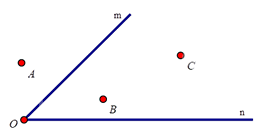
Đáp án : C
Quan sát hình vẽ để trả lời.
Các điểm B, C nằm trong góc mOn.
Đáp án C.
Điểm nào thuộc đường thẳng a?
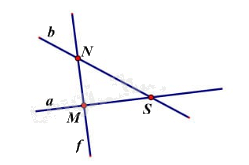
Đáp án : C
Quan sát hình vẽ để trả lời.
Hai điểm M và S thuộc đường thẳng a nên ta chọn đáp án C.
Đáp án C.
Cho hai đường thẳng a, b. Khi đó a, b có thể:
Đáp án : D
Dựa vào kiến thức về đường thẳng.
Hai đường thẳng a, b bất kì có thể song song, cắt nhau hoặc trùng nhau nên đáp án D đúng.
Đáp án D.
Cho các góc sau \(\widehat A = {30^0};\widehat B = {60^0};\widehat C = {110^0};\widehat D = {90^0}\). Chọn câu sai.
Đáp án : C
So sánh số đo các góc trên để chọn câu sai.
Vì \({60^0} < {90^0}\) nên \(\widehat B < \widehat D\).
Vì \({30^0} < {60^0}\) nên \(\widehat A < \widehat B\).
Vì \({110^0} > {90^0}\) nên \(\widehat C > \widehat D\) (C sai).
Vì \({60^0} < {110^0}\) nên \(\widehat B < \widehat C\).
Đáp án C.
So sánh các số sau:
a) \(\frac{{ - 2}}{7}\) và \(\frac{{ - 3}}{7}\)
b) 5,14 và 5,139
Sử dụng quy tắc so sánh phân số và số thập phân.
a) Vì 2 < 3 nên -2 > -3
Do đó \(\frac{{ - 2}}{7} > \frac{{ - 3}}{7}\)
b) Vì 5,140 > 5,139 nên 5,14 > 5,139.
Thực hiện phép tính: \(\frac{1}{2} - \frac{5}{4}.\frac{{ - 7}}{{10}}\).
Sử dụng quy tắc tính với phân số.
\(\begin{array}{l}\frac{1}{2} - \frac{5}{4}.\frac{{ - 7}}{{10}}\\ = \frac{1}{2} - \frac{{ - 7}}{8}\\ = \frac{1}{2} + \frac{7}{8}\\ = \frac{4}{8} + \frac{7}{8}\\ = \frac{{11}}{8}\end{array}\)
a) Hãy vẽ các đoạn thẳng sau: AB = 5 cm; CD = 3,5
b) So sánh độ dài hai đoạn thẳng AB và CD.
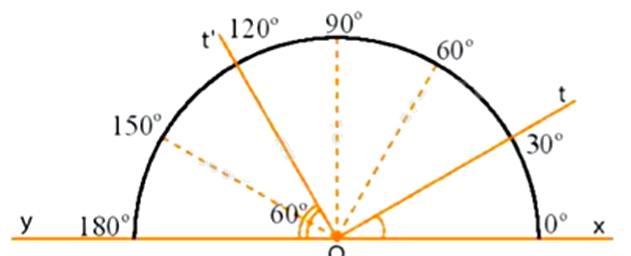
c) Nhìn hình vẽ, đọc số đo các góc xOt; tOt’; xOy.
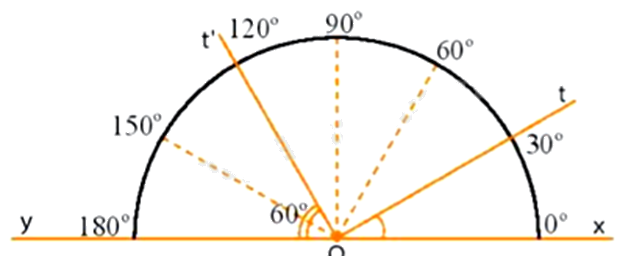
a) Sử dụng thước kẻ để vẽ đoạn thẳng.
b) Sử dụng quy tắc so sánh số thập phân để so sánh AB và CD.
c) Quan sát hình vẽ để trả lời câu hỏi.
a) Vẽ đúng kích thước các đoạn thẳng có độ dài: AB = 5cm; CD = 3,5
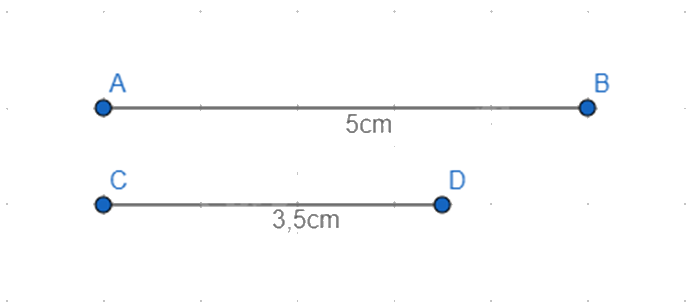
b) Vì 5 > 3,5 nên AB > CD.
c) Số đo các góc xOt; tOt’; xOy là:
\(\begin{array}{l}\widehat {xOt} = {30^0}\\\widehat {tOt'} = \widehat {xOt'} - \widehat {xOt} = {120^0} - {30^0} = {90^0}\\\widehat {xOy} = {180^0}\end{array}\)
Một lớp có 40 học sinh xếp loại học lực gồm ba loại: Giỏi, Khá, Trung bình và không có loại Yếu. Số học sinh Giỏi chiếm \(\frac{1}{5}\) số học sinh cả lớp. Số học sinh Trung bình bằng \(\frac{3}{{16}}\)số học sinh còn lại.
a) Tính số học sinh Giỏi.
b) Tính số học sinh Trung bình.
c) Tính tỉ số phần trăm số học sinh Khá so với cả lớp.
\(\frac{m}{n}\) của a là \(\frac{m}{n}.a\).
a) Số học sinh giỏi là: \(40.\frac{1}{5} = 8\) ( học sinh)
b) Số học sinh khá và trung bình là: 40 – 8 = 32 (học sinh)
Số học sinh trung bình là: \(32.\frac{3}{{16}} = 6\) ( học sinh)
c) Số học sinh khá là: 32 - 6 = 26 ( học sinh)
Tỉ số phần trăm số học sinh khá so với cả lớp là:
\(\frac{{26}}{{40}}.100\% = 65\% \)
Tìm x biết \({x^3} - {x^2} + x - 1 = 0\)
Nhóm thừa số chung để tìm x.
\(\begin{array}{l}{x^3} - {x^2} + x - 1 = 0\\{x^2}(x - 1) + (x - 1) = 0\\(x - 1)({x^2} + 1) = 0\end{array}\)
Suy ra x - 1= 0 hoặc \({x^2} + 1 = 0\)
Mà \({x^2} \ge 0\) với mọi x nên \({x^2} + 1\)> 0
Vậy x = 1
Đề thi học kì 2 Toán 6 - Đề số 12, chương trình Cánh diều, là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức và kỹ năng của học sinh sau một học kỳ học tập. Đề thi này bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, nhằm kiểm tra toàn diện các chủ đề đã được học.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi:
Để giải các bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép tính cộng, trừ, nhân, chia. Chú ý đến thứ tự thực hiện các phép tính và sử dụng các tính chất của phép tính để đơn giản hóa bài toán.
Ví dụ: Tính 123 + 456 - 789
Giải: 123 + 456 - 789 = 579 - 789 = -210
Để giải các bài toán này, học sinh cần hiểu rõ khái niệm tỉ số và tỉ lệ, cũng như các phương pháp giải bài toán tỉ lệ thuận và tỉ lệ nghịch.
Ví dụ: Hai số có tỉ số là 3:5 và tổng của chúng là 24. Tìm hai số đó.
Giải: Gọi hai số đó là 3x và 5x. Ta có: 3x + 5x = 24 => 8x = 24 => x = 3. Vậy hai số đó là 3x = 9 và 5x = 15.
Để giải các bài toán này, học sinh cần nắm vững các khái niệm cơ bản về hình học, như điểm, đường thẳng, đoạn thẳng, góc, và các tính chất của chúng. Sử dụng các công cụ hình học như thước kẻ, compa để vẽ hình và kiểm tra kết quả.
Ví dụ: Cho đoạn thẳng AB dài 5cm. Lấy điểm M nằm giữa A và B sao cho AM = 2cm. Tính độ dài đoạn thẳng MB.
Giải: Vì M nằm giữa A và B nên AM + MB = AB => MB = AB - AM = 5cm - 2cm = 3cm.
Ngoài đề thi học kì 2 Toán 6 - Đề số 12 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Đề thi học kì 2 Toán 6 - Đề số 12 - Cánh diều là một cơ hội tốt để học sinh đánh giá năng lực và chuẩn bị cho các kỳ thi tiếp theo. Chúc các em học sinh ôn thi tốt và đạt kết quả cao!