Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 6 - Đề số 1 - Cánh diều, tài liệu ôn tập quan trọng dành cho học sinh lớp 6. Đề thi được biên soạn theo chương trình Cánh diều, bám sát kiến thức trọng tâm và cấu trúc đề thi chính thức.
Đề thi này giúp học sinh rèn luyện kỹ năng giải toán, làm quen với các dạng bài tập thường gặp và tự đánh giá năng lực của bản thân trước kỳ thi. Kèm theo đề thi là đáp án chi tiết, giúp học sinh hiểu rõ phương pháp giải và khắc phục những sai lầm.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Giá trị của x trong biểu thức \(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\) là:
A. -8
B. -2
C. 8
D. 2
Câu 2:Hình bên có mấy tia:
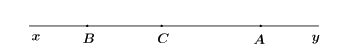
A. 6
B. 3
C. 4
D. 8
Câu 3: Để điều tra về loài hoa yêu thích nhất của \(30\) học sinh lớp 6A1, bạn lớp trưởng thu được bảng dữ liệu như sau:
H | H | M | C | C | H |
H | Đ | Đ | C | L | H |
H | C | C | L | C | C |
L | M | C | Đ | H | C |
C | M | L | L | H | C |
Viết tắt: H: Hoa Hồng; M: Hoa Mai; C: Hoa Cúc; Đ: Hoa Đào; L: Hoa Lan.
Bảng dữ liệu trên điều tra về
A. xếp loại học lực của 30 học sinh lớp 6A1.
B. loài hoa yêu thích của 30 học sinh lớp 6A1.
C. số lượng học sinh lớp 6A1.
D. loài hoa trồng được của 30 học sinh lớp 6A1
Câu 4:
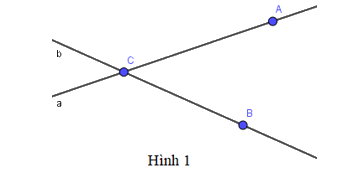
Chọn phát biểu sai trong các phát biểu sau:
A. Điểm A thuộc đường thẳng a
B. Hai điểm A, B cùng thuộc đường thẳng a
C. Điểm C thuộc đường thẳng b
D. Hai điểm B, C cùng thuộc đường thẳng b
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính hợp lý nếu có thể):
a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\)
b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\)
c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
Bài 2:(1,5 điểm)Tìm x, biết:
a) \(x - \dfrac{{ - 1}}{5} = 1\dfrac{1}{2}\)
b) \( - \dfrac{1}{2} + \left( {x - \dfrac{5}{{11}}} \right) = \dfrac{{ - 3}}{4}\)
c) \(\dfrac{3}{4} + \left( {\dfrac{2}{5} - x} \right) = \dfrac{1}{4}\)
Bài 3:(1,5 điểm)Biểu đồ trang dưới đây cho biết số lượng sách giáo khoa lớp 6 – Bộ Chân trời sáng tạo, bán được tại một hiệu sách vào ngày Chủ nhật vừa qua.
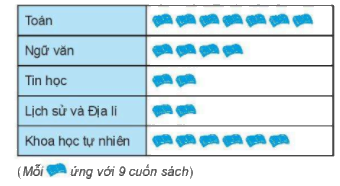
a) Sách nào bán được nhiều nhất? Tính số lượng?
b) Tổng số cuốn sách giáo khoa lớp 6 mà hiệu sách bán được trong ngày Chủ nhật vừa qua là bao nhiêu cuốn?
Bài 4: (2,5 điểm) Trên tia An lấy 2 điểm K và Q sao cho AK = 3cm, AQ = 4cm.
a) Tính độ dài đoạn thẳng KQ.
b) Lấy điểm C trên tia Am là tia đối của tia An sao cho AC = 3cm, tính CK.
Điểm A có là trung điểm của đoạn thẳng CK không? Vì sao?
c) Lấy điểm B là trung điểm của đoạn thẳng CA. So sánh BK và AQ?
Bài 5:(0,5 điểm)Tính giá trị của biểu thức: \(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\)
Phần I: Trắc nghiệm
1. B | 2. A | 3. B | 4. B |
Câu 1
Phương pháp:
Đưa về hai phân số cùng mẫu và so sánh hai phân số bằng nhau hoặc nhân chéo.
Cách giải:
Cách 1:
\(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\)
\(\begin{array}{l}\dfrac{{3x}}{{12}} = \dfrac{{ - 6}}{{12}}\\3x = - 6\\x = - 2\end{array}\)
Cách 2:
\(\begin{array}{l}\dfrac{x}{4} = \dfrac{6}{{ - 12}}\\x = \dfrac{{4.6}}{{ - 12}}\\x = - 2\end{array}\)
Chọn B.
Câu 2
Phương pháp:
Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O.
Cách giải:
Hình trên có 6 tia: Ax, Ay, Bx, By, Cx, Cy.
Chọn A.
Câu 3
Phương pháp:
Sử dụng lý thuyết bảng dữ liệu ban đầu.
Cách giải:
Bảng dữ liệu trên điều tra về loài hoa yêu thích của 30 học sinh lớp 6A1.
Chọn B.
Câu 4
Phương pháp:
Quan sát hình vẽ để xác định một điểm thuộc hay không thuộc một đường thẳng. Cách giải:
Từ hình vẽ ta thấy điểm A, C thuộc đường thẳng a; điểm B, C thuộc đường thẳng b.
Vậy phát biểu sai là hai điểm A, B cùng thuộc đường thẳng a.
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp
a) Cộng hai phân số cùng mẫu.
b) Nhóm thích hợp các phân số cùng mẫu.
c) Sử dụng tính chất phân phối của phép nhân và phép cộng.
Cách giải:
a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\)
\(\begin{array}{l} = \dfrac{{ - 7 + 3}}{{16}}\\ = \dfrac{{ - 4}}{{16}}\\ = \dfrac{{ - 1}}{4}\end{array}\)
b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\)
\(\begin{array}{l} = \left( {\dfrac{1}{7} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}} \right) + \dfrac{{ - 1}}{3}\\ = \dfrac{{1 + 10 - 4}}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{7}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{3}{3} + \dfrac{{ - 1}}{3}\\ = \dfrac{{3 - 1}}{3}\\ = \dfrac{2}{3}\end{array}\)
c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
\(\begin{array}{l} = \dfrac{4}{9}.\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{ - 45}}{{26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}.\dfrac{{ - 7 - 45}}{{26}} + \dfrac{1}{3}\\ = \dfrac{4}{9}.\left( { - 2} \right) + \dfrac{1}{3}\\ = \dfrac{{ - 8}}{9} + \dfrac{3}{9}\\ = \dfrac{{ - 8 + 3}}{9}\\ = \dfrac{{ - 5}}{9}\end{array}\)
Bài 2
Phương pháp
Chuyển vế để tìm được \(x\).
Sử dụng phép tính giá trị lũy thừa của một số.
Cách giải:
a) \(x - \frac{{ - 1}}{5} = 1\frac{1}{2}\)
\(\begin{array}{l}\frac{1}{2}x - \frac{{ - 1}}{5} = \frac{3}{2}\\x = \frac{3}{2} + \frac{{ - 1}}{5}\\x = \frac{{13}}{{10}}\end{array}\)
Vậy \(x = \frac{{13}}{{10}}\)
b) \( - \frac{1}{2} + \left( {x - \frac{5}{{11}}} \right) = \frac{{ - 3}}{4}\)
\(\begin{array}{l}x - \frac{5}{{11}} = \frac{{ - 3}}{4} + \frac{1}{2}\\x - \frac{5}{{11}} = \frac{{ - 1}}{4}\\x = \frac{{ - 1}}{4} + \frac{5}{{11}}\\x = \frac{9}{{44}}\end{array}\)
Vậy \(x = \frac{9}{{44}}\)
c) \(\frac{3}{4} + \left( {\frac{2}{5} - x} \right) = \frac{1}{4}\)
\(\frac{2}{5} - x = \frac{1}{4} - \frac{3}{4}\)
\(\frac{2}{5} - x = {\rm{\;}} - \frac{1}{2}\)
\(x = \frac{2}{5} + \frac{1}{2}\)
\(x = \frac{9}{{10}}\)
Vậy \(x = \frac{9}{{10}}\)
Bài 3
Phương pháp
Đọc dữ liệu ở biểu đồ tranh, thực hiện phép tính nhân
Cách giải:
a) Sách Toán có \(7\) hình  nên bán được nhiều nhất và số sách Toán bán được là \(7.9 = 63\) (cuốn sách)
nên bán được nhiều nhất và số sách Toán bán được là \(7.9 = 63\) (cuốn sách)
Sách Tin học, sách Lịch sử và Địa lí có \(2\) hình  nên bán được ít nhất và số sách mỗi loại là \(2.9 = 18\) (cuốn sách)
nên bán được ít nhất và số sách mỗi loại là \(2.9 = 18\) (cuốn sách)
b) Tổng số có \(21\) hình  nên số sách giáo khoa lớp 6 bán được là: \(21.9 = 189\) (cuốn sách)
nên số sách giáo khoa lớp 6 bán được là: \(21.9 = 189\) (cuốn sách)
Bài 4
Phương pháp
a) Chứng minh K nằm giữa A và Q và suy ra AK + KQ = AQ.
b) Chứng minh A nằm giữa C và K. Tính CK = AC + AK.
Chỉ ra A nằm giữa C, K và AC = AK. Từ đó suy ra A là trung điểm của CK.
c) Tính BA.
Chứng minh A nằm giữa B và K. Tính BK = BA + AK.
So sánh BK và AQ.
Cách giải:
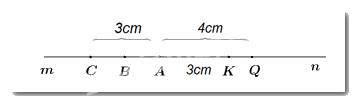
a) Vì AK < AQ (3cm < 4cm) nên K nằm giữa A và Q.
=> AK + KQ = AQ
=> 3 + KQ = 4
=> KQ = 4 – 3
=> KQ = 1 (cm)
b) Vì C và K nằm trên hai tia đối An và Am nên A nằm giữa C và K.
=> CK = AC + AK
=> CK = 3 + 3
=> CK = 6 (cm)
Ta có: A nằm giữa C và K.
AC = AK = 3cm.
=> A là trung điểm của CK.
c) Vì B là trung điểm của AC nên BA = AC : 2 = 3 : 2 = 1,5 (cm).
Vì B, K nằm trên hai tia đối nhau An và Am nên A nằm giữa B và K.
=> BK = BA + AK
=> BK = 1,5 + 3
=> BK = 4,5 (cm)
Mà AQ = 4 (cm)
=> BK > AQ.
Bài 5
Phương pháp
Nhận xét:
\(\dfrac{1}{{1.2}} = 1 - \dfrac{1}{2};\) \(\dfrac{1}{{2.3}} = \dfrac{1}{2} - \dfrac{1}{3};\)\(\dfrac{1}{{3.4}} = \dfrac{1}{3} - \dfrac{1}{4};\)…; \(\dfrac{1}{{2011.2012}} = \dfrac{1}{{2011}} - \dfrac{1}{{2012}}\) sau đó rút gọn các cặp phân số đối nhau rồi thực hiện tính.
Cách giải:
\(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\)
\( = 7.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \ldots + \dfrac{1}{{2011.2012}}} \right)\)
\( = 7.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + \ldots + \dfrac{1}{{2011}} - \dfrac{1}{{2012}}} \right)\)
\( = 7.\left( {1 - \dfrac{1}{{2012}}} \right) = \dfrac{{14077}}{{2012}}\)
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Giá trị của x trong biểu thức \(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\) là:
A. -8
B. -2
C. 8
D. 2
Câu 2:Hình bên có mấy tia:
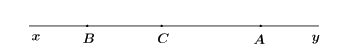
A. 6
B. 3
C. 4
D. 8
Câu 3: Để điều tra về loài hoa yêu thích nhất của \(30\) học sinh lớp 6A1, bạn lớp trưởng thu được bảng dữ liệu như sau:
H | H | M | C | C | H |
H | Đ | Đ | C | L | H |
H | C | C | L | C | C |
L | M | C | Đ | H | C |
C | M | L | L | H | C |
Viết tắt: H: Hoa Hồng; M: Hoa Mai; C: Hoa Cúc; Đ: Hoa Đào; L: Hoa Lan.
Bảng dữ liệu trên điều tra về
A. xếp loại học lực của 30 học sinh lớp 6A1.
B. loài hoa yêu thích của 30 học sinh lớp 6A1.
C. số lượng học sinh lớp 6A1.
D. loài hoa trồng được của 30 học sinh lớp 6A1
Câu 4:
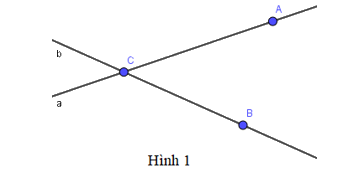
Chọn phát biểu sai trong các phát biểu sau:
A. Điểm A thuộc đường thẳng a
B. Hai điểm A, B cùng thuộc đường thẳng a
C. Điểm C thuộc đường thẳng b
D. Hai điểm B, C cùng thuộc đường thẳng b
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính hợp lý nếu có thể):
a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\)
b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\)
c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
Bài 2:(1,5 điểm)Tìm x, biết:
a) \(x - \dfrac{{ - 1}}{5} = 1\dfrac{1}{2}\)
b) \( - \dfrac{1}{2} + \left( {x - \dfrac{5}{{11}}} \right) = \dfrac{{ - 3}}{4}\)
c) \(\dfrac{3}{4} + \left( {\dfrac{2}{5} - x} \right) = \dfrac{1}{4}\)
Bài 3:(1,5 điểm)Biểu đồ trang dưới đây cho biết số lượng sách giáo khoa lớp 6 – Bộ Chân trời sáng tạo, bán được tại một hiệu sách vào ngày Chủ nhật vừa qua.
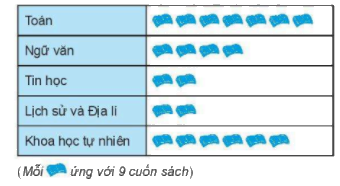
a) Sách nào bán được nhiều nhất? Tính số lượng?
b) Tổng số cuốn sách giáo khoa lớp 6 mà hiệu sách bán được trong ngày Chủ nhật vừa qua là bao nhiêu cuốn?
Bài 4: (2,5 điểm) Trên tia An lấy 2 điểm K và Q sao cho AK = 3cm, AQ = 4cm.
a) Tính độ dài đoạn thẳng KQ.
b) Lấy điểm C trên tia Am là tia đối của tia An sao cho AC = 3cm, tính CK.
Điểm A có là trung điểm của đoạn thẳng CK không? Vì sao?
c) Lấy điểm B là trung điểm của đoạn thẳng CA. So sánh BK và AQ?
Bài 5:(0,5 điểm)Tính giá trị của biểu thức: \(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\)
Phần I: Trắc nghiệm
1. B | 2. A | 3. B | 4. B |
Câu 1
Phương pháp:
Đưa về hai phân số cùng mẫu và so sánh hai phân số bằng nhau hoặc nhân chéo.
Cách giải:
Cách 1:
\(\dfrac{x}{4} = \dfrac{6}{{ - 12}}\)
\(\begin{array}{l}\dfrac{{3x}}{{12}} = \dfrac{{ - 6}}{{12}}\\3x = - 6\\x = - 2\end{array}\)
Cách 2:
\(\begin{array}{l}\dfrac{x}{4} = \dfrac{6}{{ - 12}}\\x = \dfrac{{4.6}}{{ - 12}}\\x = - 2\end{array}\)
Chọn B.
Câu 2
Phương pháp:
Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O.
Cách giải:
Hình trên có 6 tia: Ax, Ay, Bx, By, Cx, Cy.
Chọn A.
Câu 3
Phương pháp:
Sử dụng lý thuyết bảng dữ liệu ban đầu.
Cách giải:
Bảng dữ liệu trên điều tra về loài hoa yêu thích của 30 học sinh lớp 6A1.
Chọn B.
Câu 4
Phương pháp:
Quan sát hình vẽ để xác định một điểm thuộc hay không thuộc một đường thẳng. Cách giải:
Từ hình vẽ ta thấy điểm A, C thuộc đường thẳng a; điểm B, C thuộc đường thẳng b.
Vậy phát biểu sai là hai điểm A, B cùng thuộc đường thẳng a.
Chọn B.
Phần II: Tự luận
Bài 1
Phương pháp
a) Cộng hai phân số cùng mẫu.
b) Nhóm thích hợp các phân số cùng mẫu.
c) Sử dụng tính chất phân phối của phép nhân và phép cộng.
Cách giải:
a) \(\dfrac{{ - 7}}{{16}} + \dfrac{3}{{16}}\)
\(\begin{array}{l} = \dfrac{{ - 7 + 3}}{{16}}\\ = \dfrac{{ - 4}}{{16}}\\ = \dfrac{{ - 1}}{4}\end{array}\)
b) \(\dfrac{1}{7} + \dfrac{{ - 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}\)
\(\begin{array}{l} = \left( {\dfrac{1}{7} + \dfrac{{10}}{7} + \dfrac{{ - 4}}{7}} \right) + \dfrac{{ - 1}}{3}\\ = \dfrac{{1 + 10 - 4}}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{7}{7} + \dfrac{{ - 1}}{3}\\ = \dfrac{3}{3} + \dfrac{{ - 1}}{3}\\ = \dfrac{{3 - 1}}{3}\\ = \dfrac{2}{3}\end{array}\)
c) \(\dfrac{4}{9}.\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
\(\begin{array}{l} = \dfrac{4}{9}.\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{45}}{{ - 26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}\left( {\dfrac{{ - 7}}{{26}} + \dfrac{{ - 45}}{{26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}.\dfrac{{ - 7 - 45}}{{26}} + \dfrac{1}{3}\\ = \dfrac{4}{9}.\left( { - 2} \right) + \dfrac{1}{3}\\ = \dfrac{{ - 8}}{9} + \dfrac{3}{9}\\ = \dfrac{{ - 8 + 3}}{9}\\ = \dfrac{{ - 5}}{9}\end{array}\)
Bài 2
Phương pháp
Chuyển vế để tìm được \(x\).
Sử dụng phép tính giá trị lũy thừa của một số.
Cách giải:
a) \(x - \frac{{ - 1}}{5} = 1\frac{1}{2}\)
\(\begin{array}{l}\frac{1}{2}x - \frac{{ - 1}}{5} = \frac{3}{2}\\x = \frac{3}{2} + \frac{{ - 1}}{5}\\x = \frac{{13}}{{10}}\end{array}\)
Vậy \(x = \frac{{13}}{{10}}\)
b) \( - \frac{1}{2} + \left( {x - \frac{5}{{11}}} \right) = \frac{{ - 3}}{4}\)
\(\begin{array}{l}x - \frac{5}{{11}} = \frac{{ - 3}}{4} + \frac{1}{2}\\x - \frac{5}{{11}} = \frac{{ - 1}}{4}\\x = \frac{{ - 1}}{4} + \frac{5}{{11}}\\x = \frac{9}{{44}}\end{array}\)
Vậy \(x = \frac{9}{{44}}\)
c) \(\frac{3}{4} + \left( {\frac{2}{5} - x} \right) = \frac{1}{4}\)
\(\frac{2}{5} - x = \frac{1}{4} - \frac{3}{4}\)
\(\frac{2}{5} - x = {\rm{\;}} - \frac{1}{2}\)
\(x = \frac{2}{5} + \frac{1}{2}\)
\(x = \frac{9}{{10}}\)
Vậy \(x = \frac{9}{{10}}\)
Bài 3
Phương pháp
Đọc dữ liệu ở biểu đồ tranh, thực hiện phép tính nhân
Cách giải:
a) Sách Toán có \(7\) hình  nên bán được nhiều nhất và số sách Toán bán được là \(7.9 = 63\) (cuốn sách)
nên bán được nhiều nhất và số sách Toán bán được là \(7.9 = 63\) (cuốn sách)
Sách Tin học, sách Lịch sử và Địa lí có \(2\) hình  nên bán được ít nhất và số sách mỗi loại là \(2.9 = 18\) (cuốn sách)
nên bán được ít nhất và số sách mỗi loại là \(2.9 = 18\) (cuốn sách)
b) Tổng số có \(21\) hình  nên số sách giáo khoa lớp 6 bán được là: \(21.9 = 189\) (cuốn sách)
nên số sách giáo khoa lớp 6 bán được là: \(21.9 = 189\) (cuốn sách)
Bài 4
Phương pháp
a) Chứng minh K nằm giữa A và Q và suy ra AK + KQ = AQ.
b) Chứng minh A nằm giữa C và K. Tính CK = AC + AK.
Chỉ ra A nằm giữa C, K và AC = AK. Từ đó suy ra A là trung điểm của CK.
c) Tính BA.
Chứng minh A nằm giữa B và K. Tính BK = BA + AK.
So sánh BK và AQ.
Cách giải:
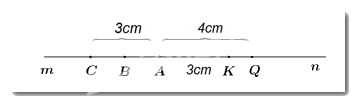
a) Vì AK < AQ (3cm < 4cm) nên K nằm giữa A và Q.
=> AK + KQ = AQ
=> 3 + KQ = 4
=> KQ = 4 – 3
=> KQ = 1 (cm)
b) Vì C và K nằm trên hai tia đối An và Am nên A nằm giữa C và K.
=> CK = AC + AK
=> CK = 3 + 3
=> CK = 6 (cm)
Ta có: A nằm giữa C và K.
AC = AK = 3cm.
=> A là trung điểm của CK.
c) Vì B là trung điểm của AC nên BA = AC : 2 = 3 : 2 = 1,5 (cm).
Vì B, K nằm trên hai tia đối nhau An và Am nên A nằm giữa B và K.
=> BK = BA + AK
=> BK = 1,5 + 3
=> BK = 4,5 (cm)
Mà AQ = 4 (cm)
=> BK > AQ.
Bài 5
Phương pháp
Nhận xét:
\(\dfrac{1}{{1.2}} = 1 - \dfrac{1}{2};\) \(\dfrac{1}{{2.3}} = \dfrac{1}{2} - \dfrac{1}{3};\)\(\dfrac{1}{{3.4}} = \dfrac{1}{3} - \dfrac{1}{4};\)…; \(\dfrac{1}{{2011.2012}} = \dfrac{1}{{2011}} - \dfrac{1}{{2012}}\) sau đó rút gọn các cặp phân số đối nhau rồi thực hiện tính.
Cách giải:
\(A = \dfrac{7}{{1.2}} + \dfrac{7}{{2.3}} + \dfrac{7}{{3.4}} + \ldots + \dfrac{7}{{2011.2012}}\)
\( = 7.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \ldots + \dfrac{1}{{2011.2012}}} \right)\)
\( = 7.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + \ldots + \dfrac{1}{{2011}} - \dfrac{1}{{2012}}} \right)\)
\( = 7.\left( {1 - \dfrac{1}{{2012}}} \right) = \dfrac{{14077}}{{2012}}\)
Đề thi giữa kì 2 Toán 6 - Đề số 1 - Cánh diều là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau nửa học kỳ. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số tự nhiên, phân số, số thập phân, tỉ số và phần trăm, hình học cơ bản và đại số sơ cấp.
Thông thường, đề thi giữa kì 2 Toán 6 - Cánh diều có cấu trúc gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 2 Toán 6 - Cánh diều:
Ví dụ 1: Tính giá trị của biểu thức: (1/2 + 1/3) x 6
Giải:
Ví dụ 2: Một cửa hàng có 120 sản phẩm, trong đó có 40 sản phẩm loại A. Tính tỉ số phần trăm của sản phẩm loại A so với tổng số sản phẩm.
Giải:
Tỉ số phần trăm của sản phẩm loại A so với tổng số sản phẩm là: (40/120) x 100% = 33.33%
Để chuẩn bị tốt nhất cho kỳ thi giữa kì 2 Toán 6 - Cánh diều, học sinh nên tham khảo thêm các tài liệu sau:
Đề thi giữa kì 2 Toán 6 - Đề số 1 - Cánh diều là một cơ hội tốt để học sinh kiểm tra và củng cố kiến thức đã học. Hy vọng với những phân tích và hướng dẫn giải chi tiết trên, các em học sinh sẽ tự tin hơn khi bước vào kỳ thi và đạt kết quả tốt nhất.